A Climatic Perspective on the Impacts of Global Warming on Water Cycle of Cold Mountainous Catchments in the Tibetan Plateau: A Case Study in Yarlung Zangbo River Basin
Abstract
1. Introduction
2. Study Area and Methodology
2.1. Description of Yarlung Zangbo River and Data Set
2.2. Quantile Regression Analysis for Investigating Changes in Flow Regimes
2.3. Groundwater Storage Trend Inferred from Daily Streamflow
2.4. Trend Analysis
3. Results
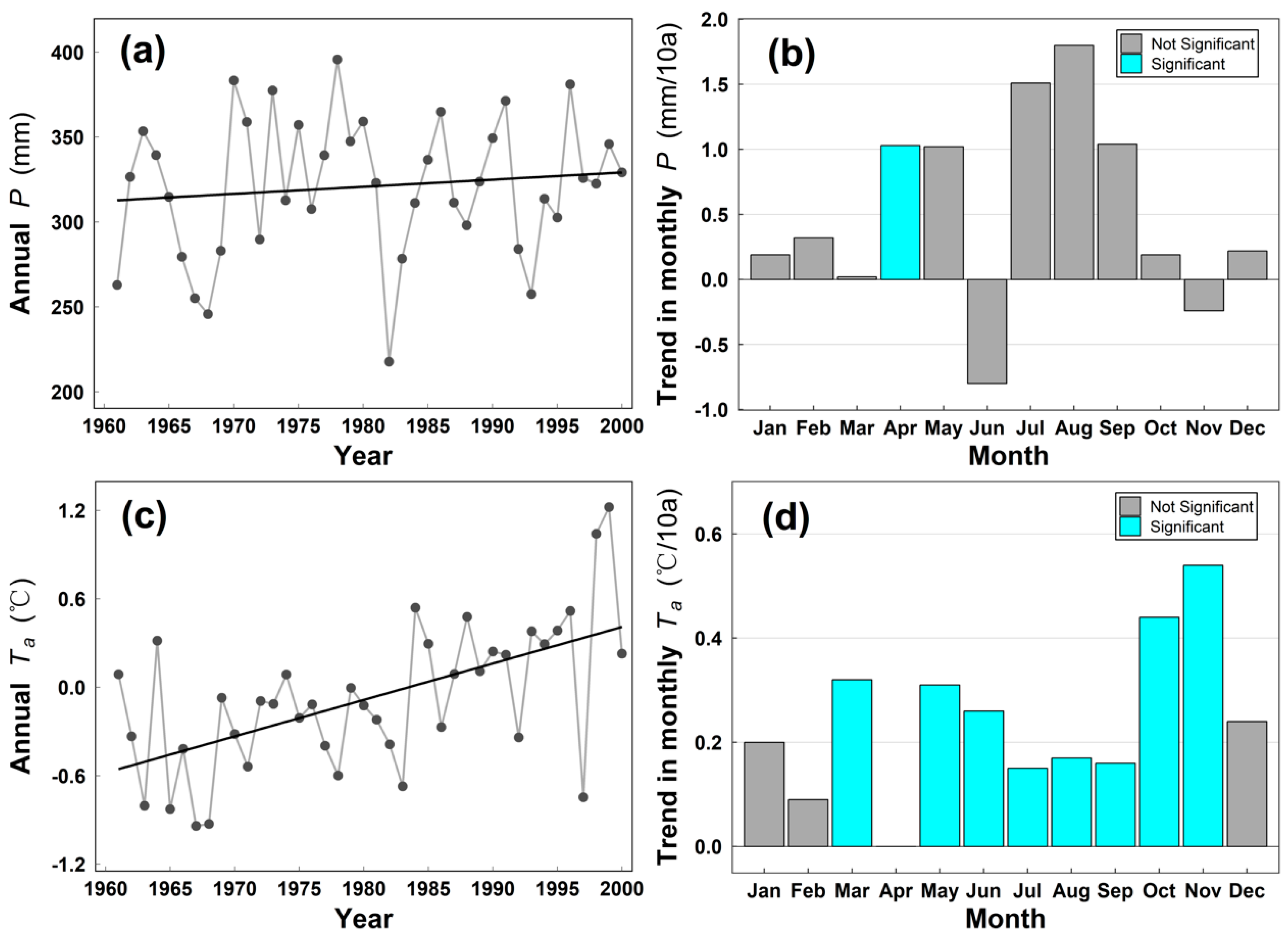
3.1. Long-Term Climate Variability of the YZRB
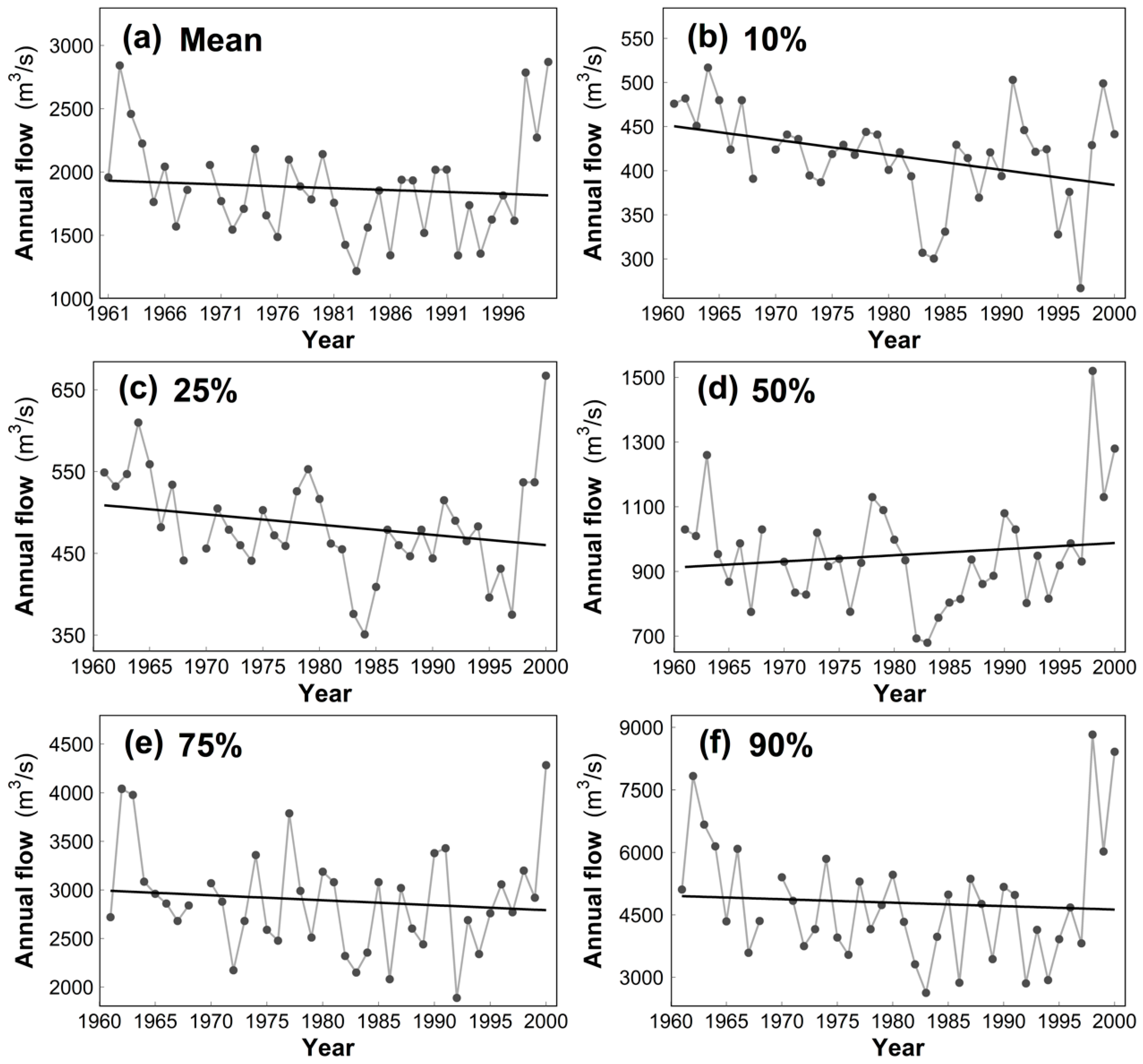
3.2. Changes in Annual Flow Regimes
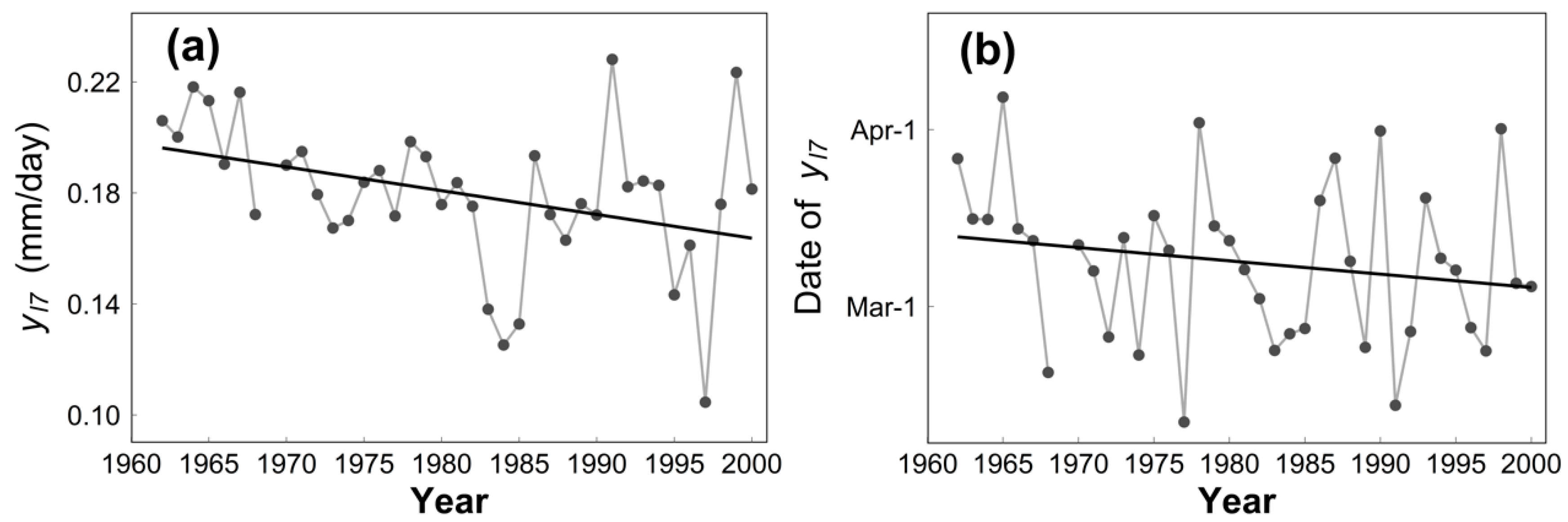
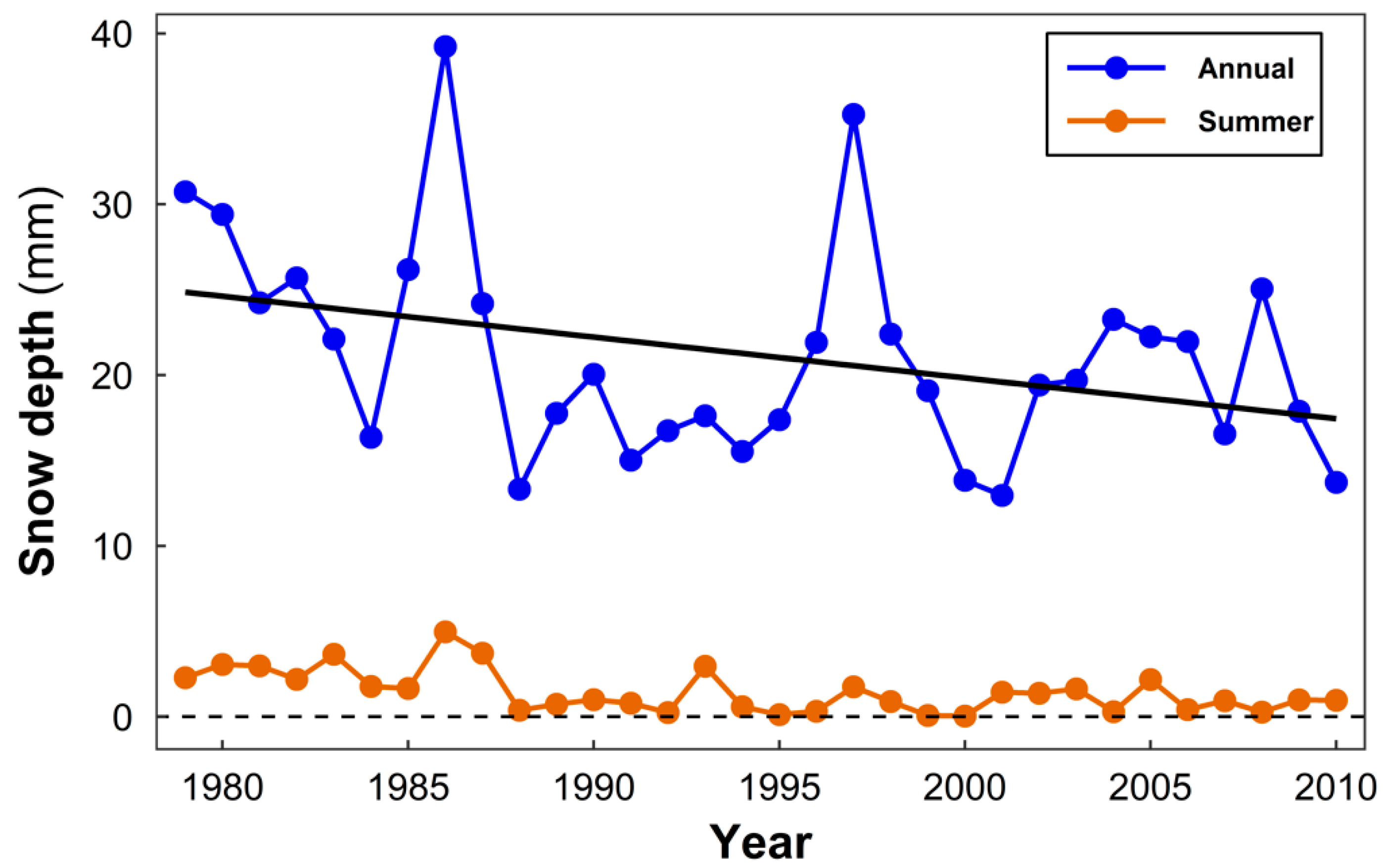
3.3. Trends in Catchment Groundwater Storage
4. Discussion
4.1. Changes in Low Flow Regime under Climate Change Conditions
4.2. Changes in Low Flow and Groundwater Storage
4.3. Impacts of Climate Warming on Groundwater Storage Decline
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Henderson, J.; Rodgers, C.; Jones, R.; Smith, J.; Strzepek, K.; Martinich, J. Economic impacts of climate change on water resources in the coterminous United States. Mitig. Adapt. Strateg. Glob. Chang. 2015, 20, 135–157. [Google Scholar] [CrossRef]
- Karl, T.R.; Melillo, J.M.; Peterson, T.C.; Hassol, S.J. Global Climate Change Impacts in the United States; Cambridge University Press: Cambridge, UK, 2009; p. 188. [Google Scholar]
- Miller, K.A.; Belton, V. Water resource management and climate change adaptation: A holistic and multiple criteria perspective. Mitig. Adapt. Strateg. Glob. Chang. 2014, 19, 289–308. [Google Scholar] [CrossRef]
- Pepin, N.; Bradley, R.S.; Diaz, H.F.; Baraer, M.; Caceres, E.B.; Forsythe, N.; Fowler, H.; Greenwood, G.; Hashmi, M.Z.; Liu, X.D.; et al. Elevation-dependent warming in mountain regions of the world. Nat. Clim. Chang. 2015, 5, 424–430. [Google Scholar]
- Gao, J.; Yao, T.; Masson-Delmotte, V.; Steen-Larsen, H.C.; Wang, W. Collapsing glaciers threaten Asia’s water supplies. Nature 2019, 565, 19–21. [Google Scholar] [CrossRef]
- Pritchard, H.D. Asia’s shrinking glaciers protect large populations from drought stress. Nature 2019, 569, 649–654. [Google Scholar] [CrossRef] [PubMed]
- Bookhagen, B. Hydrology: Himalayan groundwater. Nat. Geosci. 2012, 5, 97. [Google Scholar] [CrossRef]
- Liu, W.; Sun, F.; Li, Y.; Zhang, G.; Sang, Y.F.; Lim, W.H.; Liu, J.; Wang, H.; Bai, P. Investigating water budget dynamics in 18 river basins across the Tibetan Plateau through multiple datasets. Hydrol. Earth Syst. Sci. 2018, 22, 351–371. [Google Scholar] [CrossRef]
- Yang, K.; Ye, B.; Zhou, D.; Wu, B.; Foken, T.; Qin, J.; Zhou, Z. Response of hydrological cycle to recent climate changes in the Tibetan Plateau. Clim. Chang. 2011, 109, 517–534. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, L.L.; Li, J.; Deng, R.D.A.A. Climate and Hydrological Change Characteristics and Applicability of GLDAS Data in the Yarlung Zangbo River Basin, China. Water 2018, 10, 254. [Google Scholar] [CrossRef]
- Zhang, W.; Yi, Y.; Song, K.; Kimball, J.; Lu, Q. Hydrological Response of Alpine Wetlands to Climate Warming in the Eastern Tibetan Plateau. Remote Sens. 2016, 8, 336. [Google Scholar] [CrossRef]
- Knox, J.C. Sensitivity of modern and Holocene floods to climate change. Quat. Sci. Rev. 2000, 19, 439–457. [Google Scholar] [CrossRef]
- Smakhtin, V.U. Low flow hydrology: A review. J. Hydrol. 2001, 240, 147–186. [Google Scholar] [CrossRef]
- Arnell, N.W. The effect of climate change on hydrological regimes in Europe: A continental perspective. Glob. Environ. Chang. 1999, 9, 5–23. [Google Scholar] [CrossRef]
- Kormos, P.R.; Luce, C.H.; Wenger, S.J.; Berghuijs, W.R. Trends and sensitivities of low streamflow extremes to discharge timing and magnitude in Pacific Northwest mountain streams. Water Resour. Res. 2016, 52, 4990–5007. [Google Scholar] [CrossRef]
- Luce, C.H.; Holden, Z.A. Declining annual streamflow distributions in the Pacific Northwest United States, 1948–2006. Geophys. Res. Lett. 2009, 36, L16401. [Google Scholar] [CrossRef]
- Alley, W.M.; Healy, R.W.; LaBaugh, J.W.; Reilly, T.E. Flow and storage in groundwater systems. Science 2002, 296, 1985–1990. [Google Scholar] [CrossRef]
- Brutsaert, W. Hydrology: An Introduction; Cambridge University Press: Cambridge, UK, 2005; p. 605. [Google Scholar]
- Brutsaert, W. Are the North American deserts expanding? Some climate signals from groundwater storage conditions. Ecohydrology 2012, 5, 541–549. [Google Scholar] [CrossRef]
- Feng, W.; Shum, C.; Zhong, M.; Pan, Y. Groundwater Storage Changes in China from Satellite Gravity: An Overview. Remote Sens. 2018, 10, 674. [Google Scholar] [CrossRef]
- Döll, P.; Schmied, H.M.; Schuh, C.; Portmann, F.T.; Eicker, A. Global-scale assessment of groundwater depletion and related groundwater abstractions: Combining hydrological modeling with information from well observations and GRACE satellites. Water Resour. Res. 2015, 50, 5698–5720. [Google Scholar] [CrossRef]
- Sun, A.Y.; Green, R.; Rodell, M.; Swenson, S. Inferring aquifer storage parameters using satellite and in situ measurements: Estimation under uncertainty. Geophys. Res. Lett. 2010, 37, L10401. [Google Scholar] [CrossRef]
- Frappart, F.; Ramillien, G. Monitoring Groundwater Storage Changes Using the Gravity Recovery and Climate Experiment (GRACE) Satellite Mission: A Review. Remote Sens. 2018, 10, 829. [Google Scholar] [CrossRef]
- Guo, H.; Zhang, Z.; Cheng, G.; Li, W.; Li, T.; Jiao, J.J. Groundwater-derived land subsidence in the North China Plain. Environ. Earth Sci. 2015, 74, 1415–1427. [Google Scholar] [CrossRef]
- Xie, X.; Xu, C.; Wen, Y.; Li, W. Monitoring Groundwater Storage Changes in the Loess Plateau Using GRACE Satellite Gravity Data, Hydrological Models and Coal Mining Data. Remote Sens. 2018, 10, 605. [Google Scholar] [CrossRef]
- Brutsaert, W. Annual drought flow and groundwater storage trends in the eastern half of the United States during the past two-third century. Theor. Appl. Climatol. 2010, 100, 93–103. [Google Scholar] [CrossRef]
- Brutsaert, W. Long-term groundwater storage trends estimated from streamflow records: Climatic perspective. Water Resour. Res. 2008, 44, W2409. [Google Scholar] [CrossRef]
- Cao, Q.; Clark, E.A.; Mao, Y.; Lettenmaier, D.P. Trends and Interannual Variability in Terrestrial Water Storage Over the Eastern United States, 2003–2016. Water Resour. Res. 2019, 55, 1928–1950. [Google Scholar] [CrossRef]
- Zhang, L.; Brutsaert, W.; Crosbie, R.; Potter, N. Long-term annual groundwater storage trends in Australian catchments. Adv. Water Resour. 2014, 74, 156–165. [Google Scholar] [CrossRef]
- Gao, Z.; Zhang, L.; Cheng, L.; Zhang, X.; Cowan, T.; Cai, W.; Brutsaert, W. Groundwater storage trends in the Loess Plateau of China estimated from streamflow records. J. Hydrol. 2015, 530, 281–290. [Google Scholar] [CrossRef]
- Lin, K.; Yeh, H. Baseflow recession characterization and groundwater storage trends in northern Taiwan. Hydrol. Res. 2017, 48, 1745–1756. [Google Scholar] [CrossRef]
- Michiaki, S.; Brutsaert, W. Recent Low-Flow and Groundwater Storage Changes in Upland Watersheds of the Kanto Region, Japan. J. Hydrol. Eng. 2009, 14, 280–285. [Google Scholar]
- Brutsaert, W.; Hiyama, T. The determination of permafrost thawing trends from long-term streamflow measurements with an application in eastern Siberia. J. Geophys. Res. Atmos. 2012, 117, D22110. [Google Scholar] [CrossRef]
- Lyon, S.W.; Destouni, G.; Giesler, R.; Humborg, C.; Mörth, C.; Seibert, J.; Karlsson, J.; Troch, P.A. Estimation of permafrost thawing rates in a sub-arctic catchment using recession flow analysis. Hydrol. Earth Syst. Sci. Discuss. 2009, 6, 595–604. [Google Scholar] [CrossRef]
- Xiang, L.; Wang, H.; Steffen, H.; Wu, P.; Jia, L.; Jiang, L.; Shen, Q. Groundwater storage changes in the Tibetan Plateau and adjacent areas revealed from GRACE satellite gravity data. Earth Planet. Sci. Lett. 2016, 449, 228–239. [Google Scholar] [CrossRef]
- Shen, D.; Chen, C. Water Resources of the Qinghai-Xizang Plateau and Its Exploitation. J. Nat. Resour. 1996, 11, 8–14. [Google Scholar]
- Liu, T.; Zhang, X.; Xiong, S.; Qin, X.; Yang, X. Glacial environments on the Tibetan Plateau and global cooling. Quat. Int. 2002, 97, 133–139. [Google Scholar] [CrossRef]
- Yang, Y.C.; Gao, D.Y.; Li, B.S. Study on the moisture passage on the lower reaches of the Yarlung Zangbo River. Sci. China Ser. B 1989, 32, 580–593. [Google Scholar]
- Shangzhe, Z.; Jie, W.; Liubing, X.; Xiaoli, W.; Colgan, P.M.; Mickelson, D.M. Glacial advances in southeastern Tibet during late Quaternary and their implications for climatic changes. Quatern Int 2010, 218, 58–66. [Google Scholar] [CrossRef]
- Ying, S.; Gao, X.; Zhang, D.; Giorgi, F. Climate change over the Yarlung Zangbo–Brahmaputra River Basin in the 21st century as simulated by a high resolution regional climate model. Quat. Int. 2011, 244, 159–168. [Google Scholar]
- You, Q.; Kang, S.; Wu, Y.; Yan, Y. Climate change over the Yarlung Zangbo River Basin during 1961–2005. J. Geogr. Sci. 2007, 17, 409–420. [Google Scholar] [CrossRef]
- Zhu, X.; Wu, T.; Li, R.; Wang, S.; Hu, G.; Wang, W.; Qin, Y.; Yang, S. Characteristics of the ratios of snow, rain and sleet to precipitation on the Qinghai-Tibet Plateau during 1961–2014. Quat. Int. 2017, 444, 137–150. [Google Scholar] [CrossRef]
- Chen, X.; Long, D.; Hong, Y.; Zeng, C.; Yan, D. Improved modeling of snow and glacier melting by a progressive two-stage calibration strategy with GRACE and multisource data: How snow and glacier meltwater contributes to the runoff of the Upper Brahmaputra River basin? Water Resour. Res. 2017, 53, 2431–2466. [Google Scholar] [CrossRef]
- Wang, X.; Pang, G.; Yang, M. Precipitation over the Tibetan Plateau during recent decades: A review based on observations and simulations. Int. J. Climatol. 2017, 38, 1116–1131. [Google Scholar] [CrossRef]
- Bertrand, G.; Goldscheider, N.; Gobat, J.; Hunkeler, D. From multi-scale conceptualization to a classification system for inland groundwater-dependent ecosystems. Hydrogeol. J. 2012, 20, 5–25. [Google Scholar] [CrossRef]
- Ray, P.A.; Yang, Y.C.E.; Wi, S.; Khalil, A.; Chatikavanij, V.; Brown, C. Room for improvement: Hydroclimatic challenges to poverty-reducing development of the Brahmaputra River basin. Environ. Sci. Policy 2015, 54, 64–80. [Google Scholar] [CrossRef]
- Li, F.; Xu, Z.; Feng, Y.; Liu, M.; Liu, W. Changes of land cover in the Yarlung Tsangpo River basin from 1985 to 2005. Environ. Earth Sci. 2013, 68, 181–188. [Google Scholar] [CrossRef]
- Consortium, R.; Inventory, R.G. A Dataset of Global Glacier Outlines: Version 6.0: Technical Report. In Global Land Ice Measurements from Space; Digital Media; NSIDC: Boulder, CO, USA, 2017. [Google Scholar]
- Wu, Q.; Li, X.; Li, W. Computer simulation and mapping of the regional distribution of permafrost along the Qinghai-Xizang Highway. J. Glaciol. Geocryol. 2000, 22, 323–326. [Google Scholar]
- Douglas, E.M.; Vogel, R.M.; Kroll, C.N. Trends in floods and low flows in the United States: Impact of spatial correlation. J. Hydrol. 2000, 240, 90–105. [Google Scholar] [CrossRef]
- Huang, X.; Wang, Z.; Sang, Y.; Yang, M.; Liu, X.; Gong, T. Precision of data in three precipitation datasets of the Yarlung Zangbo River Basin. Prog. Geogr. 2016, 35, 339–348. [Google Scholar]
- Che, T.; Li, X.; Rui, J.; Armstrong, R.; Zhang, T. Snow depth derived from passive microwave remote-sensing data in China. Ann. Glaciol. 2008, 49, 145–154. [Google Scholar] [CrossRef]
- Dai, L.; Che, T.; Ding, Y. Inter-Calibrating SMMR, SSM/I and SSMI/S Data to Improve the Consistency of Snow-Depth Products in China. Remote Sens. 2015, 7, 7212–7230. [Google Scholar] [CrossRef]
- Dai, L.; Che, T.; Wang, J.; Zhang, P. Snow depth and snow water equivalent estimation from AMSR-E data based on a priori snow characteristics in Xinjiang, China (EI). Remote Sens. Environ. 2012, 127, 14–29. [Google Scholar] [CrossRef]
- Koenker, R.; Hallock, K.F. Quantile regression. J. Econ. Perspect. 2001, 15, 143–156. [Google Scholar] [CrossRef]
- Li, M.; Ma, Z.; Lv, M. Variability of modeled runoff over China and its links to climate change. Clim. Chang. 2017, 144, 433–445. [Google Scholar] [CrossRef][Green Version]
- Lins, H.; Slack, J. Seasonal and Regional Characteristics of U.S. Streamflow Trends in the United States from 1940 to 1999. Phys. Geogr. 2005, 26, 489–501. [Google Scholar] [CrossRef]
- Nasri, B.; Bouezmarni, T.; Sthilaire, A.; Ouarda, T.B.M.J. Non-stationary hydrologic frequency analysis using B-spline quantile regression. J. Hydrol. 2017, 554, 532–544. [Google Scholar] [CrossRef]
- Requena, A.I.; Ouarda, T.B.M.J.; Chebana, F. Low-flow frequency analysis at ungauged sites based on regionally estimated streamflows. J. Hydrol. 2018, 563, 523–532. [Google Scholar] [CrossRef]
- Cheng, L.; Zhang, L.; Chiew, F.H.S.; Canadell, J.G.; Zhao, F.; Wang, Y.; Hu, X.; Lin, K. Quantifying the impacts of vegetation changes on catchment storage-discharge dynamics using paired-catchment data. Water Resour. Res. 2017, 53, 5963–5979. [Google Scholar] [CrossRef]
- Brutsaert, W.; Nieber, J.L. Regionalized Drought Flow Hydrographs from a Mature Glacial Plateau. Water Resour. Res. 1977, 13, 637–643. [Google Scholar] [CrossRef]
- Cheng, L.; Zhang, L.; Wilfried Brutsaert, M.A. Automated Selection of Pure Base Flows from Regular Daily Streamflow Data: Objective Algorithm. J. Hydrol. Eng. 2016, 21, 6016008. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Charles Griffin; Oxford University Press: Oxford, UK, 1975; p. 202. [Google Scholar]
- Mann, H.B. Nonparametric tests against trend. Econom. J. Econom. Soc. 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Hirsch, R.M.; Slack, J.R.; Smith, R.A. Techniques of Trend Analysis for Monthly Water Quality Data. Water Resour. Res. 1982, 18, 107–121. [Google Scholar] [CrossRef]
- Xu, Z.X.; Li, J.Y.; Liu, C.M. Long-term trend analysis for major climate variables in the Yellow River basin. Hydrol. Process. 2010, 21, 1935–1948. [Google Scholar] [CrossRef]
- Field, C.B. Climate Change 2014—Impacts, Adaptation and Vulnerability: Regional Aspects; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Yang, Z.; Zhuo, M.; Lu, H.; Dava, C.; Ma, P.; Zhou, K. Characteristics of precipitation variation and its effects on runoff in the Yarlung Zangbo River basin during 1961–2010. J. Glaciol. Geocryol. 2014, 36, 166–172. [Google Scholar]
- Leppi, J.C.; Harrar, S.W.; Running, S.W. Impacts of climate change on August stream discharge in the Central-Rocky Mountains. Clim. Chang. 2012, 112, 997–1014. [Google Scholar] [CrossRef]
- Barnett, T.P.; Pierce, D.W.; Hidalgo, H.G.; Bonfils, C.; Santer, B.D.; Das, T.; Bala, G.; Wood, A.W.; Nozawa, T.; Mirin, A.A. Human-induced changes in the hydrology of the western United States. Science 2008, 319, 1080–1083. [Google Scholar] [CrossRef] [PubMed]
- Cheng, L.; Yaeger, M.; Viglione, A.; Coopersmith, E.; Ye, S.; Sivapalan, M. Exploring the physical controls of regional patterns of flow duration curves–Part 1: Insights from statistical analyses. Hydrol. Earth Syst. Sci. 2012, 16, 4435–4446. [Google Scholar] [CrossRef]
- Brutsaert, W. Evaporation into the Atmosphere: Theory, History and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 1, p. 302. [Google Scholar]
- Wang, D. On the base flow recession at the Panola Mountain Research Watershed, Georgia, United States. Water Resour. Res. 2011, 47, W3527. [Google Scholar] [CrossRef]
- Wang, D.; Cai, X. Detecting human interferences to low flows through base flow recession analysis. Water Resour. Res. 2009, 45, W7426. [Google Scholar] [CrossRef]
- Tague, C.; Grant, G.E. Groundwater dynamics mediate low-flow response to global warming in snow-dominated alpine regions. Water Resour. Res. 2009, 45, W7421. [Google Scholar] [CrossRef]
- Chen, J.; Sudicky, E.A.; Gula, J.; Peltier, W.R.; Park, Y.; Ross, M. Impact of Climate Change on Canadian Surface Water and Groundwater Resources: A Continental-scale Hydrologic Modelling Study using Multiple High-resolution RCM Projections. In Proceedings of the AGU Fall Meeting 2011, San Francisco, CA, USA, 12 May–12 September 2011. [Google Scholar]
- Uriostegui, S.H. Quantifying seasonal groundwater recharge in snow-dominated basin in the Sierra Nevada using cosmogenic S-35. In Proceedings of the GSA Annual Meeting, Vancouver, BC, Canada, 19–22 October 2014. [Google Scholar]
- Li, H.; Jiang, J.; Chen, B.; Li, Y.; Xu, Y.; Shen, W. Pattern of NDVI-based vegetation greening along an altitudinal gradient in the eastern Himalayas and its response to global warming. Environ. Monit. Assess. 2016, 188, 186. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Dawes, W.R.; Walker, G.R. Response of mean annual evapotranspiration to vegetation changes at catchment scale. Water Resour. Res. 2001, 37, 701–708. [Google Scholar] [CrossRef]
- Elias, E.; Rango, A.; Smith, R.; Maxwell, C.; Steele, C.; Havstad, K. Climate Change, Agriculture and Water Resources in the Southwestern United States. J. Contemp. Water Res. Educ. 2016, 158, 46–61. [Google Scholar] [CrossRef]
- Niu, L.; Ye, B.; Ding, Y.; Li, J.; Zhang, Y.; Sheng, Y.; Yue, G. Response of hydrological processes to permafrost degradation from 1980 to 2009 in the Upper Yellow River Basin, China. Hydrol. Res. 2016, 47, 1014–1024. [Google Scholar] [CrossRef]
- Wang, X.; Chen, R.; Yang, Y. Effects of Permafrost Degradation on the Hydrological Regime in the Source Regions of the Yangtze and Yellow Rivers, China. Water 2017, 9, 897. [Google Scholar] [CrossRef]
- You, Q.; Kang, S.C.; Yan, Y.; Xu, Y.; Zhang, Y.; Huang, J. Trends in Daily Temperature and Precipitation Extremes over the Yarlung Zangbo River Basin during 1961–2005. Acta Geogr. Sin. 2009, 64, 592–600. [Google Scholar]
- Pall, P.; Allen, M.R.; Stone, D.A. Testing the Clausius–Clapeyron constraint on changes in extreme precipitation under CO2 warming. Clim. Dynam. 2007, 28, 351–363. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Dai, A.; Rasmussen, R.M.; Parsons, D.B. The changing character of precipitation. Bull. Am. Meteorol. Soc. 2003, 84, 1205–1218. [Google Scholar] [CrossRef]
- Hoogmoed, W.B.; Stroosnijder, L. Crust formation on sandy soils in the Sahel I. Rainfall and infiltration. Soil Tillage Res. 1984, 4, 5–23. [Google Scholar] [CrossRef]
- Huang, J.; Wu, P.; Zhao, X. Effects of rainfall intensity, underlying surface and slope gradient on soil infiltration under simulated rainfall experiments. Catena 2013, 104, 93–102. [Google Scholar] [CrossRef]
- Liu, H.; Lei, T.W.; Zhao, J.; Yuan, C.P.; Fan, Y.T.; Qu, L.Q. Effects of rainfall intensity and antecedent soil water content on soil infiltrability under rainfall conditions using the run off-on-out method. J. Hydrol. 2011, 396, 24–32. [Google Scholar] [CrossRef]
- Wang, H.; Gao, J.E.; Zhang, M.; Li, X.; Zhang, S.; Jia, L. Effects of rainfall intensity on groundwater recharge based on simulated rainfall experiments and a groundwater flow model. Catena 2015, 127, 80–91. [Google Scholar] [CrossRef]
- Dourte, D.; Shukla, S.; Singh, P.; Haman, D. Rainfall Intensity-Duration-Frequency Relationships for Andhra Pradesh, India: Changing Rainfall Patterns and Implications for Runoff and Groundwater Recharge. J. Hydrol. Eng. 2013, 18, 324–330. [Google Scholar] [CrossRef]
- Hiscock, K.M. Groundwater in the 21st Century—Meeting the Challenges. In Sustaining Groundwater Resources: A Critical Element in the Global Water Crisis; Jones, J.A.A., Ed.; Springer: Dordrecht, The Netherlands, 2011; pp. 207–225. [Google Scholar]
- Huang, F.; Zhang, Y.; Zhang, D.; Chen, X. Environmental Groundwater Depth for Groundwater-Dependent Terrestrial Ecosystems in Arid/Semiarid Regions: A Review. Int. J. Environ. Res. Public Health 2019, 16, 763. [Google Scholar] [CrossRef]
- Larocque, M.; Levison, J.; Martin, A.; Chaumont, D. A review of simulated climate change impacts on groundwater resources in Eastern Canada. Can. Water Resour. J. Rev. Can. Ressour. Hydr. 2019, 44, 22–41. [Google Scholar] [CrossRef]
- Jin, H. Study on the cause, developing trend and control measure of land desertification in the lower middle reaches of Yarlung Zangbo River. J. Desert Res. 1997, 17, 255–260. [Google Scholar]
- Liu, Z.; Yao, Z.; Huang, H.; Wu, S.; Liu, G. Land use and climate changes and their impacts on runoff in the Yarlung Zangbo River Basin, China. Land Degrad. Dev. 2014, 25, 203–215. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Beek, L.P.H.V.; Bierkens, M.F.P. Climate change will affect the Asian water towers. Science 2010, 328, 1382–1385. [Google Scholar] [CrossRef]




© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Z.; Cheng, L.; Luo, P.; Liu, P.; Zhang, L.; Li, F.; Liu, L.; Wang, J. A Climatic Perspective on the Impacts of Global Warming on Water Cycle of Cold Mountainous Catchments in the Tibetan Plateau: A Case Study in Yarlung Zangbo River Basin. Water 2020, 12, 2338. https://doi.org/10.3390/w12092338
Xu Z, Cheng L, Luo P, Liu P, Zhang L, Li F, Liu L, Wang J. A Climatic Perspective on the Impacts of Global Warming on Water Cycle of Cold Mountainous Catchments in the Tibetan Plateau: A Case Study in Yarlung Zangbo River Basin. Water. 2020; 12(9):2338. https://doi.org/10.3390/w12092338
Chicago/Turabian StyleXu, Zhicheng, Lei Cheng, Peng Luo, Pan Liu, Lu Zhang, Fapeng Li, Liu Liu, and Jie Wang. 2020. "A Climatic Perspective on the Impacts of Global Warming on Water Cycle of Cold Mountainous Catchments in the Tibetan Plateau: A Case Study in Yarlung Zangbo River Basin" Water 12, no. 9: 2338. https://doi.org/10.3390/w12092338
APA StyleXu, Z., Cheng, L., Luo, P., Liu, P., Zhang, L., Li, F., Liu, L., & Wang, J. (2020). A Climatic Perspective on the Impacts of Global Warming on Water Cycle of Cold Mountainous Catchments in the Tibetan Plateau: A Case Study in Yarlung Zangbo River Basin. Water, 12(9), 2338. https://doi.org/10.3390/w12092338







