Assessment of the Dissimilarities of EDI and SPI Measures for Drought Determination in South Africa
Abstract
:1. Introduction
2. Materials and Methods
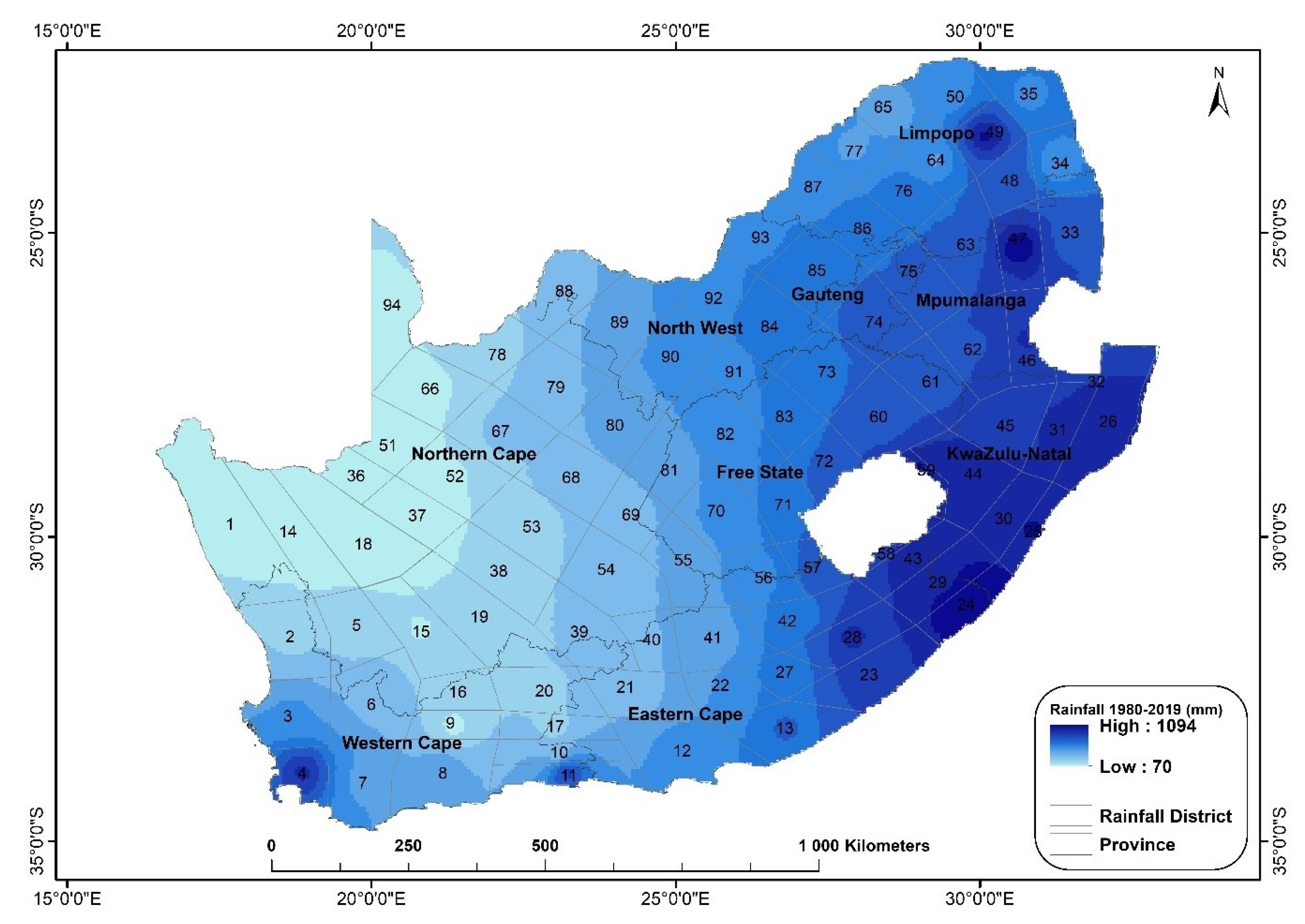
2.1. Study Area
2.2. Materials and Methods
2.2.1. Computation of Effective Drought Index (EDI)
2.2.2. Computation of Standardized Precipitation Index (SPI)
2.2.3. Methodology for Time Series Classification
2.3. Dissimilarity Measure Based on Pearson’s Correlation
2.4. Periodogram Based Dissimilarity Measure
3. Results
3.1. Comparison of SPI and EDI Using the Pearson Correlation Coefficient and p-Value
3.2. Comparison of SPI and EDI Using Periodogram Dissimilarity
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Department of Environmental Affairs, Republic of South Africa DEA. South Africa’s Second National Communication under the United Nations Framework Convention on Climate Change; Department of Environmental Affairs, Republic of South Africa DEA: Pretoria, South Africa, 2011. [Google Scholar]
- Kruger, A.C.; Nxumalo, M.P. Historical rainfall trends in South Africa: 1921-2015. Water S. Afr. 2017, 43, 285–297. [Google Scholar] [CrossRef] [Green Version]
- Yang, B.; Kang, S.; Ljungqvist, F.C.; He, M.; Zhao, Y.; Qin, C. Drought variability at the northern fringe of the Asian summer monsoon region over the past millennia. Clim. Dyn. 2014, 43, 845–859. [Google Scholar] [CrossRef]
- Frank, A.; Armenski, T.; Gocic, M.; Popov, S.; Popovic, L.; Trajkovic, S. Influence of mathematical and physical background of drought indices on their complementarity and drought recognition ability. Atmos. Res. 2017, 194, 268–280. [Google Scholar] [CrossRef]
- Sheffield, J.; Wood, E.F. Drought: Past Problems and Future Scenarios; Earthscan: London, UK, 2012. [Google Scholar]
- Botai, C.M.; Botai, J.O.; Dlamini, L.C.; Zwane, N.S.; Phaduli, E. Characteristics of droughts in South Africa: A Case Study of Free State and North West Provinces. Water 2016, 8, 439. [Google Scholar] [CrossRef]
- Botai, C.M.; Botai, J.O.; de Wit, J.C.; Ncongwane, K.P.; Adeola, A.M. Drought characteristics over the Western Cape Province, South Africa. Water 2017, 9, 876. [Google Scholar] [CrossRef] [Green Version]
- Wilhite, D.A. Drought: A Global Assessment; Routledge: New York, NY, USA, 2000; Volume 1, pp. 89–104. [Google Scholar]
- Wilhite, D.; Buchanan-Smith, M. Drought as Hazard: Understanding the Natural and Social Context. In Drought and Water Crises: Science, Technology, and Management Issues; Wilhite, D.A., Ed.; CRC Press: Boca Raton, FL, USA, 2005; pp. 3–29. [Google Scholar]
- Heim, R.R. A review of twentieth-century drought indices used in the United States. Bull. Am. Meteorol. Soc. 2002, 83, 1149–1165. [Google Scholar] [CrossRef] [Green Version]
- Valliyodan, B.T.; Nguyen, H.T. Understanding regulatory networks and engineering for enhanced drought tolerance in plants. Curr. Opin. Plant Biol. 2006, 9, 189–195. [Google Scholar] [CrossRef] [PubMed]
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Narasimhan, B.; Srinivasan, R. Development and evaluation of soil moisture deficit index (SMDI) and evapotranspiration deficit index (ETDI) for agricultural drought monitoring. Agric. For. Meteorol. 2005, 133, 69–88. [Google Scholar] [CrossRef]
- Kogan, F.N. Global drought watch from space. Bull. Am. Meteorol. Soc. 1997, 78, 621–636. [Google Scholar] [CrossRef]
- Wilhite, D.A.; Wood, D.A. Drought Management in a Changing West: New Directions for Water Policy; Utah State University: Logan, UT, USA, 1994. [Google Scholar]
- Coffel, E.; Horton, R. Climate change and the impact of extreme temperatures on aviation. Weather Clim. Soc. 2015, 7, 94–102. [Google Scholar] [CrossRef]
- Hirabayashi, Y.; Kanae, S.; Emori, S.; Oki, T.; Kimoto, M. Global projections of changing risks of floods and droughts in a changing climate. Hydrol. Sci. J. 2008, 53, 754–772. [Google Scholar] [CrossRef]
- Svoboda, M.; Fuchs, B.; IDMP Integrated. Handbook of Drought Indicators and Indices; Integrated Drought Management Programme (IDMP), Integrated Drought Management Tools and Guidelines Series 2; World Meteorological Organization and Global Water Partnership: Geneva, Switzerland, 2016; p. 52. [Google Scholar]
- Palmer, W.C. Meteorological Drought, Office of Climatology Research Paper 45; U.S. Weather Bureau: Washington, DC, USA, 1965. [Google Scholar]
- Gibbs, W.J.; Maher, J.V. Rainfall Deciles as Drought Indicators, Bureau of Meteorology Bulletin No. 48; Commonwealth of Australia: Melbourne, Australia, 1967. [Google Scholar]
- Palmer, W.C. Keeping track of crop moisture conditions nationwide: The new crop moisture index. Weatherwise 1968, 21, 156–161. [Google Scholar] [CrossRef]
- Bhalme, H.N.; Mooley, D.A. Large-scale droughts/floods and monsoon circulation. Mon. WeatherRev. 1980, 108, 1197–1211. [Google Scholar] [CrossRef] [Green Version]
- Shafer, B.A.; Dezman, L.E. 1982: Development of a surface water supply index (SWSI) to assess the severity of drought conditions in snowpack runoff areas. In Proceedings of the 50th Annual Western Snow Conference, Colorado State University, Fort Collins, CO, USA, 19–23 April 1982; pp. 164–175. (In preprints). [Google Scholar]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; pp. 179–184. [Google Scholar]
- Hollinger, S.E.; Isard, S.A.; Welford, M.R. A new soil moisture drought index for predicting crop yields. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; pp. 187–190. [Google Scholar]
- Byun, H.; Wilhite, D.A. Objective quantification of drought severity and duration. J. Clim. 1999, 12, 2747–2756. [Google Scholar] [CrossRef]
- Wu, H.; Hayes, M.J.; Weiss, A.; Hu, Q.I. An evaluation of the standardized precipitation index, the china-Z index and the statistical Z-Score. Int. J. Climatol. 2001, 21, 745–758. [Google Scholar] [CrossRef]
- Tsakiris, G.; Pangalou, D.; Vangelis, H. Regional drought assessment based on reconnaissance drought index (RDI). Water Resour. Manag. 2007, 21, 821–833. [Google Scholar] [CrossRef]
- Vicente-Serrano, SM.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef] [Green Version]
- Woli, P.; Jones, J.; Ingram, K.; Paz, J. Forecasting drought using the agricultural reference index for drought (arid): A case study. Weather Forecast. 2013, 28, 427–443. [Google Scholar] [CrossRef]
- Dalezios, N.; Blanta, A.; Spyropoulos, N.; Tarquis, A. Risk identification of agricultural drought for sustainable agroecosystems. Nat. Hazards Earth Syst. Sci. 2014, 14, 2435–2448. [Google Scholar] [CrossRef] [Green Version]
- WMO (World Meteorological Organization). Drought and Agriculture; Technical Note No. 138, Report of the CAgM Working Group on Assessment of Drough; WMO: Geneva, Switzerland, 1975; p. 127. [Google Scholar]
- Jain, V.K.; Pandey, R.P.; Jain, M.K.; Byun, H. Comparison of drought indices for appraisal of drought characteristics in the Ken River Basin. Weather Clim. Extrem. 2015, 8, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Dai, A. Characteristics and trends in various forms of the Palmer Drought Severity Index (PDSI) during 1900–2008. J. Geophys. Res. 2011, 116, D12115. [Google Scholar] [CrossRef] [Green Version]
- Morid, S.; Smakhtin, V.; Moghaddasi, M. Comparison of seven meteorological indexes for drought monitoring in Iran. Int. J. Climatol. 2006, 26, 971–985. [Google Scholar] [CrossRef]
- Keyantash, J.; Dracup, J.A. The quantification of drought: An evaluation of drought indices. Bull. Am. Meteorol. Soc. 2002, 83, 1167–1180. [Google Scholar] [CrossRef]
- Okpara, J.N.; Tarhule, A. Evaluation of drought indices in the Niger Basin, West Africa. J. Geogr. Earth Sci. 2015, 3, 1–32. [Google Scholar]
- Masinde, M.; Mwagha, M.; Tadesse, T. Downscaling Africa’s Drought Forecasts through Integration of Indigenous and Scientific Drought Forecasts Using Fuzzy Cognitive Maps. Geosciences 2018, 8, 135. [Google Scholar] [CrossRef] [Green Version]
- Bayissa, Y.; Maskey, S.; Tadesse, T.; van Andel, J.S.; Semu Moges, S.; van Griensven, A.; Solomatine, D. Comparison of the Performance of Six Drought Indices in Characterizing Historical Drought for the Upper Blue Nile Basin, Ethiopia. Geosciences 2018, 8, 81. [Google Scholar] [CrossRef] [Green Version]
- Smakhtin, V.U.; Hughes, D.A. Review, Automated Estimation and Analyses of Drought Indices in South Asia; Working Paper 83; International Water Management Institute: Colombo, Sri Lanka, 2004. [Google Scholar]
- Botai, J.O.; Botai, C.M.; de Wit, J.P.; Muthoni, M.; Adeola, A.M. Analysis of Drought Progression Physiognomies in South Africa. Water 2019, 11, 299. [Google Scholar] [CrossRef] [Green Version]
- Adisa, O.M.; Botai, J.O.; Adeola, A.M.; Botai, C.M.; Hassen, A.; Darkey, D.; Tesfamariam, E.; and Adisa, A.T.; Adisa, A.F. Analysis of drought conditions over major maize producing provinces of South Africa. J. Agric. Meteorol. 2019, 75, 173–182. [Google Scholar] [CrossRef] [Green Version]
- Hayes, M.; Svoboda, M.; Wall, N.; Widhalm, M. The Lincoln Declaration on Drought Indices: Universal Meteorological Drought Index Recommended. Bull. Am. Meteorol. Soc. 2011, 92, 485–488. [Google Scholar] [CrossRef] [Green Version]
- Edwards, D.C.; Mckee, T.B. Characteristics of 20th century drought in the United States at multiple timescales. Atmos. Sci. 1997, 63, 1–30. [Google Scholar]
- Stagee, J.H.; Tallaksen, L.M.; Gudmundsson, I.; van Loon, A.; Stahl, K. Candidate distributions for climatological drought indices (SPI and SPEI). Int. J. Climatol. 2015, 35, 4027–4040. [Google Scholar] [CrossRef]
- Caiado, J.; Crato, N.; Peña, D. A periodogram-based metric for time series classification. Comput. Stat. Data Anal. 2006, 50, 2668–2684. [Google Scholar] [CrossRef] [Green Version]
- Montero, P.; Vilar, J.A. TSclust: An R package for time series clustering. J. Stat. Softw. 2014, 62, 1–43. [Google Scholar] [CrossRef] [Green Version]
- Casado de Lucas, D. Classification Techniques for Time Series and Functional Data. Ph.D. Thesis, Universidad Carlos III de Madrid, Madrid, Spain, 2010. [Google Scholar]
- Adisa, O.M.; Botai, C.M.; Botai, J.O.; Hassen, A.; Darkey, D.; Tesfamariam, E.; Adisa, A.F.; Adeola, A.M.; Ncongwane, K.P. Analysis of agro-climatic parameters and their influence on maize production in South Africa. Theor. Appl. Climatol. 2017, 134, 991–1004. [Google Scholar] [CrossRef]









| Category | Range of Drought Index Values | |
|---|---|---|
| SPI | EDI | |
| Extremely Dry | −2.0 | −2.0 |
| Severely Dry | −1.5 to −1.99 | −1.5 to −1.99 |
| Moderately Dry | −1.0 to −1.49 | −1.0 to −1.49 |
| Normal | −0.99 to 0.99 | −0.99 to 0.99 |
| Moderately Wet | 1.0 to 1.49 | 1.0 to 1.49 |
| Severely Wet | 1.5 to 1.99 | 1.5 to 1.99 |
| Extremely Wet | 2.0 | 2.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adisa, O.M.; Masinde, M.; Botai, J.O. Assessment of the Dissimilarities of EDI and SPI Measures for Drought Determination in South Africa. Water 2021, 13, 82. https://doi.org/10.3390/w13010082
Adisa OM, Masinde M, Botai JO. Assessment of the Dissimilarities of EDI and SPI Measures for Drought Determination in South Africa. Water. 2021; 13(1):82. https://doi.org/10.3390/w13010082
Chicago/Turabian StyleAdisa, Omolola M., Muthoni Masinde, and Joel O. Botai. 2021. "Assessment of the Dissimilarities of EDI and SPI Measures for Drought Determination in South Africa" Water 13, no. 1: 82. https://doi.org/10.3390/w13010082
APA StyleAdisa, O. M., Masinde, M., & Botai, J. O. (2021). Assessment of the Dissimilarities of EDI and SPI Measures for Drought Determination in South Africa. Water, 13(1), 82. https://doi.org/10.3390/w13010082






