A Study on the Influence of Suspended Matter by the Foundation Construction of Different Offshore Wind Turbines in the Taiwan Sea Area
Abstract
:1. Introduction
2. Methodology
2.1. Hydrodynamic Model
2.2. Wave Model
2.3. Particle Tracking Model
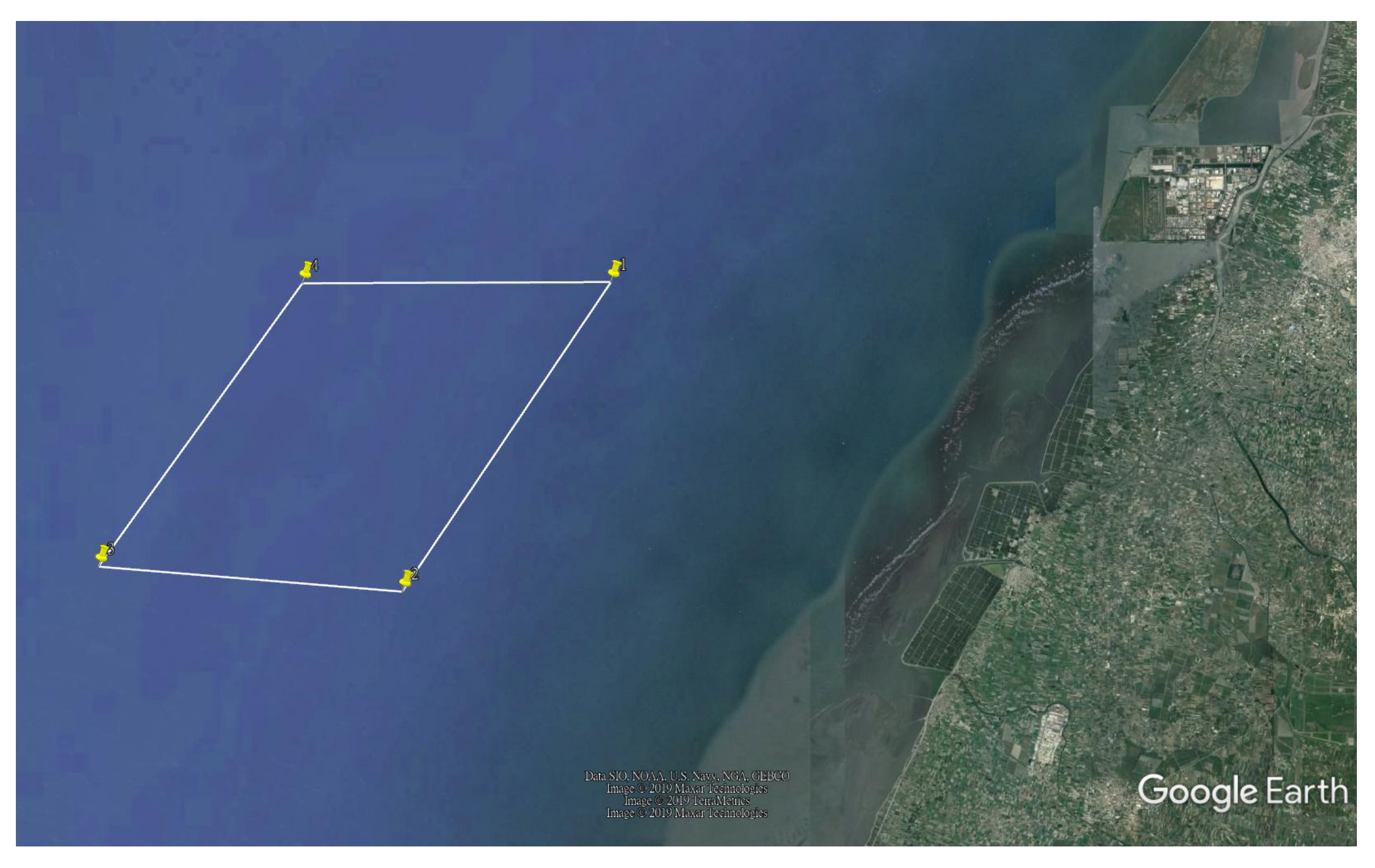
3. Model Set-Up
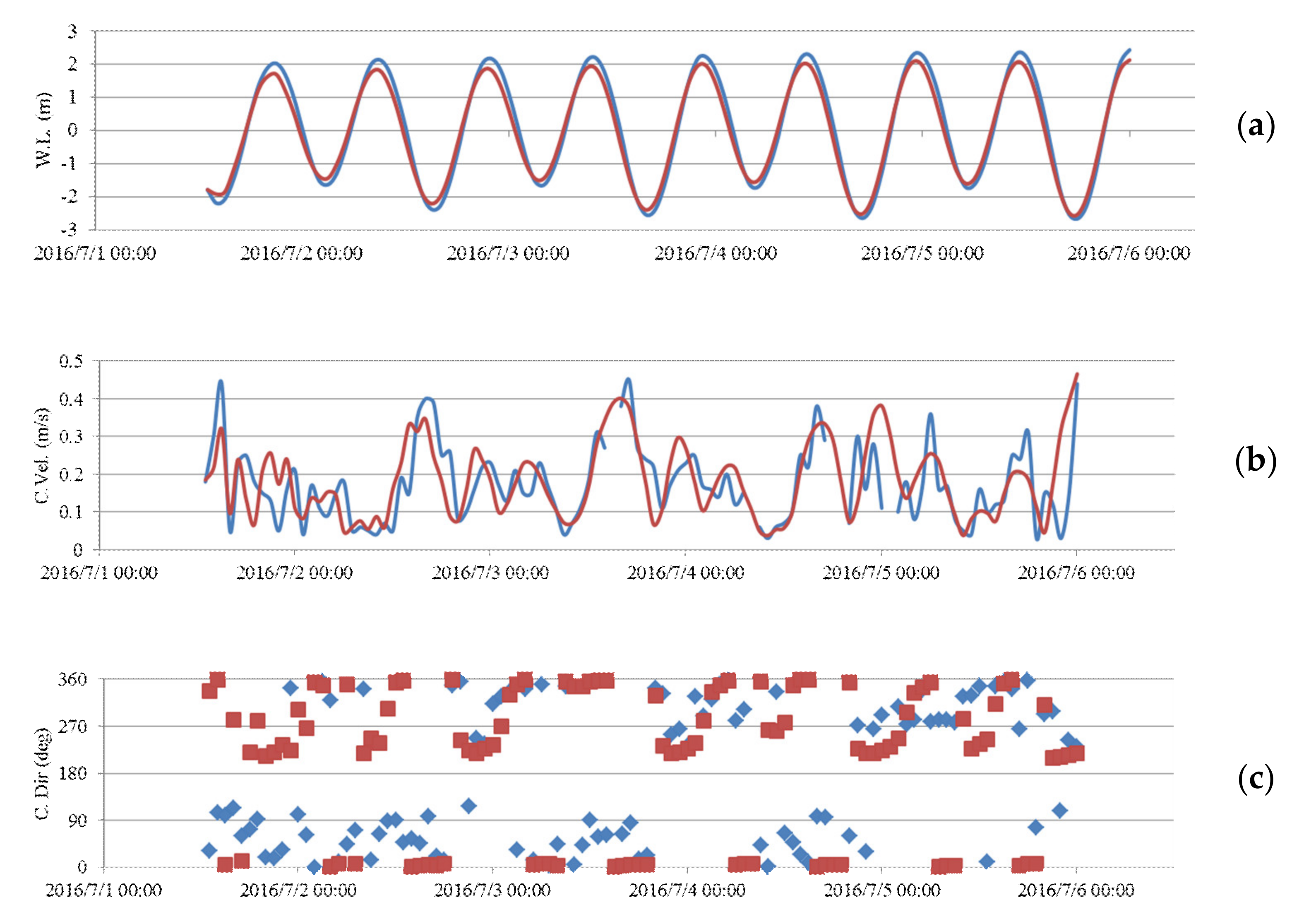
3.1. Modeling Procedure and Validation
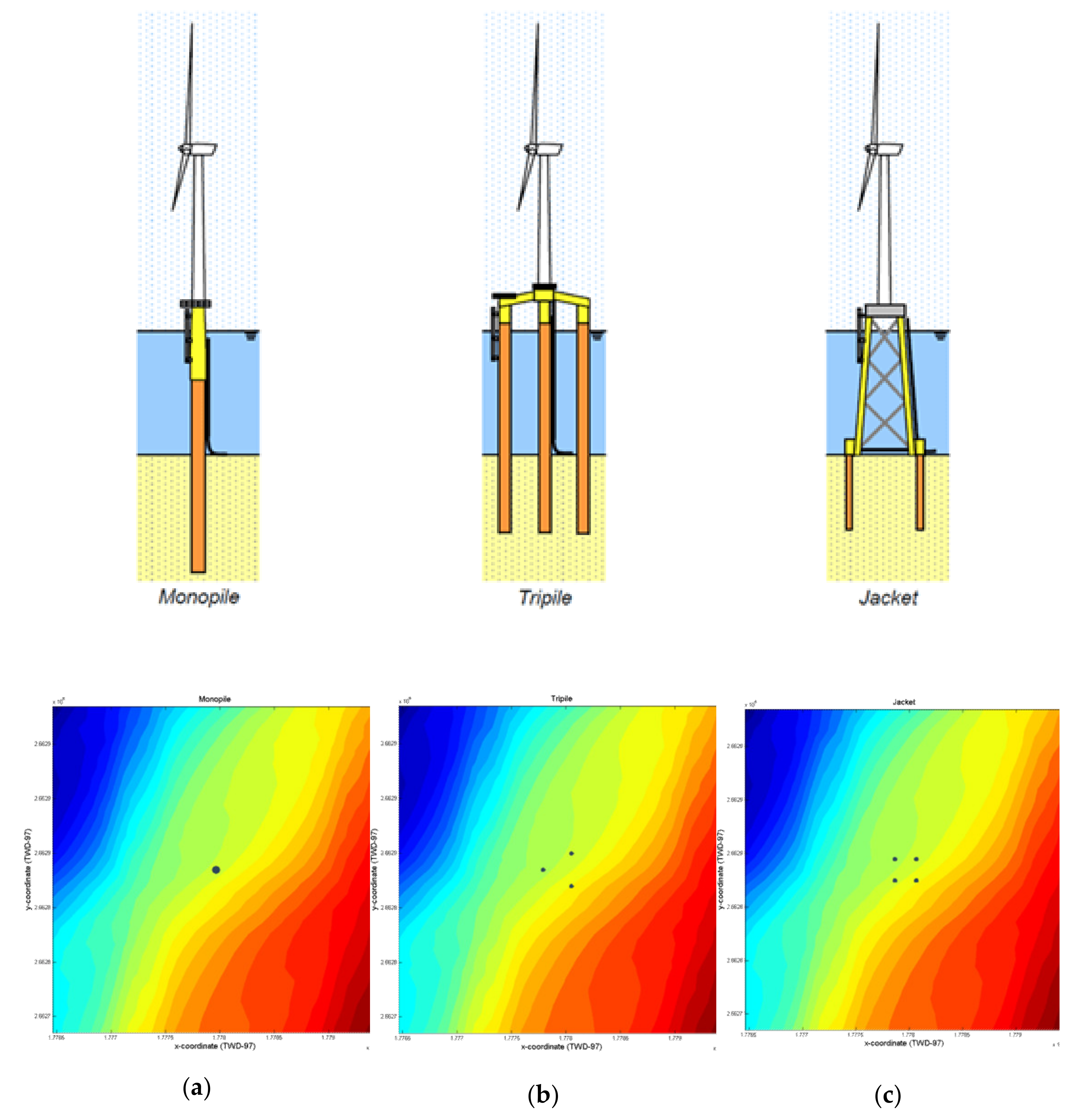
3.2. Suspended Load Characteristics at the Different Foundations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- 4C Offshore. Global Wind Speed Rankings. 2014. Available online: http://www.4coffshore.com/windfarms/windspeeds.aspx (accessed on 11 December 2014).
- Ministry of Science and Technology. Ocean Data Bank. 2018. Available online: http://www.odb.ntu.edu.tw/ (accessed on 20 September 2018).
- Elliott, D.L.; Barnard, J.C. Observations of wind turbine wakes and surface roughness effects on wind flow variability. Sol. Energy 1990, 45, 265–283. [Google Scholar] [CrossRef]
- Burton, T.; Jenkins, N.; Sharpe, D.; Bossanyi, E. Wind Energy Handbook, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2001; pp. 15–18. [Google Scholar]
- Jin, W.J. Numerical Simulation of Wind Turbine Wakes Based on Actuator Line Method in NEK5000. Master’s Thesis, Royal Institute of Technology, Stockholm, Sweden, 2013. [Google Scholar]
- Schomerus, T.; Runge, K.; Nehls, G. Strategic environmental assessment for the utilisation of offshore wind energy. In Proceedings of the 2nd Scientific Conference on the Use of Offshore Wind Energy by the Federal Ministry for the Environment, Berlin, Germany, 20–21 February 2007; pp. 57–73. [Google Scholar]
- Sivas, D.; Caldwell, M. A new vision for Californian ocean governance: Comprehensive ecosystem-based marine zoning. Stanf. Environ. Law J. 2008, 27, 209–270. [Google Scholar]
- Longuet-Higgins, M.S.; Stewart, R.W. Radiation in water waves: A physical discussion with applications. Deep-Sea Res. 1964, 11, 529–563. [Google Scholar] [CrossRef]
- Chiang, Y.C.; Hsiao, S.S.; Lin, M.C. A Quasi-3D Sediment Transport Modeling for Coastal Morphodynamics. In Proceedings of the 21st International Offshore and Polar Engineering Conference, Maui, HI, USA, 19 June 2011; pp. 1053–1058. [Google Scholar]
- Chiang, Y.C.; Hsiao, S.S.; Fang, H.M.; Wang, H.Y. A Study of The Sandbar Evolution by Tidal Current Effect. J. Coast. Ocean Eng. 2013, 13, 275–294. [Google Scholar]
- Chiang, Y.C.; Hsiao, S.S.; Fang, H.M.; Wang, H.Y. A Study of the Asymmetric Wave Parameterize. Int. J. Eng. Technol. 2017, 9, 239–243. [Google Scholar]
- Wang, H.Y.; Fang, H.M.; Hsiao, S.S. Morphological Characteristics of Tidal Inlets Subject to a Short Term Typhoon Event: A Case Study in Lanyan River Estuary. J. Mar. Sci. Technol. 2018, 26, 552–561. [Google Scholar]
- Matushevskiy, T.V. Method of separation of wave induced and turbulent motions in the near-surface layer of the ocean. In On Problems of Ocean Dynamics; Gidrometeoizdat: Leningrad, Russia, 1975; pp. 124–151. (In Russian) [Google Scholar]
- Falconer, R.A. Numerical modeling of tidal circulation in harbors. J. Waterw. Port Coastal Ocean Div. 1980, 106, 31–48. [Google Scholar] [CrossRef]
- Dean, R.G.; Dalrymple, R.A. Water Wave Mechanics for Engineers and Scientists; Prentice-Hall, Inc.: Hoboken, NJ, USA, 1984. [Google Scholar]
- Ponce, V.M.; Yabusaki, S.B. Modeling circulation in depth-averaged flow. J. Hydraul. Div. 1981, 107, 1501–1518. [Google Scholar] [CrossRef]
- Kirby, J.T. A parabolic equation for the combined refraction-diffraction of Stokes waves by mildly varying topography. J. Fluid Mech. 1983, 136, 453–466. [Google Scholar] [CrossRef] [Green Version]
- Mizuguchi, M. An heuristic model of wave height distribution in surf zone. In Proceedings of the 17th Coastal Engineering Conference, Sydney, Australia, 23–28 March 1980; pp. 278–289. [Google Scholar]
- Csanady, G.T. Turbulent Diffusion in the Environment; D. Reidel Publishing Company: Amsterdam, The Netherlands, 1973. [Google Scholar]
- Komar, P.D.; Inman, D.L. Longshore sand transport on beaches. J. Geophys. Res. 1970, 75, 5914–5927. [Google Scholar] [CrossRef]
- Watanabe, A.; Maruyama, K. Numerical modelling of nearshore wave field under combined refraction, diffraction and breaking. Coast. Eng. Jpn. 1986, 29, 19–39. [Google Scholar] [CrossRef]
- Sawaragi, T.; Deguchi, I. Distribution of sand transport rate across the surf zone. In Proceedings of the 16th Coastal Engineering Conference, Hamburg, Germany, 27 August–3 September 1978; Volume 2, pp. 1596–1613. [Google Scholar]
- Vries, W.E.D.; Vemula, N.K.; Passon, P.; Fischer, T.; Kaufer, D.; Matha, D.; Schmidt, B.; Vorpahl, F. Final Report WP 4.2: Support Structure Concepts for Deep Water Sites: Deliverable D4.2.8 (WP4: Offshore Foundations and Support Structures). 2011. Available online: https://www.researchgate.net/profile/Bjoern-Schmidt/publication/241886865_Final_report_WP_42_Support_Structure_Concepts_for_Deep_Water_Sites_Deliverable_D428_WP4_offshore_foundations_and_support_structures/links/5693cbb508ae3ad8e33b301a/Final-report-WP-42-Support-Structure-Concepts-for-Deep-Water-Sites-Deliverable-D428-WP4-offshore-foundations-and-support-structures.pdf (accessed on 15 April 2021).






| Area | Grid Size | Number of Grid Points |
| 33 × 30 km | 50 × 50 m | 660 × 600 |
| Coordinate of the origin (TWD67) | Angle of deviation (counterclockwise from the north) | Time step size |
| 147892, 2656583 | 25° | 1.5 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsiao, S.-S.; Wang, H.-Y.; Chiang, Y.-C. A Study on the Influence of Suspended Matter by the Foundation Construction of Different Offshore Wind Turbines in the Taiwan Sea Area. Water 2021, 13, 1405. https://doi.org/10.3390/w13101405
Hsiao S-S, Wang H-Y, Chiang Y-C. A Study on the Influence of Suspended Matter by the Foundation Construction of Different Offshore Wind Turbines in the Taiwan Sea Area. Water. 2021; 13(10):1405. https://doi.org/10.3390/w13101405
Chicago/Turabian StyleHsiao, Sung-Shan, Hsing-Yu Wang, and Yun-Chih Chiang. 2021. "A Study on the Influence of Suspended Matter by the Foundation Construction of Different Offshore Wind Turbines in the Taiwan Sea Area" Water 13, no. 10: 1405. https://doi.org/10.3390/w13101405
APA StyleHsiao, S.-S., Wang, H.-Y., & Chiang, Y.-C. (2021). A Study on the Influence of Suspended Matter by the Foundation Construction of Different Offshore Wind Turbines in the Taiwan Sea Area. Water, 13(10), 1405. https://doi.org/10.3390/w13101405






