Assessing the Impact of DMAs and the Use of Boosters on Chlorination in a Water Distribution Network in Greece
Abstract
:1. Introduction
2. Chlorination Boosters, Chlorine Residual Modeling, and THMs’ Formation
3. Methods and Study Area
4. Results and Discussion
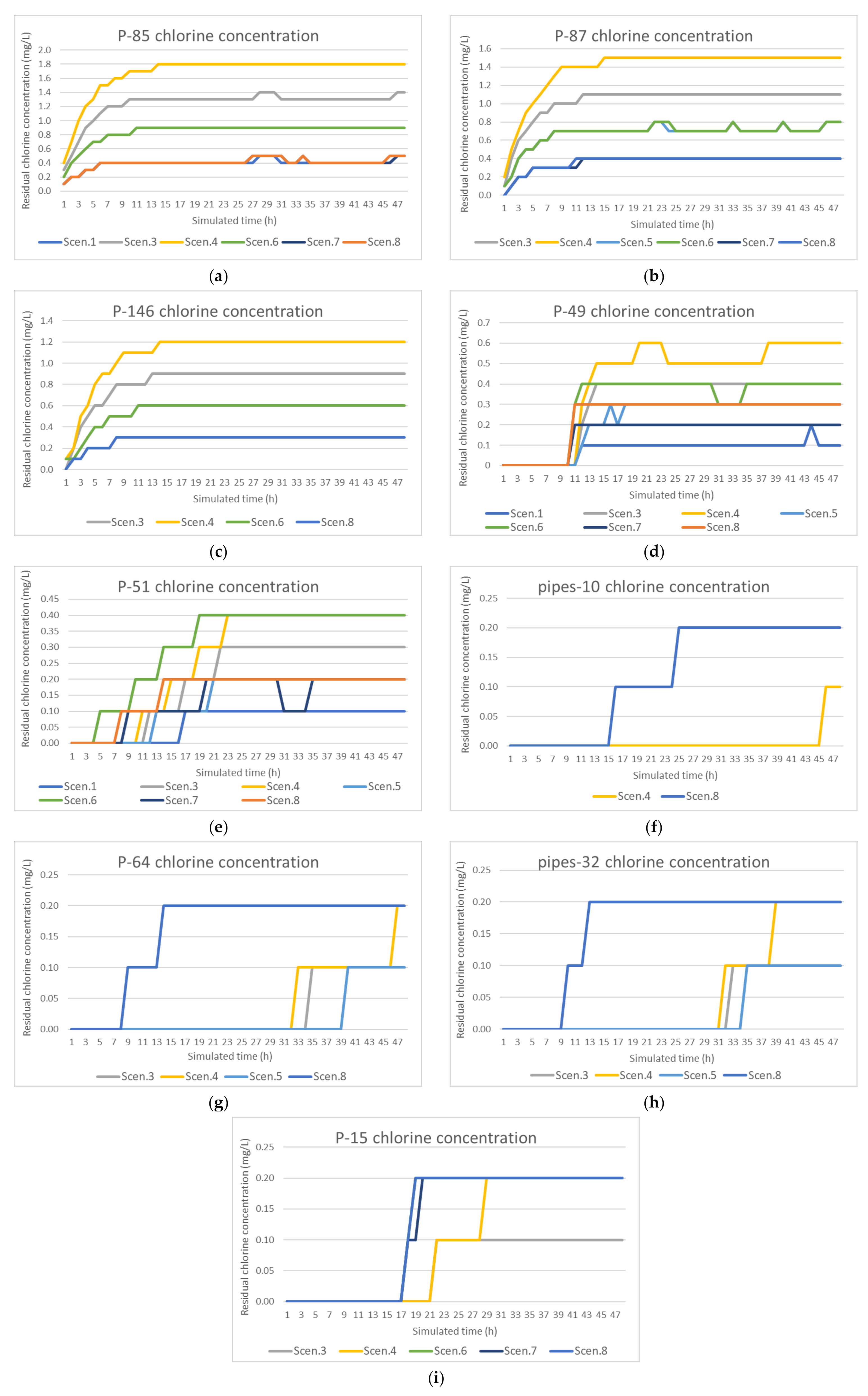
4.1. Scenario A
4.2. Scenario B
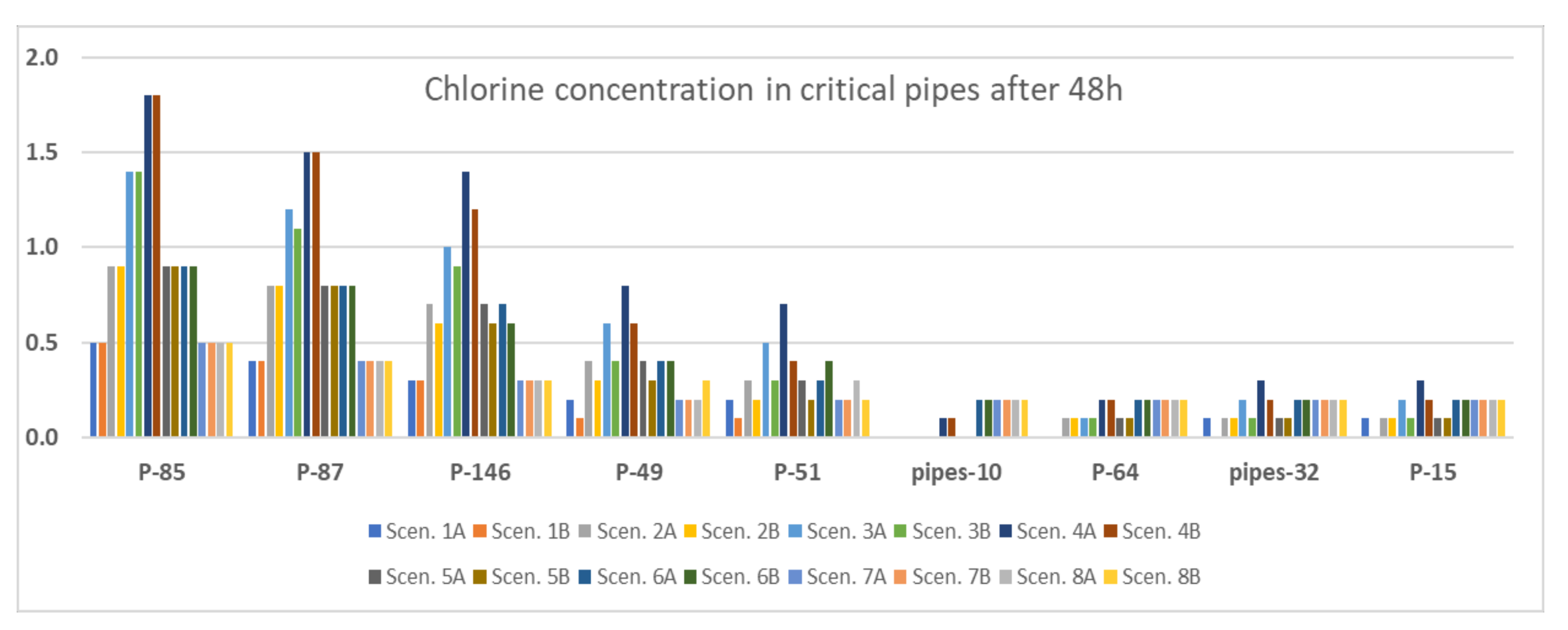
4.3. Results from the Comparison of Scenarios A and B
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tsitsifli, S.; Kanakoudis, V. Developing THMs’ Predictive Models in Two Water Supply Systems in Greece. Water 2020, 12, 1422. [Google Scholar] [CrossRef]
- Kanakoudis, V.; Muhammetoglu, H. Urban Water Pipe Networks Management Towards Non-Revenue Water Reduction: Two Case Studies from Greece and Turkey. Clean-Soil Air Water 2013, 42, 880–892. [Google Scholar] [CrossRef]
- Ciaponi, C.; Creaco, E.; Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Musmarra, D.; Santonastaso, G.F. Reducing impacts of contamination in water distribution networks: A combined strategy based on network partitioning and installation of water quality sensors. Water 2019, 11, 1315. [Google Scholar] [CrossRef] [Green Version]
- World Health Organization. Guidelines for Drinking-Water Quality, 4th ed.; WHO: Geneva, Switzerland, 2017. [Google Scholar]
- Joint Ministerial Decision, No.67322/6.9.2017 on “Quality of Water Intended for Human Consumption in Compliance with the Directive 98/83/EC of the European Council of 3rd November 1998 as Amended by the Directive 2015/1787 (L260, 7.10.2015)”. (in Greek). Available online: https://elinyae.gr/sites/default/files/2019-07/3282b_2017.1528374178932.pdf (accessed on 11 January 2021).
- Directive (EU) 2020/2184 of the European Parliament and of the Council of 16 December 2020 on the Quality of Water Intended for Human Consumption. Available online: https://eur-lex.europa.eu/eli/dir/2020/2184/oj (accessed on 11 January 2021).
- Tryby, M.E.; Boccelli, D.L.; Koechling, M.T.; Uber, J.G.; Summers, R.S.; Rossman, L.A. Booster chlorination for managing disinfectant residuals. J. Am. Water Works Assoc. 1999, 91, 95–108. [Google Scholar] [CrossRef]
- Boccelli, D.L.; Tryby, M.E.; Uber, J.G.; Rossman, L.A.; Zierolf, M.L.; Polycarpou, M.M. Optimal scheduling of booster disinfection in water distribution systems. J. Water Resour. Plan. Manag. 1998, 124, 99–111. [Google Scholar] [CrossRef]
- Munavalli, G.R.; Kumar, M.M. Optimal scheduling of multiple chlorine sources in water distribution systems. J. Water Resour. Plan. Manag. 2003, 129, 493–504. [Google Scholar] [CrossRef]
- Tryby, M.E.; Boccelli, D.L.; Uber, J.G.; Rossman, L.A. Facility location model for booster disinfection of water supply networks. J. Water Resour. Plan. Manag. 2002, 128, 322–333. [Google Scholar] [CrossRef]
- Propato, M.; Uber, J.G. Linear least-squares formulation for operation of booster disinfection systems. J. Water Resour. Plan. Manag. 2003, 130, 53–62. [Google Scholar] [CrossRef]
- Yoo, D.G.; Lee, S.M.; Lee, H.M.; Choi, Y.H.; Kim, J.H. Optimizing Re-Chlorination Injection Points for Water Supply Networks Using Harmony Search Algorithm. Water 2018, 10, 547. [Google Scholar] [CrossRef] [Green Version]
- Prasad, T.D.; Walters, G.A.; Savic, D.A. Booster disinfection of water supply networks: Multiobjective approach. J. Water Resour. Plan. Manag. 2004, 130, 367–376. [Google Scholar] [CrossRef]
- Ostfeld, A.; Salomons, E. Conjunctive optimal scheduling of pumping and booster chlorine injections in water distribution systems. Eng. Optim. 2006, 38, 337–352. [Google Scholar] [CrossRef]
- Seyoum, A.G.; Tanyimboh, T.T. Integration of hydraulic and water quality modelling in distribution networks: EPANET-PMX. Water Resour. Manag. 2017, 31, 4485–4503. [Google Scholar] [CrossRef] [Green Version]
- Seyoum, A.G.; Tanyimboh, T.T.; Siew, C. Assessment of water quality modelling capabilities of EPANET multiple species and pressure-dependent extension models. Water Sci. Technol. Water Supply 2013, 13, 1161–1166. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.M.; Lee, H.M.; Yoo, D.G.; Kim, J.H. A comparative study on a hydraulic and water-quality analysis method for determining rechlorination injection points for a water-supply network. Water 2019, 11, 697. [Google Scholar] [CrossRef] [Green Version]
- Chatzivasili, S.; Papadimitriou, K.; Kanakoudis, V. Optimizing the Formation of DMAs in a Water Distribution Network through Advanced Modelling. Water 2019, 11, 278. [Google Scholar] [CrossRef] [Green Version]
- Chatzivasili, S.; Papadimitriou, K.; Kanakoudis, V.; Patelis, M. Optimizing the Formation of DMAs in a Water Distribution Network Applying Geometric Partitioning (GP) and Gaussian Mixture Models (GMMs). Proceedings 2018, 2, 601. [Google Scholar] [CrossRef] [Green Version]
- Kourbasis, N.; Patelis, M.; Tsitsifli, S.; Kanakoudis, V. Optimizing water age and pressure in drinking water distribution networks. Environ. Sci. Proc. 2020, 2, 51. [Google Scholar] [CrossRef]
- Carrico, B.; Singer, P.C. Impact of booster chlorination on chlorine decay and THM production: Simulated analysis. J. Environ. Eng. 2009, 135, 928–935. [Google Scholar] [CrossRef]
- Vasconcelos, J.J.; Rossman, L.A.; Grayman, W.M.; Boulos, P.F.; Clark, R.M. Kinetics of chlorine decay. J. AWWA 1997, 89, 54–65. [Google Scholar] [CrossRef]
- Rossman, L.A.; Brown, R.A.; Singer, P.C.; Nuckols, J.R. DBP formation kinetics in a simulated distribution system. Water Res. 2001, 35, 3483–3489. [Google Scholar] [CrossRef]
- Blokker, M.; Vreeburg, J.; Speight, V. Residual chlorine in the extremities of the drinking water distribution system: The influence of stochastic water demands. Procedia Eng. 2014, 70, 172–180. [Google Scholar] [CrossRef] [Green Version]
- Rossman, L.A.; Clark, R.M.; Grayman, W.M. Modeling chlorine residuals in drinking-water distribution-systems. J. Environ. Eng. 1994, 120, 803–820. [Google Scholar] [CrossRef]
- Kanakoudis, V.; Gonelas, K. Properly allocating the urban waters meters’ readings to the nodes of a water pipe network simulation model in a developing water utility. Desalin. Water Treat. 2015, 54, 2190–2203. [Google Scholar] [CrossRef]
- Duan, W.; He, B.; Takara, K.; Luo, P.; Nover, D.; Sahu, N.; Yamashiki, Y. Spatiotemporal evaluation of water quality incidents in Japan between 1996 and 2007. Chemosphere 2013, 93, 946–953. [Google Scholar] [CrossRef] [PubMed]
- Duan, W.; He, B.; Nover, D.; Yang, G.; Chen, W.; Meng, H.; Zou, S.; Liu, C. Water quality assessment and pollution source identification of the eastern Poyang Lake Basin using multivariate statistical methods. Sustainability 2016, 8, 133. [Google Scholar] [CrossRef] [Green Version]

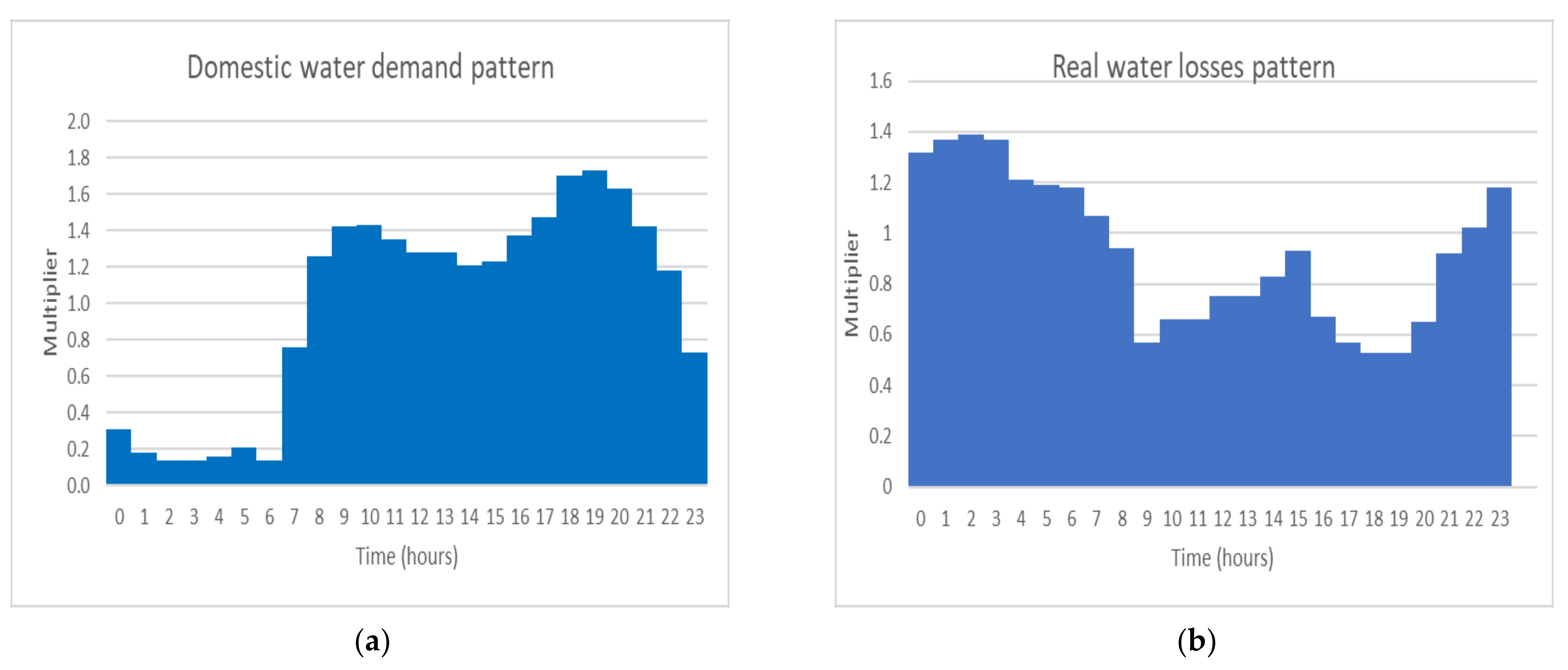
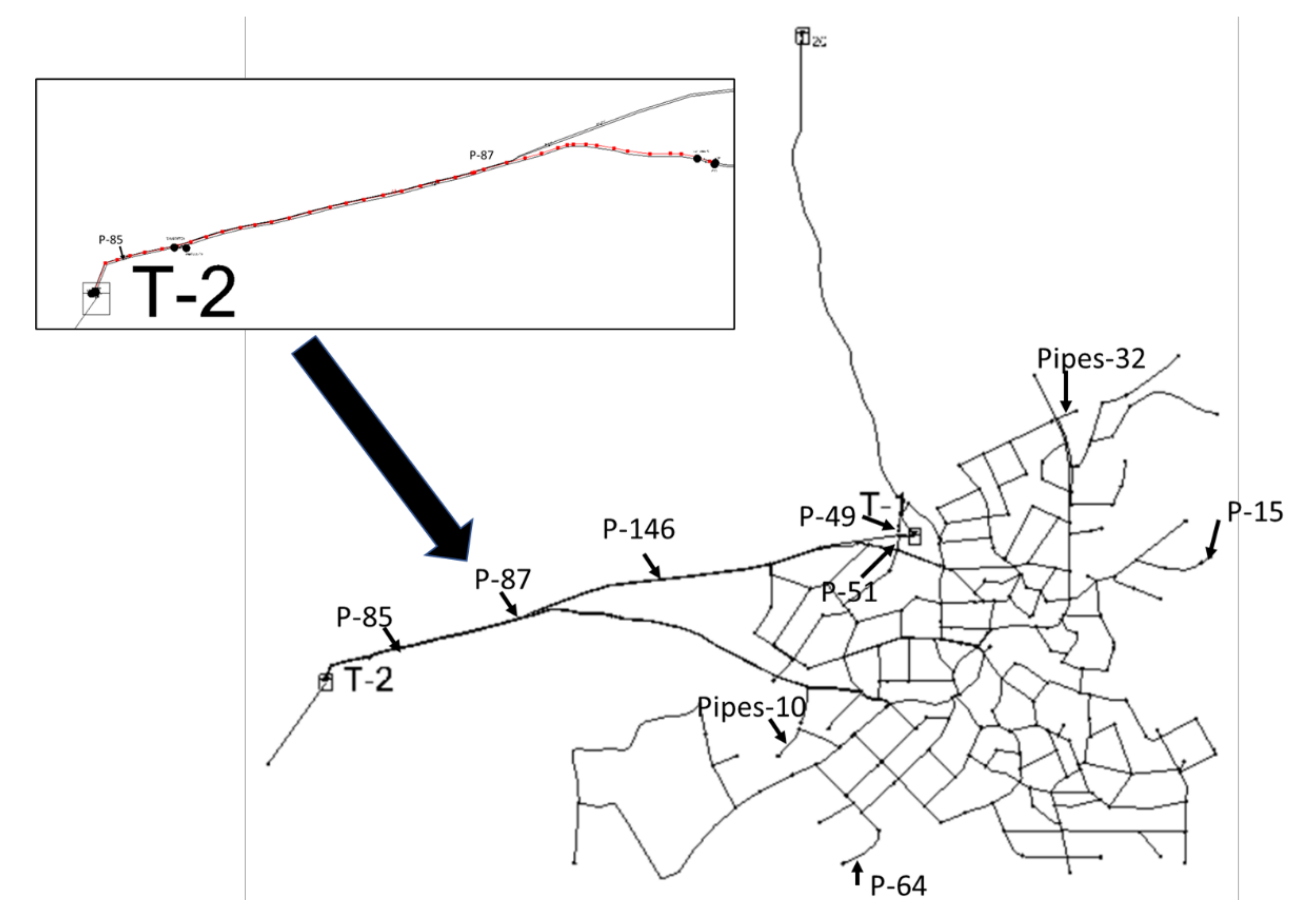
| Water Source | Water Volume (m3/Day) | Water Volume (m3/h) |
|---|---|---|
| Reservoir | 1494.72 | 62.28 |
| Springs | 72.24 | 3.01 |
| Total | 1566.96 | 65.29 |
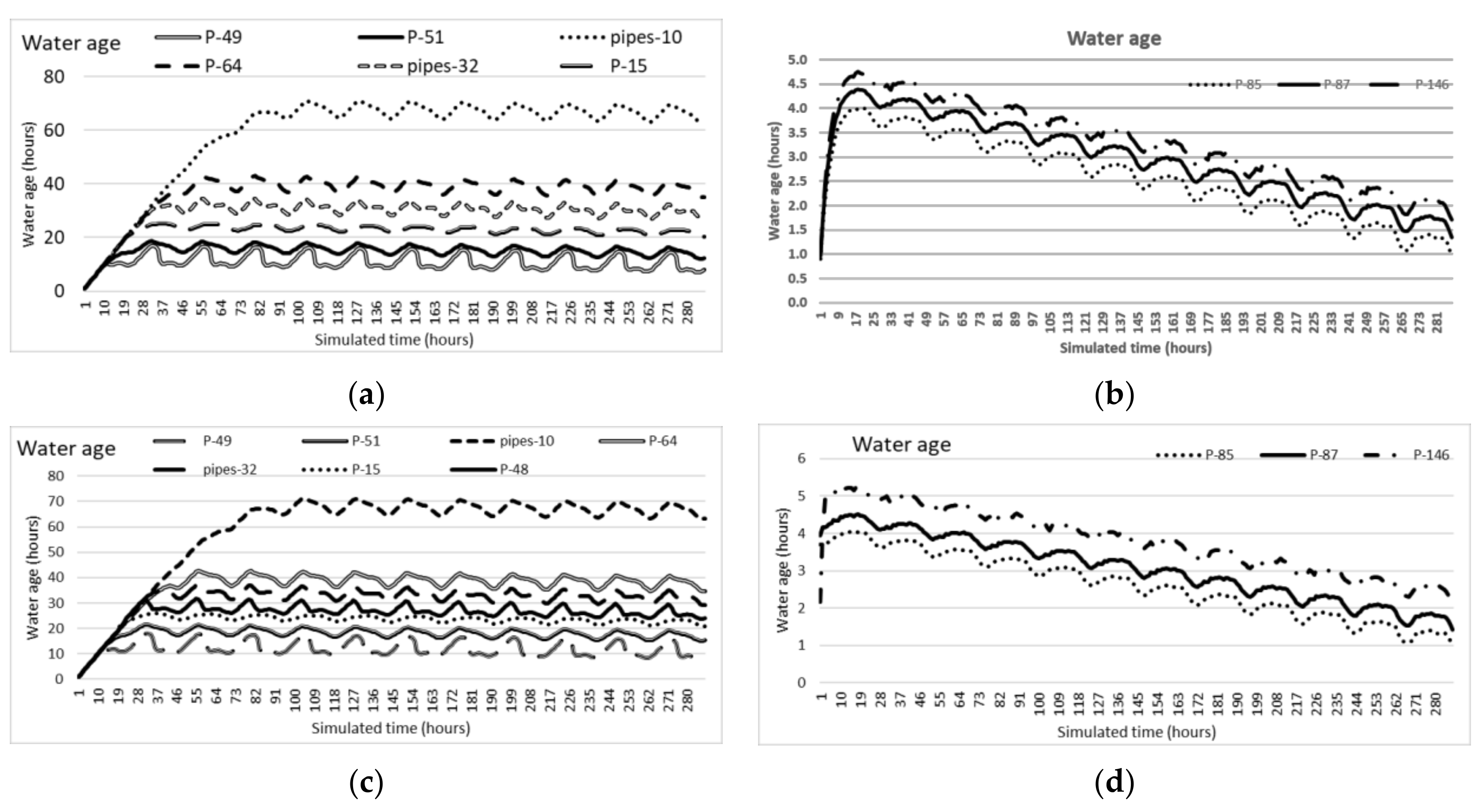
| Pipe | Water Age (Hours) | Junctions ID | Water Age (Hours) | Junctions ID | Water Age (Hours) | |||
|---|---|---|---|---|---|---|---|---|
| Scenario A | Scenario B | Scenario A | Scenario B | Scenario A | Scenario B | |||
| P-85 | 0.95 | 0.95 | J-54 | 0.95 | 0.96 | Nodes-56 | 3.98 | 3.66 |
| P-87 | 1.34 | 1.42 | J-55 | 0.95 | 0.96 | Manholes-15 | 5.37 | 5.99 |
| P-146 | 1.71 | 2.18 | J-77 | 0.95 | 0.96 | J-1 | 2.86 | 5.30 |
| P-49 | 7.90 | 9.05 | J-35 | 8.18 | 9.32 | J-34 | 18.41 | 20.97 |
| P-51 | 12.34 | 15.25 | J-36 | 20.36 | 23.50 | J-16 | 18.59 | 19.18 |
| Pipes-10 | 63.17 | 63.39 | Nodes-20 | 31.15 | 31.39 | Nodes-47 | 5.17 | 6.08 |
| P-64 | 35.07 | 34.72 | J-42 | 16.86 | 16.53 | Manholes-55 | 2.35 | 1.62 |
| Pipes-32 | 26.73 | 29.23 | Nodes-110 | 18.25 | 20.76 | 495 | 7.37 | 7.54 |
| P-15 | 20.36 | 20.89 | Manholes-87 | 2.58 | 1.84 | J-7 | 11.53 | 13.95 |
| 473 | 10.61 | 13.00 | ||||||
| Selected Junctions (ID) | Chlorine Dose (mg/L) | |||||||
|---|---|---|---|---|---|---|---|---|
| Scen.1 | Scen.2 | Scen.3 | Scen.4 | Scen.5 | Scen.6 | Scen.7 | Scen.8 | |
| Reservoir | 0.5 | 1.0 | 1.5 | 2.0 | 1.0 | 1.0 | 0.5 | 0.5 |
| Springs | 0 | 0 | 0 | 0 | 0.5 | 1.0 | 0.5 | 0.5 |
| manholes-94 | 0 | 0 | 0 | 0 | 0 | 0.6 | 0.6 | 0.5 |
| nodes-21 | 0 | 0 | 0 | 0 | 0 | 0.6 | 0.6 | 0.5 |
| manholes-4 | 0 | 0 | 0 | 0 | 0 | 0.5 | 0.5 | 0.5 |
| manholes-55 | 0 | 0 | 0 | 0 | 0 | 0.5 | 0.5 | 0.5 |
| nodes-104 | 0 | 0 | 0 | 0 | 0 | 0.5 | 0.5 | 0.5 |
| manholes-11 | 0 | 0 | 0 | 0 | 0 | 0.4 | 0.4 | 0.5 |
| 460,2 | 0 | 0 | 0 | 0 | 0 | 0.4 | 0.4 | 0 |
| 482 | 0 | 0 | 0 | 0 | 0 | 0.4 | 0.4 | 0.4 |
| manholes-2 | 0 | 0 | 0 | 0 | 0 | 0.3 | 0.3 | 0 |
| 455,6 | 0 | 0 | 0 | 0 | 0 | 0.3 | 0.3 | 0.2 |
| nodes-173 | 0 | 0 | 0 | 0 | 0 | 0.2 | 0.2 | 0.2 |
| manholes-35 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.5 |
| manholes-25 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.3 |
| 499,2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.2 |
| nodes-52 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.2 |
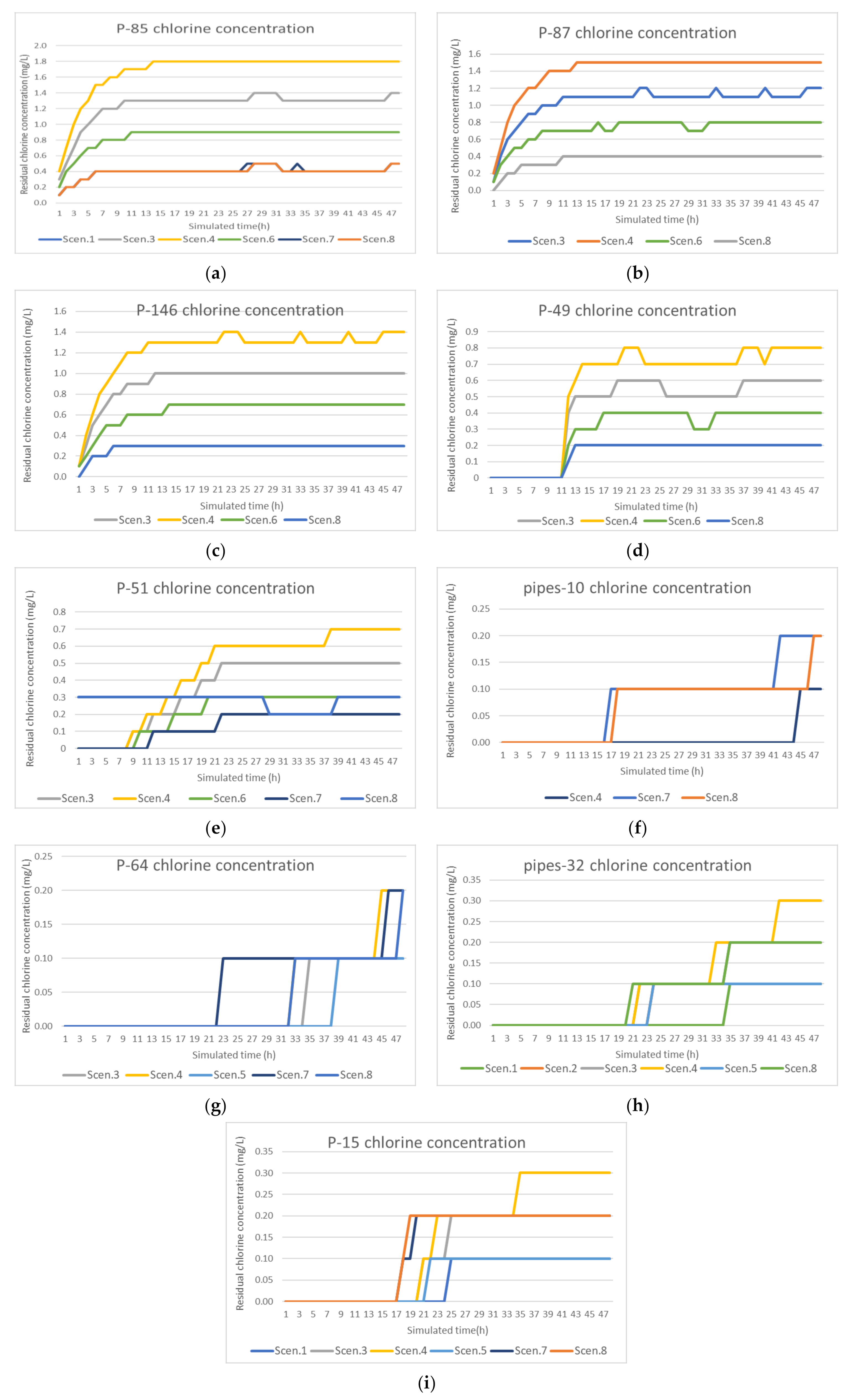
| Pipe ID | Chlorine Residual Concentration (mg/L) | |||||||
|---|---|---|---|---|---|---|---|---|
| Scen.1 | Scen.2 | Scen.3 | Scen.4 | Scen.5 | Scen.6 | Scen.7 | Scen.8 | |
| P-85 | 0.5 | 0.9 | 1.4 | 1.8 | 0.9 | 0.9 | 0.5 | 0.5 |
| P-87 | 0.4 | 0.8 | 1.2 | 1.5 | 0.8 | 0.8 | 0.4 | 0.4 |
| P-146 | 0.3 | 0.7 | 1.0 | 1.4 | 0.7 | 0.7 | 0.3 | 0.3 |
| P-49 | 0.2 | 0.4 | 0.6 | 0.8 | 0.4 | 0.4 | 0.2 | 0.2 |
| P-51 | 0.2 | 0.3 | 0.5 | 0.7 | 0.3 | 0.3 | 0.2 | 0.3 |
| pipes-10 | 0.0 | 0.0 | 0.0 | 0.1 | 0.0 | 0.2 | 0.2 | 0.2 |
| P-64 | 0.0 | 0.1 | 0.1 | 0.2 | 0.1 | 0.2 | 0.2 | 0.2 |
| pipes-32 | 0.1 | 0.1 | 0.2 | 0.3 | 0.1 | 0.2 | 0.2 | 0.2 |
| P-15 | 0.1 | 0.1 | 0.2 | 0.3 | 0.1 | 0.2 | 0.2 | 0.2 |
| Junctions ID | ||||||||
| J-54 | 0.5 | 0.9 | 1.4 | 1.8 | 0.9 | 0.9 | 0.5 | 0.5 |
| J-55 | 0.4 | 0.9 | 1.3 | 1.8 | 0.9 | 0.9 | 0.4 | 0.4 |
| J-77 | 0.4 | 0.9 | 1.3 | 1.8 | 0.9 | 0.9 | 0.4 | 0.4 |
| J-35 | 0.2 | 0.4 | 0.6 | 0.7 | 0.4 | 0.4 | 0.2 | 0.2 |
| J-36 | 0.1 | 0.3 | 0.4 | 0.6 | 0.3 | 0.3 | 0.2 | 0.2 |
| Nodes-20 | 0.1 | 0.1 | 0.2 | 0.3 | 0.1 | 0.4 | 0.4 | 0.4 |
| J-42 | 0.1 | 0.2 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
| Nodes-110 | 0.1 | 0.2 | 0.3 | 0.4 | 0.2 | 0.2 | 0.2 | 0.2 |
| Manholes-87 | 0.3 | 0.6 | 0.9 | 1.2 | 0.6 | 0.6 | 0.5 | 0.5 |
| Nodes-56 | 0.2 | 0.3 | 0.5 | 0.7 | 0.3 | 0.6 | 0.6 | 0.5 |
| Manholes-15 | 0.2 | 0.3 | 0.5 | 0.6 | 0.3 | 0.3 | 0.3 | 0.4 |
| J-1 | 0.3 | 0.6 | 0.9 | 1.1 | 0.6 | 0.6 | 0.3 | 0.3 |
| J-34 | 0.1 | 0.3 | 0.4 | 0.5 | 0.3 | 0.3 | 0.2 | 0.2 |
| J-16 | 0.1 | 0.2 | 0.2 | 0.3 | 0.2 | 0.2 | 0.2 | 0.2 |
| Nodes-47 | 0.1 | 0.2 | 0.3 | 0.4 | 0.2 | 0.2 | 0.2 | 0.3 |
| Manholes-55 | 0.3 | 0.6 | 0.9 | 1.2 | 0.6 | 0.6 | 0.5 | 0.5 |
| 495 | 0.1 | 0.2 | 0.3 | 0.4 | 0.2 | 0.3 | 0.3 | 0.3 |
| J-7 | 0.1 | 0.2 | 0.3 | 0.4 | 0.2 | 0.3 | 0.3 | 0.3 |
| 473 | 0.1 | 0.2 | 0.3 | 0.5 | 0.2 | 0.3 | 0.3 | 0.3 |
| Total chlorine dose (g/day) | 747.4 | 1494.7 | 2242.1 | 2989.4 | 1495.1 | 1522.7 | 779.7 | 777.0 |
| Safe water volume (%) | 73.06 | 93.78 | 46.16 | 22.06 | 93.82 | 93.22 | 97.98 | 100.00 |
| Min chlorine concentration at 48 h (mg/L) | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.1 | 0.1 | 0.2 |
| Max chlorine concentration at 48 h (mg/L) | 0.5 | 0.9 | 1.4 | 1.8 | 0.9 | 0.9 | 0.6 | 0.5 |
| Mean chlorine concentration at 48 h (mg/L) | 0.18 | 0.36 | 0.54 | 0.72 | 0.36 | 0.39 | 0.27 | 0.27 |
| Selected Junctions ID | Chlorine Dose (mg/L) | |||||||
|---|---|---|---|---|---|---|---|---|
| Scen.1 | Scen.2 | Scen.3 | Scen.4 | Scen.5 | Scen.6 | Scen.7 | Scen.8 | |
| Reservoir | 0.5 | 1.0 | 1.5 | 2.0 | 1.0 | 1.0 | 0.5 | 0.5 |
| Springs | 0 | 0 | 0 | 0 | 0.5 | 1.0 | 0.6 | 0.5 |
| Manholes-3 | 0 | 0 | 0 | 0 | 0 | 0.5 | 0.5 | 0.5 |
| Manholes-55 | 0 | 0 | 0 | 0 | 0 | 0.5 | 0.5 | 0.5 |
| Manholes-94 | 0 | 0 | 0 | 0 | 0 | 0.5 | 0.5 | 0.5 |
| Nodes-21 | 0 | 0 | 0 | 0 | 0 | 0.5 | 0.5 | 0.5 |
| Manholes-4 | 0 | 0 | 0 | 0 | 0 | 0.5 | 0.4 | 0.4 |
| Manholes-11 | 0 | 0 | 0 | 0 | 0 | 0.5 | 0.4 | 0.5 |
| Manholes-7 | 0 | 0 | 0 | 0 | 0 | 0.5 | 0.4 | 0.5 |
| 481,5 | 0 | 0 | 0 | 0 | 0 | 0.5 | 0.4 | 0.4 |
| Manholes-57 | 0 | 0 | 0 | 0 | 0 | 0.5 | 0.3 | 0.4 |
| 482,2 | 0 | 0 | 0 | 0 | 0 | 0.5 | 0.2 | 0.3 |
| Manholes-38 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.4 |
| 473,5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.3 |
| Pipe ID | Residual Chlorine Concentration (mg/L) | |||||||
|---|---|---|---|---|---|---|---|---|
| Scen.1 | Scen.2 | Scen.3 | Scen.4 | Scen.5 | Scen.6 | Scen.7 | Scen.8 | |
| P-85 | 0.5 | 0.9 | 1.4 | 1.8 | 0.9 | 0.9 | 0.5 | 0.5 |
| P-87 | 0.4 | 0.8 | 1.1 | 1.5 | 0.8 | 0.8 | 0.4 | 0.5 |
| P-146 | 0.3 | 0.6 | 0.9 | 1.2 | 0.6 | 0.6 | 0.3 | 0.3 |
| P-49 | 0.1 | 0.3 | 0.4 | 0.6 | 0.3 | 0.4 | 0.2 | 0.3 |
| P-51 | 0.1 | 0.2 | 0.3 | 0.4 | 0.2 | 0.4 | 0.2 | 0.2 |
| Pipes-10 | 0.0 | 0.0 | 0.0 | 0.1 | 0.0 | 0.2 | 0.2 | 0.2 |
| P-64 | 0.0 | 0.1 | 0.1 | 0.2 | 0.1 | 0.2 | 0.2 | 0.2 |
| Pipes-32 | 0.0 | 0.1 | 0.1 | 0.2 | 0.1 | 0.2 | 0.2 | 0.2 |
| P-15 | 0.0 | 0.1 | 0.1 | 0.2 | 0.1 | 0.2 | 0.2 | 0.2 |
| Junctions ID | ||||||||
| J-54 | 0.5 | 0.9 | 1.4 | 1.8 | 0.9 | 0.9 | 0.5 | 0.5 |
| J-55 | 0.4 | 0.9 | 1.3 | 1.8 | 0.9 | 0.9 | 0.4 | 0.4 |
| J-77 | 0.4 | 0.9 | 1.3 | 1.8 | 0.9 | 0.9 | 0.4 | 0.4 |
| J-35 | 0.1 | 0.3 | 0.4 | 0.6 | 0.3 | 0.4 | 0.2 | 0.3 |
| J-36 | 0.1 | 0.2 | 0.3 | 0.4 | 0.2 | 0.3 | 0.2 | 0.2 |
| Nodes-20 | 0.1 | 0. | 0.2 | 0.2 | 0.1 | 0.3 | 0.3 | 0.3 |
| J-42 | 0.1 | 0.2 | 0.2 | 0.3 | 0.2 | 0.3 | 0.3 | 0.3 |
| Nodes-110 | 0.1 | 0.1 | 0.2 | 0.3 | 0.1 | 0.2 | 0.2 | 0.2 |
| Manholes-87 | 0.3 | 0.7 | 1.0 | 1.4 | 0.7 | 0.7 | 0.5 | 0.5 |
| Nodes-56 | 0.2 | 0.3 | 0.5 | 0.6 | 0.3 | 0.5 | 0.5 | 0.5 |
| Manholes-15 | 0.1 | 0.2 | 0.3 | 0.4 | 0.2 | 0.4 | 0.3 | 0.4 |
| J-1 | 0.2 | 0.4 | 0.6 | 0.8 | 0.4 | 0.4 | 0.2 | 0.2 |
| J-34 | 0.1 | 0.2 | 0.3 | 0.3 | 0.2 | 0.3 | 0.2 | 0.2 |
| J-16 | 0.1 | 0.1 | 0.1 | 0.2 | 0.1 | 0.2 | 0.2 | 0.2 |
| Nodes-47 | 0.1 | 0.1 | 0.2 | 0.3 | 0.1 | 0.2 | 0.2 | 0.2 |
| Manholes-55 | 0.4 | 0.7 | 1.1 | 1.5 | 0.7 | 0.7 | 0.5 | 0.5 |
| 495 | 0.1 | 0.2 | 0.3 | 0.4 | 0.2 | 0.3 | 0.3 | 0.3 |
| J-7 | 0.1 | 0.1 | 0.2 | 0.3 | 0.1 | 0.2 | 0.2 | 0.3 |
| 473 | 0.1 | 0.2 | 0.2 | 0.3 | 0.2 | 0.2 | 0.2 | 0.3 |
| Total chlorine dose (g/day) | 747.4 | 1494.7 | 2242.1 | 2989.4 | 1495.1 | 1516.5 | 770.4 | 775.5 |
| Safe water volume (%) | 69.23 | 85.58 | 52.70 | 24.59 | 85.61 | 90.43 | 98.89 | 100.00 |
| Min chlorine concentration at 48 h (mg/L) | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.1 | 0.1 | 0.2 |
| Max chlorine concentration at 48 h (mg/L) | 0.5 | 0.9 | 1.4 | 1.8 | 0.9 | 0.9 | 0.5 | 0.5 |
| Mean chlorine concentration at 48 h (mg/L) | 0.16 | 0.33 | 0.49 | 0.66 | 0.33 | 0.38 | 0.27 | 0.29 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsitsifli, S.; Kanakoudis, V. Assessing the Impact of DMAs and the Use of Boosters on Chlorination in a Water Distribution Network in Greece. Water 2021, 13, 2141. https://doi.org/10.3390/w13162141
Tsitsifli S, Kanakoudis V. Assessing the Impact of DMAs and the Use of Boosters on Chlorination in a Water Distribution Network in Greece. Water. 2021; 13(16):2141. https://doi.org/10.3390/w13162141
Chicago/Turabian StyleTsitsifli, Stavroula, and Vasilis Kanakoudis. 2021. "Assessing the Impact of DMAs and the Use of Boosters on Chlorination in a Water Distribution Network in Greece" Water 13, no. 16: 2141. https://doi.org/10.3390/w13162141
APA StyleTsitsifli, S., & Kanakoudis, V. (2021). Assessing the Impact of DMAs and the Use of Boosters on Chlorination in a Water Distribution Network in Greece. Water, 13(16), 2141. https://doi.org/10.3390/w13162141







