A Forecast-Skill-Based Dynamic Pre-Storm Level Control for Reservoir Flood-Control Operation
Abstract
1. Introduction
2. Derivation of Forecast-Skill-Based Dynamic Pre-Storm Level
2.1. Typical Reservoir Flood Control Operation Strategies
- The reservoir water level at the beginning of flood forecasts should be allowed to operate below a limit operation water level;
- The water level at the start of the storm-control period should be set to a lower water level as compared to the beginning of flood forecasts. This water level (hereinafter referred to as dynamic pre-storm level, D-PSL, i.e., level A’ in Figure 1) is related to the magnitude and accuracy of forecasts for the incoming flood. Then reservoir regulates the flood from this level to some level B’ based on the difference between flood volume and reservoir release;
- After the storm-control period, the reservoir should be allowed to return to the limited operation water level.
2.2. Forecast-Skill-Based Dynamic Pre-Storm Level Derivation
2.2.1. Forecast-Skill-Based Period Flood Forecasts
2.2.2. Derivation of Dynamic Pre-Storm Level
- Step 1.
- Estimate the flood variance, , for multiple periods from historical/projected annual maximum flood series (AM) [43];
- Step 2.
- Evaluate the forecast skill ( of any applicable hydrological forecast model based on long term retroactive forecasts and observations following hydrological forecasts related research, e.g., [35];
- Step 3.
- Produce the maximum day flood volume forecast of an incoming flood using the forecast model, where the forecast is in the form of mean and variance ;
- Step 4.
- Calculate the dynamic design period flood, , according to the reservoir dynamic design-flood probability, , indicated by the exceedance probability of forecast error (e.g., 1% shown in Figure 2);
- Step 5.
- Carry out the reservoir flood-control operation according to Equation (7) based on dynamic design period flood, , and then obtain the dynamic pre-storm level, D-;
- Step 6.
- Repeat step 3 to step 5 with the time period varying from 1 day to 2 days, 3 days, and 5 days, and obtain the corresponding D-;
- Step 7.
- Define the minimum value in {D-PSL1 d, D-PSL2 d, D-PSL3 d, D-PSL5 d} as the chosen D-PSL.
2.2.3. The Relationship between Forecast Error and Flood Risk
- Overestimated flood volume—the probability of such case . The reservoir will not be filled to its capacity; thus, the outflow can be reduced according to the flood volume difference between the dynamic design period flood and actual flood volume. Compared to the static FLWL method, the D-PSL-based operation will definitely not increase flood risk, and this conclusion is irrelevant to the magnitude of a flood;
- Underestimated, but within limit forecast error—the probability of such case . This seems alert condition actually will not face flood risk. This is because the D-PSL is derived from rather than the forecast value itself. This means the proposed policy did provide an adequate margin of safety. Indeed, the result is the same as case 1;
- Significantly underestimated flood volume—the probability of such case . The actual flood is significantly larger than the forecasts. The reservoir storage reserved is insufficient to capture all excess flood. To avoid catastrophic flood damage induced by a dam failure, the reservoir must release water equals to the inflow, thus increase downstream flood risk. However, this kind of probability for each flood event is less than , which is usually as small as 1% to 0.01%.
3. Case Study
3.1. The Three Gorges Reservoir
3.2. Evaluation of Dynamic Pre-Storm Level
- Estimate the period flood variance by reviewing the historical flow using the annual maximum series method;
- Simulate flood volume for multiple time periods using the autoregressive model and Gaussian random number generator, and use them as period flood forecasts ;
- Verify the simulation model by comparing the results between historical observations and simulated forecasts;
- Compute the limit forecast error for multiple time periods under a given forecast skill using Equations (1) to (5);
- Calculate the D-PSLts based on forecast floods for multiple time periods and obtain the chosen D-PSL using Equations (6) to (9).
3.2.1. Flood Simulation based on Historical Records Using Autoregressive Model
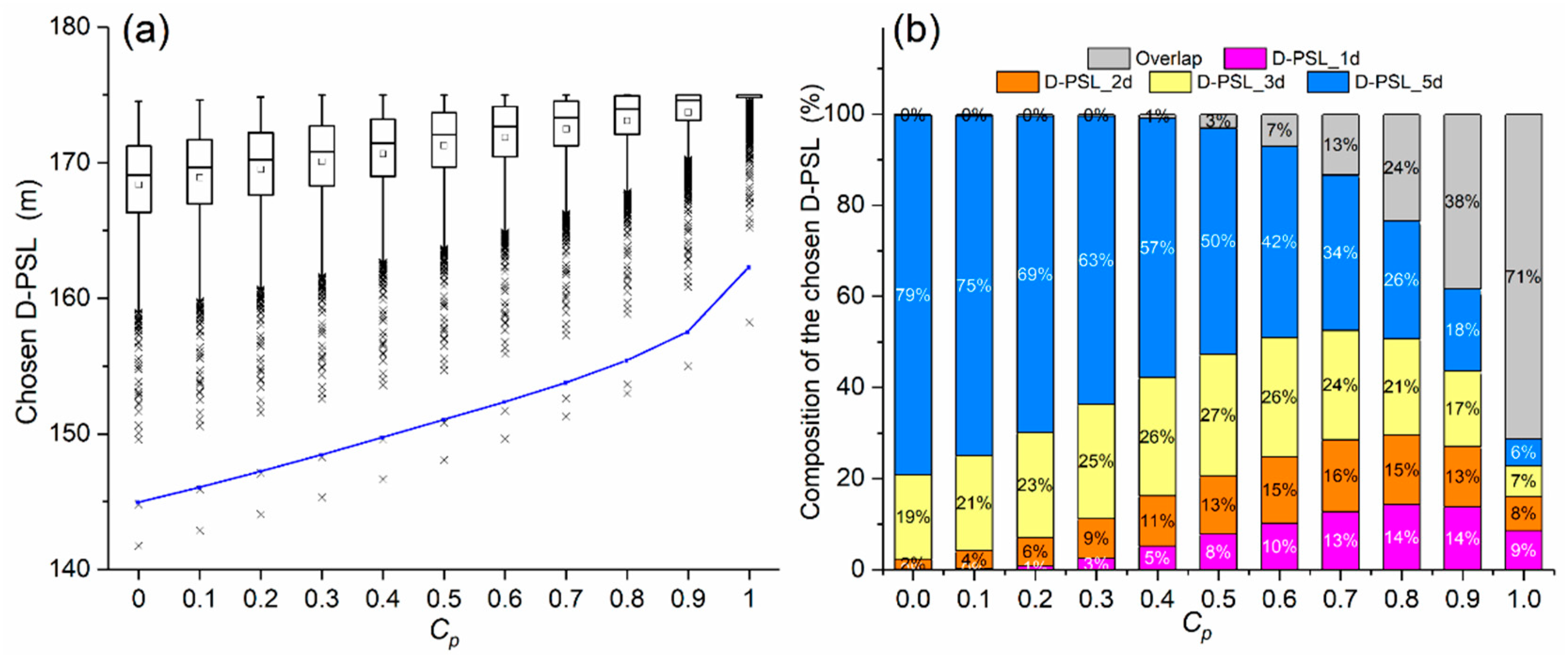
3.2.2. Forecast-Skill-Based Dynamic Pre-Storm Level
3.3. Impact of Downstream Conveyance Capacity
3.4. Impact of Reservoir Size
4. Discussion
4.1. Relationship between D-PSL and Limit Operation Water Level
4.2. Application of the Dynamic Pre-Storm Flood Control Operation Strategy
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Stedinger, J.R. Expected Probability and Annual Damage Estimators. J. Water Res. Plan. Manag. 1997, 123, 125–135. [Google Scholar] [CrossRef]
- Loucks, D.P.; Van Beek, E.; Stedinger, J.R.; Dijkman, J.P.; Villars, M.T. Water Resources Systems Planning and Management: An Introduction to Methods, Models and Applications; UNESCO: Paris, France, 2005. [Google Scholar]
- Hirsch, R.M. A Perspective on Nonstationarity and Water Management. J. Am. Water Resour. Assoc. 2011, 47, 436–446. [Google Scholar] [CrossRef]
- Milly, P.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Kundzewicz, Z.W.; Lettenmaier, D.P.; Stouffer, R.J. Stationarity Is Dead: Whither Water Management? Science 2008, 4, 20. [Google Scholar] [CrossRef] [PubMed]
- Zhao, T.; Zhao, J. Joint and respective effects of long- and short-term forecast uncertainties on reservoir operations. J. Hydrol. 2014, 517, 83–94. [Google Scholar] [CrossRef]
- García-Pintado, J.; Mason, D.C.; Dance, S.L.; Cloke, H.L.; Neal, J.C.; Freer, J.; Bates, P.D. Satellite-supported flood forecasting in river networks: A real case study. J. Hydrol. 2015, 523, 706–724. [Google Scholar] [CrossRef]
- Shiri, J.; KïSï, O. Short-term and long-term streamflow forecasting using a wavelet and neuro-fuzzy conjunction model. J. Hydrol. 2010, 394, 486–493. [Google Scholar] [CrossRef]
- Maurer, E.P.; Lettenmaier, D.P. Potential Effects of Long-Lead Hydrologic Predictability on Missouri River Main-Stem Reservoirs. J. Clim. 2004, 17, 174–186. [Google Scholar] [CrossRef]
- Anghileri, D.; Voisin, N.; Castelletti, A.; Pianosi, F.; Nijssen, B.; Lettenmaier, D.P. Value of long-term streamflow forecasts to reservoir operations for water supply in snow-dominated river catchments. Water Resour. Res. 2016, 52, 4209–4225. [Google Scholar] [CrossRef]
- Raso, L.; Schwanenberg, D.; Giesen, N.C.V.D.; Overloop, P.J.V. Short-term optimal operation of water systems using ensemble forecasts. Adv. Water Resour. 2014, 71, 200–208. [Google Scholar] [CrossRef]
- Valeriano, O.C.S.; Koike, T.; Yang, K.; Graf, T.; Xin, L.; Lei, W.; Han, X. Decision support for dam release during floods using a distributed biosphere hydrological model driven by quantitative precipitation forecasts. Water Resour. Res. 2010, 46, W10544. [Google Scholar]
- Georgakakos, A.P.; Yao, H.; Kistenmacher, M.; Georgakakos, K.P.; Graham, N.E.; Cheng, F.Y.; Spencer, C.; Shamir, E. Value of adaptive water resources management in Northern California under climatic variability and change: Reservoir management. J. Hydrol. 2012, 412, 34–46. [Google Scholar] [CrossRef]
- Schwanenberg, D.; Fan, F.M.; Naumann, S.; Kuwajima, J.I.; Montero, R.A.; Dos Reis, A.A. Short-term reservoir optimization for flood mitigation under meteorological and hydrological forecast uncertainty. Water Resour. Manag. 2015, 29, 1635–1651. [Google Scholar] [CrossRef]
- Pianosi, F.; Soncini Sessa, R. Real-time management of a multipurpose water reservoir with a heteroscedastic inflow model. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Hsu, N.S.; Wei, C.C. A multipurpose reservoir real-time operation model for flood control during typhoon invasion. J. Hydrol. 2007, 336, 282–293. [Google Scholar] [CrossRef]
- Yan, B.; Guo, S.; Chen, L. Estimation of reservoir flood control operation risks with considering inflow forecasting errors. Stoch. Environ. Res. Risk Assess. 2014, 28, 359–368. [Google Scholar] [CrossRef]
- Faber, B. Forecast-based flood control operation at Folsom reservoir using advance release. In Proceedings of the Using Precipitation and Pineapple Express Forecasts to Operate Folsom Dam and Reservoir, Rocklin, CA, USA, 22 June 2001. [Google Scholar]
- Chou, N.F.; Wu, C.W. Expected shortage based pre-release strategy for reservoir flood control. J. Hydrol. 2013, 497, 1–14. [Google Scholar] [CrossRef]
- Li, X.; Guo, S.; Liu, P.; Chen, G. Dynamic control of flood limited water level for reservoir operation by considering inflow uncertainty. J. Hydrol. 2010, 391, 124–132. [Google Scholar] [CrossRef]
- Zhou, Y.; Guo, S.; Liu, P.; Xu, C. Joint operation and dynamic control of flood limiting water levels for mixed cascade reservoir systems. J. Hydrol. 2014, 519, 248–257. [Google Scholar] [CrossRef]
- Zhao, T.; Zhao, J.; Lund, J.R.; Yang, D. Optimal Hedging Rules for Reservoir Flood Operation from Forecast Uncertainties. J. Water Res. Plan. Manag. 2014, 140, 4014041. [Google Scholar] [CrossRef]
- Hui, R.; Lund, J.; Zhao, J.; Zhao, T. Optimal Pre-storm Flood Hedging Releases for a Single Reservoir. Water Resour. Manag. 2016, 30, 5113–5129. [Google Scholar] [CrossRef]
- Ding, W.; Zhang, C.; Peng, Y.; Zeng, R.; Zhou, H.; Cai, X. An analytical framework for flood water conservation considering forecast uncertainty and acceptable risk. Water Resour. Res. 2015, 51, 4702–4726. [Google Scholar] [CrossRef]
- Ding, W.; Zhang, C.; Cai, X.; Li, Y.; Zhou, H. Multiobjective hedging rules for flood water conservation. Water Resour. Res. 2017, 53, 1963–1981. [Google Scholar] [CrossRef]
- Zhao, T.; Cai, X.; Yang, D. Effect of streamflow forecast uncertainty on real-time reservoir operation. Adv. Water Resour. 2011, 34, 495–504. [Google Scholar] [CrossRef]
- Boucher, M.A.; Tremblay, D.; Delorme, L.; Perreault, L.; Anctil, F. Hydro-economic assessment of hydrological forecasting systems. J. Hydrol. 2012, 416, 133–144. [Google Scholar] [CrossRef]
- Galelli, S.; Goedbloed, A.; Schwanenberg, D.; Overloop, P.J.V. Optimal Real-Time Operation of Multipurpose Urban Reservoirs: Case Study in Singapore. J. Water Res. Plan. Manag. 2014, 140, 511–523. [Google Scholar] [CrossRef]
- Lettenmaier, D.P. Synthetic Streamflow Forecast Generation. J. Hydraul. Eng. 1984, 110, 277–289. [Google Scholar] [CrossRef]
- Connaughton, J.; King, N.; Dong, L.; Ji, P.; Lund, J. Comparing Simple Flood Reservoir Operation Rules. Water 2014, 6, 2717–2731. [Google Scholar] [CrossRef]
- Jiang, Z.; Sun, P.; Ji, C.; Zhou, J. Credibility theory based dynamic control bound optimization for reservoir flood limited water level. J. Hydrol. 2015, 529, 928–939. [Google Scholar] [CrossRef]
- Tan, Q.; Wang, X.; Liu, P.; Lei, X.; Cai, S.; Wang, H.; Ji, Y. The dynamic control bound of flood limited water level considering capacity compensation regulation and flood spatial pattern uncertainty. Water Resour. Manag. 2017, 31, 143–158. [Google Scholar] [CrossRef]
- Bobée, B.; Cavadias, G.; Ashkar, F.; Bernier, J.; Rasmussen, P. Towards a systematic approach to comparing distributions used in flood frequency analysis. J. Hydrol. 1993, 142, 121–136. [Google Scholar] [CrossRef]
- Maurer, E.P. Predictability of seasonal runoff in the Mississippi River basin. J. Geophys. Res. Atmos. 2003, 108, D16. [Google Scholar] [CrossRef]
- Shukla, S.; Lettenmaier, D.P. Seasonal hydrologic prediction in the United States: Understanding the role of initial hydrologic conditions and seasonal climate forecast skill. Hydrol. Earth Syst. Sci. 2011, 15, 3529–3538. [Google Scholar] [CrossRef]
- Shi, X.; Wood, A.W.; Lettenmaier, D.P. How Essential is Hydrologic Model Calibration to Seasonal Streamflow Forecasting? J. Hydrometeorol. 2008, 9, 1350–1363. [Google Scholar] [CrossRef]
- Khaliq, M.N.; Ouarda, T.B.M.J.; Ondo, J.C.; Gachon, P.; Bobée, B. Frequency analysis of a sequence of dependent and/or non-stationary hydro-meteorological observations: A review. J. Hydrol. 2006, 329, 534–552. [Google Scholar] [CrossRef]
- Romanescu, G.; Stoleriu, C.; Romanescu, A.M. Water reservoirs and the risk of accidental flood occurrence. Case study: Stanca-Costesti reservoir and the historical floods of the Prut river in the period July–August 2008, Romania. Hydrol. Process. 2011, 25, 2056–2070. [Google Scholar] [CrossRef]
- Vicuna, S.; Dracup, J.A.; Lund, J.R.; Dale, L.L.; Maurer, E.P. Basin-scale water system operations with uncertain future climate conditions: Methodology and case studies. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Zhao, T.; Zhao, J. Forecast-skill-based simulation of streamflow forecasts. Adv. Water Resour. 2014, 71, 55–64. [Google Scholar] [CrossRef]
- Jiang, S.H.; Fan, Z.W. Risk analysis for flood control operation of reservoir. J. Hydraul. Eng. 2004, 35, 102–107. [Google Scholar]
- Kelly, K.S.; Krzysztofowicz, R. A bivariate meta-Gaussian density for use in hydrology. Stoch. Hydrol. Hydraul. 1997, 11, 17–31. [Google Scholar] [CrossRef]
- Montanari, A. Deseasonalisation of hydrological time series through the normal quantile transform. J. Hydrol. 2005, 313, 274–282. [Google Scholar] [CrossRef]
- Singh, V.P.; Chow, V.T. Handbook of Applied Hydrology, 2nd ed.; Mcgraw-Hill Education: New York, NY, USA, 2016. [Google Scholar]
- Markar, M.S.; Clark, S.Q.; Min, Y.; Jing, Z. Evaluation of hydrologic and hydraulic models for real-time flood forecasting use in the Yangtze River catchment. Australas. J. Water Resour. 2006, 10, 93–102. [Google Scholar] [CrossRef]
- Guo, S.; Li, X.; Liu, X.; Dai, M. Key Technologies for the Dyamic Control of the Flood Limited Water Level of Three Gorges Reservoir; China Water and Power Press: Beijing, China, 2011. [Google Scholar]
- Wang, Y.C.; Yoshitani, J.; Fukami, K. Stochastic multiobjective optimization of reservoirs in parallel. Hydrol. Process. 2005, 19, 3551–3567. [Google Scholar] [CrossRef]
- Turgeon, A. Solving a stochastic reservoir management problem with multilag autocorrelated inflows. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Sharma, A.; Tarboton, D.G.; Lall, U. Streamflow simulation: A nonparametric approach. Water Resour. Res. 1997, 2, 291–308. [Google Scholar] [CrossRef]
- Chiu, C. Stochastic methods in hydraulics and hydrology of streamflow. Geophys. Surv. 1972, 1, 61–84. [Google Scholar] [CrossRef]
- Liu, P.; Li, L.; Guo, S.; Xiong, L.; Zhang, W.; Zhang, J.; Xu, C. Optimal design of seasonal flood limited water levels and its application for the Three Gorges Reservoir. J. Hydrol. 2015, 527, 1045–1053. [Google Scholar] [CrossRef]
- Grimaldi, S.; Serinaldi, F. Asymmetric copula in multivariate flood frequency analysis. Adv. Water Resour. 2006, 29, 1155–1167. [Google Scholar] [CrossRef]
- Yue, S.; Ouarda, T.B.; Bobée, B.; Legendre, P.; Bruneau, P. Approach for describing statistical properties of flood hydrograph. J. Hydrol. Eng. 2002, 7, 147–153. [Google Scholar] [CrossRef]
- Dingman, S.L. Drainage density and streamflow: A closer look. Water Resour. Res. 1978, 14, 1183–1187. [Google Scholar] [CrossRef]
- Nash, J.E. Systematic determination of unit hydrograph parameters. J. Geophys. Res. Atmos. 1959, 64, 111–115. [Google Scholar] [CrossRef]
- Swain, R.E.; England, J.F.; Bullard, K.L.; Raff, D.A. Guidelines for Evaluating Hydrologic Hazards; US Department of the Interior, Bureau of Reclamation: Washington, DC, USA, 2006. [Google Scholar]








| Flood Period (day) | CV | CS/CV | |||
|---|---|---|---|---|---|
| 1 day | 44.06 | 0.21 | 4 | 57.18 | 83.9 |
| 2 day | 86.63 | 0.21 | 4 | 222.47 | 165.0 |
| 3 day | 127.32 | 0.21 | 4 | 483.26 | 242.6 |
| 5 day | 202.18 | 0.19 | 3.5 | 1203.12 | 359.7 |
| Flood Frequency | 1 day | 2 day | 3 day | 5 day |
|---|---|---|---|---|
| ≥0.1% | 9 | 5 | 6 | 3 |
| <0.1% | 9 | 1 | 1 | 0 |
| <0.2% | 34 | 21 | 17 | 27 |
| <1% | 615 | 669 | 529 | 719 |
| <10% | 4123 | 4053 | 4196 | 3828 |
| <50% | 5210 | 5251 | 5251 | 5423 |
| Selected Forecast Floods | Maximum Period Flood Volume Forecasts (108 m3) | |||
|---|---|---|---|---|
| 1 day | 2 day | 3 day | 5 day | |
| F1 | 84.72 | 168.09 | 244.80 | 340.02 |
| F2 | 80.78 | 155.87 | 232.18 | 335.99 |
| F3 | 75.03 | 130.80 | 194.00 | 304.11 |
| F4 | 69.05 | 132.57 | 181.96 | 267.20 |
| F5 | 65.01 | 117.84 | 175.56 | 256.68 |
| F6 | 60.03 | 118.89 | 169.69 | 281.87 |
| F7 | 55.01 | 95.66 | 125.02 | 198.59 |
| F8 | 50.02 | 89.55 | 120.64 | 190.31 |
| F9 | 44.89 | 82.27 | 117.81 | 187.98 |
| F10 | 40.48 | 73.47 | 104.33 | 157.53 |
| F11 | 35.24 | 67.66 | 98.76 | 158.68 |
| F12 | 30.63 | 57.27 | 85.05 | 138.02 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, W.; Lei, X.; Zhao, J.; Wang, M.; Khu, S.-T.; Wang, C. A Forecast-Skill-Based Dynamic Pre-Storm Level Control for Reservoir Flood-Control Operation. Water 2021, 13, 556. https://doi.org/10.3390/w13040556
Wan W, Lei X, Zhao J, Wang M, Khu S-T, Wang C. A Forecast-Skill-Based Dynamic Pre-Storm Level Control for Reservoir Flood-Control Operation. Water. 2021; 13(4):556. https://doi.org/10.3390/w13040556
Chicago/Turabian StyleWan, Wenhua, Xiaohui Lei, Jianshi Zhao, Mingna Wang, Soon-Thiam Khu, and Chao Wang. 2021. "A Forecast-Skill-Based Dynamic Pre-Storm Level Control for Reservoir Flood-Control Operation" Water 13, no. 4: 556. https://doi.org/10.3390/w13040556
APA StyleWan, W., Lei, X., Zhao, J., Wang, M., Khu, S.-T., & Wang, C. (2021). A Forecast-Skill-Based Dynamic Pre-Storm Level Control for Reservoir Flood-Control Operation. Water, 13(4), 556. https://doi.org/10.3390/w13040556









