Evaluation of Groundwater Potential and Safe Yield of Heterogeneous Unconsolidated Aquifers in Chiang Mai Basin, Northern Thailand
Abstract
:1. Introduction
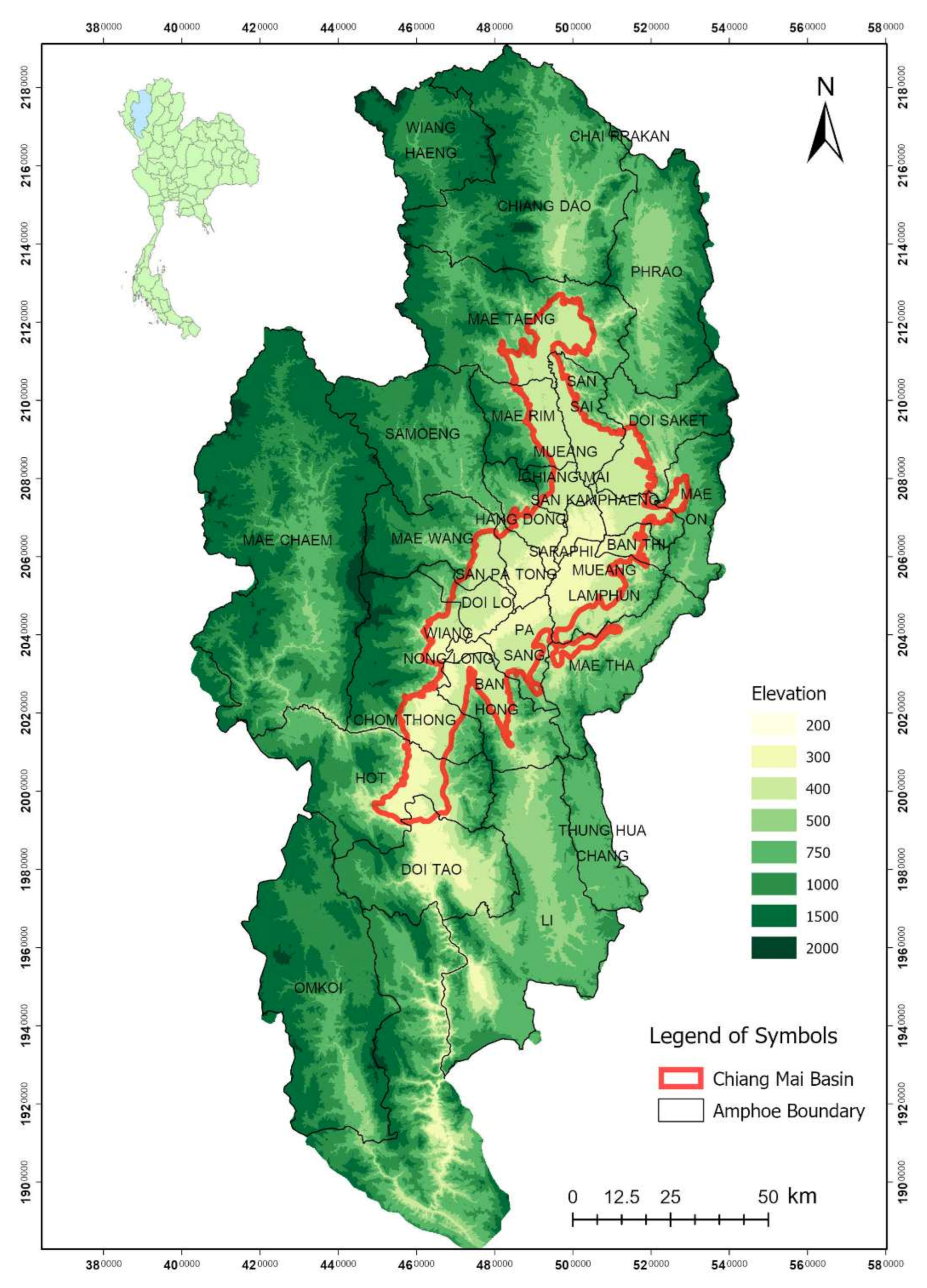
2. General Information of the Study Area and Previous Studies
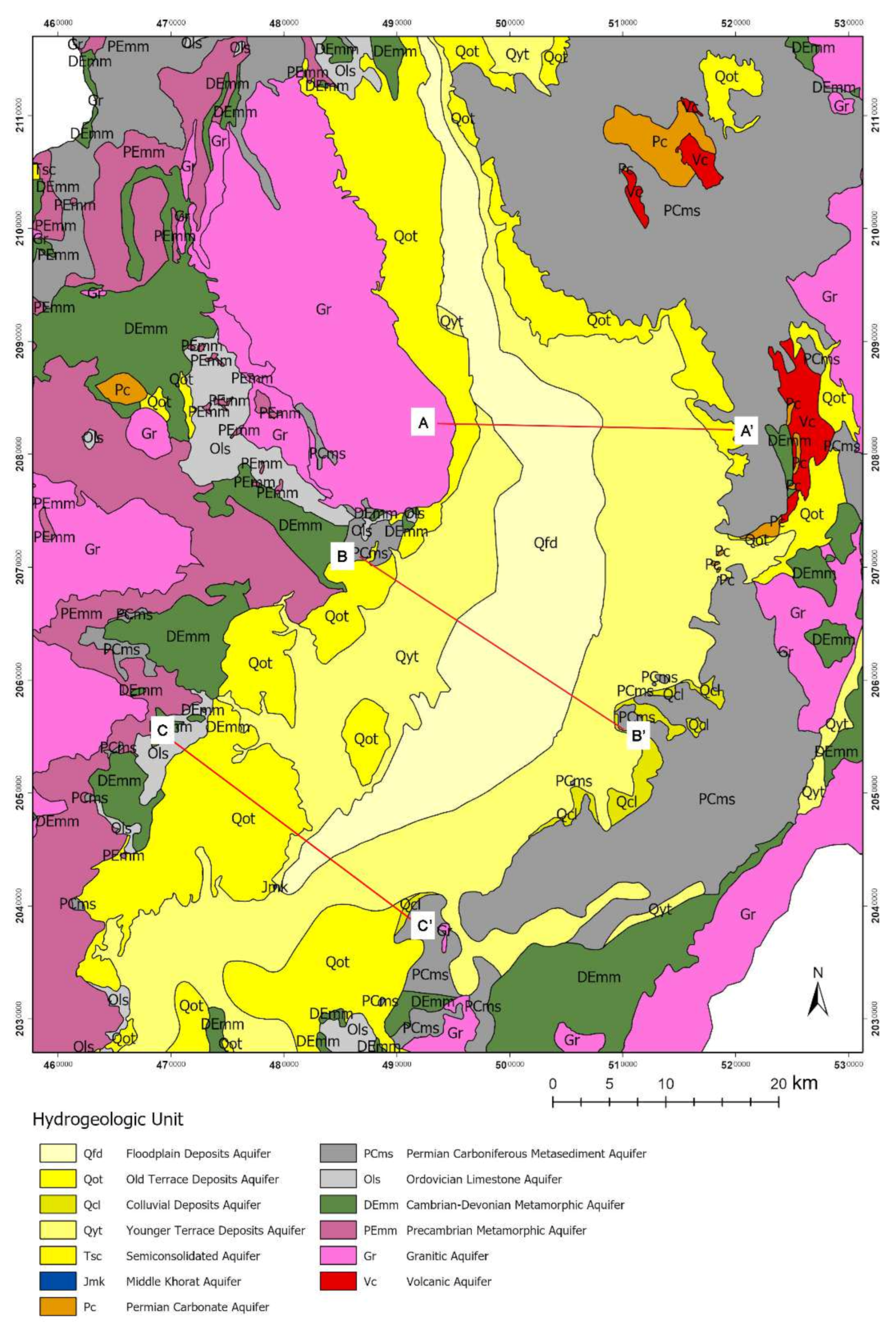
2.1. Hydrogeologic Settings
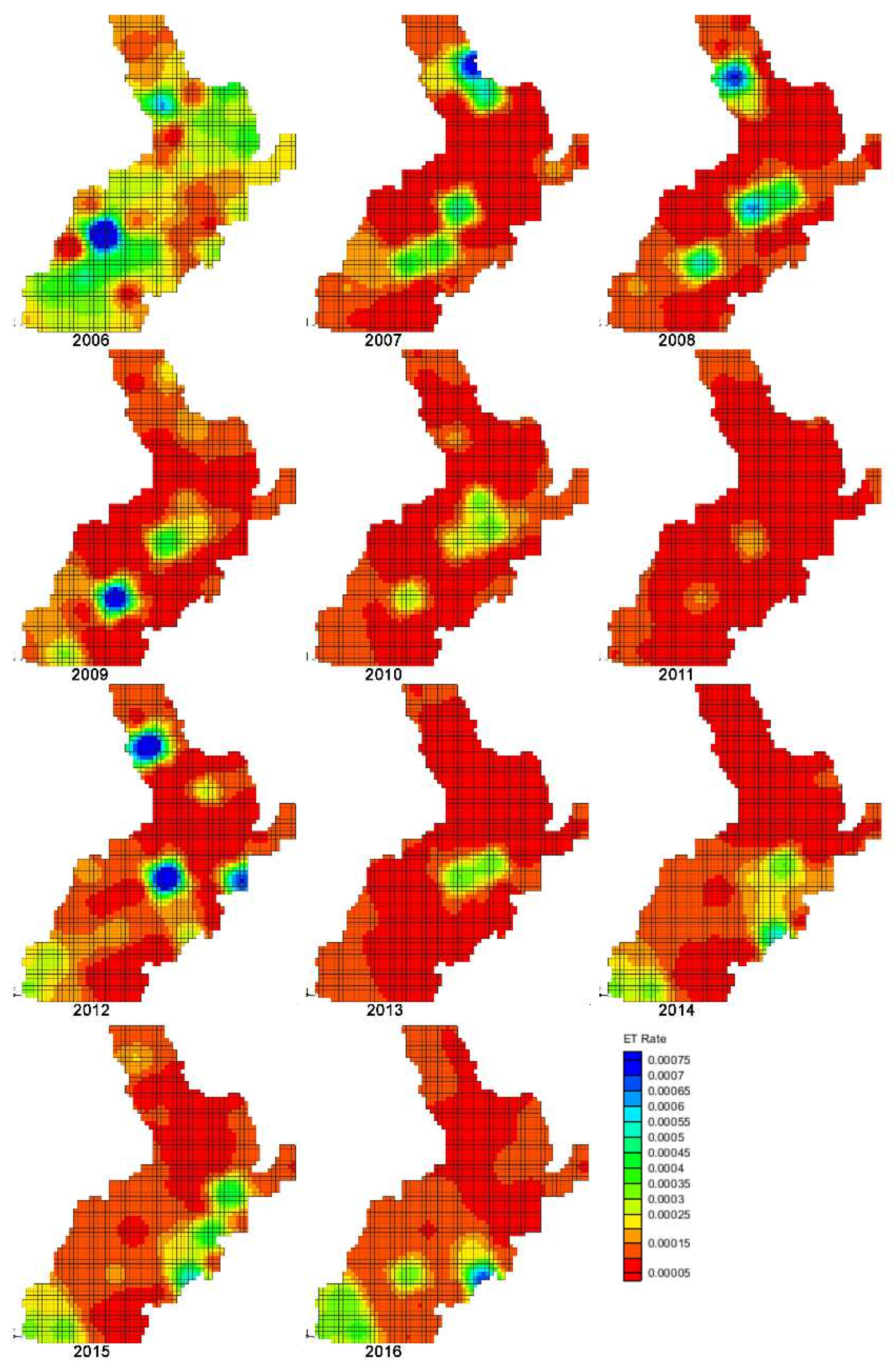
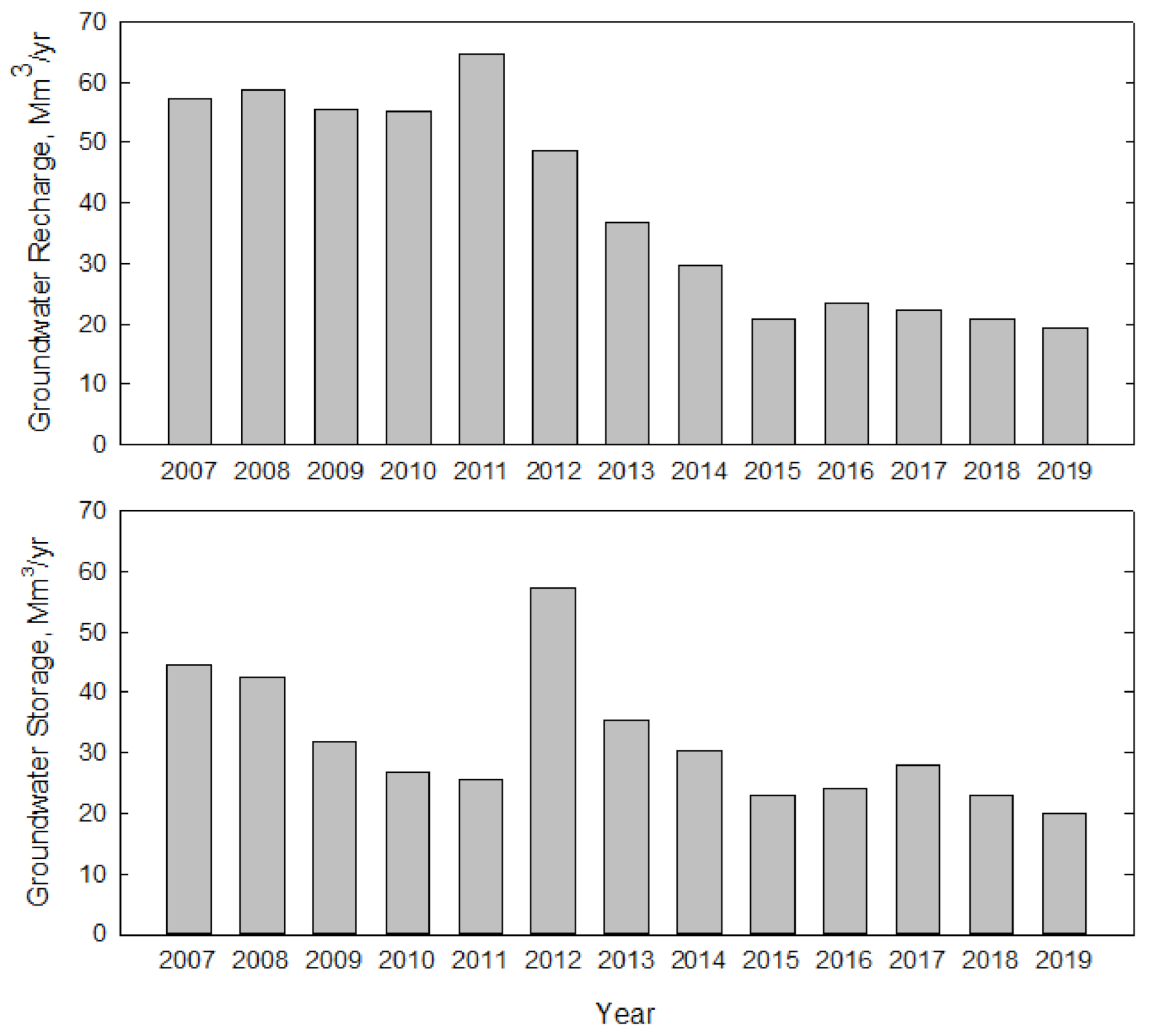
2.2. Groundwater Recharge
2.3. Previous Groundwater Modeling Studies
3. Materials and Methods
3.1. Conceptual Model Setup: Hydrostratigraphic Units and Hydraulic Properties of the Aquifers
3.2. Hydraulic Head Measurements and River Discharges and Stages Data
3.3. Groundwater Wells
3.4. Numerical Model Simulation
3.5. Model Calibration
4. Results and Discussion
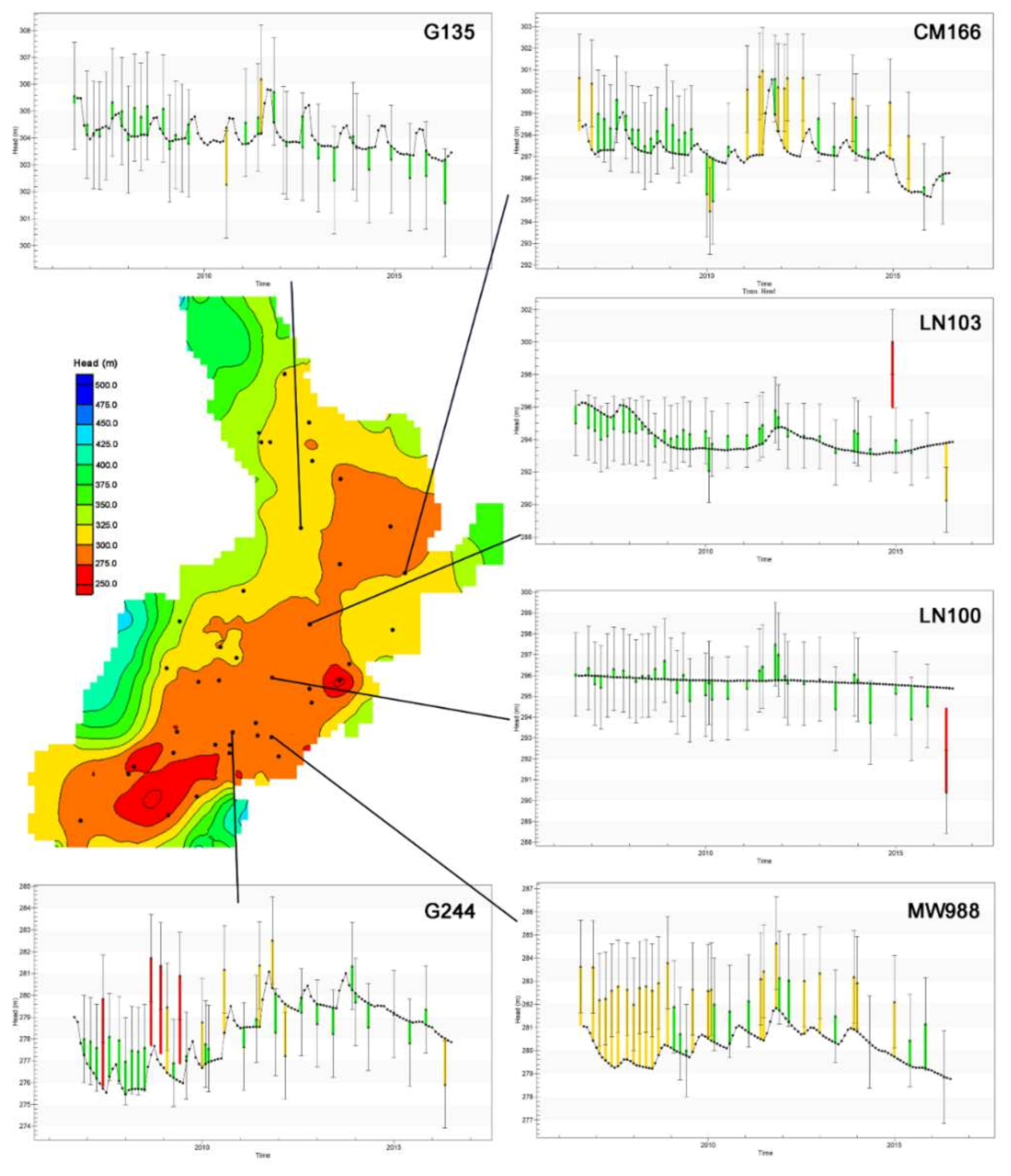
4.1. Steady-State and Transient Model Calibration
4.2. Model Validation
4.3. Groundwater Potential of the Unconsolidated Aquifers
4.4. Evaluating Groundwater Safe Yield in Unconsolidated Aquifers
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Department of Groundwater Resources (DGR). Thailand’s Conjunctive Groundwater and Surface Water Use Planning: Northern Thailand; Final Report; Department of Groundwater Resources: Bangkok, Thailand, 2010. [Google Scholar]
- Department of Groundwater Resources (DGR). The State of Groundwater Annual Report: Thailand Groundwater Monitoring Networks Project; Final Report; Department of Groundwater Resources: Bangkok, Thailand, 2013. [Google Scholar]
- Department of Groundwater Resources (DGR). The State of Groundwater Annual Report: Thailand Groundwater Monitoring Networks Project; Final Report; Department of Groundwater Resources: Bangkok, Thailand, 2018. [Google Scholar]
- Department of Groundwater Resources (DGR). Groundwater and Environmental Development and Conservation Master Plan; Final Report; Department of Groundwater Resources: Bangkok, Thailand, 2012. [Google Scholar]
- Intasutra, T. Groundwater potential in unconsolidated sediments in Chiang Mai basin. In Proceedings of the First Symposium on Geomorphology and Quaternary Geology of Thailand, Bangkok, Thailand, 28–29 October 1983; pp. 179–195. [Google Scholar]
- Department of Groundwater Resources (DGR). Groundwater Resources Assessment of the Chiang Mai, Upper Chao Phraya, and Mae Klong Basins; Final Report; Department of Groundwater Resources: Bangkok, Thailand, 2005. [Google Scholar]
- Doherty, J. PEST, Model-Independent Parameter Estimation-User Manual, 5th ed.; Watermark Numerical Computing: Brisbane, Australia, 2014. [Google Scholar]
- Doherty, J.; Hunt, R.J. Approaches to Highly Parameterized Inversion: A Guide to Using PEST for Groundwater-Model Calibration: U.S. Geological Survey Scientific Investigations Report 2010-5169; U.S. Geological Survey: Reston, VA, USA, 2010. [Google Scholar]
- Margane, A.; Tatong, T. Aspects of the hydrogeology of the Chiang Mai-Lamphun basin, Thailand that are Important for the Groundwater Management. Z. Angew. Geol. 1999, 45, 188–197. [Google Scholar]
- Wattananikorn, K.; Beshir, J.A.; Nochaiwong, A. Gravity interpretation of Chiang Mai basin, northern Thailand: Concentrating on Ban Thung Sieo area. J. SE Asian Earth Sci. 1995, 12, 53–64. [Google Scholar] [CrossRef]
- Asnachinda, P. Hydrogeochemistry of the Chiang Mai basin, northern Thailand. J. Asian Earth Sci. 1997, 15, 317–326. [Google Scholar] [CrossRef]
- Ridd, M.R.; Barber, A.J.; Crow, M.J. The Geology of Thailand; Geological Society: London, UK, 2011. [Google Scholar]
- Suvagondha, F. Hydrogeology of Amphoe Muang Lamphun. Master’s Thesis, Chiang Mai University, Chiang Mai, Thailand, 1979. [Google Scholar]
- Kiwduangta, B. Hydrostratigraphic Model of the Shallow Aquifer in the Vicinity of the Northern Region Industrial Estate Area, Lamphun Province. Master’s Thesis, Chiang Mai University, Chiang Mai, Thailand, 2012. [Google Scholar]
- Wongpornchai, P. Hydrogeology of the Western Part of Chiang Mai Basin: Amphoe Mae Rim, Amphoe Muang and Amphoe Hang Dong, Chiang Mai. Master’s Thesis, Chiang Mai University, Chiang Mai, Thailand, 1990. [Google Scholar]
- Tatong, T. Assessment of Available Groundwater Resources in the Chiang Mai Basin, Northern Thailand. Master’s Thesis, University of Birmingham, Birmingham, UK, 2000. [Google Scholar]
- Uppasit, S. Groundwater Recharge Calculation of Chiang Mai Basin Using Water-Table Fluctuation Method. Master’s Thesis, Chiang Mai University, Chiang Mai, Thailand, 2004. [Google Scholar]
- Saenton, S. Applications of Stochastic Process and Inverse Modeling Technique in Groundwater Modeling of the Chiang Mai Basin, Thailand Research Fund; Final Report; Thailand Research Fund: Bangkok, Thailand, 2010. [Google Scholar]
- Harbaugh, A.W. MODFLOW-2005, the U.S. Geological Survey Modular Groundwater Model: The Ground-Water Flow Process; U.S. Geological Survey Techniques and Methods 6-A16; US Department of the Interior: Reston, VA, USA, 2005. [Google Scholar]
- Hill, M.C.; Tiedeman, C.R. Effective Groundwater Model Calibration, with Analysis of Sensitivity, Predictions and Uncertainty; Wiley: New York, NY, USA, 2007. [Google Scholar]
- Doherty, J. Ground water model calibration using pilot points and regularization. Ground Water 2003, 41, 170–177. [Google Scholar] [CrossRef] [PubMed]
- Anderson, M.P.; Woessner, W.W.; Hunt, R.J. Applied Groundwater Modeling: Simulation of Flow and Advective Transport, 2nd ed.; Elsevier Inc.: London, UK, 2015. [Google Scholar]













| Hydrostratigraphic Units | K (m/d) | S (-) |
|---|---|---|
| Floodplain, Qfd | 0.015–18 | 0.0166–0.299 |
| Low Terrace, Qyt | 0.035–30 | 0.0153–0.204 |
| High Terrace, Qot (+Qcl) | 0.043–63 | 0.0170–0.233 |
| Semi- to consolidated aquifers (below Q’s) | 0.12–13.5 | 1.5 × 10−5–0 × 10−4 |
| Parameter Types | Parameter Name | Initial Values | Note | ||
|---|---|---|---|---|---|
| Hydraulic conductivity b (m/d) | Qfd | HK1 | 0.015–18 |  | Pilot points a (Layers 1–4) |
| Qyt | HK2 | 0.035–30 m/d | |||
| Qot | HK3 | 0.043–63 m/d | |||
| Lower aquifers | HK4 | 0.12–13.5 m/d | |||
| Storage coefficient b | Qfd | SS1 (m−1) SY1 (-) | 5.4 × 10−5–1.2 × 10−4 0.0166–0.2496 | ||
| Qyt | SS2 (m−1) SY2 (-) | 3.1 × 10−5–6.7 × 10−4 0.01532–0.1927 | |||
| Qot | SS3 (m−1) SY3 (-) | 1.8 × 10−5–4.2 × 10−4 0.01703–0.2328 | |||
| Lower aquifers | SS4 (m−1) | 1.5 × 10−5–2.0 × 10−4 | |||
| Vertical anisotropy | All units | VANI | 0.1 | - | |
| Recharge rate (mm/y) | - | RCH | 28–112 |  | Pilot points a (Layer 1) |
| Max ET rate (mm/y) | - | EVT | 88–147 | ||
| North and south GHB conductance factors | - | GHB | 0.25 m2/m/d | - | |
| River-bed conductance factors | Ping rivers | RIV_1 | 0.25 m2/m/d | - | |
| Kuang rivers | RIV_2 | 0.25 m2/m/d | - | ||
| Parameter Types | Final Parameter Values | Parameter Sensitivity | ||
|---|---|---|---|---|
| Geometric Mean | Min-Max | |||
| Hydraulic conductivity (m/d) | Qfd | 0.0469 | 0.0051–0.19 | 1.07 |
| Qyt | 0.1050 | 0.0187–2.48 | 1.78 | |
| Qot | 0.1748 | 0.0016–6.77 | 1.64 | |
| Lower aquifer | 0.1059 | 0.0003–0.42 | 0.23 | |
| Specific storage (m−1) | Qfd | 0.00026 | 1.03 × 10−6–1.60 × 10−4 | 1.22 × 10−2 |
| Qyt | 0.0002 | 4.36 × 10−6–1.31 × 10−4 | 4.76 × 10−2 | |
| Qot | 0.0001 | 1.78 × 10−6–1.82 × 10−4 | 2.37 × 10−2 | |
| Lower aquifer | 0.0003 | 2.11 × 10−6–2.17 × 10−4 | 9.60 × 10−4 | |
| Specific yield (-) | Qfd | 0.0294 | 3.37 × 10−2–0.20 | 3.32 × 10−3 |
| Qyt | 0.0029 | 6.75 × 10−2–0.10 | 8.77 × 10−3 | |
| Qot | 0.0112 | 8.35 × 10−2–0.11 | 4.32 × 10−3 | |
| Lower aquifer | n/a | - | ||
| Recharge rate (mm/y) | - | 56.5 | 0.041–289.62 | 0.71 |
| Maximum ET Rate (mm/y) | - | 37.3206 | 7.02–188.23 | 0.66 |
| Riverbed conductance factor (m2/m/d) | Ping | 0.4517 | 0.37–0.51 | 0.12 |
| Kuang | 0.4528 | 0.44–0.47 | 0.17 | |
| General-head conductance factor (m2/m/d) | North | 0.4417 | 4.11 × 10−3 | |
| South | 0.3352 | 8.32 × 10−3 | ||
| Scenario | Targeted Average Drawdown (m) | Safe Yield or Pumping Rate of Qfd, Qyt, and Qot + Qcl Aquifers (Mm3/y) | % Increase from Current Usage |
|---|---|---|---|
| Base Case | - | 24.0 (2015) | - |
| Case 1 | 1.0 | 41.6 | 73 |
| Case 2 | 2.0 | 51.2 | 114 |
| Case 3 | 3.0 | 54.1 | 125 |
| Case 4 | 4.0 | 54.9 | 129 |
| Case 5 | 5.0 | 55.4 | 131 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taweelarp, S.; Khebchareon, M.; Saenton, S. Evaluation of Groundwater Potential and Safe Yield of Heterogeneous Unconsolidated Aquifers in Chiang Mai Basin, Northern Thailand. Water 2021, 13, 558. https://doi.org/10.3390/w13040558
Taweelarp S, Khebchareon M, Saenton S. Evaluation of Groundwater Potential and Safe Yield of Heterogeneous Unconsolidated Aquifers in Chiang Mai Basin, Northern Thailand. Water. 2021; 13(4):558. https://doi.org/10.3390/w13040558
Chicago/Turabian StyleTaweelarp, Sutthipong, Morrakot Khebchareon, and Schradh Saenton. 2021. "Evaluation of Groundwater Potential and Safe Yield of Heterogeneous Unconsolidated Aquifers in Chiang Mai Basin, Northern Thailand" Water 13, no. 4: 558. https://doi.org/10.3390/w13040558
APA StyleTaweelarp, S., Khebchareon, M., & Saenton, S. (2021). Evaluation of Groundwater Potential and Safe Yield of Heterogeneous Unconsolidated Aquifers in Chiang Mai Basin, Northern Thailand. Water, 13(4), 558. https://doi.org/10.3390/w13040558








