Evaluation of the WRF Model to Simulate a High-Intensity Rainfall Event over Kampala, Uganda
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Rainfall Observational Data
2.3. WRF Model Setting and Configuration
WRF Parametrization Schemes
2.4. Model Evaluation
2.4.1. Relative Error Index (RE)
2.4.2. Verification Indices
2.4.3. Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS)
3. Results
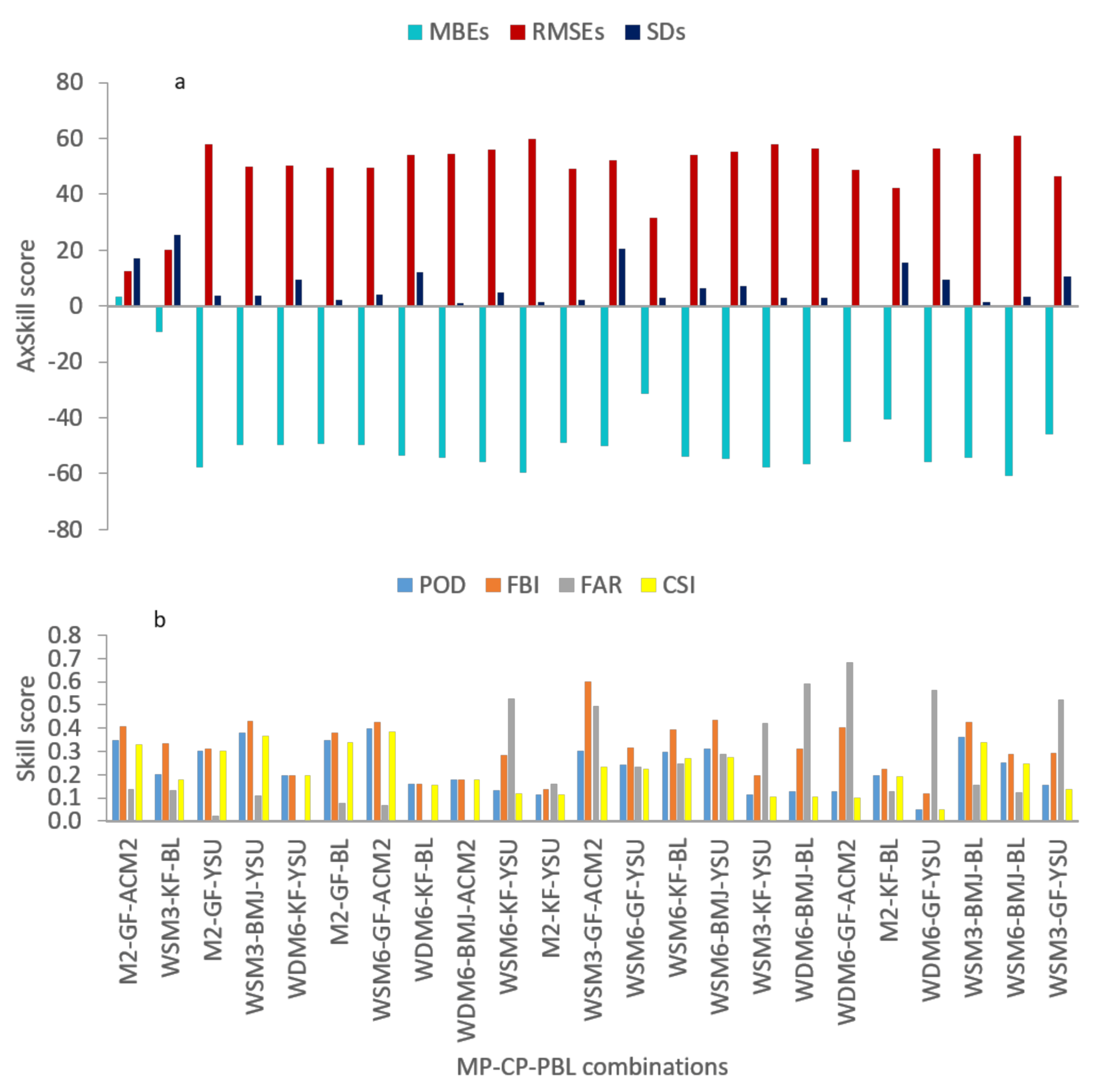
3.1. WRF Performance of the Areal 24-h Accumulated Rainfall
3.2. WRF Performance in the Temporal Dimension at AWS Location
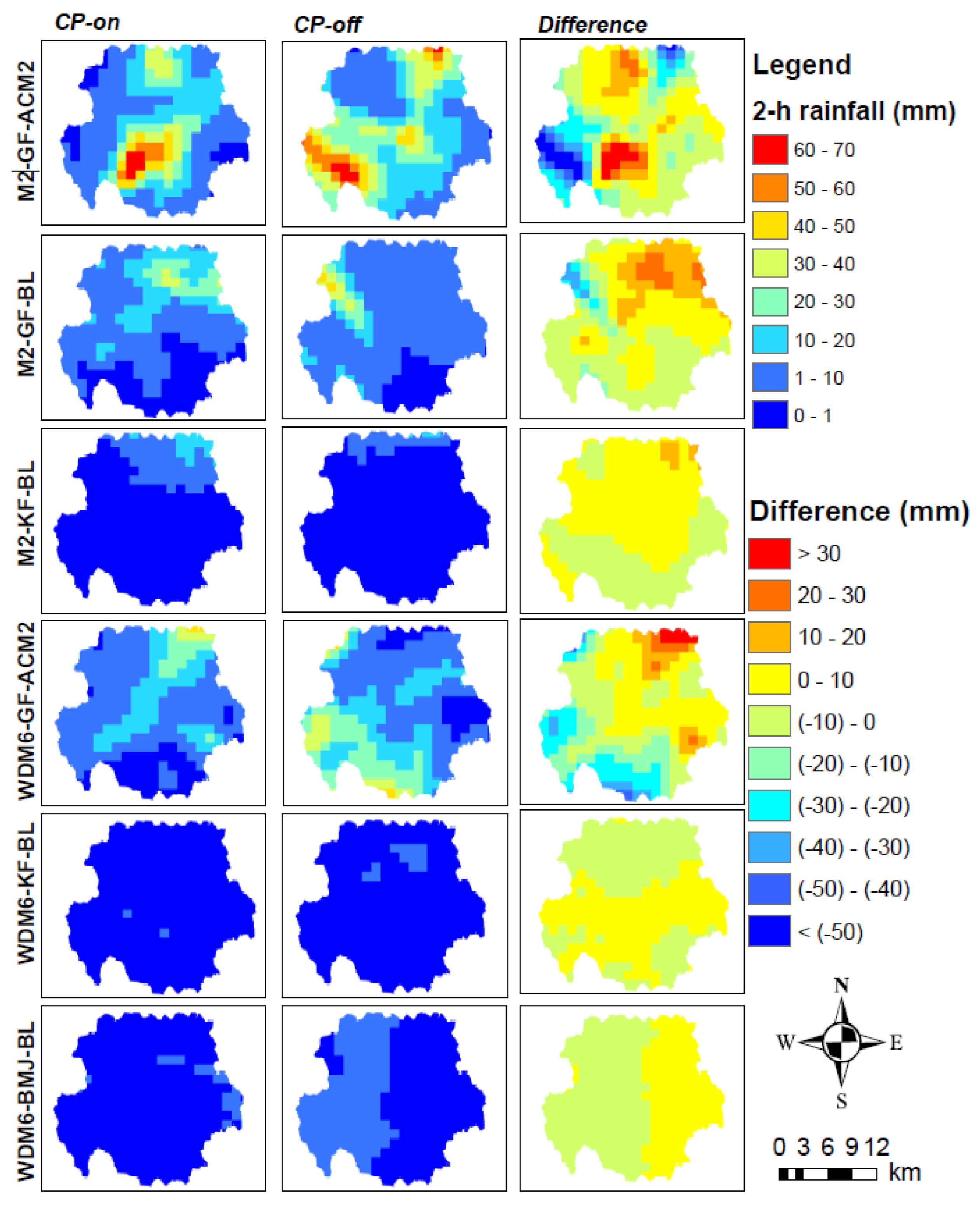
3.3. WRF Performance in the Spatial Dimension
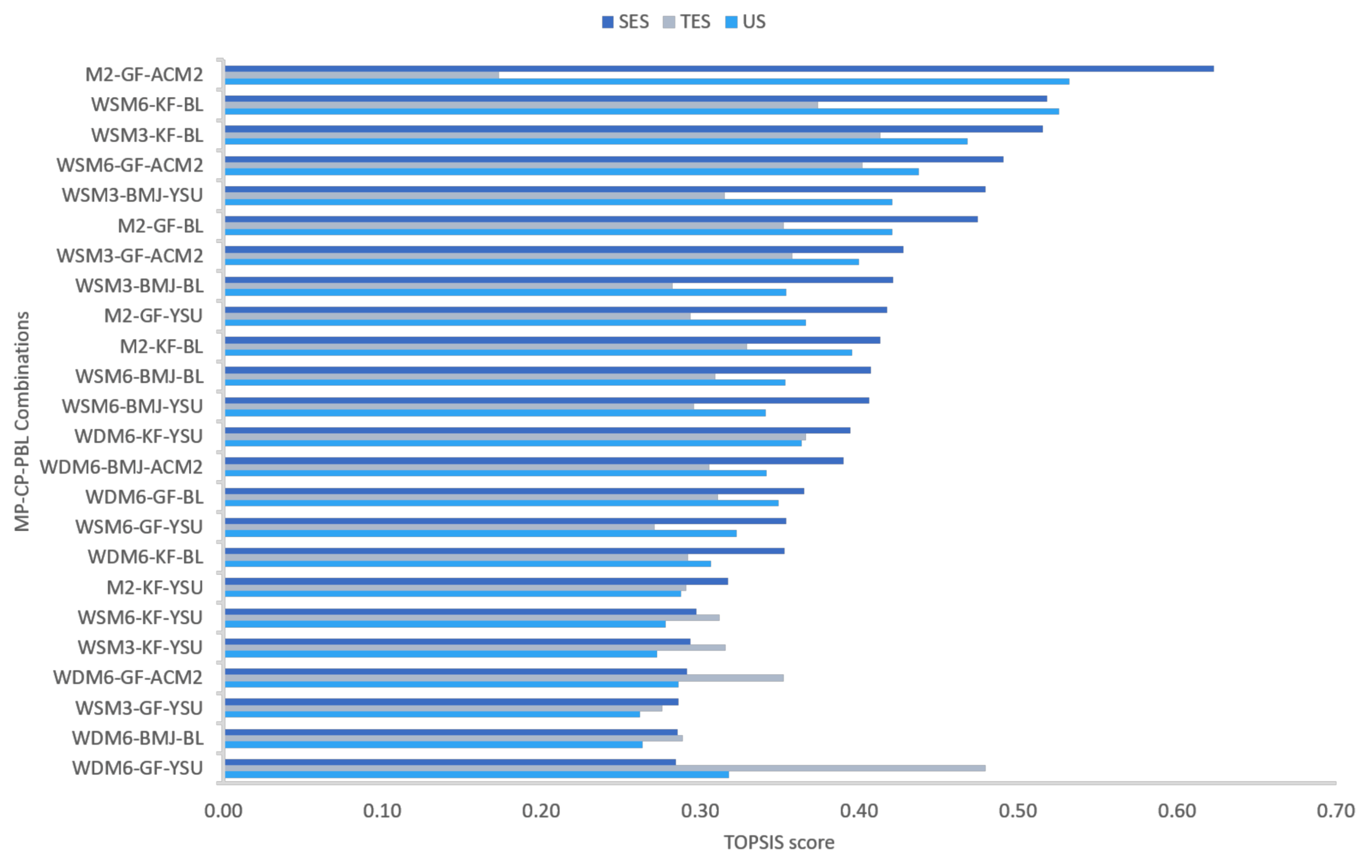
3.4. TOPSIS Analysis
3.5. The Impact of Cumulus Parameterization Schemes on the Simulated Rainfall
3.6. Best Performing Combinations for Localized Flood Modeling
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, J.; Chen, Y.; Wang, H.; Qin, J.; Chiao, S. Extending flood forecasting lead time in a large watershed by coupling WRF QPF with a distributed hydrological model. Hydrol. Earth Syst. Sci. 2017, 21, 1279–1294. [Google Scholar] [CrossRef]
- Braud, I.; Ayral, P.-A.; Bouvier, C.; Branger, F.; Delrieu, G.; Dramais, G.; Le Coz, J.; Leblois, E.; Nord, G.; Vandervaere, J.-P. Advances in flash floods understanding and modelling derived from the FloodScale project in South-East France. E3S Web Conf. 2016, 7, 04005. [Google Scholar] [CrossRef]
- Anyah, R.O. Modeling the Variability of the Climate System over Lake Victoria Basin. Ph.D. Thesis, North Carolina State University, Raleigh, NC, USA, 2005. [Google Scholar]
- Sun, X.; Xie, L.; Semazzi, F.; Liu, B. Effect of lake surface temperature on the spatial distribution and intensity of the precipitation over the Lake Victoria Basin. Mon. Weather Rev. 2015, 143, 1179–1192. [Google Scholar] [CrossRef]
- Paul, S.; Ghosh, S.; Mathew, M.; Devanand, A.; Karmakar, S.; Niyogi, D. Increased spatial variability and intensification of extreme monsoon rainfall due to urbanization. Sci. Rep. 2018, 8, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Powers, J.G.; Klemp, J.B.; Skamarock, W.C.; Davis, C.A.; Dudhia, J.; Gill, D.O.; Coen, J.L.; Gochis, D.J.; Ahmadov, R.; Peckham, S.E.; et al. The weather research and forecasting model: Overview, system efforts, and future directions. Bull. Am. Meteorol. Soc. 2017, 98, 1717–1737. [Google Scholar] [CrossRef]
- Flesch, T.K.; Reuter, G.W. WRF Model simulation of two alberta flooding events and the impact of topography. J. Hydrometeorol. 2012, 13, 695–708. [Google Scholar] [CrossRef]
- Pennelly, C.; Reuter, G.W.; Flesch, T.K. Verification of the WRF model for simulating heavy precipitation in Alberta. Atmos. Res. 2014, 135–136, 172–192. [Google Scholar] [CrossRef]
- Cassola, F.; Ferrari, F.; Mazzino, A. Numerical simulations of Mediterranean heavy precipitation events with the WRF model: A verification exercise using different approaches. Atmos. Res. 2015, 164–165, 210–225. [Google Scholar] [CrossRef]
- Ryu, Y.-H.; Smith, J.A.; Bou-Zeid, E.; Baeck, M.L. The influence of land surface heterogeneities on heavy convective rainfall in the Baltimore–Washington metropolitan area. Mon. Weather Rev. 2016, 144, 553–573. [Google Scholar] [CrossRef]
- Davolio, S.; Mastrangelo, D.; Miglietta, M.M.; Drofa, O.; Buzzi, A.; Malguzzi, P. High resolution simulations of a flash flood near Venice. Nat. Hazards Earth Syst. Sci. 2009, 9, 1671–1678. [Google Scholar] [CrossRef]
- Tian, J.; Liu, J.; Yan, D.; Li, C.; Yu, F. Numerical rainfall simulation with different spatial and temporal evenness by using a WRF multiphysics ensemble. Nat. Hazards Earth Syst. Sci. 2017, 17, 563–579. [Google Scholar] [CrossRef]
- Rodrigo, C.; Kim, S.; Jung, I.H. Sensitivity study of WRF numerical modeling for forecasting heavy rainfall in Sri Lanka. Atmosphere 2018, 9, 378. [Google Scholar] [CrossRef]
- Liu, J.; Bray, M.; Han, D. Sensitivity of the Weather Research and Forecasting (WRF) model to downscaling ratios and storm types in rainfall simulation. Hydrol. Process. 2012, 26, 3012–3031. [Google Scholar] [CrossRef]
- Tan, E. Development of a Methodology for Probable Maximum Precipitation Estimation over the American River Watershed Using The WRF Model. Ph.D. Thesis, University of California, Davis, Davis, CA, USA, 2010. [Google Scholar]
- Argüeso, D.; Hidalgo-Muñoz, J.M.; Gámiz-Fortis, S.R.; Esteban-Parra, M.J.; Dudhia, J.; Castro-Díez, Y. Evaluation of WRF parameterizations for climate studies over Southern Spain using a multistep regionalization. J. Clim. 2011, 24, 5633–5651. [Google Scholar] [CrossRef]
- Sikder, M.S.; Hossain, F. Sensitivity of initial-condition and cloud microphysics to the forecasting of monsoon rainfall in South Asia. Meteorol. Appl. 2018, 25, 493–509. [Google Scholar] [CrossRef]
- Efstathiou, G.; Zoumakis, N.; Melas, D.; Lolis, C.; Kassomenos, P. Sensitivity of WRF to boundary layer parameterizations in simulating a heavy rainfall event using different microphysical schemes. Effect on large-scale processes. Atmos. Res. 2013, 132–133, 125–143. [Google Scholar] [CrossRef]
- Sikder, S.; Hossain, F. Assessment of the weather research and forecasting model generalized parameterization schemes for advancement of precipitation forecasting in monsoon-driven river basins. J. Adv. Model. Earth Syst. 2016, 8, 1210–1228. [Google Scholar] [CrossRef]
- Douglas, I.; Alam, K.; Maghenda, M.; McDonnell, Y.; McLean, L.; Campbell, J. Unjust waters: Climate change, flooding and the urban poor in Africa. Environ. Urban. 2008, 20, 187–205. [Google Scholar] [CrossRef]
- Sliuzas, R.; Flacke, J.; Jetten, V. Modelling Urbanization and Flooding in Kampala, Uganda. In Proceedings of the 14th N-AERUS/GISDECO Conference, Enschede, The Netherlands, 12–14 September 2013; pp. 12–14. [Google Scholar]
- Sliuzas, R.; Jetten, V.; Flacke, J.; Lwasa, S.; Wasige, E.; Pettersen, K. Flood Risk Assessment, Strategies and Actions for Improving Flood Risk Management in Kampala: Final Report of Integrated Flood Management Project Kampala: E-book; University of Twente, Faculty of Geo-Information Science and Earth Observation (ITC): Enschede, The Netherlands, 2013. [Google Scholar]
- Umer, Y.; Jetten, V.; Ettema, J. Sensitivity of flood dynamics to different soil information sources in urbanized areas. J. Hydrol. 2019, 577, 123945. [Google Scholar] [CrossRef]
- Argent, R.; Sun, X.; Semazzi, F.H.M.; Xie, L.; Liu, B. The Development of a customization framework for the WRF model over the Lake Victoria Basin, Eastern Africa on seasonal timescales. Adv. Meteorol. 2015, 2015, 1–15. [Google Scholar] [CrossRef]
- Otieno, G.; Mutemi, J.; Opijah, F.; Ogallo, L.; Omondi, H. The impact of cumulus parameterization on rainfall simulations over East Africa. Atmos. Clim. Sci. 2018, 8, 355–371. [Google Scholar] [CrossRef][Green Version]
- Opio, R.; Sabiiti, G.; Nimusiima, A.; Mugume, I.; Sansa-Otim, J. WRF Simulations of extreme rainfall over Uganda’s Lake Victoria Basin: Sensitivity to parameterization, model resolution and domain size. J. Geosci. Environ. Prot. 2020, 8, 18–31. [Google Scholar] [CrossRef]
- De Luca, D.L.; Biondi, D. Bivariate return period for design hyetograph and relationship with t-year design flood peak. Water 2017, 9, 673. [Google Scholar] [CrossRef]
- Shiau, J.T. Return period of bivariate distributed extreme hydrological events. Stoch. Environ. Res. Risk Assess. 2003, 17, 42–57. [Google Scholar] [CrossRef]
- Kizza, M.; Rodhe, A.; Xu, C.-Y.; Ntale, H.K.; Halldin, S. Temporal rainfall variability in the Lake Victoria Basin in East Africa during the twentieth century. Theor. Appl. Clim. 2009, 98, 119–135. [Google Scholar] [CrossRef]
- Osman, O.E.; Hastenrath, S.L. On the synoptic climatology of summer rainfall over central Sudan. Arch. Meteorol. Geophys. Bioklimatol. Ser. B 1969, 17, 297–324. [Google Scholar] [CrossRef]
- Camberlin, P. Oxford Research Encyclopedia of Climate Science Climate of Eastern Africa Geographical Features Influencing the Region’s Climate; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef]
- Diem, J.E.; Konecky, B.L.; Salerno, J.; Hartter, J. Is equatorial Africa getting wetter or drier? Insights from an evaluation of long-term, satellite-based rainfall estimates for western Uganda. Int. J. Clim. 2019, 39, 3334–3347. [Google Scholar] [CrossRef]
- Cattani, E.; Merino, A.; Guijarro, J.A.; Levizzani, V. East Africa rainfall trends and variability 1983–2015 using three long-term satellite products. Remote. Sens. 2018, 10, 931. [Google Scholar] [CrossRef]
- Wang, W.; Beezley, C.; Duda, M. WRF ARW V3: User’s Guide. 2012. Available online: http://www.mmm.ucar.edu/wrf/users (accessed on 11 January 2013).
- Hersbach, H.; Dee, D. ERA5 reanalysis is in production. ECMWF Newsl. 2016, 147, 5–6. [Google Scholar]
- Moya-Álvarez, A.S.; Gálvez, J.; Holguín, A.; Estevan, R.; Kumar, S.; Villalobos, E.; Martínez-Castro, D.; Silva, Y. Extreme rainfall forecast with the WRF-ARW model in the Central Andes of Peru. Atmosphere 2018, 9, 362. [Google Scholar] [CrossRef]
- Lynn, B.; Khain, A. Utilization of spectral bin microphysics and bulk parameterization schemes to simulate the cloud structure and precipitation in a mesoscale rain event. J. Geophys. Res. Space Phys. 2007, 112, 112. [Google Scholar] [CrossRef]
- Morrison, H.; Pinto, J.O. Intercomparison of bulk cloud microphysics schemes in mesoscale simulations of springtime arctic mixed-phase stratiform clouds. Mon. Weather Rev. 2006, 134, 1880–1900. [Google Scholar] [CrossRef]
- Han, J.-Y.; Hong, S.-Y. Precipitation forecast experiments using the Weather Research and Forecasting (WRF) model at gray-zone resolutions. Weather Forecast. 2018, 33, 1605–1616. [Google Scholar] [CrossRef]
- Hong, S.Y.; Dudhia, J.; Chen, S.H. A revised approach to ice microphysical processes for the bulk parameterization of clouds and precipitation. J. Amer. Met. Soc. 2004, 132, 103–120. [Google Scholar] [CrossRef]
- Hong, S.-Y.; Lim, J.-O.J. The WRF single-moment 6-class microphysics scheme (WSM6). Asia Pac. J. Atmos. Sci. 2006, 42, 129–151. [Google Scholar]
- Ryan, B.F. On the global variation of precipitating layer clouds. Bull. Am. Meteorol. Soc. 1996, 77, 53–70. [Google Scholar] [CrossRef][Green Version]
- Thompson, G.; Field, P.R.; Rasmussen, R.M.; Hall, W.D. Explicit forecasts of winter precipitation using an improved bulk microphysics scheme. Part II: Implementation of a new snow parameterization. Mon. Weather Rev. 2008, 136, 5095–5115. [Google Scholar] [CrossRef]
- Morrison, H.; Thompson, G.; Tatarskii, V. Impact of cloud microphysics on the development of trailing stratiform precipitation in a simulated squall line: Comparison of one- and two-moment schemes. Mon. Weather Rev. 2009, 137, 991–1007. [Google Scholar] [CrossRef]
- Lim, K.-S.S.; Hong, S.-Y. Development of an Effective double-moment cloud microphysics scheme with prognostic Cloud Condensation Nuclei (CCN) for weather and Climate models. Mon. Weather Rev. 2010, 138, 1587–1612. [Google Scholar] [CrossRef]
- Kain, J.S. The Kain–Fritsch convective parameterization: An update. J. Appl. Meteorol. 2004, 43, 170–181. [Google Scholar] [CrossRef]
- Janjić, Z.I. Comments on “Development and evaluation of a convection scheme for use in climate models”. J. Atmos. Sci. 2000, 57, 3686. [Google Scholar] [CrossRef]
- Grell, G.A.; Freitas, S.R. A scale and aerosol aware stochastic convective parameterization for weather and air quality modeling. Atmos. Chem. Phys. Discuss. 2014, 14, 5233–5250. [Google Scholar] [CrossRef]
- Grell, G.A.; Dévényi, D. A generalized approach to parameterizing convection combining ensemble and data assimilation techniques. Geophys. Res. Lett. 2002, 29, 38-1–38-4. [Google Scholar] [CrossRef]
- Hong, S.-Y.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Pleim, J.E. A Combined local and nonlocal closure model for the atmospheric boundary layer. Part I: Model description and testing. J. Appl. Meteorol. Clim. 2007, 46, 1383–1395. [Google Scholar] [CrossRef]
- Bougeault, P.; Lacarrere, P. Parameterization of orography-induced turbulence in a mesobeta-scale model. Mon. Weather Rev. 1989, 117, 1872–1890. [Google Scholar] [CrossRef]
- Dudhia, J. Numerical study of convection observed during the winter monsoon experiment using a mesoscale two-dimensional model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. Atmos. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
- Niu, G.-Y.; Yang, Z.-L.; Mitchell, K.E.; Chen, F.; Ek, M.B.; Barlage, M.; Kumar, A.; Manning, K.; Niyogi, D.; Rosero, E.; et al. The community Noah land surface model with multiparameterization options (Noah-MP): Model description and evaluation with local-scale measurements. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Jiménez, P.A.; Dudhia, J.; González-Rouco, J.F.; Navarro, J.; Montávez, J.P.; García-Bustamante, E. A Revised Scheme for the WRF Surface Layer Formulation. Mon. Weather Rev. 2012, 140, 898–918. [Google Scholar] [CrossRef]
- Kusaka, H.; Kondo, H.; Kikegawa, Y.; Kimura, F. A simple single-layer urban canopy model for atmospheric models: Comparison with multi-layer and slab models. Bound. Layer Meteorol. 2001, 101, 329–358. [Google Scholar] [CrossRef]
- Davis, C.A.; Brown, B.G.; Bullock, R.; Halley-Gotway, J. The Method for Object-Based Diagnostic Evaluation (MODE) Applied to Numerical Forecasts from the 2005 NSSL/SPC Spring Program. Weather Forecast. 2009, 24, 1252–1267. [Google Scholar] [CrossRef]
- Stergiou, I.; Tagaris, E.; Sotiropoulou, R.-E.P. Sensitivity assessment of WRF parameterizations over Europe. Proceedings 2017, 1, 119. [Google Scholar] [CrossRef]
- Mugume, I.; Waiswa, D.; Mesquita, M.; Reuder, J.; Basalirwa, C.; Bamutaze, Y.; Twinomuhangi, R.; Tumwine, F.; Otim, J.; Ngailo, T.J. Assessing the performance of WRF model in simulating rainfall over western Uganda. J. Climatol. Weather Forecast. 2017, 5, 1–9. [Google Scholar]
- Ngailo, T.J.; Shaban, N.; Reuder, J.; Mesquita, M.D.S.; Rutalebwa, E.; Mugume, I.; Sangalungembe, C. Assessing Weather Research and Forecasting (WRF) Model Parameterization Schemes Skill to Simulate Extreme Rainfall Events over Dar es Salaam on 21 December 2011. J. Geosci. Environ. Prot. 2018, 6, 36–54. [Google Scholar] [CrossRef][Green Version]
- Stampoulis, D.; Anagnostou, E.N.; Nikolopoulos, E.I. Assessment of High-Resolution Satellite-Based Rainfall Estimates over the Mediterranean during Heavy Precipitation Events. J. Hydrometeorol. 2013, 14, 1500–1514. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Behrangi, A.; Sorooshian, S.; Hsu, K.; Amitai, E. Evaluation of satellite-retrieved extreme precipitation rates across the central United States. J. Geophys. Res. Atmos. 2011, 116, 116. [Google Scholar] [CrossRef]




| Model | WRF v 4.1 | |||
|---|---|---|---|---|
| Characteristics | Domain 1 (D01) | Domain 2 (D02) | Domain 3 (D03) | Domain 4 (D04) |
| Horizontal grid resolution | 27 km | 9 km | 3 km | 1 km |
| Horizontal Dimensions | 31 × 31 × 31 | 31 × 31 × 31 | 31 × 31 × 31 | 31 × 31 × 31 |
| Time step 60 seconds | adaptive time step | adaptive time step | adaptive time step | adaptive time step |
| Initial-boundary conditions | ERA-5 (30 km) | simulation of domain 1 | simulation of domain 2 | simulation of domain 3 |
| Model run period | 0000 UTC 24 June–1800 UTC 26 June 2012 | |||
| Physics Options | Naming | Description of Parametrization Schemes |
|---|---|---|
| Microphysics scheme (MP) | WSM 3 WSM 5 * | WRF Single Moment 3-class scheme [41] WRF Single Moment 5-class scheme [41] |
| WSM 6 EF * T * | WRF Single Moment 6-class scheme [42] The Eta Ferrier scheme [43] Thomson et al. double moment scheme [44] | |
| M2 WDM 5 * | Morrison et al. 2-Moments scheme [45] WRF Double Moment 5-class scheme [46] | |
| WDM 6 | WRF Double Moment 6-class scheme [46] | |
| Cumulus parametrization (CP) | KF | Kain-Fritsch (new Eta) scheme [47] |
| BMJ | Betts-Miller-Janjic scheme [48] | |
| GF G3D * | Grell-Freitas ensemble scheme [49] Grell 3D ensemble scheme [50] | |
| Planetary Boundary Layer (PBL) | YSU | Yonsei University PBL [51] |
| ACM2 | Asymmetrical Convective Model version 2 PBL [52] | |
| BL | Bougeault-Lacarrere PBL [53] | |
| Radiation-Shortwave | Dudhia | Dudhia Shortwave scheme [54] |
| Radiation-Longwave | RRTM | Rapid Radiative Transfer Model Longwave [55] |
| Land Surface model | NoahMP | Unified Noah land-surface model [56] |
| Surface Layer | SF_SFCLAY | Revised MM5 Monin-Obukhov scheme [57] |
| Urban Physics | SLUCM | Single-layer urban Canopy Model [58] |
| Indices Type Formula | Perfect Score | Remark |
|---|---|---|
| Percentage Relative Error (RE%) (1) Root Mean Square Error (RMSE) (2) Mean Bias Error (MBE) (3) Standard Deviation (SD) (4) Probability of detection (POD) (5) Frequency bias index (FBI) (6) False alarm ratio (FAR) (7) Critical success index (CSI) (8) | 0 0 0 0 1 1 0 1 | RE%-calculated using catchment areal 24-hour rainfall of WRF simulated and CHIRPS estimation; measures the relative error of WRF simulated accumulated areal catchment rainfall compared to CHIRPS RMSE-measures the average magnitude error of the WRF simulated rainfall corresponding to the observed rainfall; does not indicate the direction of the deviations. MBE- measures the average cumulative error of the WRF simulated rainfall but does not show the correspondence between the simulation and observation. It also shows the direction of the error whether its negative or positive SD-measures the variation of the overall magnitude of the simulation error due to MBE POD-Indicate what grid rainfall correctly simulated compared the CHIRPS grid rainfall. Sensitivity to the frequency of rainfall occurrence during the event; ignores false alarms. FBI-Indicates the tendency of overestimation (FBI > 1) or underestimation (FBI < 1) of WRF simulated rainfall occurrence FAR-Indicates the grids of the WRF simulated rainfall that have no rainfall compared to the CHIRPS grids. It ignores the misses and sensitive to the frequency of rainfall occurrence during the event CSI-Indicates how the grids rainfall simulated by WRF corresponds to the CHIRPS estimates. It penalizes both misses and false alarms and sensitive to hits |
| WRF/CHIRPS | RainCHIRPS | No Rain |
|---|---|---|
| RainWRF | RR (hits) | RN (false alarm) |
| No rain | NR (miss) | NN (correct negative) |
| Rescaled Error Indices | Threshold |
|---|---|
| PODrs = POD | |
| FBIrs = (FBImax − FBI); when FBI > 1 | |
| FBIrs = FBI; when FBI < 1 | |
| FARrs = 1 − FAR | |
| CSIrs = CSI | |
| REr = (1 − RE/REmin); when RE < 0 | REmin = −0.89 |
| RMSErt = (1 − RMSE/RMSEmax) | RMSEmax = 4 |
| MBErt = 1 − MBE/MBEmax; when MBE > 0 | MBEmax = 0.5 |
| MBErt = 1 − MBE/MBEmin; when MBE < 0 | MBEmin = −0.5 |
| SDrt = (1 − SD/Sdmax) | Sdmax = 4 |
| RMSErs = (1 − RMSE/RMSEmax) | RMSEmax = 61 |
| MBErs = 1 − MBE/MBEmax; when MBE > 0 | MBEmax = 61 |
| MBErs = 1 − MBE/MBEmin; when MBE < 0 | MBEmin = −61 |
| SDrs = (1 − SD/Sdmax) | Sdmax = 52 |
| Combinations | Areal Amount | Temporal Dimension | Spatial Dimension Indices | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Continuous | Categorical | |||||||||||
| Areal (mm) | RE (%) | MBE (mm) | RMSE (mm) | SD(mm) | MBE (mm) | RMSE (mm) | SD (mm) | POD | FBI | FAR | CSI | |
| CHIRPS | 16.8 | |||||||||||
| M2-GF-ACM2 | 16.4 | (−2.4) | 0.44 | 3.82 | 2.56 | 3.39 | 12.37 | 16.99 | 0.35 | 0.41 | 0.14 | 0.33 |
| WSM6-KF-BL | 10.1 | (−39.9) | 0.20 | 2.86 | 2.87 | (−31.43) | 31.50 | 2.99 | 0.30 | 0.40 | 0.25 | 0.27 |
| M2-KF-BL | 8.9 | (−47.0) | (−0.34) | 2.68 | 2.67 | (−48.56) | 48.56 | 0.16 | 0.20 | 0.23 | 0.13 | 0.19 |
| WSM3-GF-ACM2 | 6.7 | (−60.1) | (−0.33) | 2.54 | 2.53 | (−48.94) | 48.96 | 2.22 | 0.30 | 0.60 | 0.49 | 0.23 |
| WSM3-KF-BL | 6.3 | (−62.5) | (−0.19) | 2.89 | 2.65 | (−9.14) | 20.11 | 25.34 | 0.20 | 0.33 | 0.13 | 0.18 |
| WSM6-GF-YSU | 5.7 | (−66.1) | (−0.45) | 2.59 | 2.56 | (−50.24) | 52.28 | 20.44 | 0.24 | 0.32 | 0.23 | 0.23 |
| M2-GF-BL | 5.6 | (−66.7) | (−0.33) | 2.56 | 2.55 | (−49.55) | 49.58 | 2.35 | 0.35 | 0.38 | 0.08 | 0.34 |
| M2-GF-YSU | 5.2 | (−69.0) | (−0.42) | 2.57 | 2.54 | (−57.80) | 57.86 | 3.80 | 0.30 | 0.31 | 0.02 | 0.30 |
| WSM6-GF-ACM2 | 4.3 | (−74.4) | (−0.32) | 2.30 | 2.28 | (−49.60) | 49.68 | 4.05 | 0.40 | 0.43 | 0.07 | 0.39 |
| WDM6-KF-YSU | 3.9 | (−76.8) | (−0.30) | 2.60 | 2.60 | (−49.88) | 50.33 | 9.45 | 0.20 | 0.20 | 0.00 | 0.20 |
| WDM6-BMJ-ACM2 | 3.5 | (−79.2) | (−0.38) | 2.64 | 2.62 | (−54.40) | 54.40 | 1.17 | 0.18 | 0.18 | 0.00 | 0.18 |
| WDM6-GF-BL | 3.5 | (−79.2) | (−0.37) | 2.66 | 2.64 | (-45.89) | 46.50 | 10.63 | 0.13 | 0.16 | 0.15 | 0.13 |
| WSM6-BMJ-BL | 3.5 | (−79.2) | (−0.39) | 2.61 | 2.59 | (−54.40) | 54.41 | 1.53 | 0.25 | 0.29 | 0.12 | 0.25 |
| WSM3-BMJ-YSU | 3.4 | (−79.8) | (−0.36) | 2.66 | 2.64 | (−49.84) | 49.91 | 3.73 | 0.38 | 0.43 | 0.11 | 0.36 |
| WSM3-BMJ-BL | 3.3 | (−80.4) | (−0.43) | 2.58 | 2.55 | (−56.00) | 56.39 | 9.32 | 0.36 | 0.43 | 0.15 | 0.34 |
| M2-KF-YSU | 2.9 | (−82.7) | (−0.42) | 2.58 | 2.55 | (−59.70) | 59.71 | 1.40 | 0.12 | 0.14 | 0.16 | 0.11 |
| WDM6-GF-YSU | 2.9 | (−82.7) | (−0.21) | 2.30 | 2.30 | (−40.70) | 42.18 | 15.67 | 0.05 | 0.12 | 0.56 | 0.05 |
| WDM6-GF-ACM2 | 2.6 | (−84.5) | (−0.38) | 2.38 | 2.36 | (−56.46) | 56.50 | 2.85 | 0.13 | 0.40 | 0.68 | 0.10 |
| WSM3-GF-YSU | 2.5 | (−85.1) | (−0.44) | 2.60 | 2.57 | (−60.73) | 60.78 | 3.44 | 0.15 | 0.30 | 0.52 | 0.14 |
| WSM6-KF-YSU | 2.4 | (−85.7) | (−0.37) | 2.67 | 2.66 | (−55.89) | 55.99 | 4.67 | 0.13 | 0.28 | 0.53 | 0.12 |
| WDM6-BMJ-BL | 2.3 | (−86.3) | (−0.42) | 2.61 | 2.59 | (−57.92) | 57.95 | 2.75 | 0.13 | 0.31 | 0.59 | 0.11 |
| WDM6-KF-BL | 2.2 | (−86.9) | (−0.43) | 2.53 | 2.51 | (−53.60) | 54.26 | 11.96 | 0.16 | 0.16 | 0.01 | 0.16 |
| WSM6-BMJ-YSU | 2.1 | (−87.5) | (−0.41) | 2.62 | 2.59 | (−53.84) | 54.03 | 6.37 | 0.31 | 0.44 | 0.29 | 0.28 |
| WSM3-KF-YSU | 1.8 | (−89.3) | (−0.35) | 2.73 | 2.72 | (−54.81) | 55.04 | 7.18 | 0.11 | 0.20 | 0.42 | 0.11 |
| Combinations | RE(%) | TES | SES | US | ||||
|---|---|---|---|---|---|---|---|---|
| Score | Rank | Score | Rank | Score | Rank | Score | Rank | |
| M2-GF-ACM2 | (−2.4) | 1 | 0.36 | 7 | 0.62 | 1 | 0.53 | 1 |
| WSM6-KF-BL | (−39.9) | 2 | 0.37 | 4 | 0.52 | 2 | 0.53 | 2 |
| M2-KF-BL | (−47.0) | 3 | 0.33 | 10 | 0.41 | 10 | 0.30 | 8 |
| WSM3-GF-ACM2 | (−60.1) | 4 | 0.36 | 6 | 0.43 | 7 | 0.40 | 7 |
| WSM3-KF-BL | (−62.5) | 5 | 0.41 | 2 | 0.52 | 3 | 0.47 | 3 |
| WSM6-GF-YSU | (−66.1) | 6 | 0.31 | 13 | 0.35 | 16 | 0.32 | 16 |
| M2-GF-BL | (−66.7) | 7 | 0.35 | 8 | 0.47 | 6 | 0.42 | 6 |
| M2-GF-YSU | (−69.0) | 8 | 0.29 | 18 | 0.42 | 9 | 0.37 | 9 |
| WSM6-GF-ACM2 | (−74.4) | 9 | 0.40 | 3 | 0.49 | 4 | 0.44 | 4 |
| WDM6-KF-YSU | (−76.8) | 10 | 0.37 | 5 | 0.39 | 13 | 0.36 | 10 |
| WDM6-BMJ-ACM2 | (−79.2) | 11 | 0.31 | 16 | 0.39 | 14 | 0.34 | 14 |
| WDM6-GF-BL | (−79.2) | 12 | 0.31 | 14 | 0.37 | 15 | 0.35 | 13 |
| WSM6-BMJ-BL | (−79.2) | 13 | 0.31 | 15 | 0.41 | 11 | 0.35 | 12 |
| WSM3-BMJ-YSU | (−79.8) | 14 | 0.32 | 12 | 0.48 | 5 | 0.42 | 5 |
| WSM3-BMJ-BL | (−80.4) | 15 | 0.28 | 22 | 0.42 | 8 | 0.35 | 11 |
| M2-KF-YSU | (−82.7) | 16 | 0.29 | 20 | 0.32 | 18 | 0.29 | 19 |
| WDM6-GF-YSU | (−82.7) | 17 | 0.48 | 1 | 0.28 | 24 | 0.32 | 17 |
| WDM6-GF-ACM2 | (−84.5) | 18 | 0.35 | 9 | 0.29 | 21 | 0.29 | 20 |
| WSM3-GF-YSU | (−85.1) | 19 | 0.28 | 23 | 0.29 | 22 | 0.26 | 24 |
| WSM6-KF-YSU | (−85.7) | 20 | 0.27 | 24 | 0.30 | 19 | 0.28 | 21 |
| WDM6-BMJ-BL | (−86.3) | 21 | 0.29 | 21 | 0.29 | 23 | 0.26 | 23 |
| WDM6-KF-BL | (−86.9) | 22 | 0.29 | 19 | 0.35 | 17 | 0.31 | 18 |
| WSM6-BMJ-YSU | (−87.5) | 23 | 0.30 | 17 | 0.41 | 12 | 0.34 | 15 |
| WSM3-KF-YSU | (−89.3) | 24 | 0.32 | 11 | 0.20 | 20 | 0.27 | 22 |
| CP-on | CP-off | (CP-on)–(CP-off) | |||
|---|---|---|---|---|---|
| MP-CP-PBL Combinations | Area Average Rainfall (mm) | RE(%) | Area Average Rainfall (mm) | RE(%) | Difference (mm) |
| CHIRPS | 16.8 | ||||
| M2-GF-ACM2 | 16.4 | (−2.4) [1] | 16 | (−4.8) [1] | 0.4 |
| WSM6-KF-BL | 10.1 | (−39.9) [2] | 9.8 | (−41.7) [7] | 0.3 |
| M2-KF-BL | 8.9 | (−47.0) [3] | 1.8 | (−89.3) [18] | 7.1 |
| WSM3-GF-ACM2 | 6.7 | (−60.1) [4] | 6.1 | (−63.7) [13] | 0.6 |
| WSM3-KF-BL | 6.3 | (−62.5) [5] | 3.5 | (−79.2) [15] | 2.8 |
| WSM6-GF-YSU | 5.7 | (−66.1) [6] | 0.3 | (−98.2) [22] | 5.4 |
| M2-GF-BL | 5.6 | (−66.7) [7] | 7.7 | (−54.2) [9] | (−2.1) |
| M2-GF-YSU | 5.2 | (−69.0) [8] | 6.7 | (−60.1) [11] | (−1.5) |
| WSM6-GF-ACM2 | 4.3 | (−74.4) [9] | 10.3 | (−38.7) [6] | (−6) |
| WDM6-KF-YSU | 3.9 | (−76.8) [10] | 2.4 | (−85.7) [16] | 1.5 |
| WDM6-BMJ-ACM2 | 3.5 | (−79.2) [11] | 1.7 | (−89.9) [19] | 1.8 |
| WDM6-GF-BL | 3.5 | (−79.2) [12] | 1.5 | (−91.1) [20] | 2 |
| WSM6-BMJ-BL | 3.5 | (−79.2) [13] | 10.4 | (−38.1) [5] | (−6.9) |
| WSM3-BMJ-YSU | 3.4 | (−79.8) [14] | 8.4 | (−50.0) [8] | (−5) |
| WSM3-BMJ-BL | 3.3 | (−80.4) [15] | 4.8 | (−71.4) [14] | (−1.5) |
| M2-KF-YSU | 2.9 | (−82.7) [16] | 6.6 | (−60.7) [12] | (−3.7) |
| WDM6-GF-YSU | 2.9 | (−82.7) [17] | 0 | (−100.0) [24] | 2.9 |
| WDM6-GF-ACM2 | 2.6 | (−84.5) [18] | 13.2 | (−21.4) [3] | (−10.6) |
| WSM3-GF-YSU | 2.5 | (−85.1) [19] | 7.1 | (−57.7) [10] | (−4.6) |
| WSM6-KF-YSU | 2.4 | (−85.7) [20] | 1.9 | (−88.7) [17] | 0.5 |
| WDM6-BMJ-BL | 2.3 | (−86.3) [21] | 10.9 | (-35.1) [4] | (−8.6) |
| WDM6-KF-BL | 2.2 | (−86.9) [22] | 1 | (−94.0) [21] | 1.2 |
| WSM6-BMJ-YSU | 2.1 | (−87.5) [23] | 15.1 | (−10.1) [2] | (−13) |
| WSM3-KF-YSU | 1.8 | (−89.3) [24] | 0.1 | (−99.4) [23] | 1.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Umer, Y.; Ettema, J.; Jetten, V.; Steeneveld, G.-J.; Ronda, R. Evaluation of the WRF Model to Simulate a High-Intensity Rainfall Event over Kampala, Uganda. Water 2021, 13, 873. https://doi.org/10.3390/w13060873
Umer Y, Ettema J, Jetten V, Steeneveld G-J, Ronda R. Evaluation of the WRF Model to Simulate a High-Intensity Rainfall Event over Kampala, Uganda. Water. 2021; 13(6):873. https://doi.org/10.3390/w13060873
Chicago/Turabian StyleUmer, Yakob, Janneke Ettema, Victor Jetten, Gert-Jan Steeneveld, and Reinder Ronda. 2021. "Evaluation of the WRF Model to Simulate a High-Intensity Rainfall Event over Kampala, Uganda" Water 13, no. 6: 873. https://doi.org/10.3390/w13060873
APA StyleUmer, Y., Ettema, J., Jetten, V., Steeneveld, G.-J., & Ronda, R. (2021). Evaluation of the WRF Model to Simulate a High-Intensity Rainfall Event over Kampala, Uganda. Water, 13(6), 873. https://doi.org/10.3390/w13060873







