The Effects of Exchange Flow on the Karst Spring Hydrograph under the Different Flow Regimes: A Synthetic Modeling Approach
Abstract
:1. Introduction
2. Materials and Methods
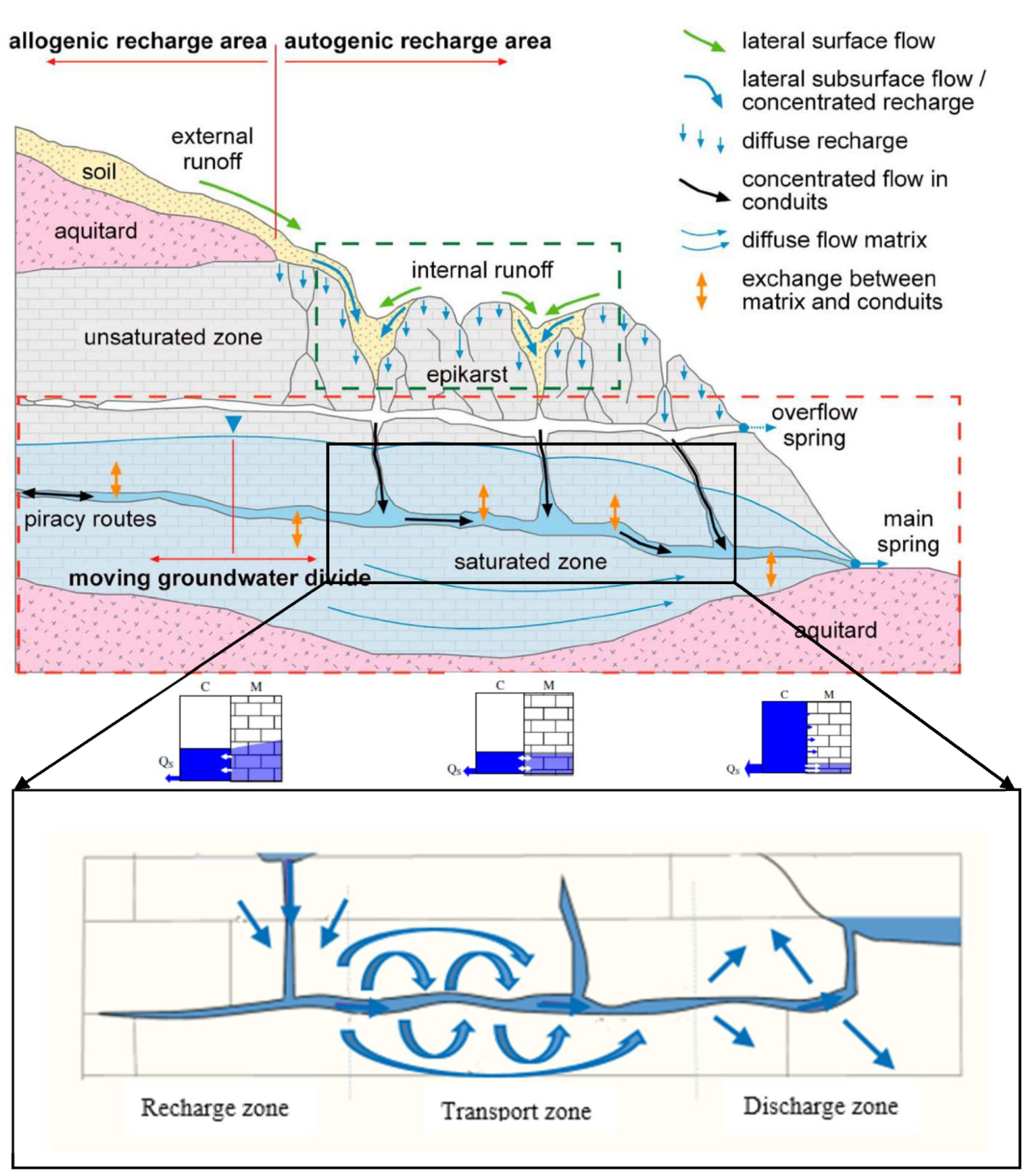
2.1. Review of the Exchange Flow and Related Parameters
2.1.1. Theoretical Background
2.1.2. Temporal and Spatial Variations of the Exchange Flow
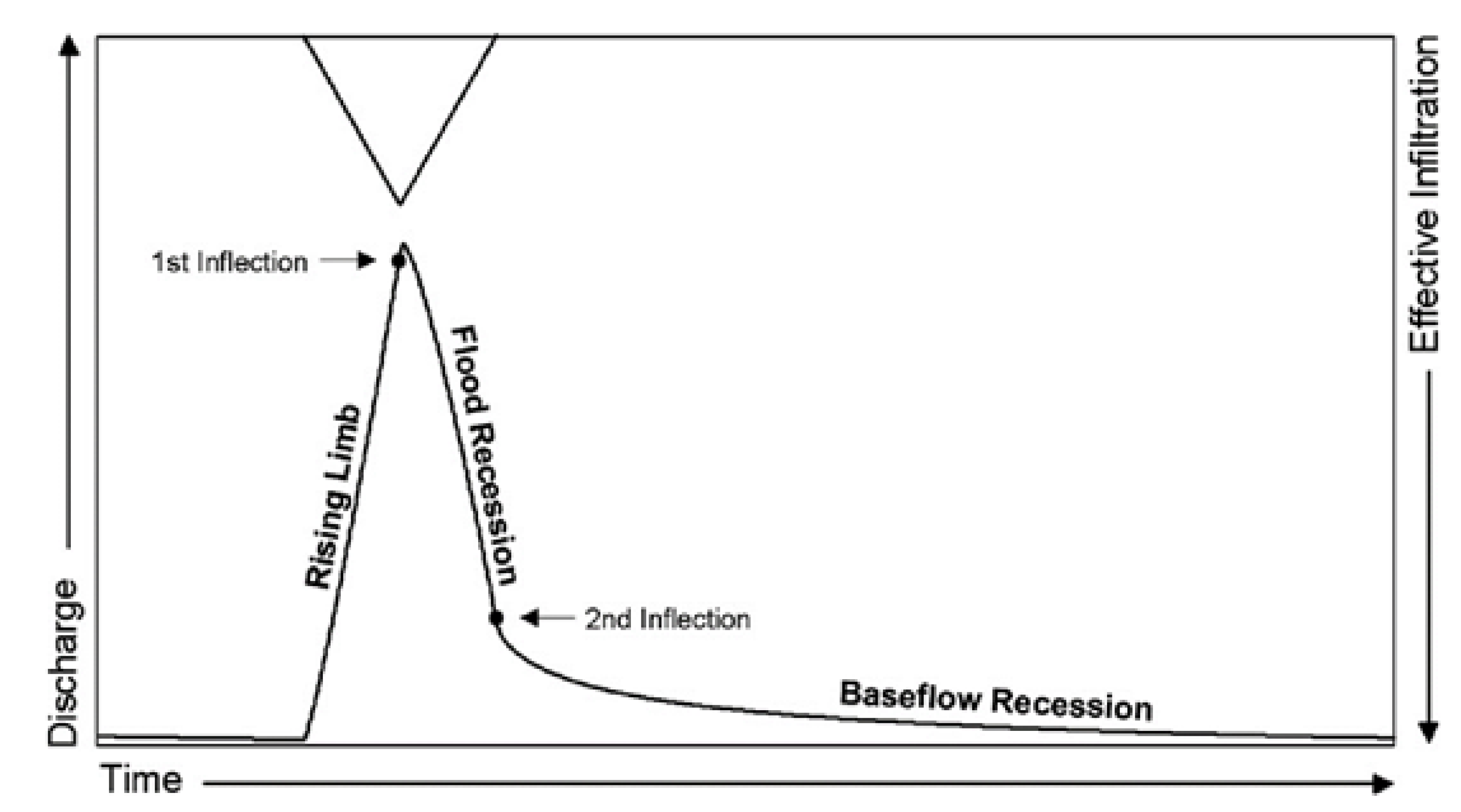
2.1.3. The Effect of the Exchange Flow and Its Direction on the Spring Hydrograph
2.2. Methodology
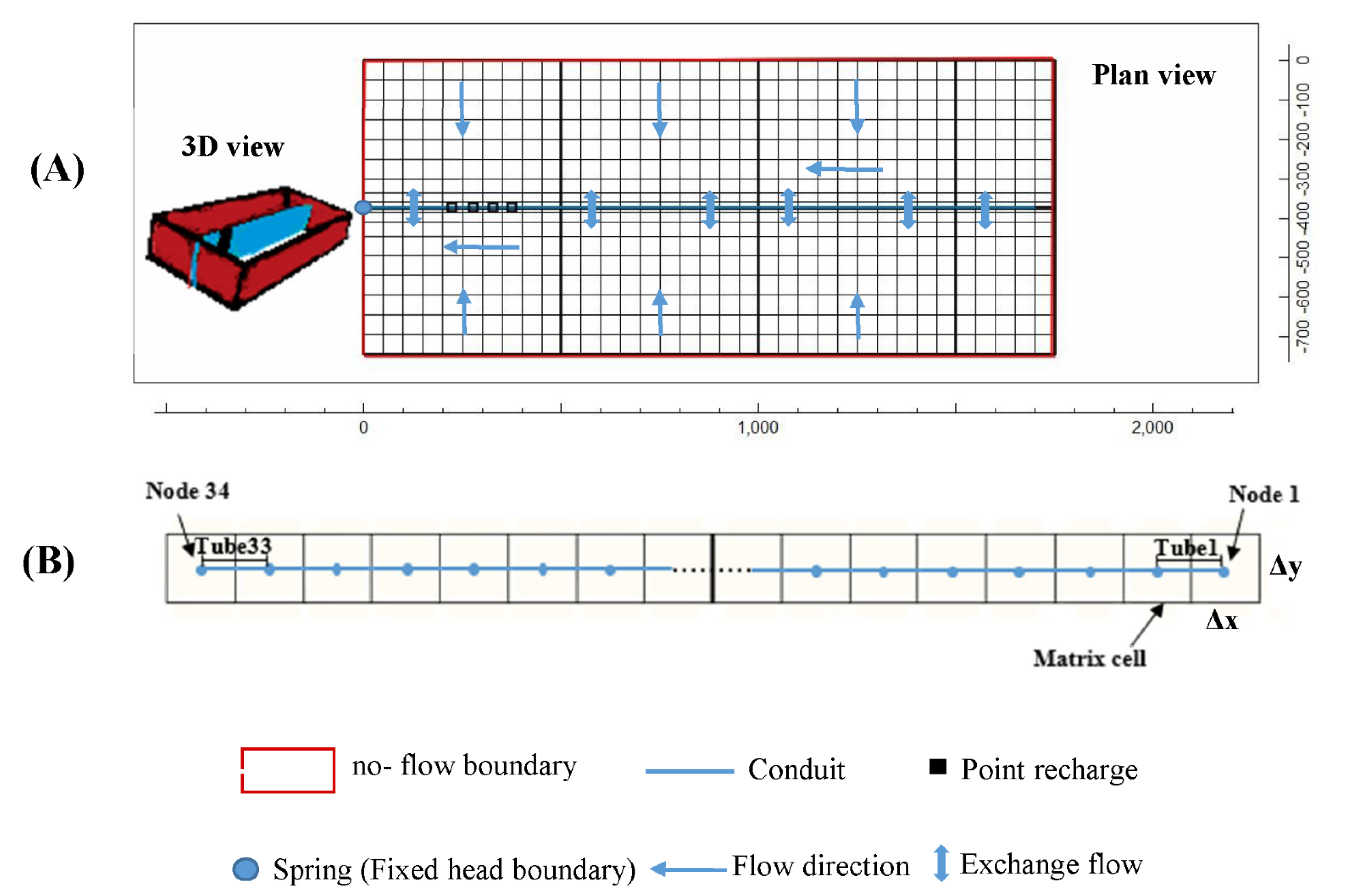
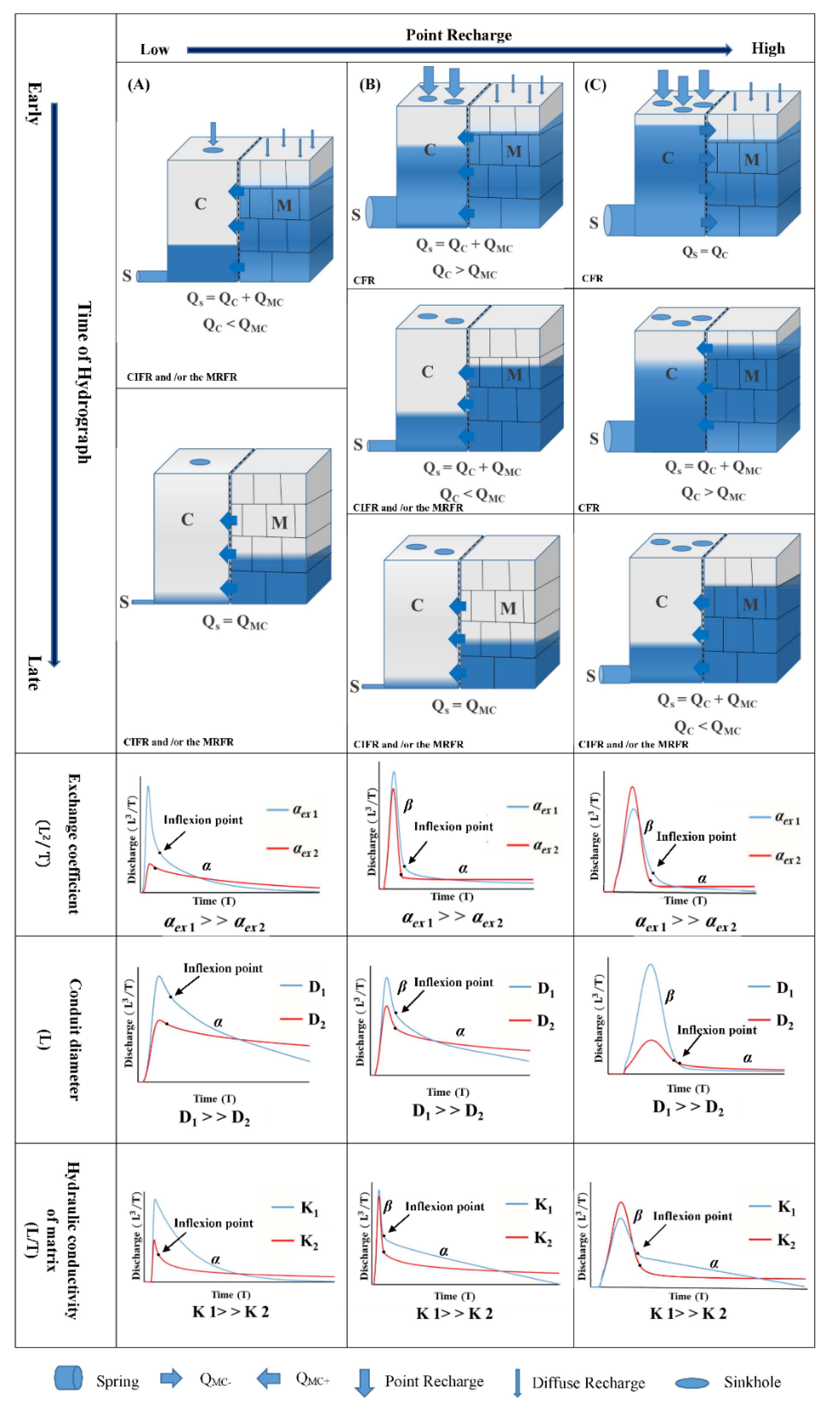
3. The Conceptual Model and Scenarios
3.1. The Geometry of the Conceptual Model
3.2. Types of Recharge
3.3. Discharge Point of the Synthetic Model
3.4. Definition of the Scenarios
4. Results and Discussion
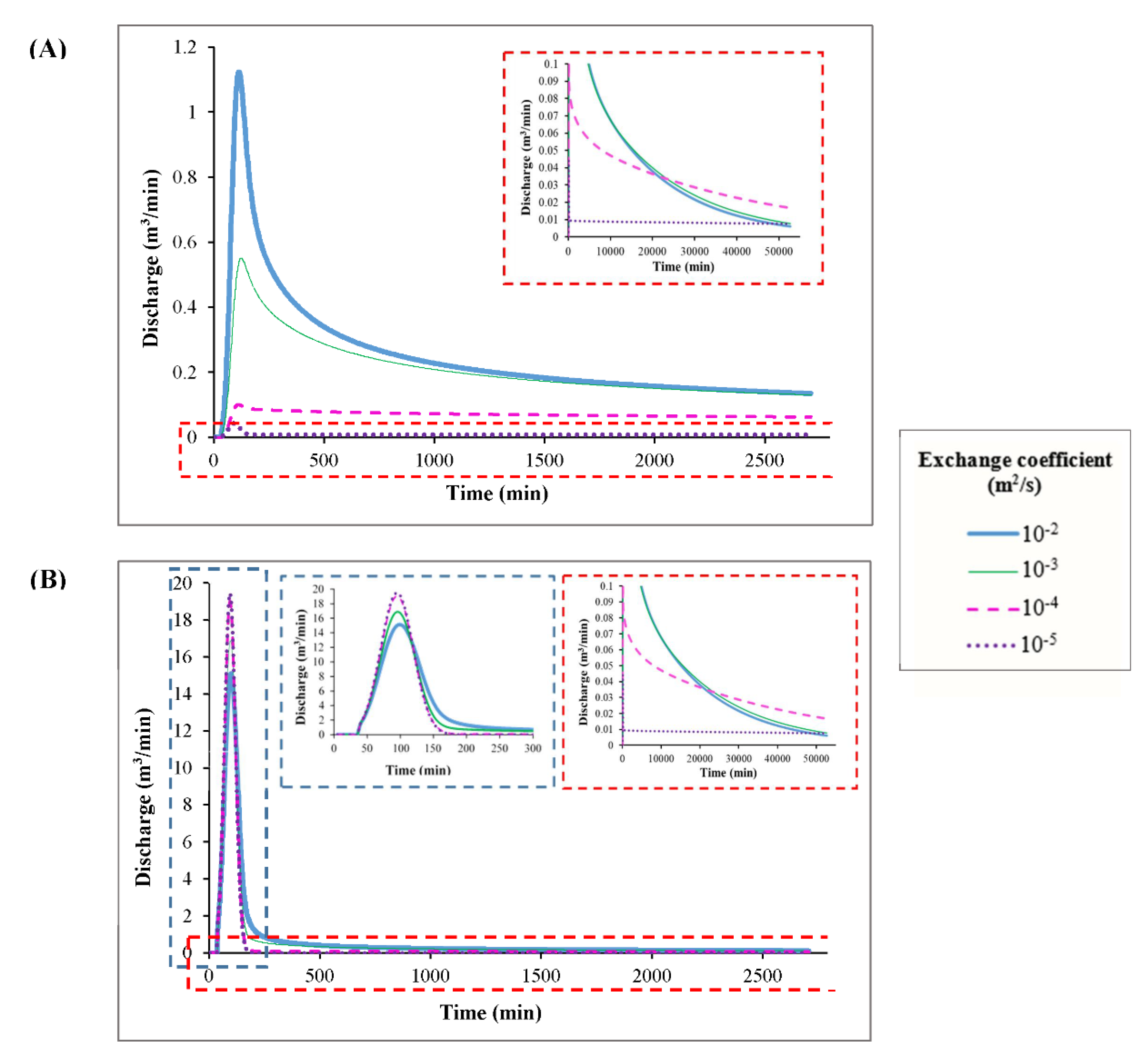
4.1. The Effect of the Exchange Coefficient on the Karst Spring Hydrograph
4.2. The Influence of the Conduit Diameter on the Karst Spring Hydrograph
4.3. The Influence of the Matrix Hydraulic Conductivity on the Karst Spring Hydrograph
4.4. Generalization of the Effect of Exchange Flow on the Spring Hydrograph
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Goldscheider, N.; Drew, D. Methods in Karst Hydrogeology; Taylor & Francis: London, UK, 2007; 264p. [Google Scholar]
- Oehlmann, S.; Geyer, T.; Licha, T.; Birk, S. Influence of aquifer heterogeneity on karst hydraulics and catchment delineation employing distributive modeling approaches. Hydrol. Earth Syst. Sci. 2013, 17, 4729–4742. [Google Scholar] [CrossRef] [Green Version]
- Hartmann, A.; Goldscheider, N.; Wagener, T.; Lange, J.; Weiler, M. Karst water resources in a changing world: Review of hydrological modeling approaches. Rev. Geophys. 2014, 52, 218–242. [Google Scholar] [CrossRef]
- White, W.B. Conceptual models for karstic aquifers. Speleogenesis 2003, 1, 1–6. [Google Scholar]
- De Rooij, R. Toward improved Numerical Modeling of Karst aquIFERS: COUPLING Trubulent Conduit Flow and Laminar Matrix Flow under Variably Saturated Conditions. Ph.D. Thesis, University of Neuchâtel, Neuchâtel, Switzerland, 2008. [Google Scholar]
- Berglund, J.L. Karst Aquifer Recharge and Conduit Flow Dynamics from High-Resolution Monitoring and Transport Modeling in Central Pennsylvania Springs. Ph.D. Thesis, Temple University, Philadelphia, PA, USA, 2019. [Google Scholar]
- Barenblatt, G.; Zheltov, I.; Kochina, I. Basic concepts in the theory of seepage of homogeneous liquids in fissured rocks [strata]. J. Appl. Math. Mech. 1960, 24, 1286–1303. [Google Scholar] [CrossRef]
- Warren, J.; Root, P. The Behavior of Naturally Fractured Reservoirs. Soc. Pet. Eng. J. 1963, 3, 245–255. [Google Scholar] [CrossRef] [Green Version]
- Narasimhan, T.N. Multidimensional numerical simulation of fluid flow in fractured porous media. Water Resour. Res. 1982, 18, 1235–1247. [Google Scholar] [CrossRef] [Green Version]
- Wang, X. On the coupled continuum pipe flow model (CCPF) for flows in karst aquifer. Discret. Contin. Dyn. Syst. B 2010, 13, 489–501. [Google Scholar] [CrossRef]
- Kazemi, H.; Seth, M.S.; Thomas, G.W. The interpretation of interference tests in naturally fractured reservoirs with uniform fracture distribution. Trans. Soc. Pet. Eng. 1969, 9, 463–472. [Google Scholar] [CrossRef]
- Moench, A.F. Double-Porosity Models for a Fissured Groundwater Reservoir With Fracture Skin. Water Resour. Res. 1984, 20, 831–846. [Google Scholar] [CrossRef]
- Chen, N.; Gunzburger, M.; Hu, B.; Wang, X.; Woodruff, C. Calibrating the exchange coefficient in the modified coupled continuum pipe-flow model for flows in karst aquifers. J. Hydrol. 2012, 414-415, 294–301. [Google Scholar] [CrossRef]
- Peterson, E.W.; Wicks, C.M. Fluid and Solute Transport from a Conduit to the Matrix in a Carbonate Aquifer System. Math. Geol. 2005, 37, 851–867. [Google Scholar] [CrossRef]
- Bauer, S.; Liedl, R.; Sauter, M. Modeling of karst aquifer genesis: Influence of exchange flow. Water Resour. Res. 2003, 39, 1–12. [Google Scholar] [CrossRef]
- Bailly-Comte, V.; Martin, J.B.; Jourde, H.; Screaton, E.J.; Pistre, S.; Langston, A. Water exchange and pressure transfer between conduits and matrix and their influence on hydrodynamics of two karst aquifers with sinking streams. J. Hydrol. 2010, 386, 55–66. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, X.; Soulsby, C. Catchment-scale conceptual modelling of water and solute transport in the dual flow system of the karst critical zone. Hydrol. Process. 2017, 31, 3421–3436. [Google Scholar] [CrossRef]
- Cornaton, F.; Perrochet, P. Analytical 1D dual-porosity equivalent solutions to 3D discrete single-continuum models. Application to karstic spring hydrograph modelling. J. Hydrol. 2002, 262, 165–176. [Google Scholar] [CrossRef] [Green Version]
- Dufoyer, A.; Massei, N.; Lecoq, N.; Marechal, J.-C.; Thiery, D.; Pennequin, D.; David, P.-Y. Links between karst hydrogeological properties and statistical characteristics of spring discharge time series: A theoretical study. Environ. Earth Sci. 2019, 78, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Reimann, T.; Geyer, T.; Shoemaker, W.B.; Liedl, R.; Sauter, M. Effects of dynamically variable saturation and matrix-conduit coupling of flow in karst aquifers. Water Resour. Res. 2011, 47, 1–19. [Google Scholar] [CrossRef]
- Saller, S.P.; Ronayne, M.J.; Long, A.J. Comparison of a karst groundwater model with and without discrete conduit flow. Hydrogeol. J. 2013, 21, 1555–1566. [Google Scholar] [CrossRef]
- Xu, Z.; Hu, B.X.; Davis, H.; Cao, J. Simulating long term nitrate-N contamination processes in the Woodville Karst Plain using CFPv2 with UMT3D. J. Hydrol. 2015, 524, 72–88. [Google Scholar] [CrossRef]
- Giese, M.; Reimann, T.; Liedl, R.; Maréchal, J.-C.; Sauter, M. Application of the flow dimension concept for numerical drawdown data analyses in mixed-flow karst systems. Hydrogeol. J. 2017, 25, 799–811. [Google Scholar] [CrossRef]
- Basha, H.A.; Zoghbi, C.A. Simplified Physically Based Models for Pressurized Flow in Karst Systems. Water Resour. Res. 2018, 54, 7198–7215. [Google Scholar] [CrossRef]
- Mohammadi, Z.; Illman, W.A.; Karimi, M. Optimization of the hydrodynamic characteristics of a karst conduit with CFPv2 coupled to OSTRICH. J. Hydrol. 2018, 567, 564–578. [Google Scholar] [CrossRef]
- Peterson, R.N.; Burnett, W.C.; Glenn, C.R.; Johnson, A.G. Quantification of point-source groundwater discharges to the ocean from the shoreline of the Big Island, Hawaii. Limnol. Oceanogr. 2009, 54, 890–904. [Google Scholar] [CrossRef]
- Johnson, A.G.; Glenn, C.R.; Burnett, W.C.; Peterson, R.N.; Lucey, P.G. Aerial infrared imaging reveals large nutrient-rich groundwater inputs to the ocean. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef] [Green Version]
- Frank, S.; Goeppert, N.; Ohmer, M.; Goldscheider, N. Sulfate variations as a natural tracer for conduit-matrix interaction in a complex karst aquifer. Hydrol. Process. 2019, 33, 1292–1303. [Google Scholar] [CrossRef]
- Duran, L.; Massei, N.; Lecoq, N.; Fournier, M.; Labat, D. Analyzing multi-scale hydrodynamic processes in karst with a coupled conceptual modeling and signal decomposition approach. J. Hydrol. 2020, 583, 124625. [Google Scholar] [CrossRef]
- Hill, M.E. An Evaluation of Conduit Conceptualizations and Model Performance. Ph.D. Thesis, Department of Geology, University of South Florida, Tampa, FL, USA, 2008. [Google Scholar]
- Joodi, A.S.; Sizaret, S.; Binet, S.; Bruand, A.; Alberic, P.; Lepiller, M. Development of a Darcy-Brinkman model to simulate water flow and tracer transport in a heterogeneous karstic aquifer (Val d’Orléans, France). Hydrogeol. J. 2009, 18, 295–309. [Google Scholar] [CrossRef] [Green Version]
- Sohi, M.H.; Koch, M.; Ashjari, J. Numerical Simulation of Ground Water Flow in Dual Porous Media of the Karun 4 Dam (Iran) Foundation and Abutments. Ph.D. Thesis, University of Kassel, Kassel, Germany, 2018. [Google Scholar]
- Binet, S.; Joigneaux, E.; Pauwels, H.; Albéric, P.; Fléhoc, C.; Bruand, A. Water exchange, mixing and transient storage between a saturated karstic conduit and the surrounding aquifer: Groundwater flow modeling and inputs from stable water isotopes. J. Hydrol. 2017, 544, 278–289. [Google Scholar] [CrossRef] [Green Version]
- Sivelle, V.; Labat, D.; Mazzilli, N.; Massei, N.; Jourde, H. Dynamics of the Flow Exchanges between Matrix and Conduits in Karstified Watersheds at Multiple Temporal Scales. Water 2019, 11, 569. [Google Scholar] [CrossRef] [Green Version]
- Shoemaker, W.B.; Kuniansky, E.L.; Birk, S.; Bauer, S.; Swain, E.D. Documentation of a Conduit Flow Process (CFP) for MODFLOW-2005. Tech. Methods 2007. [Google Scholar] [CrossRef] [Green Version]
- Bauer, S.; Liedl, R.; Sauter, M. Modelling of karst development considering conduit-matrix exchange flow. Calibration and Reliability in Groundwater Modelling. In Proceedings of the ModelCARE 99 Conference held at Zurich, Zurich, Switzerland, September 1999; IAHS 265, 2000. pp. 10–15. [Google Scholar]
- Chang, Y.; Wu, J.; Liu, L. Effects of the conduit network on the spring hydrograph of the karst aquifer. J. Hydrol. 2015, 527, 517–530. [Google Scholar] [CrossRef]
- Malenica, L.; Gotovac, H.; Kamber, G.; Simunovic, S.; Allu, S.; Divic, V. Groundwater Flow Modeling in Karst Aquifers: Coupling 3D Matrix and 1D Conduit Flow via Control Volume Isogeometric Analysis—Experimental Verification with a 3D Physical Model. Water 2018, 10, 1787. [Google Scholar] [CrossRef] [Green Version]
- De Rooij, R. Improving accuracy and efficiency in discrete-continuum karst models. Environ. Earth Sci. 2019, 78, 115. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, X.; Cheng, Q.; Soulsby, C. Storage dynamics, hydrological connectivity and flux ages in a karst catchment: Conceptual modelling using stable isotopes. Hydrol. Earth Syst. Sci. 2019, 23, 51–71. [Google Scholar] [CrossRef] [Green Version]
- Soglio, L.D.; Danquigny, C.; Mazzilli, N.; Emblanch, C. Modeling the Matrix-Conduit Exchanges in Both the Epikarst and the Transmission Zone of Karst Systems. Water 2020, 12, 3219. [Google Scholar] [CrossRef]
- Wu, P.; Shu, L.; Li, F.; Chen, H.; Xu, Y.; Zou, Z.; Mabedi, E.C. Impacts of Artificial Regulation on Karst Spring Hydrograph in Northern China: Laboratory Study and Numerical Simulations. Water 2019, 11, 755. [Google Scholar] [CrossRef] [Green Version]
- Kovács, A.; Perrochet, P. A quantitative approach to spring hydrograph decomposition. J. Hydrol. 2008, 352, 16–29. [Google Scholar] [CrossRef]
- Király, L. Introduction al’hydrogéologie des roches fissurées et karstiques, Bases théoriques al’intention des hydrogéologues; Manuscrit; Université de Neuchâtel: Neuchâtel, Switzerland, 1998. [Google Scholar]
- Kovács, A.; Perrochet, P.; Király, L.; Jeannin, P.-Y. A quantitative method for the characterisation of karst aquifers based on spring hydrograph analysis. J. Hydrol. 2005, 303, 152–164. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, S.; Geyer, T.; Guttman, J.; Marei, A.; Ries, F.; Sauter, M. Characterisation and modelling of conduit restricted karst aquifers—Example of the Auja spring, Jordan Valley. J. Hydrol. 2014, 511, 750–763. [Google Scholar] [CrossRef]
- Maillet, E. Essais d’Hydraulique Souterraine et Fluviale; Hermann: Paris, France, 1905. [Google Scholar]
- Fiorillo, F. Tank-reservoir drainage as a simulation of the recession limb of karst spring hydrographs. Hydrogeol. J. 2011, 19, 1009–1019. [Google Scholar] [CrossRef]
- Colebrook, C.F.; White, C.M. The reduction of carrying capacity of pipes with age. J. Inst. Civ. Eng. 1937, 7, 99–118. [Google Scholar] [CrossRef]
- Dreybrodt, W. Processes in Karst Systems-Physics, Chemistry, and Geology; Springer: Berlin/Heidelberg, Germany, 1988; 288p. [Google Scholar] [CrossRef]
- Kavousi, A.; Reimann, T.; Liedl, R.; Raeisi, E. Karst aquifer characterization by inverse application of MODFLOW-2005 CFPv2 discrete-continuum flow and transport model. J. Hydrol. 2020, 587, 124922. [Google Scholar] [CrossRef]
- Geng, X.; Michael, H.A. Preferential Flow Enhances Pumping-Induced Saltwater Intrusion in Volcanic Aquifers. Water Resour. Res. 2020, 56, 026390. [Google Scholar] [CrossRef]
- Kreyns, P.; Geng, X.; Michael, H.A. The influence of connected heterogeneity on groundwater flow and salinity distributions in coastal volcanic aquifers. J. Hydrol. 2020, 586, 124863. [Google Scholar] [CrossRef]



| Number of Run Models | Variable Parameter | Constant Parameters | Type of Scenario | |
|---|---|---|---|---|
| A (QMC+) | (A1) | K (10−5 m/s) | (10−2–10−5) | 4 |
| d (0.5 m) | ||||
| (10−2) | ||||
| Sy (5 × 10−3) | ||||
| SS (10−7) | ||||
| hinitial (20 m) | ||||
| (A2) | K (10−5 m/s) | (0.1–0.5 m) | 5 | |
| (10−3 m2/s) | ||||
| (10−2) | ||||
| Sy (5 × 10−3) | ||||
| SS (10−7) | ||||
| hinitial (20 m) | ||||
| (A3) | (0.5 m) | K (10−3–10−6) | 4 | |
| (10−3 m2/s) | ||||
| (10−2) | ||||
| Sy (5 × 10−3) | ||||
| SS(10−7) | ||||
| hinitial (20 m) | ||||
| B (QMC− and QMC+) | (B1) | K (10−5 m/s) | (10−2–10−5) | 4 |
| (0.5 m) | ||||
| (10−2) | ||||
| Sy (5 × 10−3) | ||||
| SS (10−7) | ||||
| hinitial (20 m) | ||||
| (B2) | K (10−5 m/s) | (0.1–0.5 m) | 5 | |
| (10−3 m2/s) | ||||
| (10−2) | ||||
| Sy (5 × 10−3) | ||||
| SS (10−7) | ||||
| hinitial (20 m) | ||||
| (B3) | (0.5 m) | K (10−3–10−6) | 4 | |
| (10−3 m2/s) | ||||
| (10−2) | ||||
| Sy (5 × 10−3) | ||||
| SS (10−7) | ||||
| hinitial (20 m) | ||||
| State | I | II | III | IV | |
|---|---|---|---|---|---|
| Spring hydrograph | 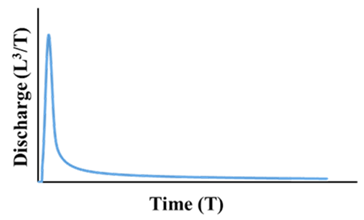 | 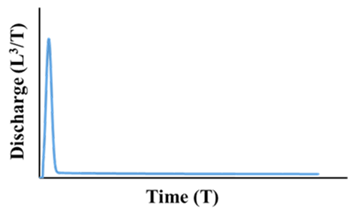 | 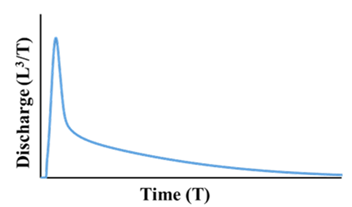 |  | |
| Recession curve | 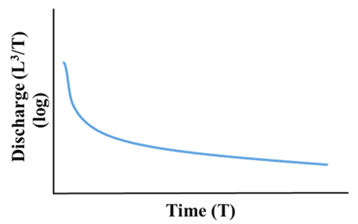 | 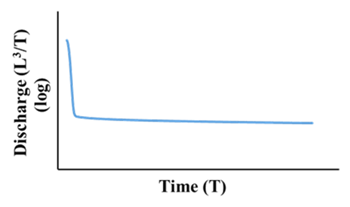 | 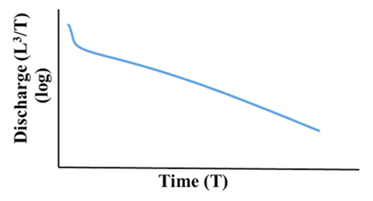 |  | |
| Inflection point | Clear | Clear | Clear | Unclear | |
| The position of inflection point | Before an arc region | Before a non-arc region | Before a non-arc region | - | |
| α | αI, αIII, αIV > αII | ||||
| Characteristics of the internal structure | αex | Large | Small | Large | Large |
| T | Small | Small or Large | Large | Large | |
| Δh | ΔhI, ΔhIII, ΔhIV < ΔhII | ||||
| Potential Scenario in the synthetic forward modeling | Scenario A and B | Scenario A and B | Scenario B | Scenario A | |
| Characteristics of Scenarios A and B | RCH in Scenario A = RCH in Scenario B CRCH in Scenario A << CRCH in Scenario B Aquifer thickness in Scenario A = Aquifer thickness in Scenario B The effective porosity of the matrix in Scenario A = The effective porosity of the matrix in Scenario B | ||||
| αex: Exchange coefficient T: Transmissivity α: The slope of recession curve under the condition of baseflow Δh: The difference of the hydraulic head between the matrix and the conduit RCH: Diffuse recharge to the matrix CRCH: Concentrated recharge to conduits | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shirafkan, M.; Mohammadi, Z.; Sivelle, V.; Labat, D. The Effects of Exchange Flow on the Karst Spring Hydrograph under the Different Flow Regimes: A Synthetic Modeling Approach. Water 2021, 13, 1189. https://doi.org/10.3390/w13091189
Shirafkan M, Mohammadi Z, Sivelle V, Labat D. The Effects of Exchange Flow on the Karst Spring Hydrograph under the Different Flow Regimes: A Synthetic Modeling Approach. Water. 2021; 13(9):1189. https://doi.org/10.3390/w13091189
Chicago/Turabian StyleShirafkan, Malihe, Zargham Mohammadi, Vianney Sivelle, and David Labat. 2021. "The Effects of Exchange Flow on the Karst Spring Hydrograph under the Different Flow Regimes: A Synthetic Modeling Approach" Water 13, no. 9: 1189. https://doi.org/10.3390/w13091189
APA StyleShirafkan, M., Mohammadi, Z., Sivelle, V., & Labat, D. (2021). The Effects of Exchange Flow on the Karst Spring Hydrograph under the Different Flow Regimes: A Synthetic Modeling Approach. Water, 13(9), 1189. https://doi.org/10.3390/w13091189