Influence of Meteorological Factors on the Potential Evapotranspiration in Yanhe River Basin, China
Abstract
:1. Introduction
2. Data and Methods
2.1. Study Area
2.2. Data
2.3. ET0
2.4. Calculation of Sensitivity Coefficient
2.5. Calculation of Contribution Rate
2.6. Analytical Method
3. Results
3.1. Temporal and Spatial Characteristics of ET0 and Meteorological Factors
3.2. Sensitivity of ET0 to Meteorological Factors
3.2.1. Temporal Characteristics
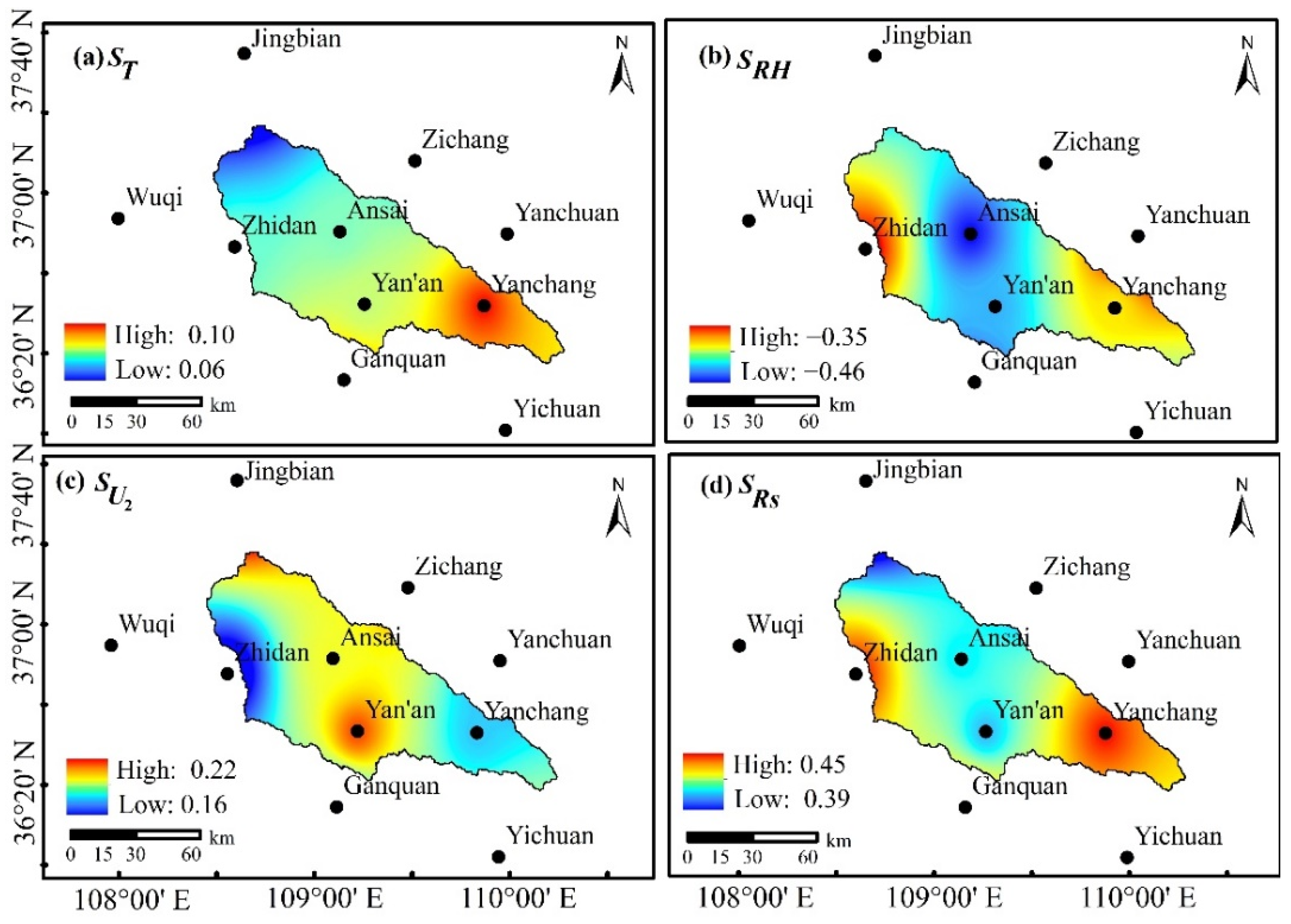
3.2.2. Spatial Characteristics
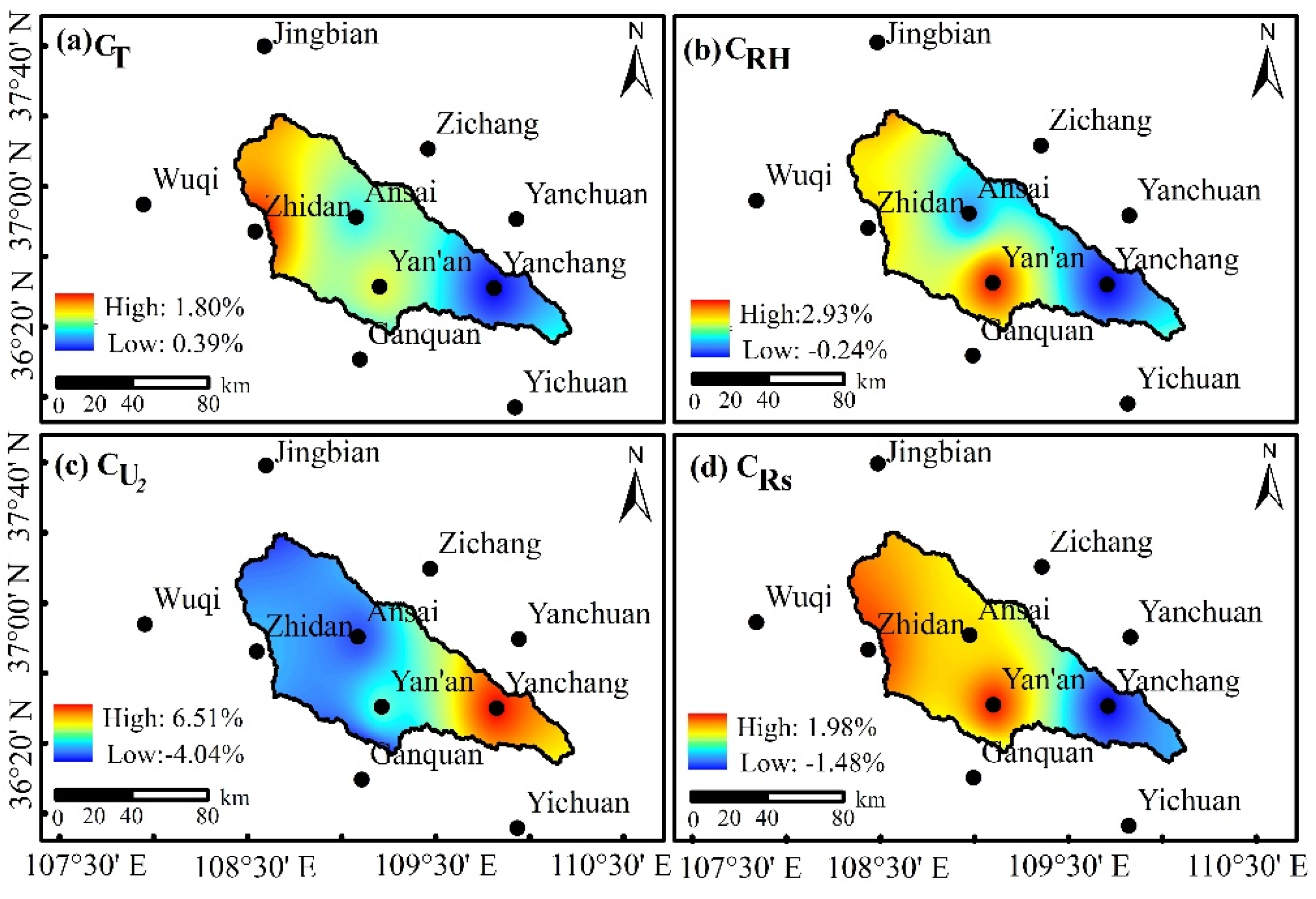
3.3. Contribution Rate of Meteorological Factors
4. Discussion
4.1. Dominant Factors of ET0 Variation in the YRB
4.2. Evaporation Paradox in the YRB
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IPCC. Summary for Policymakers. In Global Warming of 1.5 C. An IPCC Special Report on the Impacts of Global Warming of 1.5 C Above Pre-Industrial Levels and Related Global Greenhouse Gas Emission Pathways, in the Context of Strengthening the Global Response to the Threat of Climate Change, Sustainable Development, and Efforts to Eradicate Poverty; Masson-Delmotte, V.P., Zhai, H.-O., Pörtner, D., Roberts, J., Skea, P.R., Shukla, A., Pirani, W., Moufouma-Okia, C., Péan, R., Pidcock, S., Eds.; IPCC: Geneva, Switzerland, 2008; in press. [Google Scholar]
- Zhou, J. Spatial and Temporal Variation of Droughts Over China Based on Various Potential Evapotranspiration Formulas; Nanjing University of Information Science and Technology: Nanjing, China, 2019. [Google Scholar]
- Food and Agriculture Organization of the United Nations. Crop Evapotranspiration: Guidelines for Computing Crop Requirements; Food & Agriculture Organization: Rome, Italy, 1998. [Google Scholar]
- Li, X.C. Spatio-Temporal Variation of Actual Evapotranspiration in the Pearl, Haihe and Tarim Basins of China; Nanjing University of Information Science and Technology: Nanjing, China, 2013. [Google Scholar]
- Onyutha, C. Statistical analyses of potential evapotranspiration changes over the period 1930–2012 in the Nile River riparian countries. Agric. For. Meteorol. 2016, 226-227, 80–95. [Google Scholar] [CrossRef]
- Cohen, S.; Ianetz, A.; Stanhill, G. Evaporative climate changes at Bet Dagan, Israel, 1964–1998. Agric. For. Meteorol. 2002, 111, 83–91. [Google Scholar] [CrossRef]
- Yin, Y.; Wu, S.; Chen, G.; Dai, E. Attribution analyses of potential evapotranspiration changes in China since the 1960s. Theor. Appl. Clim. 2010, 101, 19–28. [Google Scholar] [CrossRef]
- Roderick, M.L.; Farquhar, G.D. The cause of decreased pan evaporation over the past 50 years. Science 2002, 298, 1410–1411. [Google Scholar]
- Roderick, M.L.; Farquhar, G.D. Changes in Australian pan evaporation from 1970 to 2002. Int. J. Clim. 2004, 24, 1077–1090. [Google Scholar] [CrossRef]
- Burn, H.D.; Hesch, M.N. Trends in evaporation for the Canadian Prairies. J. Hydrol. 2007, 336, 61–73. [Google Scholar] [CrossRef]
- Fu, G.; Charles, S.P.; Yu, J. A critical overview of pan evaporation trends over the last 50 years. Clim. Chang. 2009, 97, 193–214. [Google Scholar] [CrossRef]
- Dinpashoh, Y.; Jhajharia, D.; Fakheri-Fard, A.; Singh, V.P.; Kahya, E. Trends in reference crop evapotranspiration over Iran. J. Hydrol. 2011, 399, 422–433. [Google Scholar] [CrossRef]
- Chattopadhyay, N.; Hulme, M. Evaporation and potential evapotranspiration in India under conditions of recent and future climate change. Agric. For. Meteorol. 1997, 87, 55–73. [Google Scholar] [CrossRef]
- Liu, C.M.; Zhang, D.; Liu, X.M.; Zhao, C.S. Spatial and temporal change in the potential evapotranspiration sensi-tivity to meteorological factors in China (1960–2007). J. Geogr. Sci. 2012, 22. [Google Scholar] [CrossRef]
- Liu, Q.; Yang, Z.F.; Cui, B.S.; Sun, T. The temporal trends of reference evapotranspiration and its sensitivity to key meteoro-logical variables in the Yellow River Basin, China. Hydrol. Process. 2010, 24, 2171–2181. [Google Scholar]
- Gong, L.B.; Xu, C.Y.; Chen, D.L.; Halldin, S.; Chen, Y.Q. Sensitivity of the Penman-Monteith reference evapotranspi-ration to key climatic variables in the Changjiang (Yangtze River) basin. J. Hydrol. Amst. 2006, 329, 620–629. [Google Scholar] [CrossRef]
- Wang, Y.; Jiang, T.; Bothe, O.; Fraedrich, K. Changes of pan evaporation and reference evapotranspiration in the Yangtze River basin. Theor. Appl. Clim. 2006, 90, 13–23. [Google Scholar] [CrossRef]
- Luo, K.; Tao, F.; Deng, X.; Moiwo, J.P. Changes in potential evapotranspiration and surface runoff in 1981-2010 and the driving factors in Upper Heihe River Basin in Northwest China. Hydrol. Process. 2016, 31, 90–103. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Liu, C.M.; Tang, Y.H.; Yang, Y.H. Trends in pan evaporation and reference and actual evapotran-spiration across the Tibetan Plateau. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, F.L.; Liu, W.Z. Spatiotemporal characteristics of reference evapotranspiration during 1961–2009 and its pro-jected changes during 2011–2099 on the Loess Plateau of China. Agricultural & Forest Meteorology; Elsevier: Amsterdam, The Netherlands, 2012; Volume 154, pp. 147–155. [Google Scholar]
- Liu, X.M.; Zheng, H.X.; Liu, C.M.; Cao, Y.J. Sensitivity of the potential evapotranspiration to key climatic variables in the Haihe River Basin. Resour. Sci. 2009, 31, 1470–1476. [Google Scholar]
- Su, X.L.; Song, Y.; Niu, J.P.; Ji, F. Sensitivity and attribution of potential evapotranspiration in Jinghuiqu irrigation district. J. Nat. Resour. 2015, 1, 115–123. [Google Scholar]
- Yang, X.N. Effects of Landscape Pattern on Runoff Andsediment in the Loess Plateau: A Multi-Scale Study. Dissertation Submitted to Northwest A & F University, Xianyang, China, 2019. [Google Scholar]
- Jiao, J.Y.; Wang, Z.J.; Wei, Y.H.; Su, Y.; Cao, B.T.; Li, Y.J. Characteristics of erosion sediment yield with extreme rainstorms in Yanhe Watershed based on field. Trans. Chin. Soc. Agric. Eng. 2017, 33, 159–167. [Google Scholar]
- Zhang, X.L.; Xiong, L.H.; Lin, L.; Long, H.F. Application of five potential evapotranspiration equations in Hanjiang Basin. Arid. Land Geogr. 2012, 35, 229–237. [Google Scholar]
- McCuen, R.H. A Sensitivity and Error Analysis Cf Procedures Used for Estimating Evaporation. JAWRA J. Am. Water Resour. Assoc. 1974, 10, 486–497. [Google Scholar] [CrossRef]
- Beven, K. A sensitivity analysis of the Penman-Monteith actual evapotranspiration estimates. J. Hydrol. 1979, 44, 169–190. [Google Scholar] [CrossRef]
- Rana, G.; Katerji, N. A Measurement Based Sensitivity Analysis of the Penman-Monteith Actual Evapotranspiration Model for Crops of Different Height and in Contrasting Water Status. Theor. Appl. Clim. 1998, 60, 141–149. [Google Scholar] [CrossRef]
- Hupet, F.; Vanclooster, M. Effect of the sampling frequency of meteorological variables on the estimation of the reference evapotranspiration. J. Hydrol. 2001, 243, 192–204. [Google Scholar] [CrossRef]
- Mann, H.B. Non-Parametric Test against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Measures; Charles Griffin: London, UK, 1975; p. 202. [Google Scholar]
- Lin, Z.H.; Mo, X.G.; Li, H.X.; Li, H.B. Comparison of Three Spatial Interpolation Methods for Climate Variables in China. Acta Geogr. Sin. 2002, 57, 47–56. [Google Scholar]



| Time | Mean | M-K Statistics | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T/°C | RH/% | U2/(m s−1) | Rs/(MJ mm−2 Day−1) | P/mm | ET0/(mm) | T | RH | U2 | Rs | P | ET0 | |
| Jan. | −6.07 | 53.85 | 1.03 | 304.92 | 3.00 | 23.37 | 1.68 | 0.72 | 0.93 | 0.51 | 0.63 | 0.49 |
| Feb. | −2.05 | 52.44 | 1.13 | 336.89 | 5.65 | 33.90 | 2.73 | 1.1 | −0.09 | 0.61 | 2.14 | 1.7 |
| Mar. | 4.33 | 50.53 | 1.32 | 478.71 | 14.28 | 66.43 | 3.12 | −2.31 | −0.19 | 2.42 | −2.33 | 3.36 |
| Apr. | 11.76 | 46.48 | 1.48 | 580.06 | 24.05 | 104.39 | 2.24 | −0.47 | −3.03 | 1.44 | 1.07 | 0.49 |
| May. | 17.20 | 50.93 | 1.40 | 664.94 | 43.40 | 133.22 | 0.75 | −0.37 | −2.07 | 1 | 0.54 | 0.28 |
| Jun. | 21.29 | 57.66 | 1.26 | 655.36 | 60.54 | 139.72 | 1.68 | −1.17 | −0.93 | 0.93 | −1.1 | 1 |
| Jul. | 22.99 | 69.01 | 1.11 | 631.68 | 115.24 | 134.55 | 2.63 | −1.24 | 0.72 | 0.72 | 0.3 | 1.63 |
| Aug. | 21.24 | 74.17 | 1.03 | 573.99 | 107.19 | 114.22 | 1.7 | −2.21 | 1.12 | −0.42 | −1 | 0.7 |
| Sep. | 16.04 | 74.92 | 0.98 | 453.95 | 71.85 | 78.29 | 2.82 | −0.21 | 1.84 | −1.86 | 0.98 | −0.49 |
| Oct. | 9.63 | 70.20 | 1.02 | 384.49 | 34.76 | 53.65 | 1.61 | 1.26 | 0.05 | −1.05 | 0.72 | −0.21 |
| Nov. | 2.22 | 62.64 | 1.07 | 304.19 | 12.64 | 32.13 | 1.98 | −0.19 | −0.23 | −0.02 | −0.3 | 0.68 |
| Dec. | −4.23 | 57.03 | 1.04 | 276.63 | 2.60 | 22.07 | 0.89 | −0.68 | 1.35 | 0.63 | 0.56 | 0.96 |
| Year | 9.59 | 60.05 | 1.16 | 5645.81 | 495.19 | 935.92 | 3.8 | −1.12 | −0.7 | 0.56 | 0.42 | 1.65 |
| Time | Mean | M-K Statistics | ||||||
|---|---|---|---|---|---|---|---|---|
| ST | SRH | SU2 | SRs | ST | SRH | SU2 | SRs | |
| Jan. | −0.12 | −0.51 | 0.32 | 0.09 | 1.33 | −2.31 | 1.35 | −0.56 |
| Feb. | −0.05 | −0.43 | 0.25 | 0.27 | 2.10 | −1.77 | 0.56 | −0.58 |
| Mar. | 0.04 | −0.36 | 0.20 | 0.40 | −0.33 | 1.82 | 2.82 | −2.21 |
| Apr. | 0.09 | −0.28 | 0.20 | 0.48 | 0.19 | 0.89 | 0.16 | 1.12 |
| May. | 0.12 | −0.25 | 0.16 | 0.56 | −0.19 | 1.07 | 0.30 | 0.09 |
| Jun. | 0.14 | −0.24 | 0.13 | 0.63 | −0.89 | 1.24 | 0.93 | −0.07 |
| Jul. | 0.19 | −0.28 | 0.09 | 0.70 | −1.98 | −0.02 | 1.70 | −1.07 |
| Aug. | 0.22 | −0.33 | 0.07 | 0.70 | −2.54 | −1.37 | 2.63 | −2.83 |
| Sep. | 0.20 | −0.44 | 0.09 | 0.61 | −1.33 | −2.77 | 1.37 | −2.38 |
| Oct. | 0.13 | −0.54 | 0.16 | 0.43 | 0.61 | −1.82 | −0.42 | −0.37 |
| Nov. | 0.02 | −0.62 | 0.29 | 0.16 | 1.00 | −0.91 | 1.12 | −1.19 |
| Dec. | −0.07 | −0.61 | 0.37 | −0.01 | 2.84 | −0.93 | 1.40 | −1.21 |
| Year | 0.08 | −0.41 | 0.19 | 0.42 | 0.82 | −1.51 | 2.80 | −1.82 |
| Station | Mean | M-K Statistics | ||||||
|---|---|---|---|---|---|---|---|---|
| ST | SRH | SU2 | SRs | ST | SRH | SU2 | SRs | |
| Jingbian | 0.03 | −0.46 | 0.26 | 0.34 | 1.12 | 3.05 | 2.89 | −0.40 |
| Wuqi | 0.07 | −0.36 | 0.17 | 0.43 | 0.56 | 2.07 | −0.07 | 1.54 |
| Zichang | 0.07 | −0.43 | 0.21 | 0.40 | 0.51 | −3.57 | 1.42 | −1.30 |
| Zhidan | 0.08 | −0.34 | 0.16 | 0.45 | 2.77 | −1.21 | 2.10 | −0.77 |
| Ansai | 0.08 | −0.45 | 0.20 | 0.41 | 1.26 | −0.16 | 1.07 | 0.72 |
| Yan’an | 0.08 | −0.44 | 0.21 | 0.41 | −1.56 | 0.05 | 1.33 | −1.30 |
| Ganquan | 0.09 | −0.46 | 0.17 | 0.45 | 2.68 | 3.38 | 0.54 | 1.72 |
| Yanchuan | 0.08 | −0.28 | 0.17 | 0.44 | 0.61 | −2.68 | 4.24 | −3.36 |
| Yanchang | 0.10 | −0.39 | 0.18 | 0.45 | −1.72 | −2.96 | 3.36 | −3.22 |
| Yichuan | 0.09 | −0.45 | 0.20 | 0.42 | −1.56 | −2.49 | 3.61 | −3.84 |
| Time | RT/% | CT/% | RRH/% | CRH/% | RU2/% | CU2/% | RRS/% | CRS/% |
|---|---|---|---|---|---|---|---|---|
| Jan. | −16.15 | 1.95 | 3.10 | −1.59 | 2.34 | 0.76 | 0.53 | 0.05 |
| Feb. | −123.61 | 6.68 | 8.25 | −3.57 | 0.71 | 0.18 | 1.79 | 0.49 |
| Mar. | 63.48 | 2.86 | −23.68 | 8.61 | −4.53 | −0.92 | 11.87 | 4.79 |
| Apr. | 12.65 | 1.15 | −4.60 | 1.26 | −23.55 | −4.70 | 5.30 | 2.54 |
| May. | 2.77 | 0.33 | −3.47 | 0.88 | −22.31 | −3.66 | 4.09 | 2.31 |
| Jun. | 4.57 | 0.64 | −6.65 | 1.58 | −11.78 | −1.57 | 2.65 | 1.68 |
| Jul. | 6.11 | 1.16 | −5.64 | 1.59 | 3.95 | 0.34 | 2.25 | 1.58 |
| Aug. | 4.48 | 0.96 | −6.40 | 2.09 | 6.20 | 0.43 | −2.29 | −1.60 |
| Sep. | 9.70 | 1.95 | −0.57 | 0.25 | 8.53 | 0.73 | −9.20 | −5.58 |
| Oct. | 11.47 | 1.44 | 4.18 | −2.25 | −5.09 | −0.81 | −6.80 | −2.89 |
| Nov. | 66.20 | 1.26 | −0.04 | 0.03 | −4.10 | −1.17 | −2.04 | −0.33 |
| Dec. | −21.83 | 1.46 | −4.92 | 3.01 | 10.80 | 3.96 | 2.62 | −0.04 |
| Year | 14.35 | 1.09 | 2.09 | −0.85 | −3.24 | −0.63 | 1.32 | 0.55 |
| Station | RT/% | CT/% | RRH/% | CRH/% | RU2/% | CU2/% | RRS/% | CRS/% |
|---|---|---|---|---|---|---|---|---|
| Jingbian | 27.75 | 2.02 | −9.00 | 3.91 | −31.68 | −6.76 | 2.79 | 1.12 |
| Wuqi | 12.34 | 0.94 | −3.92 | 1.35 | −17.78 | −2.82 | 8.81 | 3.95 |
| Zichang | 16.19 | 1.25 | 0.74 | −0.34 | 10.52 | 2.10 | −0.21 | −0.08 |
| Zhidan | 19.71 | 1.86 | −4.56 | 2.10 | −8.13 | −1.40 | 4.27 | 1.90 |
| Ansai | 11.10 | 0.89 | −1.46 | 0.40 | −18.65 | −3.13 | 2.23 | 0.98 |
| Yan’an | 12.91 | 1.25 | −7.57 | 2.93 | 0.16 | 0.03 | 4.43 | 1.98 |
| Ganquan | 18.00 | 0.54 | −2.99 | 1.37 | −35.71 | −9.16 | −2.18 | −0.74 |
| Yanchuan | 8.27 | 0.54 | −0.51 | 0.18 | 40.06 | 6.90 | −1.17 | −0.50 |
| Yanchang | 4.70 | 0.39 | 0.74 | −0.24 | 34.65 | 6.51 | −3.42 | −1.48 |
| Yichuan | 15.34 | 1.33 | −4.67 | 2.12 | 8.13 | 1.64 | −2.58 | −1.09 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Y.; Gao, P.; Mu, X. Influence of Meteorological Factors on the Potential Evapotranspiration in Yanhe River Basin, China. Water 2021, 13, 1222. https://doi.org/10.3390/w13091222
Luo Y, Gao P, Mu X. Influence of Meteorological Factors on the Potential Evapotranspiration in Yanhe River Basin, China. Water. 2021; 13(9):1222. https://doi.org/10.3390/w13091222
Chicago/Turabian StyleLuo, Yu, Peng Gao, and Xingmin Mu. 2021. "Influence of Meteorological Factors on the Potential Evapotranspiration in Yanhe River Basin, China" Water 13, no. 9: 1222. https://doi.org/10.3390/w13091222
APA StyleLuo, Y., Gao, P., & Mu, X. (2021). Influence of Meteorological Factors on the Potential Evapotranspiration in Yanhe River Basin, China. Water, 13(9), 1222. https://doi.org/10.3390/w13091222







