Probabilistic Approach to Precipitation-Runoff Relation in a Mountain Catchment: A Case Study of the K?odzka Valley in Poland
Abstract
:1. Introduction
2. Study Area and Methods
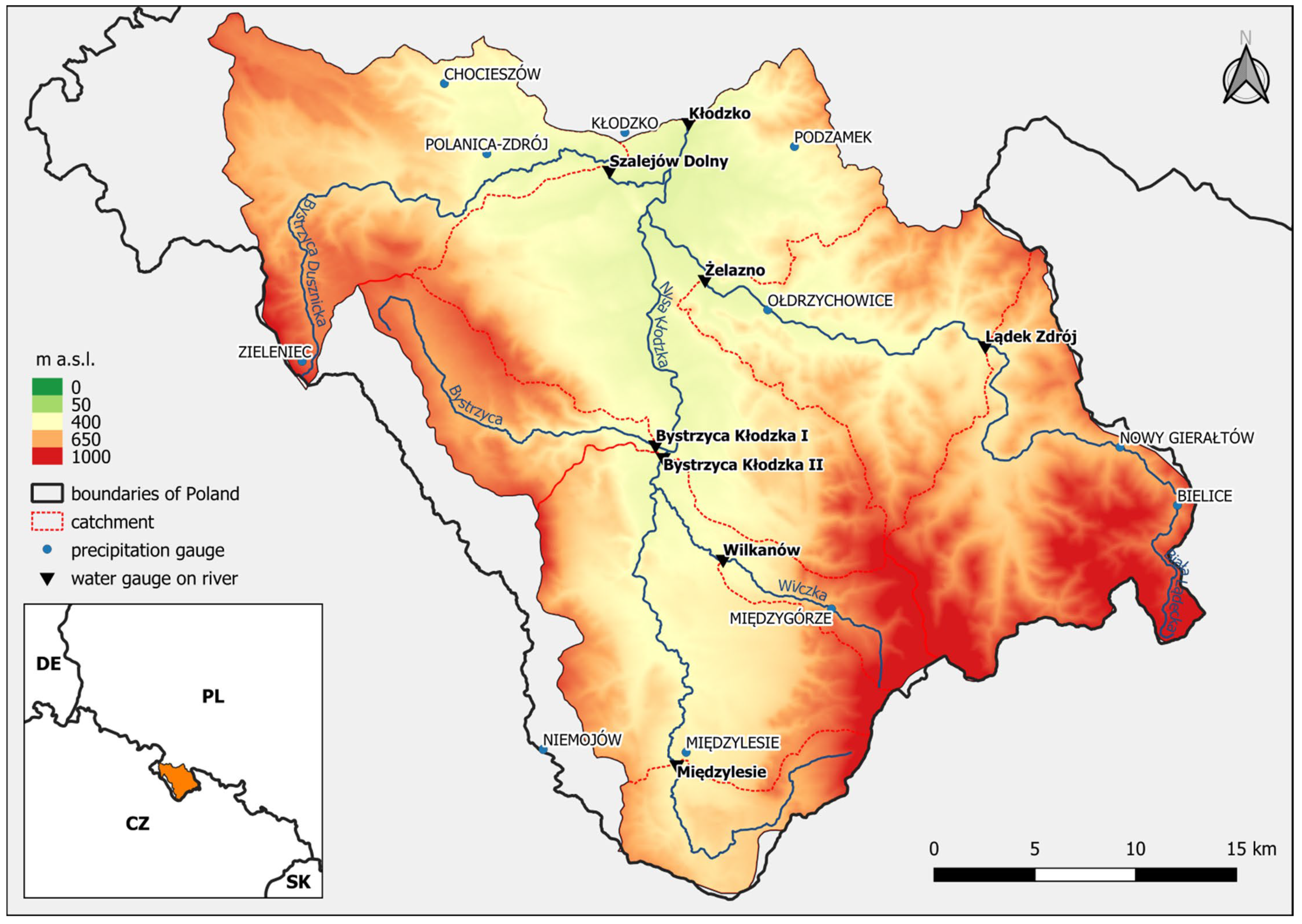
2.1. Study Area
2.2. Data Sets
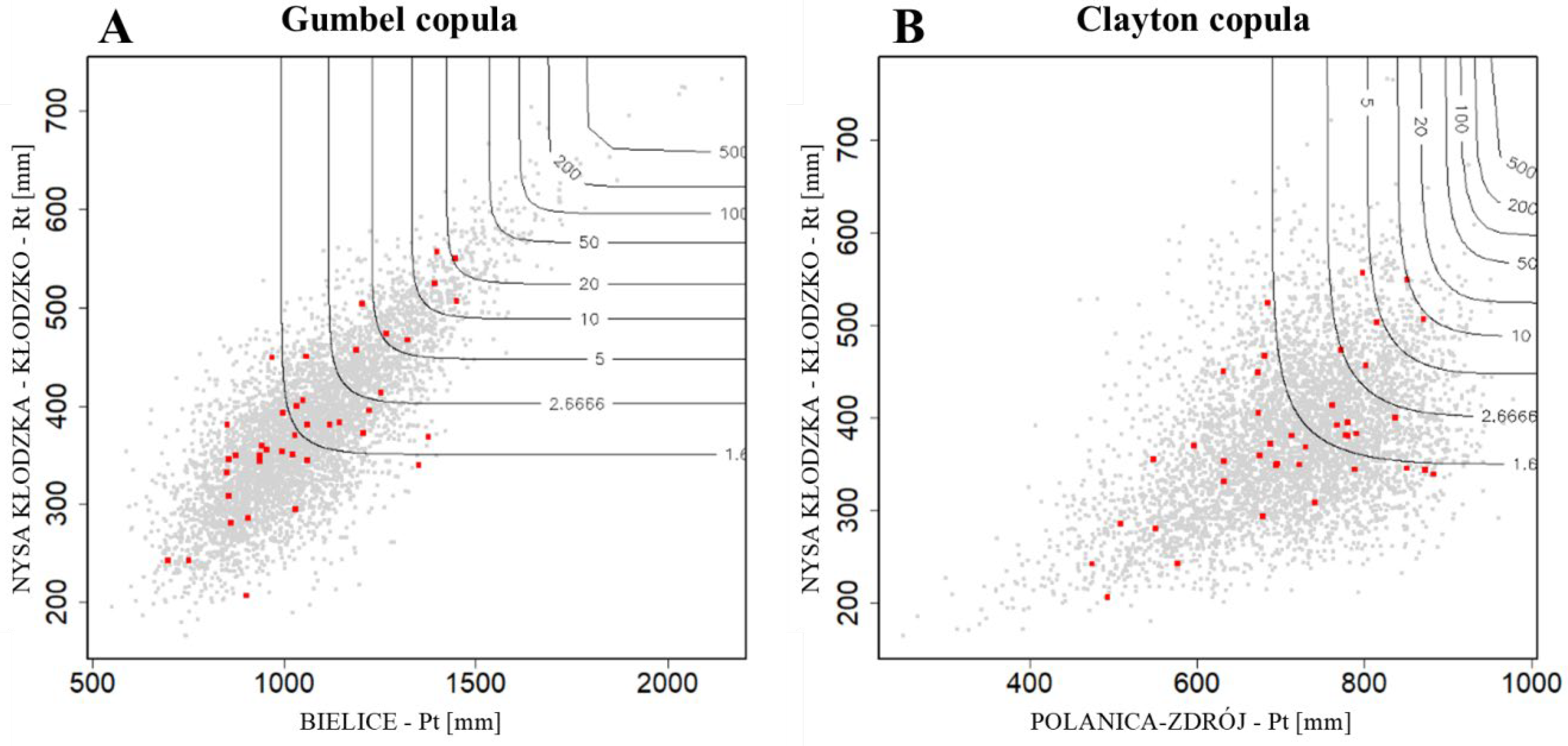
2.3. Methods
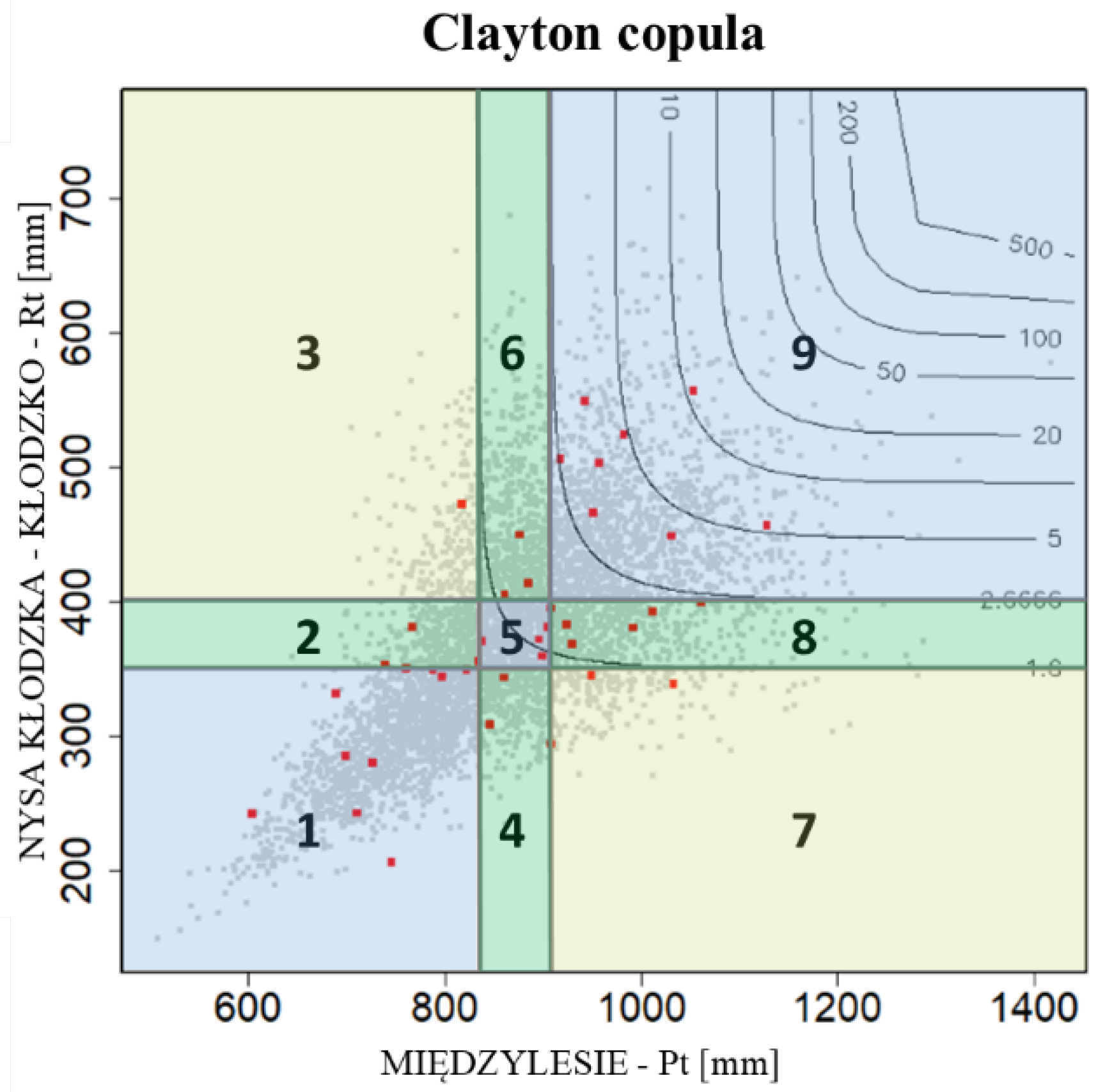
- Sector 1: LPt–LRt (X ≤ Pt62.5%, Y ≤ Rt62.5%);
- Sector 5: MPt–MRt (Pt62.5% < X ≤ Pt37.5%, Rt62.5% < Y ≤ Rt37.5%);
- Sector 9: HPt–HRt (X > Pt37.5%, Y > Rt37.5%);
- Sector 2: LPt–MRt (X ≤ Pt62.5%, Rt62.5% < Y ≤ Rt37.5%);
- Sector 3: LPt–HRt (X ≤ Pt62.5%, Y > Rt37.5%);
- Sector 4: MPt–LRt (Pt62.5% < X ≤ Pt37.5%, Y ≤ Rt62.5%);
- Sector 6: MPt–HRt (Pt62.5% < X ≤ Pt37.5%, Y > Rt37.5%);
- Sector 7: HPt–LRt (X > Pt37.5%, Y ≤ Rt62.5%);
- Sector 8: HPt–MRt (X > Pt37.5%, R62.5% < Y ≤ Rt37.5%).
- Probable values with a probability of occurrence of <62.5% were designated as LPt/LRt;
- Probable values with a probability of occurrence in a range >62.5% and <37.5% were designated as MPt/MRt;
- Probable values with a probability of occurrence > 37.5% were designated as HPt/HRt.
3. Results
3.1. Probable Values of Pt and Rt
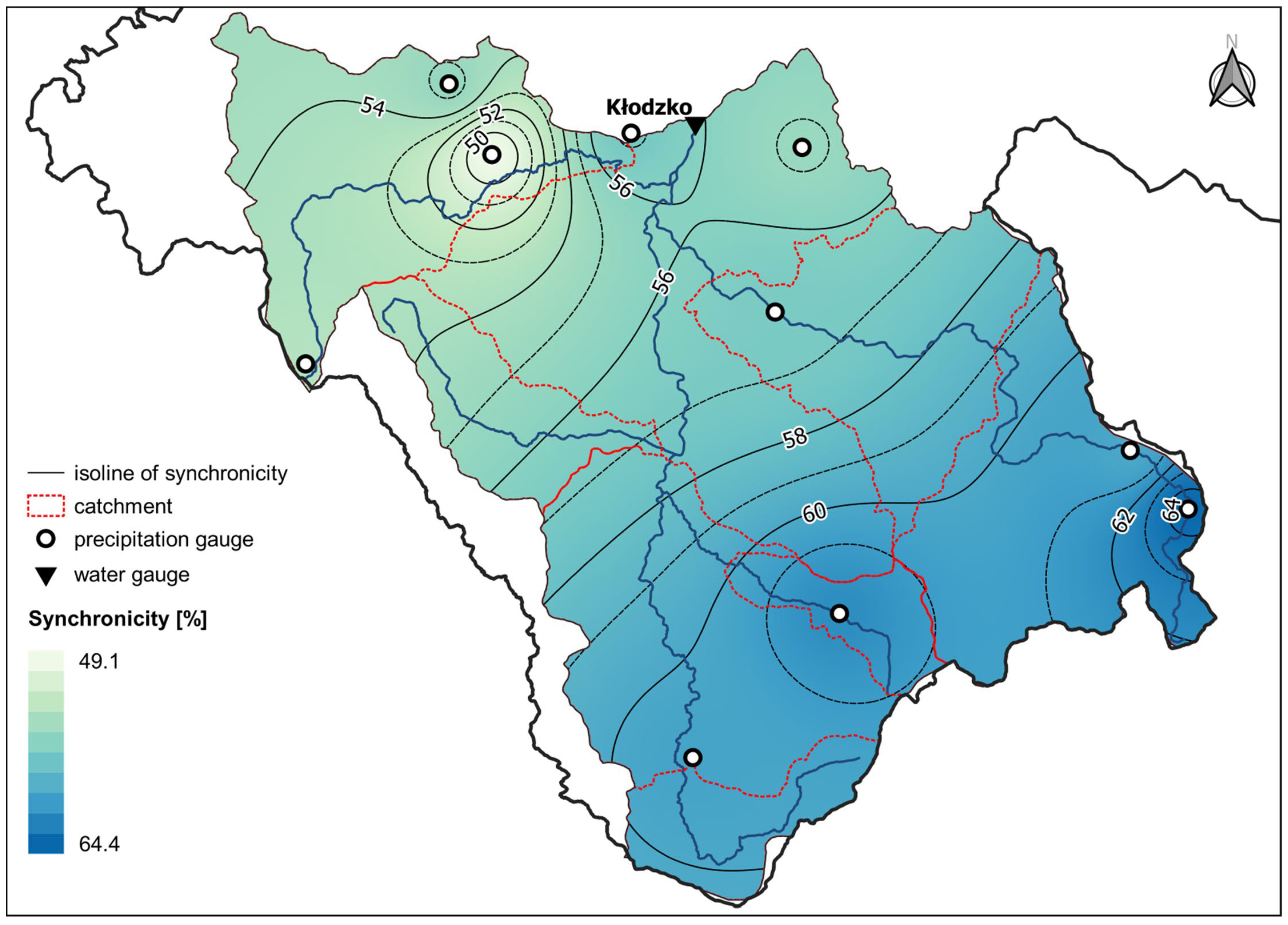
3.2. Synchronicity of Pt and Rt
4. Discussion and Conclusions
- Copulas can be used in studies on regional precipitation-runoff relations and to determine probabilistic values of analyzed variables.
- The precipitation-runoff relationship can be presented as the synchronous occurrence of these variables, and graphically depicted using isolines of synchronicity.
- The eastern tributaries of the Nysa Kłodzka River are more hydrologically active than the western ones, and they determine the amount of water resources of the study area.
- The regime features of rivers in KV depend on the type and distribution of precipitation over the year, and consequently on its relation with runoff in the sub-catchments of the Nysa Kłodzka River and its tributaries.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sitterson, J.; Knightes, C.; Parmar, R.; Wolfe, K.; Muche, M.; Avant, B. An Overview of Rainfall-Runoff Model Types; U.S. Environmental Protection Agency: Washington, DC, USA, 2017.
- Moradkhani, H.; Sorooshian, S. General Review of Rainfall-Runoff Modeling: Model Calibration, Data Assimilation, and Uncertainty Analysis. In Hydrological Modelling and the Water Cycle; Sorooshian, S., Hsu, K.L., Coppola, E., Tomassetti, B., Verdecchia, M., Visconti, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–24. [Google Scholar] [CrossRef] [Green Version]
- Beven, K.J. Rainfall-Runoff Modelling: The Primer, 2nd ed.; Wiley-Blackwell: Hoboken, NJ, USA, 2012; ISBN 978-0-470-71459-1. [Google Scholar]
- Teng, F.; Huang, W.R.; Cai, Y.; Zheng, C.M.; Zou, S.B. Application of Hydrological Model PRMS to Simulate Daily Rainfall Runoff in Zamask-Yingluoxia Subbasin of the Heihe River Basin. Water 2017, 9, 769. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.-Y. Application of NRCS-CN Method for Estimation of Watershed Runoff and Disaster Risk. Geomat. Nat. Hazards Risk 2019, 10, 2220–2238. [Google Scholar] [CrossRef] [Green Version]
- Młyński, D. Analysis of Problems Related to the Calculation of Flood Frequency Using Rainfall-Runoff Models: A Case Study in Poland. Sustainability 2020, 12, 7187. [Google Scholar] [CrossRef]
- Młyński, D.; Wałęga, A. Identification of the Relationship between Rainfall and the CN Parameter in Western Carpathian Mountain Catchments in Poland. Sustainability 2020, 12, 9317. [Google Scholar] [CrossRef]
- Młyński, D.; Wałęga, A.; Książek, L.; Florek, J.; Petroselli, A. Possibility of Using Selected Rainfall-Runoff Models for Determining the Design Hydrograph in Mountainous Catchments: A Case Study in Poland. Water 2020, 12, 1450. [Google Scholar] [CrossRef]
- Bednorz, E.; Wrzesiński, D.; Tomczyk, A.M.; Jasik, D. Classification of Synoptic Conditions of Summer Floods in Polish Sudeten Mountains. Water 2019, 11, 1450. [Google Scholar] [CrossRef] [Green Version]
- Wrona, B. Meteorological and Morphological Conditions of Extreme Precipitation in the Upper and Middle Odra River Basin; Materiały Badawcze, Seria: Meteorologia 41; IMGW: Warszawa, Poland, 2008. (In Polish) [Google Scholar]
- Szalińska, W.; Urban, G.; Otop, I. Assessment of Precipitation Volumes causing Summer Floods in the Middle Odra River Basin. Infrastrukt. Ekol. Teren. Wiej. 2008, 9, 227–238. (In Polish) [Google Scholar]
- Łach, J. The History of Floods in the Kłodzko Land and their Impact on the Direction of Transformation of the Valley Bottoms of the Nysa Kłodzka and Biała Lądecka Rivers. Nauka Przyr. Technol. 2009, 3, 93. (In Polish) [Google Scholar]
- Łach, J. The Role of Torrential Rains and Floods in Modeling the Relief of the Kłodzka Valley and the Western Mountain Ranges of the Eastern Sudetes; Instytut Geografii i Rozwoju Regionalnego Uniwersytet Wrocławski: Wrocław, Poland, 2012; ISBN 978-83-62673-24-7. (In Polish) [Google Scholar]
- Rutkowska, A.; Willems, P.; Niedzielski, T. Relation between Design Floods based on Daily Maxima and Daily Means: Use of the Peak Over Threshold Approach in the Upper Nysa Kłodzka Basin (SW Poland). Geomat. Nat. Hazards Risk 2016, 8, 585–606. [Google Scholar] [CrossRef]
- Niedzielski, T.; Miziński, B. Real-Time Hydrograph Modelling in the Upper Nysa Kłodzka River Basin (SW Poland): A Two-Model Hydrologic Ensemble Prediction Approach. Stoch. Environ. Res. Risk Assess. 2017, 31, 1555–1576. [Google Scholar] [CrossRef] [Green Version]
- Stodolak, R.; Baran, J.; Knap, E. Influence of the Assumed Time Distributions of Rain Variability on the Results of RainFall-Runoff Modeling. Inż. Ekol. 2018, 19, 87–93. (In Polish) [Google Scholar] [CrossRef]
- Jeziorska, J.; Niedzielski, T. Applicability of TOPMODEL in the Mountainous Catchments in the Upper Nysa Kłodzka River Basin (SW Poland). Acta Geophys. 2018, 66, 203–222. [Google Scholar] [CrossRef] [Green Version]
- Olichwer, T. Long-Term Variability of Water Resources in Mountainous Areas: Case Study—Klodzko Region (SW Poland). Carpathian J. Earth Environ. Sci. 2018, 14, 29–38. [Google Scholar] [CrossRef]
- Perz, A. Characteristics of the Flow Regime of the Kłodzka Valley Rivers. Badania Fizjograficzne Seria A Geografia Fizyczna 2019, 70, 65–83. (In Polish) [Google Scholar] [CrossRef]
- Xing, Z.Q.; Yan, D.H.; Zhang, C.; Wang, G.; Zhang, D.D. Spatial Characterization and Bivariate Frequency Analysis of Precipitation and Runoff in the Upper Huai River Basin, China. Water Resour. Manag. 2015, 29, 3291–3304. [Google Scholar] [CrossRef]
- Perz, A.; Sobkowiak, L.; Wrzesiński, D. Spatial Differentiation of the Maximum River Runoff Synchronicity in the Warta River Catchment, Poland. Water 2020, 12, 1782. [Google Scholar] [CrossRef]
- Sobkowiak, L.; Perz, A.; Wrzesiński, D.; Faiz, M.A. Estimation of the River Flow Synchronicity in the Upper Indus River Basin Using Copula Functions. Sustainability 2020, 12, 5122. [Google Scholar] [CrossRef]
- Kondracki, J. Regional Geography of Poland; Wydawnictwo Naukowe PWN: Warszawa, Poland, 2013. (In Polish) [Google Scholar]
- Solon, J.; Borzyszkowski, J.; Jodłowski, M.; Kistowski, M.; Kot, R.; Krąż, P.; Lechnio, J.; Macias, A.; Majchrowska, A.; Malinowska, E.; et al. Physico-Geographical Mesoregions of Poland: Verification and Adjustment of Boundaries on the Basis of Contemporary Spatial Data. Geogr. Pol. 2018, 91, 143–170. [Google Scholar] [CrossRef]
- Staffa, M. Dictionary of Tourist Geography of the Sudetes. Vol. 15: The Kłodzko Valley and the Upper Nysa Trench; I-BiS: Wrocław, Poland, 1993; pp. 315–318. (In Polish) [Google Scholar]
- Regional Water Management Authority (RZGW) in Wrocław. Development of the Nysa Kłodzka River Balance Catchment Characteristics. 2013. Available online: https://wroclaw.rzgw.gov.pl/files_mce/Planowanie%20w%20gospodarowaniu%20wodami/charakterystyka_nysa_klodzka.pdf (accessed on 10 March 2021). (In Polish)
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated World Map of the Köppen-Geiger Climate Classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef] [Green Version]
- Wrzesiński, D. Use of Entropy in the Assessment of Uncertainty of River Runoff Regime in Poland. Acta Geophys. 2016, 64, 1825–1839. [Google Scholar] [CrossRef] [Green Version]
- Wrzesiński, D. Flow Regime Patterns and Their Changes. In Management of Water Resources in Poland; Zeleňáková, M., Kubiak-Wójcicka, K., Negm, A.M., Eds.; Springer Water: Cham, Switzerland, 2021; pp. 163–180. [Google Scholar] [CrossRef]
- Sklar, A. Fonction de re´Partition an Dimensions et Leurs Marges; Publications de L´Institute de Statistique de l’Université de Paris: Paris, France, 1959; Volume 8, pp. 229–231. [Google Scholar]
- Fan, L.L.; Wang, H.R.; Wang, C.; Lai, W.L.; Zhao, Y. Exploration of Use of Copulas in Analysing the Relationship between Precipitation and Meteorological Drought in Beijing, China. Adv. Meteorol. 2017, 2017, 1–11. [Google Scholar] [CrossRef]
- Akaike, H. A New Look at the Statistical Model Identification. IEEE Trans. Autom. Control. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Nelsen, R.B. An Introduction to Copulas; Springer: New York, NY, USA, 1999. [Google Scholar]
- Chen, L.; Guo, S. Copulas and Its Application in Hydrology and Water Resources; Springer: Singapore, 2019. [Google Scholar] [CrossRef]
- Genest, C.; Favre, A.-C. Everything You Always Wanted to Know about Copula Modeling but Were Afraid to Ask. J. Hydrol. Eng. 2007, 12, 347–368. [Google Scholar] [CrossRef]
- Zhang, J.; Ding, Z.; You, J. The Joint Probability Distribution of Runoff and Sediment and its Change Characteristics with Multi-Time Scales. J. Hydrol. Hydromech. 2014, 62, 218–225. [Google Scholar] [CrossRef] [Green Version]
- Gu, H.; Yu, Z.; Li, G.; Ju, Q. Nonstationary Multivariate Hydrological Frequency Analysis in the Upper Zhanghe River Basin, China. Water 2018, 10, 772. [Google Scholar] [CrossRef] [Green Version]
- Wrzesiński, D. Uncertainty of Flow Regime Characteristics of Rivers in Europe. Quaest. Geogr. 2013, 32, 43–53. [Google Scholar] [CrossRef] [Green Version]
- Wrzesiński, D.; Sobkowiak, L. Detection of Changes in Flow Regime of Rivers in Poland. J. Hydrol. Hydromech. 2018, 66, 55–64. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Wang, B.; Li, H. Analysis of Asynchronism-Synchronism of Regional Precipitation in Inter-Basin Water Transfer Areas. Trans. Tianjin Univ. 2012, 18, 384–392. [Google Scholar] [CrossRef]
- Chen, J.; Gu, S.X.; Zhang, T. Synchronous-Asynchronous Encounter Probability Analysis of High-Low Runoff for Jinsha River, China, using Copulas. MATEC Web Conf. 2018, 246, 01094. [Google Scholar] [CrossRef]
- Zhou, N.Q.; Zhao, L.; Shen, X.P. Copula-based Probability Evaluation of Rich-Poor Runoff and Sediment Encounter in Dongting Lake Basin. Sci. Geogr. Sin. 2014, 34, 242–248. (In Chinese) [Google Scholar] [CrossRef]
- You, Q.; Jiang, H.; Liu, Y.; Liu, Z.; Guan, Z. Probability Analysis and Control of River Runoff–sediment Characteristics based on Pair-Copula Functions: The Case of the Weihe River and Jinghe River. Water 2019, 11, 510. [Google Scholar] [CrossRef] [Green Version]
- Ozga-Zielinski, B.; Ciupak, M.; Adamowski, J.; Khalil, B.; Malard, J. Snow-Melt Flood Frequency Analysis by Means of Copula based 2D Probability Distributions for the Narew River in Poland. J. Hydrol. Reg. Stud. 2016, 6, 26–51. [Google Scholar] [CrossRef] [Green Version]
- Plewa, K.; Perz, A.; Wrzesiński, D.; Sobkowiak, L. Probabilistic Assessment of Correlations of Water Levels in Polish Coastal Lakes with Sea Water Level with the Application of Archimedean Copulas. Water 2019, 11, 1292. [Google Scholar] [CrossRef] [Green Version]
- Zhang, B.; Wang, S.; Wang, Y. Probabilistic Projections of Multidimensional Flood Risks at a Convection-Permitting Scale. Water Resour. Res. 2021, 57, 57. [Google Scholar] [CrossRef]
- Liu, Z.; Zhou, P.; Chen, X.; Guan, Y. A Multivariate Conditional Model for Streamflow Prediction and Spatial Precipitation Refinement. J. Geophys. Res. Atmos. 2015, 120. [Google Scholar] [CrossRef] [Green Version]
- Zhang, B.; Wang, S. Probabilistic Characterization of Extreme Storm Surges Induced by Tropical Cyclones. J. Geophys. Res. Atmos. 2021, 126. [Google Scholar] [CrossRef]

| Rain Gauge Station | Coordinates | Altitude (m a.s.l.) | Annual Precipitation (mm) | |
|---|---|---|---|---|
| Latitude | Longitude | |||
| Bielice | 50°16′ N | 17°00′ E | 695 | 935.9 |
| Chocieszów | 50°27′ N | 16°29′ E | 405 | 765.2 |
| Kłodzko | 50°26′ N | 16°36′ E | 356 | 577.2 |
| Międzygórze | 50°13′ N | 16°46′ E | 585 | 985.4 |
| Międzylesie | 50°09′ N | 16°40′ E | 450 | 860.3 |
| Niemojów | 50°09′ N | 16°34′ E | 570 | 1005.8 |
| Nowy Gierałtów | 50°18′ N | 16°57′ E | 635 | 900.4 |
| Ołdrzychowice | 50°21′ N | 16°43′ E | 340 | 747.5 |
| Podzamek | 50°25′ N | 16°43′ E | 400 | 765.3 |
| Polanica-Zdrój | 50°25′ N | 16°31′ E | 390 | 873.3 |
| Zieleniec | 50°19′ N | 16°23′ E | 845 | 1277.8 |
| River | Gauge | Coordinates | Altitude (m a.s.l.) | Catchment Area (km2) | Runoff Depth (mm) | River Regime Type 1 | |
|---|---|---|---|---|---|---|---|
| Latitude | Longitude | ||||||
| Nysa Kłodzka | Międzylesie | 50°09′ N | 16°39′ E | 426 | 49.7 | 444 | 2 |
| Bystrzyca Kłodzka II | 50°17′ N | 16°39′ E | 338 | 260.0 | 481 | 4 | |
| Kłodzko | 50°26′ N | 16°39′ E | 281 | 1084.0 | 375 | 4 | |
| Wilczka | Wilkanów | 50°14′ N | 16°41′ E | 363 | 35.1 | 715 | 2 |
| Bystrzyca | Bystrzyca Kłodzka I | 50°17′ N | 16°39′ E | 340 | 64.0 | 484 | 2 |
| Biała Lądecka | Lądek Zdrój | 50°20′ N | 16°52′ E | 421 | 166.0 | 649 | 4 |
| Żelazno | 50°22′ N | 16°40′ E | 317 | 305.0 | 508 | 4 | |
| Bystrzyca Dusznicka | Szalejów Dolny | 50°25′ N | 16°34′ E | 305 | 175.0 | 388 | 2 |
| Copula Family | Generator | Parameter | Kendall’s | |
|---|---|---|---|---|
| Clayton | ||||
| Gumbel–Hougaard | ||||
| Frank |
| Rain Gauge Station | Sectors | Syn. | Asyn. | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 5 | 9 | 2 | 4 | 8 | 6 | 3 | 7 | Total | Moderate | High | ||
| Nysa Kłodzka River at gauge Międzylesie | |||||||||||||
| Międzylesie | 27.7 | 10.2 | 26.9 | 7.2 | 7.5 | 7.4 | 7.7 | 2.4 | 2.9 | 64.8 | 35.2 | 29.8 | 5.3 |
| Nysa Kłodzka River at gauge Bystrzyca Kłodzka II | |||||||||||||
| Międzylesie | 26.4 | 8.8 | 22.6 | 7.2 | 6.2 | 10.1 | 10.2 | 3.7 | 4.8 | 57.8 | 42.2 | 33.7 | 8.5 |
| Międzygórze | 22.6 | 7.9 | 23.3 | 9.0 | 9.7 | 8.0 | 7.6 | 6.0 | 5.9 | 53.7 | 46.3 | 34.4 | 11.9 |
| Nysa Kłodzka River at gauge Kłodzko | |||||||||||||
| Międzylesie | 26.9 | 8.9 | 24.5 | 6.0 | 6.3 | 9.7 | 10.3 | 3.7 | 3.7 | 60.4 | 39.6 | 32.3 | 7.3 |
| Międzygórze | 27.8 | 8.8 | 25.4 | 6.7 | 6.8 | 9.3 | 9.2 | 2.9 | 3.2 | 62.0 | 38.0 | 32.0 | 6.1 |
| Bielice | 26.7 | 10.2 | 27.5 | 8.5 | 8.2 | 7.2 | 6.5 | 2.3 | 2.9 | 64.4 | 35.6 | 30.5 | 5.1 |
| Nowy Gierałtów | 25.5 | 9.1 | 25.5 | 8.2 | 9.4 | 7.4 | 7.0 | 4.2 | 3.8 | 60.0 | 40.0 | 32.0 | 8.0 |
| Ołdrzychowice | 23.9 | 8.1 | 24.8 | 9.0 | 9.1 | 7.8 | 7.1 | 5.1 | 5.1 | 56.8 | 43.2 | 33.0 | 10.2 |
| Zieleniec | 24.3 | 7.9 | 21.0 | 7.3 | 7.1 | 9.6 | 10.2 | 6.4 | 6.1 | 53.3 | 46.7 | 34.2 | 12.5 |
| Chocieszów | 25.6 | 8.0 | 21.6 | 6.7 | 6.6 | 10.2 | 10.2 | 5.5 | 5.6 | 55.2 | 44.8 | 33.7 | 11.1 |
| Polanica-Zdrój | 22.4 | 7.5 | 19.2 | 7.6 | 7.7 | 9.9 | 10.1 | 7.3 | 8.2 | 49.1 | 50.9 | 35.4 | 15.5 |
| Podzamek | 22.5 | 8.3 | 24.1 | 9.2 | 9.2 | 8.3 | 8.0 | 5.1 | 5.3 | 54.9 | 45.1 | 34.7 | 10.4 |
| Kłodzko | 26.4 | 8.5 | 22.3 | 7.3 | 6.8 | 9.3 | 9.9 | 4.8 | 4.9 | 57.1 | 42.9 | 33.3 | 9.7 |
| Wilczka River at gauge Wilkanów | |||||||||||||
| Międzygórze | 25.6 | 9.1 | 26.3 | 8.3 | 9.4 | 7.1 | 6.2 | 4.1 | 3.8 | 61.0 | 39.0 | 31.1 | 7.9 |
| Biała Lądecka River at gauge Lądek Zdrój | |||||||||||||
| Bielice | 25.3 | 9.1 | 28.9 | 8.2 | 8.7 | 6.3 | 7.2 | 3.1 | 3.1 | 63.3 | 36.7 | 30.5 | 6.2 |
| Nowy Gierałtów | 26.8 | 8.7 | 25.5 | 8.3 | 7.9 | 8.3 | 8.3 | 3.1 | 3.0 | 61.0 | 39.0 | 32.8 | 6.1 |
| Biała Lądecka River at gauge Żelazno | |||||||||||||
| Bielice | 25.9 | 9.5 | 26.4 | 8.4 | 8.9 | 7.3 | 7.1 | 3.0 | 3.4 | 61.9 | 38.1 | 31.7 | 6.4 |
| Nowy Gierałtów | 27.1 | 8.9 | 24.3 | 6.3 | 6.3 | 10.0 | 9.3 | 3.4 | 4.4 | 60.3 | 39.7 | 31.9 | 7.8 |
| Ołdrzychowice | 21.5 | 7.3 | 20.5 | 7.4 | 7.8 | 10.3 | 10.1 | 7.5 | 7.5 | 49.4 | 50.6 | 35.6 | 15.0 |
| Bystrzyca Dusznicka River at gauge Szalejów Dolny | |||||||||||||
| Zieleniec | 28.6 | 9.6 | 27.4 | 6.9 | 7.2 | 7.3 | 8.0 | 2.4 | 2.4 | 65.7 | 34.3 | 29.5 | 4.8 |
| Chocieszów | 26.6 | 8.3 | 24.9 | 6.7 | 6.9 | 10.0 | 9.2 | 3.7 | 3.7 | 59.8 | 40.2 | 32.8 | 7.4 |
| Polanica-Zdrój | 23.4 | 7.4 | 21.1 | 7.8 | 7.5 | 10.0 | 10.9 | 5.9 | 6.0 | 51.9 | 48.1 | 36.2 | 11.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perz, A.; Sobkowiak, L.; Wrzesiński, D. Probabilistic Approach to Precipitation-Runoff Relation in a Mountain Catchment: A Case Study of the K?odzka Valley in Poland. Water 2021, 13, 1229. https://doi.org/10.3390/w13091229
Perz A, Sobkowiak L, Wrzesiński D. Probabilistic Approach to Precipitation-Runoff Relation in a Mountain Catchment: A Case Study of the K?odzka Valley in Poland. Water. 2021; 13(9):1229. https://doi.org/10.3390/w13091229
Chicago/Turabian StylePerz, Adam, Leszek Sobkowiak, and Dariusz Wrzesiński. 2021. "Probabilistic Approach to Precipitation-Runoff Relation in a Mountain Catchment: A Case Study of the K?odzka Valley in Poland" Water 13, no. 9: 1229. https://doi.org/10.3390/w13091229
APA StylePerz, A., Sobkowiak, L., & Wrzesiński, D. (2021). Probabilistic Approach to Precipitation-Runoff Relation in a Mountain Catchment: A Case Study of the K?odzka Valley in Poland. Water, 13(9), 1229. https://doi.org/10.3390/w13091229






