Numerical Analysis of Free-Surface Flows over Rubber Dams
Abstract
1. Introduction
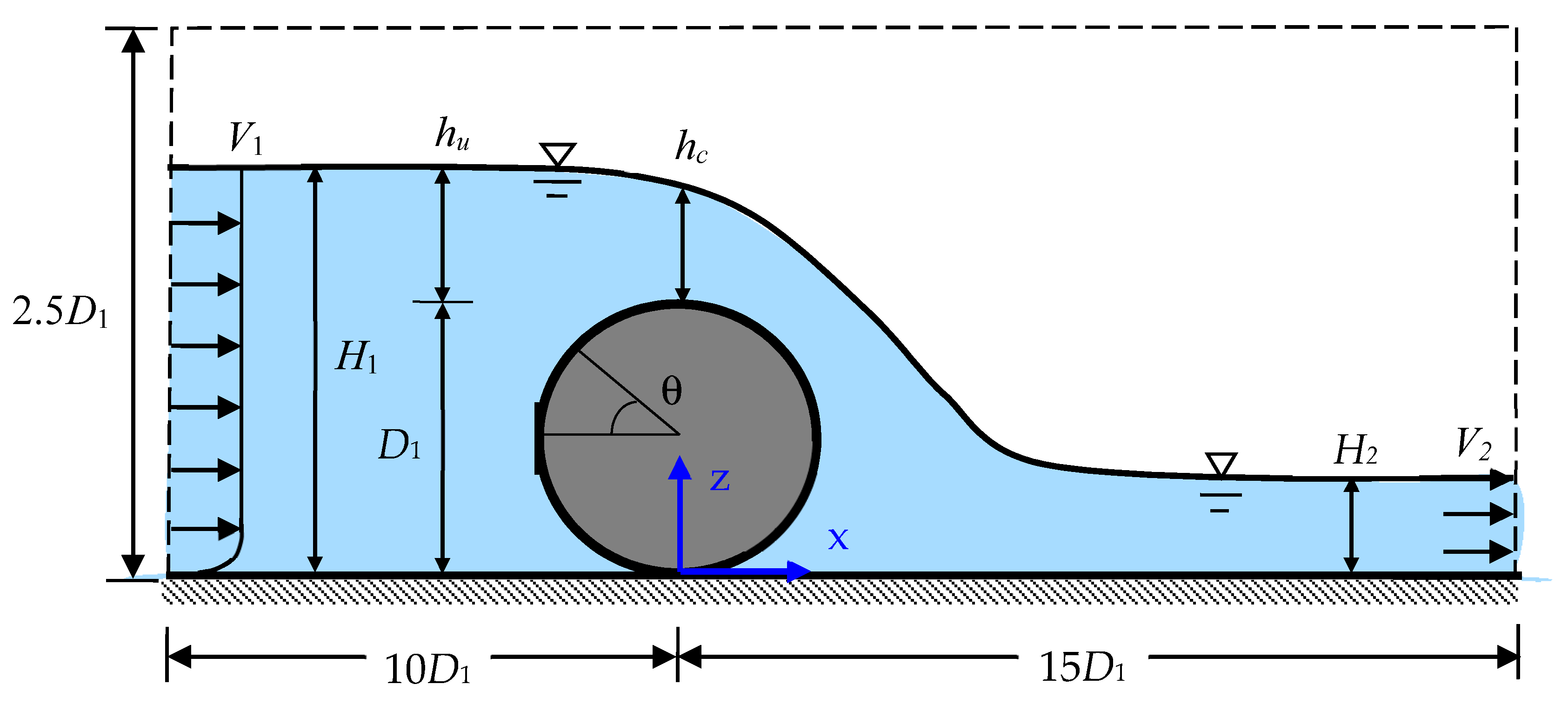
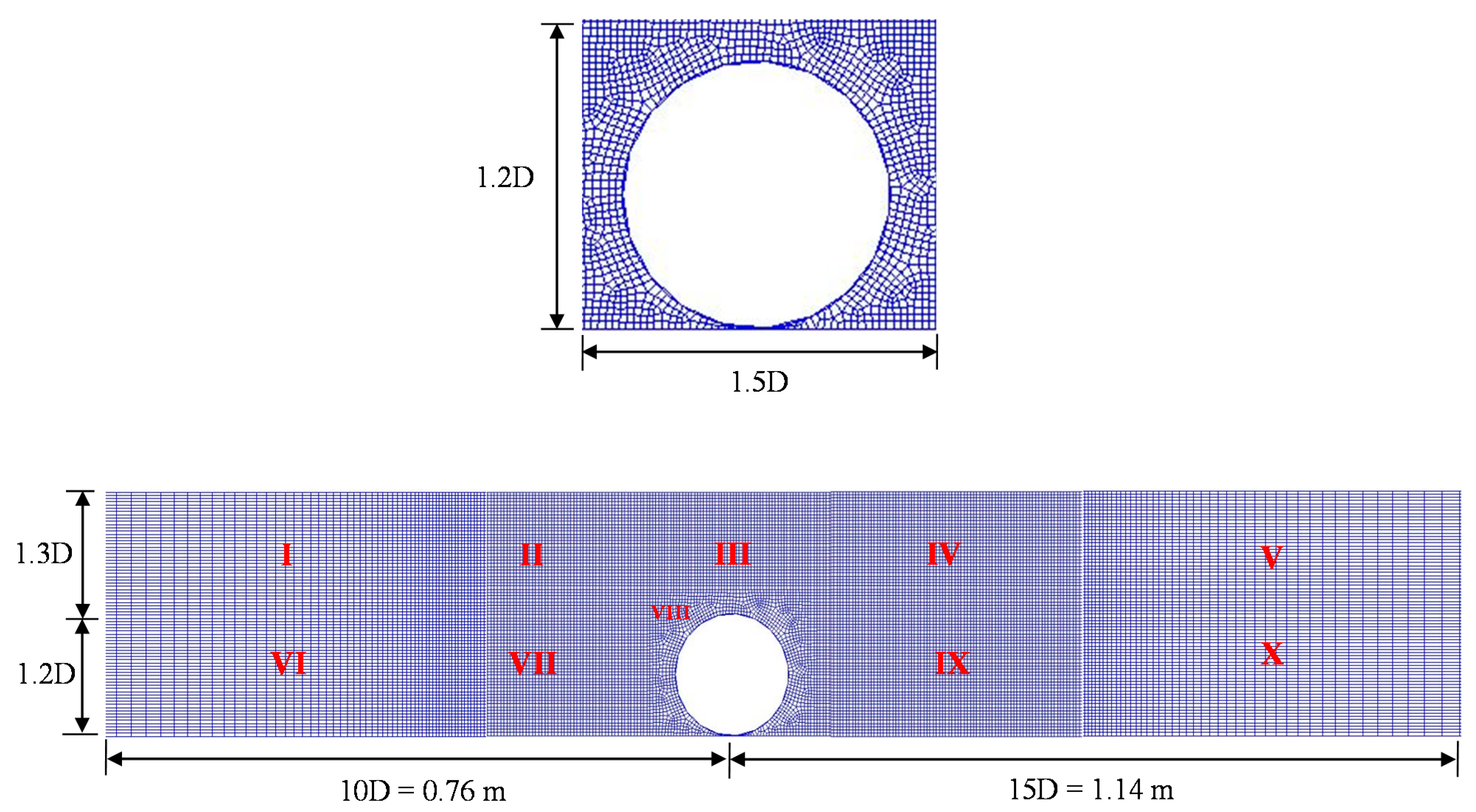
2. Numerical Model
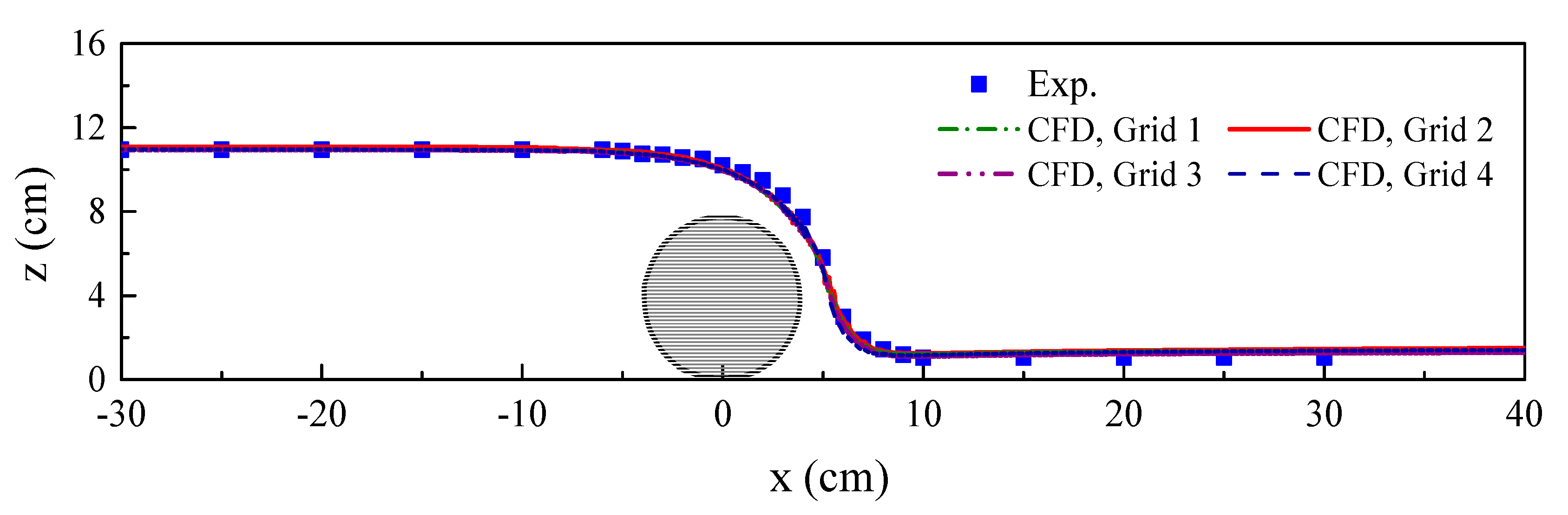
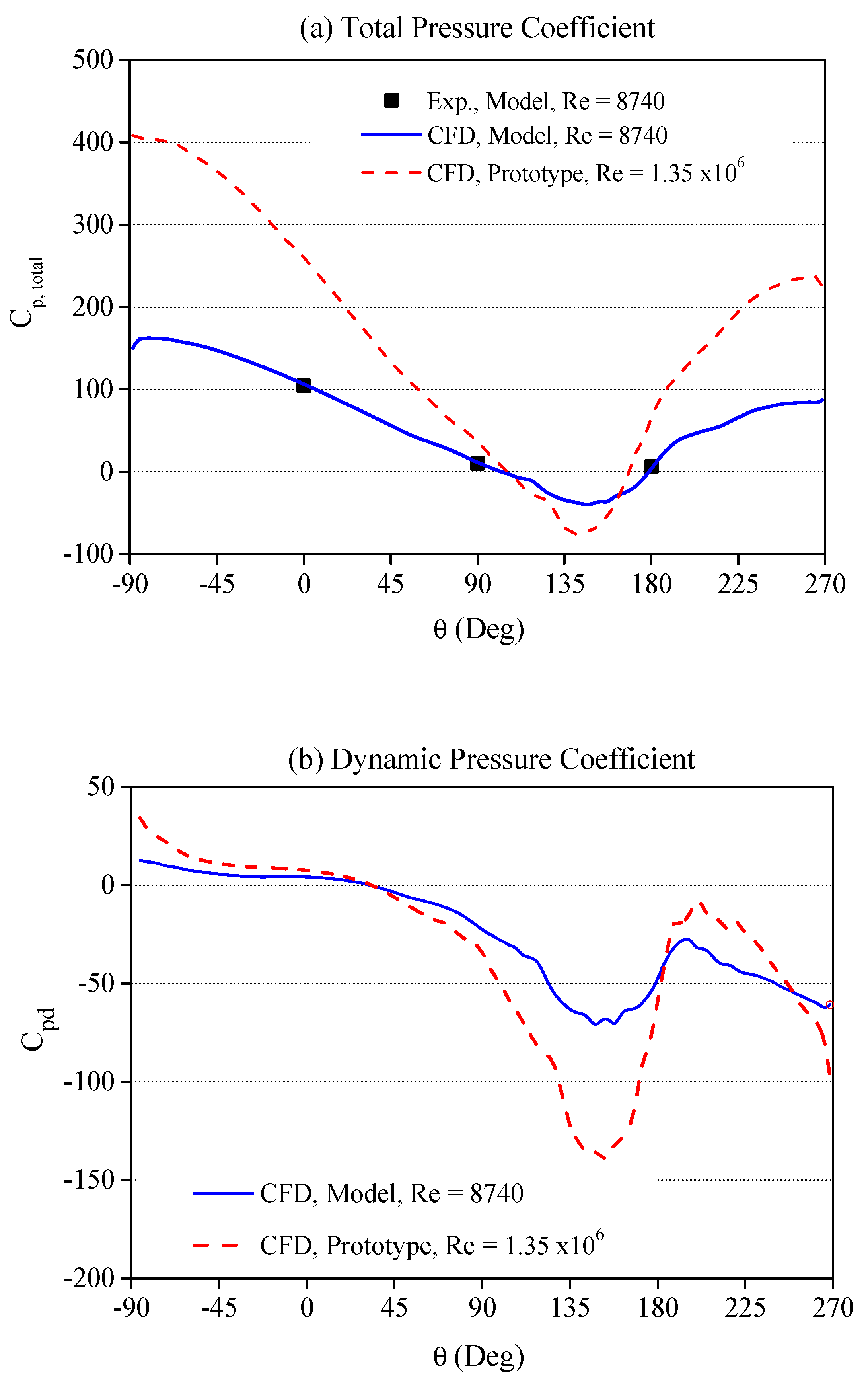
3. Model Validation
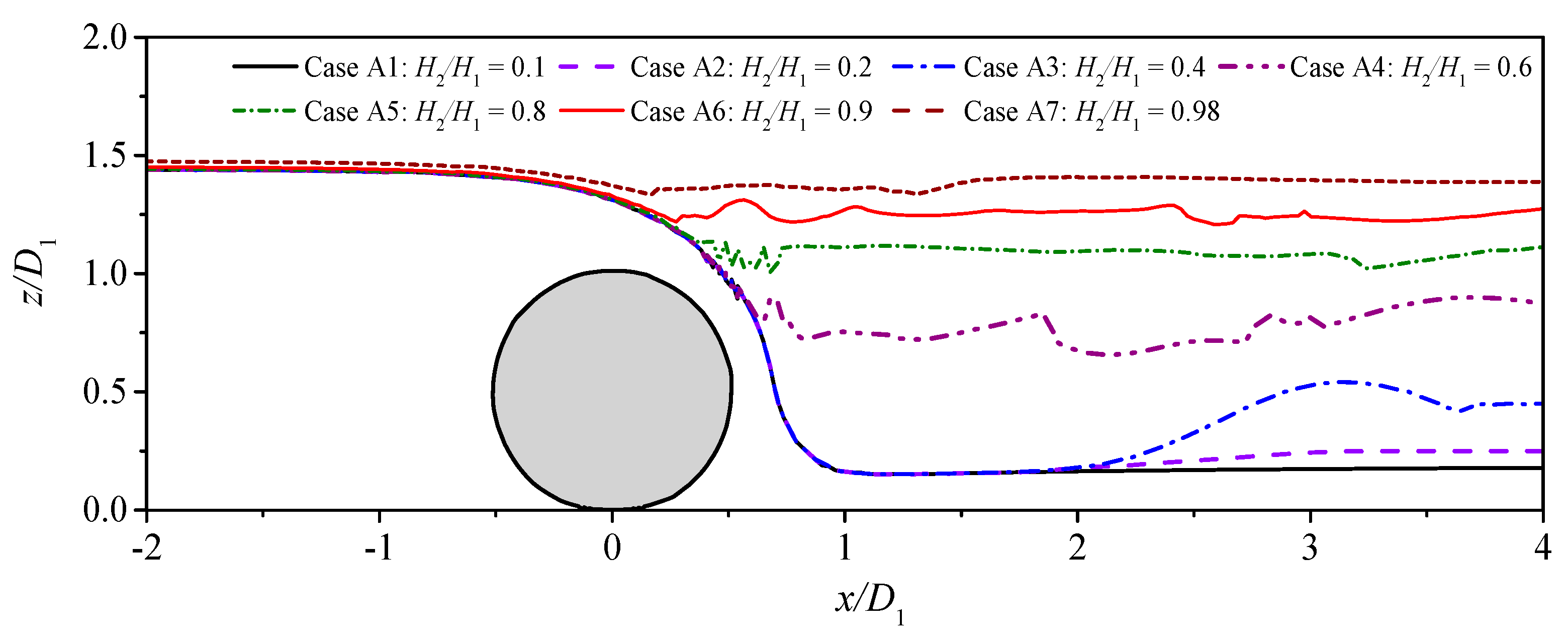
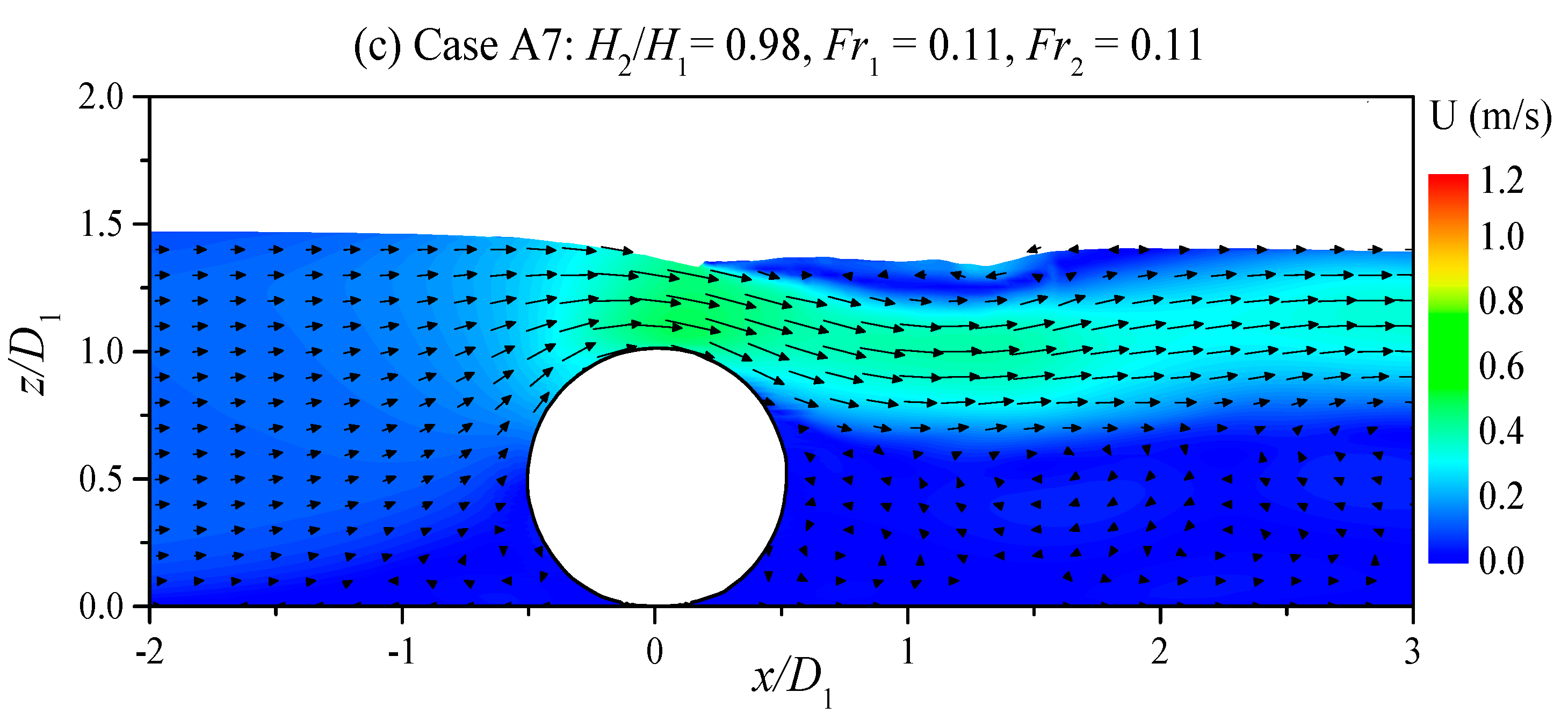
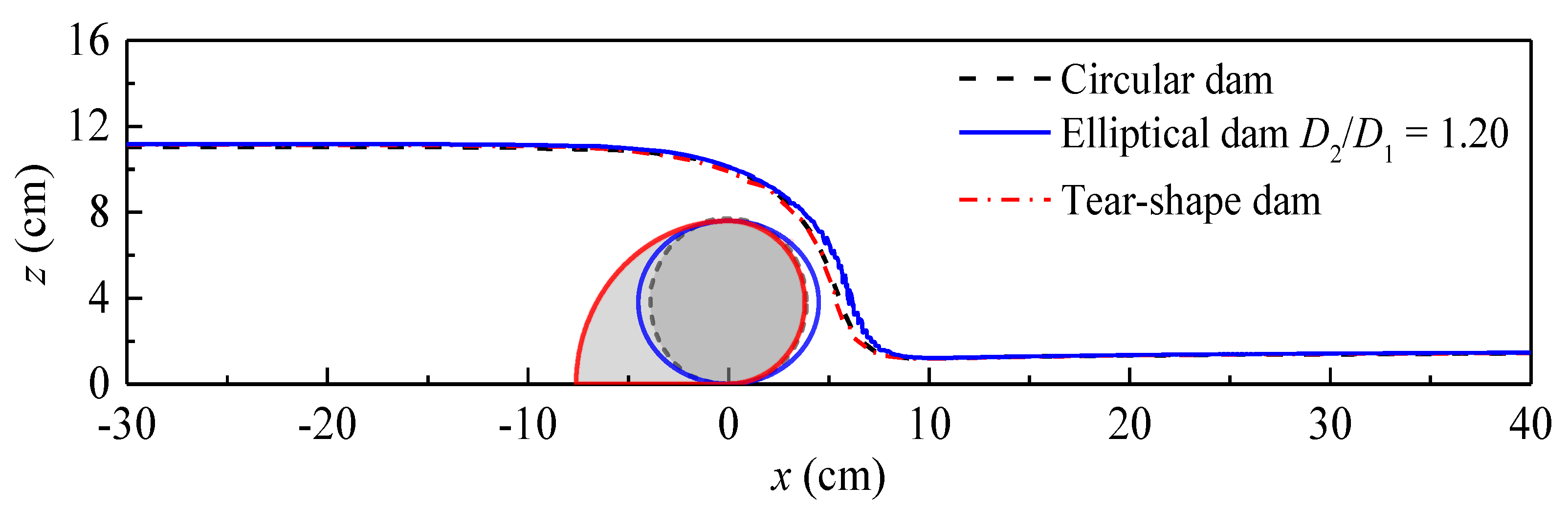
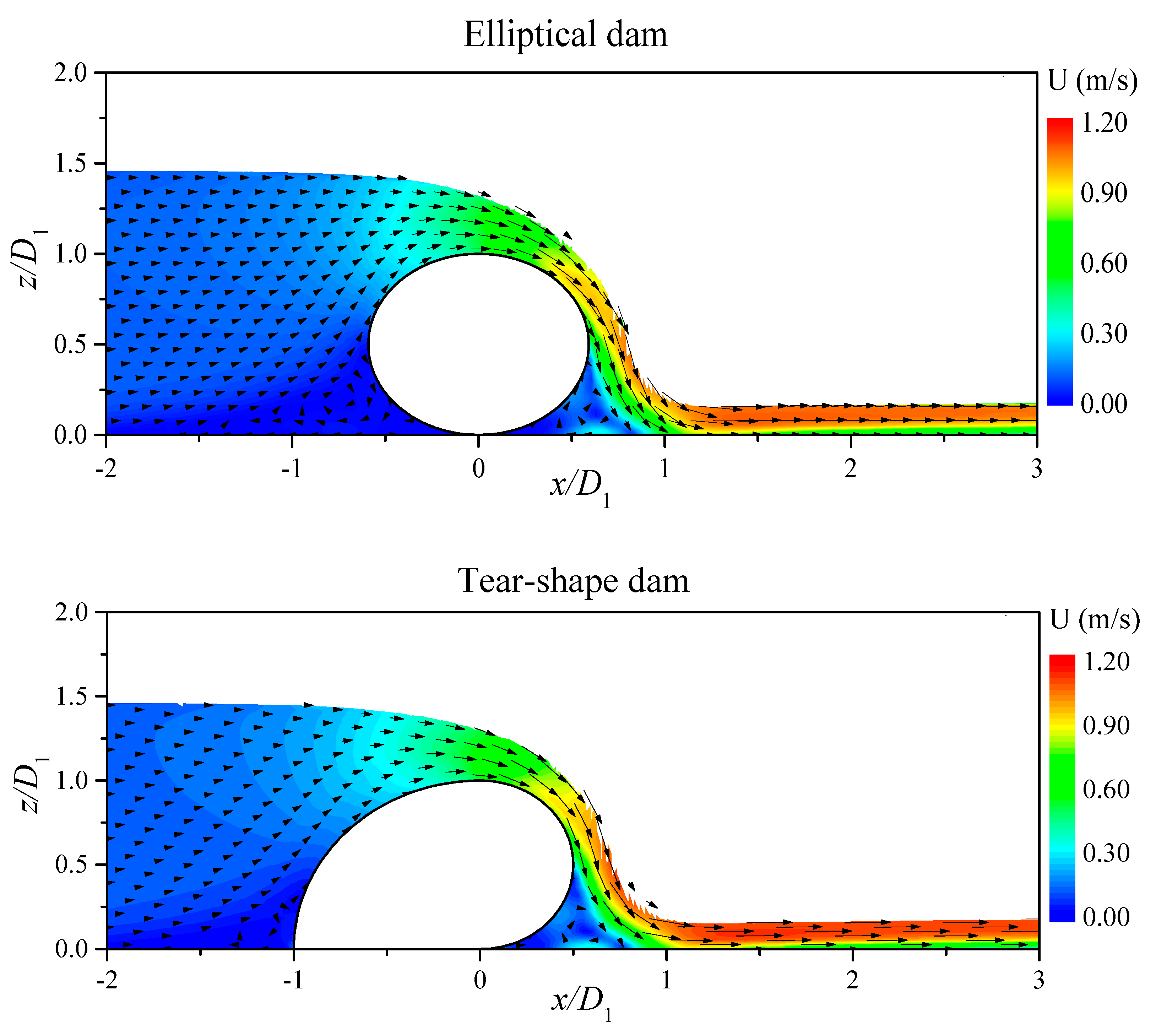
4. Results and Discussion
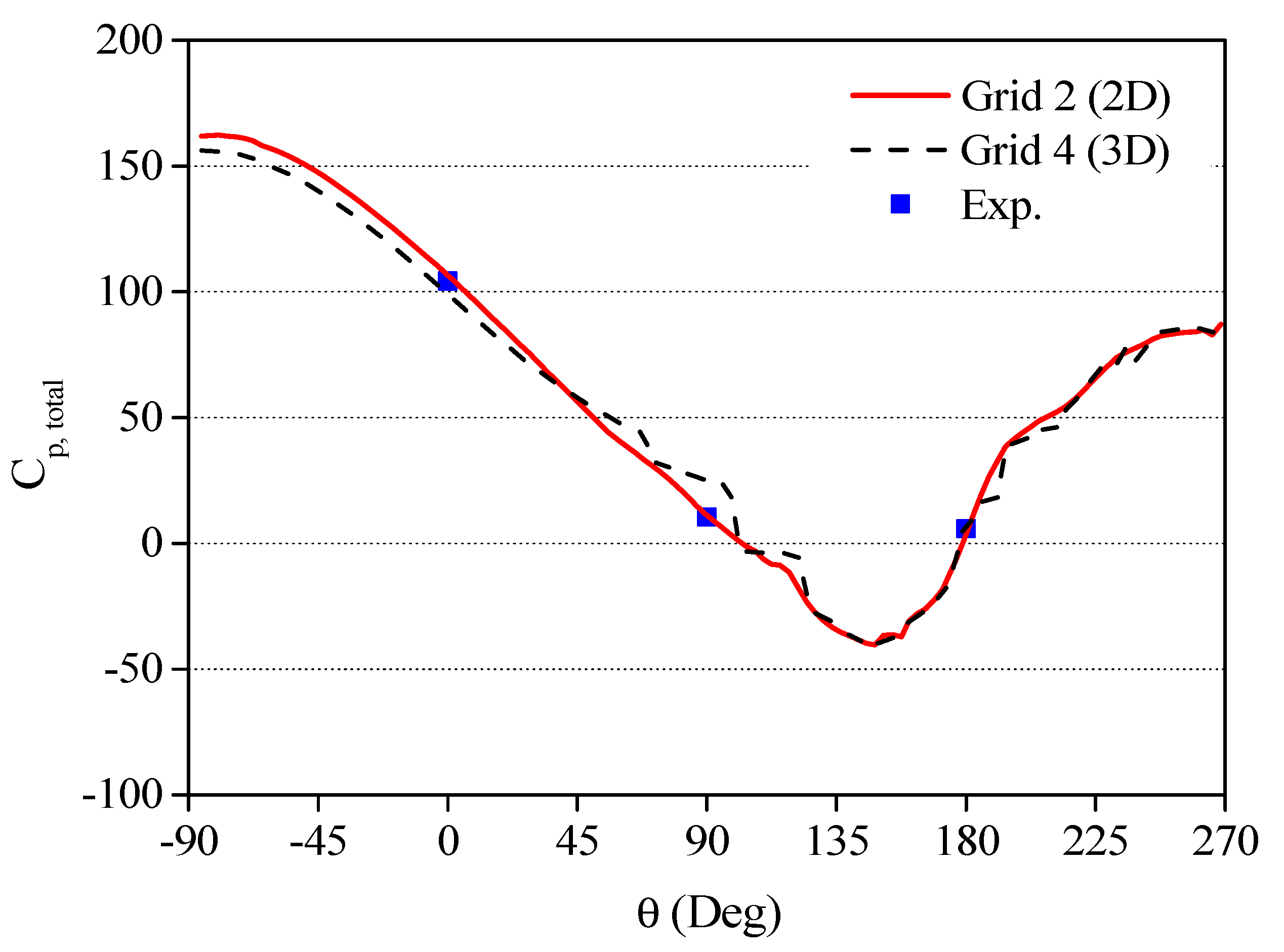
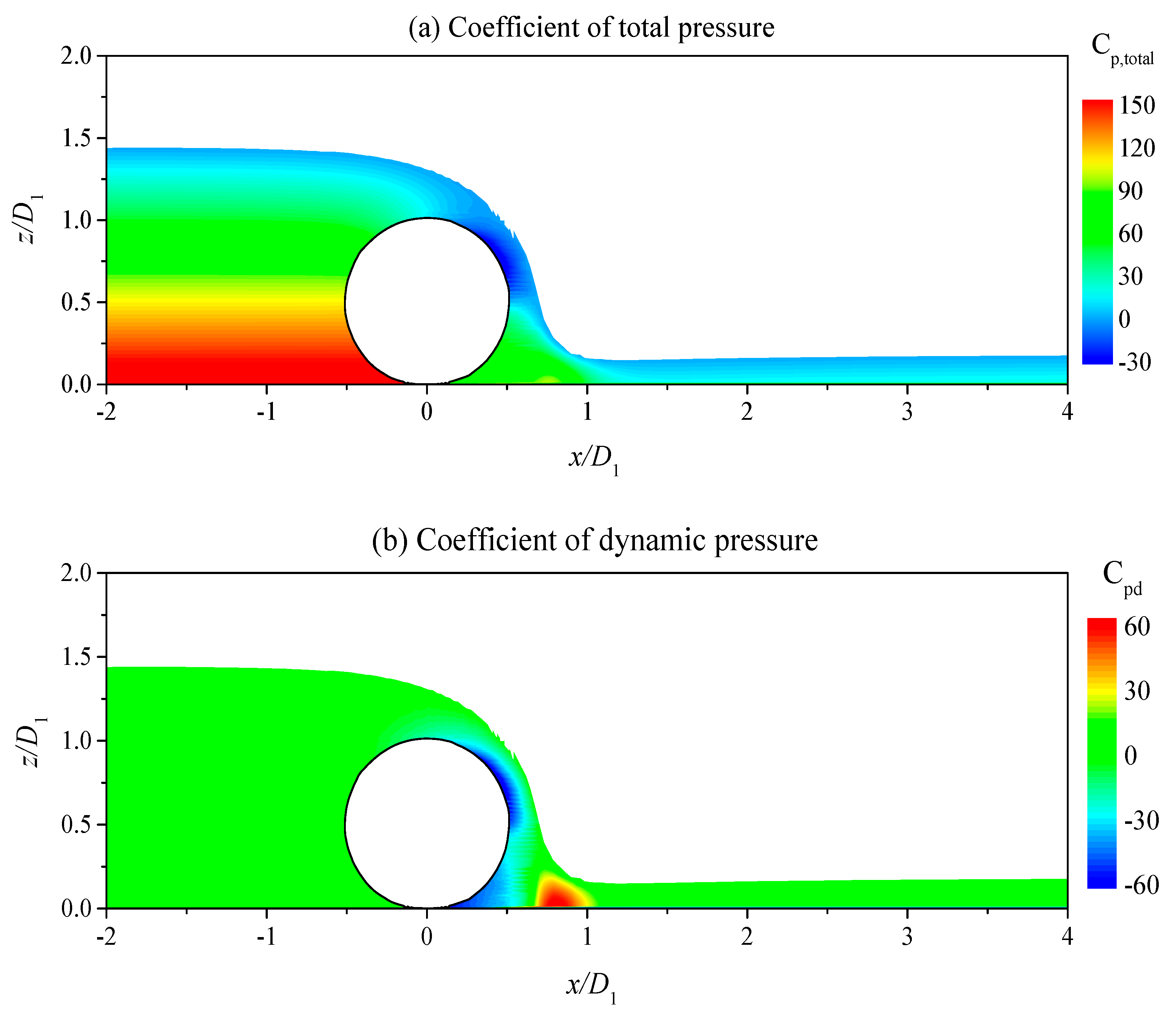
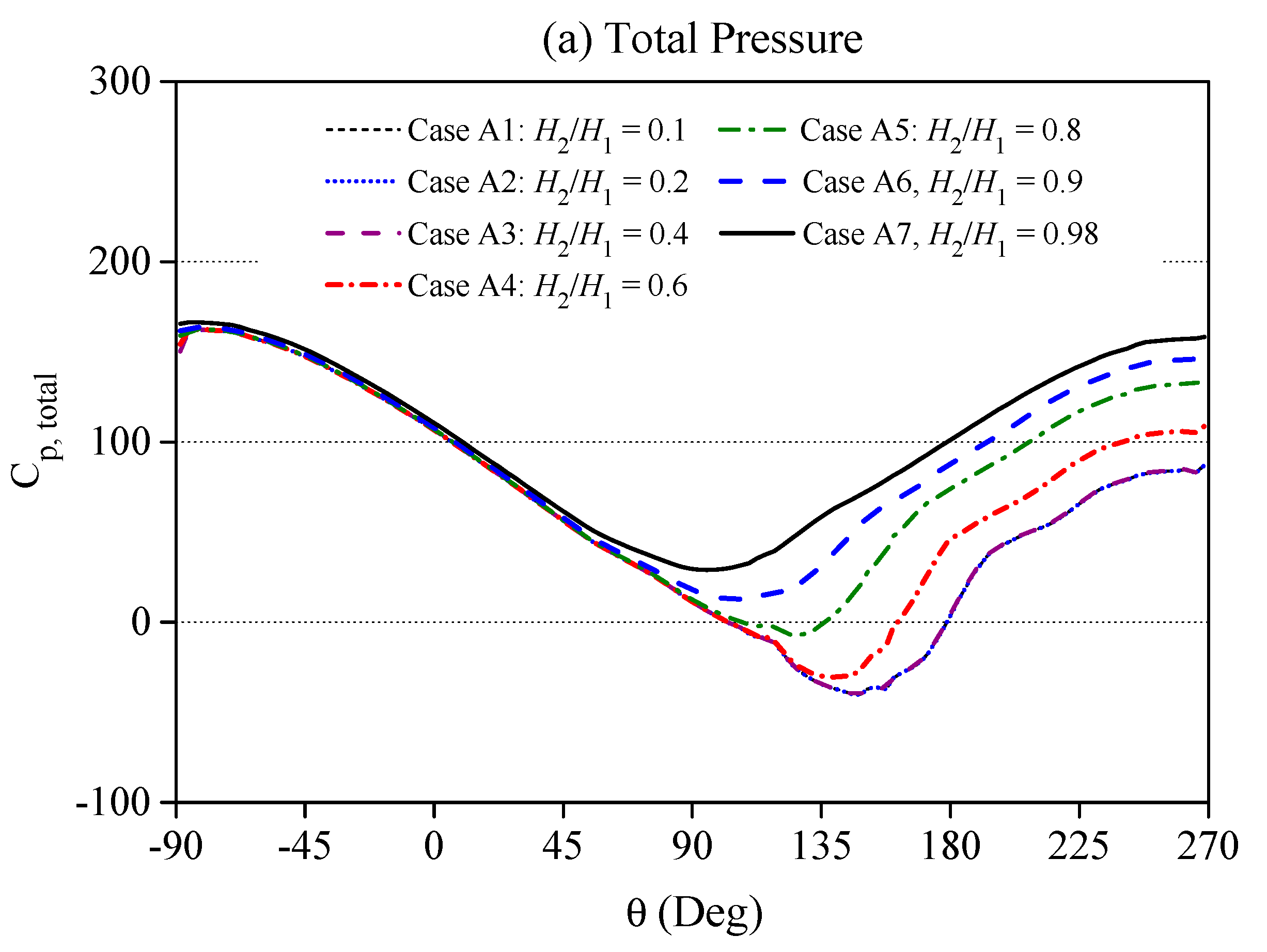
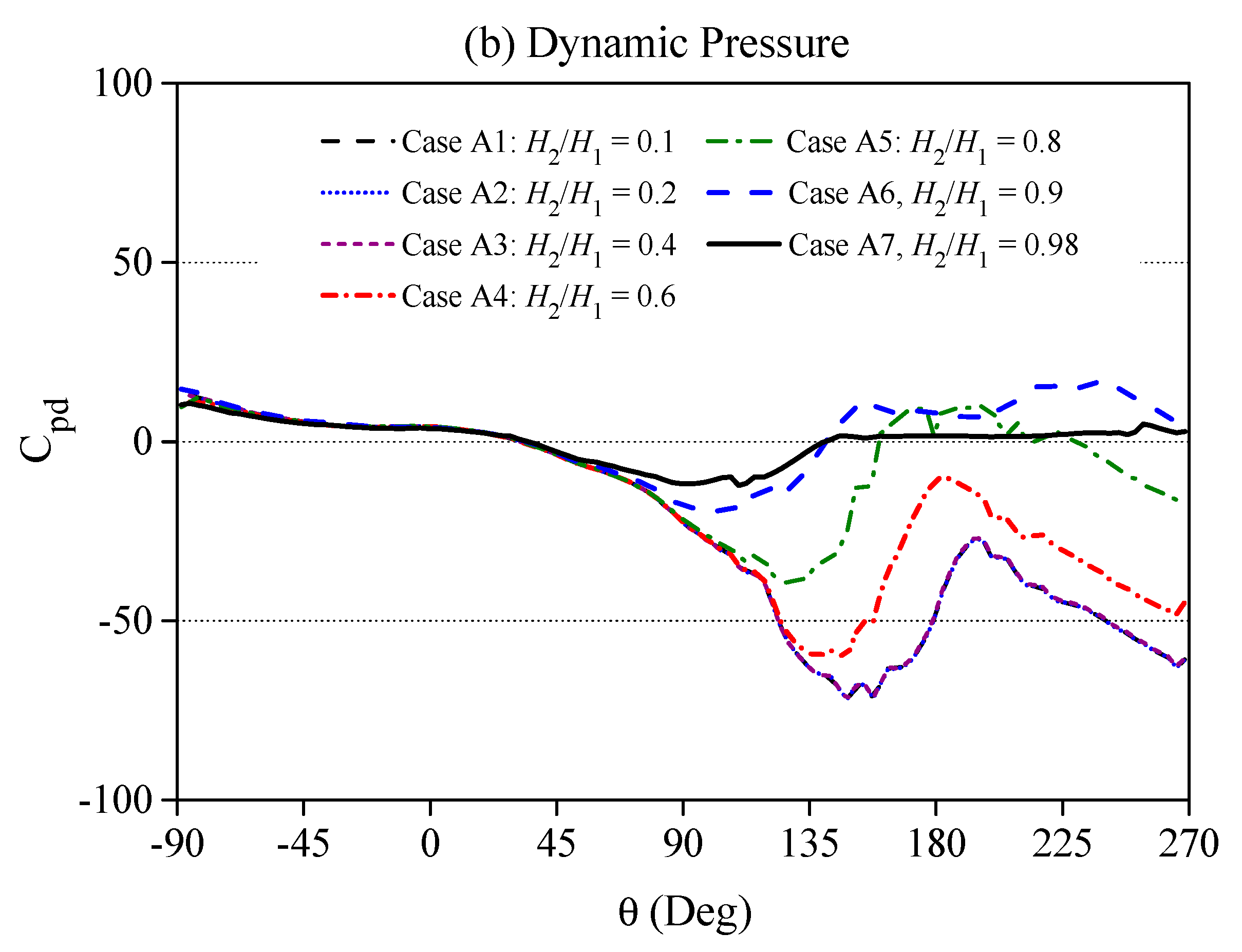
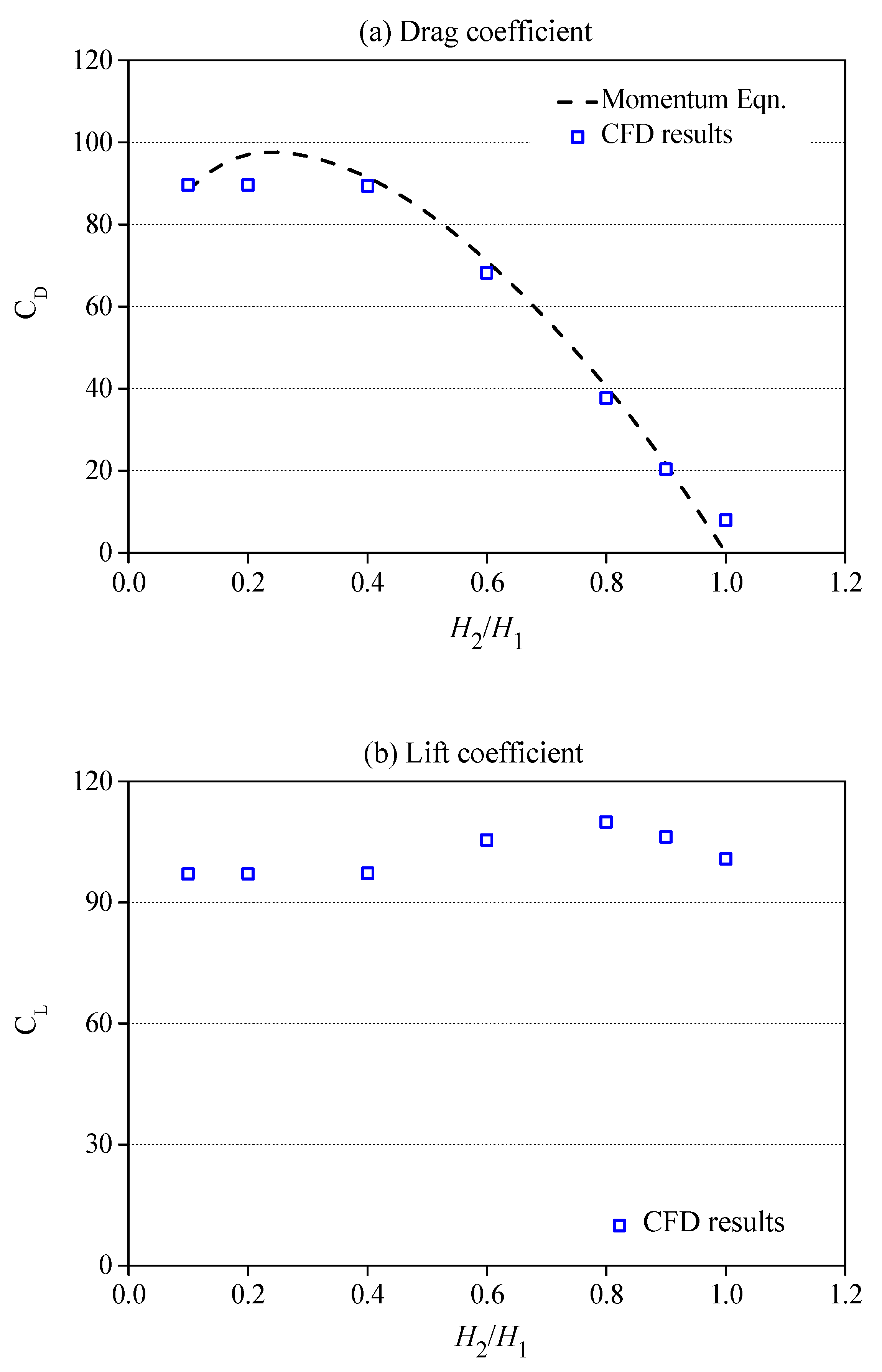
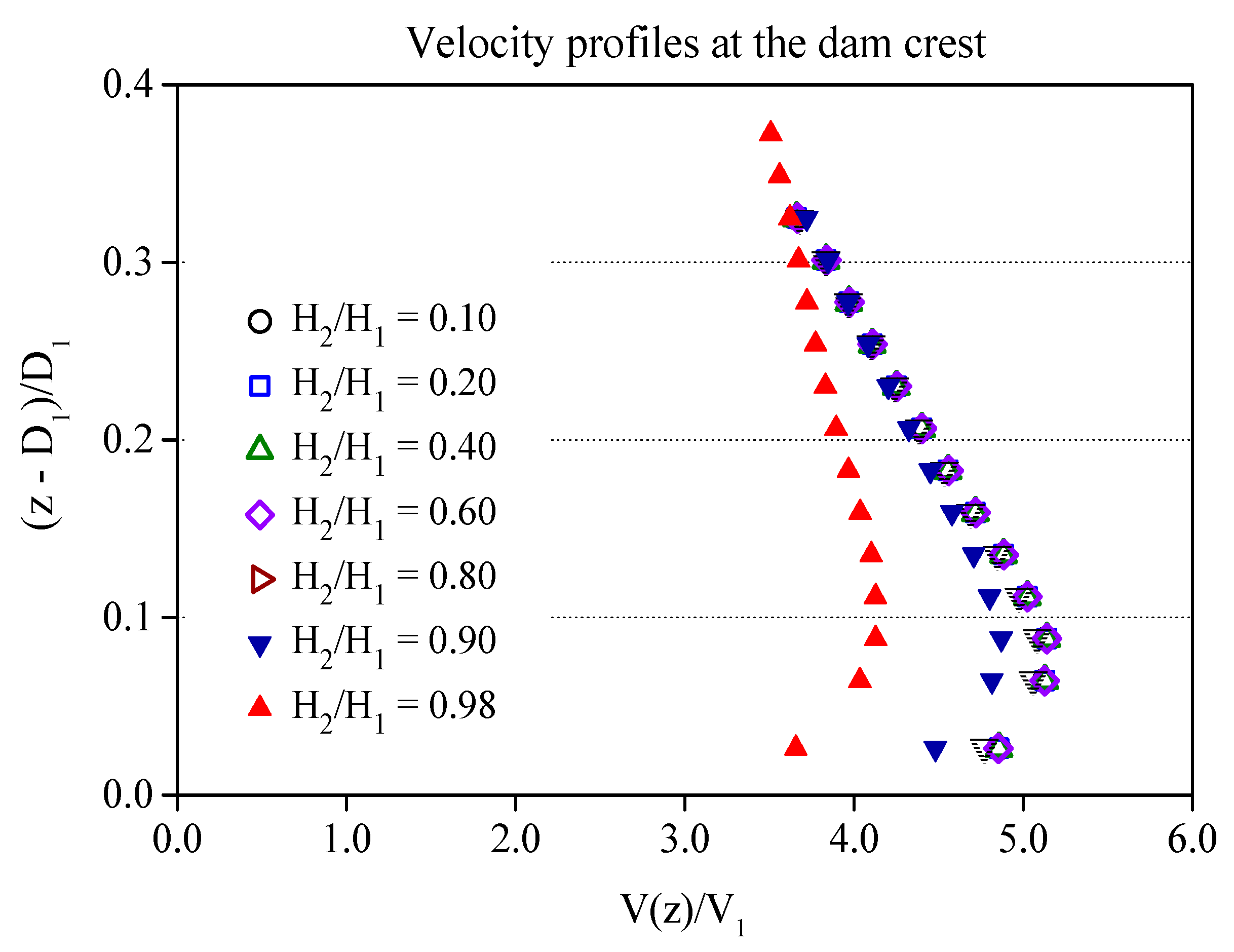
4.1. Hydrodynamic Loading
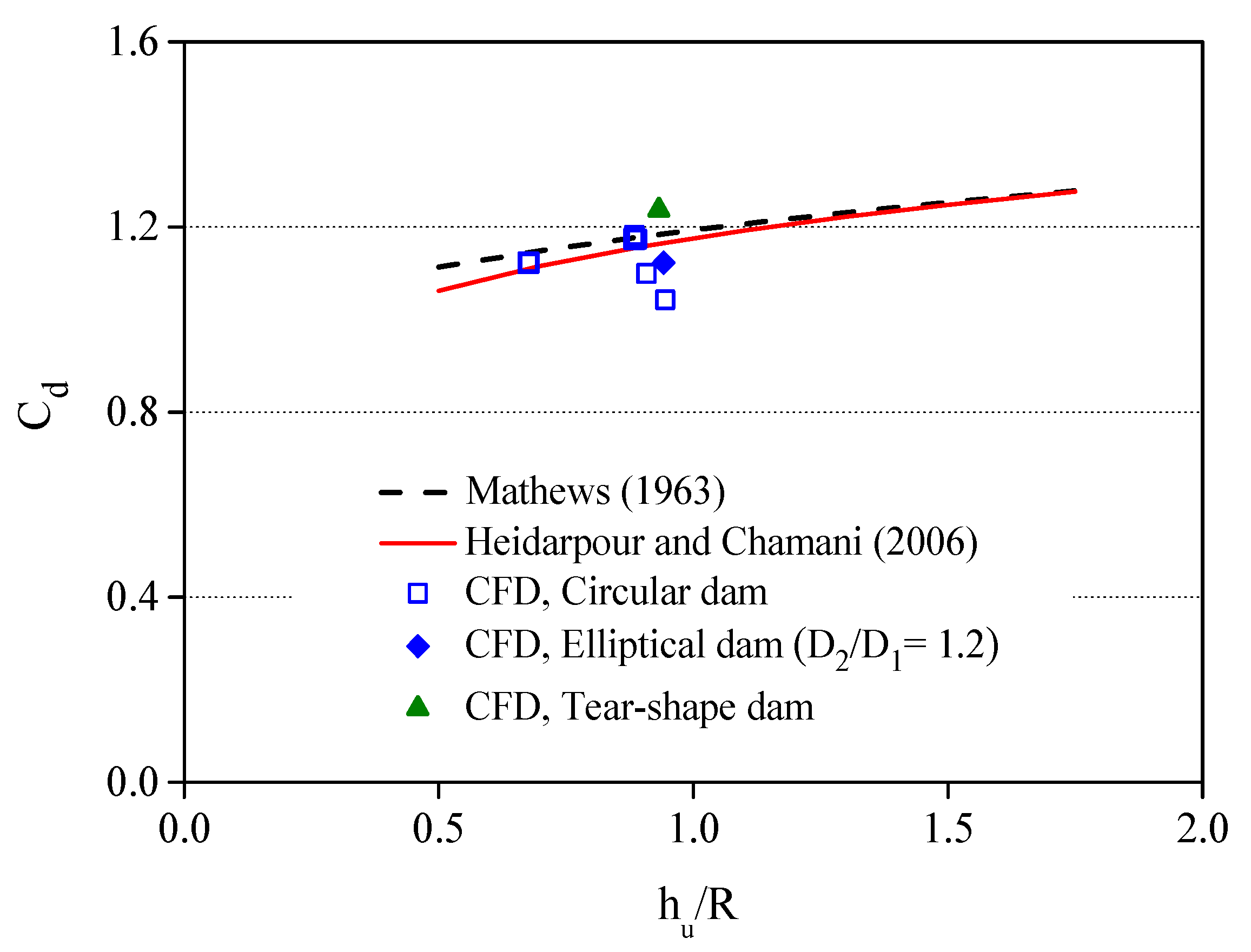
4.2. Discharge Coefficient
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ramamurthy, A.S.; Vo, N.-D. Characteristics of Circular-Crested Weir. J. Hydraul. Eng. 1993, 119, 1055–1062. [Google Scholar] [CrossRef]
- Zhang, X.Q.; Tam, P.W.M.; Zheng, W. Construction, operation, and maintenance of rubber dams. Can. J. Civ. Eng. 2002, 29, 409–420. [Google Scholar] [CrossRef]
- Saleh, A.F.M.; Mondal, M.S. Performance evaluation of rubber dam projects of Bangladesh in irrigation development. Irrig. Drain. 2001, 50, 237–248. [Google Scholar] [CrossRef]
- Chanson, H. A review of the overflow of inflatable flexible membrane dams. Aust. Civ. Eng. Trans. 1997, 39, 107–116. [Google Scholar]
- Wu, P.-H.; Plaut, R. Analysis of the vibrations of inflatable dams under overflow conditions. Thin-Walled Struct. 1996, 26, 241–259. [Google Scholar] [CrossRef][Green Version]
- Chanson, H.; Tam, P.W.M. Discussion and Closure: Use of Rubber Dams for Flood Mitigation in Hong Kong. J. Irrig. Drain. Eng. 1998, 124, 181–184. [Google Scholar] [CrossRef]
- Chanson, H. Hydraulics of rubber dam overflow: A simple design approach. In Proceedings of the 13th Australasian Fluid Mechanics Conference, Melbourne, Australia, 13–18 December 1998; pp. 255–258. [Google Scholar]
- Hager, W.H. Critical flow condition in open channel hydraulics. Acta Mech. 1985, 54, 157–179. [Google Scholar] [CrossRef]
- Hager, W.H. Discussion of “Characteristics of Circular-Crested Weirs” by A.S. Ramamurthy and N.-D. Vo (1993, 119). J. Hydraul. Eng. 1994, 120, 1494–1495. [Google Scholar] [CrossRef]
- Chanson, H.; Montes, J.S. Overflow Characteristics of Circular Weirs: Effects of Inflow Conditions. J. Irrig. Drain. Eng. 1998, 124, 152–162. [Google Scholar] [CrossRef]
- Heidarpour, M.; Chamani, M. Velocity distribution over cylindrical weirs. J. Hydraul. Res. 2006, 44, 708–711. [Google Scholar] [CrossRef]
- Bagheri, S.; Heidarpour, M. Overflow characteristics of circular-crested weirs. J. Hydraul. Res. 2010, 48, 515–520. [Google Scholar] [CrossRef]
- Schmocker, L.; Halldórsdóttir, B.R.; Hager, W.H. Effect of Weir Face Angles on Circular-Crested Weir Flow. J. Hydraul. Eng. 2011, 137, 637–643. [Google Scholar] [CrossRef]
- Naghavi, B.; Esmaili, K.; Yazdi, J.; Vahid, F.K. An experimental and numerical study on hydraulic characteristics and theoretical equations of circular weirs. Can. J. Civ. Eng. 2011, 38, 1327–1334. [Google Scholar] [CrossRef]
- Cheraghi-Shirazi, N.; Kabiri-Samani, A.; Boroomand, B. Numerical analysis of rubber dams using fluid–structure interactions. Flow Meas. Instrum. 2014, 40, 91–98. [Google Scholar] [CrossRef]
- Yuce, M.I.; Al-Babely, A.A.; Al-Dabbagh, M.A. Flow simulation over oblique cylindrical weirs. Can. J. Civ. Eng. 2015, 42, 389–407. [Google Scholar] [CrossRef]
- Cheraghi-Shirazi, N.; Kabiri-Samani, A.; Boroomand, B. Flow field over the rubber dams based on fluid-structure interactions. J. Civ. Eng. 2017, 49, 141–144. [Google Scholar] [CrossRef]
- Deardorff, J.W. A numerical study of three-dimensional turbulent channel flow at large Reynolds numbers. J. Fluid Mech. 1970, 41, 453–480. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- O’Neil, J.; Meneveau, C. Subgrid-scale stresses and their modelling in a turbulent plane wake. J. Fluid Mech. 1997, 349, 253–293. [Google Scholar] [CrossRef]
- Smagorinsky, J. General circulation experiments with the primitive equations: I. The basic experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Rodi, W.; Constantinescu, G.; Stoesser, T. Large Eddy Simulation in Hydraulic; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- DeLong, M. Two Examples of the Impact of Partitioning with Chaco and Metis on the Convergence of Additive-Schwarz Preconditioned FGMRES; Technical Report LA-UR-97-4181; Los Alamos National Laboratory: Los Alamos, NM, USA, 1997. [Google Scholar]
- Hirt, C.; Nichols, B. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Cabot, W.; Moin, P. Approximate Wall Boundary Conditions in the Large-Eddy Simulation of High Reynolds Number Flow. Flow Turbul. Combust. 2000, 63, 269–291. [Google Scholar] [CrossRef]
- Korzekwa, D.A. Truchas—A multi-physics tool for casting simulation. Int. J. Cast Met. Res. 2009, 22, 187–191. [Google Scholar] [CrossRef]
- Chu, C.-R.; Wu, Y.-R.; Wu, T.-R.; Wang, C.-Y. Slosh-induced hydrodynamic force in a water tank with multiple baffles. Ocean Eng. 2018, 167, 282–292. [Google Scholar] [CrossRef]
- Chu, C.-R.; Chung, C.-H.; Wu, T.-R.; Wang, C.-Y. Numerical analysis of free surface flow over a submerged rectangular bridge deck. J. Hydraul. Eng. 2016, 142. [Google Scholar] [CrossRef]
- Chu, C.-R.; Lin, Y.-A.; Wu, T.-R.; Wang, C.-Y. Hydrodynamic force of circular cylinder close to the water surface. Comput. Fluids 2018, 171, 154–165. [Google Scholar] [CrossRef]
- Wu, T.-R.; Vuong, T.-H.-N.; Lin, J.-W.; Chu, C.-R.; Wang, C.-Y. Three-Dimensional Numerical Study on the Interaction between Dam-Break Wave and Cylinder Array. J. Earthq. Tsunami 2018, 12, 1–35. [Google Scholar] [CrossRef]
- Matthew, G.D. On the influence of the curvature, surface tension and viscosity on flow over round-crested weirs. Proc. Inst. Civil Eng. 1963, 25, 511–524. [Google Scholar] [CrossRef]


| Title | Grid 1 (2D) | Grid 2 (2D) | Grid 3 (2D) | Grid 4 (3D) | ||||
| Total grid no. | 104,048 | 159,212 | 233,859 | 955,272 | ||||
| Grid no. on the cylinder surface | 90 | 120 | 150 | 120 | ||||
| Grid size near the cylinder | 2.65 mm | 2.0 mm | 1.60 mm | 2.0 mm | ||||
| Smallest grid size | Δx = 3 mm Δz = 3 mm | Δx = 2 mm Δz = 2 mm | Δx = 1.5 mm Δz = 1.5 mm | Δx = 2 mm Δy = 5 mm Δz = 2 mm | ||||
| Water surface Δh | 8.53% | 5.59% | 5.06% | 6.97% | ||||
| Force coeff. | CD | CL | CD | CL | CD | CL | CD | CL |
| 89.7 | 95.5 | 89.6 | 88.5 | 93.1 | 93.1 | 90.3 | 97.8 | |
| CPU time | 18 h | 26 h | 40 h | 768 h | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chu, C.-R.; Tran, T.T.T.; Wu, T.-R. Numerical Analysis of Free-Surface Flows over Rubber Dams. Water 2021, 13, 1271. https://doi.org/10.3390/w13091271
Chu C-R, Tran TTT, Wu T-R. Numerical Analysis of Free-Surface Flows over Rubber Dams. Water. 2021; 13(9):1271. https://doi.org/10.3390/w13091271
Chicago/Turabian StyleChu, Chia-Ren, Truc Thi Thu Tran, and Tso-Ren Wu. 2021. "Numerical Analysis of Free-Surface Flows over Rubber Dams" Water 13, no. 9: 1271. https://doi.org/10.3390/w13091271
APA StyleChu, C.-R., Tran, T. T. T., & Wu, T.-R. (2021). Numerical Analysis of Free-Surface Flows over Rubber Dams. Water, 13(9), 1271. https://doi.org/10.3390/w13091271








