Numerical Analysis of Free-Surface Flows over Rubber Dams
Abstract
:1. Introduction
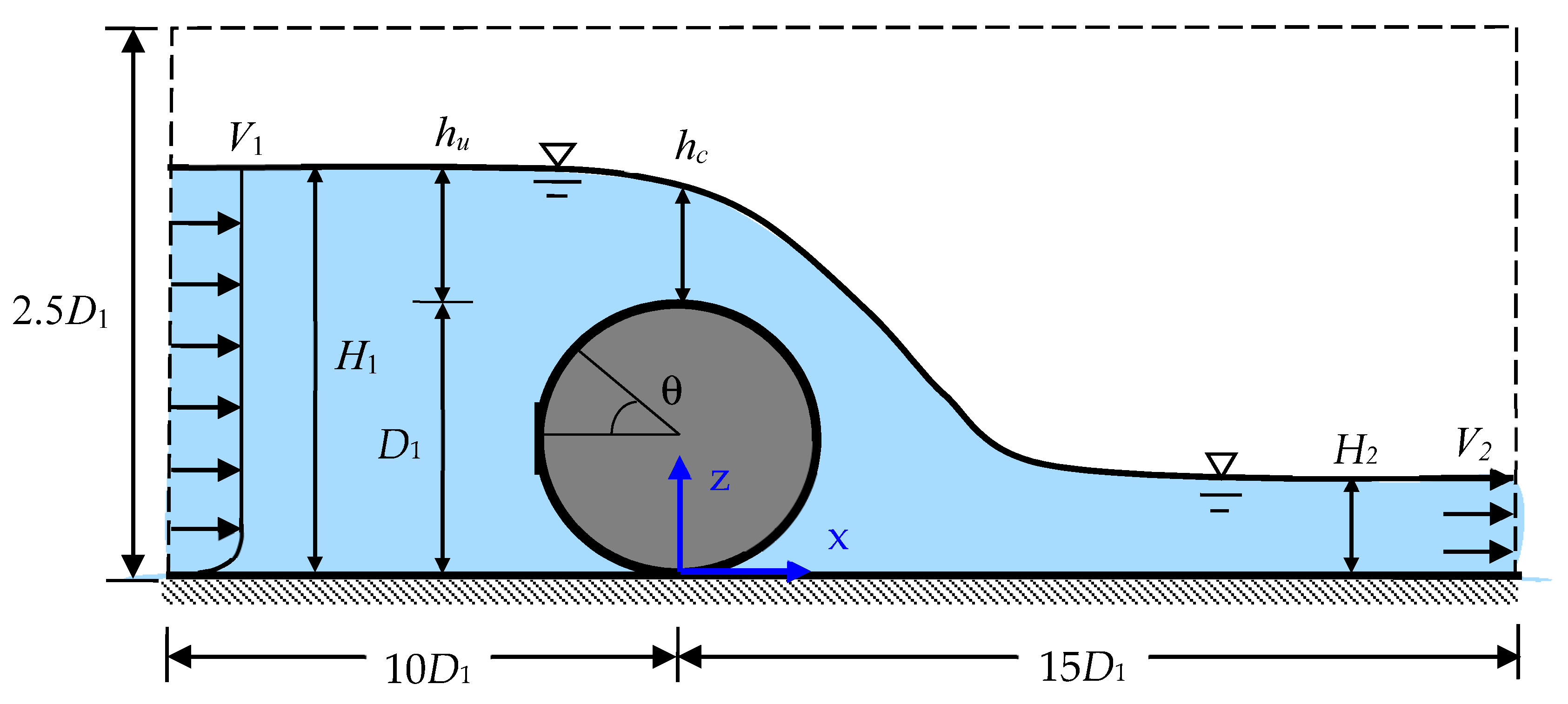
2. Numerical Model
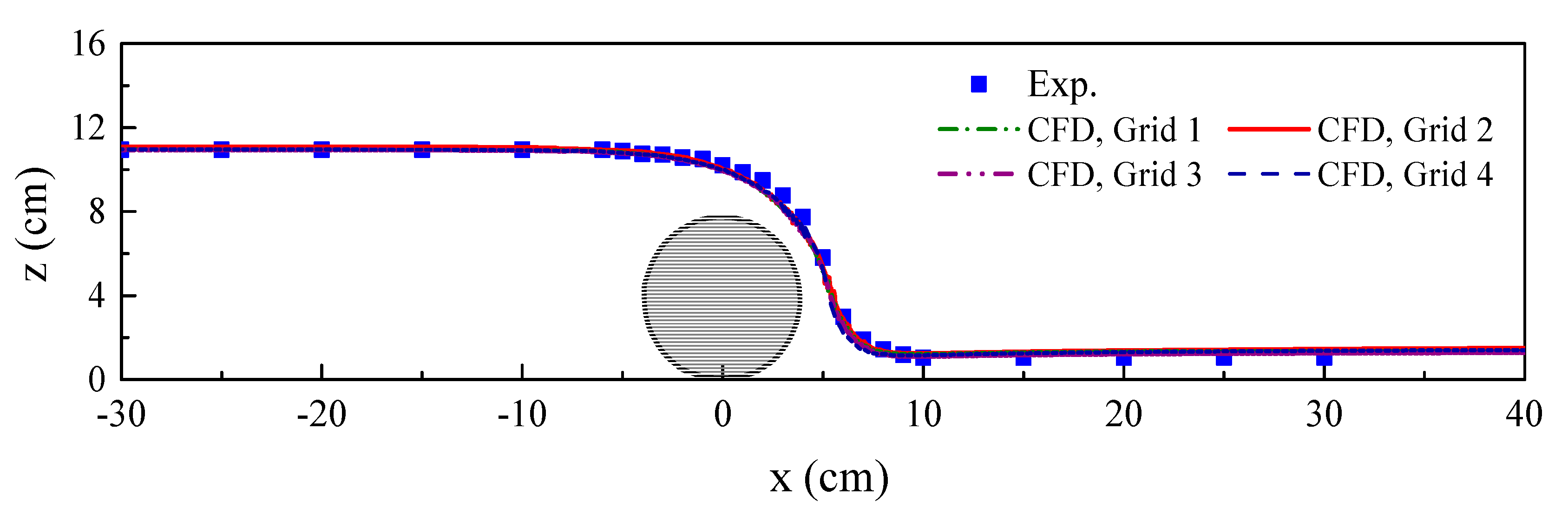
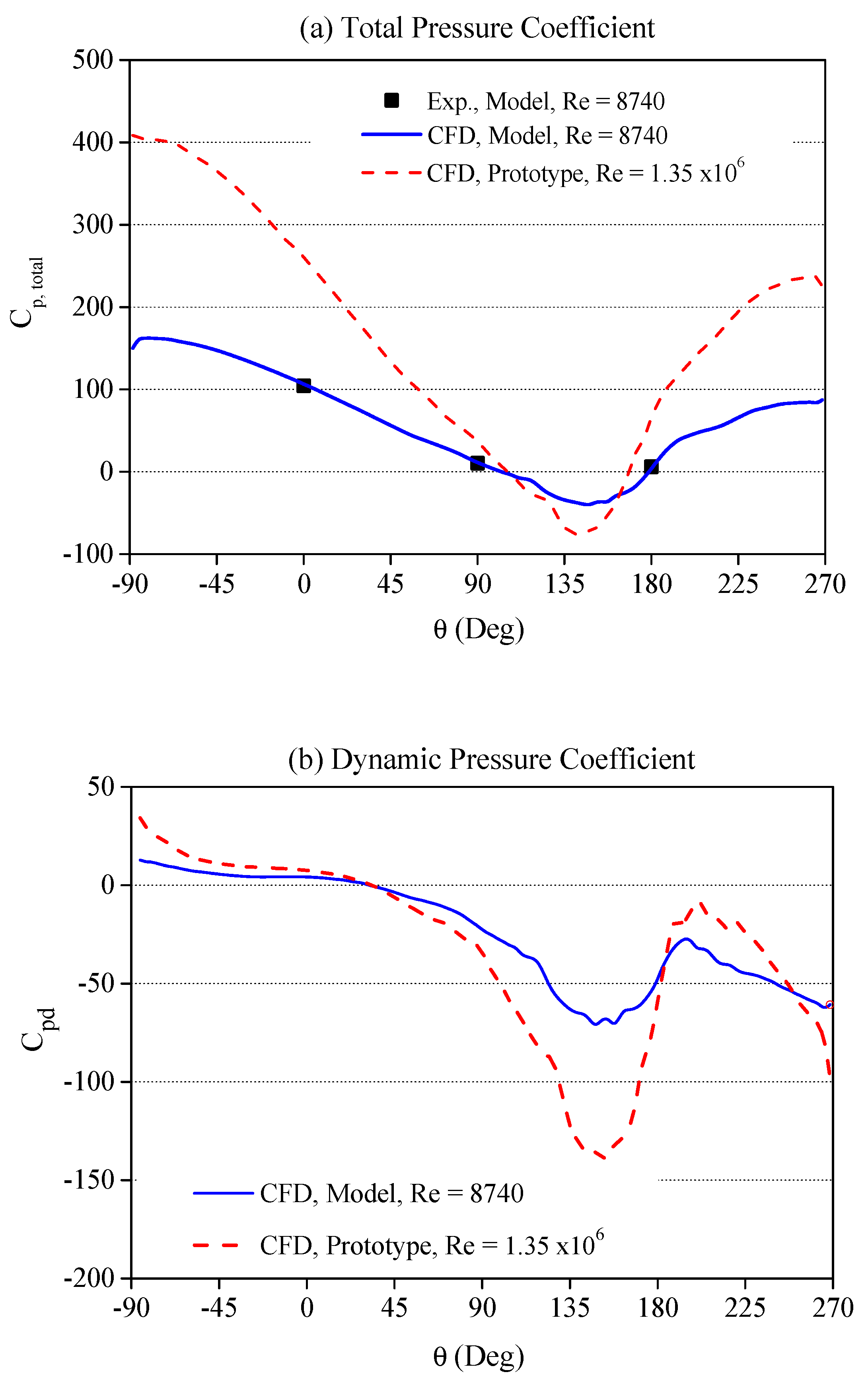
3. Model Validation
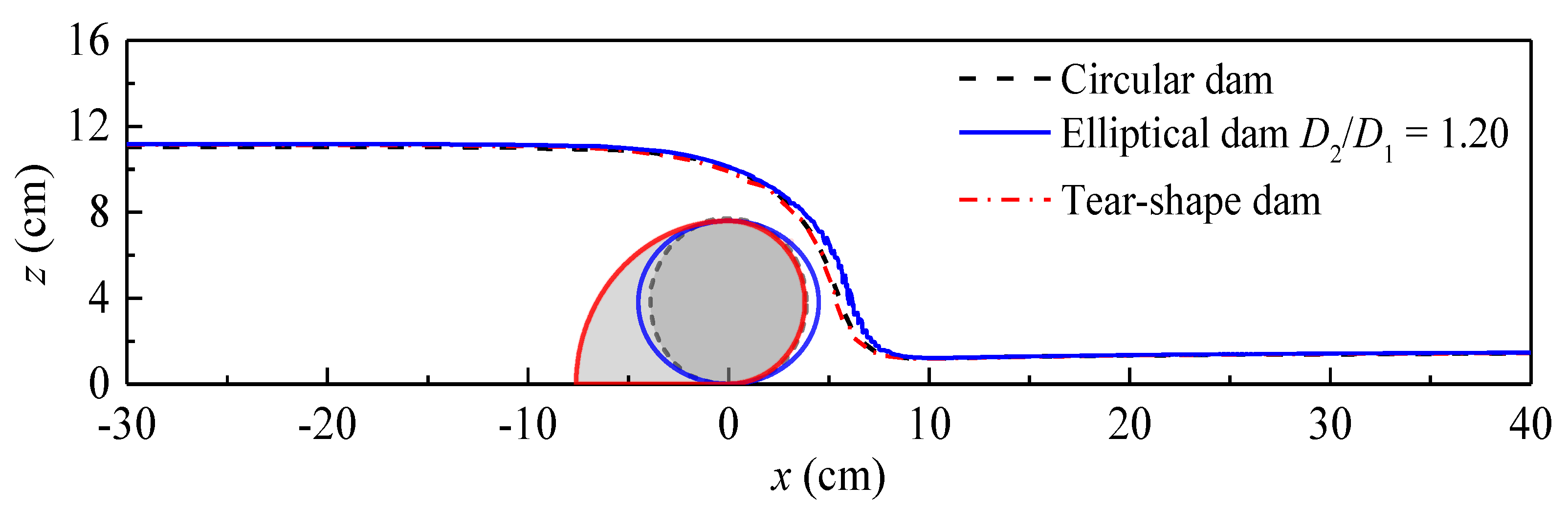
4. Results and Discussion
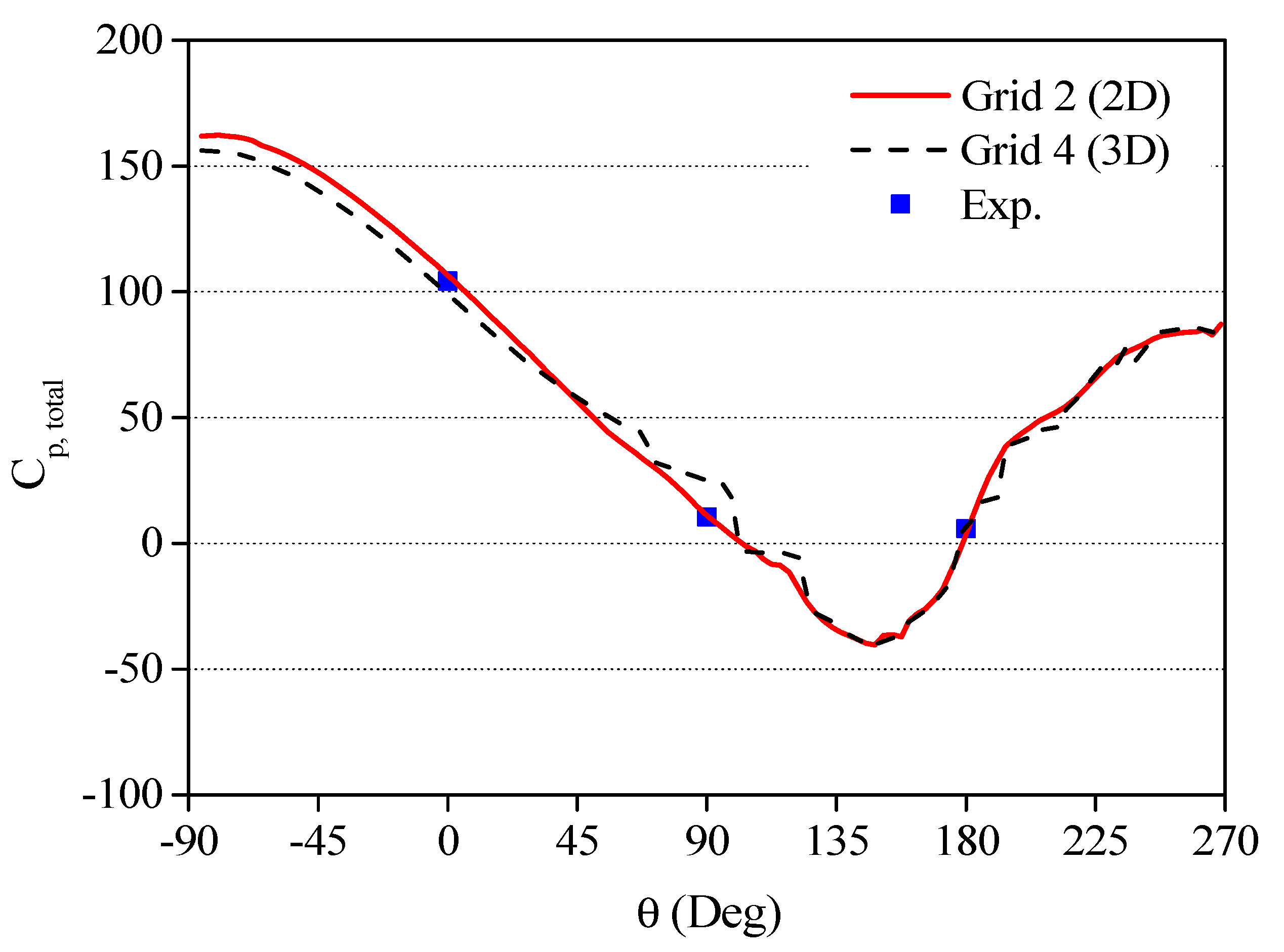
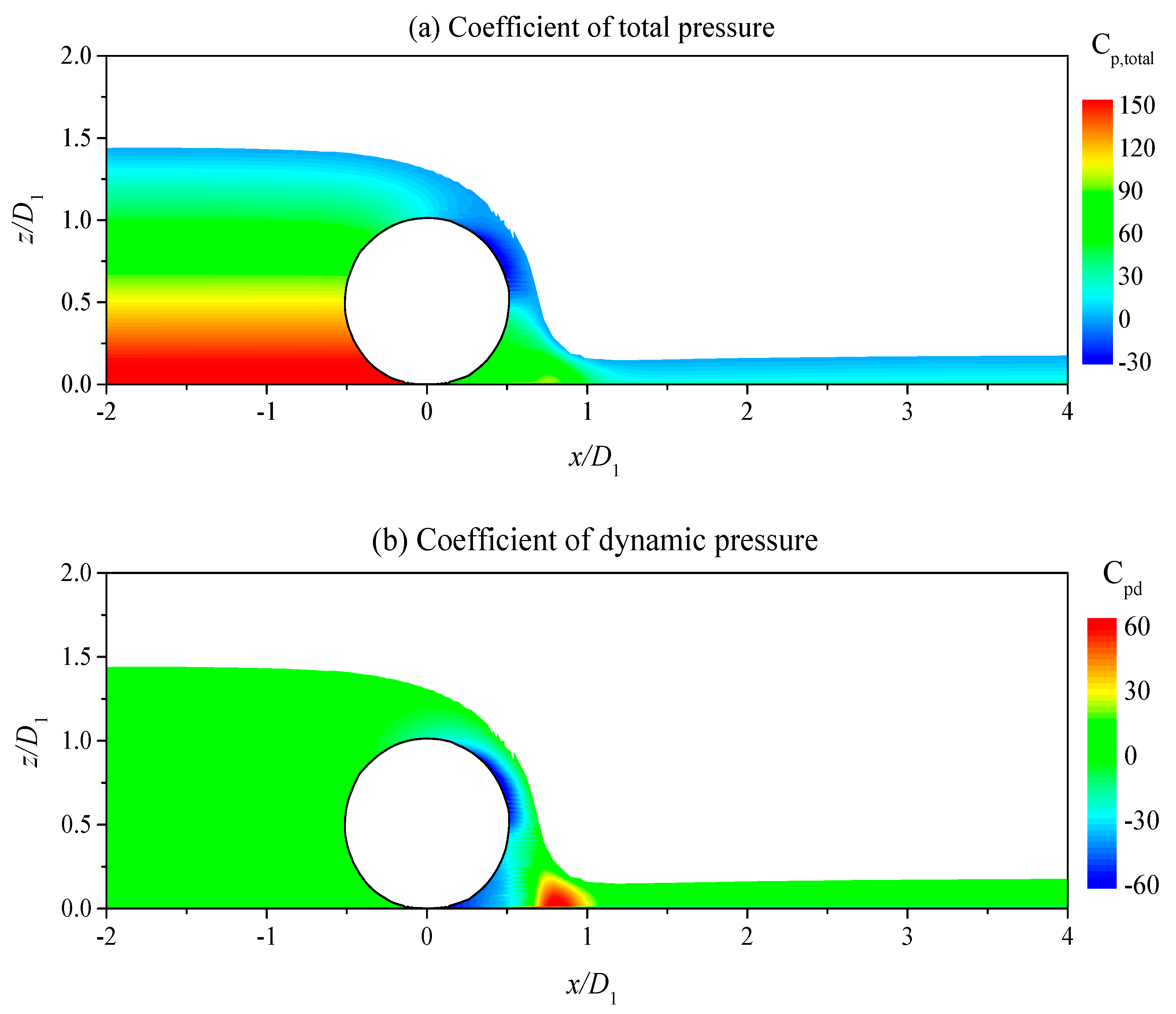
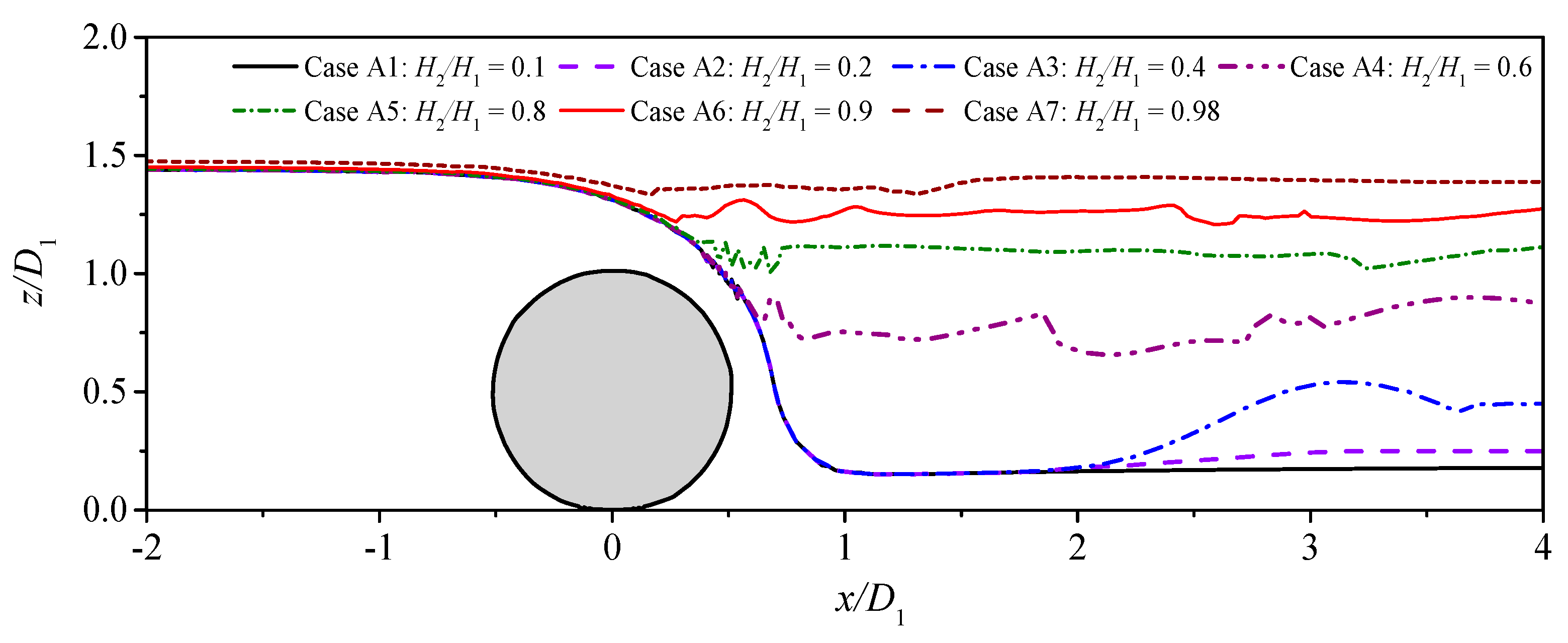
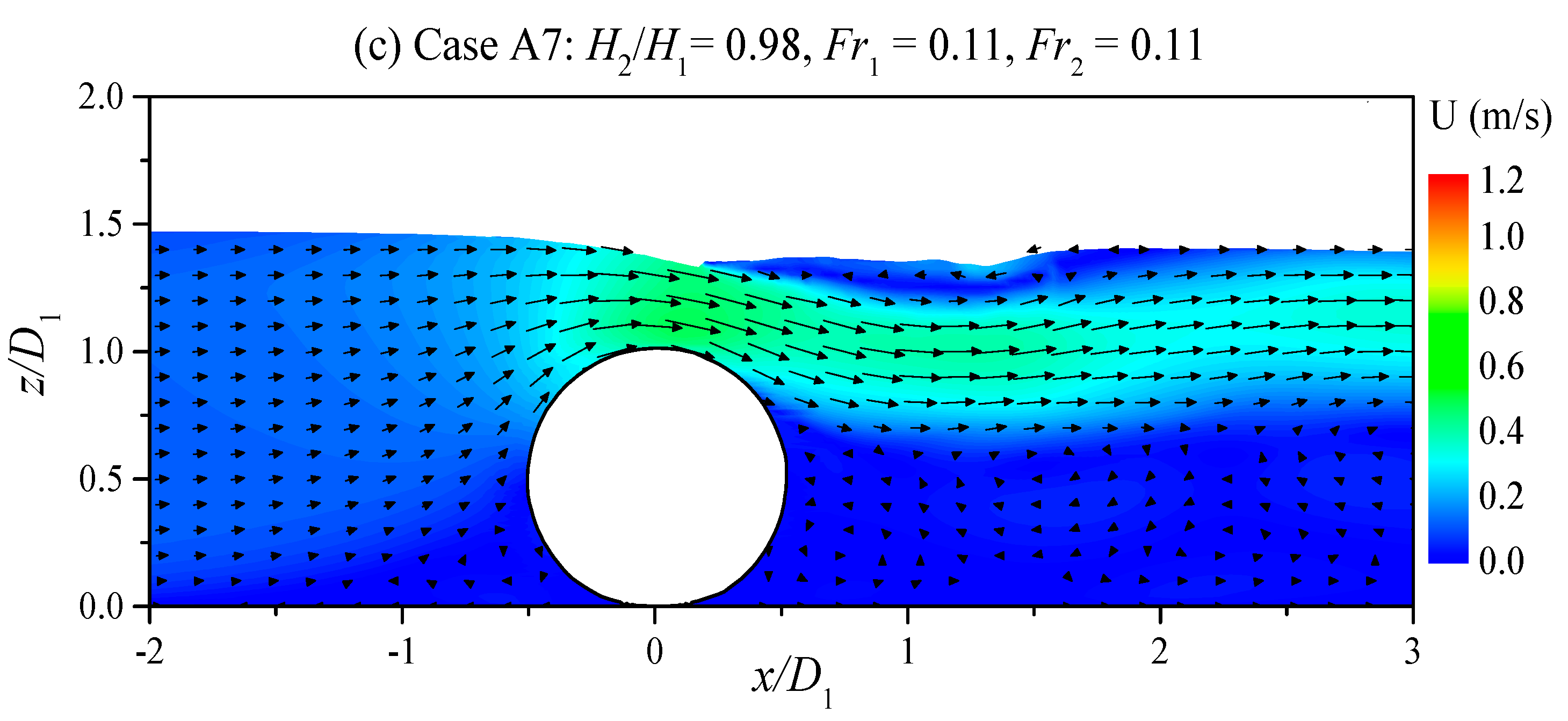
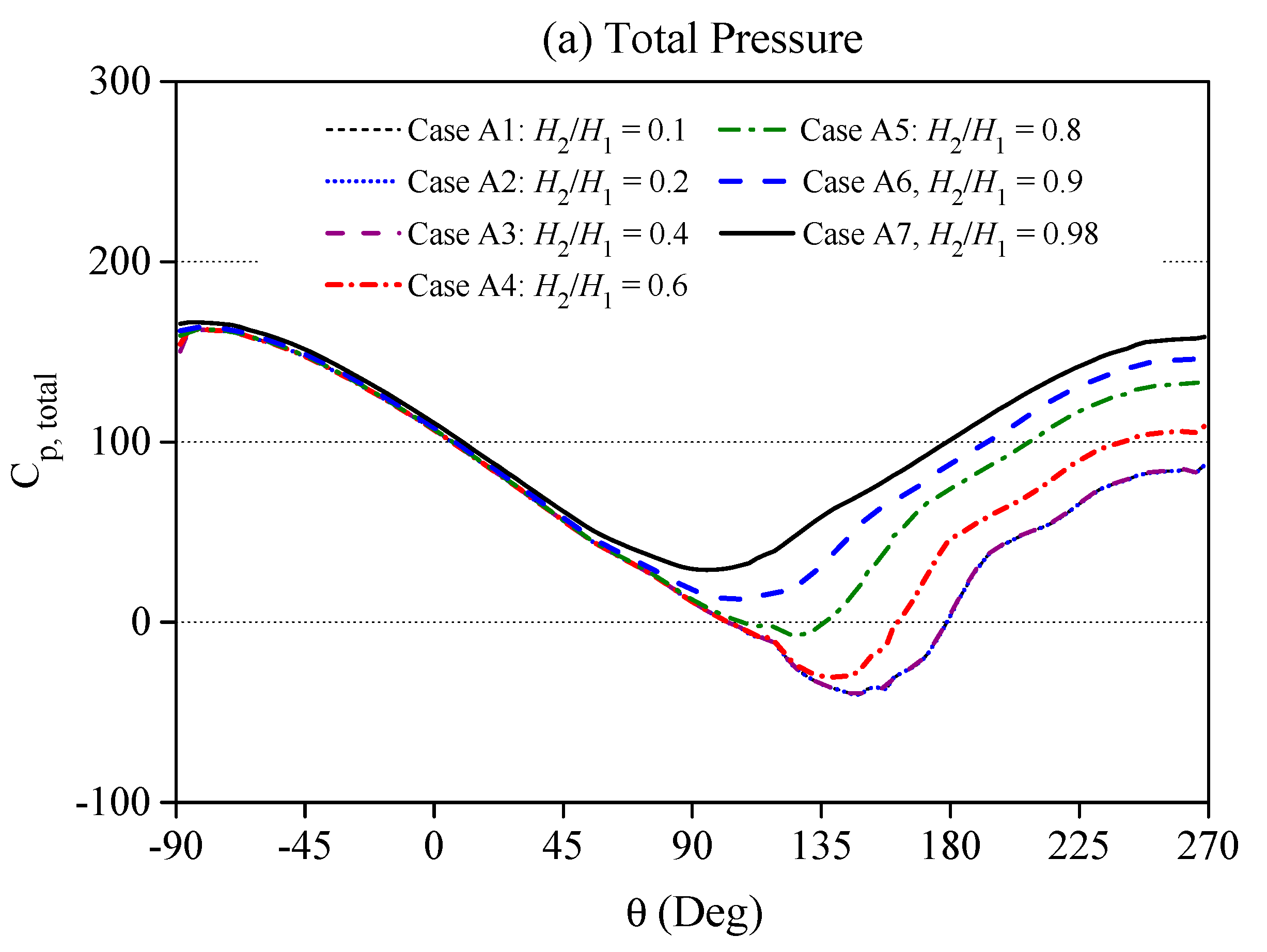
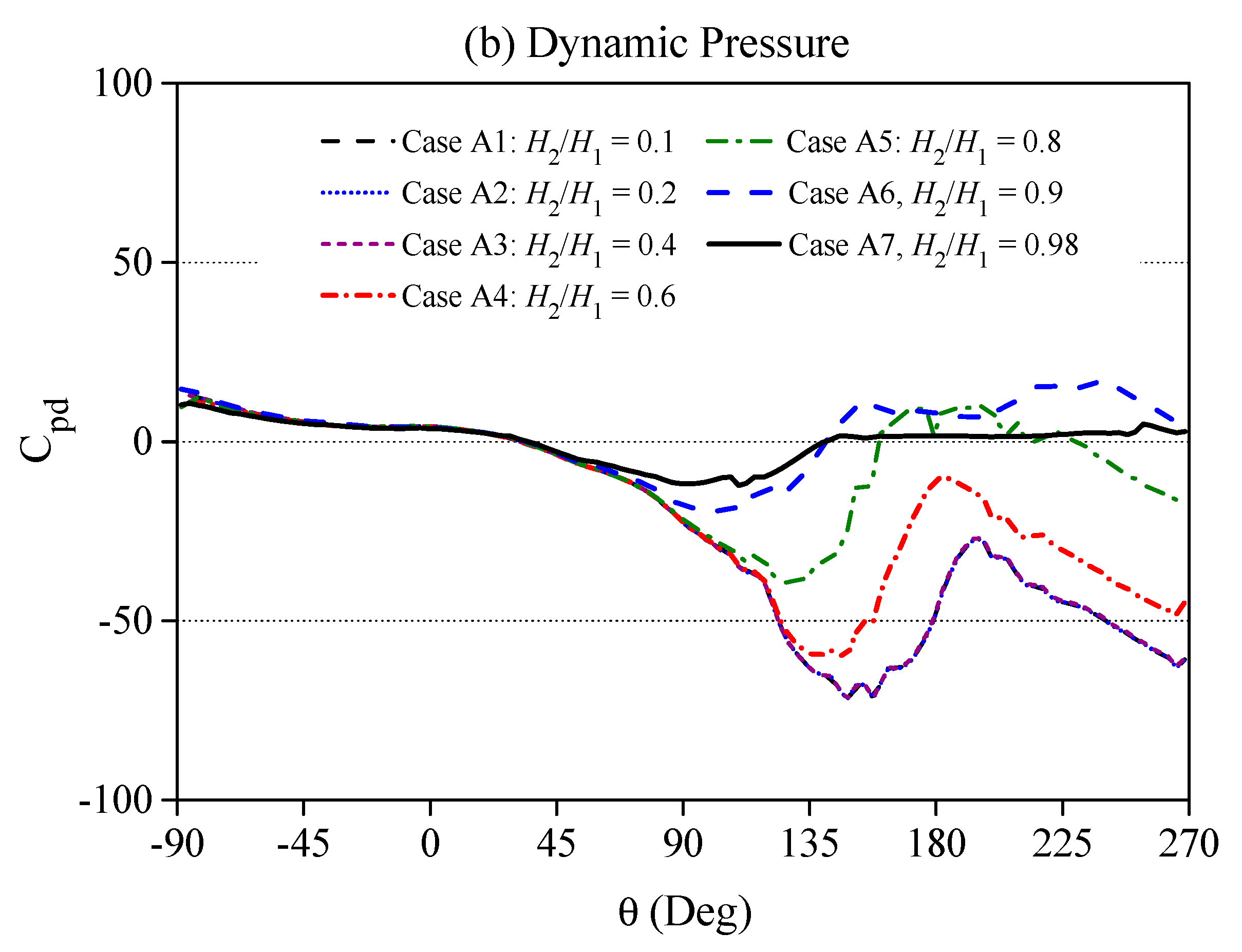
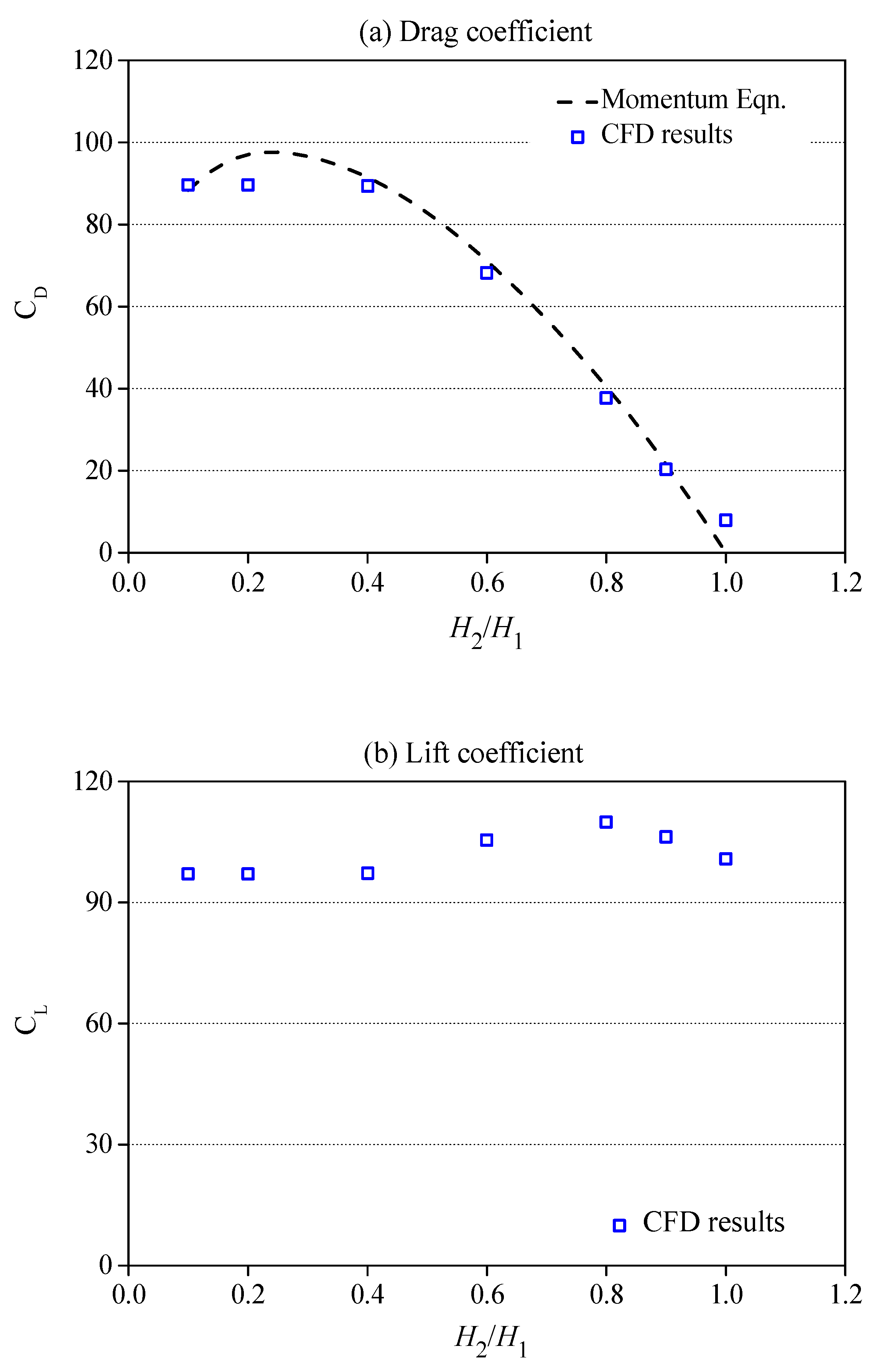
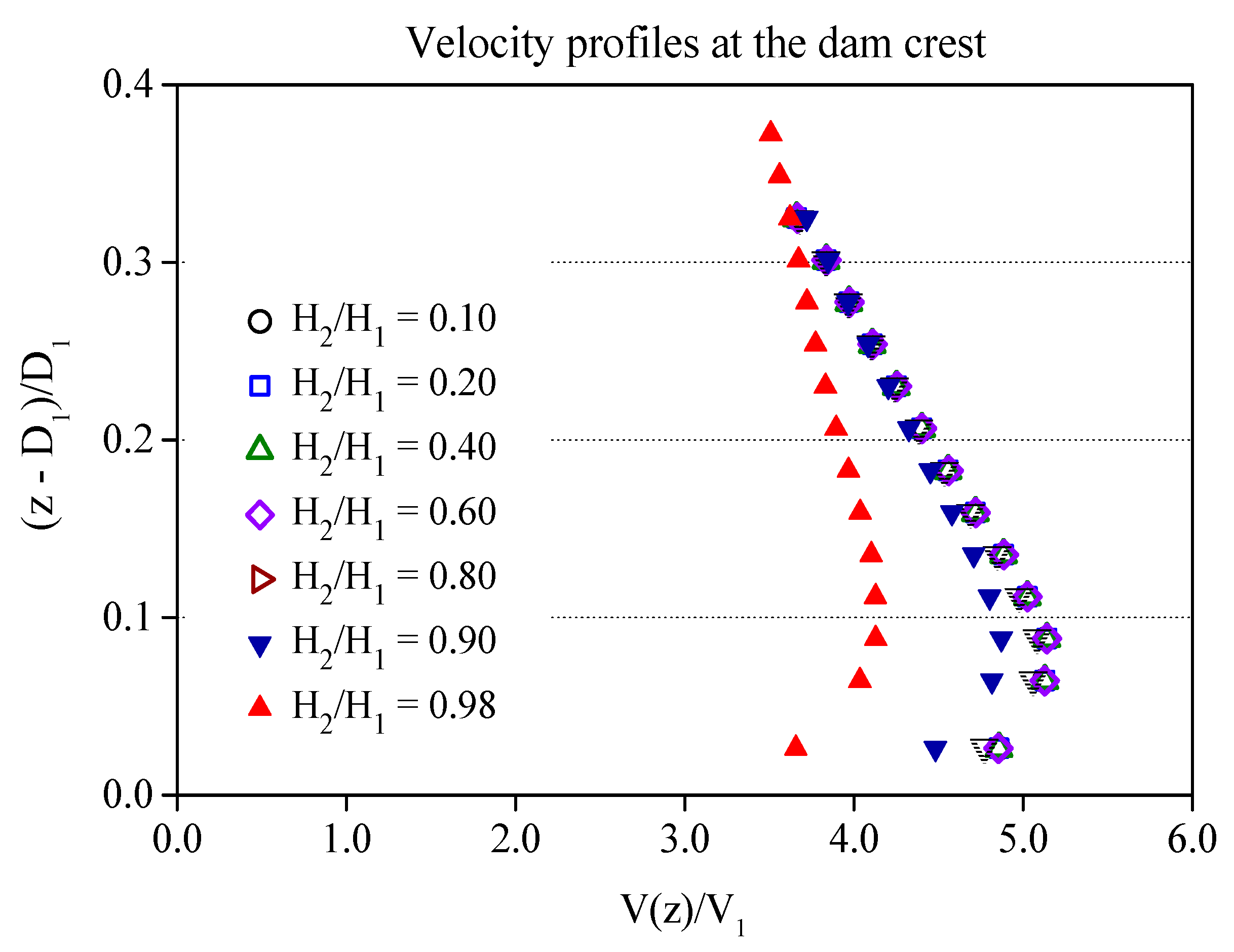
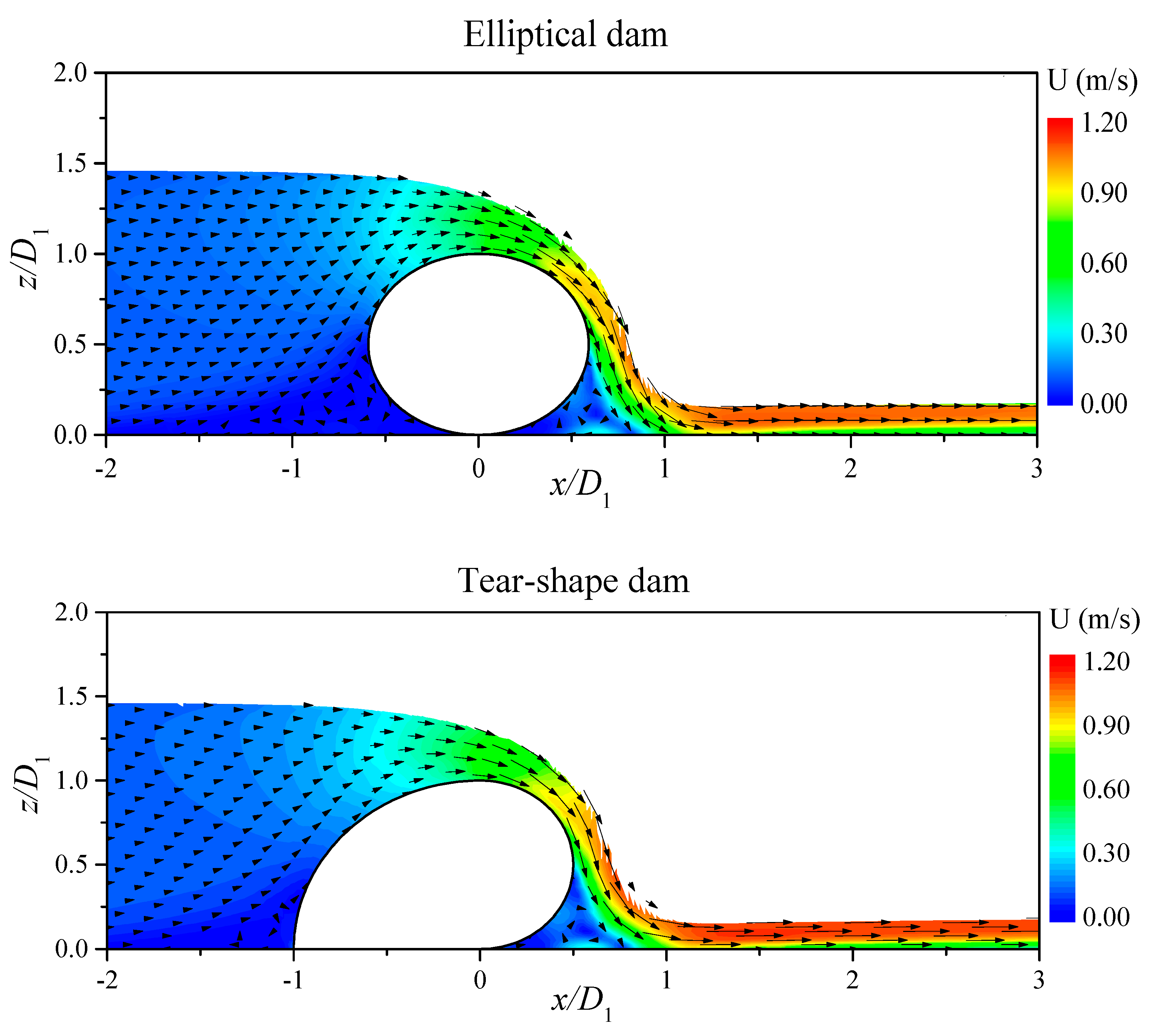
4.1. Hydrodynamic Loading
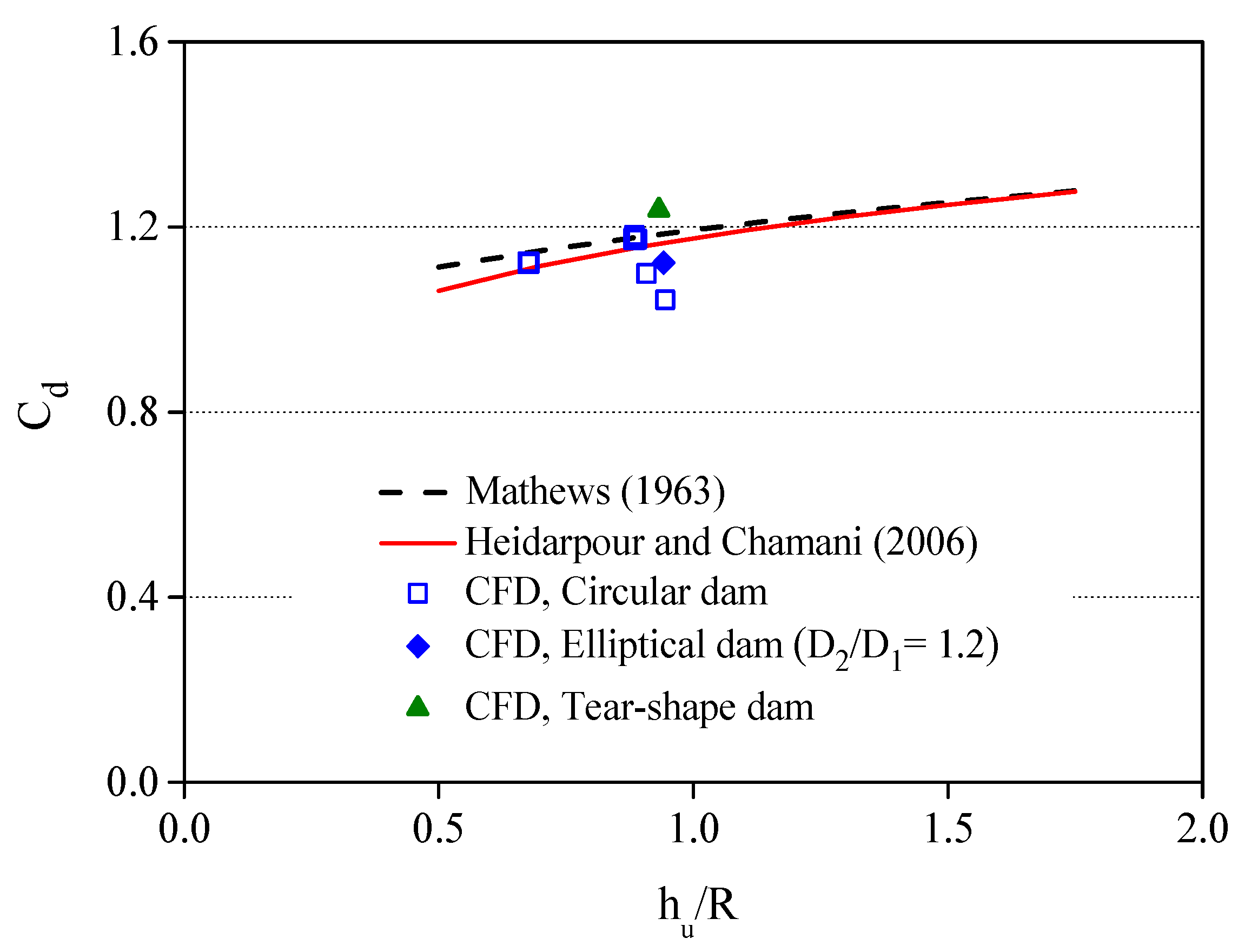
4.2. Discharge Coefficient
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ramamurthy, A.S.; Vo, N.-D. Characteristics of Circular-Crested Weir. J. Hydraul. Eng. 1993, 119, 1055–1062. [Google Scholar] [CrossRef]
- Zhang, X.Q.; Tam, P.W.M.; Zheng, W. Construction, operation, and maintenance of rubber dams. Can. J. Civ. Eng. 2002, 29, 409–420. [Google Scholar] [CrossRef] [Green Version]
- Saleh, A.F.M.; Mondal, M.S. Performance evaluation of rubber dam projects of Bangladesh in irrigation development. Irrig. Drain. 2001, 50, 237–248. [Google Scholar] [CrossRef]
- Chanson, H. A review of the overflow of inflatable flexible membrane dams. Aust. Civ. Eng. Trans. 1997, 39, 107–116. [Google Scholar]
- Wu, P.-H.; Plaut, R. Analysis of the vibrations of inflatable dams under overflow conditions. Thin-Walled Struct. 1996, 26, 241–259. [Google Scholar] [CrossRef] [Green Version]
- Chanson, H.; Tam, P.W.M. Discussion and Closure: Use of Rubber Dams for Flood Mitigation in Hong Kong. J. Irrig. Drain. Eng. 1998, 124, 181–184. [Google Scholar] [CrossRef]
- Chanson, H. Hydraulics of rubber dam overflow: A simple design approach. In Proceedings of the 13th Australasian Fluid Mechanics Conference, Melbourne, Australia, 13–18 December 1998; pp. 255–258. [Google Scholar]
- Hager, W.H. Critical flow condition in open channel hydraulics. Acta Mech. 1985, 54, 157–179. [Google Scholar] [CrossRef]
- Hager, W.H. Discussion of “Characteristics of Circular-Crested Weirs” by A.S. Ramamurthy and N.-D. Vo (1993, 119). J. Hydraul. Eng. 1994, 120, 1494–1495. [Google Scholar] [CrossRef]
- Chanson, H.; Montes, J.S. Overflow Characteristics of Circular Weirs: Effects of Inflow Conditions. J. Irrig. Drain. Eng. 1998, 124, 152–162. [Google Scholar] [CrossRef] [Green Version]
- Heidarpour, M.; Chamani, M. Velocity distribution over cylindrical weirs. J. Hydraul. Res. 2006, 44, 708–711. [Google Scholar] [CrossRef]
- Bagheri, S.; Heidarpour, M. Overflow characteristics of circular-crested weirs. J. Hydraul. Res. 2010, 48, 515–520. [Google Scholar] [CrossRef]
- Schmocker, L.; Halldórsdóttir, B.R.; Hager, W.H. Effect of Weir Face Angles on Circular-Crested Weir Flow. J. Hydraul. Eng. 2011, 137, 637–643. [Google Scholar] [CrossRef]
- Naghavi, B.; Esmaili, K.; Yazdi, J.; Vahid, F.K. An experimental and numerical study on hydraulic characteristics and theoretical equations of circular weirs. Can. J. Civ. Eng. 2011, 38, 1327–1334. [Google Scholar] [CrossRef]
- Cheraghi-Shirazi, N.; Kabiri-Samani, A.; Boroomand, B. Numerical analysis of rubber dams using fluid–structure interactions. Flow Meas. Instrum. 2014, 40, 91–98. [Google Scholar] [CrossRef]
- Yuce, M.I.; Al-Babely, A.A.; Al-Dabbagh, M.A. Flow simulation over oblique cylindrical weirs. Can. J. Civ. Eng. 2015, 42, 389–407. [Google Scholar] [CrossRef]
- Cheraghi-Shirazi, N.; Kabiri-Samani, A.; Boroomand, B. Flow field over the rubber dams based on fluid-structure interactions. J. Civ. Eng. 2017, 49, 141–144. [Google Scholar] [CrossRef]
- Deardorff, J.W. A numerical study of three-dimensional turbulent channel flow at large Reynolds numbers. J. Fluid Mech. 1970, 41, 453–480. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- O’Neil, J.; Meneveau, C. Subgrid-scale stresses and their modelling in a turbulent plane wake. J. Fluid Mech. 1997, 349, 253–293. [Google Scholar] [CrossRef]
- Smagorinsky, J. General circulation experiments with the primitive equations: I. The basic experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Rodi, W.; Constantinescu, G.; Stoesser, T. Large Eddy Simulation in Hydraulic; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- DeLong, M. Two Examples of the Impact of Partitioning with Chaco and Metis on the Convergence of Additive-Schwarz Preconditioned FGMRES; Technical Report LA-UR-97-4181; Los Alamos National Laboratory: Los Alamos, NM, USA, 1997. [Google Scholar]
- Hirt, C.; Nichols, B. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Cabot, W.; Moin, P. Approximate Wall Boundary Conditions in the Large-Eddy Simulation of High Reynolds Number Flow. Flow Turbul. Combust. 2000, 63, 269–291. [Google Scholar] [CrossRef]
- Korzekwa, D.A. Truchas—A multi-physics tool for casting simulation. Int. J. Cast Met. Res. 2009, 22, 187–191. [Google Scholar] [CrossRef]
- Chu, C.-R.; Wu, Y.-R.; Wu, T.-R.; Wang, C.-Y. Slosh-induced hydrodynamic force in a water tank with multiple baffles. Ocean Eng. 2018, 167, 282–292. [Google Scholar] [CrossRef]
- Chu, C.-R.; Chung, C.-H.; Wu, T.-R.; Wang, C.-Y. Numerical analysis of free surface flow over a submerged rectangular bridge deck. J. Hydraul. Eng. 2016, 142. [Google Scholar] [CrossRef]
- Chu, C.-R.; Lin, Y.-A.; Wu, T.-R.; Wang, C.-Y. Hydrodynamic force of circular cylinder close to the water surface. Comput. Fluids 2018, 171, 154–165. [Google Scholar] [CrossRef]
- Wu, T.-R.; Vuong, T.-H.-N.; Lin, J.-W.; Chu, C.-R.; Wang, C.-Y. Three-Dimensional Numerical Study on the Interaction between Dam-Break Wave and Cylinder Array. J. Earthq. Tsunami 2018, 12, 1–35. [Google Scholar] [CrossRef] [Green Version]
- Matthew, G.D. On the influence of the curvature, surface tension and viscosity on flow over round-crested weirs. Proc. Inst. Civil Eng. 1963, 25, 511–524. [Google Scholar] [CrossRef]

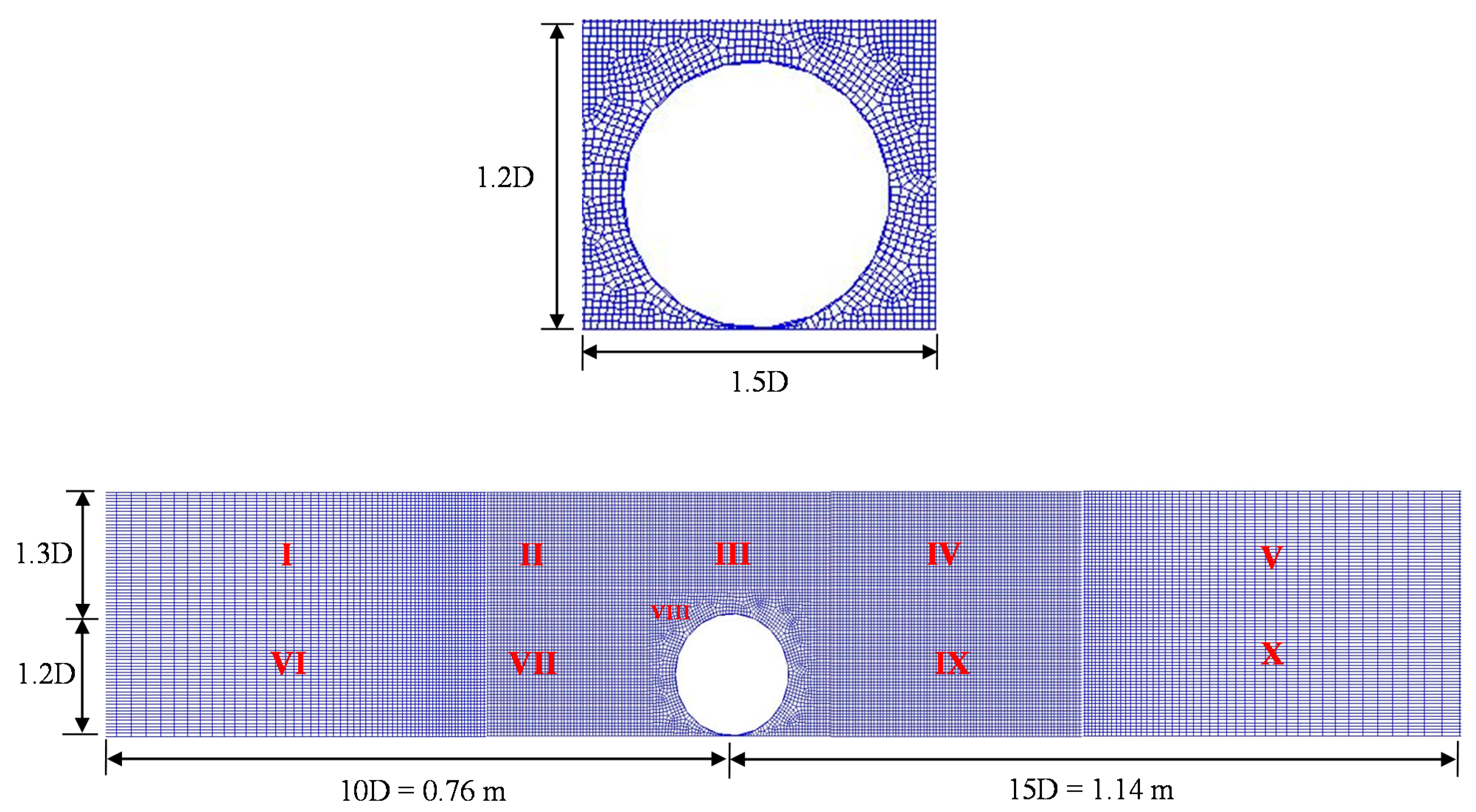

| Title | Grid 1 (2D) | Grid 2 (2D) | Grid 3 (2D) | Grid 4 (3D) | ||||
| Total grid no. | 104,048 | 159,212 | 233,859 | 955,272 | ||||
| Grid no. on the cylinder surface | 90 | 120 | 150 | 120 | ||||
| Grid size near the cylinder | 2.65 mm | 2.0 mm | 1.60 mm | 2.0 mm | ||||
| Smallest grid size | Δx = 3 mm Δz = 3 mm | Δx = 2 mm Δz = 2 mm | Δx = 1.5 mm Δz = 1.5 mm | Δx = 2 mm Δy = 5 mm Δz = 2 mm | ||||
| Water surface Δh | 8.53% | 5.59% | 5.06% | 6.97% | ||||
| Force coeff. | CD | CL | CD | CL | CD | CL | CD | CL |
| 89.7 | 95.5 | 89.6 | 88.5 | 93.1 | 93.1 | 90.3 | 97.8 | |
| CPU time | 18 h | 26 h | 40 h | 768 h | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chu, C.-R.; Tran, T.T.T.; Wu, T.-R. Numerical Analysis of Free-Surface Flows over Rubber Dams. Water 2021, 13, 1271. https://doi.org/10.3390/w13091271
Chu C-R, Tran TTT, Wu T-R. Numerical Analysis of Free-Surface Flows over Rubber Dams. Water. 2021; 13(9):1271. https://doi.org/10.3390/w13091271
Chicago/Turabian StyleChu, Chia-Ren, Truc Thi Thu Tran, and Tso-Ren Wu. 2021. "Numerical Analysis of Free-Surface Flows over Rubber Dams" Water 13, no. 9: 1271. https://doi.org/10.3390/w13091271
APA StyleChu, C.-R., Tran, T. T. T., & Wu, T.-R. (2021). Numerical Analysis of Free-Surface Flows over Rubber Dams. Water, 13(9), 1271. https://doi.org/10.3390/w13091271








