Evaluation of Subsurface Drip Irrigation Designs in a Soil Profile with a Capillary Barrier
Abstract
:1. Introduction
2. Materials and Methods
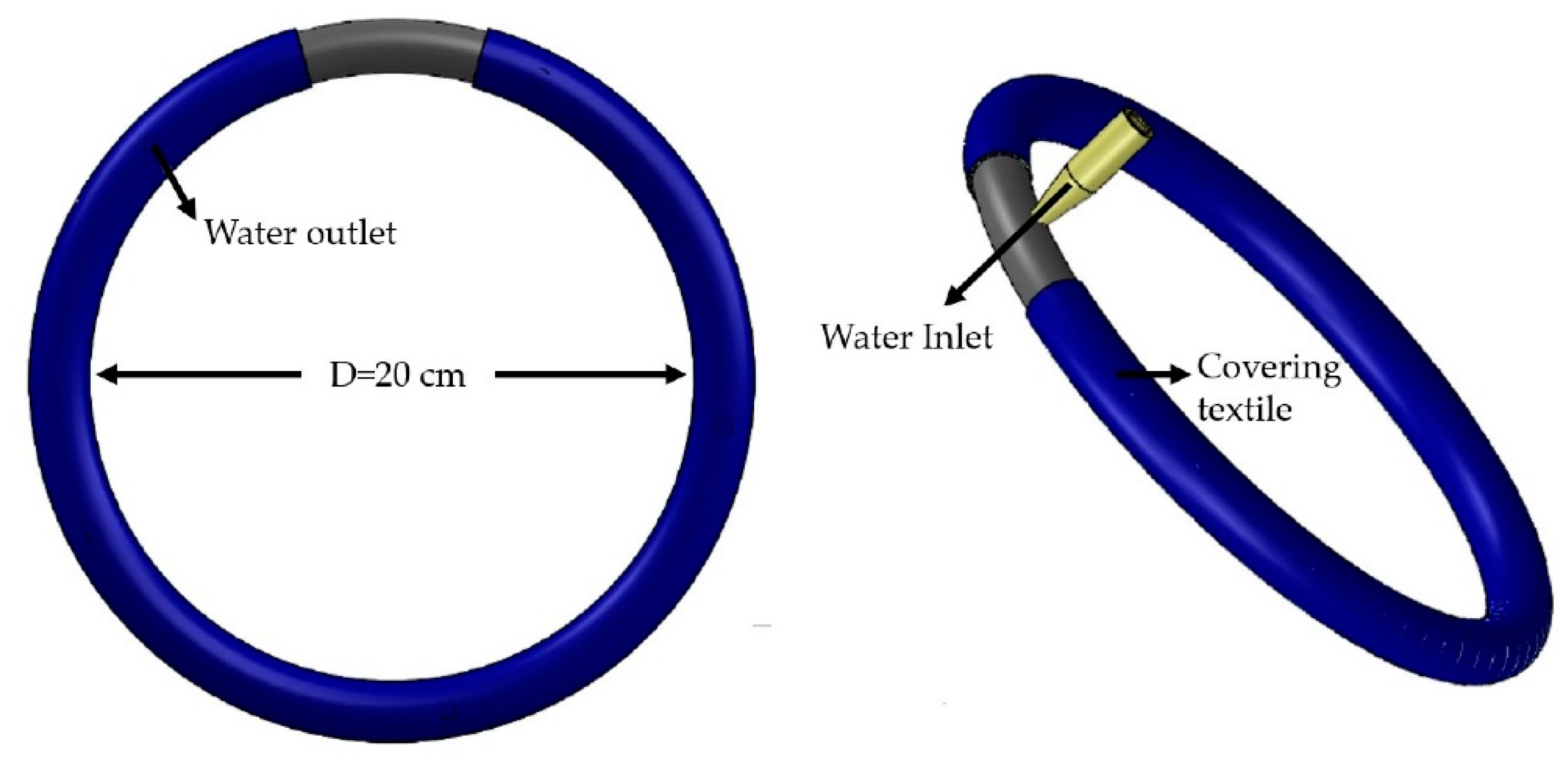
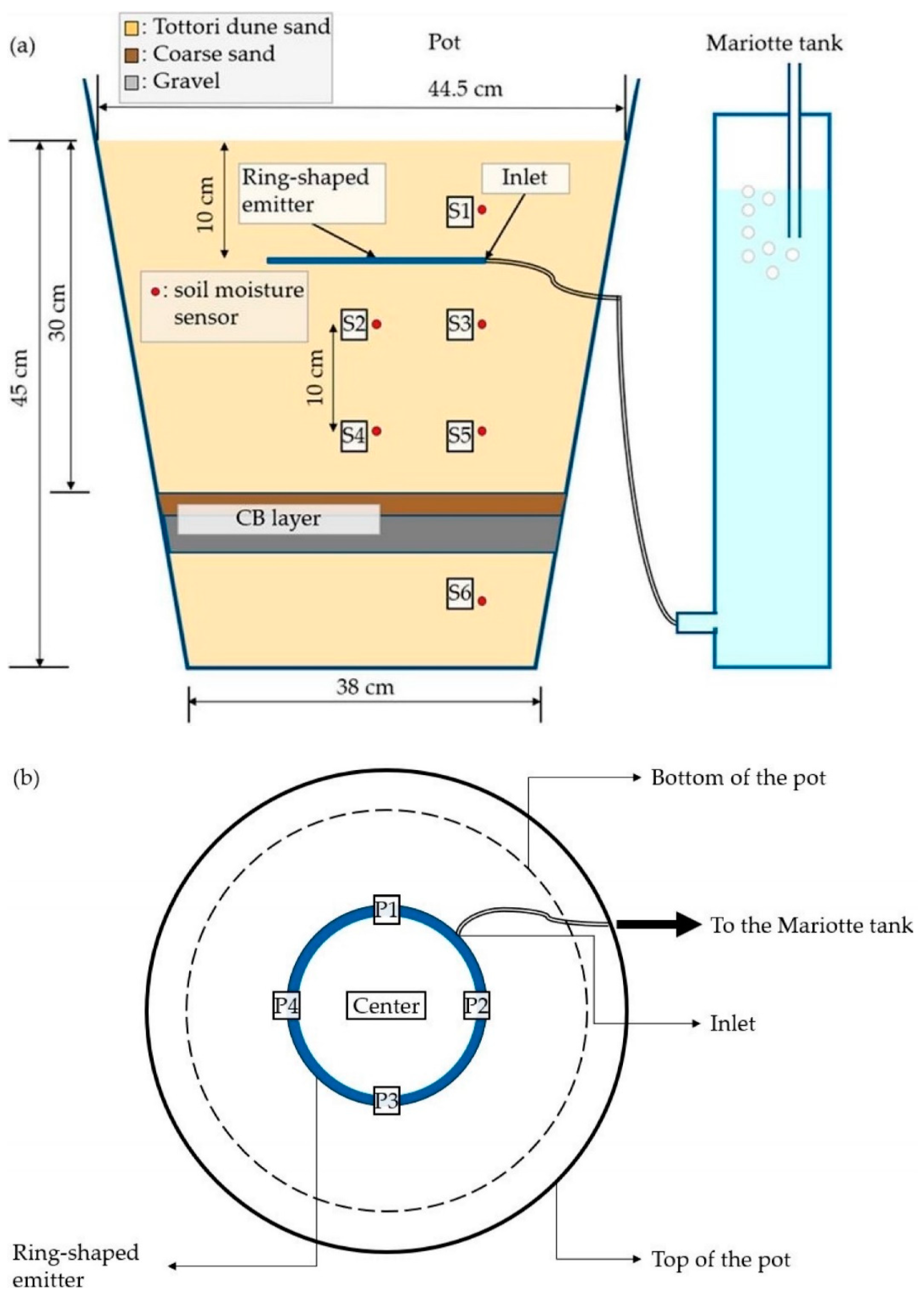
2.1. A Laboratory Experiment with a Ring-Shaped Emitter and a CB
2.2. The HYDRUS (2D/3D) Inverse Estimation of Soil Hydraulic Parameters and Simulation of the Pot Experiment
2.3. Numerical Analysis of the Optimal SDI Setup
2.3.1. The RWU Model of HYDRUS (2D/3D)
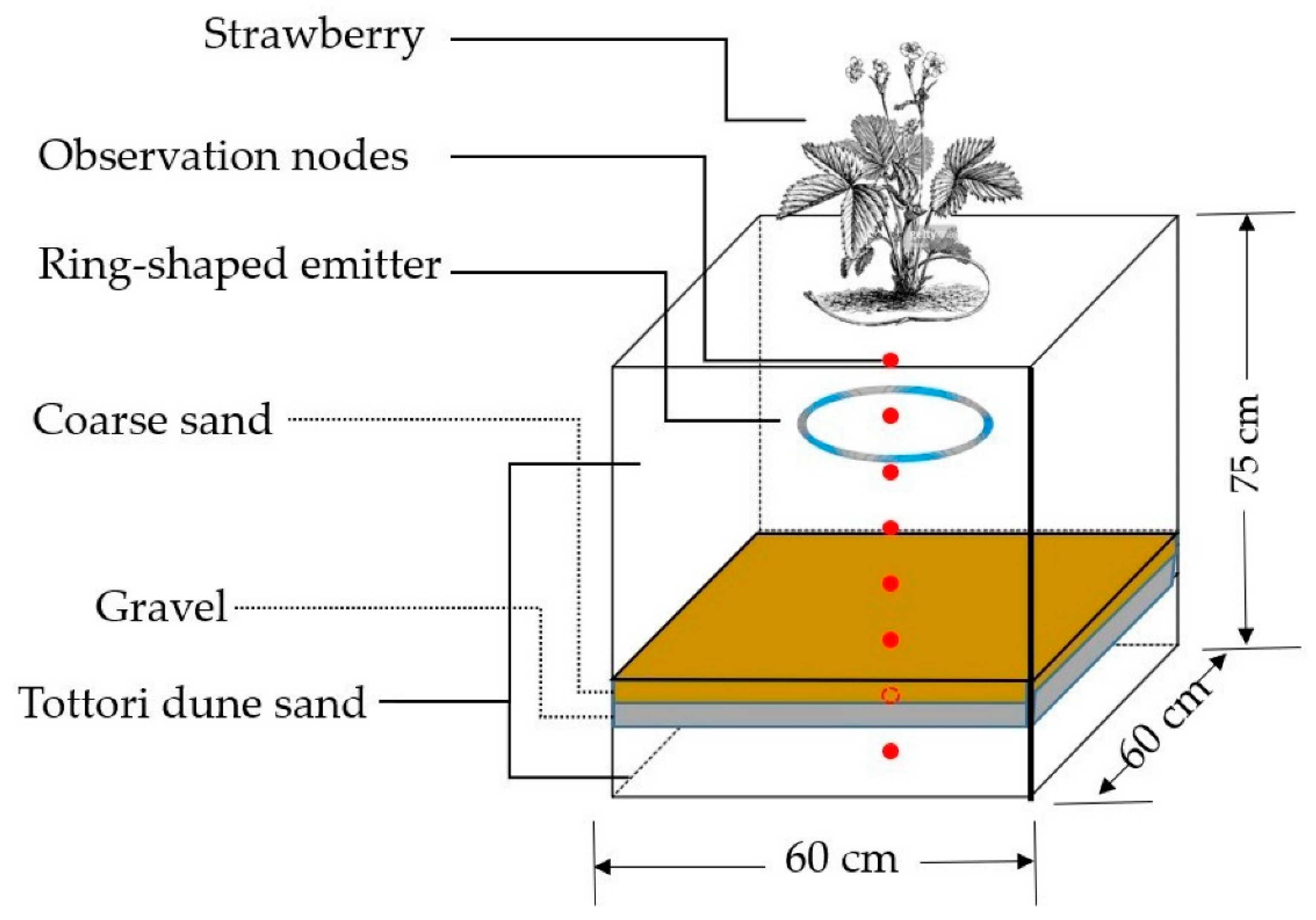
2.3.2. Simulation Domain Setups
3. Results
3.1. A Laboratory Experiment with a Ring-Shaped Emitter and a CB
3.2. Inverse Estimation of Soil Hydraulic Parameters and Simulation of the Pot Experiment
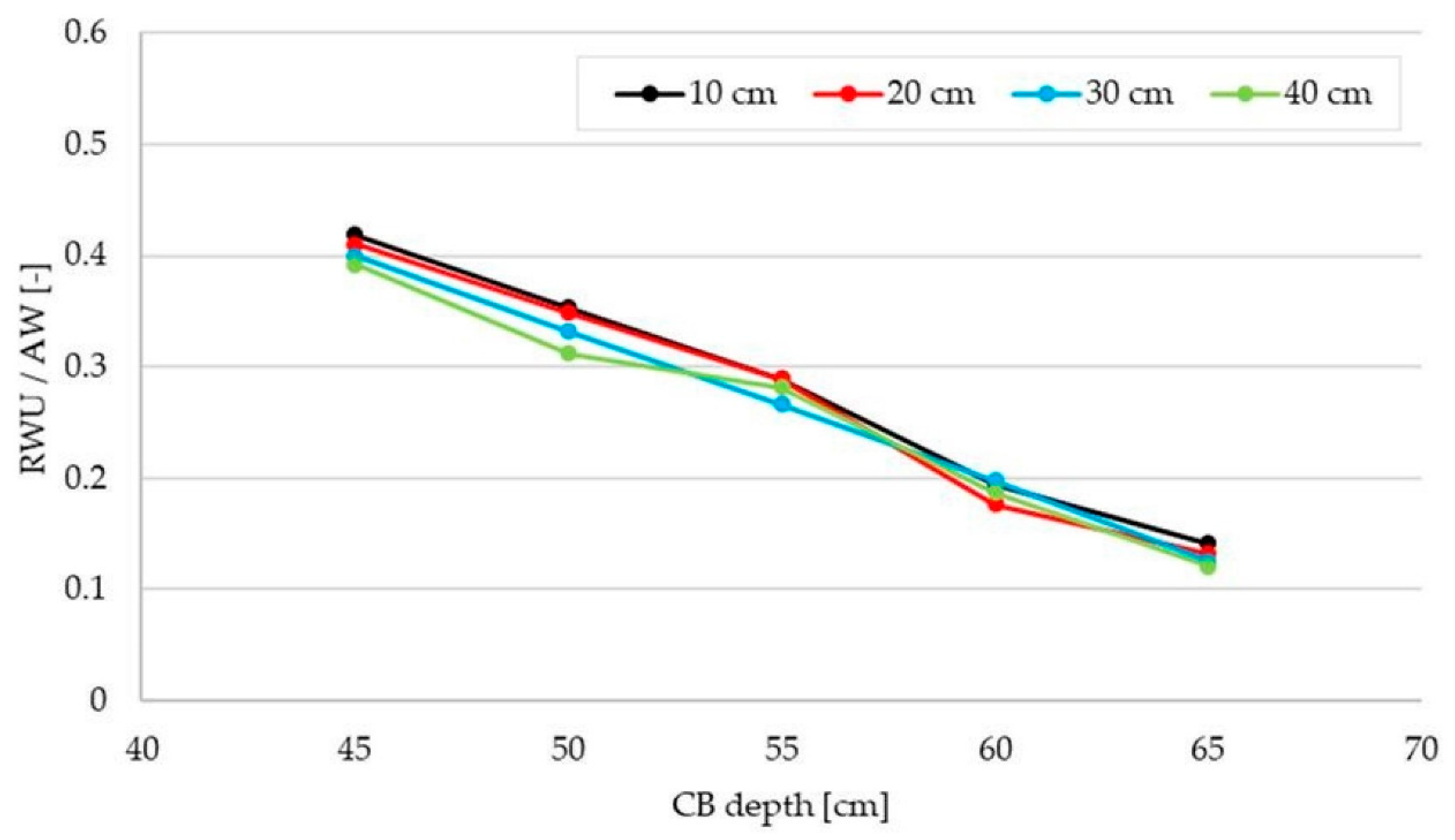
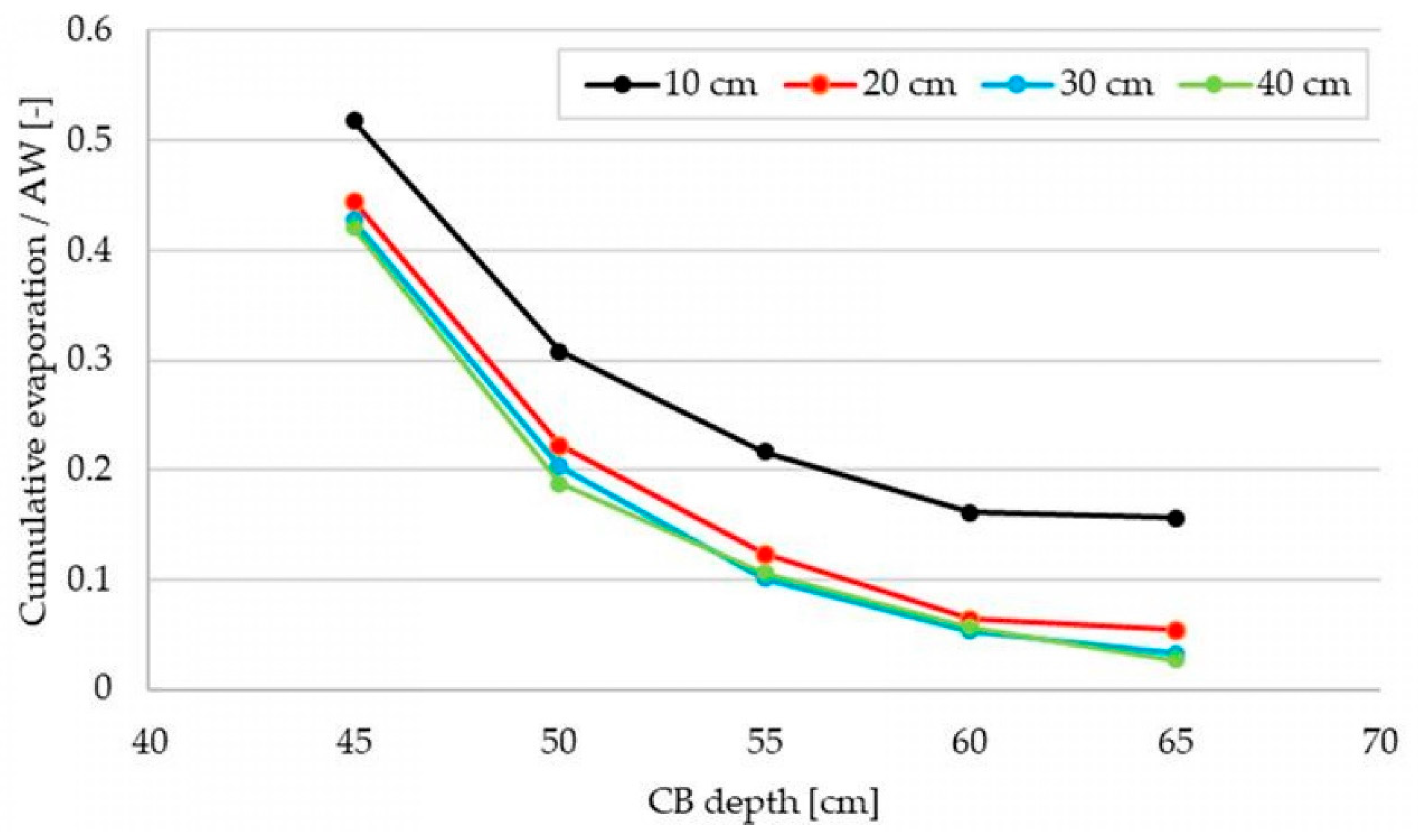
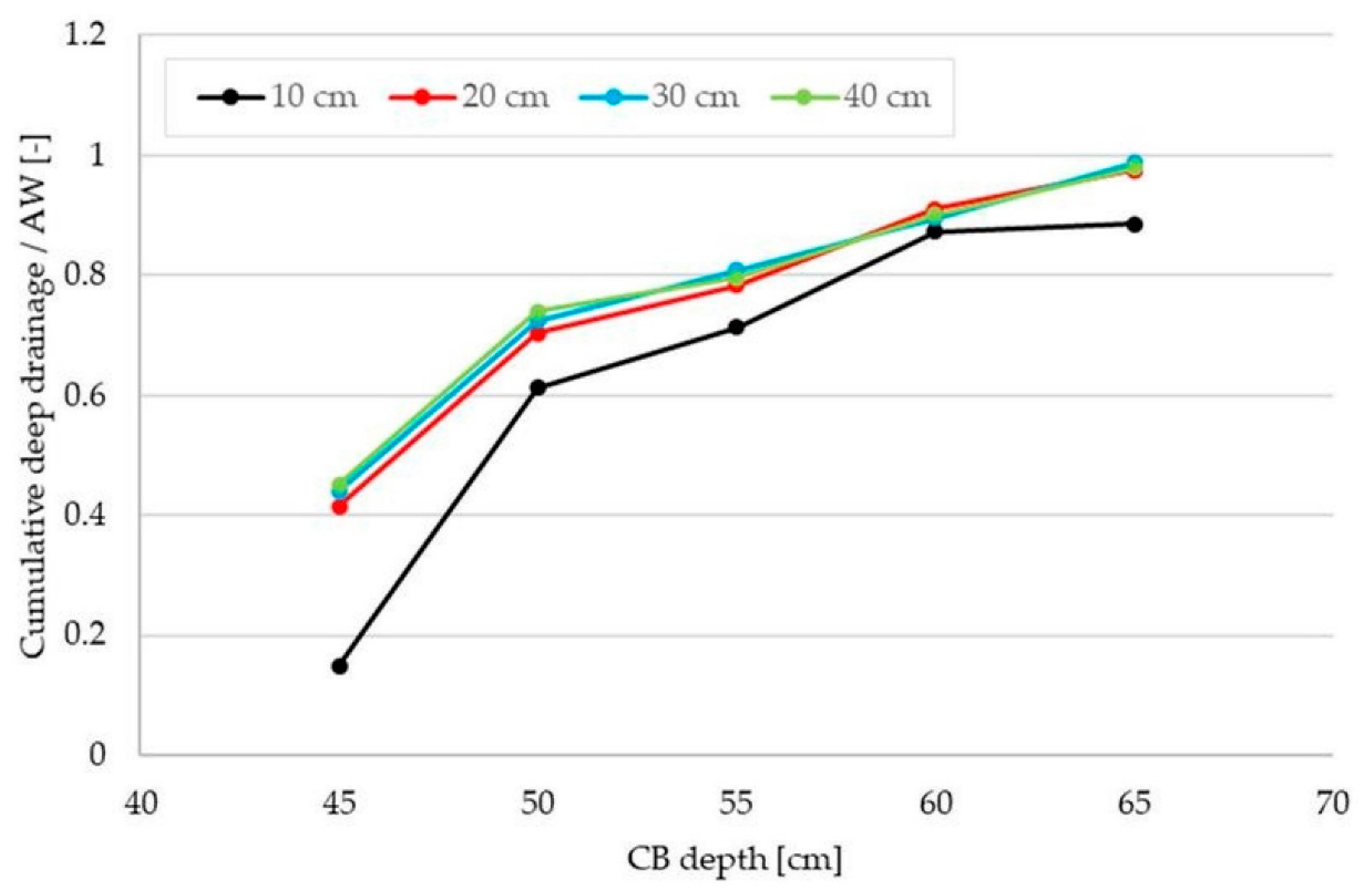
3.3. Numerical Analysis of the Effect of the Ring-Shaped Emitter and CB Installation Depths
4. Discussion
4.1. Water Dynamics in a System with a CB under SDI
4.2. The Comparison between the Pot Experiment and the HYDRUS (2D/3D) Simulation
4.3. Effects of the Installation Depths of the Ring-Shaped Emitter and CB on Water Balance
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Steduto, P.; Faurès, J.-M.; Hoogeveen, J.; Winpenny, J.; Burke, J. Coping with Water Scarcity: An Action Framework for Agricultural and Food Security; FAO WATER REPORTS 38; Food and Agricultural Organization of the United Nations: Rome, Italy, 2012; pp. 11–13, ISSN 1020-1203. [Google Scholar]
- Grasham, C.F.; Korzenevica, M.; Charles, K.J. On considering climate resilience in urban water security: A review of the vulnerability of the urban poor in sub-Saharan Africa. WIREs Water 2019, 6, e1344. [Google Scholar] [CrossRef] [Green Version]
- Niang, I.; Ruppel, O.C.; Abdrabo, M.A.; Essel, A.; Lennard, C.; Padgham, J.; Urquhart, P. Climate Change 2014: Impacts Adaptation, and Vulnerability. Part B: Regional Aspects. Contribution of Working Group 2 to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2014; pp. 1199–1265. [Google Scholar] [CrossRef] [Green Version]
- Sousa, P.M.; Blamey, R.C.; Reason, C.J.C.; Ramos, A.M.; Trigo, R.M. The ‘Day Zero’ Cape Town drought and the poleward migration of moisture corridors. Environ. Res. Lett. 2018, 13, 124025–124035. [Google Scholar] [CrossRef] [Green Version]
- Ityel, E.; Lazarovitch, N.; Silberbush, M.; Ben-Gal, A. An artificial capillary barrier to improve root zone conditions for horticultural crops: Physical effects on water content. Irrig. Sci. 2010, 29, 171–180. [Google Scholar] [CrossRef]
- Ityel, E.; Lazarovitch, N.; Silberbush, M.; Ben-Gal, A. An artificial capillary barrier to improve root zone conditions for horticultural crops: Response of pepper, lettuce, melon, and tomato. Agric. Water Manag. 2012, 30, 293–301. [Google Scholar] [CrossRef]
- Ityel, E.; Lazarovitch, N.; Silberbush, M.; Ben-Gal, A. An artificial capillary barrier to improve root zone conditions for horticultural crops: Response of pepper plants to matric head and irrigation water salinity. Irrig. Sci. 2012, 105, 13–20. [Google Scholar] [CrossRef]
- Miyake, M.; Otsuka, M.; Fujimaki, H.; Inoue, M.; Saito, H. Evaluation of an Artificial Capillary Barrier to Control Infiltration and Capillary Rise at Root Zone Areas. J. Arid Land Stud. 2015, 25, 117–120. [Google Scholar] [CrossRef]
- Wongkaew, A.; Saito, H.; Fujimaki, H.; Šimůnek, J. Numerical analysis of soil water dynamics in a soil column with an artificial capillary barrier growing leaf vegetables. Soil Use Manag. 2018, 34, 206–215. [Google Scholar] [CrossRef]
- Mohammed, S.A.; Rashid, A.; Said, S.A.; Anvar, R.K.; Hamed, A. Use of Soil-Structured Capillary Barrier can Mitigate the Impact of Saline Irrigation Water on Marigold Grown Under Field Condition. J. Agri. Mar. Sci. 2020, 25, 9–19. [Google Scholar] [CrossRef]
- Yunasa, G.H.; Kassim, A.; Umar, M.; Talib, Z.A.; Abdulfatah, A.Y. Laboratory investigation of suction distribution in a modified capillary barrier system. IOP Conf. Ser. Earth Environ. Sci. 2020, 476, 012047. [Google Scholar] [CrossRef]
- Morris, C.E.; Stormont, J.C. Evaluation of numerical simulations of capillary barrier field tests. Geotech. Geol. Eng. 1998, 16, 201–213. [Google Scholar] [CrossRef]
- Fala, O.; Molson, J.; Aubertin, M.; Bussière, B. Numerical Modelling of Flow and Capillary Barrier Effects in Unsaturated Waste Rock Piles. Mine Water Environ. 2005, 24, 172–185. [Google Scholar] [CrossRef]
- Stroosnijder, L. Soil evaporation: Test of a practical approach under semi-arid conditions. Neth. J. Agri. Sci. 1987, 35, 417–426. [Google Scholar] [CrossRef]
- Bonachela, S.; Orgaz, F.; Villalobos, F.J.; Fereres, E. Soil evaporation from drip-irrigated olive orchards. Irrig. Sci. 2001, 20, 65–71. [Google Scholar] [CrossRef]
- Martinez, J.; Reca, J. Water use efficiency of surface drip irrigation versus an alternative subsurface drip irrigation method. Irrig. Drain. Eng. 2014, 140, 04014030. [Google Scholar] [CrossRef]
- Friedman, S.P.; Gamliel, A. Wetting Patterns and Relative Water-Uptake Rates from a Ring-Shaped Water Source. Soil Sci. Soc. Am. J. 2019, 83, 48–57. [Google Scholar] [CrossRef]
- O’Brien, D.M.; Rogers, D.H.; Lamm, F.R.; Clark, G.A. An Economic Comparison of Subsurface Drip and Center Pivot Sprinkler Irrigation Systems. Appl. Eng. Agric. 1998, 14, 391–398. [Google Scholar] [CrossRef]
- Saefuddin, R.; Saito, H. Performance of a ring-shaped emitter for subsurface irrigation in bell pepper (Capsicum annum L.) cultivation. Paddy Water Environ. 2019, 17, 101–107. [Google Scholar] [CrossRef]
- Saefuddin, R.; Saito, H.; Šimůnek, J. Experimental and numerical evaluation of a ring-shaped emitter for subsurface irrigation. Agric. Water Manag. 2019, 211, 111–122. [Google Scholar] [CrossRef]
- Sumarsono, J.; Setiawan, B.I.; Subrata, I.D.M.; Saptomo, S.K. Ring-typed emitter subsurface irrigation performances in dryland farmings. Int. J. Civ. Eng. Technol. 2018, 9, 797–806. [Google Scholar]
- Šimůnek, J.; van Genchten, M.T.; Sejna, M. Recent Developments and Applications of the HYDRUS. Computer Software Packages. Vadose Zone J. 2016, 6, 1–25. [Google Scholar] [CrossRef] [Green Version]
- Skaggs, T.H.; Trout, T.J.; Šimůnek, J.; Shouse, P.J. Comparison of HYDRUS-2D Simulations of Drip Irrigation with Experimental Observations. Irrig. Drain. Eng. 2004, 130, 304–310. [Google Scholar] [CrossRef]
- Kandelous, M.M.; Šimůnek, J. Comparison of numerical, analytical, and empirical models to estimate wetting patterns for surface and subsurface drip irrigation. Irrig. Sci. 2010, 97, 1070–1076. [Google Scholar] [CrossRef] [Green Version]
- Šimůnek, J.; van Genuchten, M.T.; Šejna, M. The HYDRUS Software Package for Simulating Two- and Three-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably-Saturated Media, Technical Manual, 3rd ed.; PC Progress: Prague, Czech Republic, 2018; pp. 103–106. [Google Scholar]
- Provenzano, G. Using HYDRUS-2D simulation model to evaluate wetted soil volume in subsurface drip irrigation system. Irrig. Drain. Eng. 2007, 133, 342–349. [Google Scholar] [CrossRef]
- El-Nesr, M.N.; Alazba, A.A.; Šimůnek, J. HYDRUS simulations of the effects of dual-drip subsurface irrigation and a physical barrier on water movement and solute transport in soils. Irrig. Sci. 2014, 32, 111–125. [Google Scholar] [CrossRef] [Green Version]
- Brunetti, G.; Šimůnek, J.; Piro, P. A comprehensive analysis of the variably saturated hydraulic behavior of a green roof in a Mediterranean climate. Vadose Zone J. 2016, 5, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Durner, W. Hydraulic conductivity estimation for soils with heterogeneous pore structure. Water Resour. Res. 1994, 30, 211–223. [Google Scholar] [CrossRef]
- van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Šimůnek, J.; van Genuchten, M.T.; Sejna, M. Development and applications of the HYDRUS and STANMOD software packages and related codes. Vadose Zone J. 2008, 7, 587–600. [Google Scholar] [CrossRef] [Green Version]
- Vrugt, J.A.; van Wijk, M.T.; Hopmans, J.W.; Šimůnek, J. One-, two-, and three-dimensional root water uptake functions for transient modeling. Water Resour. Res. 2001, 37, 2457–2470. [Google Scholar] [CrossRef] [Green Version]
- Feddes, R.A.; Kowalik, P.J.; Zaradny, H. Simulation of Field Water Use and Crop Yield; John Wiley & Sons: New York, NY, USA, 1978; ISBN 9789022006764. [Google Scholar]
- Jury, W.A.; Horton, R. Soil Physics, 6th ed.; John Wiley & Sons: New York, NY, USA, 2004; pp. 139–146. ISBN 978-0-471-05965-3. [Google Scholar]
- Kandelous, M.M.; Kamai, T.; Vrugt, J.A.; Šimůnek, J.; Hanson, B.; Hopmans, J.W. Evaluation of subsurface drip irrigation design and management parameters for alfalfa. Agric. Water Manag. 2012, 109, 81–93. [Google Scholar] [CrossRef]

| Materials | θr [-] | θs [-] | α1 [cm−1] | n [-] | Ks [cm/min] | w1 [-] | w2 [-] | α2 [cm−1] | n2 [-] | l [-] |
|---|---|---|---|---|---|---|---|---|---|---|
| Tottori Dune sand | 0.006 | 0.384 | 0.030 | 6.675 | 2.15 | 1.0 | 0 | 0 | 1.5 | 0.5 |
| Coarse sand | 0.004 | 0.371 | 0.133 | 20.8 | 4.97 | 0.99 | 0.01 | 0.25 | 1.5 | 0.5 |
| Gravel | 0.005 | 0.274 | 0.204 | 15.5 | 13.8 | 0.99 | 0.01 | 0.25 | 1.5 | 0.5 |
| Vrugt et al. (2001) Parameter Description | Variable | Value |
|---|---|---|
| Maximum rooting radius [cm] | Xm | 20 |
| Radius of maximum intensity [cm] | x* | 0 |
| Maximum rooting radius [cm] | Ym | 20 |
| Radius of maximum intensity [cm] | y* | 0 |
| Maximum rooting depth [cm] | Zm | 30.5 |
| Depth with maximum rooting density [cm] | z* | 5 |
| Non-symmetry coefficient [-] | Px, Py, Pz | 1, 1, 1 |
| Surface area associated with transpiration [cm2] | - | 1200 |
| Feddes et al. [33] Parameters | Value |
|---|---|
| h1 [cm] | −5 |
| h2 [cm] | −10 |
| h3 [cm] | −40 |
| h4 [cm] | −45 |
| Measurement Depth | VWC | Ave. | SD. | ||||
|---|---|---|---|---|---|---|---|
| P1 | P2 | P3 | P4 | Center | |||
| 5 cm | 0.071 | 0.031 | 0.061 | 0.023 | 0.014 | 0.040 | 0.022 |
| 10 cm | 0.085 | 0.071 | 0.087 | 0.049 | 0.053 | 0.069 | 0.016 |
| 15 m | 0.136 | 0.150 | 0.177 | 0.178 | 0.145 | 0.157 | 0.017 |
| 20 cm | 0.213 | 0.224 | 0.238 | 0.255 | 0.244 | 0.235 | 0.015 |
| 25 cm | 0.294 | 0.331 | 0.338 | 0.331 | 0.326 | 0.324 | 0.016 |
| Coarse sand layer | 0.084 | 0.083 | 0.085 | 0.082 | 0.089 | 0.085 | 0.003 |
| Gravel layer | 0.032 | 0.041 | 0.039 | 0.030 | 0.036 | 0.036 | 0.004 |
| 40 cm | 0.212 | 0.199 | 0.194 | 0.163 | 0.218 | 0.197 | 0.019 |
| α [cm−1] | n [-] | l [-] | |
|---|---|---|---|
| Initial estimates | 0.03 | 6.665 | 0.5 |
| Optimized values | 0.0502 | 4.748 | 0.00227 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noguchi, K.; Saito, H.; Saefuddin, R.; Šimůnek, J. Evaluation of Subsurface Drip Irrigation Designs in a Soil Profile with a Capillary Barrier. Water 2021, 13, 1300. https://doi.org/10.3390/w13091300
Noguchi K, Saito H, Saefuddin R, Šimůnek J. Evaluation of Subsurface Drip Irrigation Designs in a Soil Profile with a Capillary Barrier. Water. 2021; 13(9):1300. https://doi.org/10.3390/w13091300
Chicago/Turabian StyleNoguchi, Koichi, Hirotaka Saito, Reskiana Saefuddin, and Jiří Šimůnek. 2021. "Evaluation of Subsurface Drip Irrigation Designs in a Soil Profile with a Capillary Barrier" Water 13, no. 9: 1300. https://doi.org/10.3390/w13091300
APA StyleNoguchi, K., Saito, H., Saefuddin, R., & Šimůnek, J. (2021). Evaluation of Subsurface Drip Irrigation Designs in a Soil Profile with a Capillary Barrier. Water, 13(9), 1300. https://doi.org/10.3390/w13091300







