Roman Water Transport: Pressure Lines
Abstract
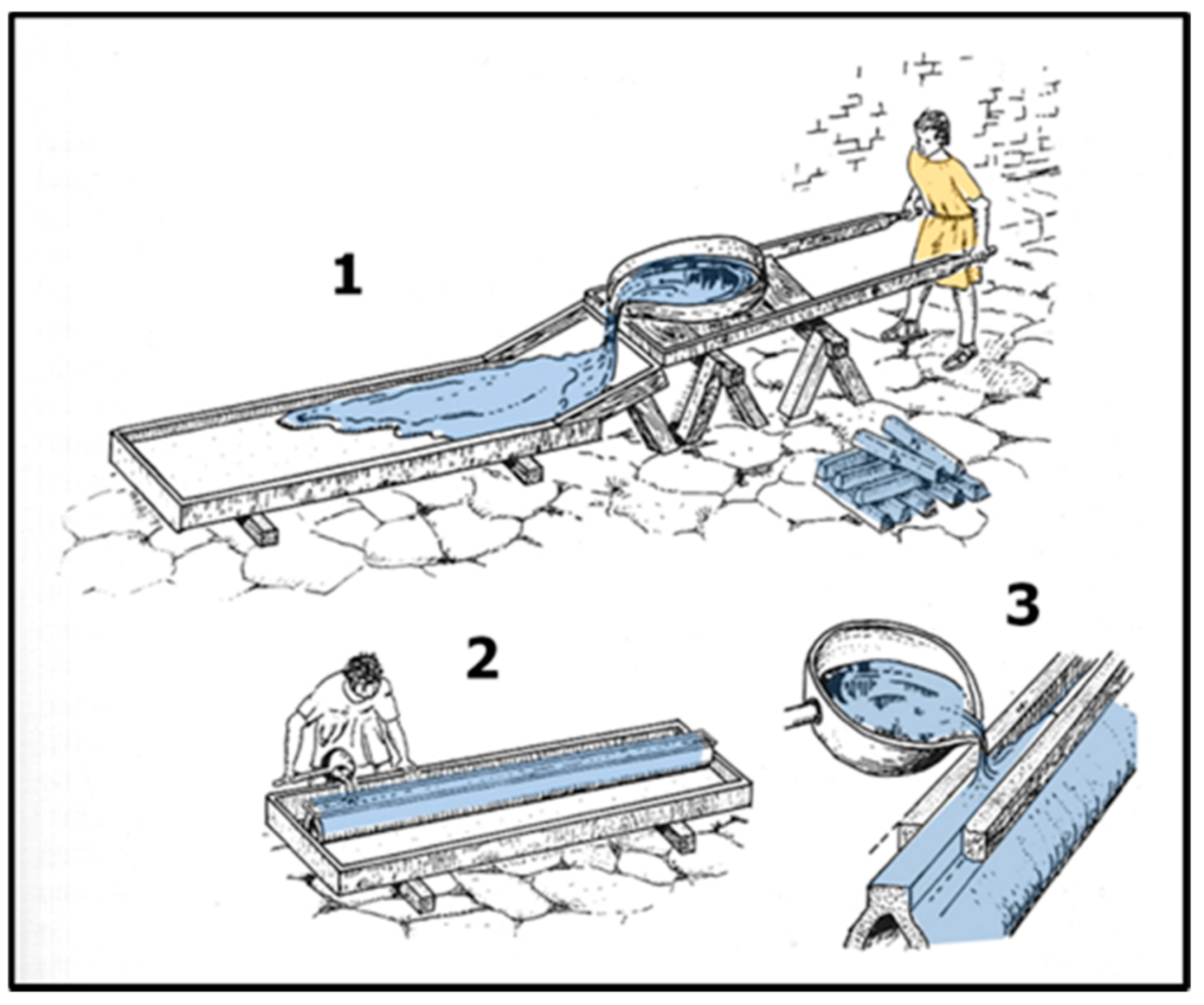
:1. Some Aspects of Roman Aqueducts
2. Pressure Conduits: Inverted Siphons
3. Siphon Conduits and Water Pressure
4. Static Pressure
5. Bends in the Line
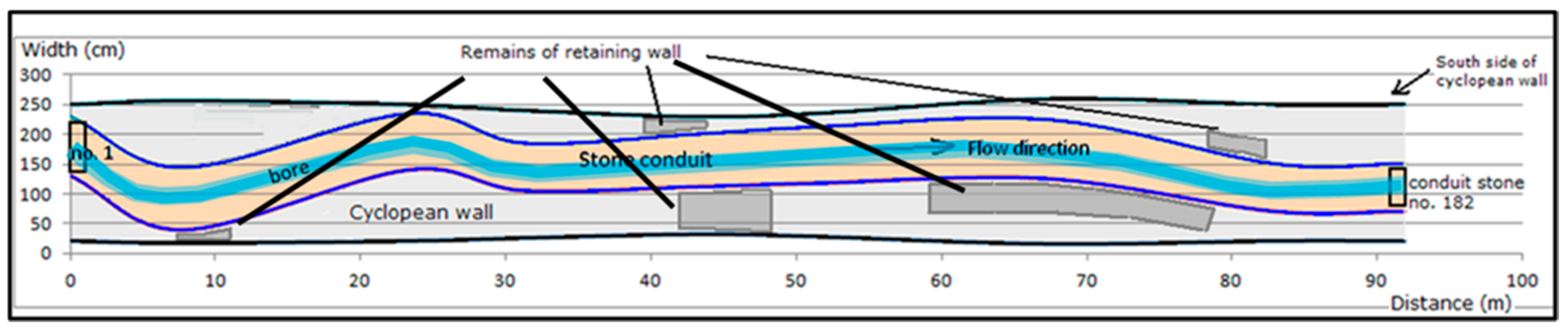
6. The Delik Kemer Siphon of the Patara Aqueduct
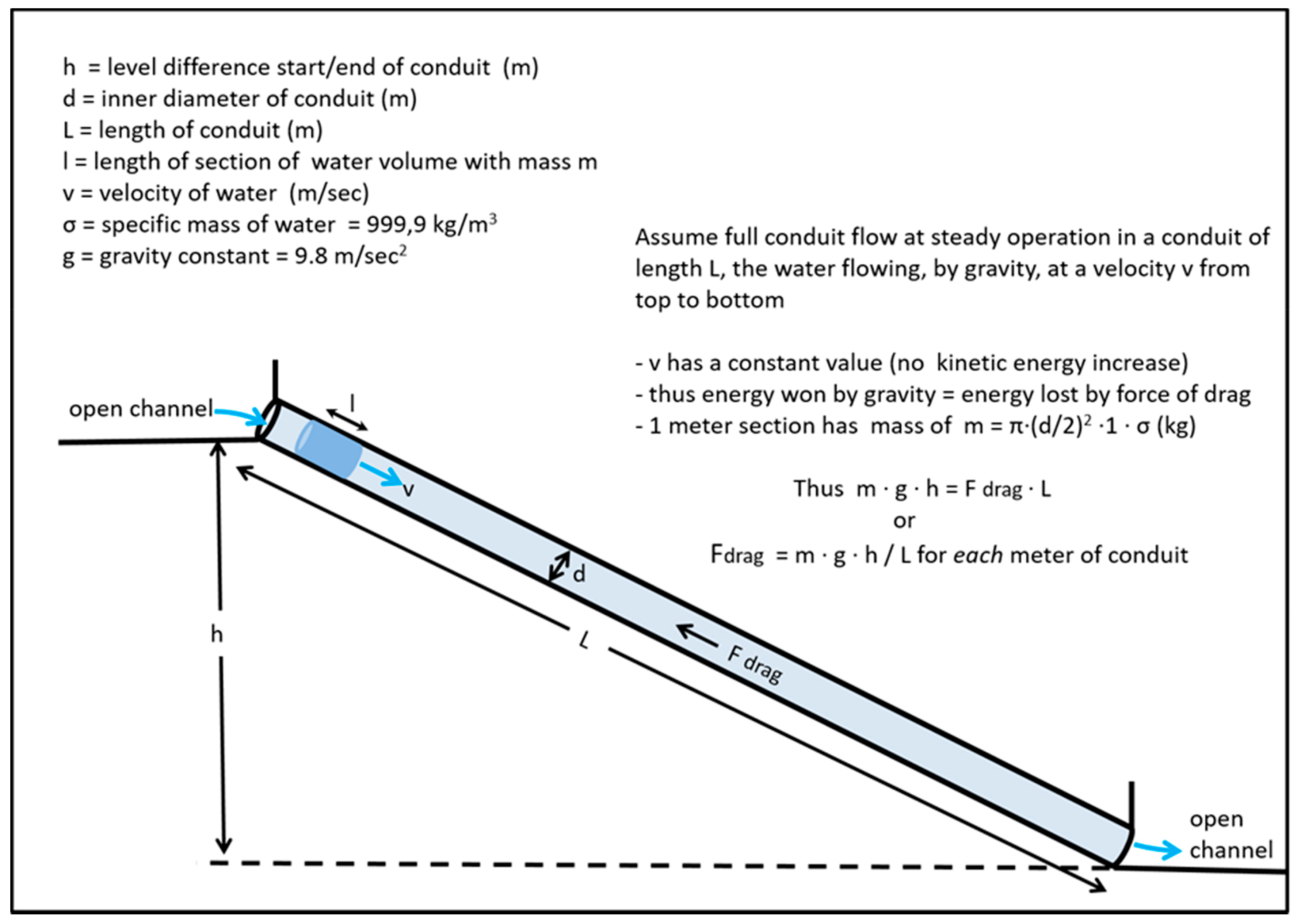
7. Effects from the Flow of Water
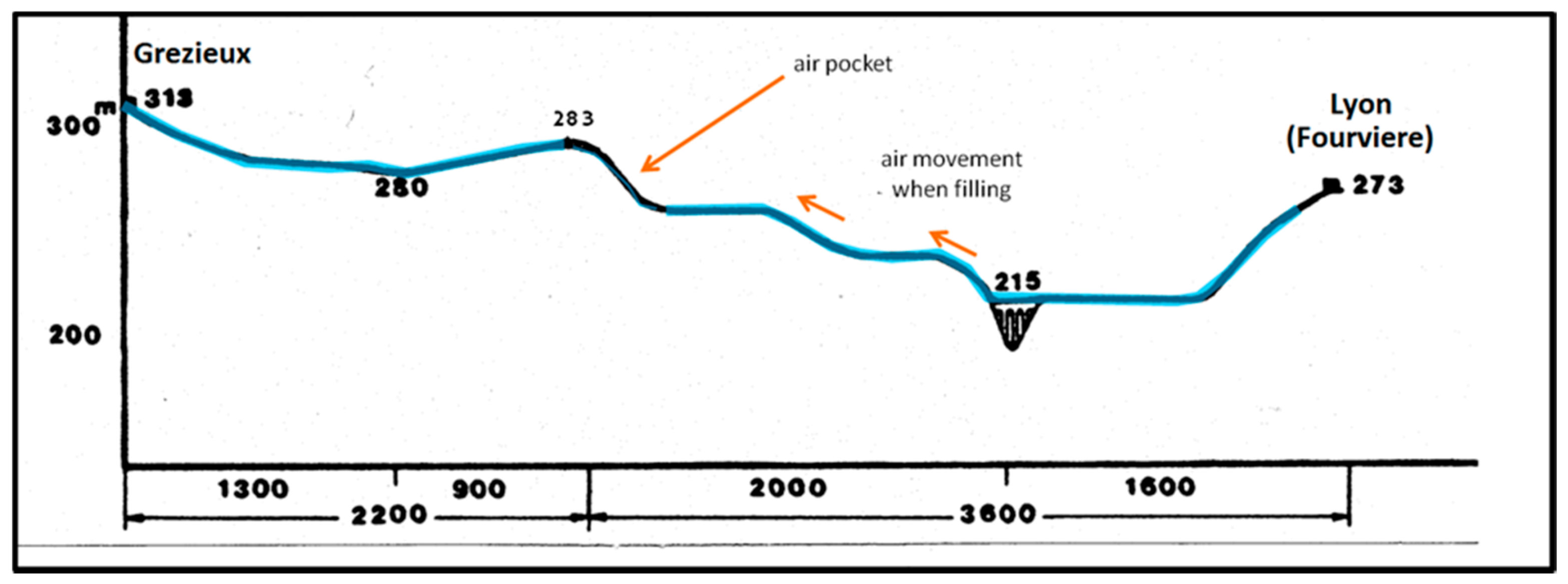
8. The Presence of Air in the Line
9. Air in Water Conduits
10. Leaking Conduits
11. Cat.II Siphons with Horizontal Bends
12. Vitruvius
13. Discussion
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
- www.romaq.org (7 April 2021); Hodge 1992, 1.
- Aqueducts exclusively built for water mills are known. Near Barbegal in France, not far from Arles, remains of a complex with 16 water-driven grain mills have been identified. The vertical wheel mills were located on a hill side in two parallel rows of eight mills one below the other. The mills were supplied by a separate aqueduct (Sellin 1983, Hodge 1992, Leveau 1996, Sürmelehindi et al. 2019. For a history of water mills, see, e.g., Reynolds 1983, also Ritti-Grewe-Kessener 2007).
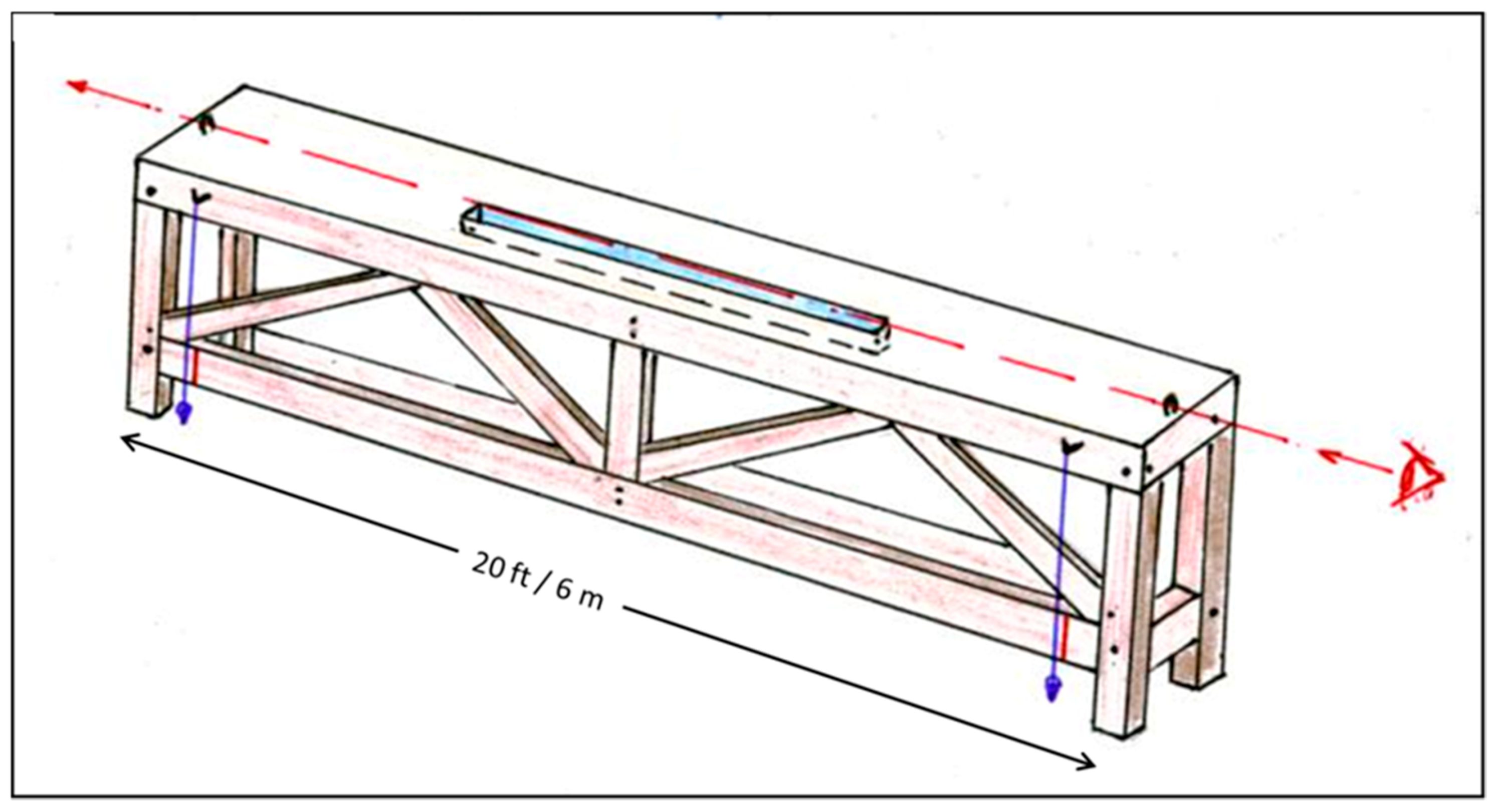
- For Roman surveying, see Lewis 2001; also Grewe 1998, 2017.
- This was not always the case. In the first century CE, a 17 km aqueduct was planned for ancient Saldae, present-day Bejaja in Algeria. In order to pass a hill, a 428 m-long tunnel was planned, to be dug from two sides to meet in the middle. At one instance, the two stretches that were excavated had a joint length that exceeded the distance to be covered. Then, an engineer from the Roman army, Nonius Datus, was called in for help, and he solved the problem. This was commemorated in an inscription, still to be seen in Bejaja, mentioning the three virtues that an able engineer should possess: Spes, Virtus, Patientia. Copies of the inscription are in the Museo della Cività in Rome, and in the Museum für antike Schiffahrt in Mainz (de Waele 1996; Grewe 2002).
- Marcus Vitruvius Pollio, first century BCE, is the author of ‘De Archtectura Libri Decem’ (‘Ten Books on Architecture‘). His book VIII treats issues on water and water transport.
- Vitruvius VIII, 5, 1–3.
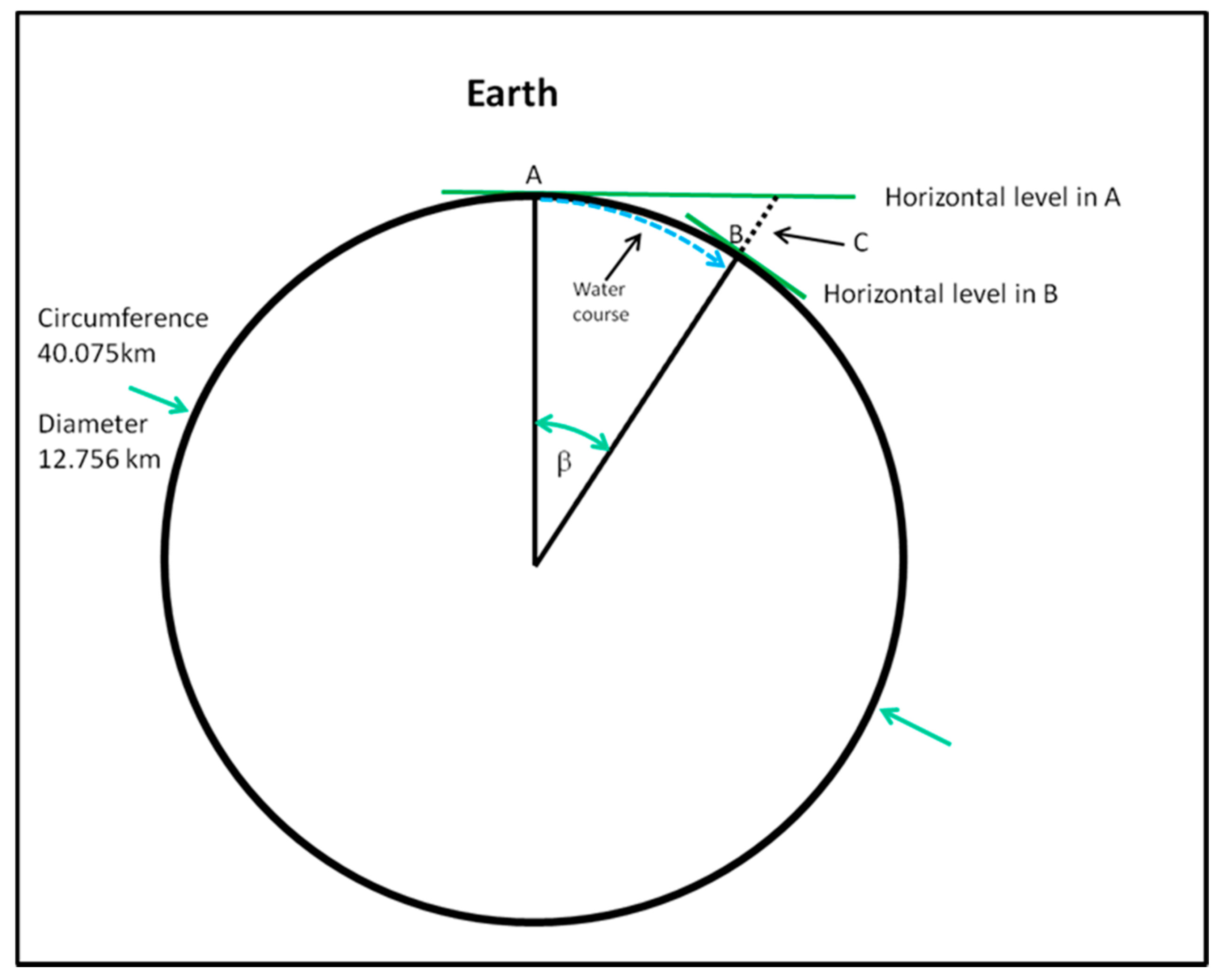
- For a distance between A and B, corresponding to an angle β in Figure 7, the error C becomes= R (1/cosβ − 1), where R = radius of the earth. β may be determined by dividing the distance between A and B by the circumference of the earth, and multiplying it by 360 (degrees).
- Grewe 2014, 38.
- Lubbers 2018.
- Büyükyιldιrιm 2017, 72.
- Rakob 1983.
- Hodge 1992, 187–190.
- Kessener 2000, 109.
- Malinowski 1979; also 1996.
- Grewe 2014, 298/382 for an overview.
- Kessener 2016, 263.
- Passchier et al. 2016.
- Sürmelihindi et al. 2019.
- Sürmelihindi et al. 2021.
- See, e.g., Hodge 1992, 347–348.
- http://www.romanaqueducts.info/siphons/siphons.htm (17 February 2021).
- For a discussion see Smith 1979, 2007a/b; Hodge 1983, 1992; Kessener 2004, 2016.
- For the Gades and its two siphons, see Perez et al. 2012; Smyrna: Weber 1899; for the Lyon aqueducts and their nine siphons: Burdy 2002; Pergamon: Fahlbusch 1982, Garbrecht 2001, Manvroudis 2015; Alatri: Lewis 1999; Aspendos: Kessener 2000, 2011; Termini Imerese: Belvedere 1986; Laodikeia ad Lykum: Weber 1989; Oinoanda: Stenton and Coulton 1986; Patara: Passchier et al. 2016.
- For the water provision of Pergamon both in Hellenistic and Roman times, see the work of Günther Garbrecht (Garbrecht 2001).
- Pérez and Bestué 2008, 2010.
- Lyon (Lugdunum) was founded in 43 BCE. The aqueducts are dated 20 BCE (Mont d’Or), 10 BCE (Yzeron),CE (Brevenne), and 120 CE (du Gier). Burdy 1991, 1996, 2002.
- Hodge 1992, 156.
- For Roman soldering techniques, see, e.g., Hodge 1992, 307–309.
- As assumed for the lead pipe elements of Pergamon’s Madradag siphon, Garbrecht 2001, 128.
- Grewe/Kessener/Piras, 1999. The Seljuk bridge was restored in the 1990s, losing some of its charm.
- For the Hellenistic Karabunar siphon of Smyrna, see Weber1899, also Lewis 1999, 158–162.
- Malinowski 1979, 1996.
- Burdy and Cochet 1992.
- Hansen 1992.
- The unit of pressure is Pa(scal), where 1 Pa = 1 newton/m2; 100,000 Pa = 1 bar ≈ 1 Atm ≈ 14.5 pound/sq inch.
- Fahlbusch 1982, 73; Garbrecht 2001, 121.
- Vitr. VIII, 6, 8. It is not known what type of stone Vitruvius points to. Calabat 1973, 179, suggests a porphyry-type stone; Lewis suggests trachyte or andesite for its strength (Lewis 1999, 169, n.90).
- Vitr. VIII, 6, 9.
- Şahin 2007: the inscription reads: ‘the Emperor Caesar Flavius Vespasianus Augustus restored the analemna [the cyclopean wall] of the aqueduct, which was destroyed by an earthquake, from its base with the from stone blocks constructed conduit on top; along the analemna of the pressure line he had installed three four-inch wide ceramic conduits, in order that, because of the two conduits, in case repairs are needed, the water flow and its use remain continuously possible. Furthermore he restored other parts of the water conduit and brought water [to the town]—after an interruption of thirty months—by his legate and propraetor Sextus Marcius Priscus; the costs were accounted from saved taxes of the town, and the union made *** denarii [unknown amount] available, without that a written request was drawn up. The construction was already started by Vilius Flaccus, the legate and proprietor of Claudius Caesar Augustus, it was finished and water flowed to the town during the administration of Epirus Marcellus, legate and proprietor of Claudius Caesar Augustus (after German translation by Şahin 2007). See also Passchier et al. 2016.
- Büyükyildirim 1994, 57–59.
- The July 21, 365 CE earthquake of Crete of magnitude 8.6, lifted the west of the island 10 m upwards. It was responsible for extensive destructions throughout the Eastern Mediterranean as far as Cyprus, Palestine and Egypt, generating a giant tsunami (Pararis-Carayannis 2010). The Roman historian Ammianus Marcellinus (330–400 CE) described the effects on Alexandria: ‘Slightly after daybreak, and heralded by a thick succession of fiercely shaken thunderbolts, the solidity of the whole earth was made to shake and shudder, and the sea was driven away, its waves were rolled back, and it disappeared, so that the abyss of the depths was uncovered and many-shaped varieties of sea-creatures were seen stuck in the slime; the great wastes of those valleys and mountains, which the very creation had dismissed beneath the vast whirlpools, at that moment, as it was given to be believed, looked up at the sun’s rays. Many ships, then, were stranded as if on dry land, and people wandered at will about the paltry remains of the waters to collect fish and the like in their hands; then the roaring sea as if insulted by its repulse rises back in turn, and through the teeming shoals dashed itself violently on islands and extensive tracts of the mainland, and flattened innumerable buildings in towns or wherever they were found. Thus in the raging conflict of the elements, the face of the earth was changed to reveal wondrous sights. For the mass of waters returning when least expected killed many thousands by drowning, and with the tides whipped up to a height as they rushed back, some ships, after the anger of the watery element had grown old, were seen to have sunk, and the bodies of people killed in shipwrecks lay there, faces up or down. Other huge ships, thrust out by the mad blasts, perched on the roofs of houses, as happened at Alexandria, and others were hurled nearly two miles from the shore, like the Laconian vessel near the town of Methone which I saw when I passed by, yawning apart from long decay.’ (https://en.wikipedia.org/wiki/365_Crete_earthquake (19 May 2021)).
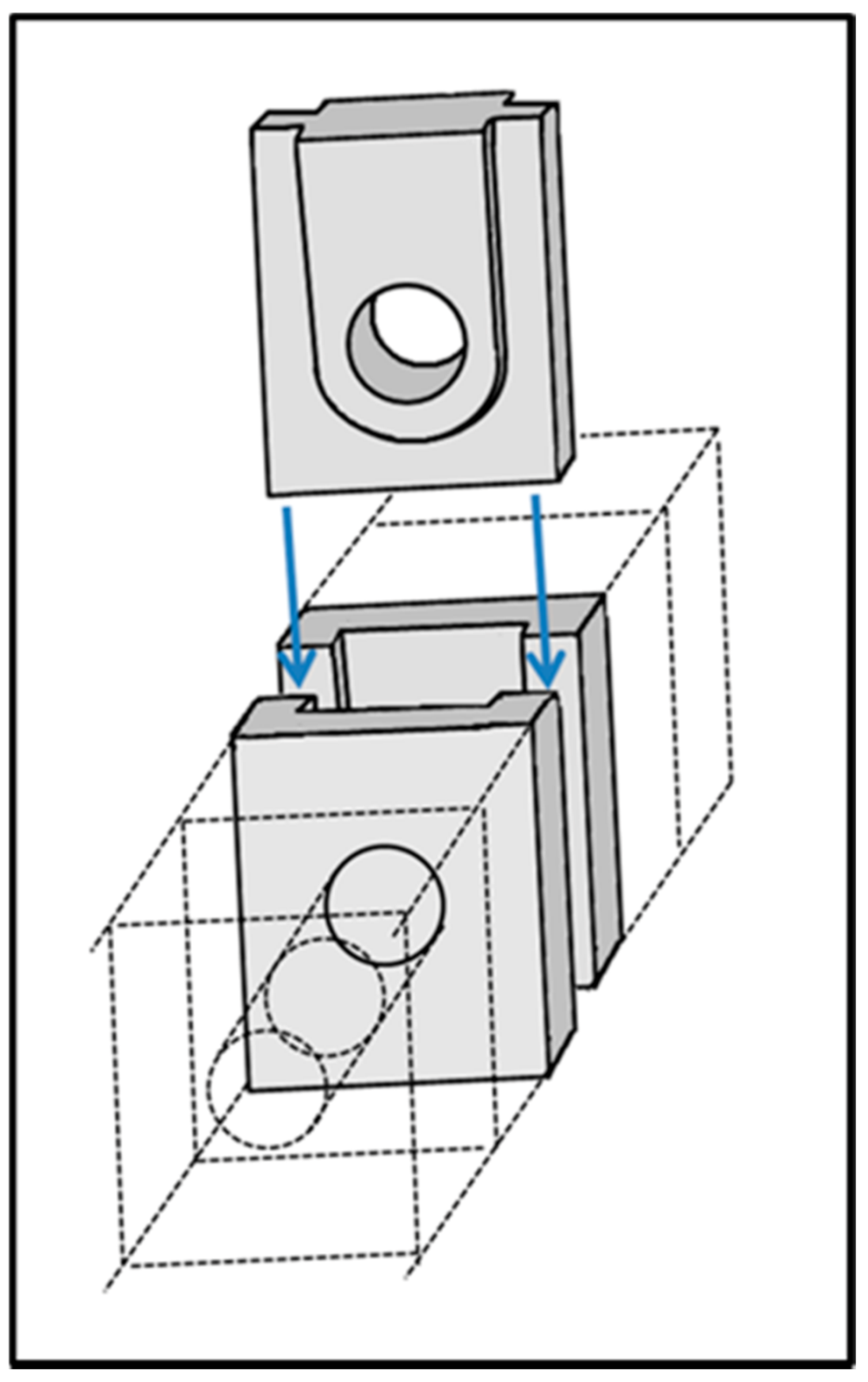
- For siphons made of lead pipes soldered together, Cat.I conduits, such precautions were not needed as, at bends, the forces from static pressure are transferred away from the bend via the pipe wall (see Figure 40). The conduit, as a whole, may need to be fixed to prevent sliding out of place, but the conduit would only burst, along its length, where pressure is highest: in the lowest part of the siphon.
- Number of explanations for the presence of these holes have been proposed, such as safety valves, devices to alleviate pressure surges, and giant whistles when filling the siphon (the tone would indicate the degree of filling). Most probably, the holes were cut in a diagnostic procedure to pinpoint obstructions, after which the clog-up could be removed by poking with a rod and the holes closed off with a stone plug (Kessener 2017, 364–370).
- Patara and Laodikeia a/L: Kessener 2017, 364–371; Smyrna: Lewis 1999, Figure 3, on a hole tapered to a 1 cm opening, presumably related to an air release valve; Hippos Susita: Tsuk et al. 2002, 208.
- Narrow spots in the conduit may cause additional drag forces at such points.
- After http://www.pipeflow.co.uk/public/articles/Darcy_Weisbach_Formula (19 May 2021).
- The force may be calculated as follows: F = dP/dt = (2·ρ·A·dx·v·sin(β/2))/dt = 2·ρ·A·dx/dt·v·sin(β/2) = 2·ρ·A·v2·sin(β/2), where ρ = 1000 kg/m3, diameter of conduit = 28 cm, water velocity = 1 m/sec, and β = 55 degrees; it follows that F = 2·1000·π/4·(0.28)2·12·sin(55ο/2) = 57 newtons, or a force of about 6 kgf.
- Ortloff and Kassinos 2003.
- Ganderberger 1957, 99: ‘Alte Praktiker füllen ihre Rohrleitungen sehr langsam. Sie benötigen oft 2 bis 3 Tage für eine Rohrleitung van 6 bis 10 km Länge‘ (‘Experienced practiciens fill their piped conduits very slowly. They often use 2 to 3 days for a pipe line 6 to 10 km long‘). For the 3250 m Madradag siphon of Pergamon the filling procedure would thus take at least a 24 h day. Comment by Charles Ortloff [48]: This low input flow rate would not have been prescribed by Roman engineers unless flow disturbances were observed at high filling rates during start-up operations of the Aspendos aqueduct system. The low and slow input flow rate mandate likely derives from prior start-up observations of instabilities generated at higher slow rates. For example, for a too-high input flow rate into the first siphon, water flow would accelerate to high velocity flowing down the siphon slope, causing a partial flow with air space above at a high supercritical Froude number value. Upon the water flow reaching the horizontal section at the bottom of the siphon, a hydraulic jump is formed with the subcritical post hydraulic jump flow entering the upward part of the siphon. As flow continues, the increased static pressure and frictional flow resistance in the upward section of the siphon causes the hydraulic jump to rise in the declination part of the siphon until it reaches the inlet to reinstate full flow conditions and a possible inlet overflow. Note here that the open basin at the top of the first tower/end of the first siphon limits static back pressure and regulates the hydraulic jump position. A siphon entry overflow will then signal that the input flow rate is too high as a back flow now may exist at the siphon inlet. Now as water height increases in the upward part of the siphon, it reaches the open basis at the top—this limits the backflow static pressure and stabilizes the hydraulic jump position close to the inlet and like permits continuation of full flow into the next sequential siphon with similar flow conditions as noted in the first upstream siphon. Some backflow into the open top basin occurs that may cause static pressure instabilities to occur that can effect subcritical flows within the first siphon. Now backflow problems can be largely eliminated by reducing the input flow rate to a stable value, where the hydraulic jump effect is now minor and no backflow exists at the siphon inlet—this lower flow rate promotes stable flow in the entire system after initial start-up instabilities occur.
- See, e.g., Corcos, 1989.
- Volume V of the air pocket is inversely related to air pressure P: P · V is a constant.
- Knauss 1983.
- Kamma and van Zijl 2002.
- For details, see Garbrecht 2001, 149–151; 203–206; Tafel 20-1 and 26-2.
- Kessener, 2016.
- See also Kessener 2001.
- Lanckoronski 1890, 93–94.
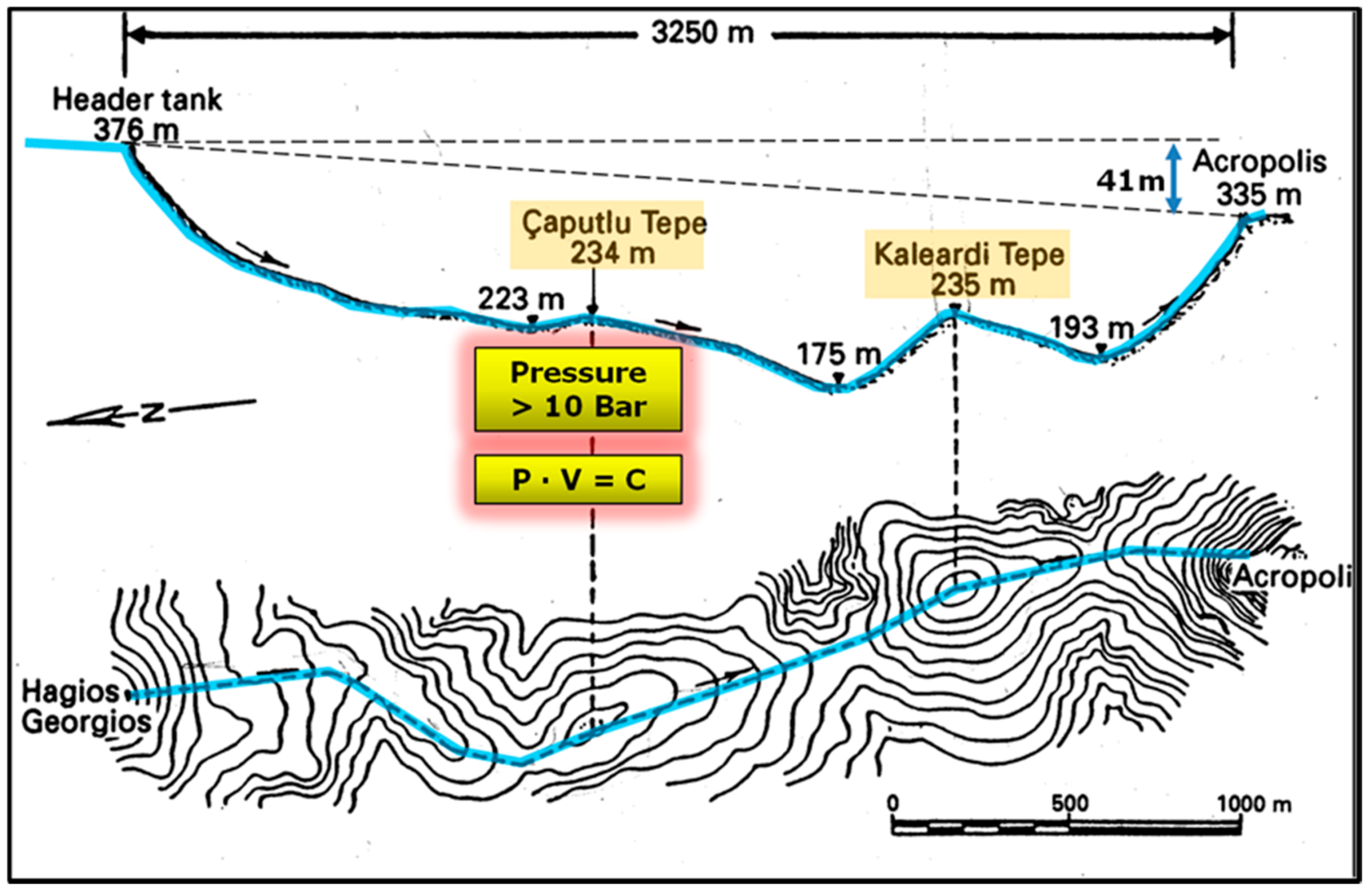
- One may of course ask why the course of the Madradag siphon runs over the tops of intermediate hills and not around them in order to avoid these high points in the line. For one thing, by choosing the hill tops, the static pressure was reduced as much as possible. However, more probably, the trajectory was chosen to prevent damage by environmental events. Along the entire course, the terrain slopes down on either side of the conduit: it ran on the local watershed. Damage from torrential rains and storms was prevented.
- Garbrecht 2001, 121–123.
- Burdy 1991, 100–103.
- Burdy 1991, 101.
- Falvey 1980, 48. A similar formula for Vcr was used by Kamma and van Zijl 2002, 56: Vcr = 1.23·(g·Db·sinα)1/2, where Cb = 0.88 in Falvey’s formula.
- Aksoy 1997.
- Falvey 1980, 50–52; 61–65.
- Baines and Wilkinson 1986.
- For further literature on pressure surges from air in conduits, see e.g., Burrows et al.1995; Zhou et al. 2002.
- Stern 1983, 177–179.
- Schnapauff 1966.
- Falvey 1980, 57–77.
- Falvey 1980, Figure 45.
- In modern pressure lines automatically operating air release valves may thus result to—at times detrimental—water hammer effects, which effects may be reduced by proper dimensions of the orifice through which air escapes.
- Kessener, 2000.
- Assuming that the conduit between the header tank and receiving tank had a fixed inner diameter.
- Which would have been an option (Kessener 2000, 258–259).
- Pérez 2012; Pérez et al. 2014.
- Not much is known about Marcus Vitruvius Pollio. He was born ca. 80 BCE, and his manuscript was presumably written ca. 20 BCE. The oldest manuscript is a Carolingian copy from about 800 CE, the Harleianus, kept at the British Library (MS Harley 2767) (www.bl.uk/catalogues/illuminatedmanuscripts/record.asp?MSID=8557&CollID=8&NStart=2767, accessed on 24 May 2018).
- Among others, Rowland 2001 (English), Peters 1997 (Dutch), Fensterbusch 1976 (German), Callebat 1973 (French), Choisy 1971 (French), Granger 1962 (English), Morgan 1960 (English), Krohn 1912 (Latin text).
- See note 37. Additionally, Kessener 2001, 150 n.77.
- Vitr, VIII, 6, 6.
- Fahlbusch and Peleg 1992; Lewis 1999; Kessener 2001; 2002; Ohlig, 2006.
- Kessener 2003, 2016.
- Hodge 1992, 124; Lewis 1999, 145 and 171.
References
- Amin, A.; Kim, C.G.; Kee, Y.H. Numerical analysis of free surface vortices behavior in a pump sump. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Busan, Korea, 2017. [Google Scholar]
- Aksoy, S. Gedanken über Luftblasen in Druckleitungen. Mitt. des Leichtweiss-Institut für Wasserbau, 1997; Unpublished work. [Google Scholar]
- Baines, W.D.; Wilkinson, D.L. The motion of large air bubbles in ducts of moderate slope. J. Hydraul. Res. 1986, 25, 157–169. [Google Scholar] [CrossRef]
- Belvedere, O. L’Acquedotto Cornelio di Termini Imerese; L’Erma di Bretschneide: Rome, Italy, 1986. [Google Scholar]
- Burdy, J. L’Aqueduc Romain de l’Yzeron; Conseil Général du Rhône: Lyon, France, 1991. [Google Scholar]
- Burdy, J. L’Aqueduc Romain du Gier; Conseil Général du Rhône: Lyon, France, 1991. [Google Scholar]
- Burdy, J. Les Aqueducs Romains de Lyon; Presses Universitaires de Lyon: Lyon, France, 2002. [Google Scholar]
- Burdy, J.; Cochet, A. Une date consulaire (213 après J.-C.) sur un tuyau de plomb viennois. Gallia 1992, 49, 89–97. [Google Scholar] [CrossRef]
- Burrows, R.; Qiu, D.Q. Effect of air pockets on pipeline surge pressure. Proc. Inst. Civ. Eng.-Water Marit. Energy 1995, 112, 349–361. [Google Scholar]
- Büyükyιldιrιm, G. Tarihi Su Yapιlarι; Antalya Bölgesi: Ankara, Turkey, 1994. [Google Scholar]
- Büyükyιldιrιm, G. 20.Yüzyιlda Su İşleri ve Antalya; Devlet Su İşleri: Antalya, Turkey, 2017. [Google Scholar]
- Callebat, L. Vitruve de l’Architecture, Livre VIII; Les Belles Lettres: Paris, France, 1973. [Google Scholar]
- Çeçen, K. The Longest Roman Water Supply Line; Türkiye Sιnai Kalkιnma Bankasι: Istanbul, Turkey, 1996. [Google Scholar]
- Choisy, A. Vitruve; F. de Nobele: Paris, France, 1971. [Google Scholar]
- Corcos, G. Air in Water Pipes; Agua Para La Vida: Berkeley, CA, USA, 1989. [Google Scholar]
- Fahlbusch, H. Vergleich antiker griechischer und römischer Wasserversorgungsanlagen. Mitt. des Leichtweiss-Institut für Wasserbau 1982, 73. Available online: https://www.oeaw.ac.at/resources/Record/990000779540504498#usercomments (accessed on 12 October 2021).
- Fahlbusch, H. Die Wasserversorgung in der Antike. Schr. Frontinus-Gesell. 1992, 17, 85–106. [Google Scholar]
- Fahlbusch, H.; Peleg, J. Die Colliviaria Vitruvs, Möglichkeiten der Interpretation. Mitt. des Leichtweiss-Institut für Wasserbau 1992, 117, 105–140. [Google Scholar]
- Falvey, H.T. Air-Water flow in Hydraulic structures. Eng. Monogr. 1980, 81, 26429. [Google Scholar]
- Fensterbusch, C. Vitruv zehn Bücher Über Architektur; Wissensch. Buchgesell.: Darmstadt, Germany, 1976. [Google Scholar]
- Ganderberger, W. Über Die Wirtschaftliche und Betriegssichere Gestaltung von Fernwasserleitungen; Oldenburg Verlag: München, Germany, 1957. [Google Scholar]
- Garbrecht, G. Die Wasserversorgung des antiken Pergamon, die Druckleitung. Mitt. des Leichtweiss-Institut für Wasserbau 1978, 60. [Google Scholar] [CrossRef]
- Garbrecht, G. Die Wasserversorgung des antiken Pergamon, In Die Wasserversorgung Antiker Städte; Philip von Zabern: Mainz am Rhein, Germany, 1987; Volume II, pp. 13–47. [Google Scholar]
- Garbrecht, G. Altertümer von Pergamon, Band 1-Teil 4. In Die Wasserversorgung Von Pergamon; DAI: Berlin, Germany; New York, NY, USA,, 2001. [Google Scholar]
- Gräber, F. Vorläufigen Bericht über Untersuchung der Pergamenischen Wasserleitungen; Reimer Verlag: Berlin, Germany, 1906. [Google Scholar]
- Gräber, F. Altertümer Von Pergamon-Stadt und Landschaft-Die Wasserleitungen; Gesellschaft der Freunde Universität Heidelberg e.v.: Berlin, Germany, 1913; (accessed on 12 October 2021). [Google Scholar] [CrossRef]
- Granger, F. De Architectura; Heinemann: London, UK, 1962. [Google Scholar]
- Grewe, K. Der antike Vermessungsingenieur Nonius Datus und sein Platz in de Geschichte der Technik. Schr. Front.-Ges. 2002, 25, 39–52. [Google Scholar]
- Grewe, K. Aquädukte, Wasser für Rom’s Städte; Regionalia Verlag: Rheinbach, Gernamy, 2014. [Google Scholar]
- Grewe, K. Neues aus der Aquäduktforschung. In Wasserwesen zur Zeit des Frontinus; Wiplinger, G., Letzner, W., Eds.; Babesch Supplements: Leuven, Belgium; Peeters Publishers: Leuven, Belgium, 2017; Volume 32, pp. 15–30. [Google Scholar]
- Grewe, K.; Kessener, H.P.M.; Piras, S.A.G. Im Zickzack-Kurs über den Fluß, die römisch/seldschukische Eurymedon-Brücke von Aspendos (Türkei). Antike Welt 1999, 30, 1–12. [Google Scholar]
- Haberey, W. Die Römischen Wasserleitungen Nach Köln; Rheinland Verlag: Bonn, Gernamy, 1972. [Google Scholar]
- Hansen, J. Die antike Wasserleitung unter der Rhône bei Arles. Mitt. des Leichtweiss-Institut für Wasserbau 1992, 117, 470–531. [Google Scholar]
- Hodge, A.T. Siphons in Roman Aqueducts; Publications of the British School at Rome (PBSR): Rome, Italy, 1985; p. 51. [Google Scholar]
- Hodge, A.T. Roman Aqueducts and Watersupply; Duckworth: London, UK, 1992. [Google Scholar]
- Kamma, P.S.; van Zijl, F.P. De weerstand in persleidingen voor afvalwater tijdens de gebruiksfase. Rioleringswetenschap 2002, 5, 45–64. [Google Scholar]
- Kessener, H.P.M.; Piras, S.A.G. The pressure line of the Aspendos Aqueduct. Adalya 2002, 2, 159–187. [Google Scholar]
- Kessener, H.P.M. The Aqueduct at Aspendos and its inverted siphon. J. Rom. Archaeol. 2000, 13, 105–132. [Google Scholar] [CrossRef]
- Kessener, H.P.M. Vitruvius and the Conveyance of Water. BABesch 2001, 76, 139–158. [Google Scholar]
- Kessener, H.P.M. Vitruvius rehabilitandus est. In Cura Aquarum in Israel; Ohlig, C., Peleg, Y., Tsuk, T., Eds.; Books on Demand: Siegburg, Germany, 2002; pp. 187–200. [Google Scholar]
- Kessener, H.P.M. Roman Watertransport: Problems in Operating Pressurized Pipeline Systems. In Wasserhistorische Forschungen—Schwerpunkt Antike; Schriften der Deutschen Wasserhistorischen Gesellschaft: Solingen, Germany, 2003; Volume 2, pp. 147–160. Available online: https://www.abebooks.com/9783833003400/Wasserhistorische-Forschungen-Schwerpunkt-Antike-Crais-3833003405/plp (accessed on 12 October 2021).
- Kessener, H.P.M. Moderne persleidingen en Romeinse hydraulische technieken. Rioleringswetenschap–Tech. 2004, 15, 10–44. [Google Scholar]
- Kessener, H.P.M. The Aspendos Siphon and Roman Hydraulics. In De Aquaeductu atque Aqua Urbium Lyciae Pamphiliae Pisidiae; Wiplinger, G., Ed.; BABesch Supplements: Leuven, Belgium; Peeters Publishers: Leuven, Belgium, 2016; Volume 27, pp. 261–274. [Google Scholar]
- Kessener, H.P.M. Roman Water Ditribution and Inverted Siphons; Ipskamp: Nijmegen, The Netherlands, 2017. [Google Scholar]
- Knauss, J. Wirbelbildung an Einlaufwerken-Luft-und Dralleintrag. In Schriftenreihe des Deutschen Verbandes für Wasserwirtschaft und Kulturbau e.V.; DVWK: Bonn, Germany, 1983; Volume 63. [Google Scholar]
- Krohn, F. (Ed.) Vitruvii de Architectura Libri Decem; Nabu Press: Leipzig, Germany, 1912. [Google Scholar]
- Lanckoronski, K. Grafen Städte Pamphiliens und Pisidiens; Band 1; Vienna, Austria, 1890. Available online: https://books.google.com.sg/books?id=8yghEAAAQBAJ&pg=PT188&lpg=PT188&dq=Grafen+St%C3%A4dte+Pamphiliens+und+Pisidiens&source=bl&ots=nC-OokaEOM&sig=ACfU3U3dQrUwlioFZMvbFunSbjWMOeMm3g&hl=en&sa=X&ved=2ahUKEwjAzMnP9Pj0AhVBTGwGHUqaDu8Q6AF6BAgDEAM#v=onepage&q=Grafen%20St%C3%A4dte%20Pamphiliens%20und%20Pisidiens&f=false (accessed on 12 October 2021).
- Leveau, P. The Barbegal water mill in its environment: Archaeology and the economic and social history of antiquity. J. Rom. Archaeol. 1996, 9, 137–153. [Google Scholar] [CrossRef]
- Lewis, M.J.T. Vitruvius and Greek Aqueducts; Publications of the British School at Rome (PBSR): Rome, Italy, 1999; Volume 67, pp. 145–172. [Google Scholar]
- Lewis, M.J.T. Surveying Instruments of Greece and Rome; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Lubbers, J.P. Aquaducten in Ancient Rome; Plannen en Bouwen van Aqueducten in Ancient Rome zonder Hoogtemeetinstrumenten: Hoorn, The Netherlands, 2018. [Google Scholar]
- Malinowski, R. Concretes and Mortars in Ancient Aqueducts. Concr. Int. 1979, 1, 66–75. [Google Scholar]
- Malinowski, R. Dichtungsmörtel und Betone in der Antike. In Cura Aquarum in Campania; de Haan, N., Jansen, G., Eds.; Peeters: Leiden, The Netherlands, 1996; pp. 191–198. [Google Scholar]
- Manvroudis, D. Precedent Ancient Hydraulic Works & Reconstruction of Operations of the Hellenistic Madradag Aqueduct & Inverted Siphon of Pergamon. Thesis, Belgrade, Serbia, 2015. Available online: https://www.academia.edu/36816887/Aspects_of_Roman_Water_Provision_and_related_Hydraulics_in_Aquam_Ducere_II_Proceedings_of_the_second_international_Summer_School_Water_in_the_City_Hydraulic_Systems_in_the_Roman_Age_held_in_Feltre_August_24_28_2015_Seren_del_Grappa_2018_31_52(accessed on 12 October 2021).
- Morgan, H. Vitruvius, the Ten Books on Architecture; Dover Publcations: New York, NY, USA, 1960. [Google Scholar]
- Ortloff, C.H.; Kassinos, A. Computational Fluid Dynamics Investigation of the Hydraulic Behaviour of the Roman Inverted Siphon System at Aspendos, Turkey. J. Archaeol. Sci. 2003, 30, 417–428. [Google Scholar] [CrossRef]
- Ohlig, C.J.P. Vitruvs colliviaria und die vis spiritus–(keine) Luft in Wasserleitungen? In Cura Aquarum in Ephesos; Wiplinger, G., Ed.; Peeters: Leuven, Belgium, 2006; pp. 319–326. [Google Scholar]
- Pararis-Carayannis, G. The Earthquake and Tsunami of July 21, 365 AD in the Eastern Mediterrenean Sea. J. Tsunami Soc. Int. 2011, 30, 253–292. [Google Scholar]
- Passchier, C.W.; Sürmelihindi, G.; Spötl, C. A High-resolution palaeoenvironmental record from carbonate deposits in the Roman Aqueduct of Patara, SW Turkey, from the time of Nero. Sci. Rep. 2016, 6, 28704. [Google Scholar] [CrossRef] [Green Version]
- Peters, T. Vitruvius; Polak & van Gennep: Amsterdam, The Netherlands, 1997. [Google Scholar]
- Pérez Marrero, J.; Bestué Cardiel, I. Avance del Estudio Hidraulico del Acueducto Romano de Gades. In Proceedings of the Actas IV Congreso de Obras Públicas en la Ciudad romana (Lugo-Guitiriz 2008), Lugo-Guitiriz, Spain, 6–8 November 2008; 2008; pp. 1–24. [Google Scholar]
- Perez Marrero, J.; Bestué Cardiel, I. Nuevas Aportaciones al estudio Hidraulico del Acueducto Roman de Tempul. In Aquam Perducendam Curavit, Captación; Barrios, L.G.L., Palacios, J.L.C., Pujol, L.P., Eds.; Imprenta La Isla: Cádiz, Spain, 2010; pp. 184–196. [Google Scholar]
- Pérez Marrero, J. Nuevo Análisis del Sifón Invertido de los Arquillos, Acueducto Romano de Gades. CPAG 2012, 21, 91–126. [Google Scholar]
- Pérez Marrero, J.; Bestué Cardiel, I.; Lucas Ruíz, R. 2014 Route of the Roman Aqueduct of Cádiz. Poster Universidád de Cádiz: Cadiz, Spain, 2012. Available online: https://www.academia.edu/22378624/route_of_roman-aquaduct_of_Cádiz (accessed on 15 May 2021).
- Rakob, F. Das Quellenheiligtum in Zaghouan und die römischen Wasseleitung nach Karthago. In Mitteilingen des deutschen achäologischen Instituts; DAI: Berlin, Germany, 1983; Volume 81, pp. 41–88. Available online: https://books.google.com/books/about/Das_Quellenheiligtum_in_Zaghouan_und_die.html?id=BtMTuQAACAAJ (accessed on 12 October 2021).
- Ritti, T.; Grewe, K.; Kessener, H.P.M. A relief of a water-powered stone saw mill at Hierapolis. J. Rom. Archaeol. 2007, 20, 101–125. [Google Scholar]
- Rowland, I.D. Noble Howe. In Vitruvius: Ten Books on Architecture; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- SŞahin, S. Die Bauinschrift auf dem Druckrohraquädukt von Delikkemer bei Patara. In Griechische Epigrafik in Lykien; Schuler, C., Ed.; Börsedruck: Vienna, Austria, 2007; pp. 99–110. [Google Scholar]
- Schnapauff, J. Luftblasen in Rohrleitungen—Vereinfachend betrachtet. Neue Deliwa Zeitschrift 1966, 10, 371–373. [Google Scholar]
- Smith, N.A.F. Attitudes to Roman Engineering and the question of the Inverted Siphon. In History of Technology; Routledge: London, UK, 1979; Volume I, pp. 45–71. [Google Scholar]
- Smith, N.A.F. The Hydraulics of Ancient Pipes and Pipelines. Trans. Newcomen Soc. 2007, 77, 1–49. [Google Scholar] [CrossRef]
- Smith, N.A.F. The Roman Aqueduct at Aspendos. Trans. Newcomen Soc. 2007, 77, 217–244. [Google Scholar] [CrossRef]
- Stenton, E.C.; Coulton, J.J. Oinoanda: The Watersupply and Aqueduct. Anatol. Stud. 1986, 36, 15–59. [Google Scholar] [CrossRef]
- Stern, P. Field Engineering; Intermediate Technology Publications: London, UK, 1983. [Google Scholar]
- Sürmelihindi, G.; Passchier, C.W.; Leveau, P.; Spötl, C.; Bourgeois, M.; Bernard, V. Bargegal: Carbonate imprints give a voice to the first industrial complex of Europe. J. Archaeol. Sci. Rep. 2019, 24, 1041–1058. [Google Scholar]
- Sürmelihindi, G.; Passchier, C.; Crow, J.; Spötl, C. Carbonates from the ancient world’s longest aqueduct: A testament of Bysantine water management. Geoarchaeology 2021, 36, 643–659. Available online: Wileyonlinelibrary.com/journal/gea (accessed on 8 September 2021). [CrossRef]
- Tsuk, T.; Peleg, Y.; Fahlbusch, H.; Meshel, Z. A new survey of the aqueducts of Hippos-Susita. In The Aqueducts of Israel; Thomson Shore: Portsmouth, UK, 2002; pp. 207–209. [Google Scholar]
- de Waele, J.A.K.E. Een Romeins ingenieursproject—De tunnel van Nonius Datus. Hermeneus 1996, 68, 173–181. [Google Scholar]
- Weber, G. Die Hochdruck-Wasserleitung von Loadikeia ad Lycum. Jahrb. Dtsch. Inst. (JdI) 1898, 13, 1–13. [Google Scholar]
- Weber, G. Die Wasserleitungen von Smyrna. Jahrb. Dtsch. Inst. (JdI) 1899, 14, 4–24. [Google Scholar]
- Zhou, F.; Hicks, F.E.; Steffler, P.M. Transient Flow in a Rapidly Filling Horizontal Pipe Containing Trapped Air. J. Hydraul. Eng. 2002, 128, 625–634. [Google Scholar] [CrossRef]





















































































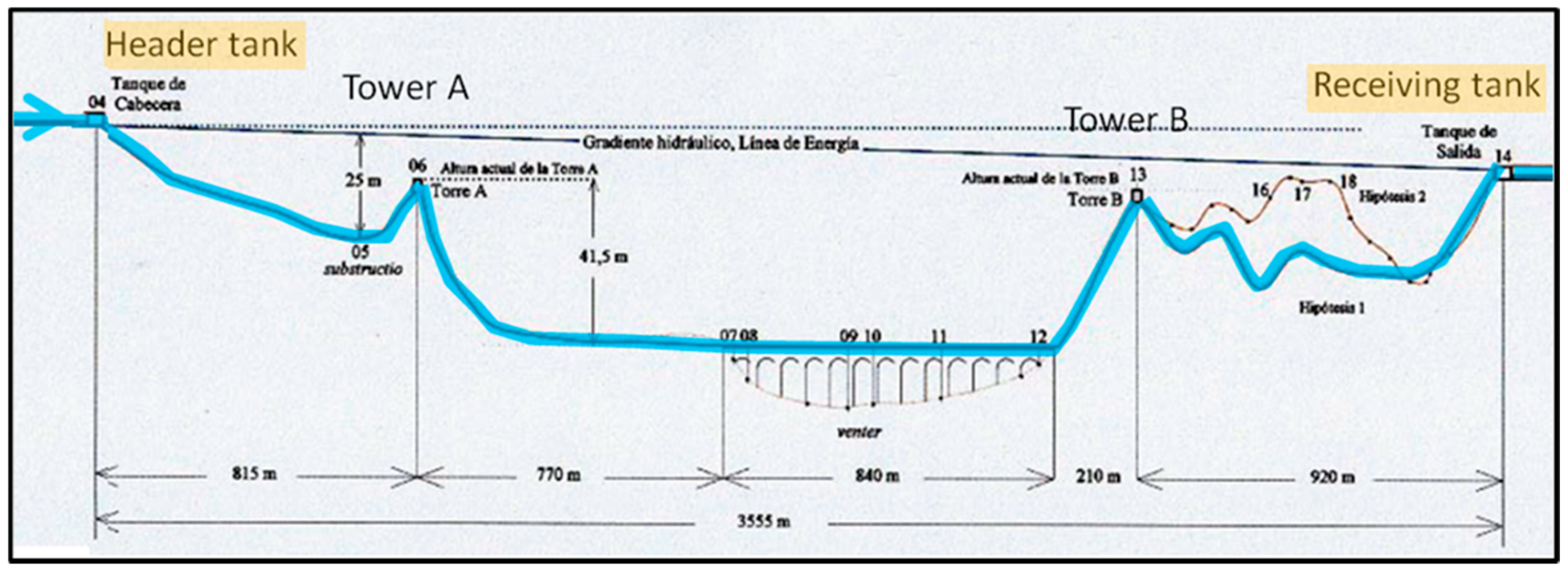
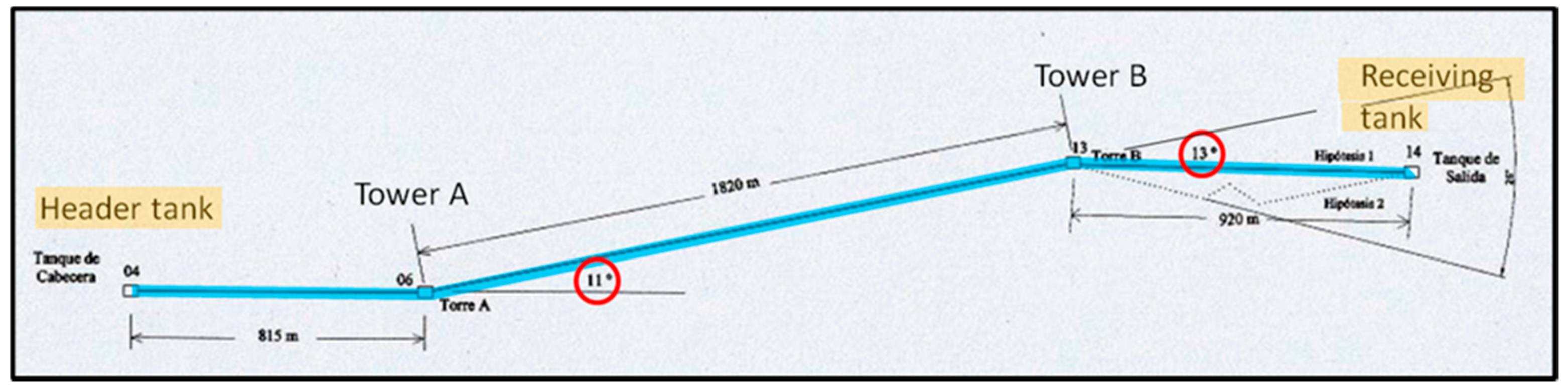



| Location | Country | Length (km) |
|---|---|---|
| Constantinople | Turkey | >250 |
| Carthage | Tunesia | 95 |
| Cologne | Germany | 95 |
| Rome (Aqua Marcia) | Italy | 91 |
| Rome (Anio Novus) | Italy | 87 |
| Cadiz (Tempul) | Spain | 83 |
| Lyon (Gier) | France | 75 |
| Rome (Aqua Claudia) | Italy | 69 |
| Lyon (Brevenne) | France | 66 |
| Rome (Anio Vetus) | Italy | 64 |
| Romen (Aqua Traiana) | Italy | 58 |
| Pergamon (Kaikos) | Turkey | 50 |
| Nîmes | France | 50 |
| Arles | France | 48 |
| Cherchel | Algeria | 45 |
| Alcanadre | Spain | 30 |
| Noviomagus | Netherlands | 5 |
| Aqueduct | City/Country | Inside Channel Dimension (Height × Width, cm) |
|---|---|---|
| Degirmendere | Ephesos/Turkey | 245 × 80 |
| Aqua Marcia | Rome | 240 × 90 |
| Carthago | Tunesia | 190 × 85 |
| Brevenne | Lyon/France | 166 × 120 |
| Cologne | Germany | 142 × 70 |
| Aspendos | Turkey, south coast | 90 × 50 |
| Mont d’Or | Lyon/France | 74 × 44 |
| Patara | Turkey, south coast | 35 × 40 |
| Distance | Error |
|---|---|
| 100 m | 1 mm |
| 500 m | 2 cm |
| 1 km | 8 cm |
| 5 km | 2 m |
| 10 km | 7.8 m |
| 100 km | 784 m |
| 250 km | 4.9 km |
| City | Aqueduct | Siphon | Material of Conduit | Length (m) | Max Depth (m) | Hydraulic Gradient (m/km) |
|---|---|---|---|---|---|---|
| Gades (Spain) | Tempul | de la Playa | stone | 19,500 | 20 | not known |
| Smyrna (Turkey) | Kara-Bunar | Kara-Bunar | clay/stone | 4400 | 158 | 1.1 (estimate) |
| Lyon (France) | Yzeron | Craponne-Lyon | lead | 3600 | 91 | 9.2 |
| Gades | Tempul | de los Arquilles | stone | 3555 | 50 | 3.1 |
| Lyon | Mont d’Or | d’Ecully | lead | 3500 | 70 | 3.1 |
| Lyon | Brevenn | Grange-Blanche | lead | 3500 | 90 | 4–5.6 (estimate) |
| Pergamon (Turkey) | Madradag | Madradag | lead | 3250 | 190 | 12.6 |
| Alatri (Italy) | Alatri | Alatri | lead | 3000 | 100 | 9 (estimate) |
| Lyon | Gier | Beaunant | lead | 2660 | 122 | 3.0 |
| Lyon | Yzeron | Grezieux-Craponne | lead | 2200 | 33 | 3.2 |
| Aspendos (Turkey) | Aspendos | Aspendos | stone | 1670 | 45 | 8.3 |
| Termini Imerese (Sicily) | Cornelio | Barratina | lead | 1300 | 40 | 3.8 |
| Lyon | Gier | Soucieu (le Garon) | lead | 1210 | 93.5 | not known |
| Laodikeia ad Lykum (Turkey) | Laodikeia | Laodikeia | stone | 800 | 50 | 26 |
| Lyon | Gier | St. Genis | lead | 700 | 79 | 8.3 |
| Lyon | Gier | St. Irenée | lead | 575 | 38 | 4 |
| Oinoanda (Turkey) | Oinoanda | Oinoanda | stone | 500–700 | 22 | 6–16 (estimate) |
| Lyon | Mont d’Or | Cotte-Chally | lead | 420 | 30 | 19 |
| Patara (Turkey) | Patara | Delik Kemer | stone | 260 | 20 | 18.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kessener, P.M. Roman Water Transport: Pressure Lines. Water 2022, 14, 28. https://doi.org/10.3390/w14010028
Kessener PM. Roman Water Transport: Pressure Lines. Water. 2022; 14(1):28. https://doi.org/10.3390/w14010028
Chicago/Turabian StyleKessener, Paul M. 2022. "Roman Water Transport: Pressure Lines" Water 14, no. 1: 28. https://doi.org/10.3390/w14010028
APA StyleKessener, P. M. (2022). Roman Water Transport: Pressure Lines. Water, 14(1), 28. https://doi.org/10.3390/w14010028





