County-Level Irrigation Water Demand Estimation Using Machine Learning: Case Study of California
Abstract
:1. Introduction
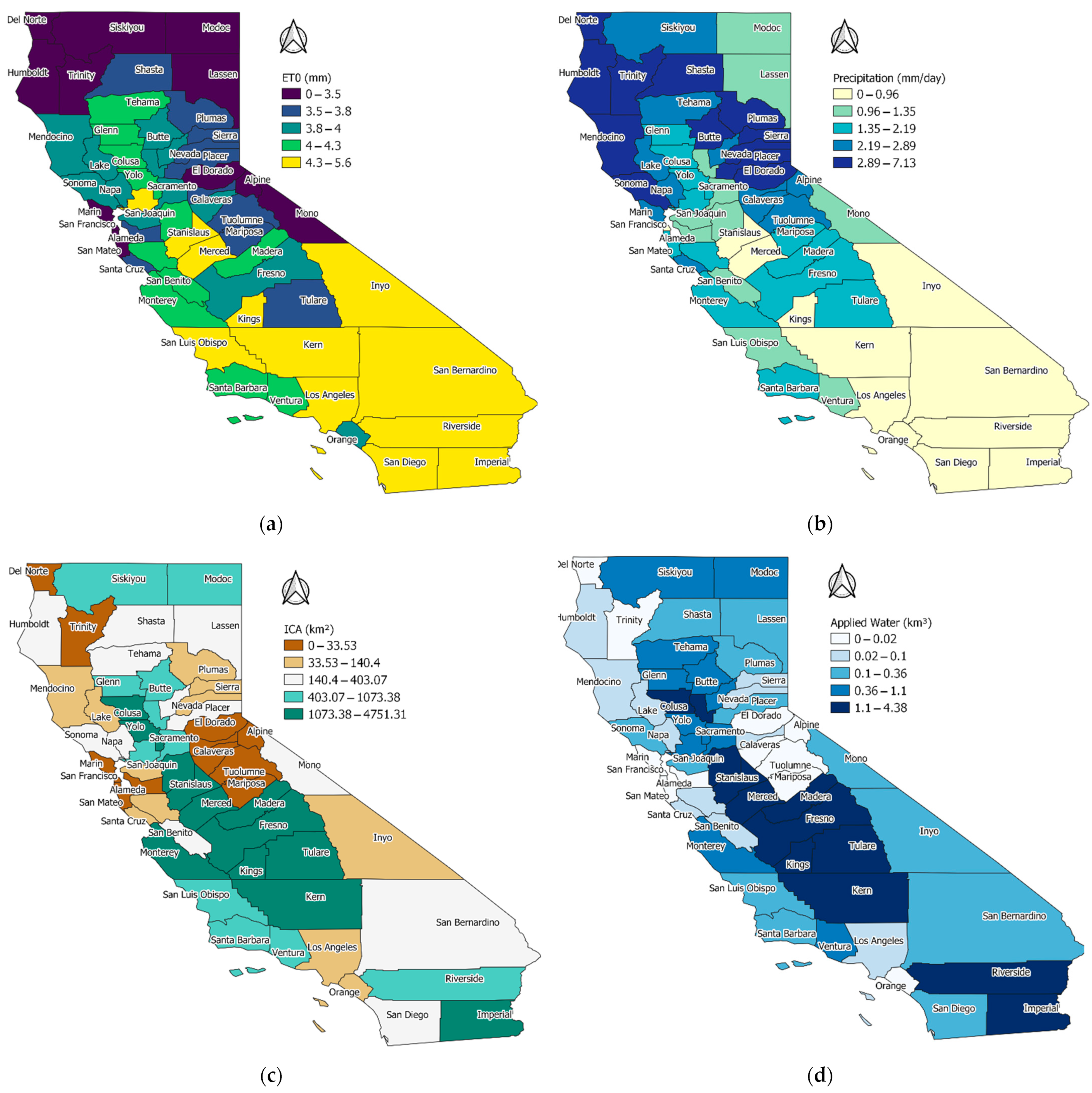
1.1. Study Site
1.2. Database and Data Management
2. Methodology
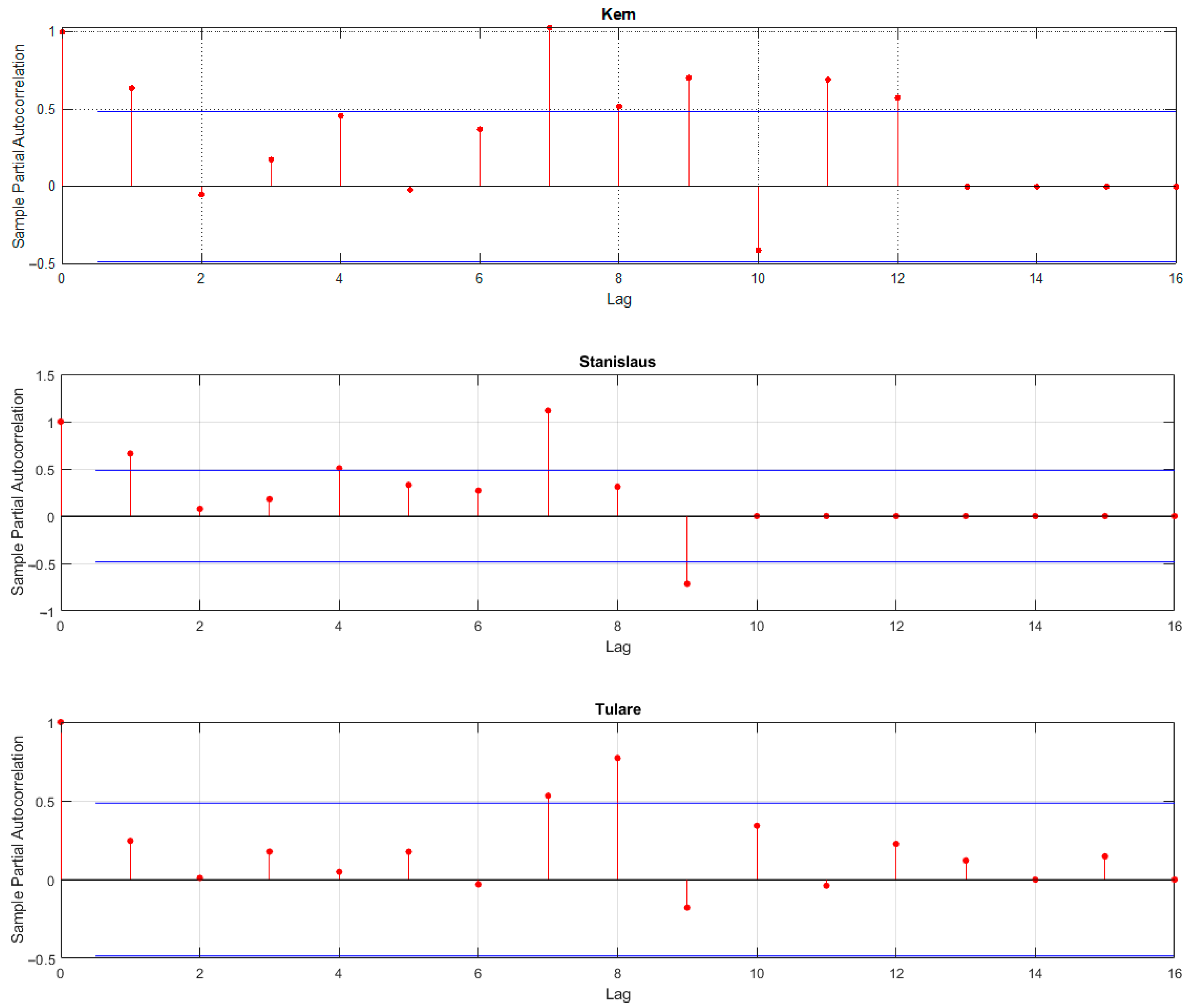
2.1. Model Selection and Training
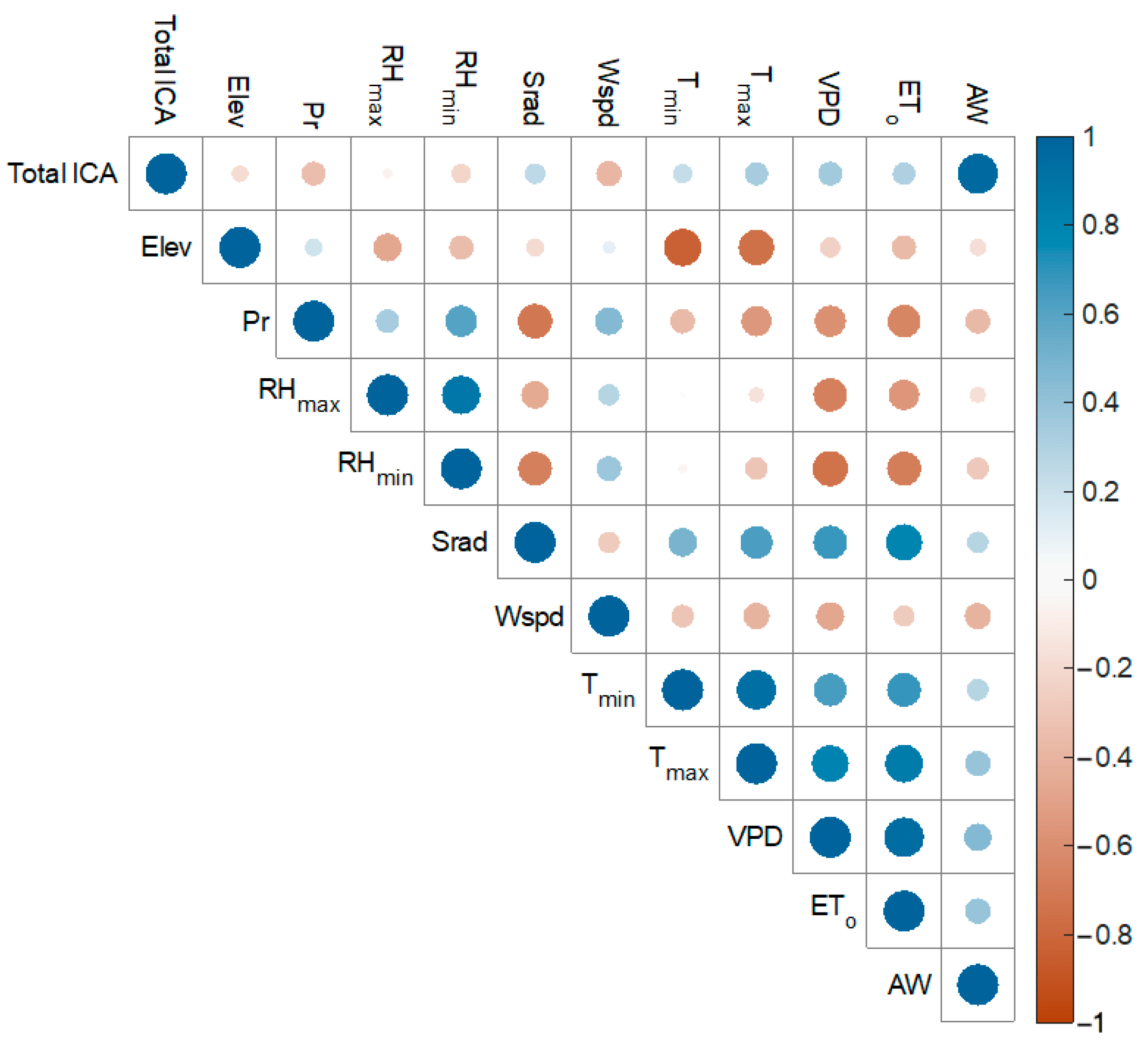
2.2. Input Data Combination
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bayer, P.E.; Edwards, D. Machine learning in agriculture: From silos to marketplaces. Plant Biotechnol. J. 2020, 19, 648–650. [Google Scholar] [CrossRef] [PubMed]
- Liakos, K.G.; Busato, P.; Moshou, D.; Pearson, S.; Bochtis, D. Machine learning in agriculture: A review. Sensors 2018, 18, 2674. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tantalaki, N.; Souravlas, S.; Roumeliotis, M. Data-driven decision making in precision agriculture: The rise of big data in agricultural systems. J. Agric. Food Inf. 2019, 20, 344–380. [Google Scholar] [CrossRef]
- Vasisht, D.; Kapetanovic, Z.; Won, J.; Jin, X.; Chandra, R.; Sinha, S.; Kapoor, A.; Sudarshan, M.; Stratman, S. Farmbeats: An IoT platform for data-driven agriculture. In Proceedings of the 14th {USENIX} Symposium on Networked Systems Design and Implementation ({NSDI} 17), Boston, MA, USA, 27–29 March 2017; pp. 515–529. [Google Scholar]
- Chlingaryan, A.; Sukkarieh, S.; Whelan, B. Machine learning approaches for crop yield prediction and nitrogen status estimation in precision agriculture: A review. Comput. Electron. Agric. 2018, 151, 61–69. [Google Scholar] [CrossRef]
- Crane-Droesch, A. Machine learning methods for crop yield prediction and climate change impact assessment in agriculture. Environ. Res. Lett. 2018, 13, 114003. [Google Scholar] [CrossRef] [Green Version]
- Van Klompenburg, T.; Kassahun, A.; Catal, C. Crop yield prediction using machine learning: A systematic literature review. Comput. Electron. Agric. 2020, 177, 105709. [Google Scholar] [CrossRef]
- Ahmadi, A.; Emami, M.; Daccache, A.; He, L. Soil Properties Prediction for Precision Agriculture Using Visible and Near-Infrared Spectroscopy: A Systematic Review and Meta-Analysis. Agronomy 2021, 11, 433. [Google Scholar] [CrossRef]
- Ebrahimi, M.A.; Khoshtaghaza, M.H.; Minaei, S.; Jamshidi, B. Vision-based pest detection based on SVM classification method. Comput. Electron. Agric. 2017, 137, 52–58. [Google Scholar] [CrossRef]
- Pantazi, X.E.; Tamouridou, A.A.; Alexandridis, T.K.; Lagopodi, A.L.; Kontouris, G.; Moshou, D. Detection of Silybum marianum infection with Microbotryum silybum using VNIR field spectroscopy. Comput. Electron. Agric. 2017, 137, 130–137. [Google Scholar] [CrossRef]
- Pantazi, X.E.; Moshou, D.; Bravo, C. Active learning system for weed species recognition based on hyperspectral sensing. Biosyst. Eng. 2016, 146, 193–202. [Google Scholar] [CrossRef]
- Emami, M.; Nazif, S.; Mousavi, S.F.; Karami, H.; Daccache, A. A hybrid constrained coral reefs optimization algorithm with machine learning for optimizing multi-reservoir systems operation. J. Environ. Manag. 2021, 286, 112250. [Google Scholar] [CrossRef]
- El Bilali, A.; Taleb, A. Prediction of irrigation water quality parameters using machine learning models in a semi-arid environment. J. Saudi Soc. Agric. Sci. 2020, 19, 439–451. [Google Scholar] [CrossRef]
- Navarro-Hellín, H.; Martinez-del-Rincon, J.; Domingo-Miguel, R.; Soto-Valles, F.; Torres-Sánchez, R. A decision support system for managing irrigation in agriculture. Comput. Electron. Agric. 2016, 124, 121–131. [Google Scholar] [CrossRef] [Green Version]
- Torres-Sanchez, R.; Navarro-Hellin, H.; Guillamon-Frutos, A.; San-Segundo, R.; Ruiz-Abellón, M.C.; Domingo-Miguel, R. A decision support system for irrigation management: Analysis and implementation of different learning techniques. Water 2020, 12, 548. [Google Scholar] [CrossRef] [Green Version]
- Goap, A.; Sharma, D.; Shukla, A.K.; Krishna, C.R. An IoT based smart irrigation management system using machine learning and open source technologies. Comput. Electron. Agric. 2018, 155, 41–49. [Google Scholar] [CrossRef]
- Vij, A.; Vijendra, S.; Jain, A.; Bajaj, S.; Bassi, A.; Sharma, A. IoT and machine learning approaches for automation of farm irrigation system. Procedia Comput. Sci. 2020, 167, 1250–1257. [Google Scholar] [CrossRef]
- Goldstein, A.; Fink, L.; Meitin, A.; Bohadana, S.; Lutenberg, O.; Ravid, G. Applying machine learning on sensor data for irrigation recommendations: Revealing the agronomist’s tacit knowledge. Precis. Agric. 2018, 19, 421–444. [Google Scholar] [CrossRef]
- Mekonnen, Y.; Namuduri, S.; Burton, L.; Sarwat, A.; Bhansali, S. Machine learning techniques in wireless sensor network based precision agriculture. J. Electrochem. Soc. 2019, 167, 037522. [Google Scholar] [CrossRef]
- Pulido-Calvo, I.; Montesinos, P.; Roldán, J.; Ruiz-Navarro, F. Linear regressions and neural approaches to water demand forecasting in irrigation districts with telemetry systems. Biosyst. Eng. 2007, 97, 283–293. [Google Scholar] [CrossRef]
- Zhang, J.; Li, H.; Shi, X.; Hong, Y. Wavelet-nonlinear cointegration prediction of irrigation water in the irrigation district. Water Resour. Manag. 2019, 33, 2941–2954. [Google Scholar] [CrossRef]
- Khan, M.A.; Islam, M.Z.; Hafeez, M. Evaluating the Performance of Several Data Mining Methods for Predicting Irrigation Water Requirement. In Proceedings of the Tenth Australasian Data Mining Conference, Sidney, Australia, 5–7 December 2012; Australian Computer Society, Inc.: Sydney, Australia, 2012; pp. 199–207. [Google Scholar]
- Qin, Y.; Mueller, N.D.; Siebert, S.; Jackson, R.B.; AghaKouchak, A.; Zimmerman, J.B.; Tong, D.; Hong, C.; Davis, S.J. Flexibility and intensity of global water use. Nat. Sustain. 2019, 2, 515–523. [Google Scholar] [CrossRef]
- Atsalakis, G.; Minoudaki, C.; Markatos, N.; Stamou, A.; Beltrao, J.; Panagopoulos, T. Daily irrigation water demand prediction using adaptive neuro-fuzzy inferences systems (ANFIS). In Proceedings of the 3rd IASME/WSEAS International Conference on Energy, Environment, Ecosystems & Sustainable Development (EEESD’07), Agios Nikolaos, Greece, 24–26 July 2007; World Scientific and Engineering Academy and Society Press (WSEAS Press): Agios Nikolaos, Greece, 2007. [Google Scholar]
- Mo, X.; Liu, S.; Lin, Z.; Xu, Y.; Xiang, Y.; McVicar, T.R. Prediction of crop yield, water consumption and water use efficiency with a SVAT-crop growth model using remotely sensed data on the North China Plain. Ecol. Model. 2005, 183, 301–322. [Google Scholar] [CrossRef]
- Weatherhead, E.K.; Knox, J.W. Predicting and mapping the future demand for irrigation water in England and Wales. Agric. Water Manag. 2000, 43, 203–218. [Google Scholar] [CrossRef]
- Wada, Y.; Wisser, D.; Eisner, S.; Flörke, M.; Gerten, D.; Haddeland, I.; Hanasaki, N.; Masaki, Y.; Portmann, F.T.; Stacke, T.; et al. Multimodel projections and uncertainties of irrigation water demand under climate change. Geophys. Res. Lett. 2013, 40, 4626–4632. [Google Scholar] [CrossRef] [Green Version]
- Wisser, D.; Frolking, S.; Douglas, E.M.; Fekete, B.M.; Vörösmarty, C.J.; Schumann, A.H. Global irrigation water demand: Variability and uncertainties arising from agricultural and climate data sets. Geophys. Res. Lett. 2008, 35, L24408. [Google Scholar] [CrossRef] [Green Version]
- Ehteram, M.; Allawi, M.F.; Karami, H.; Mousavi, S.-F.; Emami, M.; El-Shafie, A.; Farzin, S. Optimization of Chain-Reservoirs’ Operation with a New Approach in Artificial Intelligence. Water Resour Manag. 2017, 31, 2085–2104. [Google Scholar] [CrossRef]
- Ehteram, M.; Mousavi, S.-F.; Karami, H.; Farzin, S.; Emami, M.; Othman, F.B.; Amini, Z.; Kisi, O.; El-Shafie, A. Fast convergence optimization model for single and multi-purposes reservoirs using hybrid algorithm. Adv. Eng. Inform. 2017, 32, 287–298. [Google Scholar] [CrossRef]
- Mehta, V.K.; Haden, V.R.; Joyce, B.A.; Purkey, D.R.; Jackson, L.E. Irrigation demand and supply, given projections of climate and land-use change, in Yolo County, California. Agric. Water Manag. 2013, 117, 70–82. [Google Scholar] [CrossRef]
- Ahmadi, A.; Nasseri, M.; Solomatine, D.P. Parametric uncertainty assessment of hydrological models: Coupling UNEEC-P and a fuzzy general regression neural network. Hydrol. Sci. J. 2019, 64, 1080–1094. [Google Scholar] [CrossRef]
- Ahmadi, A.; Nasseri, M. Do direct and inverse uncertainty assessment methods present the same results? J. Hydroinformatics 2020, 22, 842–855. [Google Scholar] [CrossRef]
- Ahmadi, A.; Kerachian, R.; Skardi, M.J.E.; Abdolhay, A. A stakeholder-based decision support system to manage water resources. J. Hydrol. 2020, 589, 125138. [Google Scholar] [CrossRef]
- Loucks, D.P.; Da Costa, J.R. (Eds.) Decision Support Systems: Water Resources Planning; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 26. [Google Scholar]
- California Department of Water Resources. Agricultural Land & Water Use Estimates, 2019–2020; California Department of Water Resources: Sacramento, CA, USA, 2020. Available online: https://water.ca.gov/Programs/Water-Use-And-Efficiency/Land-And-Water-Use/Agricultural-Land-And-Water-Use-Estimates (accessed on 1 February 2021).
- Wilson, T.S.; Sleeter, B.M.; Cameron, D.R. Future land-use related water demand in California. Environ. Res. Lett. 2016, 11, 054018. [Google Scholar] [CrossRef]
- Parker, L.E.; McElrone, A.J.; Ostoja, S.M.; Forrestel, E.J. Extreme heat effects on perennial crops and strategies for sustaining future production. Plant Sci. 2020, 295, 110397. [Google Scholar] [CrossRef] [PubMed]
- California Department of Food and Agriculture. Agricultural Statistics Review, 2019–2020; California Department of Food and Agriculture: Sacramento, CA, USA, 2020.
- Johnson, R.; Cody, B.A. California Agricultural Production and Irrigated Water Use; Congressional Research Service: Sacramento, CA, USA, 2015; p. 28. [Google Scholar]
- Cooley, H. California Agricultural Water Use: Key Background Information; Pacific Institute: Oakland, CA, USA, 2015; pp. 1–9. [Google Scholar]
- Abatzoglou, J.T. Development of gridded surface meteorological data for ecological applications and modelling. Int. J. Climatol. 2013, 33, 121–131. Available online: https://www.climatologylab.org/gridmet.html (accessed on 1 February 2021). [CrossRef]
- Orang, M.N.; Snyder, R.L.; Shu, G.; Hart, Q.J.; Sarreshteh, S.; Falk, M.; Beaudette, D.; Hayes, S.; Eching, S. California simulation of evapotranspiration of applied water and agricultural energy use in California. J. Integr. Agric. 2013, 12, 1371–1388. [Google Scholar] [CrossRef]
- Rasmussen, C.; Williams, C. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]




| Variable (Definition) | Acronym | Unit |
|---|---|---|
| Applied Water (the quantity of volumetric water applied to all crops in a county) | AW | km3 (Billion m3) |
| Irrigated Crop Area (the total amount of land irrigated for the purpose of growing a crop, including multi-cropping acres) | ICA | km2 |
| Elevation (elevation above mean sea level) | El | m |
| Precipitation (daily accumulated precipitation) | Pr | mm |
| Daily maximum relative humidity | RHmax | % |
| Daily minimum relative humidity | RHmin | % |
| Daily mean downward shortwave radiation at the surface | Srad | W/m3 |
| Daily mean wind speed | Wspd | m/s |
| Daily minimum temperature | Tmin | K |
| Daily maximum temperature | Tmax | K |
| Mean vapor pressure deficit | VPD | kPa |
| Reference evapotranspiration (short grass) | ET0 | mm |
| Number | Crop Category | Acronym | Definition |
|---|---|---|---|
| 1 | Grain | GR | Wheat, barley, oats, miscellaneous grain and hay, and mixed grain and hay |
| 2 | Rice | RI | Rice and wild rice |
| 3 | Cotton | CO | Cotton |
| 4 | Sugar beet | SB | Sugar beets |
| 5 | Corn | CN | Corn (field and sweet) |
| 6 | Dry beans | DB | Beans (dry) |
| 7 | Safflower | SA | Safflower |
| 8 | Other field crops | FL | Flax, hops, grain sorghum, sudan, castor beans, miscellaneous fields, sunflowers, hybrid sorghum/sudan, millet, and sugar cane |
| 9 | Alfalfa | AL | Alfalfa and alfalfa mixtures |
| 10 | Pasture | PA | Clover, mixed pasture, native pastures, induced high water table native pasture, miscellaneous grasses, turf farms, bermuda grass, rye grass, and klein grass |
| 11 | Tomato (processing) | TP | Tomatoes for processing |
| 12 | Tomato (fresh) | TF | Tomatoes for market |
| 13 | Cucurbits | CU | Melons, squash, and cucumbers |
| 14 | Onion and garlic | OG | Onions and garlic |
| 15 | Potato | PO | Potatoes |
| 16 | Miscellaneous truck crops | TR | Artichokes, asparagus, beans (green), carrots, celery, lettuce, peas, spinach, flowers nursery and tree farms, bush berries, strawberries, peppers, broccoli, cabbage, cauliflower, and brussels sprouts |
| 17 | Almond and pistachios | AP | Almonds and pistachios |
| 18 | Other deciduous orchards | OR | Apples, apricots, cherries, peaches, nectarines, pears, plums, prunes, figs, walnuts, and miscellaneous deciduous |
| 19 | Citrus and subtropical | CS | Grapefruit, lemons, oranges, dates, avocados, olives, kiwis, jojoba, eucalyptus, and miscellaneous subtropical fruit |
| 20 | Vineyards | VI | Table grapes, wine grapes, and raisin grapes |
| 21 | Multi-cropping | MC | Multi-cropping |
| Parameter | Search Range | Optimal Value |
|---|---|---|
| Basis function coefficients | Zero, Constant, and Linear | Zero |
| Kernel function | Rational Quadratic, Squared Exponential, Matern 5/2, Matern 3/2, and Exponential | Matern 5/2 |
| Kernel mode | Isotropic Kernel, Nonisotropic Kernel | Nonisotropic Kernel |
| Kernel scale | 2.4338–2433.828 | 1747.9647 |
| Sigma | Observation noise standard deviation | 5.6562 |
| Model Name | Predictors |
|---|---|
| M1 | ICAi:i = 1:21 *, ETcj, j = 1:20 ** Elevation, Precipitation, Maximum relative humidity, Minimum relative humidity, Surface radiation, Wind speed, Maximum air temperature, Minimum air temperature, Vapor pressure deficit, ETo grass |
| M2 | ICAi:i = 1:21, Elevation, Precipitation, Maximum relative humidity, Minimum relative humidity, Surface radiation, Wind speed, Maximum air temperature, Minimum air temperature, Vapor pressure deficit, ETo grass |
| M3 | ICAi:i = 1:21, Elevation, Precipitation, Maximum relative humidity, Minimum relative humidity, Surface radiation, Wind speed, Maximum air temperature, Minimum air temperature, ETo grass |
| M4 | ICAi:i = 1:21, Precipitation, Maximum relative humidity, Minimum relative humidity, Surface radiation, Wind speed, Maximum air temperature, Minimum air temperature, ETo grass |
| M5 | ICAi:i = 1:21, Precipitation, Maximum relative humidity, Minimum relative humidity, Surface radiation, Wind speed, Maximum air temperature, Minimum air temperature |
| M6 | ICAi:i = 1:21 *, ETcj, j = 1:20 ** Elevation, Precipitation, Maximum relative humidity, Minimum relative humidity, Surface radiation, Wind speed, Maximum air temperature, Minimum air temperature, Vapor pressure deficit, ETo grass, IWU(t−1) |
| M7 | ICAi:i = 1:21, Elevation, Precipitation, Maximum relative humidity, Minimum relative humidity, Surface radiation, Wind speed, Maximum air temperature, Minimum air temperature, Vapor pressure deficit, ETo grass, IWU(t−1) |
| M8 | ICAi:i = 1:21, Elevation, Precipitation, Maximum relative humidity, Minimum relative humidity, Surface radiation, Wind speed, Maximum air temperature, Minimum air temperature, ETo grass, IWU(t−1) |
| M9 | ICAi:i = 1:21, Precipitation, Maximum relative humidity, Minimum relative humidity, Surface radiation, Wind speed, Maximum air temperature, Minimum air temperature, ETo grass, IWU(t−1) |
| M10 | ICAi:i = 1:21, Precipitation, Maximum relative humidity, Minimum relative humidity, Surface radiation, Wind speed, Maximum air temperature, Minimum air temperature, IWU(t−1) |
| df | SS | MS | F | Significance F | |
|---|---|---|---|---|---|
| Regression | 11 | 912.4558127 | 82.95052842 | 1508.74493 | 0 |
| Residual | 1001 | 55.03480246 | 0.054979823 | ||
| Total | 1012 | 967.4906151 |
| Estimate | Standard Error | t Stat | p-Value | Lower 95% | Upper 95% | |
|---|---|---|---|---|---|---|
| Intercept | 19.1920 | 4.8588 | 3.9499 | 0.0001 | 9.6574 | 28.7267 |
| ICA | 0.0009 | 0.0000 | 99.2910 | 0.0000 | 0.0009 | 0.0009 |
| El | −0.0001 | 0.0001 | −2.0762 | 0.0381 | −0.0003 | 0.0000 |
| Pr | −0.0270 | 0.0092 | −2.9374 | 0.0034 | −0.0450 | −0.0090 |
| RHmax | −0.0008 | 0.0033 | −0.2475 | 0.8046 | −0.0074 | 0.0057 |
| RHmin | 0.0091 | 0.0060 | 1.5237 | 0.1279 | −0.0026 | 0.0209 |
| Srad | −0.0032 | 0.0019 | −1.6533 | 0.0986 | −0.0069 | 0.0006 |
| Wspd | 0.0231 | 0.0286 | 0.8073 | 0.4197 | −0.0330 | 0.0791 |
| Tmin | 0.0335 | 0.0122 | 2.7502 | 0.0061 | 0.0096 | 0.0574 |
| Tmax | −0.0984 | 0.0206 | −4.7681 | 0.0000 | −0.1389 | −0.0579 |
| VPD | 1.1808 | 0.1394 | 8.4703 | 0.0000 | 0.9072 | 1.4543 |
| ET0 | −0.1056 | 0.0968 | −1.0908 | 0.2756 | −0.2955 | 0.0843 |
| Model | M1 | M2 | M3 | M4 | M5 | M6 | M7 | M8 | M9 | M10 |
|---|---|---|---|---|---|---|---|---|---|---|
| R2 | 0.9945 | 0.9828 | 0.9825 | 0.9792 | 0.9814 | 0.9949 | 0.9760 | 0.9760 | 0.9768 | 0.9776 |
| RMSE (km3) | 0.0669 | 0.1185 | 0.1197 | 0.1303 | 0.1232 | 0.0642 | 0.1401 | 0.1399 | 0.1376 | 0.1351 |
| MAE (km3) | 0.0335 | 0.0550 | 0.0556 | 0.0617 | 0.0556 | 0.0322 | 0.0616 | 0.0632 | 0.0624 | 0.0603 |
| STD_predict | 0.9084 | 0.9203 | 0.9138 | 0.9188 | 0.9134 | 0.9089 | 0.9281 | 0.9287 | 0.9266 | 0.9270 |
| RMSPE | 4.2218 | 7.6086 | 5.5558 | 2.4232 | 4.0605 | 3.9646 | 2.7092 | 2.4763 | 2.6975 | 2.3970 |
| NRMSE | 0.1071 | 0.1897 | 0.1916 | 0.2085 | 0.1972 | 0.1028 | 0.2242 | 0.2240 | 0.2202 | 0.2162 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Emami, M.; Ahmadi, A.; Daccache, A.; Nazif, S.; Mousavi, S.-F.; Karami, H. County-Level Irrigation Water Demand Estimation Using Machine Learning: Case Study of California. Water 2022, 14, 1937. https://doi.org/10.3390/w14121937
Emami M, Ahmadi A, Daccache A, Nazif S, Mousavi S-F, Karami H. County-Level Irrigation Water Demand Estimation Using Machine Learning: Case Study of California. Water. 2022; 14(12):1937. https://doi.org/10.3390/w14121937
Chicago/Turabian StyleEmami, Mohammad, Arman Ahmadi, Andre Daccache, Sara Nazif, Sayed-Farhad Mousavi, and Hojat Karami. 2022. "County-Level Irrigation Water Demand Estimation Using Machine Learning: Case Study of California" Water 14, no. 12: 1937. https://doi.org/10.3390/w14121937
APA StyleEmami, M., Ahmadi, A., Daccache, A., Nazif, S., Mousavi, S.-F., & Karami, H. (2022). County-Level Irrigation Water Demand Estimation Using Machine Learning: Case Study of California. Water, 14(12), 1937. https://doi.org/10.3390/w14121937










