Random Forest Model Has the Potential for Runoff Simulation and Attribution
Abstract
:1. Introduction
2. Study Area, Data Sets, and Methods
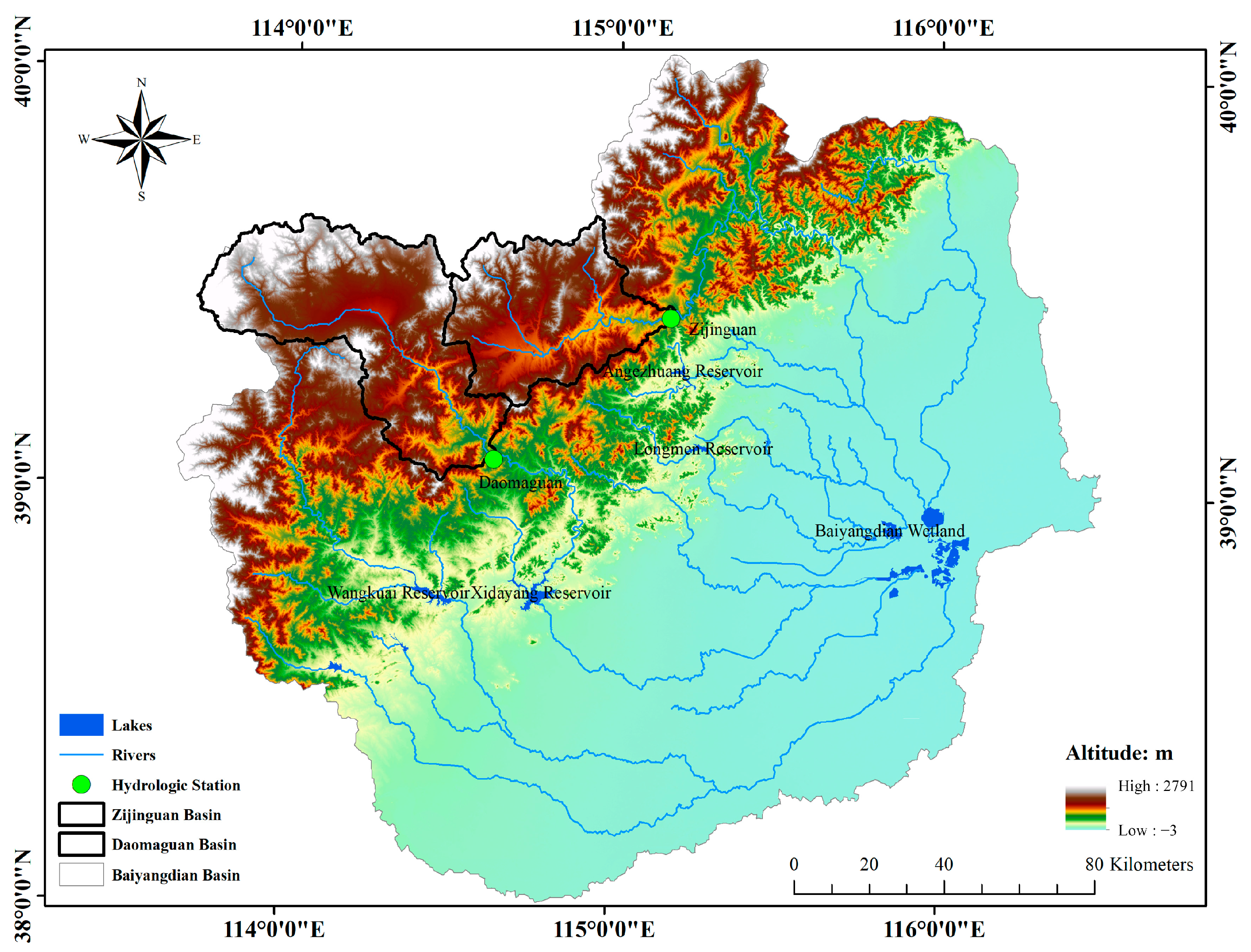
2.1. Study Area
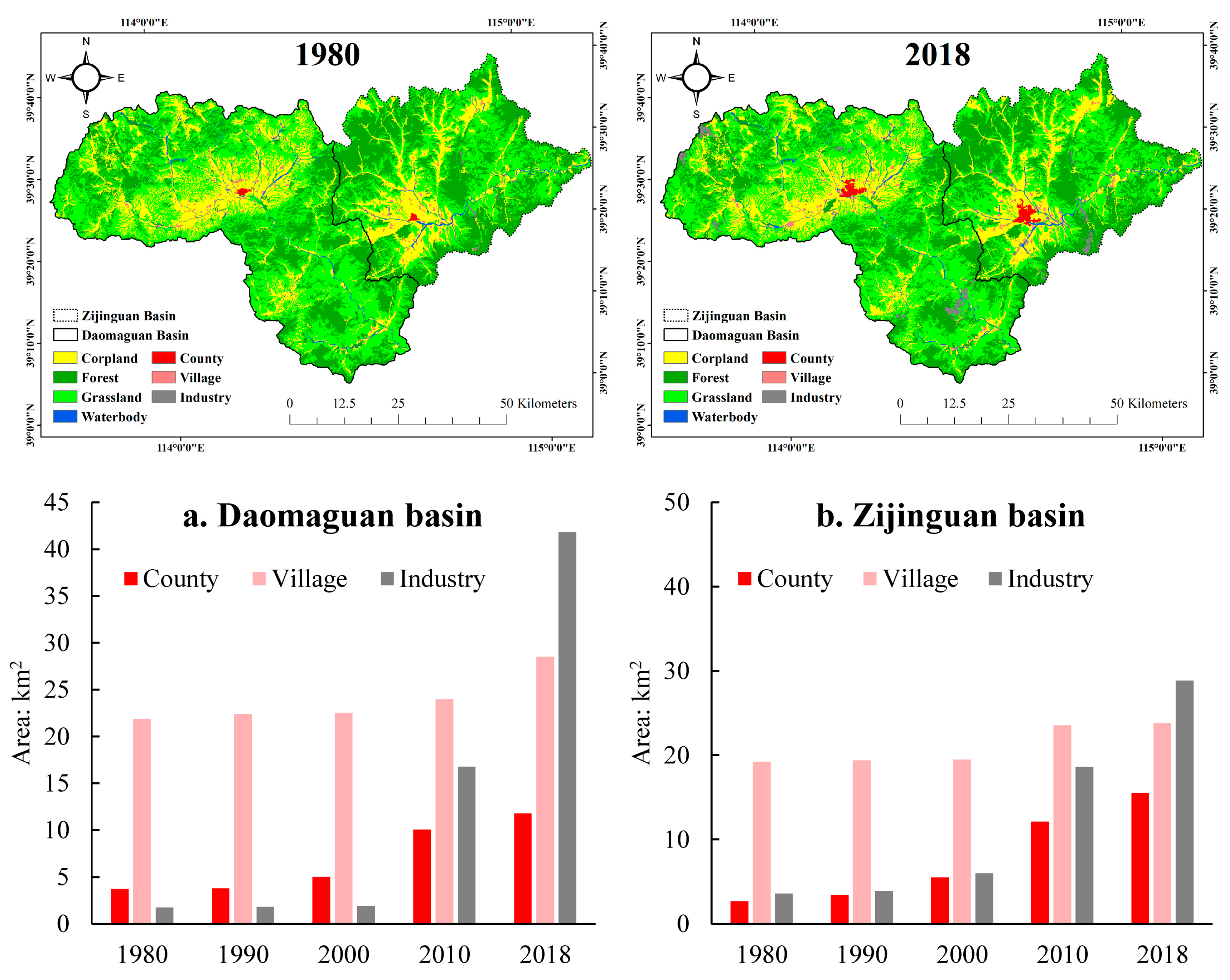
2.2. Data Sets
2.3. Methods
2.3.1. Trend and Breakpoint Analysis
2.3.2. Elasticity-Based Methods
2.3.3. Assessment Based on Random Forest Model
2.3.4. Assessment Based on Double-Mass Curve Method
3. Results
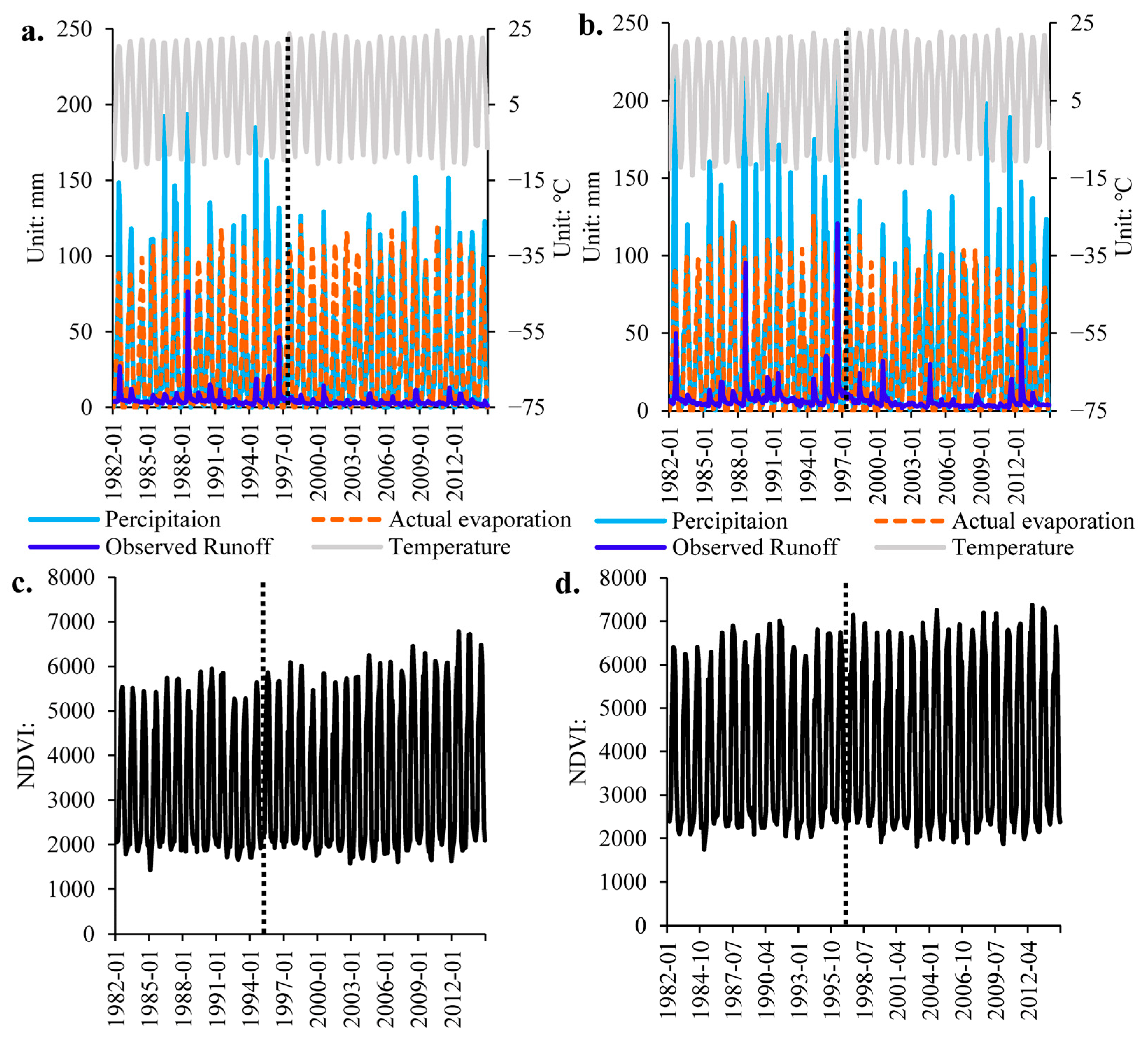
3.1. Trends of Climatic, Hydrological, and Anthropogenic Variables
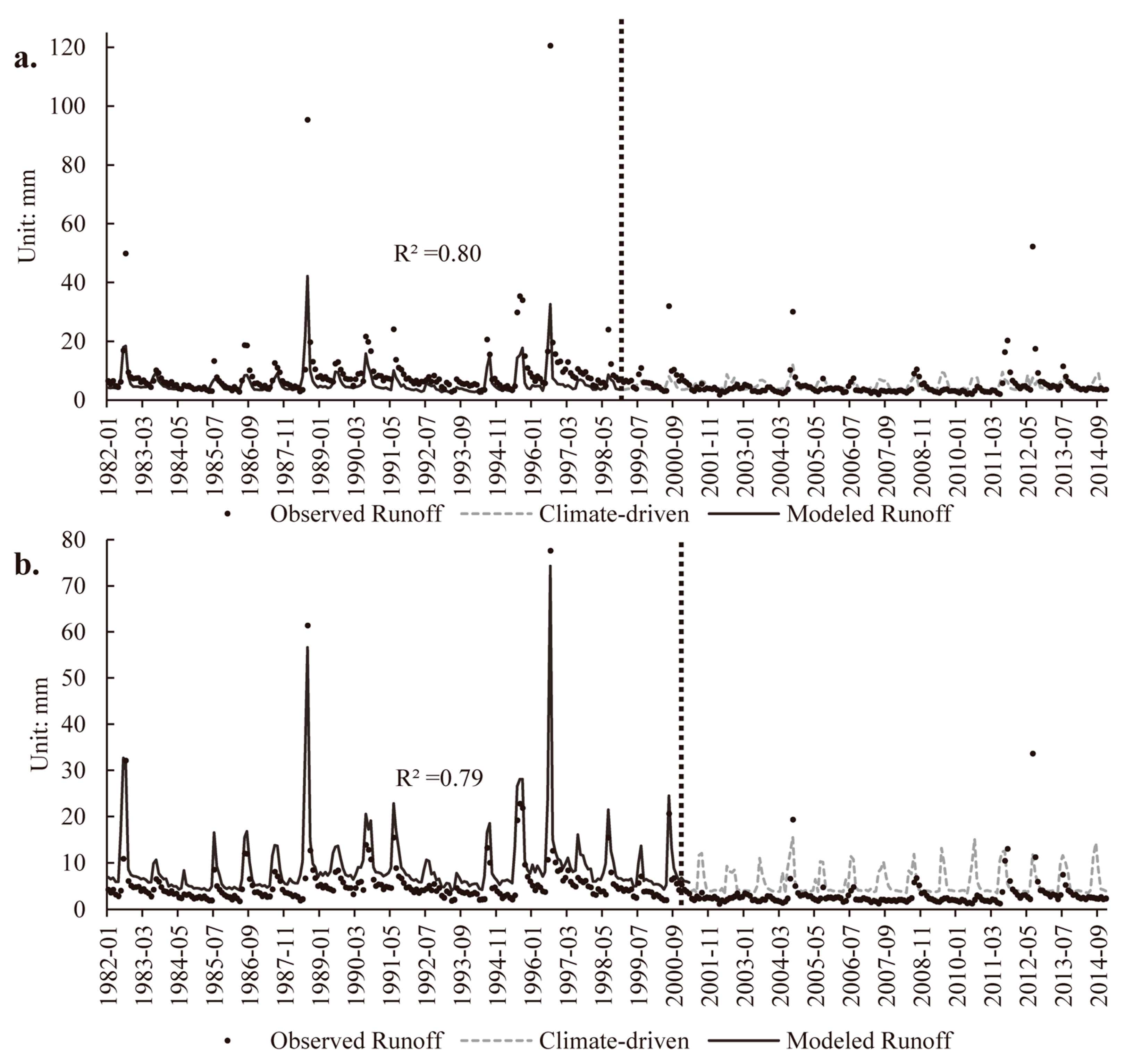
3.2. Performance of Different Models
3.3. Quantifying the Runoff Change Response to Climate Change and Human Activities in the Target Basins
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Millán, M.M. Extreme hydrometeorological events and climate change predictions in Europe. J. Hydrol. 2014, 518, 206–224. [Google Scholar] [CrossRef]
- Liang, W.; Bai, D.; Wang, F.; Fu, B.; Yan, J.; Wang, S.; Yang, Y.; Long, D.; Feng, M. Quantifying the impacts of climate change and ecological restoration on streamflow changes based on a Budyko hydrological model in China’s Loess Plateau. Water Resour. Res. 2015, 51, 6500–6519. [Google Scholar] [CrossRef]
- Amin, M.Z.M.; Shaaban, A.J.; Ercan, A.; Ishida, K.; Kavvas, M.L.; Chen, Z.Q.; Jang, S. Future climate change impact assessment of watershed scale hydrologic processes in Peninsular Malaysia by a regional climate model coupled with a physically-based hydrology modelo. Sci. Total Environ. 2017, 575, 12–22. [Google Scholar] [CrossRef] [PubMed]
- Zhou, G.; Wei, X.; Chen, X.; Zhou, P.; Liu, X.; Xiao, Y.; Sun, G.; Scott, D.F.; Zhou, S.; Han, L.; et al. Global pattern for the effect of climate and land cover on water yield. Nat. Commun. 2015, 6, 5918. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Berghuijs, W.R.; Woods, R.A. Correspondence: Space-time asymmetry undermines water yield assessment. Nat. Commun. 2016, 7, 11603. [Google Scholar] [CrossRef] [Green Version]
- Remondi, F.; Burlando, P.; Vollmer, D. Exploring the hydrological impact of increasing urbanisation on a tropical river catchment of the metropolitan Jakarta, Indonesia. Sustain. Cities Soc. 2016, 20, 210–221. [Google Scholar] [CrossRef]
- Vollmer, D.; Pribadi, D.O.; Remondi, F.; Rustiadi, E.; Grêt-Regamey, A. Prioritizing ecosystem services in rapidly urbanizing river basins: A spatial multi-criteria analytic approach. Sustain. Cities Soc. 2016, 20, 237–252. [Google Scholar] [CrossRef]
- Deng, X.; Shi, Q.; Zhang, Q.; Shi, C.; Yin, F. Impacts of land use and land cover changes on surface energy and water balance in the Heihe River Basin of China, 2000–2010. Phys. Chem. Earth Parts A/B/C 2015, 79, 2–10. [Google Scholar] [CrossRef]
- Yang, W.; Long, D.; Bai, P. Impacts of future land cover and climate changes on runoff in the mostly afforested river basin in North China. J. Hydrol. 2019, 570, 201–219. [Google Scholar] [CrossRef]
- Wang, S.; Yan, M.; Yan, Y.; Shi, C.; He, L. Contributions of climate change and human activities to the changes in runoff increment in different sections of the Yellow River. Quat. Int. 2012, 282, 66–77. [Google Scholar] [CrossRef]
- Zhan, C.S.; Jiang, S.S.; Sun, F.B.; Jia, Y.W.; Niu, C.W.; Yue, W.F. Quantitative contribution of climate change and human activities to runoff changes in the Wei River basin, China. Hydrol. Earth Syst. Sci. 2014, 18, 3069–3077. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Huang, Q.; Zhang, Q.; Gu, L.; Chen, K.; Yu, Q. Changes in the long-term hydrological regimes and the impacts of human activities in the main Wei River, China. Hydrol. Sci. J. 2016, 61, 1054–1068. [Google Scholar] [CrossRef]
- Yin, J.; Gentine, P.; Zhou, S.; Sullivan, S.C.; Wang, R.; Zhang, Y.; Guo, S. Large increase in global storm runoff extremes driven by climate and anthropogenic changes. Nat. Commun. 2018, 9, 4389. [Google Scholar] [CrossRef] [Green Version]
- Gudmundsson, L.; Boulange, J.; Do, H.X.; Gosling, S.N.; Grillakis, M.G.; Koutroulis, A.G.; Leonard, M.; Liu, J.; Schmied, H.M.; Papadimitriou, L.; et al. Globally observed trends in mean and extreme river flow attributed to climate change. Science 2021, 371, 1159. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Y.; Zhang, C.; Zeng, G.; Liang, J.; Guo, S.; Huang, L.; Wu, H.; Hua, S. Quantitative assessment of the contribution of climate variability and human activity to streamflow alteration in Dongting Lake, China. Hydrol. Process. 2016, 30, 1929–1939. [Google Scholar] [CrossRef]
- Yang, H.; Yang, D.; Hu, Q. An error analysis of the Budyko hypothesis for assessing the contribution of climate change to runoff. Water Resour. Res. 2014, 50, 9620–9629. [Google Scholar] [CrossRef]
- Li, Z.; Xu, X.; Yu, B.; Xu, C.; Liu, M.; Wang, K. Quantifying the impacts of climate and human activities on water and sediment discharge in a karst region of southwest China. J. Hydrol. 2016, 542, 836–849. [Google Scholar] [CrossRef]
- Wu, J.; Miao, C.; Zhang, X.; Yang, T.; Duan, Q. Detecting the quantitative hydrological response to changes in climate and human activities. Sci. Total Environ. 2017, 586, 328–337. [Google Scholar] [CrossRef]
- Rakhimova, M.; Liu, T.; Bissenbayeva, S.; Mukanov, Y.; Gafforov, K.S.; Bekpergenova, Z.; Gulakhmadov, A. Assessment of the Impacts of Climate Change and Human Activities on Runoff Using Climate Elasticity Method and General Circulation Model (GCM) in the Buqtyrma River Basin, Kazakhstan. Sustainability 2020, 12, 4968. [Google Scholar] [CrossRef]
- Hu, J.; Ma, J.; Nie, C.; Xue, L.; Zhang, Y.; Ni, F.; Deng, Y.; Liu, J.; Zhou, D.; Li, L.; et al. Attribution Analysis of Runoff Change in Min-Tuo River Basin based on SWAT model simulations, China. Sci. Rep. 2020, 10, 2900. [Google Scholar] [CrossRef] [Green Version]
- He, Y.; Qiu, H.; Song, J.; Zhao, Y.; Zhang, L.; Hu, S.; Hu, Y. Quantitative contribution of climate change and human activities to runoff changes in the Bahe River watershed of the Qinling Mountains, China. Sustain. Cities Soc. 2019, 51, 101729. [Google Scholar] [CrossRef]
- Zhao, G.; Tian, P.; Mu, X.; Jiao, J.; Wang, F.; Gao, P. Quantifying the impact of climate variability and human activities on streamflow in the middle reaches of the Yellow River basin, China. J. Hydrol. 2014, 519, 387–398. [Google Scholar] [CrossRef]
- Maheswaran, R.; Khosa, R. Wavelet–Volterra coupled model for monthly stream flow forecasting. J. Hydrol. 2012, 450, 320–335. [Google Scholar] [CrossRef]
- Ouali, D.; Chebana, F.; Ouarda, T.B.M.J. Fully nonlinear statistical and machine-learning approaches for hydrological frequency estimation at ungauged sites. J. Adv. Model. Earth Syst. 2017, 9, 1292–1306. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Tikhamarine, Y.; Souag-Gamane, D.; Ahmed, A.N.; Sammen, S.S.; Kisi, O.; Huang, Y.F.; El-Shafie, A. Rainfall-runoff modelling using improved machine learning methods: Harris hawks optimizer vs. particle swarm optimization. J. Hydrol. 2020, 589, 125133. [Google Scholar] [CrossRef]
- Wang, Z.; Lai, C.; Chen, X.; Yang, B.; Zhao, S.; Bai, X. Flood hazard risk assessment model based on random forest. J. Hydrol. 2015, 527, 1130–1141. [Google Scholar] [CrossRef]
- Kun, Y.; Jie, H. China Meteorological Forcing Dataset (1979–2015). 2016. Available online: https://doi.org/10.3972/westdc.002.2014.db (accessed on 21 June 2022).
- Ma, N.; Jozsef, S.; Zhang, Y.; Liu, W. Terrestrial Evapotranspiration Dataset across China (1982–2017); National Tibetan Plateau Data Center: Beijing, China, 2019. [Google Scholar]
- Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods, 4th ed.; Charles Griffin: London, UK, 1975. [Google Scholar]
- Li, B.F.; Shi, X.; Lian, L.S.; Chen, Y.N.; Chen, Z.S.; Sun, X.Y. Quantifying the effects of climate variability, direct and indirect land use change, and human activities on runoff. J. Hydrol. 2020, 584, 124684. [Google Scholar] [CrossRef]
- Song, X.Y.; Sun, W.Y.; Zhang, Y.Q.; Song, S.B.; Li, J.Y.; Gao, Y.J. Using hydrological modelling and data-driven approaches to quantify mining activities impacts on centennial streamflow. J. Hydrol. 2020, 585, 124764. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Xu, X.; Yang, D.; Yang, H.; Lei, H. Attribution analysis based on the Budyko hypothesis for detecting the dominant cause of runoff decline in Haihe basin. J. Hydrol. 2014, 510, 530–540. [Google Scholar] [CrossRef]
- Pettitt, A.N. A Non-Parametric Approach to the Change-Point. Problem. J. R. Stat. Soc. Ser. C 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Yang, H.; Yang, D.; Lei, Z.; Sun, F. New analytical derivation of the mean annual water-energy balance equation. Water Resour. 2008, 44, 893–897. [Google Scholar] [CrossRef]
- Fu, G.; Charles, S.P.; Chiew, F.H.S. A two-parameter climate elasticity of streamflow index to assess climate change effects on annual streamflow. Water Resour. Res. 2007, 43, 2578–2584. [Google Scholar] [CrossRef]
- Zhang, L.; Dawes, W.R.; Walker, G.R. Response of mean annual evapotranspiration to vegetation changes at catchment scale. Water Resour. Res. 2001, 37, 701–708. [Google Scholar] [CrossRef]
- Chadalawada, J.; Herath, H.; Babovic, V. Hydrologically Informed Machine Learning for Rainfall-Runoff Modeling: A Genetic Programming-Based Toolkit for Automatic Model Induction. Water Resour. Res. 2020, 56, e2019WR026933. [Google Scholar] [CrossRef]
- Oppel, H.; Schumann, A.H. Machine learning based identification of dominant controls on runoff dynamics. Hydrol. Process. 2020, 34, 2450–2465. [Google Scholar] [CrossRef]
- Wen, X.H.; Feng, Q.; Deo, R.C.; Wu, M.; Yin, Z.L.; Yang, L.S.; Singh, V.P. Two-phase extreme learning machines integrated with the complete ensemble empirical mode decomposition with adaptive noise algorithm for multi-scale runoff prediction problems. J. Hydrol. 2019, 570, 167–184. [Google Scholar] [CrossRef]
- Breiman, L. Bagging Predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
- Kehoe, M.J.; Chun, K.P.; Baulch, H.M. Who Smells? Forecasting Taste and Odor in a Drinking Water Reservoir. Environ. Sci. Technol. 2015, 49, 10984–10992. [Google Scholar] [CrossRef]
- Strobl, C.; Malley, J.; Tutz, G. An Introduction to Recursive Partitioning: Rationale, Application and Characteristics of Classification and Regression Trees, Bagging and Random Forests. Psychol. Methods 2009, 14, 323–348. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hu, S.; Zheng, H.; Liu, C.; Yu, J.; Wang, Z. Assessing the Impacts of Climate Variability and Human Activities on Streamflow in the Water Source Area of Baiyangdian Lake. J. Geogr. Sci. 2012, 22, 895–905. [Google Scholar] [CrossRef]
- Shen, Q.; Cong, Z.; Lei, H. Evaluating the impact of climate and underlying surface change on runoff within the Budyko framework: A study across 224 catchments in China. J. Hydrol. 2017, 554, 251–262. [Google Scholar] [CrossRef]
- Amanambu, A.C.; Obarein, O.A.; Mossa, J.; Li, L.; Ayeni, S.S.; Balogun, O.; Oyebamiji, A.; Ochege, F.U. Groundwater system and climate change: Present status and future considerations. J. Hydrol. 2020, 589, 125163. [Google Scholar] [CrossRef]

| Slope | ||
|---|---|---|
| Daomaguan | Zijinguan | |
| Precipitation | −0.003 | 0.003 |
| Air temperature | 0.011 * | 0.006 |
| Actual evapotranspiration | 0.001 | <0.001 |
| NDVI | 0.579 * | 0.359 |
| Runoff | −0.005 * | −0.008 * |
| Data Period | Method | Before and after Breakpointperiods | ΔP (mm) | ΔET0 (mm) | ΔR (mm) | Contribution to Runoff Changes (%) | |
|---|---|---|---|---|---|---|---|
| Human | Climate | ||||||
| Daomaguan Basin | Double-mass curve method | 1982–1998 1999–2014 | −43.64 | 82.41 | −29.76 | 69% | 31% |
| Elasticity-based method | 56% | 44% | |||||
| Random Forest method | 66% | 34% | |||||
| Zijinguan Basin | Double-mass curve method | 1982–2000 2001–2014 | 0.71 | 23.58 | −50.18 | 94% | 6% |
| Elasticity-based method | 91% | 9% | |||||
| Random Forest method | 94% | 6% | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Zhang, X.; Kong, X.; Shen, Y.-J. Random Forest Model Has the Potential for Runoff Simulation and Attribution. Water 2022, 14, 2053. https://doi.org/10.3390/w14132053
Liu X, Zhang X, Kong X, Shen Y-J. Random Forest Model Has the Potential for Runoff Simulation and Attribution. Water. 2022; 14(13):2053. https://doi.org/10.3390/w14132053
Chicago/Turabian StyleLiu, Xia, Xiaolong Zhang, Xiaole Kong, and Yan-Jun Shen. 2022. "Random Forest Model Has the Potential for Runoff Simulation and Attribution" Water 14, no. 13: 2053. https://doi.org/10.3390/w14132053
APA StyleLiu, X., Zhang, X., Kong, X., & Shen, Y.-J. (2022). Random Forest Model Has the Potential for Runoff Simulation and Attribution. Water, 14(13), 2053. https://doi.org/10.3390/w14132053






