A Field Experiment Verification of Theoretical Exponent N1 for FAVAD Method in Defining the Relationship of Pressure and Water Losses
Abstract
1. Introduction
2. Materials and Methods
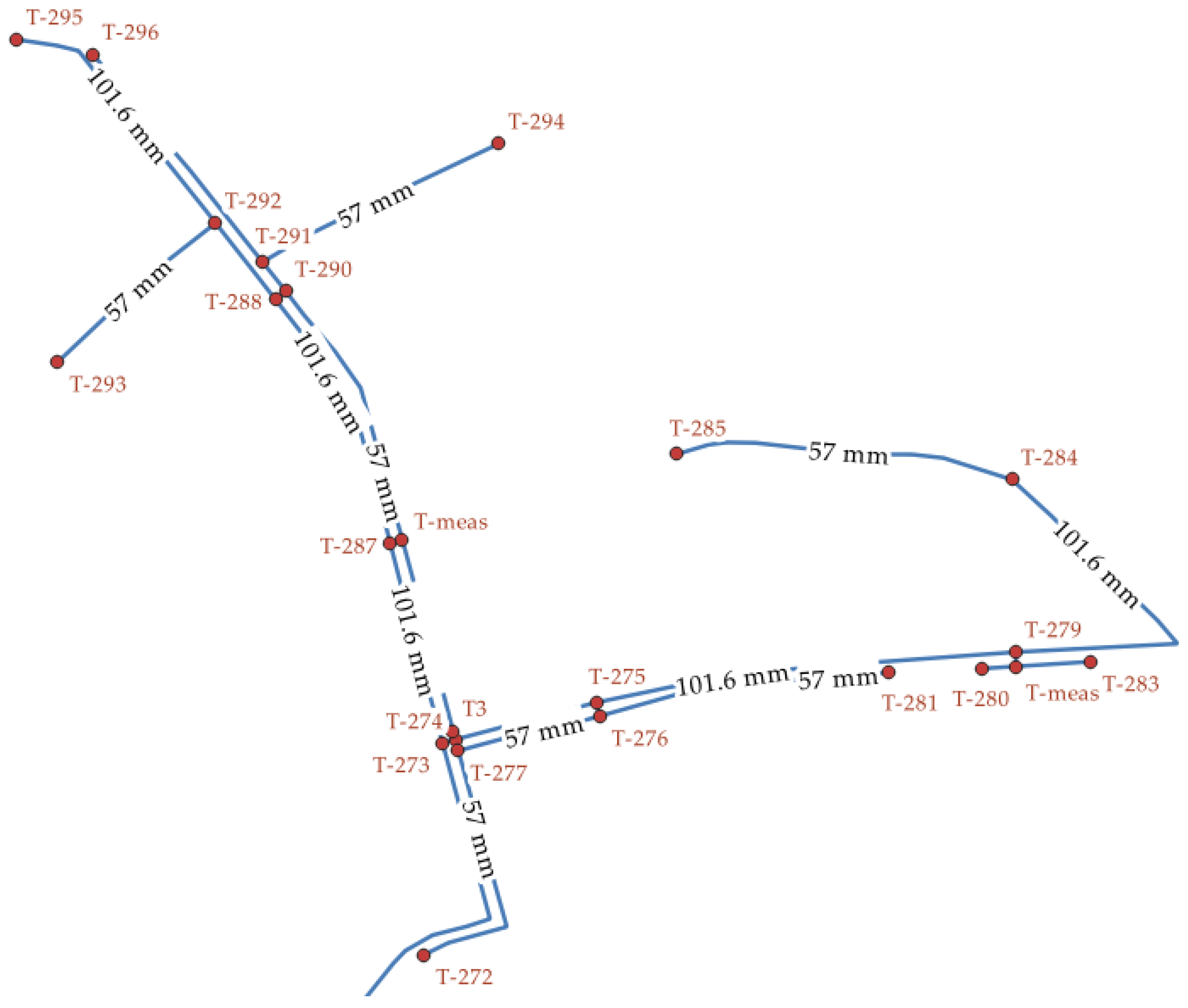
2.1. Study Area
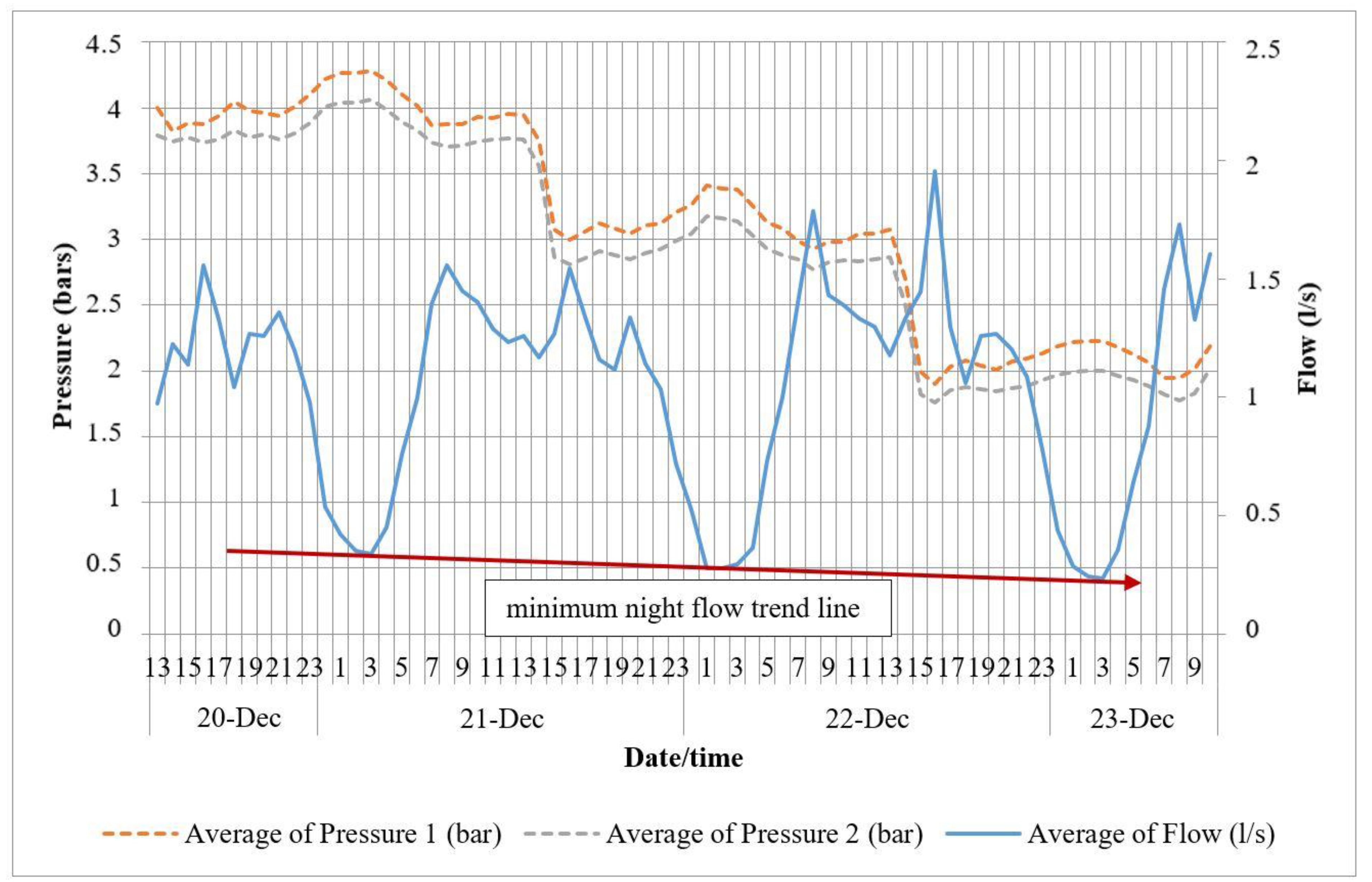
2.2. Measurements
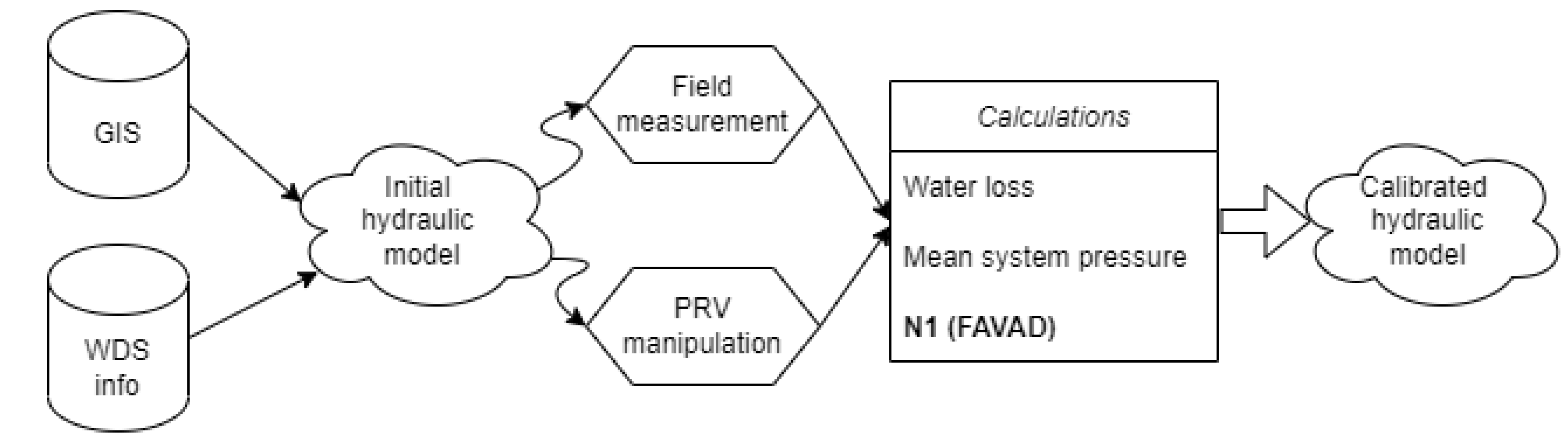
2.3. Formulas and Calculation Methods
2.3.1. Mean Pressure
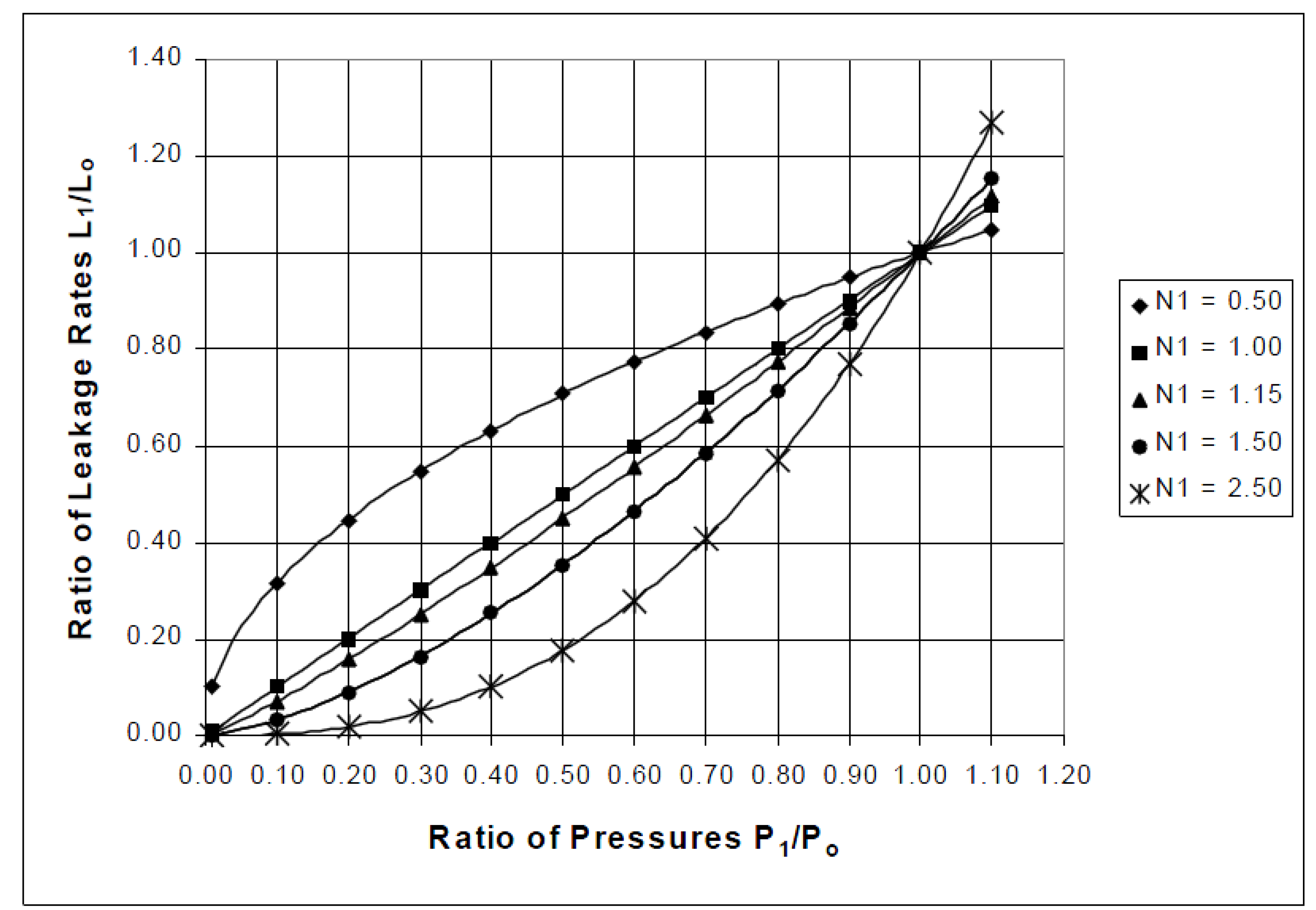
2.3.2. N1 Exponent
3. Results and Discussion
3.1. Water Loss Calculation for Measured Dates
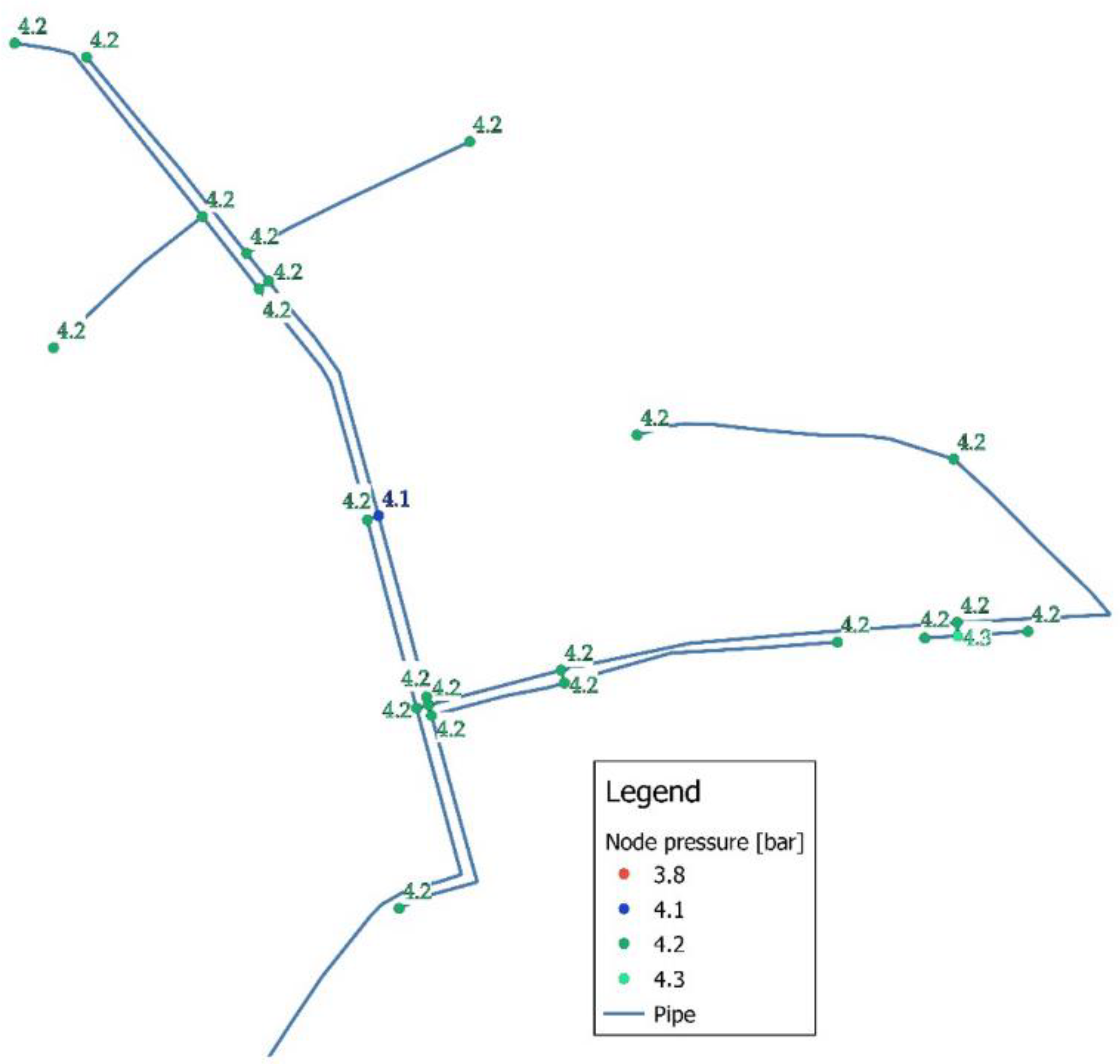
3.2. Calculations of Mean System Pressure
3.3. Calculation of N1 Exponent for FAVAD Method
3.4. Hydraulic Model of Subject WDS
3.5. Result Comparison
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Lambert, A.O.; Thornton, J. The Relationships between Pressure and Bursts—A ‘State-of-the-Art’ Update. IWA Water 2011, 21, 37–38. [Google Scholar]
- Thornton, J. Managing Leakage by Managing Pressure. Water 2003, 21, 43–44. [Google Scholar]
- Samir, N.; Kansoh, R.; Elbarki, W.; Fleifle, A. Pressure Control for Minimizing Leakage in Water Distribution Systems. Alex. Eng. J. 2017, 56, 601–612. [Google Scholar] [CrossRef]
- Lambert, A.O.; Fantozzi, M.; Shepherd, M. Pressure: Leak Flow Rates Using FAVAD: An Improved Fast-Track Practitioner’s Approach. CCWI 2017-15th Int. Conf. Comput. Control Water Ind. 2017. [Google Scholar] [CrossRef]
- May, J. Pressure Dependent Leakage. World Water Environ. Eng. 1994, 17. [Google Scholar]
- Van Zyl, J.E.; Clayton, C.R.I. The Effect of Pressure on Leakage in Water Distribution Systems. Proc. Inst. Civ. Eng. Water Manag. 2007, 160, 109–114. [Google Scholar] [CrossRef]
- Lambert, A.O. International Report: Water losses management and techniques. Water Supply 2002, 2, 1–20. [Google Scholar] [CrossRef]
- Greyvenstein, B.; Van Zyl, J.E. An Experimental Investigation into the Pressure-Leakage Relationship of Some Failed Water Pipes. J. Water Supply Res. Technol.-AQUA 2007, 56, 117–124. [Google Scholar] [CrossRef]
- Fuchs-Hanusch, D.; Steffelbauer, D.; Günther, M.; Muschalla, D. Systematic Material and Crack Type Specific Pipe Burst Outflow Simulations by Means of EPANET2. Urban Water J. 2016, 13, 108–118. [Google Scholar] [CrossRef]
- Piller, O.; Van Zyl, J.E. Incorporating the FAVAD Leakage Equation into Water Distribution System Analysis. Procedia Eng. 2014, 89, 613–617. [Google Scholar] [CrossRef]
- Sebbagh, K.; Safri, A.; Zabot, M. Pre-Localization Approach of Leaks on a Water Distribution Network by Optimization of the Hydraulic Model Using an Evolutionary Algorithm. In Proceedings of the 3rd EWaS International Conference on “Insights on the Water-Energy-Food Nexus”, Lefkada Island, Greece, 27–30 June 2018; p. 588. [Google Scholar]
- Mathye, R.P.; Scholz, M.; Nyende-Byakika, S. Optimal Pressure Management in Water Distribution Systems: Efficiency Indexes for Volumetric Cost Performance, Consumption and Linear Leakage Measurements. Water 2022, 14, 805. [Google Scholar] [CrossRef]
- Taghlabi, F.; Sour, L.; Agoumi, A. Prelocalization and Leak Detection in Drinking Water Distribution Networks Using Modeling-Based Algorithms: A Case Study for the City of Casablanca (Morocco). Drink. Water Eng. Sci 2020, 13, 29–41. [Google Scholar] [CrossRef]
- Cassa, A.M.; Van Zyl, J.E. Predicting the Leakage Exponents of Elastically Deforming Cracks in Pipes. Procedia Eng. 2014, 70, 302–310. [Google Scholar] [CrossRef]
- Price, E.; Ostfeld, A. Battle of Background Leakage Assessment for Water Networks Using Successive Linear Programing. Procedia Eng. 2014, 89, 45–52. [Google Scholar] [CrossRef]
- Boian, R.F.; Macedo, D.O.; de Oliveira, P.J.A.; Janzen, J.G. Comparison between FAVAD and General Equations to Evaluate the Leakage Lost Flow in Urban Water Distribution Systems. Eng. Sanit. Ambient. 2019, 24, 1073–1080. [Google Scholar] [CrossRef]
- van Zyl, J.E.; Lambert, A.O.; Collins, R. Realistic Modeling of Leakage and Intrusion Flows through Leak Openings in Pipes. J. Hydraul. Eng. 2017, 143, 04017030. [Google Scholar] [CrossRef]
- Van Zyl, J.E. Theoretical Modeling of Pressure and Leakage in Water Distribution Systems. Procedia Eng. 2014, 89, 273–277. [Google Scholar] [CrossRef]
- Fox, S.; Collins, R.; Boxall, J. Traditional Leakage Models for Leakage Modelling: Effective or Not? Procedia Eng. 2015, 119, 35–42. [Google Scholar] [CrossRef][Green Version]
- Muranho, J.; Ferreira, A.; Sousa, J.; Gomes, A.; Sá Marques, A. Pressure-Dependent Demand and Leakage Modelling with an EPANET Extension-WaterNetGen. Procedia Eng. 2014, 89, 632–639. [Google Scholar] [CrossRef]
- Schwaller, J.; Van Zyl, J.E.; Kabaasha, A.M. Characterising the Pressure-Leakage Response of Pipe Networks Using the FAVAD Equation. Water Sci. Technol. Water Supply 2015, 15, 1373–1382. [Google Scholar] [CrossRef]
- Tuhovcak, L.; Suchacek, T.; Rucka, J. The Dependence of Water Consumption on the Pressure Conditions and Sensitivity Analysis of the Input Parameters. In Proceedings of the 3rd EWaS International Conference on “Insights on the Water-Energy-Food Nexus”, Lefkada Island, Greece, 3 August 2018; p. 592. [Google Scholar]
- Deyi, M.; Van Zyl, J.; Shepherd, M. Applying the FAVAD Concept and Leakage Number to Real Networks: A Case Study in Kwadabeka, South Africa. Procedia Eng. 2014, 89, 1537–1544. [Google Scholar] [CrossRef]
- Latchoomun, L.; Ah King, R.T.F.; Busawon, K.; Mawooa, D.; Kaully, R.G. Laboratory Investigation of the Leakage Characteristics of Unburied HDPE Pipes. Procedia Eng. 2015, 119, 91–100. [Google Scholar] [CrossRef][Green Version]
- Schwaller, J.; Van Zyl, J.E. Implications of the Known Pressure-Response of Individual Leaks for Whole Distribution Systems. Procedia Eng. 2014, 70, 1513–1517. [Google Scholar] [CrossRef]
- Van Zyl, J.E.; Malde, R. Evaluating the Pressure-Leakage Behaviour of Leaks in Water Pipes. J. Water Supply Res. Technol.-AQUA 2017, 66, 287–299. [Google Scholar] [CrossRef]
- Özdemir, Ö.; Fırat, M.; Yılmaz, S.; Usluer, M. Analysis of the Effect of Pressure Control on Leakages in Distribution Systems by Favad Equation and Field Applications. Water Pract. Technol. 2021, 16, 320–332. [Google Scholar] [CrossRef]
- Marzola, I.; Alvisi, S.; Franchini, M. Analysis of MNF and FAVAD Models for Leakage Characterization by Exploiting Smart-Metered Data: The Case of the Gorino Ferrarese (Fe-Italy) District. Water 2021, 13, 643. [Google Scholar] [CrossRef]
- Lambert, A.O. Ten Years Experience in Using the UARL Formula to Calculate Infrastructure Leakage Index. In Proceedings of the IWA Waterloss 2009 Conference, Cape Town, South Africa, 28–30 April 2009. [Google Scholar]
- WLRandA, L. Water Leakage and Pressure Management. Available online: http://www.leakssuite.com/concepts/favad/ (accessed on 5 February 2019).
- Fantozzi, M.; Lambert, A. Residential Night Consumption–Assessment, Choice of Scaling Units and Calculation of Variability. In Proceedings of the IWA Water Loss Conference, Manila, Philipp, 26–29 February 2012; pp. 26–29. [Google Scholar]
- Loureiro, D.; Borba, R.; Rebelo, M.; Alegre, H.; Coelho, S.T.; Covas, D.I.C.; Amado, C.; Pacheco, A.; Pina, A. Analysis of Household Night-Time Consumption. In Proceedings of the 10th CCWI, Conference: Integrating Water Systems, Sheffield, UK, 1–3 September 2010; pp. 557–562. [Google Scholar]
- WSAA. Targeting Leakage Using Nightflow Measurements. In Guidlines by Wide Bay Water Corporation; Australia and Water Loss Research & Analysis Ltd.: Halifax, UK, 2011; pp. 1–29. [Google Scholar]
- Costanzo, F.; Fiorini Morosini, A.; Veltri, P.; Savić, D. Model Calibration as a Tool for Leakage Identification in WDS: A Real Case Study. Procedia Eng. 2014, 89, 672–678. [Google Scholar] [CrossRef][Green Version]
- Lambert, A.; Fantozzi, M.; Thornton, J. Practical Approaches to Modeling Leakage and Pressure Management in Distribution Systems–Progress since 2005. In Proceedings of the 12th International; Available online: https://www.semanticscholar.org/paper/Practical-approaches-to-modeling-leakage-and-in-Lambert-Fantozzi/f74b9452b8a0457af3c466867ea63b00df6d37dd (accessed on 2 May 2022).

| Crack Type | N1 Exponent for Pipe Materials | ||
|---|---|---|---|
| PVC | Asbestos–Cement | Iron | |
| Round hole | 0.524 | - | 0.518 |
| Longitudinal cracks | 1.38–1.85 | 0.79–1.04 | - |
| Circumferential cracks | 0.41–0.53 | - | - |
| Corroded hole | - | - | 0.67–2.3 |
| Date and Time | Pressure Setting (Bar) |
|---|---|
| 20 December 13:00 h | 4.0 |
| 21 December 15:00 h | 3.0 |
| 22 December 15:00 h | 2.0 |
| Measurement Day | RNC (A) | Night Flow (B) | Water Loss (C = B − A) |
|---|---|---|---|
| 21 December | 0.112 | 0.320 | 0.209 |
| 22 December | 0.250 | 0.139 | |
| 23 December | 0.140 | 0.029 |
| PRV Setting Mark | Average Flow (l/s) | Model Time | Mean System Pressure (Bar) | Water Loss (l/s) |
|---|---|---|---|---|
| PRV1 | 0.958 | 7 h | 3.9 | 0.209 |
| PRV2 | 1.040 | 23 h | 3.1 | 0.139 |
| PRV3 | 1.013 | 43 h | 2.0 | 0.029 |
| Variable | Value |
|---|---|
| L1 | 0.139 |
| L0 | 0.209 |
| P1 | 31.5 |
| P0 | 39.7 |
| N1 | 1.76 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dundović, I.; Tadić, L. A Field Experiment Verification of Theoretical Exponent N1 for FAVAD Method in Defining the Relationship of Pressure and Water Losses. Water 2022, 14, 2067. https://doi.org/10.3390/w14132067
Dundović I, Tadić L. A Field Experiment Verification of Theoretical Exponent N1 for FAVAD Method in Defining the Relationship of Pressure and Water Losses. Water. 2022; 14(13):2067. https://doi.org/10.3390/w14132067
Chicago/Turabian StyleDundović, Igor, and Lidija Tadić. 2022. "A Field Experiment Verification of Theoretical Exponent N1 for FAVAD Method in Defining the Relationship of Pressure and Water Losses" Water 14, no. 13: 2067. https://doi.org/10.3390/w14132067
APA StyleDundović, I., & Tadić, L. (2022). A Field Experiment Verification of Theoretical Exponent N1 for FAVAD Method in Defining the Relationship of Pressure and Water Losses. Water, 14(13), 2067. https://doi.org/10.3390/w14132067







