1. Introduction
According to the Romanian legislation, the water dams are designed and verified at the values of the maximum water discharges with different probabilities of being exceeded [
1], depending on the importance class of the dams [
2].
Rigorous determination of these maximum flows is of particular importance given the costs and risks associated with these types of hydrotechnical works, especially in the context of climate change. The availability of hydrological data from the last period allows the recalculation of maximum flows for the imposition of constructive/non-constructive measures regarding the increase of the capacity of large water discharges.
For a better prediction of floods and the adoption of appropriate mitigation and protection measures, it is essential to know the hydrological and hydraulic characteristics of watercourses [
3].
The current legislation [
4] requires a correlation with international recommendations and modern practices, as well as the implementation of computer applications for the normative, to be used by engineers without advanced knowledge of mathematics and computer science.
In Romania, the method of ordinary moments (MOM) is established, but taking into account the fact that hydrometric monitoring is deficient, in most cases, the data series are not older than 25 years, and it is necessary to achieve a regionalization based on the L-moments method [
5,
6], which is generally a method less influenced by the length of the data series and the existence of extreme values. Another solution is the use of partial series (POT), which is much more laborious to achieve, requiring additional checks of data independence and criteria for establishing threshold values [
7,
8,
9].
The comparative presentation, in this article, of the two methods for estimating the parameters, MOM and L-moments, for certain distributions used in Romania and correlated with international regulations [
10,
11,
12] represents a starting point in achieving a regionalization based on the L-moments method. It should be emphasized that the L-moments method has not been presented, analyzed and applied to specific hydrography in Romania. Switching to the L-moment can be done by linear regressions between the coefficient of variation based on the MOM (C
V) and the coefficient of variation based on L-moments (L-C
V), HC
S and L-C
S, where HC
S is Hazen’s unbiased skewness or C
s adopted depending on the genesis of the flows, and L-C
S is the L-moment’s skewness. The genesis of the flows represents the generating mechanism of the maximum flows given by the spatio-temporal conditions of the precipitations and the physiographic characteristics of the hydrographic basin [
13,
14,
15].
This article analyses Pearson III, the most used three parameters of statistical distribution in Romania (parent distribution), as well as LogPearson and GEV distributions, which are recommended by the Romanian legislation [
4]. In addition to these distributions, two distributions commonly used internationally are analyzed and applied, the LogNormal and the Wakeby distributions [
5,
10,
11,
12,
16,
17,
18,
19]. This article describes the latest methods for estimating distribution parameters using engineering mathematics software, by presenting, for the first time, some expressions of the functions, moments and frequency factors, facilitating the ease of use of these distributions.
Thus, novelty elements, such as the Pearson III expressions of the probability density function using the dgamma built-in function, the cumulative probability function using pgamma and pchisq built-in functions, the quantile function expressed with qgamma and qchisq functions and the form of the L-skewness coefficient expressed with ibeta and pbeta built-in functions; the LogPearson III expressions of the probability density function using the dgamma function, the cumulative probability function using the pgamma function, the quantile function expressed with the qgamma function, the form of the three L-moments and the expression of the frequency factor; the GEV expression for the third L-moment; the LogNormal expressions of the probability density function using the dnorm built-in function and dlnorm function, the cumulative probability function (using pnorm, plnorm and cnorm functions) and the expressions of the three conditions for L-moments using the quantile function and the Wakeby expressions for high order moments and the frequency factor.
All of these novelty elements help hydrology researchers understand and apply the processes behind dedicated softwares, in which they select some options without knowing the mathematics behind them. We consider that the use of these kinds of softwares (not knowing the mathematics behind them) is not beneficial in the long run.
2. Flood Frequency Analysis—Determination of Maximum Flows
In Romania, the series of maximum flows used to estimate the parameters of statistical distributions are those of the annual maximum series (AM). A disadvantage of this series is that the values resulting from the theoretical distributions are conservative and, in some cases, exaggerated, especially in the field of low probabilities, and there are underestimated values for exceeding probabilities higher than 80%. The probability of exceeding 80% has a special importance because, according to Romanian legislation Order no. 326/2007, it represents a criterion for determining the bankfull channel. Currently, according to Romanian legislation Order no. 2.115/2021, the annual probability of exceeding 50% is used, but it is too high for mountain river areas.
The annual maximum series consists of the values of the maximum flows characterizing each hydrological year. The advantage of this analysis is the certainty of data independence. Large datasets with length n ≥ 20 [
12,
13,
14,
15] are required for these analyses. Based on these considerations, it is necessary to impose an analysis based on the L-moments method.
The determination of the maximum flows was carried out in stages, according to
Figure 1. The verification of the character of outliers, normality and homogeneity were carried out in the data-curation phase.
In the next section, the theoretical distributions used in this article for the calculation of the maximum flows are presented [
5,
16,
17,
19]. Only the notation of MOM and L-moments will be used to represent the two methods of estimating the parameters of statistical distributions.
2.1. Pearson III Distribution (PE3)
Pearson III distribution is a particular case of the four-parameter exponential gamma distribution (FPEGD) under the condition of b = 1. The probability density function of FPEGD is [
20]:
The probability density function,
; the complementary cumulative distribution function,
, and quantile function,
, of the Pearson III distribution are:
where
are the shape, the scale and the position parameters, with conditions
if
or
if
and
;
represent the mean and standard deviation.
Appendix C presents the built-in mathematical functions in Mathcad.
2.2. LogPearson Distribution (LP3)
The probability density function,
; the complementary cumulative distribution function,
, and the quantile function,
, of the LogPearson distribution are:
where
are the shape, the scale and the position parameters. For case
, the quantile takes the form of
.
2.3. Generalized Extreme Value Distribution (GEV)
The probability density function,
; the complementary cumulative distribution function,
, and the quantile function,
, of the GEV distribution are [
17]:
where
are the shape, the scale and the position parameters;
if
, and
if
.
2.4. LogNormal Distribution (LN3)
The probability density function,
; the complementary cumulative distribution function,
, and the quantile function,
, of the LN3 distribution are:
where
are the shape, the scale and the position parameters;
represent the mean and standard deviation. There are also other forms of expression of the functions [
16,
17,
19].
2.5. Four-Parameters Wakeby Distribution (WK4)
The four-parameters Wakeby distribution represents an alternative to the LogNormal distribution. The four-parameters Wakeby distribution has no form for density and cumulative function, being classified as a quantile function.
The quantile function of WK4 distributions is [
5,
17]:
where
are the scale parameters, and
are the shape parameters.
4. Confidence Intervals
In the previous Romanian normatives, the statistical distributions were selected that for probabilities of exceeding less than 0.1%, the values did not exceed ±20% of the value determined by genetic methods [
1]. This approach is difficult to apply, because there are no well-founded hydrological syntheses and regionalizations that are valid for this domain of small probabilities. Thus, it is recommended to use a reference distribution, which is scientifically confirmed over time, and to report on it using the confidence interval. The confidence interval for the MOM is defined, in the World Meteorological Organization (WMO 718) [
10], for a statistical distribution, as the 90% confidence level. This assumes that the confidence interval is variable depending on the exceedance probability and standard error specific to each statistical distribution. The confidence limits represent the upper and lower bounds of the interval. The confidence interval can be expressed in three ways: with the frequency factor (
), with the standard error of the theoretical distribution or based on the Kite equation [
17].
In this article, only the confidence interval based on the frequency factor is analyzed, due to the ease of application in a normative.
where
is the frequency factor of the theoretical distribution, and
is the confidence level;
represents the arithmetic mean, and
is the standard deviation.
The frequency factor of theoretical distributions analyzed for MOM is:
- -
Pearson III:
The frequency factor can also be expressed with the qchisq function or, for approximate solutions, using the Kite, Wilson Hilferty of Cornish–Fisher frequency factor [
17].
- -
LogPearson:
- -
Generalized extreme value distribution (GEV):
- -
LogNormal distribution (LN3):
- -
Wakeby distribution (WK4):
For situations where the quantile is derived by only two parameters, which generally refer to the mean and the dispersion, a standard error is obtained depending on the CV. The confidence interval obtained is a simplification, being easy to determine and narrow (small). The confidence interval with the derivation of skewness is very wide for low probabilities. Because, in Romania, the skewness is chosen according to the genesis of the maximum flows, it is recommended to apply the confidence interval that does not take into account the errors given by the skewness. In Romania, the confidence interval (depending on the standard error) can be defined with the Pearson III distribution by choosing the skewness coefficient from regionalization studies regarding the origin of the maximum flows.
6. Discussion
For the current situation of hydrology in Romania, it is recommended to estimate the parameters by the MOM, because there are studies, including regionalization, based on the coefficient of variation and skewness. The transition to L-moments or LH-moments [
30] can only be done after regionalization studies are conducted based on the L-moment ratio diagrams, which requires considerable but necessary efforts.
In this article, the maximum flows were determined for two rivers that have different origins of their maximum flows, through the MOM and L-moments, using statistical distributions suitable for Romania. The data series of maximum annual flows, according to Bulletin 17C [
12], must have a minimum of 20 records. In the case of the Prigor river, the data series has a length of 21 records, and in the case of the Ialomita river, the data series has a length of 33 records.
Pearson III was chosen as the reference statistical distribution for the case studies. This was chosen for two reasons: the long-term use in Romania and the values close to the L-moments method with the MOM. The relative mean error (RME) and the relative absolute error (RAE) criteria [
31] were used to compare the results, as well as the framing of the quantile values in the confidence interval of the reference distribution.
where
represent the sample size, the observed value and the estimated value for a given probability.
The validation of some distributions using these two criteria is not recommended, because they are determined by the differences only in the probability domain of the observed values, so it is recommended to approach validation with the criterion of the confidence interval for the MOM. The results of the performance indicators for L-moments were presented to note that their values were very small, but the significance was not valid.
For the Prigor river, where there is certainty of the natural registration of hydrometric data, the results were similar in the case of estimating the parameters with the MOM, with all distributions falling within the confidence interval of the reference distribution. For the L-moments method, all distributions fell within the confidence interval up to the probability of exceeding 0.1%, except for the GEV, which fell within 0.5%. Poor results for low probabilities are too influenced by small annual maximum flows in the case of a short data series [
30].
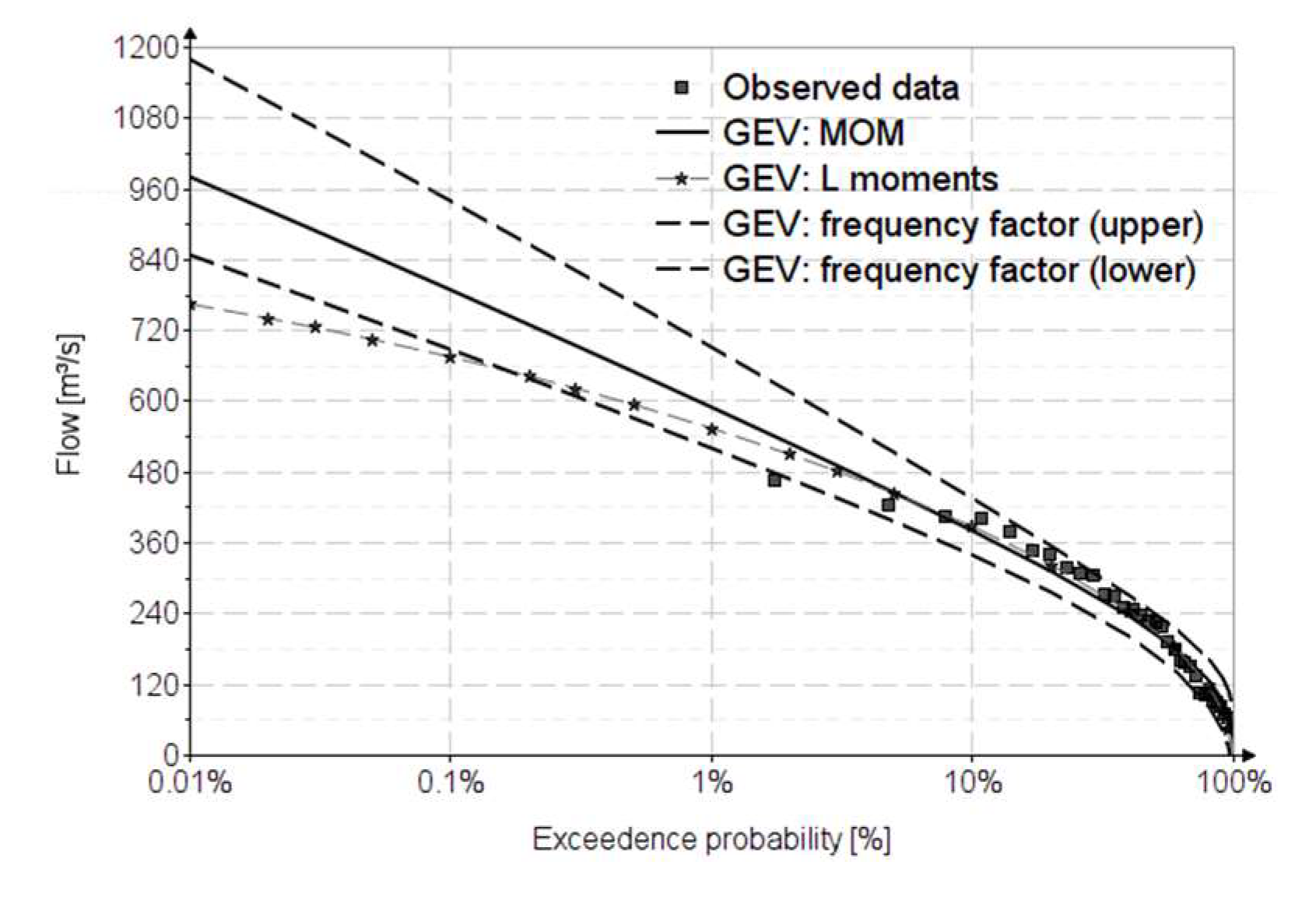
Figure 13 shows the statistical distributions analyzed compared to the chosen reference distribution for the Prigor case study.
For the Ialomita river (Tandarei hydrometric station), the observed data were in the influenced regime, and the reconstruction of the data in the natural regime was with relatively large errors. In general, for large river basins and long river lengths, especially in low-altitude areas, there is also a high degree of natural attenuation of maximum flows. Furthermore, in this case, the results with the MOM were in accordance with NP 129/2011, all falling within the confidence interval of the reference distribution. For the L-moments method, the Wakeby, Log-Pearson and GEV distributions gave different shapes, possibly due to the high degree of attenuation of the maximum flows, with there being a threshold of the maximum values at low probabilities.
Figure 14 shows the statistical distributions analyzed compared to the chosen reference distribution for the Ialomita case study.
In the case of the Prigor river, the L-skewness (τ
3) and L-kurtosis (τ
4) values of the observed data did not differ much from those of the characteristic values of the τ
4–τ
3 variation of the analyzed theoretical distributions (
Figure 15). Thus, all analyzed distributions had a similar graphic appearance.
The resulting values for τ
3 and τ
4 for the two rivers are presented in
Table 9.
In the case of the Ialomita river, the τ
3 and τ
4 values of the observed data differed greatly from those of the characteristic values of the τ
4–τ
3 variation of the analyzed theoretical distributions. Thus, for the three-parameter distributions, with the calibration being done only as a function of τ
3, the L-kurtosis τ
4 took values consistent with the variation of τ
4–τ
3 of the theoretical distribution, disregarding the τ
4 of the observed data, because for larger moments, they became unstable, making the resulting values unrealistic [
32]. The Wakeby distribution is a distribution that was introduced in the flood frequency analysis in order to fulfil the “separation effect”, described by Matalas et al. 1975 [
33], as much as possible, namely, to carry out an analysis so that the maximum flows were not excessively influenced by much of the small flows. The Wakeby distribution separates the right-hand side from the left-hand side of the distribution [
33]. The Wakeby distribution has the property of a very thick left-hand tail (high flows) and a right-hand tail that is thick (small flow) enough to decrease the average skew [
33], which makes the middle part of the distribution steeper than traditional skewed curves.
In the case of the four-parameter Wakeby distribution, the resulting values of the parameters matched those of a particular case of the distribution, namely, the generalized Pareto [
17]. Thus, in the particular case of the Ialomita river dataset, the Wakeby distribution turned into the generalized Pareto distribution, which has the expression of the quantile function, as follows:
The term on the right of the Wakeby quantile has a constant value of −40.9 m3/s, which, due to the “–“ sign in front of the term, acquires positive values. The value of this term represents the value of the position parameter γ from the Pareto quantile, with the rest of the terms remaining unchanged. It can also be seen on the graph that the value of τ4 corresponding to τ3 is that of the particular Wakeby distribution, namely, the generalized Pareto, respecting the τ4 of the observed data.
In the case of the Log-Pearson distribution, calculated based on the moments obtained from the density function, it had a similar appearance to the Wakeby distribution, but the latter had, in some cases, better results [
32]. The τ
4–τ
3 variation in the case of the LogPearson (
Figure 16) distribution was varied depending on the asymmetry values in the log space [
34].
The graphs between τ
3 and τ
4 also represent a criterion for choosing the best distributions to use in achieving a regionalization based on L-moments [
5,
17].
7. Conclusions
This article briefly described the most used statistical distributions for the maximum discharge and the latest methods for estimating the distribution parameters using engineering mathematical software.
The use of the Pearson III distribution in Romania must be maintained for the MOM, because the estimation of the parameters was simple and gave good results. A statistical distribution that can be a good alternative to Pearson III is LogNormal (LN3), being the most widely used distribution in Europe for maximum flows [
10,
24].
The introduction of other statistical distributions should be done after the regionalization studies are conducted, and it should be a simpler alternative, if this proves to be the case.
The method of estimating the parameters must remain the method of ordinary moments, because it has proven to be effective for Romania. The adoption of other estimation methods (L-moments) is useful but requires a long transition period, in which the two methods must be used in parallel.
In the regulations for calculating the maximum flows, it is recommended that statistical distributions should be presented in full, i.e., the functions of density, distribution and quantile, where they exist, as well as the inclusion of computer applications for estimating the parameters of statistical distributions and calculation examples.
The calibration of the three-parameter distributions is easy with the method of ordinary moments. Since asymmetry does not characterize short data strings, it is generally correct, highlighting two methods. A method of correcting the asymmetry according to the genesis of the data was presented in this article, which is based on choosing the asymmetry as a multiple of the coefficient of variation. Another method is to use skewness correction coefficients depending on the relatively short length of the observed data string. A disadvantage of this method is that it is not possible to calibrate the kurtosis function (non-linear function), because it has large differences for a sample compared to that of a population.
The L-moments for the samples were very close to those of the population; thus, no correction of τ
3 and τ
4 was necessary, being thus more robust and less influenced by the effects of sampling variability [
5] due to the fact that the L-moments are linear functions. The use of a four-parameter distribution allows calibration as a function of τ
3 and τ
4, which is an advantage in achieving a regionalization based on L-moments.