Three-Dimensional Engineering Geological Model and Its Applications for a Landslide Site: Combination of Grid- and Vector-Based Methods

Abstract

A three-dimensional engineering geological model (EGM), which provides an approximation of the geological conditions, is a key element in any engineering project. The slope at Huafan University, Mt. Dalun, in the Western Foothills of northern Taiwan, is a dip slope that has been assumed to be unstable. The bedrock is mainly composed of intercalated sandstone and shale, where the thickness of the sandstone varies from thin to massive, interbedded with shale from the Miocene age. By interpolating the thickness of the colluvium derived from borehole data and analyzing the contours of the interpolation surface result, we find that the landslide material accumulates at the slope foot, towards the southwest in the direction of movement. Due to tectonic control—in particular, considering the two local faults that pass through the study area—the strata’s orientation significantly changes over the studied slope. As a basis for the 3D EGM, polynomial surface fitting is applied for detailed analysis of the sub-surface geological structure, as well as to compute the regressive orientation of the bedding plane derived from the borehole data. Based on the calculated regression plane passing through the elevations of the geological interface (key bed), the results indicate that the regression plane’s direction is consistent with the outcrop measurements. Moreover, several cross-sectional profiles are considered to visualize and clarify the 3D EGM. Finally, surface and sub-surface monitoring data are compared with the result, in order to refine the 3D EGM. The proposed geological model is expected to contribute to the comprehensive understanding of gravitational slope deformation, and may serve as a guideline to minimize potential disasters.

1. Introduction

An engineering geological model (EGM) is, according to the IAEG C25, an approximation of the geological conditions created for the purpose of solving an engineering problem [1], and it is an element of utmost importance in an engineering project [2].

Traditionally, geological maps and geological profiles are used as geological models, representing the sub-surface 3D structure in a two-dimensional manner [3], in order to communicate complex spatial geological information [4]. However, it is quite difficult for a broader audience without extensive geological knowledge to conceive of and comprehend sub-surface geological information through a two-dimensional (2D) view. Although skilled geologists know how to translate 2D information into three-dimensional (3D) information qualitatively or conceptually, inaccurate and sometimes incorrect translation may still occur [5]. Moreover, limited geological profiles are not necessarily coincident with the critical cross-sections that are important to a given engineering project. The shortcomings of this traditional presentation mode include: (1) Being unfavorable for communication between geologists and engineers, due to the knowledge gap; (2) when hard data (e.g., outcrops or boreholes) are lacking, it is difficult to obtain the geological profiles required for engineering design; (3) difficulties in constructing the 3D geometry for 3D numerical simulations; and (4) the monitoring results may be hard to interpret. Therefore, a 3D EGM may essentially contribute to better sub-surface understanding in engineering projects such as natural hazard assessment, underground work planning, hydrogeological analysis for aquifer recharge assessment, and so on [6]. Such 3D EGMs play a significant role in visualizing and communication, synthesizing all available data, and providing more accurate representations of specific geological conditions or simulating stratified geology [7,8,9], as well as allowing engineering geologists to test the validity of geological assumptions or hypotheses.

Three-dimensional EGMs have widely been used over the past 40 years, mainly in the hydrocarbon and mining industries [10]. They have also been used extensively for groundwater flow modelling (see, e.g., [11,12,13], especially for Quaternary sedimentary rocks. Although quite a few studies have applied 3D EGMs for civil engineering purposes in urban areas (e.g., [6]), 2D EGMs are still used for most landslide studies. The more efficient 3D EGMs, however, have recently been increasingly used in landslide research; for example, to reconstruct the spatial structure of a landslide [14,15], or to integrate the 3D geology of sub-surface geometry and properties to visualize landslide susceptibility and evaluate the risk of natural landslides [16,17,18]. Moreover, Gu et al. [18] have calculated the stability of each unit after establishing a 3D EGM to generate regional slope stability. Li et al. [19] have created a 3D EGM of a landslide, in order to assess the relationship between landslide deformation and groundwater level change beneath the sliding surface. The application of a 3D EGM in geologically vulnerable areas that might lead to disaster landslides is necessary, as the potential presence of peculiar geological properties influenced by the geometry of the bedrock and overlying soil can create unstable slopes, leading to a reduction in the resistance forces that retain them. The geological features and structures are the most important factors in the movement development of a rock mass [20]. Landslide deformation patterns and the processes that cause them can be determined through analysis of the geometry of the bedrock, the interior layers, and the slip surfaces [21,22], which can be detected from a 3D EGM. However, studies considering the monitoring and mitigation of landslides based on a critical 3D EGM remain rare, and determination of the surface or sub-surface displacement of slope mass is still a difficulty. Therefore, there is not yet any meaningful cohesiveness in the relevant literature.

Three methods can be used to model a 3D EGM of sedimentary rocks [3]: (1) Using borehole observations to create a triangle defining a surface. In geographic information system (GIS) terms, this is a triangulated irregular network (TIN); (2) by applying any of several surface-generation and contouring procedures to the borehole observations; or (3) by developing a series of parallel or intersecting interpretive cross-sections between boreholes, in order to better control the surface geometries. These surfaces can be modelled using grid-based methods [13] or vector-based methods [23]. Generally, the geological data derived from borehole or stratigraphic sections are processed to form discrete points. To make full use of these points, a grid-based method with geological contour can be carried out in the map [24]. Grid-based methods use a mesh that is either regularly spaced (triangular, square, or rectangular), or has angular grids that are consistently spaced. Grid layering is used to simulate planes (e.g., paleo-depositional surfaces or bedding planes, which should possess continuity). In particular, a GIS grid-based data model may be used to describe slope-related items such as strata, sliding surfaces, and groundwater-surface in 3D slope models in slope stability research [25]. Additionally, the bounding surface in vector-based methods computes the elevations of the contour surfaces utilizing complicated geo-modelling computations. This means that each contour line must be properly digitized, in the form of (X, Y) pairs along each contour line of specified elevation [26] (Moore et al., 1993). The vectorial foundation of the model structure is very adaptable and reasonably simple to modify computationally. Hence, a complete modelling system that integrates grid- and vector-based methodologies to stimulate the natural geological structure is required. These combined capabilities provide the essential framework and a degree of trust for a 3D EGM.

To build a reliable 3D model, all accessible geological data should be reconciled [27]. Borehole data can clearly reveal the stratification of the underlying rock, allowing for direct observation of samples [3], and are currently utilized to create 3D EGMs [7,13]; however, the construction of a 3D EGM is still a challenging task for engineering geologists.

In this study, an example of an ancient, recently re-activated landslide is presented, in order to argue the necessity of a 3D EGM for its comprehensive understanding. The 3D model building process calls for complex feedback between the interpretation of the data (observational model approach) and the model (conceptual model approach). In the interpretation, the 3D framework forces us to make interpretive decisions that would be left on the side in map-based or cross-section interpretations [5]. The slope on which Huafan University, in the Mt. Dalun region of Taiwan, is located, has been identified as a possible unstable dip slope. Numerous site investigation projects have been carried out, in order to understand the sub-surface geology and possible landslide mechanisms. There are almost 50 drilling boreholes from diverse sources. Moreover, extensive monitoring systems including surface and sub-surface displacement measurements, groundwater table measurements, and rainfall measurements, indicating a creep phenomenon in the study area [28,29,30]. However, the monitoring data are mainly compared with geological profiles or plan view of the landslide boundary in a two-dimensional manner. Although 3D numerical modelling has been conducted [29], the sliding surface determined from inclinometer was used to define the model boundary without incorporating a 3D EGM. The design of drainage wells, which has been carried out by a local consultant company, was also based on two-dimensional information. This indicates that previous studies have not provided a comprehensive geological model for the entire area, in the form of a 3D EGM. Therefore, the 3D EGM presented in this paper provides a comprehensive geological model for the sloping area, which can help to determine the potential landslide extent. This is crucial for anticipating the failure mechanism and assessing the slope’s stability; it may also serve as a guideline for future civil engineering and geotechnical methods aimed at preventing landslides.

2. Study Area

Mt. Dalun is located in northern Taiwan’s Western Foothills belt. The Huafan University campus is built on the upper part of the mountain, and it is elevated between 240 and 580 m above sea level. This location is the headstream of the Pengshan River (Figure 1).

According to the 1:50,000 geological map published by the Central Geological Survey of Taiwan [31], the main exposed strata near the study area are those of the Mushan Formation (Ms) in the early Miocene age. One of the prominent lithological features is “white sandstone” (orthoquartzite). These sandstones are mainly composed of quartz, indicating a continental shelf sedimentary environment. The sandstones in the Mushan Formation are fine- to coarse-grained, mostly in thick or massive layers with thicknesses of 8–20 m, and usually have an obvious cross-bedding sedimentary structure. Grayish black shale or thin beds of sandstone are well-developed, often alternating with thick sandstones to form interbeds [28]. The bedding plane with the strike of the rock is roughly in the east–west direction, and is inclined between 10° and 20° to the south, being consequent to the topographical slope [29,31].

There are three major faults in the study area: The Hsiaokotou Fault, the Chuchih Fault, and the Tungshihko Fault. The Hsiaokotou and Chuchih Faults are thrust faults with a strike along ENE–WSW, trending and dipping to the southeast. The fault traces are intercepted by the left-lateral, strike-slip Tungshihko Fault with NE trend.

The geological structure and local lithology have determined the topographical features in the study area. The topography is defined by mountain ranges in the form of a bowl that trends northeast–southwest and has a surface slope of 20–25°. The catchment area in Mt. Dalun is represented by the mountain ridgelines that resemble the shape of a bowl on the terrain. The surface runoff within the mountain ridgelines flows down to streams, consisting of nature erosion gullies (marked as blue lines in Figure 1) on the slope surface.

By means of thorough site investigations, Jeng and Sue [28] have documented two minor faults which influence the local geological structure: (1) The Nanshihkeng Fault is a thrust fault with trace trending northeast and with a fault plane dipping 60–70° to the southeast; and (2) the A Fault is an oblique-slip fault truncated by the Nanshihkeng Fault. The strike is roughly NW–SE and dipping to the south with a dip angle of 65–70°. The A Fault is likely a normal fault with a left-lateral slip component, with its footwall relatively throwing up. Two sets of joints cut the bedrock, whose strikes are average NW–SE and NNE–SSW, thus being roughly parallel to the two local aforementioned faults [29].

Based on the results of the site investigation [28], the bedrock of the study area is overlaid by colluvium (slope wash), thick (more than 40 m) ancient landslide deposits (to the southeast of the study area), and artificial fill materials (ranging from 10 to 20 m). Due to the thick colluvium and fill materials, rock outcrops in the study area can only be found in eroded creeks or on the artificially excavated surfaces. In areas with thick landfill (e.g., the northeastern part of the study area), such as the sports ground and basketball court of Huafan University, surface displacement is significant due to inadequate compaction of the filled land or sliding along the bottom of the landfill [28,30]. These creeping areas revealed multiple listric sliding surfaces [30].

Due to the unstable slope and existing landslide potential in Mt. Dalun region, a monitoring system has been in operation since 2000, in order to determine the slope failure mechanism and to enhance the effective risk management. This includes inclinometer casings, standpipes for groundwater pressures, rainfall gauges, and a nail network for surficial deformation of the slope. To measure the sub-surface displacement and possible depth of sliding surfaces, every inclinometer casing in the borehole is recorded every month. Every six months, a network of monitoring points on the slope surface enables the measurement and monitoring of surficial displacement. It is possible to link changes in slope displacement to changes in the groundwater table and the magnitude of earthquakes by monitoring these variables after heavy rainfall or earthquakes. In addition, a countermeasure system has also been implemented in order to diminish the slope moment and to prevent the failure of the slope, including a drainage system and ground anchors. The installed drainage systems, comprising catch pits and trenches for collecting groundwater, have been carried out by a local consultant company, in order not to allow the water table to increase and submerge the sliding surface. In the future, it may be necessary to expand the number of drainages to ensure the safety of the slope.

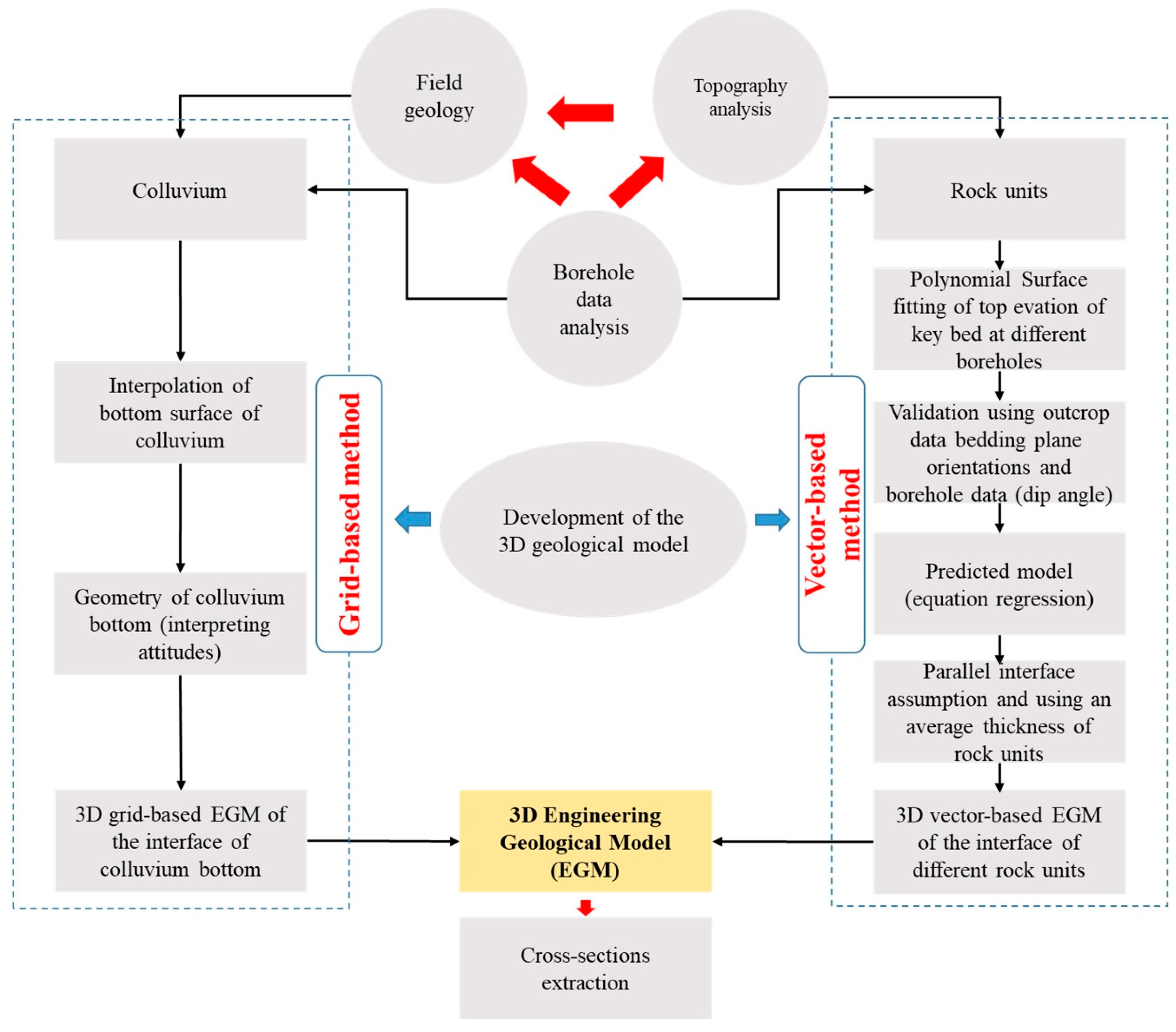
3. Methodology to Develop a 3D EGM

The data used to develop the 3D EGM included: (1) field works; (2); interpretations of borehole cores; and (3) airborne LiDAR data. The field data included existing ground-surface geological map provided by numerous geologists, publicly available data collected by companies over dozens of years [28,30], and field investigation data obtained during field trips Mt. Dalun. The approach is described in detail below, following the flow chart depicted in Figure 2.

3.1. Topography Analysis

Based on a high-resolution (1 m) LiDAR DEM, a topographic map of the study area was generated with contour line interpretation. Moreover, the large-scale topographic features, such as geological structures, scarp, hummocky topography, and gully paths could be detected. We also analyzed the terrain in an attempt to anticipate the distribution of sandstone outcrops.

3.2. Field Investigation

The field investigation was a critical step to identify the interface between the colluvium and bedrocks, the boundaries of rock units, and bedding planes’ orientation. We divided the field investigation into two stages. The first stage was a general overall view of the slope, including a preliminary assessment of terrain features and landforms and collecting outcrop information along the road in the eastern part (Figure 1). We examined classifications of lithological unit, discontinuity features, rock masses, and deposits on outcrops. In the second stage, we investigated the fields along the Pengshan River, near the toe of the slope, in order to evaluate the rock outcrop lithology for certain characteristics of rock unit classification, and investigated the dipping direction of the exposures of sedimentary strata on both sides of the riverbed. This work aims to confirm whether the type of exposure belongs to the in situ rocks or moving blocks that were deposited after ancient landslides in the past. The information gained from the field investigations and the geological map provide basic data for the establishment of a geological model in the study area. In addition, the field investigation aimed to re-examine and compare our geological records with those obtained in earlier investigations.

3.3. Borehole Data Analysis

The 3D EGM developed in this study was mainly based on the stratigraphic column interpreted from rock cores. Drilling data from 50 boreholes of various depths were utilized for the analysis. The main process of borehole data analysis was as follows:

(1)

Borehole data quality check. To begin, we thoroughly checked the reported locations and elevations of the boreholes, in order to ensure the correctness of the basic information. If the X and Y input values were inaccurate, the elevation of each borehole will be changed significantly, such that the elevation of the rock unit boundary will also be misjudged. The TWD97 TM2 (i.e., Taiwan Datum 1997, 2-degree Transverse Mercator) coordinate system was employed in this work, in order to ensure data coherence. As a result, this step is critical for further analysis. We used the LiDAR DEM to obtain the elevations (i.e., Z values) of the boreholes at given horizontal coordinates (i.e., X for E–W direction and Y for N–S direction), and compared them with the documented elevations of boreholes. In addition, the quality of the rock core must not have been significantly impacted by weathering (i.e., preserved in fresh bedrock) or shearing or fracturing by tectonic processes. We preferred boreholes with an adequate depth, which permit comparisons between a sequence of units in different boreholes. Only the boreholes that passed this checking step were used for subsequent 3D EGM development. In this way, we ensured that only reliable borehole data were considered prior to the following steps.

(2)

Rock unit classification. The fundamental interpretation consisted of lithology identification and rock unit boundary determination. Sandstone (SS) and thin alternating layers of sandstone and shale (SS and SH, respectively) constitute the main lithology in the study area. The sedimentary features of rock units, such as whitish sandstone, particularly form thick or massive layers. The grayish-black shale and thin interbeds of sandstone and shale are also well-developed, often alternating with thick sandstones [28]. The sedimentary sequences were considered when we analyzed the rock cores; in particular, we considered a sequence of continuous rock units throughout the borehole, as opposed to focusing on a single rock unit (i.e., homogeneous in a sequence of rock units). Lithostratigraphic bodies were distinguished by distinct lithological minor structures, such as lamina and flaser structures, as a criterion for determining the sedimentary sequence. The proportion of sandstones and shales was used to classify the alternated layers of sandstone and shale into different rock units. The descriptive reference proportions are:

(I)

Interlayer 1:1 ≤ Mj:Mn ≤2:1,

(II)

Interbedded 2:1 ≤ Mj:Mn ≤ 4:1,

(III)

Occasionally 4:1 ≤ Mj:Mn ≤ 8:1,

(IV)

Main lithology 8:1 ≤ Mj:Mn,

where Mj denotes major lithology and Mn denotes minor lithology.

We summarized all the descriptive properties of the rock, and then split the observation data into two separate parts: colluvium on the top, and sedimentary rock beneath each drilling borehole.

(3)

Comparison between rock units from different boreholes. In the advanced step, we conducted a comparison of the lithology from the 26 complete boreholes among the 50 boreholes in the study area, in order to prepare the necessary material for the building of the geological model. To make the comparisons accessible and reliable, we started with the boreholes that were close to each other. We grouped the boreholes together and compared the lithology of the strata. We assumed that the features of the strata lithology of these boreholes should be the same; however, the boreholes were distributed sporadically and also outside the campus on the downward slope. Both petrographic properties and the distribution of boreholes had changed slightly. When the rock cores were compared to each other, this aspect also had been carefully considered. There are comparison criteria that may be depended upon to ensure reliability. In this context, sedimentary characteristics, including the texture and internal structures created by bioturbation and bio-erosion, are essential for classifying rock units to build correlatively connected boreholes. Furthermore, every objective layer’s thickness must have minimal change; that is, the standard deviation of the thickness should be small. Furthermore, a structural dip was recognized in the borehole description and the rock core photos, handled in laminated or thinly bedded to bedded shale and sandstone sequences. Such a structural dip is best-identified from cross-bedded sections thought to have been horizontally stratified originally, which we call cross-bedding, accordingly. As a result, a side-by-side comparison of lithological borehole data was conducted.

(4)

Selection of key marker bed. The thick sandstone was selected as the key bed of the rock unit, as it was readily distinguishable. To obtain a reliable result, the thick sandstone must be identifiable over a large number of boreholes (i.e., be unique and widespread), ensuring that it exists at most locations in the study area through these boreholes. The sedimentary sequences are significant, as they help us to identify which sandstone is the proper one among the boreholes. This is based strictly on the distinguished lithology in the sedimentary sequences, as mentioned above (e.g., the laminated structure in the alternating sandstone and shale units). In addition, the key bed must fulfill the requirements for the comparison of rock units from different boreholes, as described in step (3) above.

The elevation of the colluvium bottom (top of the bedrocks), in combination with the borehole elevation and recorded depth, can be obtained in each borehole. Based on the rock unit classification results, the elevations of the top and bottom of each rock unit can also be identified. Meanwhile, the average thickness of each rock unit can be determined considering the thicknesses obtained from different boreholes.

3.4. Development of the 3D EGM

3.4.1. Interpolation of Colluvium Bottom Boundary (Depth of Bedrock Top Surface): Grid-Based Method

A dataset including the X, Y, and Z values of the interface between the colluvium and underlying bedrocks from 50 boreholes were utilized for interpolation. In addition, we assumed that the elevation of the bottom boundary of the colluvium was equal to the elevation along the Pengshan River and the water divides (ridges) and the bedrock outcrops along these lineaments. The elevation data points along these lineaments were used to interpolate the elevation of the bottom boundary of the colluvium (i.e., the bedrock top surface). These lineaments are marked with the orange dotted line in Figure 1. The 3D software Surfer 16.0 [32] was used to interpolate the boundary surface elevation at each grid with 12 × 12 m resolution using the Kriging method. Equation (1) describes the process of calculating the estimated value:

$$Z_A={\sum }_{i=1}^n{W}_i{Z}_i,$$

(1)

where $Z_A$ is the estimated value, $Z_i$ refers to the value at position i, $W_i$ expresses the weight at position i, and n identifies the number of neighboring data values utilized in the estimation (derived from the Golden software).

We gridded the datasets using the default properties of the Kriging interpolation. From unevenly spaced datasets, this approach creates structural contour maps which represent the colluvium bottom. The data were acquired from a total of 50 available boreholes for the whole study area. To make the result of interpolation reliable, we attempted to exclude the extrapolation when there was no data outside the borehole network in the study area. Consequently, visualization of the bedrock depth distribution in the study area was achieved (see Section 4.2).

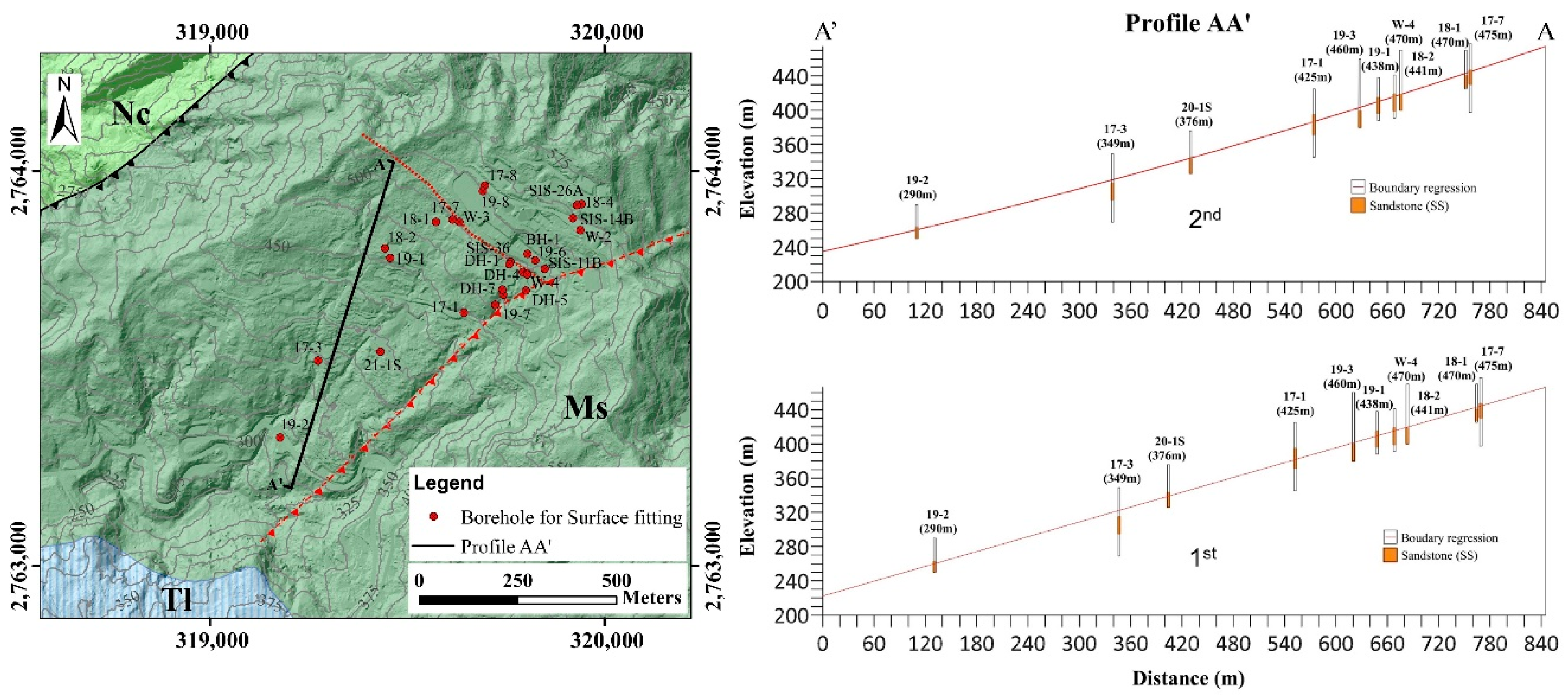
3.4.2. Determining the Polynomial Surfaces Representing the Rock Boundaries: Vector-Based Method

Polynomial surface fitting is a mathematical approach that involves identifying and measuring trends in the characteristics of the dispersed observed data, in which the sum of the squared deviations from the trend surface is minimized. With this analysis, our purpose was to develop a fitting surface for the boundaries of each rock unit, representing a geological boundary to create the spatial geometry of the interfaces between the rock units. Thus, we decided to use a prediction model which creates an interpolated geological contact surface extending in a continuous layer from the data (i.e., the geological observations obtained from the boreholes). This is a type of regression analysis expressing each initial observation, using the product of a deterministic polynomial function of the geographic location with a general Function (2):

$$Z_A=f \left(X_A,Y_A\right)=b_0+b_{1}X+b_{2}Y+b_3{X}^n+b_{4}XY+b_3{Y}^n+\dots ,$$

(2)

where Z_A is the value of a property at location A, X_A and Y_A are the coordinate values at location A, f is the regression function, b_i is a polynomial constant, and n is the order of the polynomial [33,34,35,36]. The dataset collection step is heavily reliant on stage 2 of the borehole data analysis, including X and Y representing the longitude and latitude of boreholes, respectively, and Z is the elevation value of the top of the thick sandstone, the so-called key bed (i.e., the occurrence depth of thick sandstone).

We began our spatial distribution analysis procedure with the aforementioned 26 data points corresponding to the 16 boreholes (

Table 1. Error of the first- and second-order polynomial regression models in comparison with the real data from the boreholes in Zone 1. Z represents the elevation of the sandstone top (key bed).

Borehole	X	Y	Z	Error
				2nd	1st
W-4	319,803.7	2,763,737.5	413	4.10	7.00
19-7	319,722.7	2,763,660.8	390.6	5.46	2.20
19-3	319,743.2	2,763,686.7	399	3.95	2.53
DH-5	319,800.2	2,763,697.0	411	−3.14	2.79
DH-7	319,740.0	2,763,699.7	403.8	1.95	1.23
DH-4	319,792.5	2,763,743.6	422	−3.75	−0.98
DH-1	319,758.2	2,763,763.9	423	−1.00	1.57
SIS-36	319,761	2,763,769.8	427	−3.40	−0.53
18-2	319,443.5	2,763,803.5	418	−2.21	−2.63
19-1	319,456.7	2,763,780.4	414	−4.36	−4.38
18-1	319,572.3	2,763,871.3	440	4.90	3.16
17-7	319,614.1	2,763,867.3	444.4	1.03	0.32
17-3	319,273.8	2,763,519.9	314.3	4.06	8.91
17-1	319,643.2	2,763,641.1	394	−7.46	−12.01
19-2	319,177.7	2,763,324.5	262	−1.79	−0.88
21-1S	319,431.5	2,763,541.8	342.5	1.58	−2.70

) which were irregularly distributed over the research region, spanning from the middle to the lower part of the slope, as well as the 10 data points distributed around the campus (

Table 2. Difference between actual and predicted data using first-order regression model in Zone 2.

Borehole	X	Y	Z	Error
W-3	319,631.7	2,763,871.4	443.8	3.68
17-8	319,696.5	2,763,972	472.8	−2.5
19-8	319,691.3	2,763,949.3	466.2	−1.22
BH-1	319,823.9	2,763,774.3	428.6	−5.38
19-6	319,804.5	2,763,789.9	424.8	2.21
W-2	319,938.1	2,763,849.8	440.3	−0.67
18-4	319,941.3	2,763,915.9	452.8	2.11
SIS-14B	319,919.3	2,763,880	446.9	−0.01
SIS-26A	319,929.6	2,763,913	453.7	0.7
SIS-11B	319,848	2,763,752	416.7	1.1

). The top of the key bed in these boreholes was extracted with respect to elevation values (i.e., Z). Then, these values were used to carry out regression-based surface fitting, in order to get the best fit. We began by employing a polynomial function of order one, and gradually increased the order until the result fit the data well. The prediction methods for spatial computing data were then established. According to the goodness-of-fit statistics, the best polynomial surface regression model was selected, with respect to the data, in order to describe the surface trend, thus simulating the spatial distribution of the rock units. This function then could be used as a critical model to evaluate the vertical spatial distribution of the geological sub-surface at any location with geographic coordinates inside the study area. To display the surface of the interfaces (i.e., geological contacts) or the top of the thick sandstone (key bed) obtained from the model, the contour map was processed as a resultant map. This structural map guaranteed smooth boundaries and fit the data well. In order to obtain a reliable resultant interface of rock units, the contour map was validated with respect to the bedding plane orientation from outcrops. In addition, validation of the borehole data (structural dip angle) from rock core logging was significant. We assumed that all rock units were parallel to one another (i.e., the principle of sedimentary rock), and then used the average thickness of each rock unit to generate the other interfaces, based on the fitting interface of the key bed. This means that every interface of the rock units was introduced into a polynomial function. This led to creating of a so-called 3D vector-based grid of the interfaces of different rock units. Finally, cross-sections were used to visualize the spatial distribution of the rock units.

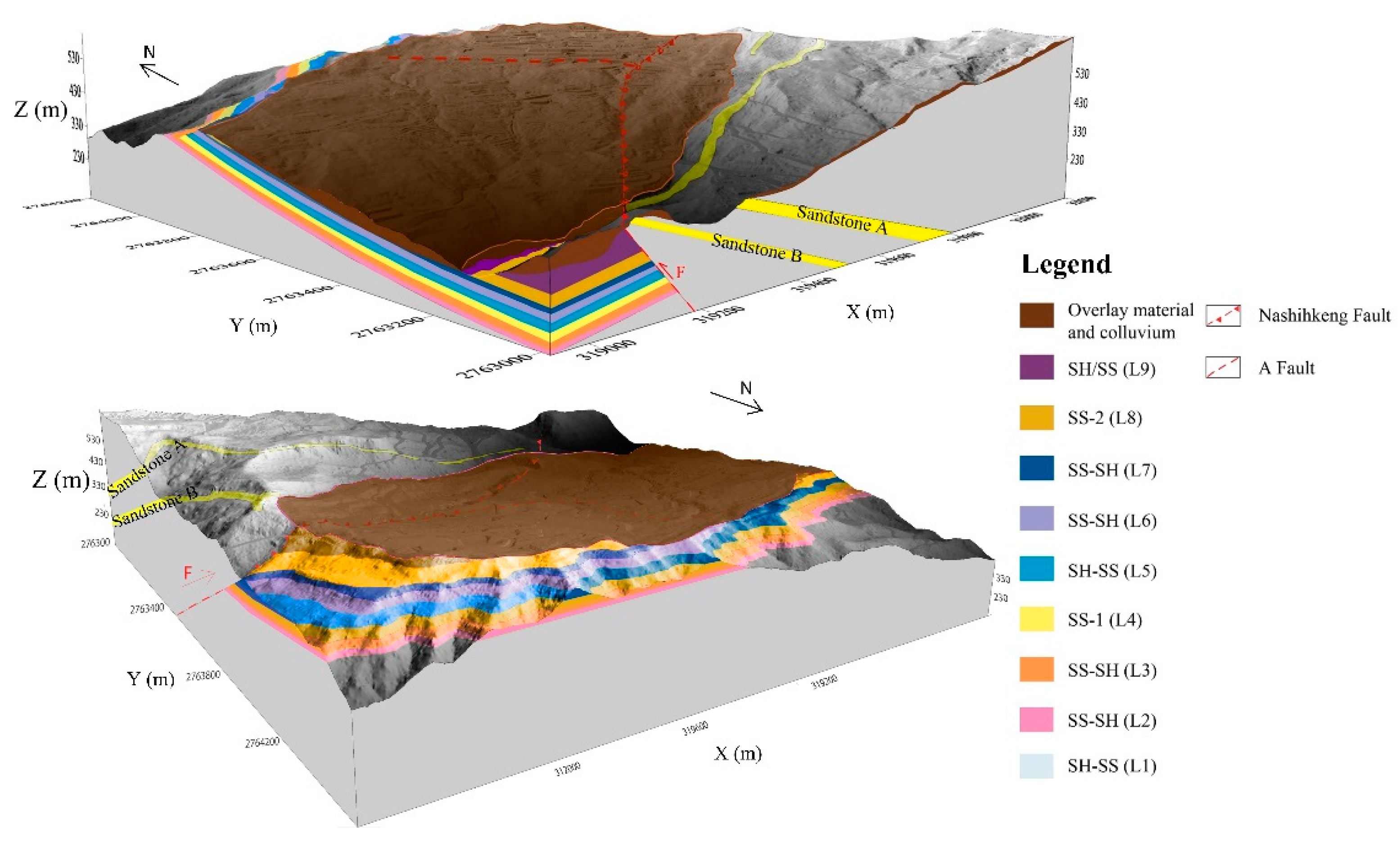
4. Results of 3D EGM Development

4.1. Boundary of Paleo Landslide Deposits

Widely sporadic outcrops are exposed along both sides of the Pengshan River (Figure 3). The Mushan Formation is characterized by a preponderance of whitish fine- to medium-grained sandstone, which is easy to identify and track along the outcrops. The orientations measured at the outcrops almost differ from the background orientations (i.e., the Mushan Formation). In some places, the orientations are almost toward the south with orientation groups of steep dip angles, ranging from 49° to 55°. Particularly, in the confluence of the two creeks, there is mudstone exposure which differs from the previous rock description. In contrast, the orientation measured not far to the southeast of the intersection is almost equal to the orientations of the background, with a dip angle of about 20°. Thus, they look like the Mushan Formation, indicating that the strata in this area were not affected by tectonic activities.

Therefore, the outcrop measurements can be categorized into two groups, with a change in orientation. The first, representing a majority of the outcrops, is positioned on the northern bank of the river, with orientation differing from that of the Mushan Formation. As boreholes 20-4W and 17-4 near creeks indicate 36 and 40 m of colluvium, this rock may originate from ancient landslides. As a result, a boundary for the paleo landslide deposits is proposed in this study, shown as the orange dotted line in Figure 3. On the other side (i.e., on the southern bank of the river), the dip angle of the bedding is steep in the same direction, indicating that the geology in the area must be influenced by tectonic forces. There is a possibility that the Nanshihkeng Fault passes through this area, but there is not much evidence to support this claim. In addition, there are still normal orientations (i.e., background orientation) that should belong to the Mushan Formation.

4.2. Grid-Based Interface between Colluvium and Bedrock

The large-scale terrain interpretation derived from the LiDAR DEM indicated that the eastern, northern, and western sides of the Mt. Dalun area have relatively high altitudes, and the topography is bowl-shaped with collapsed cliffs. Several hummocky areas dominate the topography of the study region, characterized by many small hills and closed depressions. The contour lines, in particular, indicate that the crown is dense while the toe of the avalanche protrudes with a V or U shape. The surface of the study area was previously formed by an ancient landslide debris and by erosion caused by typhoon events. The slope surface is in a current state of equilibrium of material accumulation (Figure 4a). Figure 4b additionally depicts a Kriging map showing the elevation of the interface between the colluvium and the bedrock, which represents the depth of the colluvium. This result incorporates topographical features, outcrops, and borehole data as well. The areas constrained by the rock outcrops, such as steep terrain and the paleo-landslide boundary (cf. Section 4.1), are denoted on the map by red solid crosses (i.e., the thickness of loose materials, including the colluvium and artificial filled land, is assumed to be 0 m). This map may even reveal that the geometry of the bedding plane underneath the surface is covered by loose materials, which dips toward the southwest with an inclination of approximately 15°. Furthermore, the relationship between the colluvium and the bedrock is viewed, through several profiles, in the following sections.

4.3. Geologically Uniform Zones

According to previous studies, two small-scale faults may exist in the study area: The Nanshihkeng Fault and A Fault. The potential Nanshihkeng Fault striking in NE–SW can be observed from the drilling data, in which the fault plane is inclined about 60° to the southeast and cuts through the bedrock in the slope [28]. The hanging wall dominates the eastern portion, with steep terrain to the southeast representing a reversal topography caused by the uplift phenomenon of the two thick sandstone layers in the surrounding geology. In additional, Jeng and Sue [28] have analyzed 2D resistivity data to hypothesize that a probable NW–SE striking oblique-slip fault (i.e., A Fault) intersecting the Nanshihkeng Fault might be characterized by high angle dipping. However, this fault is unclear, without any difference in topographical features.

Based on rock core analysis of the boreholes around the A Fault on the map, extensively fragmented rock and a non-cohesive crush zone as a shear zone were revealed. The shear zone is made up of gouges and rock pieces, as well as clay-rich material. This information provides evidence supporting the existence of the A Fault structure in the study area. The orientation of the A Fault can be detected from the three-point method, which corresponds to 55° NW, 75° N, suggesting that the borehole data applied in this study are consistent with the existence of the A Fault from previous studies. Notably, in following additional rock core data analysis of the borehole 20-4W around the foot part of the slope to the southwest, a piece of especially significant evidence for the presence of this fault was revealed. Figure 5a shows the shear zone like a crush and scratches, as well as a change in the bedding dip angle along with the depth of the borehole, which is a steep bedding dip angle at a depth of over 47 m. The mean inclination value ranges between 60–70°, and seems to change gradually from this depth to become a gentle bedding dip angle toward bottom of this borehole. Even though borehole 17-4 is almost filled by colluvium, the high bedding dip angle track is also indicated obviously. This implies that both boreholes 20-4W and 17-4 pass through the fault plane of the Nanshihkeng Fault, which is evolving in a drag fold pattern. Hence, the existence of these two faults is reasonable, and their distribution might dominate the bedrock orientation in a local area.

However, the lithology of the sedimentary rock in the study area did not change, as revealed from the rock core analysis and field investigation. One of the lithological features was white sandstone and alternation of sandstone and shale, characteristic of the Mushan Formation, which can be easily found from the rock core logging and the outcrops. The bedding plane revealed a gentle (about 20°) dip angle for most of the rock units (borehole data). This finding was also consistent with that provided by the CGS geological survey [31]. The evolution of the Nanshihkeng Fault and the A Fault will result in a change in the spatial distribution of the bedrock; even so, the geological characteristics were the same over the whole region. Based on these conditions, the research area was divided into three zones—Zone 1, Zone 2, and Zone 3—with the two faults serving as boundaries for geological uniform zones of the study area (Figure 5b).

4.4. Development of Geological Model in Zones 1 and 2

4.4.1. Classification of Rock Units

In the Mt. Dalun area, a detailed rock core description was revealed through lithological sediment analysis of the 26 boreholes. We attempted to separate these boreholes into two groups, based on the above-mentioned fault division (cf. Section 4.3): one for the boreholes located to the north of the A Fault and another for the boreholes located to the south of the A Fault. In other words, the boreholes indicated in the western portion of the research area (Zone 1) and the boreholes around the Huafan University campus (Zone 2).

Nine rock units could be distinguished with various types of rock, correspondingly shown in Figure 6. Of these, the key bed in the geological feature was the thick sandstone (L4), with thickness ranging from 16 to 22 m. This rock unit was critical for interpolation and surface fitting in constructing the 3D EGM, as mentioned in the methodology section. In Zone 1, according to the rock core interpretation, eight rock units were revealed, excluding the colluvium layer. The group of boreholes 17-1, 17-3, 17-7, 18-1, 18-2, 19-1, 19-2, and 21-1S covered L1 to L6 in the rock unit, while the other boreholes (19-3, 19-7, W-4, DH-5, DH-7, DH-4, DH-1, and SIS-36) penetrated through L4 and above. In Zone 2, nine rock units could depict the northern stratigraphy of the research region. The borehole BH-1 had a depth of 100 m and penetrates through nine rock units. As an outcome, the stratigraphy in both Zones 1 and 2, as well as the study area overall, could be connected continuously based on the borehole BH-1. Their standard deviation was within an acceptable range, with not much difference between the boreholes in Zone 1 and Zone 2. The characteristics of the colluvium and each rock unit are described in the following.

• Colluvium (Co). The cover material layer consists of loose and unconsolidated sediments characterized by weathered sandstone pieces and blocks with brownish color and gray matrices, fragments, debris, and soil. The fragments differ in size, shape, and crack density. In some boreholes, the fill material (dark yellowish, fine-grained) is fairly thick, which is due to the constructions, especially in the group of boreholes within the university campus. The thickness of the cover material varied, with the thickest section reaching approximately 40 m (borehole 17-4) towards the toe of the slope located to the southwest of the mountain. Based on the geological processing in the Mt. Dalun area, as well as topographical analysis, the colluvium may have originated from two sources: Loose material belonging to the ancient deep-seated landslides and so-called slope wash (i.e., debris slide).
• Sandstone (SS). Two rock units were identified as sandstone: L4 (SS-1) and L8 (SS-2). The lithology in L4 was mostly composed of thick, medium-grained whitish sandstone intercalated with thin dark black shale layers scattered in a few places in the massive sandstone. A shear zone containing mud was found in some rock cores. The rock core contains a number of joints. As previously stated, L4 is a key bed identified in the sedimentary sequence, and the overlaying and underlying units are L5 and L3, respectively, characterized by laminated alternations of sandstone and shale. As for L8, grayish sandstone occasionally intercalated with laminated shale is the main lithology. L8 had a higher average thickness than L4, about 25 m and 16 m, respectively. Therefore, the L4 was comparatively identifiable from L8.
• Alternations of sandstone and shale (SS, SH). This type of rock unit included L1 (SH/SS), L2 (SS/SH), L3 (SS-SH), L5 (SH/SS), L6 (SS/SH), L7 (SS-SH), and L9 (SH/SS). The ratio of sandstone and shale proportion in the recovered rock core significantly varied among these rock units. Each rock unit is described, respectively, in the following:

  a.

  Rock unit SH/SS (Shales occasionally interbedded with sandstones). This rock is characterized by black to gray shale interbedded with fine sandstone, very thin-bedded sandstone and shale, and mainly dominant shale percentage. It contains sandstone and shale, with shale constituting up to 70–90% of the rock core.

  b.

  Rock unit SS-SH (Sandstones interlayered with shales). The lithology is composed of interbedded sandstone and black to gray shale, with the thickness ranging from thinly laminated to thickly laminated, and extremely thinly bedded. The sandstone content throughout the portion is approximately 50%, with beds containing parallel lamination and, occasionally, ripple cross-stratification.

  c.

  Rock unit SS/SH (Sandstones occasionally interbedded with shales). The lithology composed of gray to whitish sandstone is the dominant lithology, with black shale interspersed and occasionally locally interbedded sandstone and shale. The sandstone beds range from medium bedded to very thickly bedded, accounting for about 70–80% of the composition.

According to the rock core interpretation, the dip angle of the bedding plane of the sedimentary rock in the above regions mostly ranged from 10° to more than 20°, implying that the bedding plane and slope topography are easily compatible. The results were also supported by the topographical features, field survey, and observations.

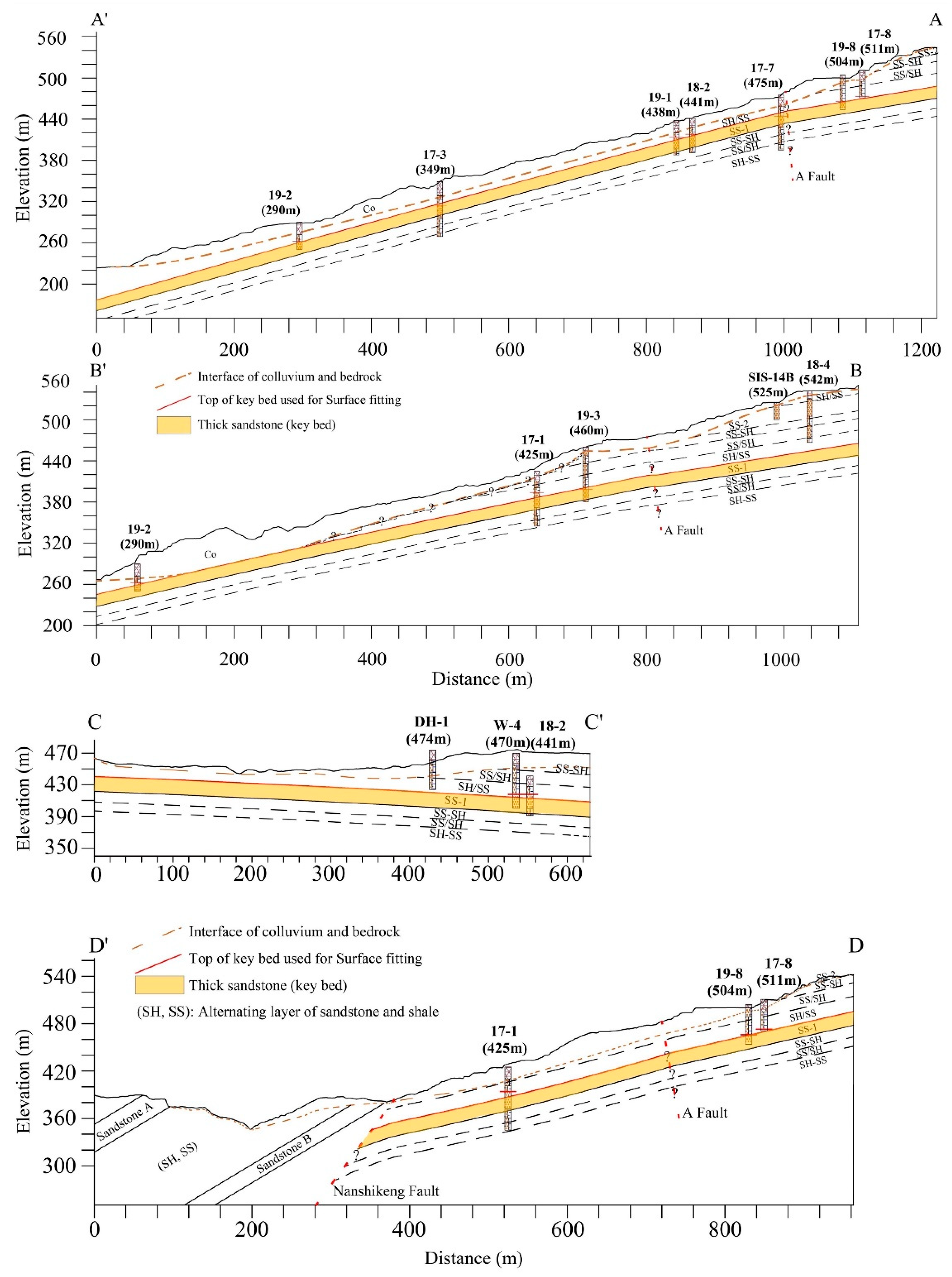
4.4.2. Upper Boundary of Key Bed

The application of the polynomial surface fitting method for modelling was applied to determine the geometry of the interface between L4 and L5. In further analyses, this sandstone (L4) top surface was used to estimate the boundaries of other rock units, where the boundaries were assumed to be parallel to each other. For Zone 1, the spatial distribution of the strata was created using both first- and second-order polynomial regression. The first-order polynomial was formulated as shown in Equation (3):

$$Z=-\mathrm{810,375.5140}+0.065242 X+0.285820 Y.$$

(3)

This equation denotes that assumed bedding is planar; that is, based on a linear equation. Meanwhile, the top elevation of the key bed using the second-order polynomial regression equation, which had high accuracy (R² = 0.99) is shown in Equation (4):

$$Z= \mathrm{a} + \mathrm{b}X+ \mathrm{c}Y+ \mathrm{d}{X}^2+ \mathrm{e}{Y}^2+ \mathrm{f}XY,$$

(4)

where $\mathrm{a}=1.18\times {10}^9; \mathrm{b}=4.83\times {10}^2;\mathrm{c}=-9.07\times {10}^2;\mathrm{d}=-7.07\times {10}^{-5};\mathrm{e}=1.73\times {10}^{-4};\mathrm{and} \mathrm{f}=-1.58\times {10}^{-4}.$

The error between the actual data obtained directly from the boreholes and the values from the regression processing is critical to validate the effective model fitting. In order to study the difference between the actual and interpolated data, Table 1 shows the errors obtained when using first- and second-order models. It can be seen that the maximum errors with the second-order model were lower than those with the first-order model, implying that the uncertainties in spatial formation were lower. Then, a cross-section A-A’ was plotted to visualize the errors in Table 1 for a borehole group, when using the different models in both orders (Figure 7). The sandstone layer is highlighted in yellow color in the boreholes. The red line, which indicates the geological boundary, was obtained by using regression values of the top elevation of the sandstone in the cross-section. The curved line represents the physical shape of the second-order surface polynomial regression, which was more likely to satisfy and better fit the surface than the first-order model, which is a straight line (or linear resultant). For example, borehole 17-1 displays the most obvious case of a comparison between the first- and second-order models with a decreased mismatch between the borehole and regressed data with the latter. The red line (i.e., second-order model) is more consistent with the top of the sandstone in this borehole, implying that the error was improved significantly.

For Zone 2, we only used first-order regression to generate the bedding distribution model, as there was not enough data in this region to perform second-order polynomial regression surface fitting, given that the majority of the boreholes did not reach the interface between L4 (the key bed) and L5. As a result, only the first order was used as the function of the polynomial regression for the geological model in Zone 2. The linear surface fitting regression equation is as follows:

$$\mathrm{Z} =-636796.2239-0.009296\mathrm{X} +0.231637 \mathrm{Y}.$$

(5)

The root-mean-square (RMS) error values, which can demonstrate the difference between the actual and predicted data in regression, were also computed. This number was high (R² = 0.98), indicating that the estimated coefficients in the regression equation were credible. Moreover, after determining the surface equation of the fitted bedding, the regression results demonstrated that the first-order model were fairly consistent with the real data, with the error being acceptable and not changing significantly (Table 2). Except for two boreholes—BH-1 and W-3—the majority of the observed data had low error.

Based on the results of the surface fitting regression, a structural contour map of the thick sandstone (key bed) was created, in order to visualize the pattern (trend) of the sedimentary rock in the two zones. To ensure the continuity of the geological structure map of the thick sandstone (key bed, L4), Figure 8 illustrates a structural contour map comprised of two groups: Zone 1 and Zone 2. It can be seen that the shape and direction of the contours had a high association with the inferred structures. To the north of the research area, the largest portion of the location is Zone 2, with the bedding plane striking almost in the E–W direction and dipping to the south with a gentle inclination of approximately 13°. This implies that the geological structure underneath the Huafan University campus is a dip slope in the literally strictest sense. Then, progressively moving towards the downslope direction, the contour seems likely to become bent, turning towards the southwestern direction. The tangent line of these contours gradually changes, implying that the strike of the bedding plane adjusts as well, with a steeper inclination towards the southwest. Based on this contour map, a proposed geological structure can be detected with a left-lateral strike-slip fault, and the strike-slip movement on the map does not have vertical displacement of stratum. However, the displacement becomes progressively unclear along the southeastern direction of the fault, and appears to be somewhat of a slip at the intersection with the Nanshihkeng Fault. The evidence for this assumption needs to be investigated through supplementary data in the future. Furthermore, the structural contour map was consistent with the attitude of the geology (the purple attitudes) and, in particular, it fit well in the dip direction of the bedding plane, which has also been recorded by Jeng and Sue [28] and measured in the field survey (Figure 8). These orientation data (i.e., strike and dip) may be expressed as vectors that are orthogonal to the strike in their locality. Therefore, the polynomial surface fitting method procedure was used to represent the geometry of the geological contact surface between strata in the Mt. Dalun area, which was considered reasonable.

4.4.3. The Average Thickness of Each Rock Unit in Zones 1 and 2

The thickness of the rock units varied with the distribution of the boreholes. The stratigraphical sedimentary rock was constituted of a succession of rock units, which were constructed according to their sequence. These rock units are characterized by a series of boundary horizons, which represent the geological contacts between the various layers, shown as a stratigraphic column in Figure 9.

4.5. Development of Geological Model in Zone 3

Zone 3 represents the eastern section of the study area, which lacked boreholes to analyze the underground stratigraphical conditions. According to the study of Jeng and Sue [28], two layers of thick sandstone and thin interbedded shale and sandstone shale can be found in this area. The thicknesses of these two thick sandstones are 30 m and 10 m, respectively (Figure 1). However, new outcrop measurements and geological descriptions have been carried out, such that the boundary of these two sandstone layers should be modified. Several attitudes in the outcrops were confirmed along the road to the southeast, where the topography is steep. Most of the exposures were discovered only by excavation on a construction road, which provided easy access to the outcrops. Exposures mostly included interbedded shale and sandstone. These were moderately to heavily weathered, covered by vegetation, and dip 20–40° to the southwest. The Nanshihkeng Fault may have changed the bedding plane’s orientation, resulting in a steep oblique slope in this area. The result of this work is consistent with that of previous studies. A total of 15 measurements were recorded during this survey, and the statistical results indicated the orientation of the bedding plane in the stereonet (Figure 10a). The average attitude of the representative bedding plane was selected to draw a structural contour map (68° NW, 31° SW). We observed the real contact exposure between the sandstone and interbedded sandstone; shale, in particular, may be seen extending from 30 to 40 m, having a light gray tint (i.e., red circle), in Figure 11. In addition, a high-resolution slope inclination map derived from the LiDAR DEM was constructed, in order to determine and deduce the reasonable boundaries of the rock units. Then, the proposed geological map for Zone 3 was redrawn. Figure 10b exhibits the distribution of the two sandstone layers, as well as the attitudes of bedding planes. We named the thicker sandstone sandstone A, while the other was sandstone B. The distribution of sandstone A on the geological map was corroborated by the contact observed in the field. Even though the outcrop of sandstone B was not exposed in the field trip, the thick sandstone should be exposed to become the ridge. This seems to be compatible with the distribution of the thinner sandstone layer observed in the study of Jeng and Sue [28]. As a result, the outcrops drawn by Jeng and Sue [28] around the ridge are realistic, working in conjunction with the average orientation to illustrate the distribution of these two thick sandstones, particularly sandstone B. These two sandstone layers on the southeastern oblique slope are distributed along NE–SW striking steep slopes or ridges, and may turn gradually to the westward direction and terminate at the Nanshihkeng Fault. For terrain compatibility, it can be inferred that sandstone A lies above sandstone B, meaning that the top of sandstone B will be the bottom of sandstone A in the spatial distribution. This can be seen in the geological profiles provided in the following section.

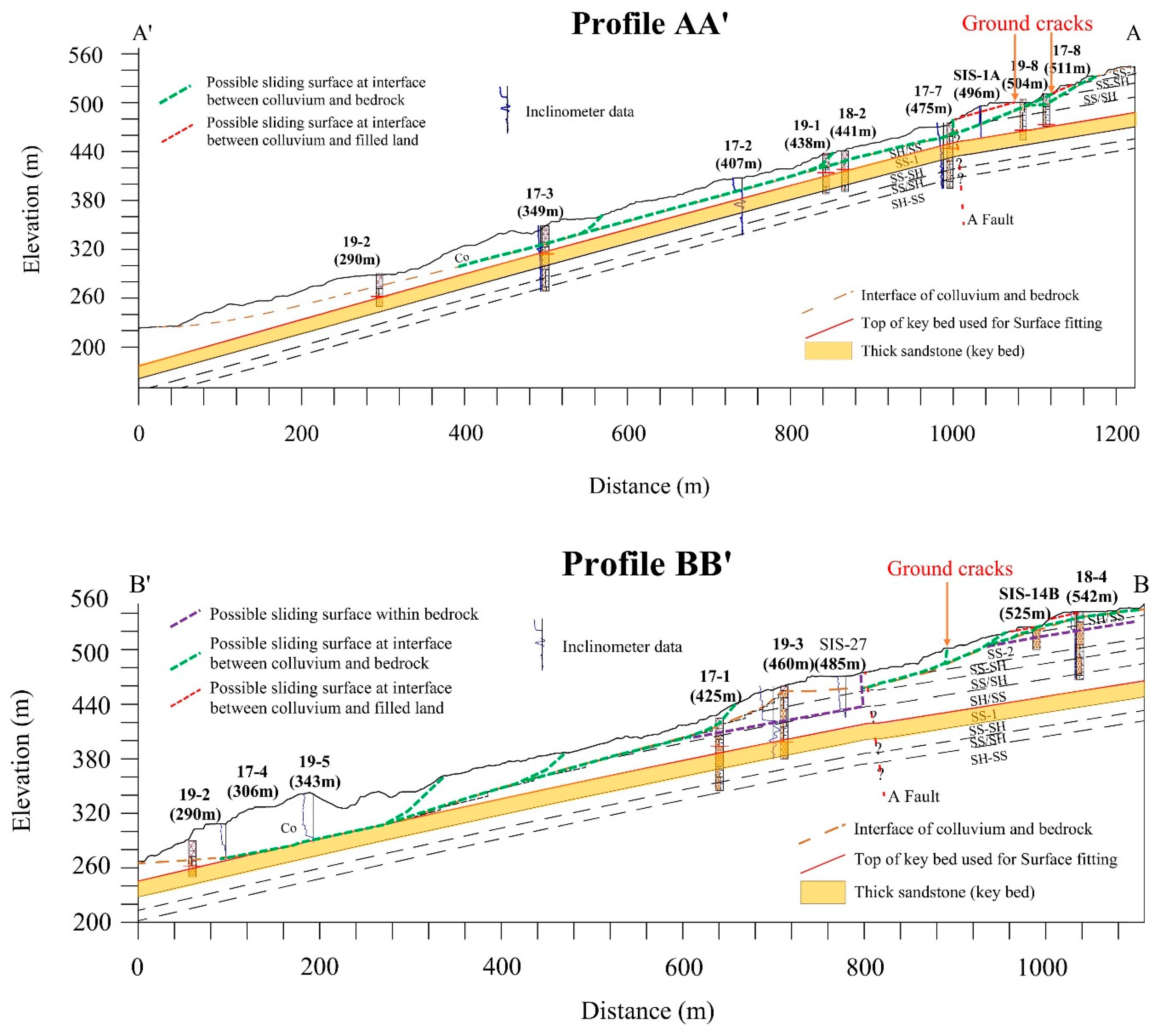
4.6. Three-Dimensional Engineering Geological Model and Geological Profiles

The three-dimensional engineering geological model, derived from the integration of the grid-based method (i.e., colluvium bottom elevation) and vector-based method (i.e., the geological interface of rock units) mentioned above, as well as field outcrop geological data in the research region, is shown in Figure 11. Cross-sections were also generated to interpret the 3D engineering geological model (Figure 12). The colluvium and bedrock were characterized by the rock units identifiable through the geological contact (interface) of strata. Two geological profiles (A-A’ and B-B’) from the northeastern to the southwestern part of the slope, along with their geological explanations, are detailed in Figure 12. It can be observed that the profile B-B’ passes through the eastern part of the Huafan University campus, revealing that the covered colluvium in the upper part around the campus is thin. However, their thickness becomes progressively larger toward the southwest. In particular, at the bottom of this slope where the riverbank is located to the north, there is a massive and thick colluvium accumulation area. For the sedimentary rock, the strata are parallel to each other, which is compatible with the topography. There is a thick sandstone layer (SS-2) of approximately 25 m thickness beneath the interbedded sandstone and shale (SH/SS) cover, to the north of the A Fault. However, this sandstone layer disappears in a portion in the profile A-A’, meaning that it had been eroded due to erosion of the exposed surface. Through two profiles extracted from the geological model, the interface between the colluvium and the underlying rock was found to be almost parallel to the geological boundary of the strata. The thick colluvium layer with the maximum depth lies roughly on the top of the sandstone (SS-1), which is acceptable as the sandstone at that altitude in those profiles is quite persistent and difficult to break. While other layers are mostly composed of narrow interbeds of shale and sand, this material has partly transformed into the colluvium due to long-term weathering and erosion. The two profiles also show that these outcrops of the bedrock on the ground surface here form the steps of a staircase in the topography. Therefore, the sources of colluvium almost entirely originated from this bedrock of alternative shale and sandstone (SS, SH). A cross-section in the northwestern to the southeastern direction (C-C’) was additionally drawn (Figure 13). It can be observed that the bedding was nearly consistent with the topographical surface and interface between the colluvium and itself. To visualize the spatial distribution of the two thick sandstones in the southeastern part (Zone 3), a profile D-D’ in an almost N–S direction passing across the A and Nanshihkeng Faults was also created (Figure 13). Even though the rock units of alternating sandstone and shale cannot be distinguished in the profile, the steep terrain can be explained by the uplift of the Nanshihkeng Fault as a reverse fault, based on this profile. In the southern part of the profile, the thickness of the colluvium is extremely thin, and the bedrock is virtually exposed around this part.

5. Applications of the 3D EGM

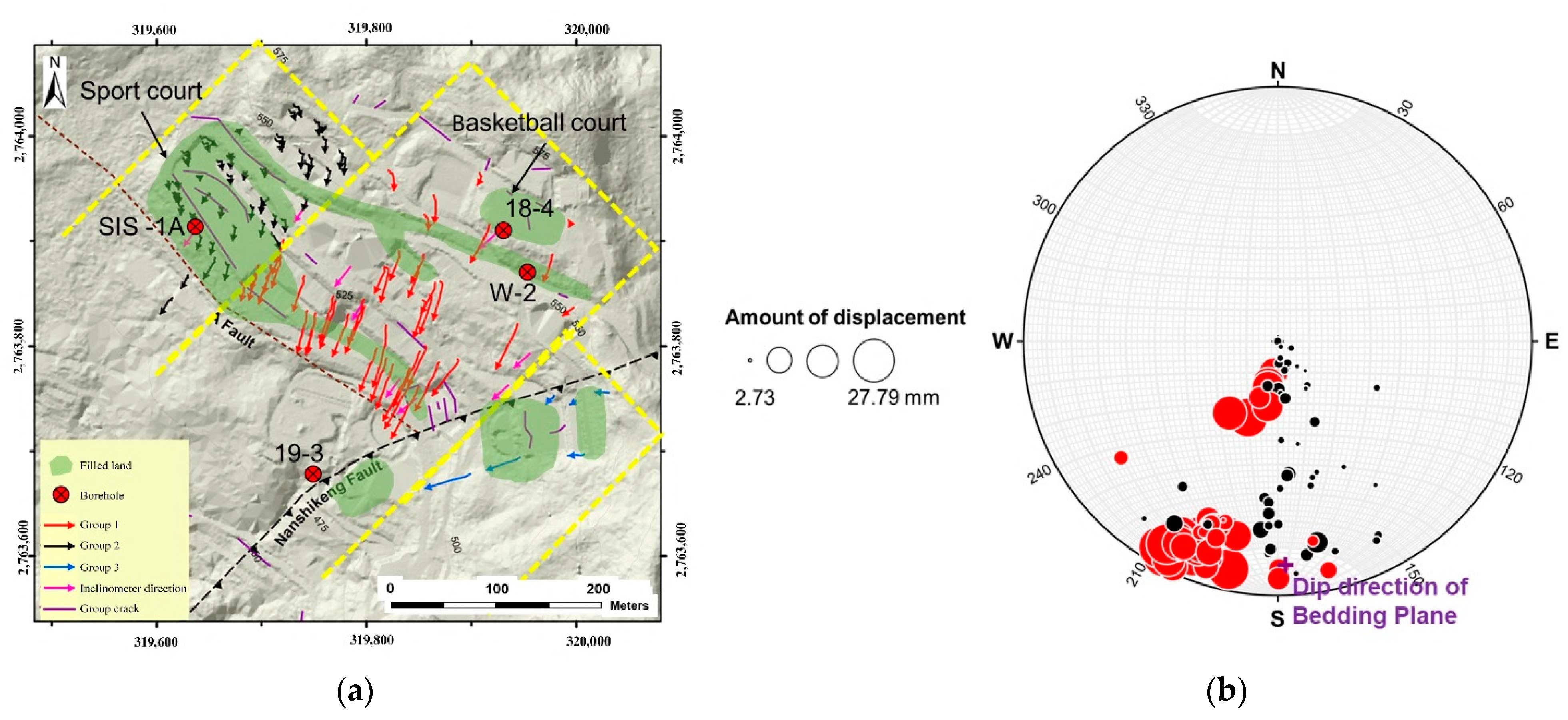
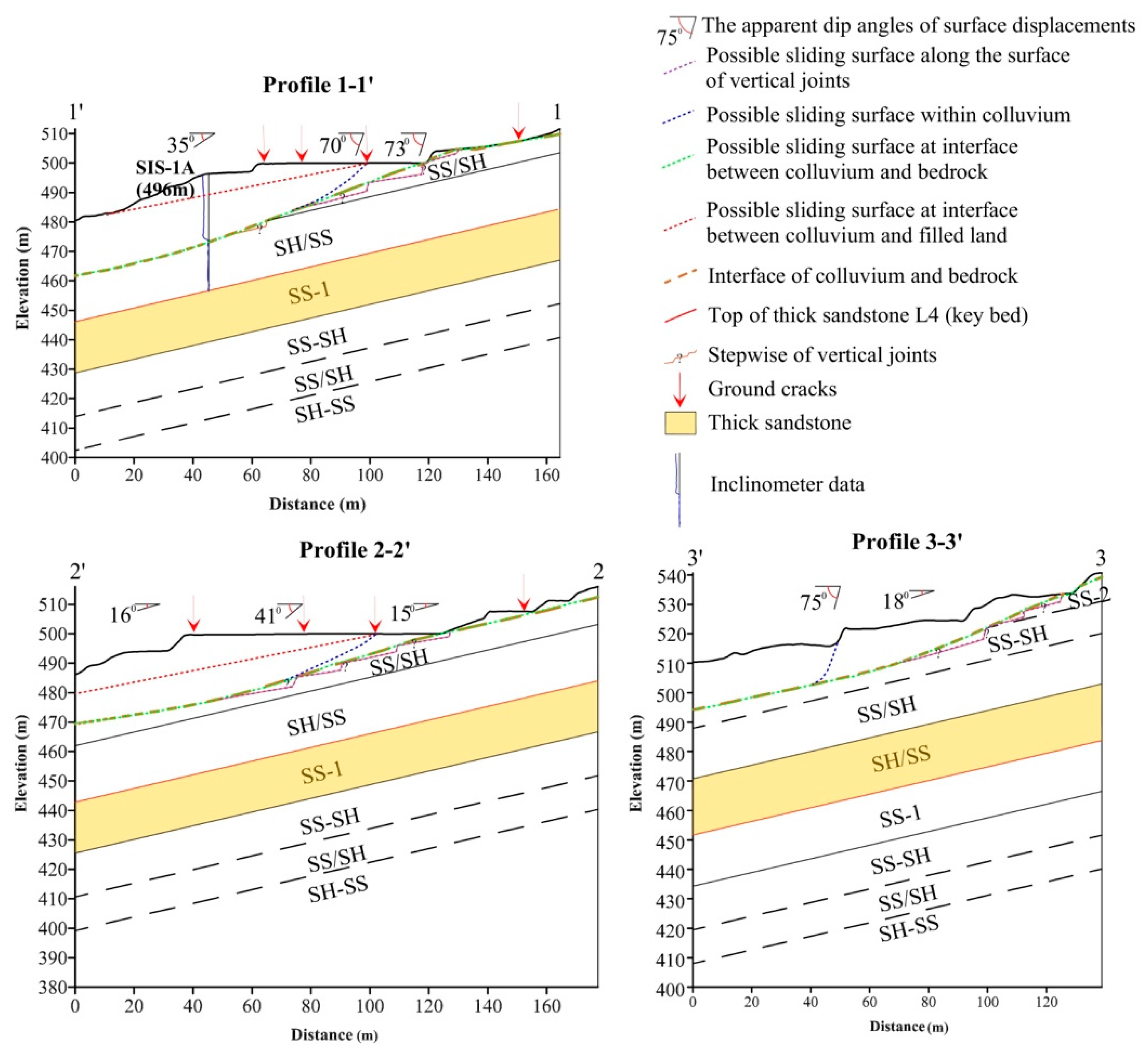
5.1. Surface and Sub-Surface Displacement Monitoring

5.1.1. Surficial Displacement Interpretation

According to the study of Tseng et al. [30], hundreds of displacement monitoring points were established and recorded in the study area from April 2010 to July 2017. This is a part of the long-term monitoring of surface and underground movements based on time-series data. On the map, Figure 14a displays the displacement tracks of each observation point within the Huafan University campus, from which the quantity and direction of horizontal displacement at each monitoring point throughout each period can be seen. This surficial displacement can be classified into three groups, as shown on the map. One is a larger displacement, with the main direction being down to the slope in the south-southwestern direction, denoted by red color (group 2); the second is towards the northwestern part, revealed by the black, as well as a smaller displacement movement toward almost the south (group 1). The displacement monitoring points outside the intersection part of the A Fault and the Nanshihkeng Fault are marked by dark blue color, in which the western components of displacement are more visible (group 3).

To obtain detailed movement behavior of the multiple sliding blocks within the campus, the displacement vectors are indicated using a stereonet from the beginning to the ending of the monitoring period. The displacement trend was a two-dimensional resultant vector in the E and N horizontal components. To show three-dimensional surficial displacement, horizontal and vertical displacements were combined to compute the sliding surface’s spatial dip, also displayed using a stereonet (Figure 14b). The red and black solid circles represent surface monitoring data groups 1 and 2, respectively. They are indicated with different diameters, according to displacement amount and direction at each monitoring site. If the vertical displacement is larger than the horizontal, the displacement vector will approach the stereonet’s center, implying that the campus may have multiple sliding surfaces with different characteristics. In the results, the group 1 displacement vectors can be seen as being dispersed in the stereonet. Smaller solid circles represent less displacement. This movement is not happening in a pre-determined direction, nor is it similar to sliding on the same weak layer inside the bedrock. For further insight, the surficial displacement in the northwest (group 1) may be separated into two smaller groupings. As each small group’s stereonet displacement vector is scattered from inside to outside, each group should be represented by a separate sliding block, comprising Blocks 1 and 2, respectively (Figure 15). In addition, these surface displacement vectors were also compared with the shape of the interpolated colluvium bottom (i.e., the colluvium–bedrock interface), as shown in Figure 15. The primary slope angle of the colluvium was approximately equivalent to the slope surface angle. The majority of horizontal displacements ware almost downslope or deviated from the tangent line of the colluvium contour line at a small angle. Moreover, the displacement direction of the inclinometer SIS-1A coincided well with the dip direction of the interface of colluvium and bedrock (Figure 15). This suggests that the direction of the sliding blocks should be similar to the tangential direction of the colluvium plane. Particularly, in the southwest part of the map in Figure 15 or the south portion of the A Fault, the dip direction of two displacement vectors is similar to the direction of displacement indicated by inclinometer SIS-1A. These two displacement vectors almost correlate with the dip direction of the colluvium and bedrock interface. In the stereonet of Block 2, these two displacement vectors are denoted as hollow triangles pointing southwest, even though their dip angle deviated from the dip angle of the interface (i.e., colluvium and bedrock) by about 15–20° and 20–30° in trend, respectively (Figure 15). The reason for this difference is that the shape of the contact between the colluvium and bedrock may be influenced by the outcome of interpolating this interface. In the stereonet, the green displacement vector in each sliding block denotes the head of the block when the vertical displacement is larger than horizontal displacement, producing a steep angle, while the orange vector supposedly represents a gradual change in the dip angle from the main body to the toe of the sliding block. Overall, the displacement vectors in both blocks almost follow the downward trend in the shape of the interface between the colluvium and bedrock. However, it can be seen that Block 2 has a number of displacement vectors turning toward the southeast. It can be speculated that these displacements were influenced by other blocks nearby, as an extrusion of the slope slide would have affected the opposite direction component when Block 1 slid downslope. This displacement would progressively deviate from the downward direction. One more probable reason is the shifting shape of the sliding blocks, which resemble a curved sliding boundary at the edge of the filled land distribution with the original topographical surface. This led Block 2 to slide on the simplest sliding surface, as long as it could slide under the driving force on the slope. Variation of the surface displacement vector with respect to the common sliding direction may reflect stress and other slope deformations. Block 1, with a high altitude without ground cracks nearby, could only exist at the contact between the colluvium and the underneath bedrock. This possible sliding surface could be one of multiple bottom colluvium surfaces connecting Block 1 to Block 2 in profile 3-3′, due to the apparent dip angles of surface displacements on the profile switching from gentle (18°) in Block 1 to steep (75°) at the head of Block 2. Block 2 was also identified as having a sliding block head around the filled land’s distributed border, and the possibility that the sliding surface occurs at the filled land–colluvium interface is remarkable. It could be parallel to the topographical surface and plane; the red dashed lines in profiles 1-1’ and 2-2’ indicate the sliding surface geometry for the inferred interface between filled land and colluvium (Figure 16). The upward termination of these sliding surfaces on the ground surface also presents with ground cracks. However, a sliding surface may only appear at the boundary between the colluvium and bedrock in the southwest, where the two displacement vectors as mentioned above are not greatly impacted by the thick filled land in Block 2. Similar to Block 1, the geometry of the sliding surfaces changes slightly along Block 2 in the profiles, almost reflecting the apparent dip angles of surface displacements on profiles (i.e., the surface sliding parallel to apparent surface displacement angles). For the sliding surface at the colluvium–bedrock interface, the interface seems to be the consequence of a steeply vertical, stepped joint system. The depth of the sliding surface should be proportional to the depth of joints formed in the bedrock and the advent of weathering (Figure 16). These vertical joints might create blocks of mass slope failure on the surface of the bedrock, as the bedrock platform typically makes it impossible to develop “daylight” on the slope without a significant amount of the maximum principal stress; particularly in persistent, thick sandstone.

As the stereonet in Figure 14b shows, the displacement vectors for group 2 had significantly larger diameter. The vertical displacement for this group was almost smaller than the horizontal displacement, as they were distributed densely at the edge of the stereonet (i.e., far away from the center). In addition, it can be seen that group 2 displayed a relatively similar amount of displacement. However, there were still some displacement vectors with dominant vertical displacement, meaning that the sliding surface was nearly vertical elsewhere in group 2. One possible explanation is that the sliding surface near the head of the sliding block had greater vertical displacement, being relatively consistent with these displacement vectors towards the center of the stereonet. Considering this phenomenon, it can be assumed that the entire surficial monitoring data of group 2 were recorded for one sliding block. However, from the stereonet (Figure 14b), the dip direction of bedding (dark purple solid cross) proposed by the 3D EGM within the campus was not consistent with the surficial displacement vectors.

5.1.2. Sub-Surface Displacement Interpretation

Based on the 3D EGM indicated by the profiles provided in Section 4.6 and inclinometer measurements, the correlations between the sliding surface and geological features were revealed. The profile A-A’ suggests that the sliding surface was located approximately 15–22 m deep, with multiple surfaces (green dashed line in Figure 17). The inclinometer data of SIS-1A, 17-7, 17-2, and 17-3 indicated that the sliding surface was the interface between the colluvium and the underlying bedrock, with the inclinometer SIS-1A also having been correlated to the bottom of colluvium in the study of Tseng et al. [30]. The profile B-B’ passes through the main Huafan University campus in the eastern part, near the intersection of the Nanshihkeng and A Faults. In the upper part, the inclinometer set in the borehole 18-4 indicated a sliding surface (purple dashed line) deep in the sandstone layer (SS-2). In many instances, a break in persistent sandstone is rare; consequently, this deep sliding surface is a so-called local slope failure (e.g., a thin, soft interlayer of shale and mudstone inside sandstone, which easily slips). With reference to the underground monitoring evidence revealed by the inclinometers in boreholes 19-3 and SIS-27, it was possible to infer the presence of a sliding surface inside the bedrock at a specific depth of 38 m (purple dashed line). The sliding surface developed continuously in the rock mass at the SS/SH unit. In cooperation of the inclinometer monitoring of the boreholes 19-5 and 17-4 near the toe of the slope, the sliding surfaces at these locations were found to possibly occur deeper, at depths of 25–45 m, likely in a curved shape (green dashed line). The depth of the sliding surface was not found to lie on a plane, meaning that the sliding surface is curved.

5.1.3. Slope Instability Mechanisms Based on 3D EGM

The slope failure mechanism depends on the geological structure and spatial distribution of the objective geology of the slope. Multiple mechanisms of slope instability may occur at different locations, as revealed by the monitoring of surface and sub-surface displacements and the 3D EGM.

According to the study of Jeng and Sue [28], the sports court and the western part of the campus overlie thick artificial fill, from 2 to 20 m, used for the construction of Huafan University (Figure 14a). The surficial displacement in this area (i.e., the western part of the campus) should not only have happened at the interface between the colluvium and the bedrock, but also at the interface between the fill and the colluvium (i.e., on the original topographical surface before the construction). Similarly, considering the green curving dashed lines indicating the lower portion of the slope (i.e., the location where a large volume of colluvium has accumulated), the sliding surface was determined to be within the colluvium or at the interface between the colluvium and the bedrock. These sliding blocks suggest that, at the interface between the colluvium and the bedrock, the fill and the colluvium may exhibit creeping behavior. This can be explained by the fact that, due to the unconsolidated and permeable nature of the colluvium, when the infiltrated water flows along the interface, the resistance force at the interface decreases and sliding may be triggered. The colluvium has progressively slid downstream, due to a combination of gravity, erosion, and rainfall, resulting in the emergence of several sliding surfaces. Another proposed explanation is that the heterogeneous material between the colluvium and the fill, where the heterogeneities resulting from their uneven elasticity gradually create tiny cracks within the interface. Water infiltrates and then separates the layers through a sliding surface. The cracks on the ground surface might be the consequence of the movement of fill on the original surface (i.e., the interface between the fill and the colluvium).

In addition, the inclinometer results based on the 3D EGM suggested that the sliding surface occurred inside the bedrock. The eastern slope might act under this particular mechanism for slope failure. This circumstance suggests, again, that the sliding block advances downslope, and behaves like a translational dip-slope landslide on a planar sliding surface developing parallel to the bedding plane. That means the sliding surface can develop continuously at an interbedded layer with weak strength in the rock mass, such as sandstones interbedded with shales. The vertical joints inside the slope may cause the sliding surface to break up into a series of block-like slides. Then, the entire slope toe daylights, leading to the interlayer sliding within the bedding plane, creating tension cracks at the head. Once the deformation of the bedding plane surpasses a certain threshold, surface ruptures spread along the deformation face and combine to produce a sliding surface.

In summary, based on the scenario of development shown through analysis of the 3D EGM and sub-surface/surface displacement monitoring, sliding surfaces can be detected, which cause the whole slope to become increasingly unstable. Slope failure can occur on multiple sliding surfaces through a variety of depths and mechanisms. In this case, three sliding surfaces were inferred, including both at the interface between the colluvium and the bedrock, and at the interface between the fill and the colluvium. Finally, a remarkable sliding surface mechanism was also located within the bedrock.

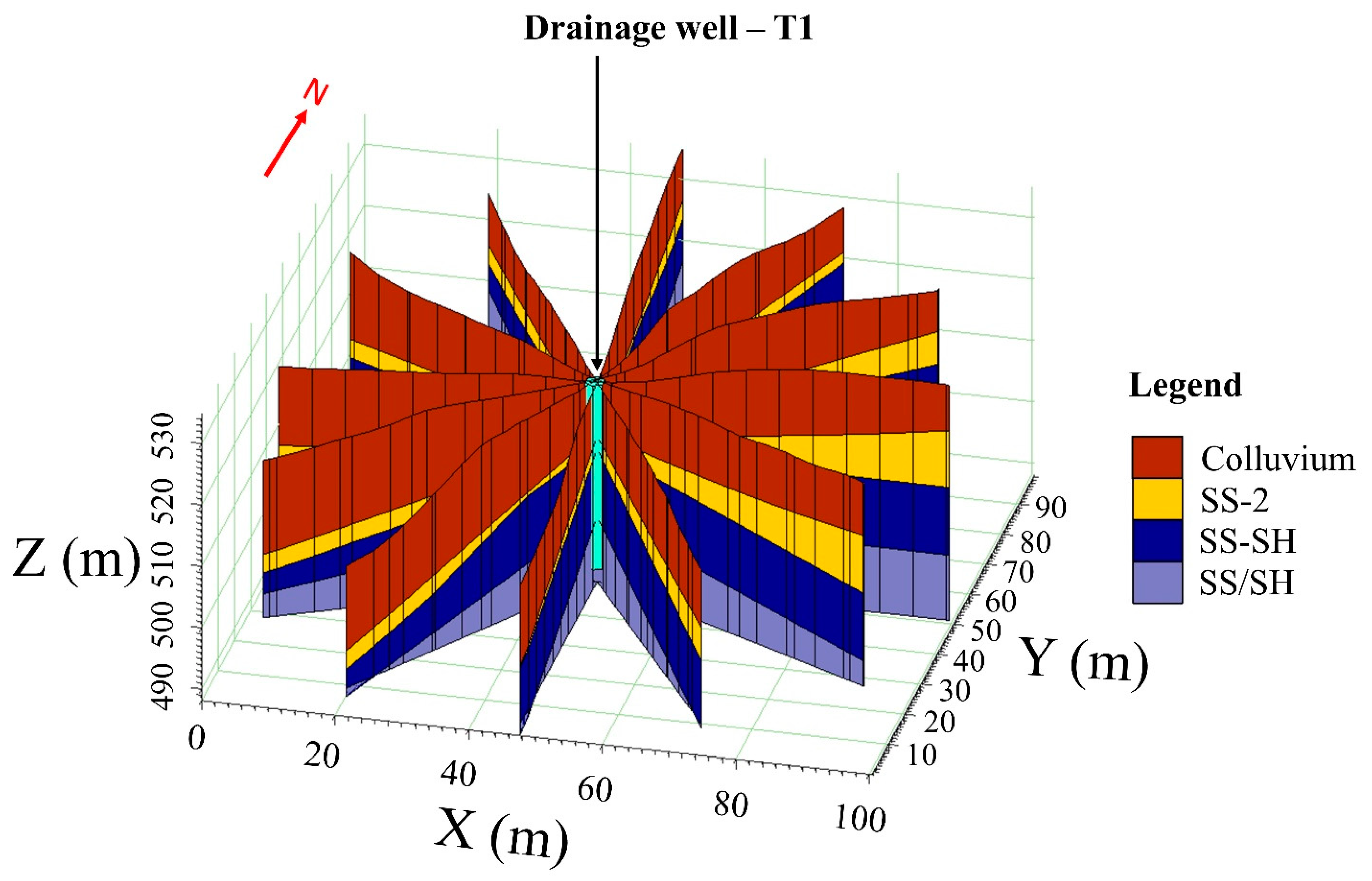
5.2. Application of the 3D EGM to Drainage Well Design

To improve slope stability, the installation of sub-surface drainage wells is the most common approach. As a result, we attempted to optimize the number and spacing of horizontal drains. An effective design for sub-surface drainage utilizes horizontal drains capable of capturing groundwater flow before it infiltrates an unstable region susceptible to landslides [37]. Moreover, a reasonable drainage well site can only be achieved by first understanding the potential sliding surface, as well as the ground water flow and flow pattern, which can be accomplished by using a 3D EGM. The 3D EGM proposed in this study, therefore, can also be used to optimize the drainage efficiency of the considered slope in the future. Figure 18 depicts the position of the vertical drainage well, T1, that has already been constructed in the middle of the Huafan University campus by a local consultant company, in order to illustrate the spatial distribution of geological characteristics that interact with it through the three-dimensional profiles considered in this work.

6. Conclusions

In this study, we attempted to construct a 3D EGM of the dip slope located in the Mt. Dalun area, incorporating field geology and rock core data analysis. The spatial distribution of the colluvium and bedrock stratum interface was determined using interpolation and surface regression approaches, based on polynomial functions. The following conclusions were reached in this study:

(1)

The study area can be divided into three uniform geological zones belonging to the Mushan Formation. Two faults—the Nanshihkeng Fault and the A Fault—formed the boundaries of these three zones.

(2)

The interpretation of the borehole cores provided a clear overall stratigraphy of the sedimentary rocks in the area. In particular, there were nine rock units that could be distinguished, including thick sandstone and a variable proportion of interbedded shale and sandstone for Zones 1 and 2, in the following order of stratigraphic history: L1 (SH/SS), L2 (SS/SH), L3 (SS-SH), L4 (SS-1), L5 (SH/SS), L6 (SS/SH), L7(SS-SH), L8 (SS-2), and L9 (SH/SS). The thick sandstone (L4) identified as the key bed is dominated by thick medium-grained whitish sandstone, intercalated with thin dark black shale layers dispersed in a few spots in the massive sandstone. The top boundary of this rock unit was observed from the borehole samples, following which this key bed was used for surface regression. In Zone 3, the spatial distribution of the two thick sandstones was proposed in the 3D EGM model as the consequence of outcrop field geology measurements and topographical analysis, by applying a high-resolution DEM.

(3)

Loose material covered the slope with varying thicknesses. It was most densely distributed in the southwestern slope, at approximately 50 m thick, and became thinner in the upper elevations along the mountain ridge. According to the topographical features, the colluvium may consist of material from various sources, such as ancient landslides or bedrock deterioration. The geometry of the bedding plane was calculated, based on its distribution, as a plane generally dipping 15° to the southwest.

(4)

Along with the 3D EGM, the structural contour map obtained by bedding surface fitting using a second-order model revealed that the geometry of the geological interface (i.e., the top surface of the key bed) gradually changes its direction and dip inclination (Zone 1). Even though the bedding in Zones 2 and 3 proposed in this study was found to be planar, its orientation changed significantly in space. Therefore, the underground information in both zones needs to be supplemented in future research.

(5)

The possibility of the future dip slope failure might be assessed through the use of a combination of surficial/underground monitoring. The geological model that incorporated the time-series of the displacement of the slope surface, revealed three sliding mechanism types. The first one comprises the sliding surface at the interface between the fill and the colluvium. The second one involves creeping on the contact surface between the colluvium and the underlying bedrock. The third mechanism is sliding occurring within the interlayer as a bedding plane. The development of deep-seated landslides through gully erosion was also proposed. However, the slope failure occurs only as local sliding and it is spatially very limited.

The three-dimensional engineering-geological model was approved as a powerful tool for further landslide hazard and risk mitigation.