Lagrangian Coherent Structure Analysis on the Vegetated Compound Channel with Numerical Simulation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Governing Equations
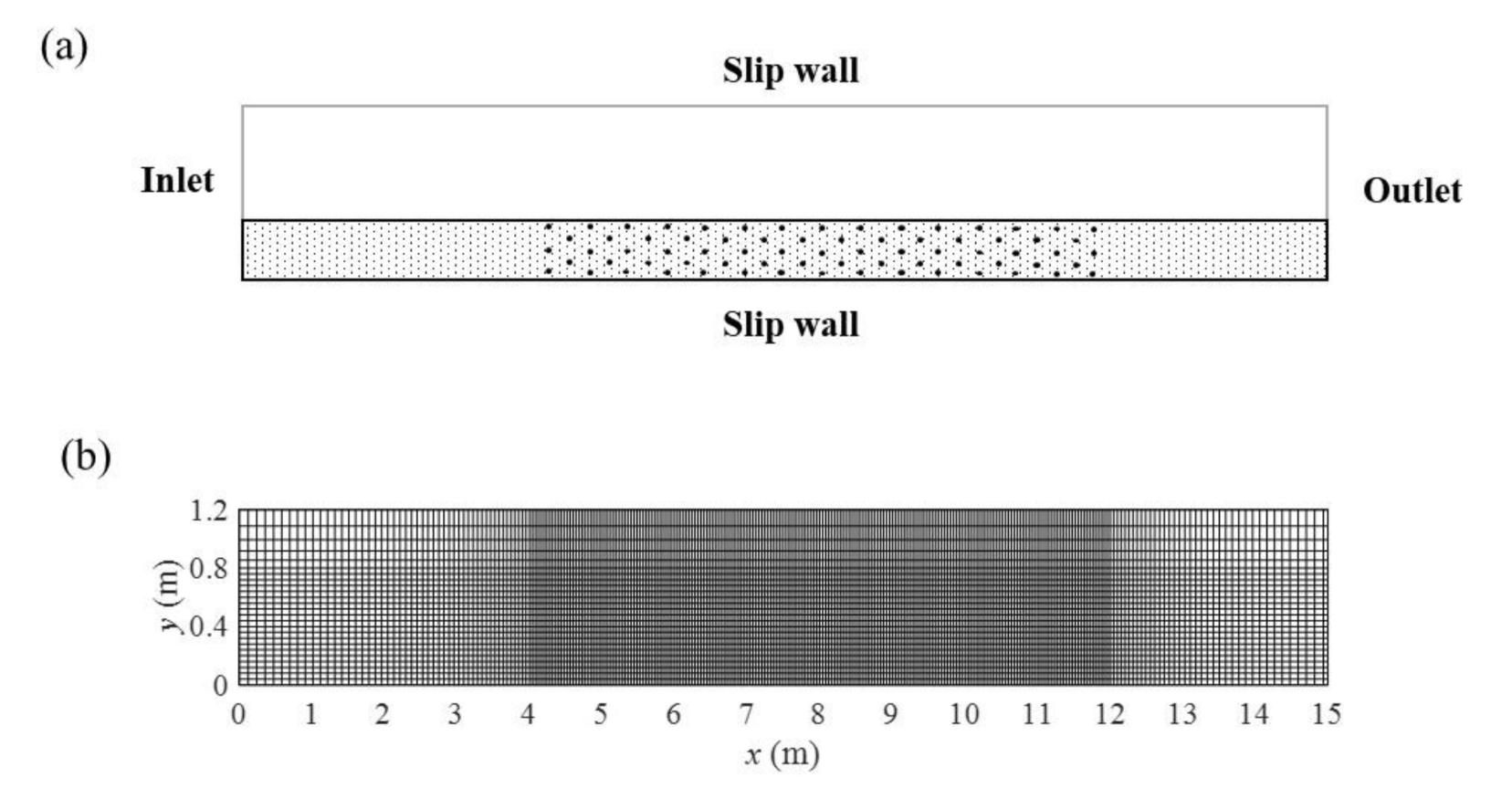
2.2. Numerical Model Setup
2.3. Finite-Time Lyapunov Exponent (FTLE)
2.4. Particle Tracking Method
3. Results and Discussion
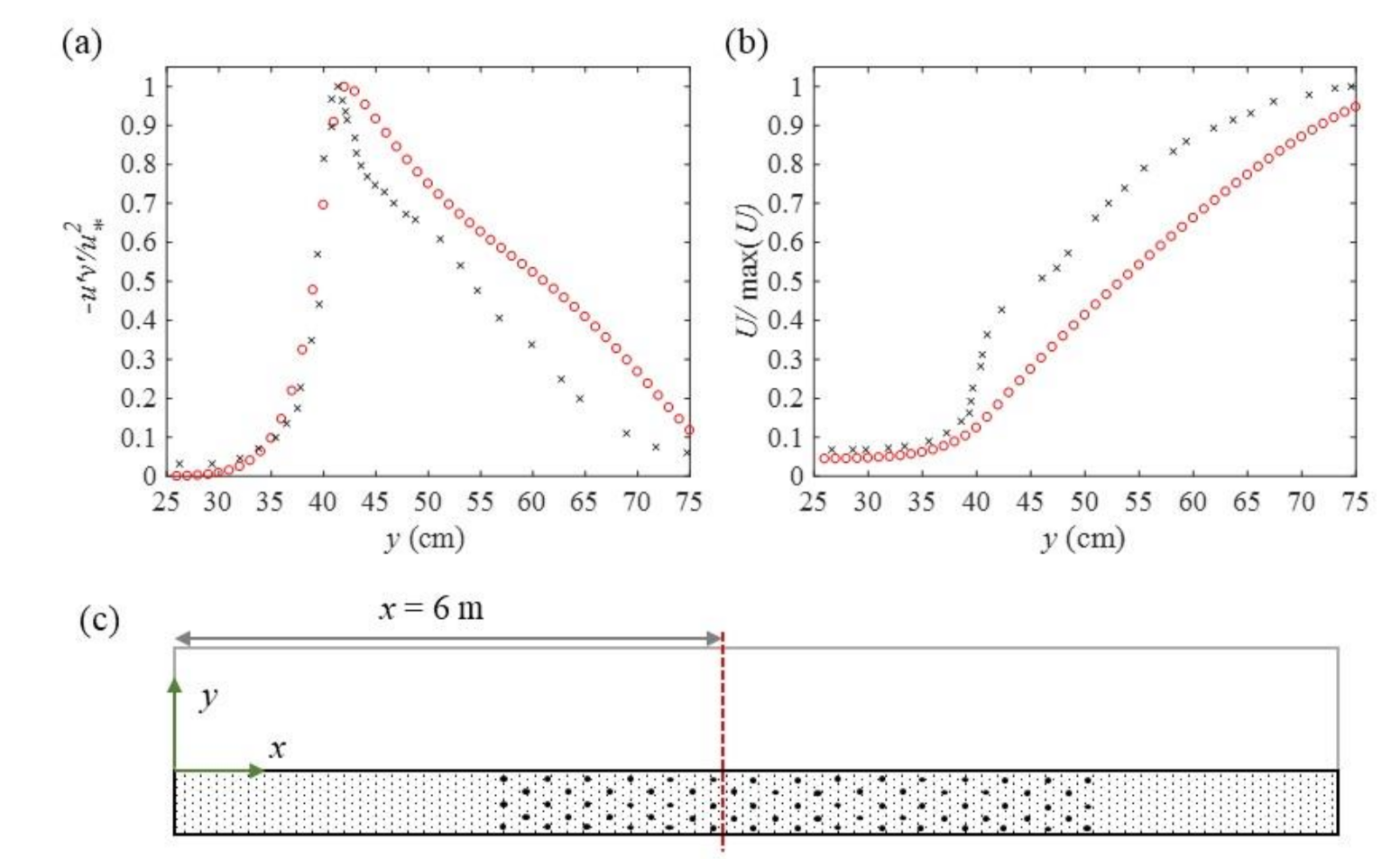
3.1. Validation of the LCS and CFD
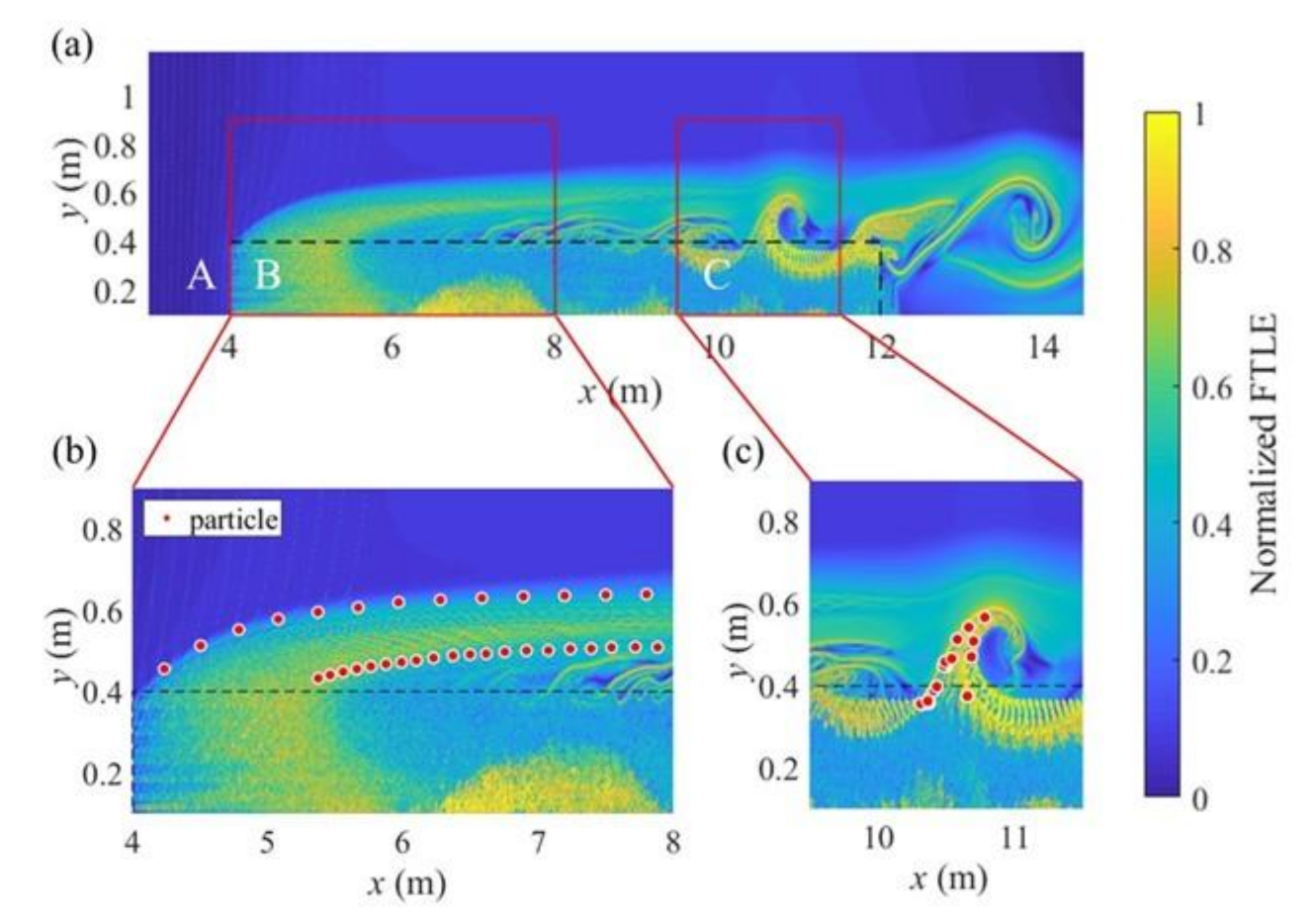
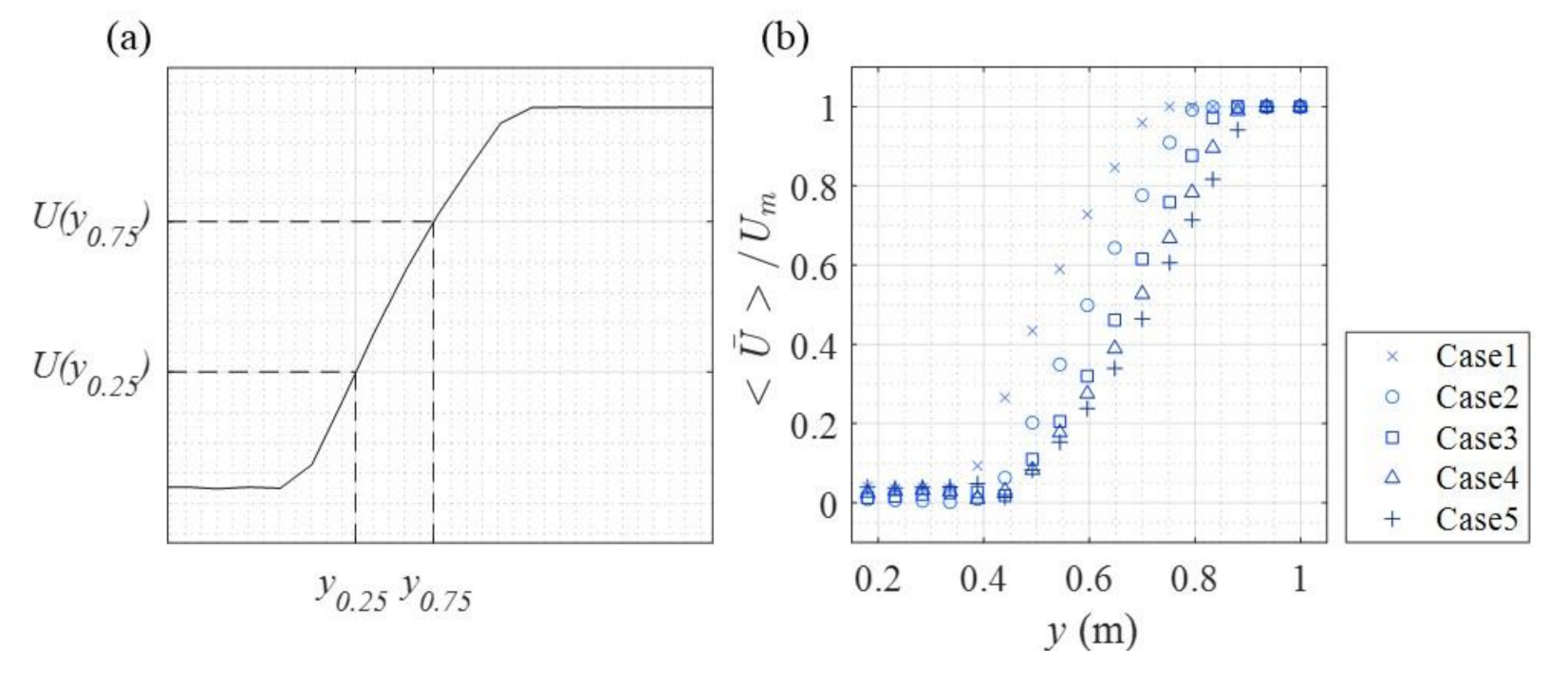
3.2. Simulation Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, P.L.F.; Chang, C.W.; Mei, C.C.; Lomonaco, P.; Martin, F.L.; Maza, M. Periodic water waves through an aquatic forest. Coast. Eng. 2015, 96, 100–117. [Google Scholar] [CrossRef]
- Kobayashi, N.; Raichle, A.W.; Asano, T. Wave attenuation by vegetation. J. Waterw. Port Coast. Ocean Eng. 1993, 119, 30–48. [Google Scholar] [CrossRef]
- Brunone, B.; Tomasicchio, G.R. Wave kinematics at steep slopes: Second-order model. J. Waterw. Port Coast. Ocean Eng. 1997, 123, 223–232. [Google Scholar] [CrossRef]
- Grove, A.S.; Shair, F.H.; Petersen, E.E. An experimental investigation of the steady separated flow past a circular cylinder. J. Fluid Mech. 1964, 19, 60–80. [Google Scholar] [CrossRef]
- Anderson, E.A.; Szewczyk, A.A. Effects of a splitter plate on the near wake of a circular cylinder in 2 and 3-dimensional flow configurations. Exp. Fluids 1997, 23, 161–174. [Google Scholar] [CrossRef]
- Brandon, D.J.; Aggarwal, S.K. A numerical investigation of particle deposition on a square cylinder placed in a channel flow. Aerosol Sci. Technol. 2001, 34, 340–352. [Google Scholar] [CrossRef]
- Vu, H.C.; Ahn, J.; Hwang, J.H. Numerical simulation of flow past two circular cylinders in tandem and side-by-side arrangement at low Reynolds numbers. KSCE J. Civ. Eng. 2016, 20, 1594–1604. [Google Scholar] [CrossRef]
- Zinke, P. Application of Porous Media Approach for Vegetation Flow Resistance; CRC Press: Boca Raton, FL, USA, 2012; pp. 301–307. [Google Scholar]
- Brito, M.; Fernandes, J.; Leal, J.B. Porous media approach for RANS simulation of compound open-channel flows with submerged vegetated floodplains. Environ. Fluid Mech. 2016, 16, 1247–1266. [Google Scholar] [CrossRef] [Green Version]
- Bennett, S.J.; Pirim, T.; Barkdoll, B.D. Using simulated emergent vegetation to alter stream flow direction within a straight experimental channel. Geomorphology 2002, 44, 115–126. [Google Scholar] [CrossRef]
- White, B.L.; Nepf, H.M. Shear instability and coherent structures in shallow flow adjacent to a porous layer. J. Fluid Mech. 2007, 593, 1–32. [Google Scholar] [CrossRef]
- White, B.L.; Nepf, H.M. A vortex-based model of velocity and shear stress in a partially vegetated shallow channel. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Zhang, J.T.; Su, X.H. Numerical model for flow motion with vegetation. J. Hydrodyn. 2008, 20, 172–178. [Google Scholar] [CrossRef]
- Zong, L.; Nepf, H. Flow and deposition in and around a finite patch of vegetation. Geomorphology 2010, 116, 363–372. [Google Scholar] [CrossRef]
- Park, H.; Hwang, J.H. Quantification of vegetation arrangement and its effects on longitudinal dispersion in a channel. Water Resour. Res. 2019, 55, 4488–4498. [Google Scholar] [CrossRef] [Green Version]
- Truong, S.H.; Uijttewaal, W.S.J. Transverse momentum exchange induced by large coherent structures in a vegetated compound channel. Water Resour. Res. 2019, 55, 589–612. [Google Scholar] [CrossRef]
- Tominaga, A.; Nezu, I. Turbulent structure in compound open-channel flows. J. Hydraul. Eng. 1991, 117, 21–41. [Google Scholar] [CrossRef]
- Sofialidis, D.; Prinos, P. Compound open-channel flow modeling with nonlinear low-Reynolds k-ϵ models. J. Hydraul. Eng. 1998, 124, 253–262. [Google Scholar] [CrossRef]
- Van Prooijen, B.C.; Battjes, J.A.; Uijttewaal, W.S. Momentum exchange in straight uniform compound channel flow. J. Hydraul. Eng. 2005, 131, 175–183. [Google Scholar] [CrossRef]
- Salamon, P.; Fernàndez-Garcia, D.; Gómez-Hernández, J.J. A review and numerical assessment of the random walk particle tracking method. J. Contam. Hydrol. 2006, 7, 277–305. [Google Scholar] [CrossRef]
- Zhang, P.F.; Wang, J.J.; Huang, L.X. Numerical simulation of flow around cylinder with an upstream rod in tandem at low Reynolds numbers. Appl. Ocean Res. 2006, 28, 183–192. [Google Scholar] [CrossRef]
- Shadden, S.C.; Lekien, F.; Marsden, J.E. Definition and properties of Lagrangian coherent structures from finite-time Lyapunov exponents in two-dimensional aperiodic flows. Phys. D Nonlinear Phenom. 2005, 212, 271–304. [Google Scholar] [CrossRef]
- Haller, G. Lagrangian coherent structures. Annu. Rev. Fluid Mech. 2015, 47, 137–162. [Google Scholar] [CrossRef] [Green Version]
- Son, Y.B.; Kim, Y.H.; Choi, B.-J.; Park, Y.-G. Lagrangian coherent structures and the dispersion of green algal bloom in the Yellow and East China Sea. J. Coast. Res. 2015, 75, 1237–2141. [Google Scholar] [CrossRef]
- Ku, H.; Hwang, J.H. The Lagrangian Coherent Structure and the Sediment Particle Behavior in the Lock Exchange Stratified Flows. J. Coast. Res. 2018, 85, 976–980. [Google Scholar] [CrossRef]
- Fischer-Antze, T.; Stoesser, T.; Bates, P.; Olsen, N.R.B. 3D numerical modelling of open-channel flow with submerged vegetation. J. Hydraul. Res. 2001, 39, 303–310. [Google Scholar] [CrossRef]
- Neary, V.S. Numerical solution of fully developed flow with vegetative resistance. J. Eng. Mech. 2003, 129, 558–563. [Google Scholar] [CrossRef]
- Woelke, M. Eddy Viscosity Turbulence Models employed by Computational Fluid Dynamic. Prace Inst. Lotnictwa 2007, 4, 92–113. [Google Scholar]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model. Turbul. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Open, C.F.D. OpenFOAM user guide. OpenFOAM Found. 2011, 2, 103. [Google Scholar]
- López, A.; Nicholls, W.; Stickland, M.T.; Dempster, W.M. CFD study of jet impingement test erosion using Ansys Fluent® and OpenFoam®. Comput. Phys. Commun. 2015, 197, 88–95. [Google Scholar] [CrossRef] [Green Version]
- Luo, K.; Fan, J.; Jin, H.; Cen, K. LES of the turbulent coherent structures and particle dispersion in the gas–solid wake flows. Powder Technol. 2004, 147, 49–58. [Google Scholar] [CrossRef]
- Green, M.A.; Rowley, C.W.; Haller, G. Detection of Lagrangian coherent structures in three-dimensional turbulence. J. Fluid Mech. 2007, 572, 111–120. [Google Scholar] [CrossRef] [Green Version]
- Voth, G.A.; Haller, G.; Gollub, J.P. Experimental measurements of stretching fields in fluid mixing. Phys. Rev. Lett. 2002, 88, 254501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mathur, M.; Haller, G.; Peacock, T.; Ruppert-Felsot, J.E.; Swinney, H.L. Uncovering the Lagrangian skeleton of turbulence. Phys. Rev. Lett. 2007, 98, 144502. [Google Scholar] [CrossRef]
- Rempel, E.L.; Chian, A.C.; Brandenburg, A. Lagrangian chaos in an ABC-forced nonlinear dynamo. Phys. Scr. 2012, 86, 018405. [Google Scholar] [CrossRef] [Green Version]
- John, O.D. LCS MATLAB Kit Version 2.3; California Institute of Technology, Pasadena, California, USA. Available online: http://dabirilab.com/software/. (accessed on 26 March 2016).
- Vallier, A. Tutorial icolagrangianfoam/solidparticle. In Peer Reviewed Tutorial, Hakan Nilsson, CFD with OpenSource Software; Chalmers University of Technology: Goteborg, Sweden, 2009. [Google Scholar]
- Lau, T.C.; Nathan, G.J. The effect of Stokes number on particle velocity and concentration distributions in a well-characterised, turbulent, co-flowing two-phase jet. J. Fluid Mech. 2016, 809, 72–110. [Google Scholar] [CrossRef] [Green Version]
- Mahir, N.; Altaç, Z. Numerical investigation of convective heat transfer in unsteady flow past two cylinders in tandem arrangements. Int. J. Heat Fluid Flow 2008, 29, 1309–1318. [Google Scholar] [CrossRef]




| Test Case | Case 1 | Case 2 | Case 3 | Case 4 | Case 4-1 | Case 5 | |
|---|---|---|---|---|---|---|---|
| ) | 0.050 | 0.103 | 0.077 | 0.062 | 0.051 | 0.130 | 0.044 |
| Domain Size ) | |||||||
| ) | 4.0 | 0.6 | 0.6 | 0.6 | 0.6 | 0.6 | 0.6 |
| 1.00 | 1.00 | 0.67 | 0.50 | 0.40 | 0.40 | 0.33 |
| Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | |
|---|---|---|---|---|---|
| ) | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, S.; Hwang, J.H. Lagrangian Coherent Structure Analysis on the Vegetated Compound Channel with Numerical Simulation. Water 2022, 14, 406. https://doi.org/10.3390/w14030406
Choi S, Hwang JH. Lagrangian Coherent Structure Analysis on the Vegetated Compound Channel with Numerical Simulation. Water. 2022; 14(3):406. https://doi.org/10.3390/w14030406
Chicago/Turabian StyleChoi, Seongeun, and Jin Hwan Hwang. 2022. "Lagrangian Coherent Structure Analysis on the Vegetated Compound Channel with Numerical Simulation" Water 14, no. 3: 406. https://doi.org/10.3390/w14030406






