Scour Propagation Rates around Offshore Pipelines Exposed to Currents by Applying Data-Driven Models
Abstract
:1. Introduction
2. Overview of Databases
2.1. Dimensional Analysis
2.2. Description of Experimental Data
3. Implementation of ML Models
3.1. Gene-Expression Programming
3.2. Multivariate Adaptive Regression Splines
3.3. Evulotionary Polynomial Regression
3.4. M5 Model Tree
4. Discussion
4.1. Statistical Measures
4.2. Statistical Performance of ML Models
4.3. Comparisons between ML Models and Related Works Regarding Complexity
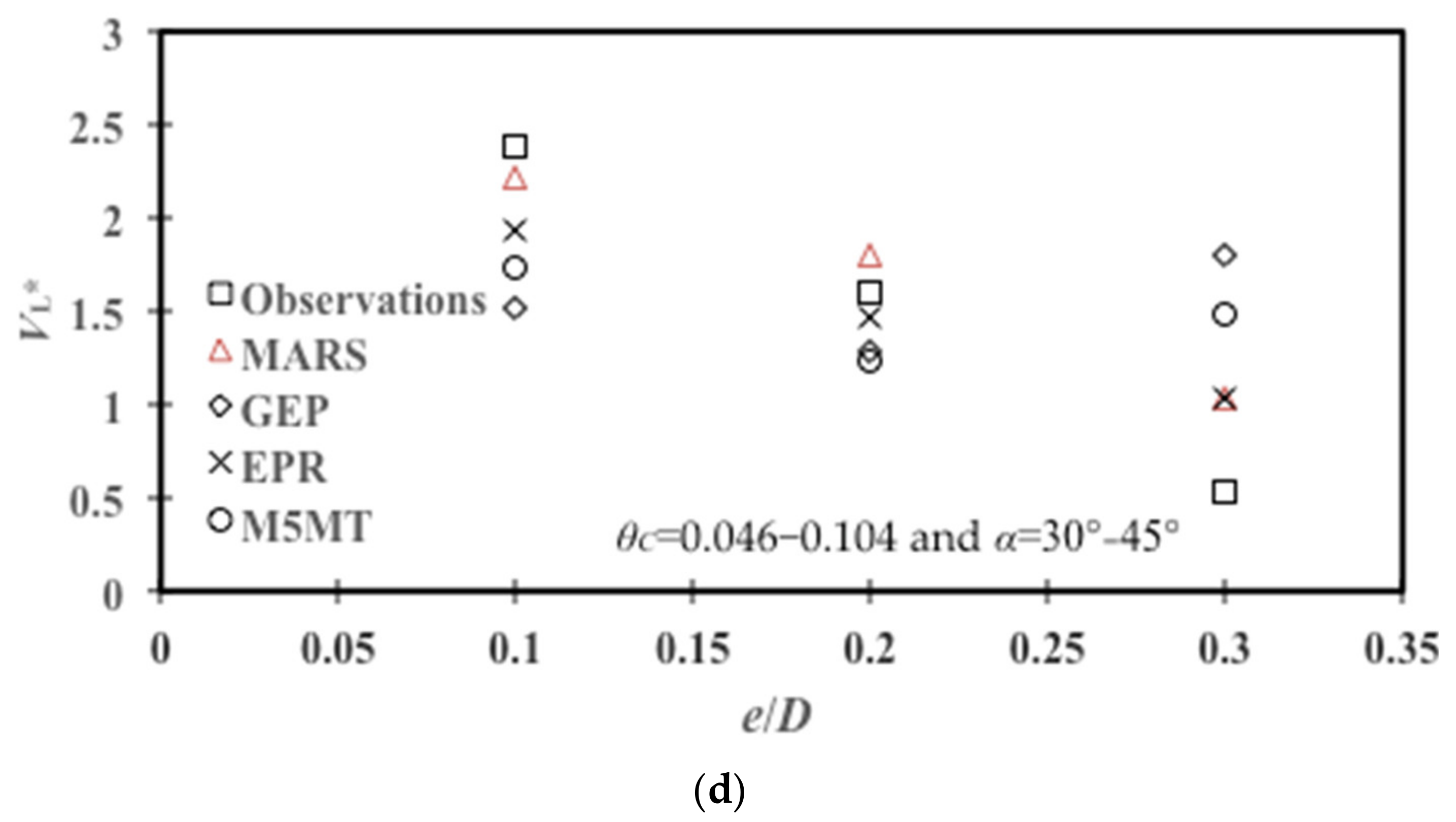
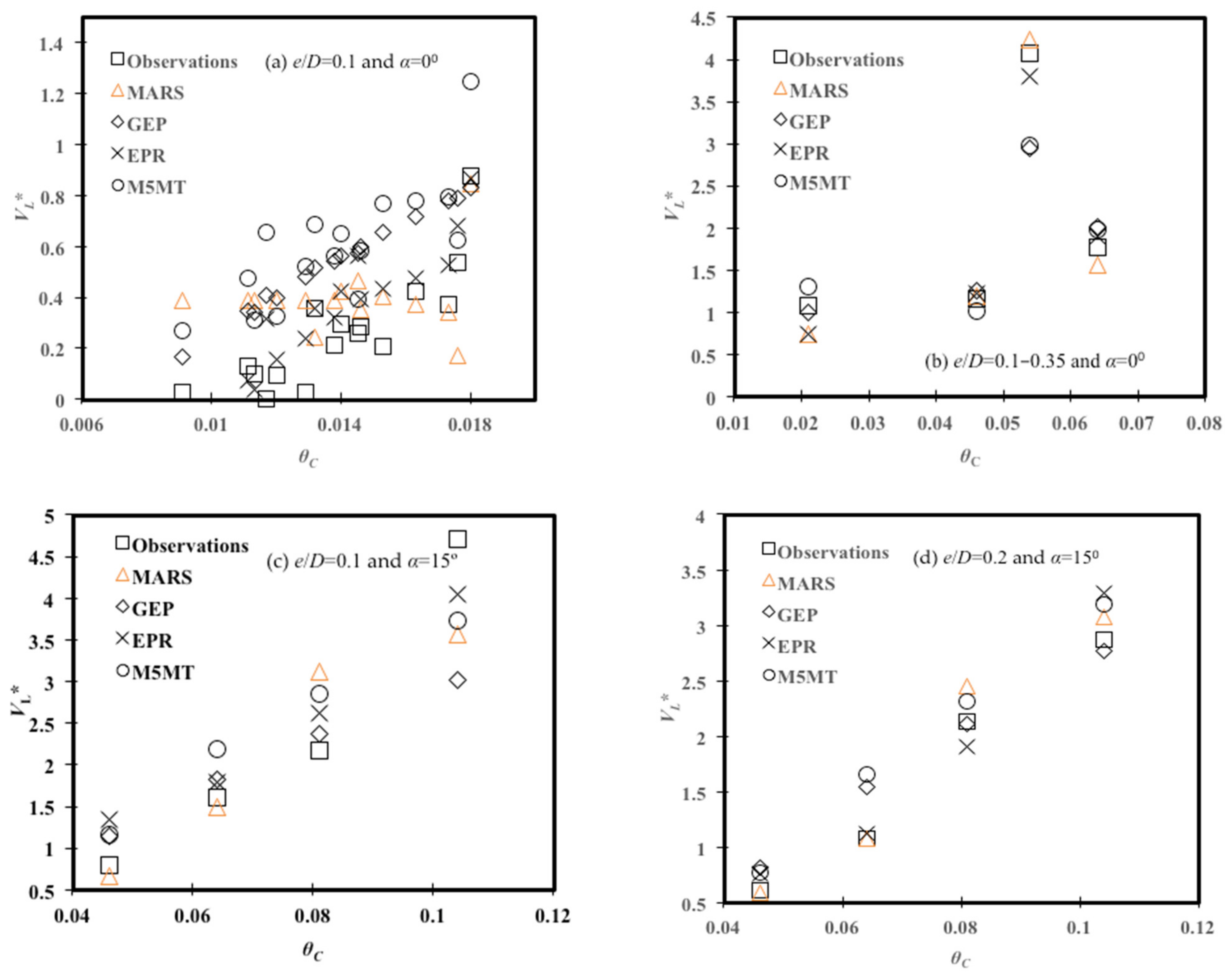
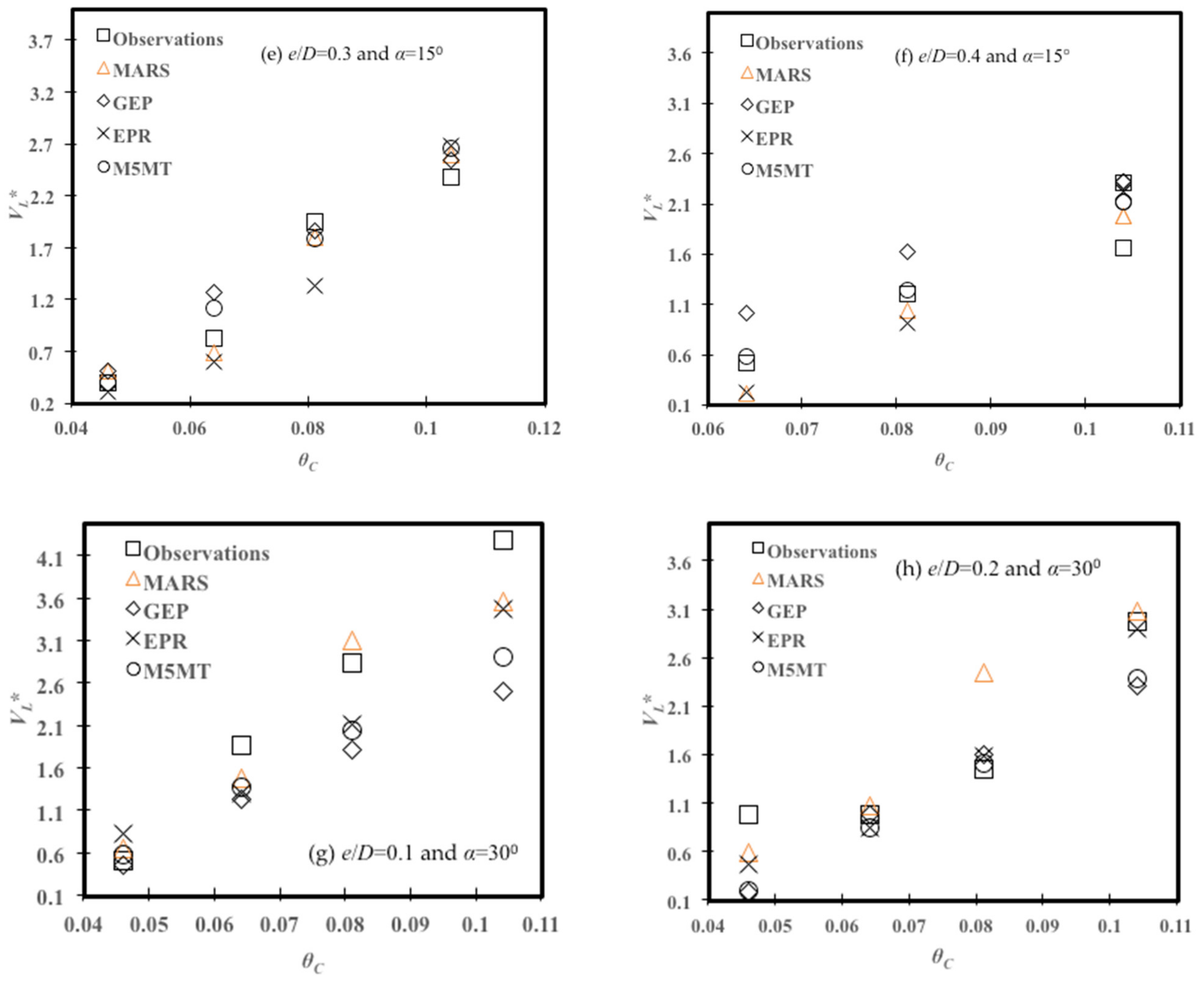
4.4. Effects of the Pipeline Embedment Depth
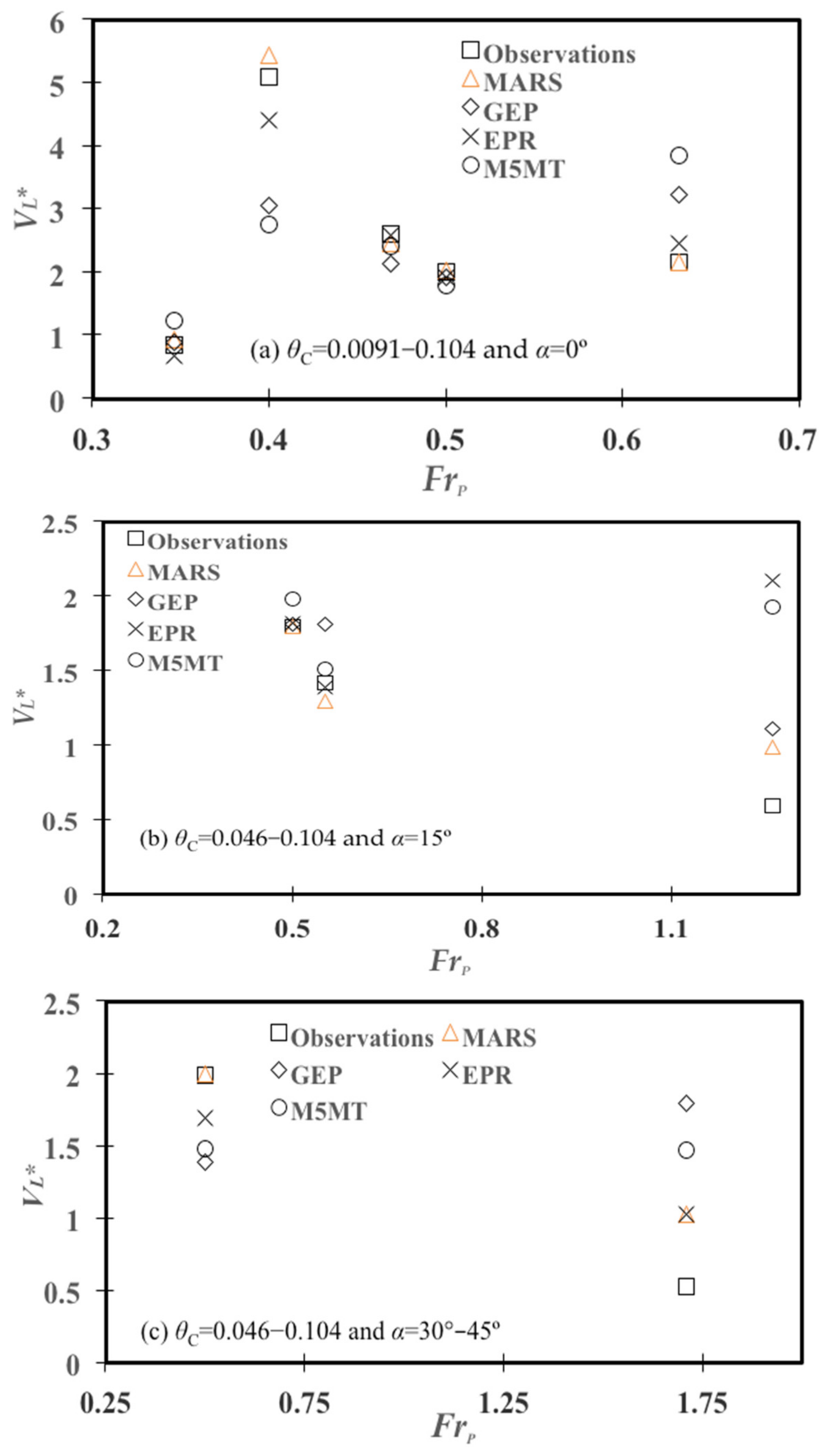
4.5. Effects of the Shields Parameter
4.6. Effects of the Approach Flow Froude Number
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bai, Y.; Bai, Q. Subsea Engineering Handbook; Gulf Professional Publishing: Burlington, MA, USA, 2010. [Google Scholar]
- Barrette, P. Offshore pipeline protection against seabed gouging by ice: An overview. Cold Reg. Sci. Technol. 2011, 69, 3–20. [Google Scholar] [CrossRef]
- Palmer, A.C.; Been, K. Pipeline geohazards for Arctic conditions. In Deepwater Foundations and Pipeline Geomechanics; McCarron, W.O., Ed.; J. Ross Publishing: Fort Lauderdale, FL, USA, 2011; pp. 171–178. [Google Scholar]
- Palmer, A.C.; King, R.A. Subsea Pipeline Engineering, 2nd ed.; PennWell Corporation: Tulsa, OK, USA, 2008. [Google Scholar]
- Ramakrishnan, T.V. Offshore Engineering; Gene-Tech Books: New Delhi, India, 2008. [Google Scholar]
- Cheng, L.; Yeow, K.; Zhang, Z.; Teng, B. Three-dimensional scour below offshore pipelines in steady currents. Coast. Eng. 2009, 56, 577–590. [Google Scholar] [CrossRef]
- Wu, Y.; Chiew, Y.-M. Three-dimensional scour at submarine pipelines. J. Hydraul. Eng. ASCE 2012, 138, 788–795. [Google Scholar] [CrossRef]
- Wu, Y.; Chiew, Y.-M. Mechanics of three-dimensional pipeline scour in unidirectional steady current. J. Pipeline Syst. Eng. 2013, 4, 3–10. [Google Scholar] [CrossRef]
- Cheng, L.; Yeow, K.; Zang, Z.; Li, F. 3D scour below pipelines under waves and combined waves and currents. Coast. Eng. 2014, 83, 137–149. [Google Scholar] [CrossRef] [Green Version]
- Fredsøe, J.; Sumer, B.M.; Arnskov, M.M. Time scale for wave/current scour below pipelines. Int. J. Offshore Polar Eng. 1992, 2, 13–17. [Google Scholar]
- Sumer, B.M.; Fredsøe, J. Scour around pipelines in combined waves and current. In Proceedings of the 15th Conference on Offshore Mechanics and Arctic Engineering (OMAE), Florence, Italy, 16–20 June 1996. [Google Scholar]
- Sumer, B.M.; Truelsen, C.; Sichmann, T.; Fredsøe, J. Onset of scour below pipelines and self-burial. Coast. Eng. 2001, 42, 313–335. [Google Scholar] [CrossRef]
- Arya, A.K.; Shingan, B. Scour-mechanism, detection and mitigation for subsea pipeline integrity. Int. J. Eng. Technol. 2012, 1, 1–14. [Google Scholar]
- Zhang, B.; Gong, R.; Wang, T.; Wang, Z. Causes and treatment measures of submarine pipeline free-spanning. J. Mar. Sci. Eng. 2020, 8, 329. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Saberi-Movahed, F. GMDH-GEP to predict free span expansion rates below pipelines under waves. Mar. Georesour. Geotec. 2019, 37, 375–392. [Google Scholar] [CrossRef]
- Ehteram, M.; Ahmed, A.N.; Ling, L.; Fai, C.M.; Latif, S.D.; Afan, H.A.; Banadkooki, F.B.; El-Shafie, A. Pipeline scour rates prediction-based model utilizing a Multilayer Perceptron-Colliding Body algorithm. Water 2020, 12, 902. [Google Scholar] [CrossRef] [Green Version]
- Najafzadeh, M.; Oliveto, G. Exploring 3D wave-induced scouring patterns around subsea pipelines with artificial intelligence techniques. Appl. Sci. 2021, 11, 3792. [Google Scholar] [CrossRef]
- Hansen, E.A.; Staub, C.; Fredsøe, J.; Sumer, B.M. Time-development of scour induced free spans of pipelines. In Proceedings of the 10th Conference on Offshore Mechanics and Arctic Engineering (OMAE), Stavanger, Norway, 23–28 June 1991. [Google Scholar]
- Ferreira, C. Gene expression programming: A new adaptive algorithm for solving problems. Complex Syst. 2001, 13, 87–129. [Google Scholar]
- Ferreira, C. Gene Expression Programming, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Friedman, J.H. Multivariate adaptive regression splines. Ann. Statist. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Giustolisi, O.; Savic, D.A. A symbolic data-driven technique based on evolutionary polynomial regression. J. Hydroinf. 2006, 8, 207–222. [Google Scholar] [CrossRef] [Green Version]
- Giustolisi, O.; Savic, D.A. Advances in data-driven analyses and modelling using EPR-MOGA. J. Hydroinf. 2009, 11, 225–236. [Google Scholar] [CrossRef]
- Giustolisi, O.; Doglioni, A.; Savic, D.A.; Webb, B.W. A multi-model approach to analysis of environmental analysis. Environ. Modell. Softw. 2007, 22, 674–682. [Google Scholar] [CrossRef] [Green Version]
- Savic, D.A.; Giustolisi, O.; Berardi, L.; Shepherd, W.; Djordjevic, S.; Saul, A. Modelling sewer failure by evolutionary computing. In Proceedings of the Institution of Civil Engineers-Water Management; Thomas Telford Ltd: London, UK, 2006; Volume 159, pp. 111–118. [Google Scholar] [CrossRef]
- Berardi, L.; Giustolisi, O.; Kapelan, Z.; Savic, D.A. Development of pipe deterioration models for water distribution systems using EPR. J. Hydroinf. 2008, 10, 113–126. [Google Scholar] [CrossRef] [Green Version]
- Quinlan, J.R. Learning with continuous classes. In Proceedings of the Australian Joint Conference on Artificial Intelligence (AI’92), Hobart, Australia, 16–18 November 1992. [Google Scholar]
- Mokhtia, M.; Eftekhari, M.; Saberi-Movahed, F. Dual-manifold regularized regression models for feature selection based on hesitant fuzzy correlation. Knowl Based Syst. 2021, 229, 107308. [Google Scholar] [CrossRef]
- Mokhtia, M.; Eftekhari, M.; Saberi-Movahed, F. Feature selection based on regularization of sparsity based regression models by hesitant fuzzy correlation. Appl. Soft Comput. 2020, 91, 106255. [Google Scholar] [CrossRef]
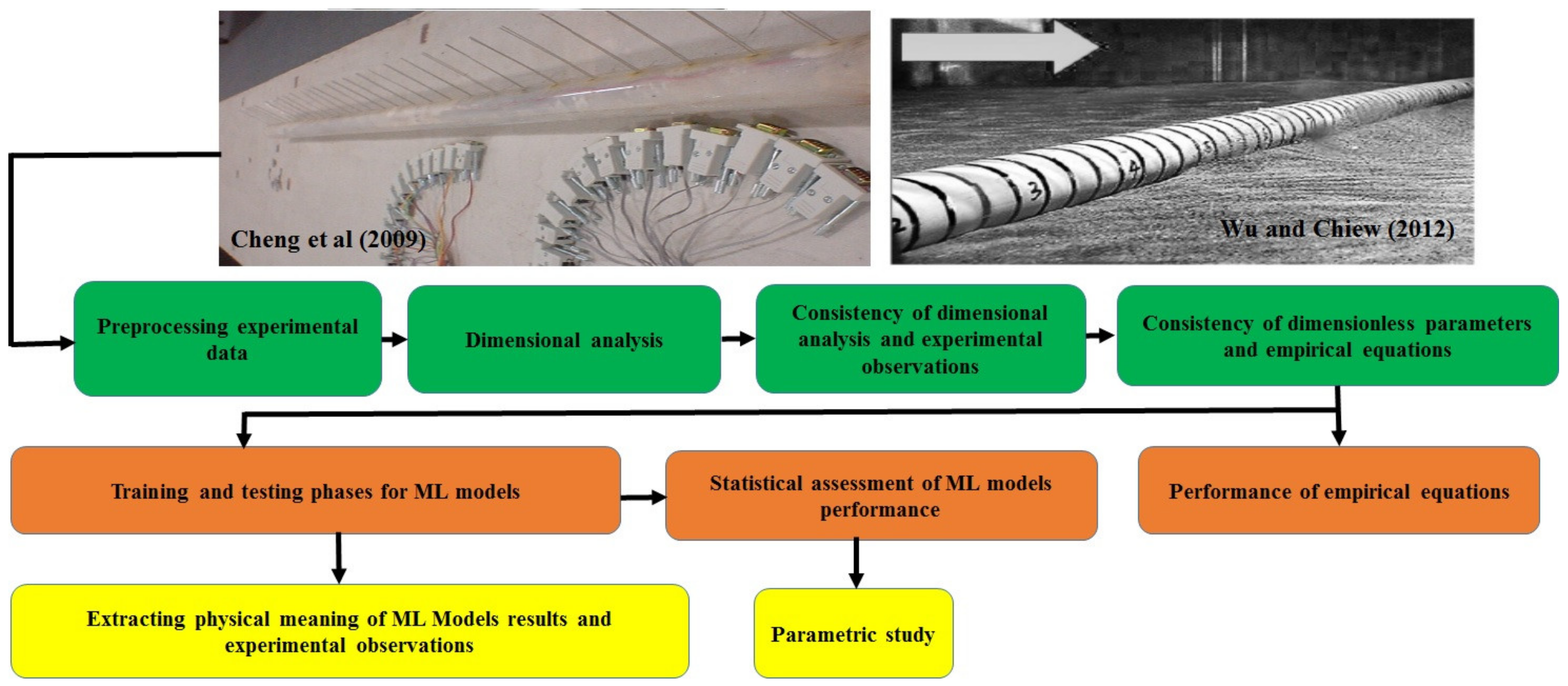



| Dimensional Variables | Minimum | Maximum | Average | Standard Deviation | Skewness |
| D (m) | 0.020 | 0.116 | 0.04425 | 0.012 | 1.538 |
| e (m) | 0.0 | 0.025 | 0.00848 | 0.00643 | 1.168 |
| d50 (m) | 0.0002 | 0.00057 | 0.00055 | 0.0000719 | −4.7055 |
| u* (m/s) | 0.0091 | 0.0314 | 0.02065 | 0.00624 | 0.2595 |
| α (degree) | 0 | 45 | 5.454 | 10.1027 | 1.8212 |
| UC (m/s) | 0.158 | 0.42 | 0.2817 | 0.07571 | 0.5154 |
| y (m) | 0.09 | 0.470 | 0.2992 | 0.156 | 0.1067 |
| VL (m/s) | 0.0000084 | 0.0056 | 0.00154 | 0.00122 | 1.2503 |
| Dimensionless Parameters | Minimum | Maximum | Average | Standard Deviation | Skewness |
| e/D | 0 | 0.5 | 0.1782 | 0.1256 | 1.224 |
| θC | 0.0091 | 0.104 | 0.04527 | 0.03221 | 0.5974 |
| FrP | 0.225 | 0.6321 | 0.4354 | 0.0927 | 0.4613 |
| ReP | 5600 | 21,000 | 14,087.02 | 3917.98 | 0.40736 |
| VL* | 0.0000481 | 5.1082 | 0.9057 | 1.277 | 1.4825 |
| Parameters | Description of Parameters | Setting of Parameters |
|---|---|---|
| P1 | Function set | +, −, ×, /, Power(x2), (1-x), Average(x1, x2), Tanh(x), 3Rt, Ln, Min, Max |
| P2 | Linking function | Addition |
| P3 | Mutation rate | OE (0.003), CFT (0), MFT (0), SSS (0) |
| P4 | Inversion rate | OE (0.00546), CFT (0), MFT (0), SSS (0.0082) |
| P5 | One-point and two-point recombination rates | OE (0.00277), CFT (0), MFT (0), SSS (0.0028) |
| P6 | Gene recombination rate | OE (0.00277), CFT (0), MFT (0.0129), SSS (0.0028) |
| P7 | Permutation | OE (0.00546), CFT (0), MFT (0), SSS (0.0082) |
| P8 | Maximum tree depth | OE (4), CFT (3), MFT (5), SSS (4) |
| P9 | Number of genes | 3 |
| P10 | Number of chromosomes | 30 |
| P11 | Number of generations | OE (1713), CFT (961), MFT (2700), SSS (909) |
| P12 | Best fitness value | OE (544.516), CFT (467.144), MFT (565.876), SSS (536.205) |
| k-Fold | Number of BFs in the Final Model | Total Effective Number of Parameters | Executive Time (s) |
|---|---|---|---|
| 1 | 11 | 26 | 0.57 |
| 2 | 7 | 16 | 0.69 |
| 3 | 14 | 33.5 | 0.99 |
| 4 | 9 | 21 | 0.71 |
| 5 | 12 | 28.5 | 0.74 |
| 6 | 12 | 28.5 | 0.66 |
| 7 | 11 | 26 | 0.67 |
| 8 | 12 | 28.5 | 0.99 |
| 9 | 6 | 13.5 | 0.71 |
| 10 | 14 | 33.5 | 0.58 |
| Basis Functions | Basis Functions | ||
|---|---|---|---|
| BF1 | max (0, 0.1−e/D) | BF9 | max (0, FrP−0.34623)·max (0, 0.3−e/D) |
| BF2 | max (0, FrP−0.34623) | BF10 | max (0, FrP−0.34623)·max (0, e/D−0.3) |
| BF3 | max (0, FrP−0.34623)·max (0, 0.046−θC) | BF11 | max (0, FrP−0.47128) |
| BF4 | max (0, θC−0.018)·max (0, 0.1−e/D) | BF12 | max (0, 0.47128−FrP)·max (0, θC−0.014) |
| BF5 | max (0, FrP−0.34623)·max (0, 0.054−θC) | BF13 | max (0, θC−0.014) |
| BF6 | max (0, 1−sinα)·max (0, θC−0.021) | BF14 | max (0, e/D−0.6) |
| BF7 | max (0, 0.1−e/D)·max (0, FrP−0.52841) | BF15 | max (0, 0.6−e/D) |
| BF8 | max (0, 0.1−e/D)·max (0, 0.52841−FrP) | BF16 | 0 |
| Model No. | Expression | MSE |
|---|---|---|
| Model #1 | 0.582 | |
| Model #2 | 0.460 | |
| Model #3 | 0.449 | |
| Model #4 | 0.437 | |
| Model #5 | 0.341 |
| Model No. | Expression | MSE |
|---|---|---|
| Model #1 | 0.747 | |
| Model #2 | 0.646 | |
| Model #3 | 0.620 | |
| Model #4 | 0.596 | |
| Model #5 | 0.585 |
| Rules of M5MT#1 Focusing on Pruning and Smoothing Phases | |
|---|---|
| If θC ≤ 0.018: | |
| | If θC ≤ 0.013:LM1 | |
| | If θC > 0.013:LM2 | |
| If θC > 0.018 : | |
| | If θC ≤ 0.05:LM3 | |
| | If θC > 0.05:LM4 | |
| Multilinear Regression Equations | |
| LM1 | VL* = −2.0495 + 20.7493θC + 1.4622(1 − e/D) − 0.8277(1 + sinα) + 5.2496FrP |
| LM2 | VL* = −2.1368 + 16.5994θC + 1.4622(1 − e/D) − 0.8277(1 + sinα) + 5.7554FrP |
| LM3 | VL* = 0.062 + 18.2934θC + 3.8163(1 − e/D) − 2.4011(1 + sinα) − 0.3838FrP |
| LM4 | VL* = −2.0857 + 24.1656θC + 5.3836(1 − e/D) − 3.3503(1 + sinα) + 4.4672FrP |
| Multilinear Regression Equations | |
|---|---|
| LM1 | VL* = 0.0512 |
| LM2 | VL* = −0.6047 + 2.5289FrP |
| LM3 | VL* = 0.062 + 37.1095θC + 4.4068(1 − e/D) − 2.899(1 + sinα) − 10.5248FrP |
| LM4 | VL* = −1.1712 + 45.4636θC + 7.2873(1 − e/D) − 4.6271(1 + sinα) |
| If θC ≤ 0.018 : | If θC ≤ 0.013 : LM1 | If θC > 0.013 : | | If FrP ≤ 0.367 : LM2 | | If FrP > 0.367 : | | | If θC ≤ 0.015 : LM3 | | | If θC > 0.015 : LM4 If θC > 0.018 : | If θC ≤ 0.05 : | | If FrP ≤ 0.361 : | | | If 1 − e/D ≤ 0.89 : | | | | If 1 − e/D ≤ 0.82 : LM5 | | | | If 1 − e/D > 0.82 : LM6 | | | If 1 − e/D > 0.89 : | | | | If 1 − e/D ≤ 0.94 : LM7 | | | | If 1 − e/D > 0.94 : LM8 | | If FrP > 0.361 : | | | If 1 + sinα ≤ 1.129 : | | | | If θC ≤ 0.019 : | | | | | If FrP ≤ 0.425 : LM9 | | | | | If FrP > 0.425 : LM10 | | | | If θC > 0.019 : | | | | | If FrP ≤ 0.387 : LM11 | | | | | If FrP > 0.387 : | | | | | | If 1 − e/D < = 0.7 : LM12 | | | | | | If 1 − e/D > 0.7 : | | | | | | | If FrP ≤ 0.42 : LM13 | | | | | | | If FrP > 0.42 : LM14 | | | If 1 + sinα > 1.129 : | | | | If 1 − e/D ≤ 0.85 : LM15 | | | | If 1 − e/D > 0.85 : LM16 | If θC > 0.05 : | | If 1 + sinα ≤ 1.129 : | | | If 1 − e/D ≤ 0.75 : | | | | If θC ≤ 0.092 : | | | | | If 1 − e/D ≤ 0.65 : LM17 | | | | | If 1 − e/D > 0.65 : LM18 | | | | If θC > 0.092 : LM19 | | | If 1 − e/D > 0.75 : | | | | If 1 − e/D ≤ 0.95 : | | | | | If θC ≤ 0.073 : | | | | | | If θC ≤ 0.059 : LM20 | | | | | | If θC ≤ 0.059 : LM20 | | | | | | If θC > 0.059 : LM21 | | | | | If θC > 0.073 : LM22 | | | | If 1 − e/D > 0.95 : LM23 | | If 1 + sinα > 1.129 : | | | If θC ≤ 0.092 : | | | | If 1 − e/D ≤ 0.85 : | | | | | If θC ≤ 0.073 : LM24 | | | | | If θC > 0.073 : | | | | | | If 1 − e/D ≤ 0.75 : LM25 | | | | | | If 1 − e/D > 0.75 : LM26 | | | | If 1 − e/D > 0.85 : LM27 | | | If θC > 0.092 : | | | | If 1 − e/D ≤ 0.75 : LM28 | | | | If 1 − e/D > 0.75 : LM29 |
| Multilinear Regression Equations | |
|---|---|
| LM1 | VL* = −2.0495 + 20.7493θC + 1.4622(1 − e/D) − 0.8277(1 + sinα) + 5.2496FrP |
| LM2 | VL* = −2.0955 + 16.5994θC + 1.46222(1 − e/D) − 0.8277(1 + sinα) + 5.629FrP |
| LM3 | VL* = −2.0867 + 16.5994θC + 1.46222(1 − e/D) − 0.8277(1 + sinα) + 5.629FrP |
| LM4 | VL* = −2.0876 + 16.5994θC + 1.46222(1 − e/D) − 0.8277(1 + sinα) + 5.629FrP |
| LM5 | VL* = −1.5165 + 11.9305θC + 4.4349(1 − e/D) − 1.904(1 + sinα) + 1.4209FrP |
| LM6 | VL* = −1.5153 + 11.9305θC + 4.4349(1 − e/D) − 1.904(1 + sinα) + 1.4209FrP |
| LM7 | VL* = −1.3564 + 11.9305θC + 4.4349(1 − e/D) − 1.904(1 + sinα) + 1.4209FrP |
| LM8 | VL* = −1.3597 + 37.1095θC + 4.4068(1 − e/D) − 1.904(1 + sinα) + 1.4209FrP |
| LM9 | VL* = −0.9468 + 14.6674θC + 3.2431(1 − e/D) − 1.9373(1 + sinα) + 2.3725FrP |
| LM10 | VL* = −0.9462 + 14.6674θC + 3.2431(1 − e/D) − 1.9373(1 + sinα) + 2.3725FrP |
| LM11 | VL* = −1.0046 + 14.6674θC + 3.2431(1 − e/D) − 1.9373(1 + sinα) + 2.5936FrP |
| LM12 | VL* = −0.9923 + 14.1337θC + 3.2539(1 − e/D) − 1.9373(1 + sinα) + 2.5434FrP |
| LM13 | VL* = −0.9881 + 14.1337θC + 3.2505(1 − e/D) − 1.9373(1 + sinα) + 2.5434FrP |
| LM14 | VL* = −0.9880 + 14.1337θC + 3.2505(1 − e/D) − 1.9373(1 + sinα) + 2.5434FrP |
| LM15 | VL* = −0.7742 + 13.7781θC + 3.2258(1 − e/D) − 2.0772(1 + sinα) + 2.3725FrP |
| LM16 | VL* = −0.7732 + 13.7781θC + 3.2258(1 − e/D) − 2.0772(1 + sinα) + 2.3725FrP |
| LM17 | VL* = −3.6161 + 26.0093θC + 5.6375(1 − e/D) − 2.1206(1 + sinα) + 4.4672FrP |
| LM18 | VL* = −3.6169 + 26.0093θC + 5.6465(1 − e/D) − 2.1206(1 + sinα) + 4.4672FrP |
| LM19 | VL* = −3.6173 + 26.7266θC + 5.5808(1 − e/D) − 2.1206(1 + sinα) + 4.4672FrP |
| LM20 | VL* = −2.6839 + 21.7296θC + 4.8669(1 − e/D) − 2.1206(1 + sinα) + 4.4672FrP |
| LM21 | VL* = −2.6847 + 21.7296θC + 4.8669(1 − e/D) − 2.1206(1 + sinα) + 4.4672FrP |
| LM22 | VL* = −2.7195 + 22.4079θC + 4.8669(1 − e/D) − 2.1206(1 + sinα) + 4.4672FrP |
| LM23 | VL* = −2.6416 + 21.516θC + 4.8669(1 − e/D) − 2.1206(1 + sinα) + 4.4672FrP |
| LM24 | VL* = −3.2052 + 24.0158θC + 4.6143(1 − e/D) − 2.0809(1 + sinα) + 4.4672FrP |
| LM25 | VL* = −3.1911 + 23.9395θC + 4.6105(1 − e/D) − 2.0809(1 + sinα) + 4.4672FrP |
| LM26 | VL* = −3.1909 + 23.9395θC + 4.6105(1 − e/D) − 2.0809(1 + sinα) + 4.4672FrP |
| LM27 | VL* = −3.1238 + 23.2431θC + 4.6001(1 − e/D) − 2.0809(1 + sinα) + 4.4672FrP |
| LM28 | VL* = −3.1293 + 21.0132θC + 4.9544(1 − e/D) − 2.0809(1 + sinα) + 4.4672FrP |
| LM29 | VL* = −3.1079 + 21.0132θC + 4.9544(1 − e/D) − 2.0809(1 + sinα) + 4.4672FrP |
| Equation | VL* | Equation | VL* |
|---|---|---|---|
| LM1 | 0.0512 | LM16 | 0.6642 |
| LM2 | 0.2208 | LM17 | 1.2584 |
| LM3 | 0.4659 | LM18 | 2.8566 |
| LM4 | 0.3353 | LM19 | 3.4517 |
| LM5 | 0.2568 | LM20 | 3.4984 |
| LM6 | 0.5315 | LM21 | 2.3073 |
| LM7 | 2.6256 | LM22 | 4.3984 |
| LM8 | 1.8337 | LM23 | 4.6448 |
| LM9 | 0.4239 | LM24 | 0.7799 |
| LM10 | 0.6153 | LM25 | 1.5781 |
| LM11 | 0.8379 | LM26 | 1.7987 |
| LM12 | 0.5844 | LM27 | 1.8874 |
| LM13 | 1.1963 | LM28 | 1.8927 |
| LM14 | 1.3669 | LM29 | 3.5284 |
| LM15 | 0.5064 | LM30 | 0 |
| ML Models | Training Stage | |||
| IOA | RMSE | MAE | SI | |
| MARS | 0.972 | 0.474 | 1.619 | 0.322 |
| GEP | 0.914 | 0.836 | 3.514 | 0.567 |
| EPR | 0.912 | 0.557 | 2.754 | 0.378 |
| M5MT | 0.962 | 0.847 | 5.347 | 0.574 |
| ML Models | Testing Stage | |||
| IOA | RMSE | MAE | SI | |
| MARS | 0.969 | 0.379 | 0.449 | 0.330 |
| GEP | 0.935 | 0.556 | 0.490 | 0.483 |
| EPR | 0.975 | 0.342 | 0.300 | 0.296 |
| M5MT | 0.924 | 0.599 | 0.922 | 0.507 |
| ML Models | Variation of e/D | |||
| θC = 0.018 and α = 0° | θC = 0.0091–0.061 and α = 0° | θC = 0.081–0.104 and α = 15° | θC = 0.046–0.104 and α = 30–45° | |
| MARS | 0.431 | 0.933 | 0.197 | 0.331 |
| GEP | 0.315 | 1.514 | 0.323 | 0.910 |
| EPR | 0.481 | 1.100 | 0.682 | 0.398 |
| M5MT | 0.681 | 1.767 | 0.618 | 0.698 |
| ML Models | Variation of θC | |||
| e/D = 0.1 and α = 0° | e/D = 0.1–0.35 and α = 0° | e/D = 0.1 and α = 15° | e/D = 0.2 and α = 15° | |
| MARS | 0.223 | 0.183 | 0.746 | 0.191 |
| GEP | 0.308 | 0.630 | 0.880 | 0.258 |
| EPR | 0.185 | 0.212 | 0.490 | 0.251 |
| M5MT | 0.681 | 0.573 | 0.690 | 0.349 |
| ML Models | Variation of θC | |||
| e/D = 0.3 and α = 15° | e/D = 0.4 and α = 15° | e/D = 0.1 and α = 30° | e/D = 0.2 and α = 30° | |
| MARS | 0.165 | 0.286 | 0.542 | 0.439 |
| GEP | 0.248 | 0.462 | 0.532 | 1.075 |
| EPR | 0.368 | 0.347 | 0.278 | 0.639 |
| M5MT | 0.218 | 0.249 | 0.502 | 0.835 |
| ML Models | Variation of FrP | |||
| θC = 0.0091–0.1045 and α = 0° | θC = 0.046–0.104 and α = 15° | θC = 0.046–0.104 and α = 30–45° | ||
| MARS | 0.173 | 0.235 | 0.359 | |
| GEP | 1.063 | 0.376 | 0.993 | |
| EPR | 0.356 | 0.872 | 0.412 | |
| M5MT | 1.315 | 0.778 | 0.762 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Najafzadeh, M.; Oliveto, G. Scour Propagation Rates around Offshore Pipelines Exposed to Currents by Applying Data-Driven Models. Water 2022, 14, 493. https://doi.org/10.3390/w14030493
Najafzadeh M, Oliveto G. Scour Propagation Rates around Offshore Pipelines Exposed to Currents by Applying Data-Driven Models. Water. 2022; 14(3):493. https://doi.org/10.3390/w14030493
Chicago/Turabian StyleNajafzadeh, Mohammad, and Giuseppe Oliveto. 2022. "Scour Propagation Rates around Offshore Pipelines Exposed to Currents by Applying Data-Driven Models" Water 14, no. 3: 493. https://doi.org/10.3390/w14030493
APA StyleNajafzadeh, M., & Oliveto, G. (2022). Scour Propagation Rates around Offshore Pipelines Exposed to Currents by Applying Data-Driven Models. Water, 14(3), 493. https://doi.org/10.3390/w14030493







