Impacts of Rainfall Data Aggregation Time on Pluvial Flood Hazard in Urban Watersheds
Abstract
:1. Introduction
2. Case Study
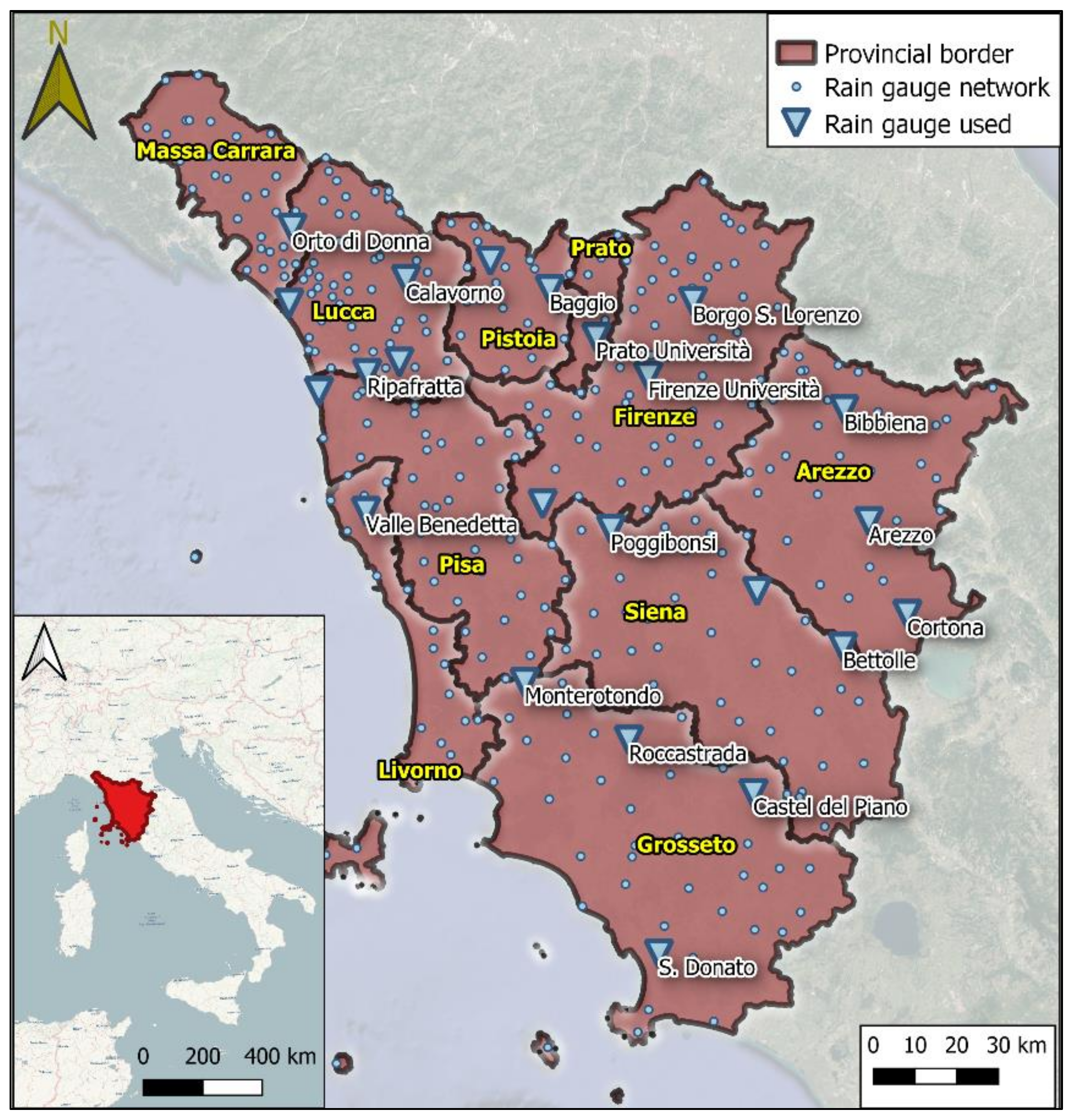
2.1. Tuscany Region
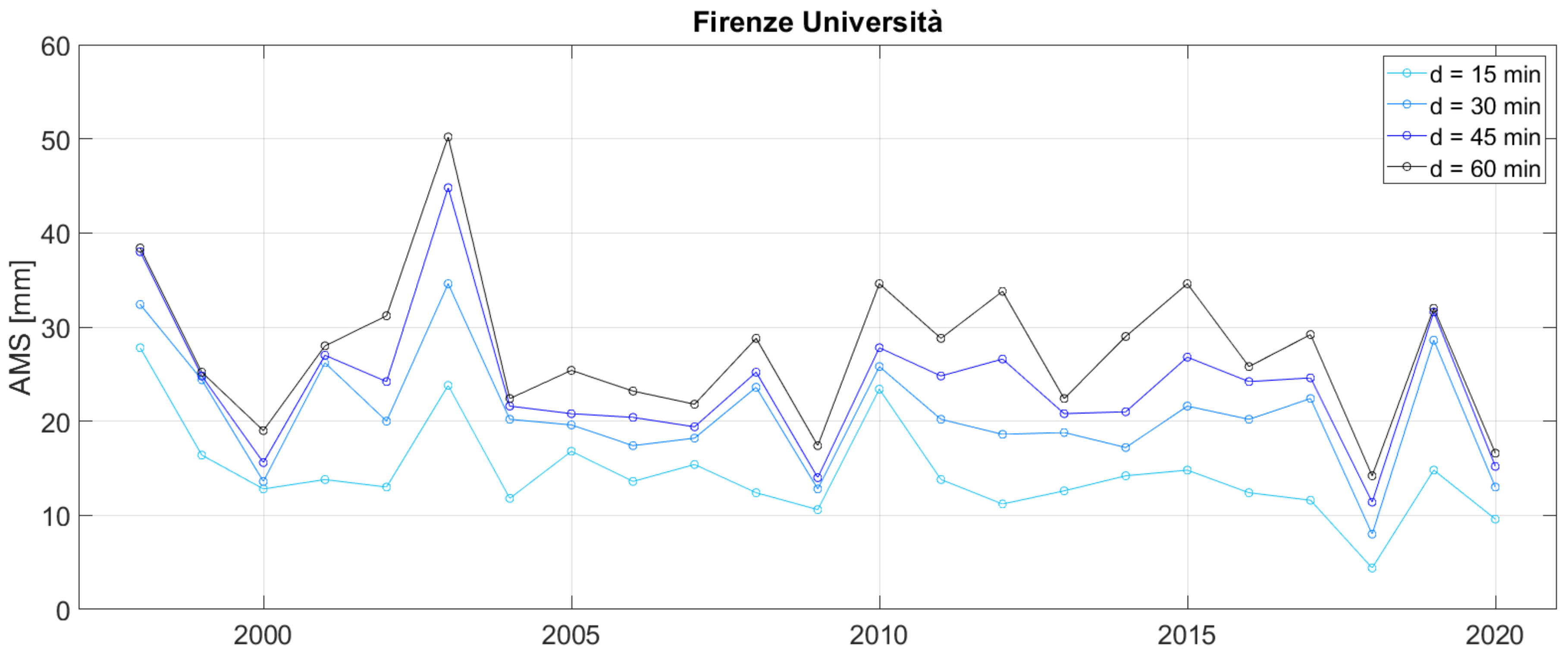
2.2. Florence Urban Watershed
3. Methodology
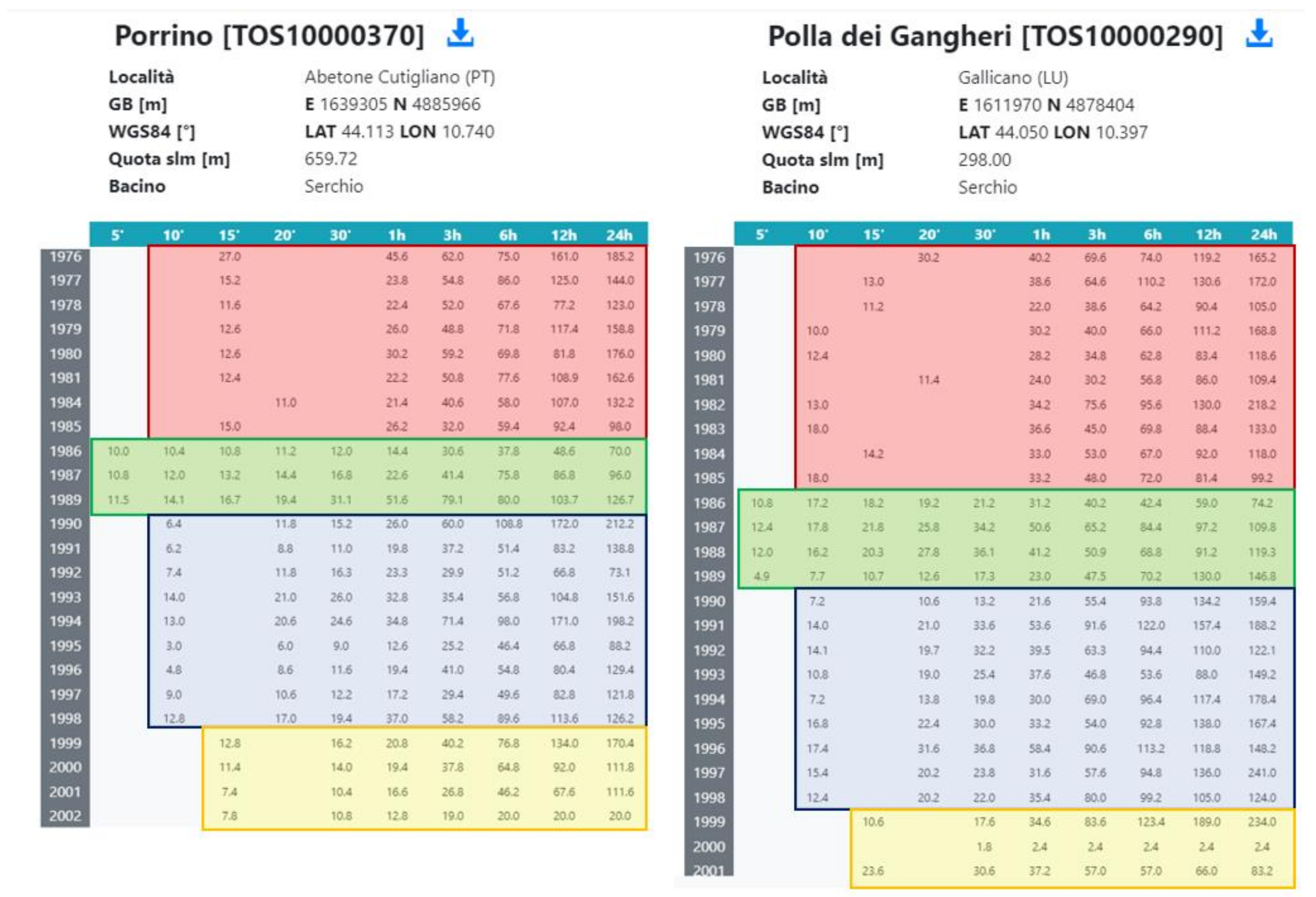
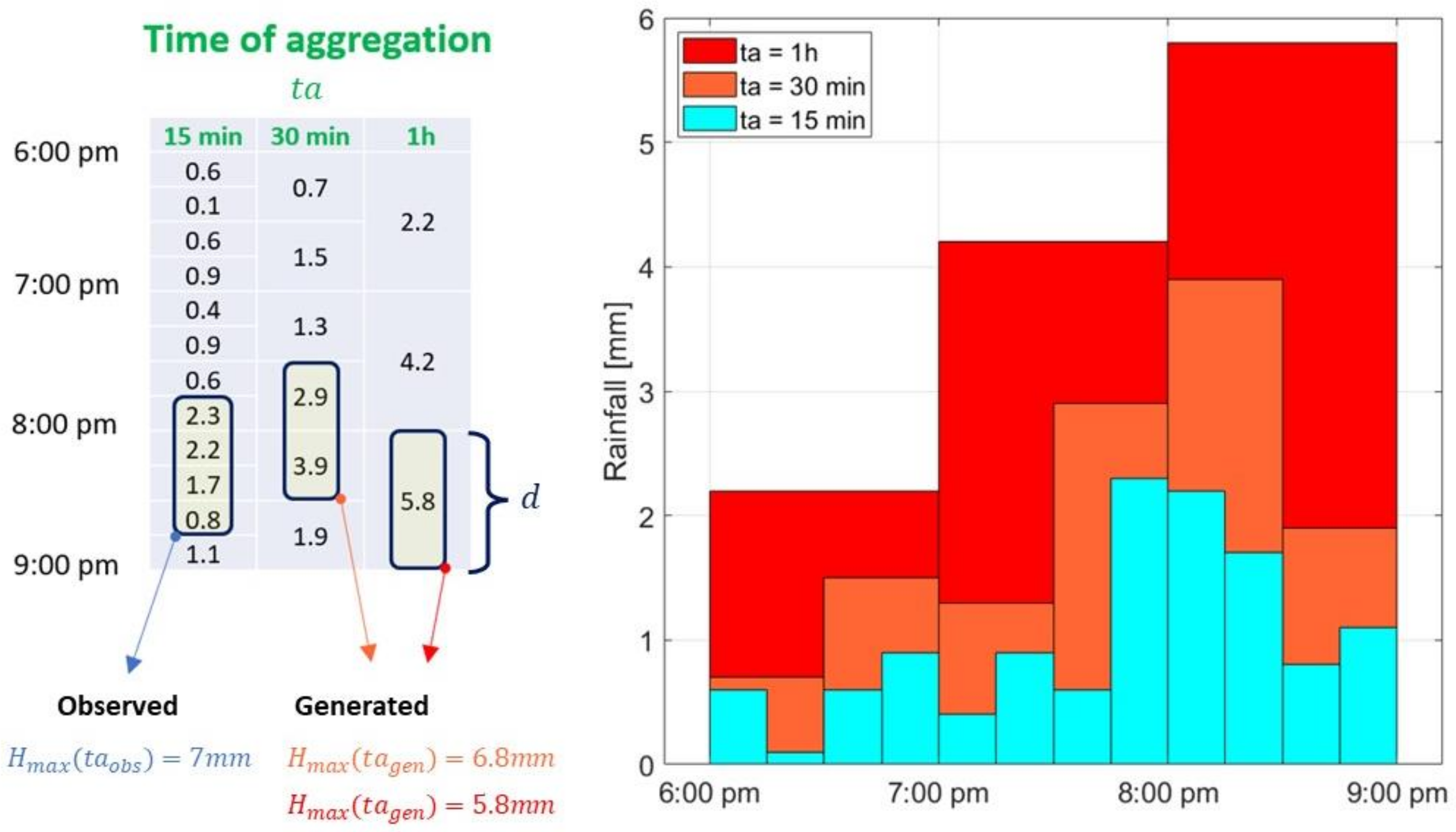
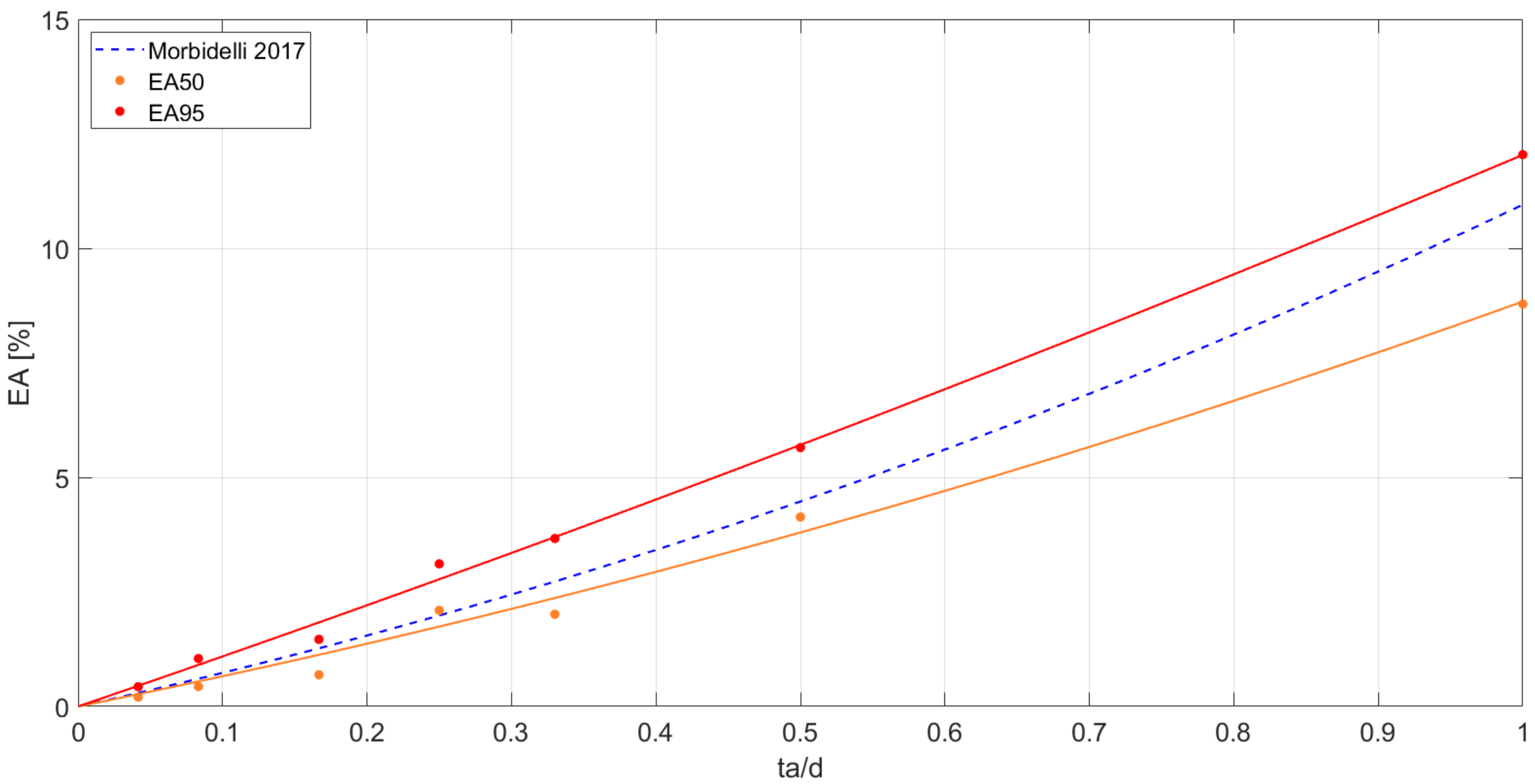
3.1. Underestimation of the Annual Maxima Rainfall Depth
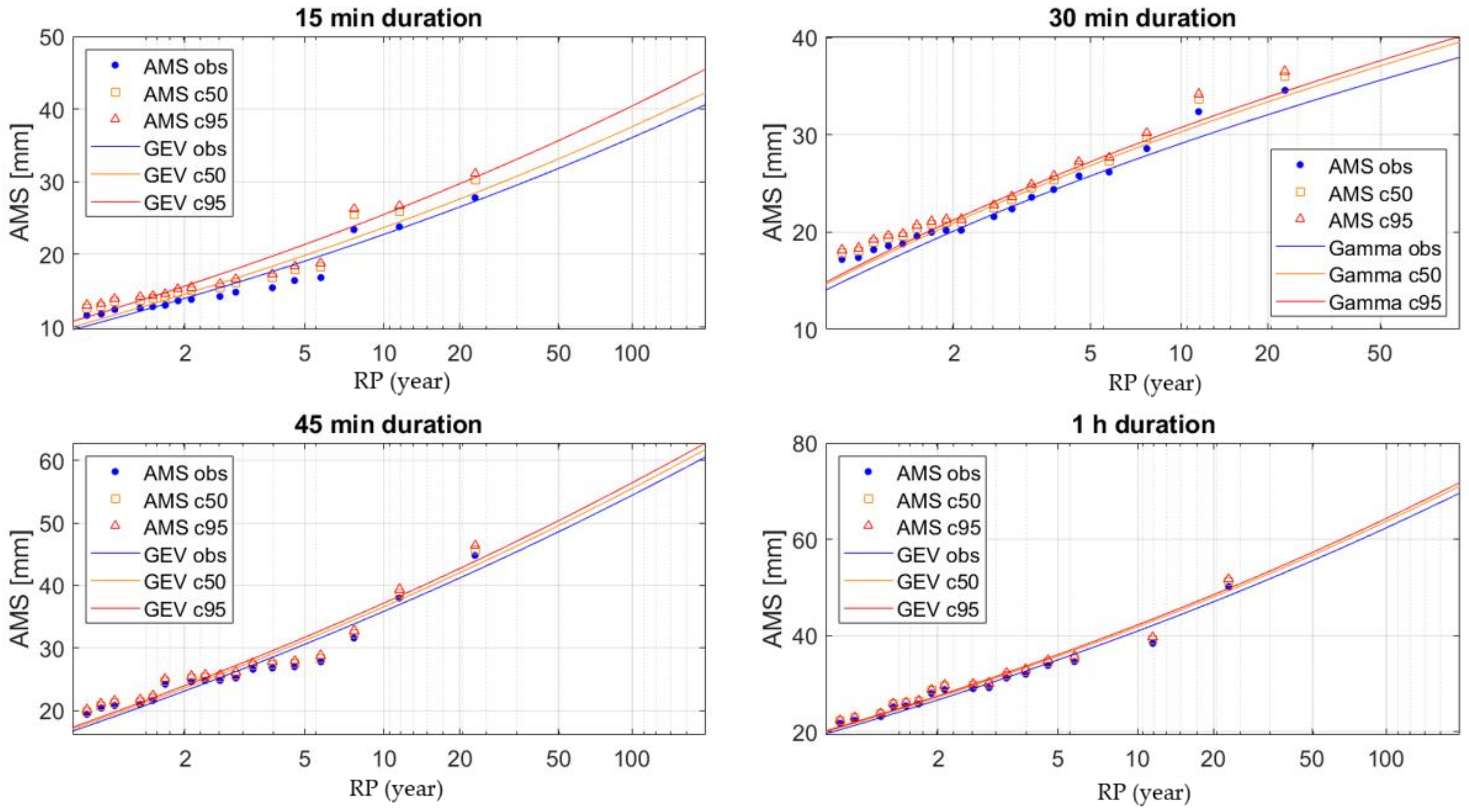
3.2. Correction of the Rainfall Series and Design Event Estimation
3.3. Hydrological and Hydraulic Modelling of the Urban Watershed
4. Results and Discussions
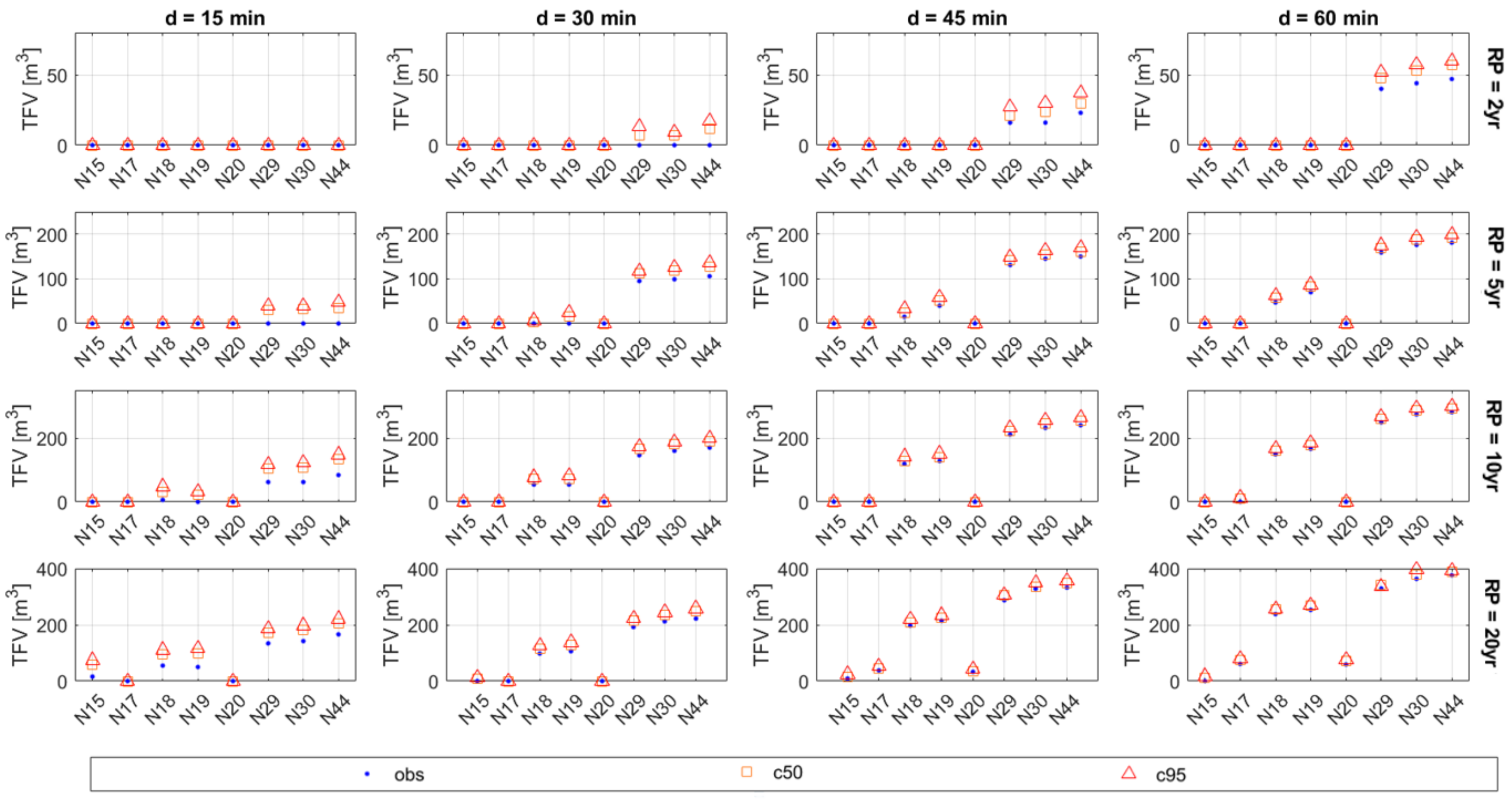
4.1. Hydrological Results
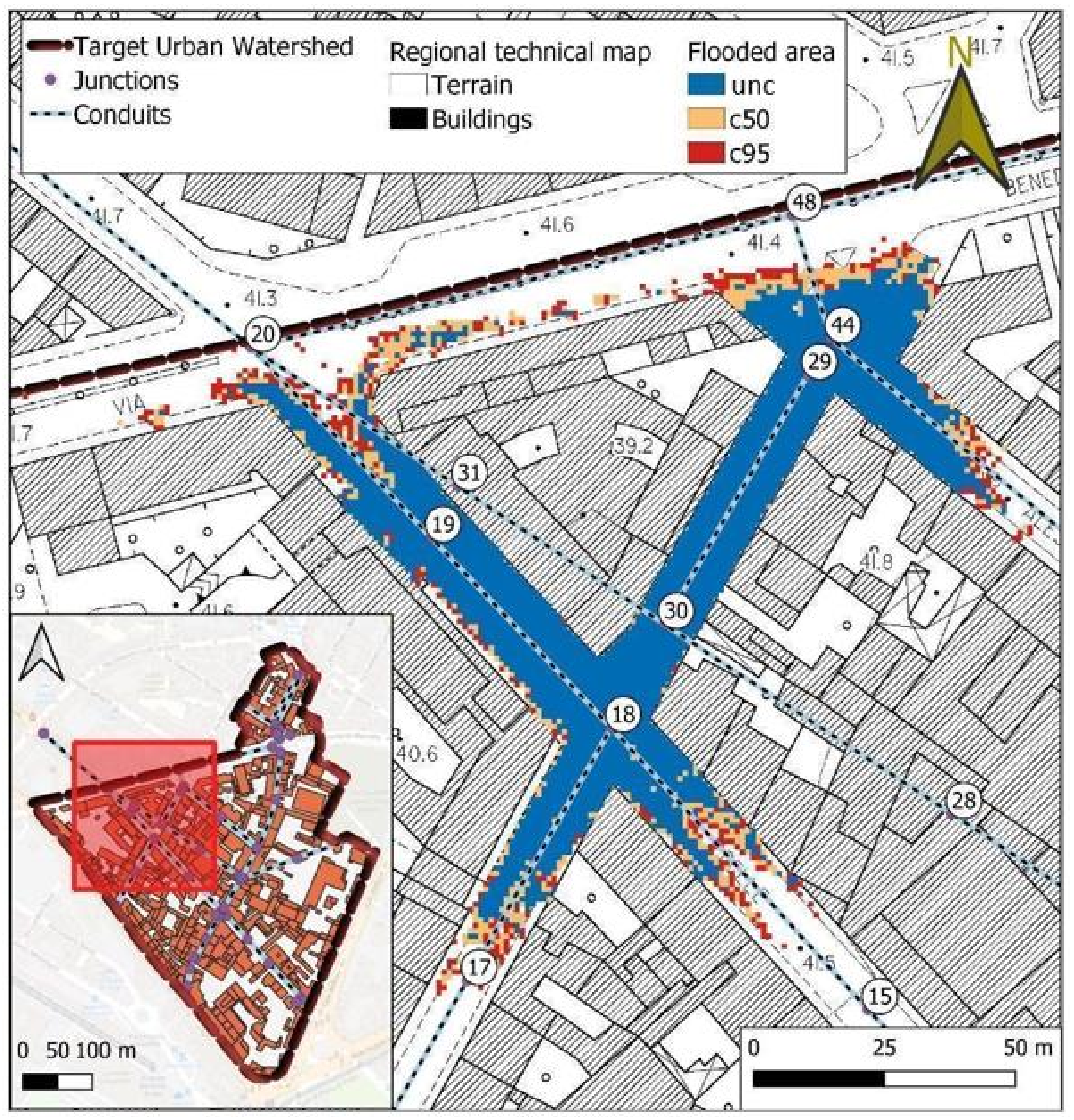
4.2. Hydraulic Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rosenzweig, B.R.; McPhillips, L.; Chang, H.; Cheng, C.; Welty, C.; Matsler, M.; Iwaniec, D.; Davidson, C.I. Pluvial flood risk and opportunities for resilience. WIREs Water 2018, 5, e1302. [Google Scholar] [CrossRef]
- Schmitt, T.G.; Scheid, C. Evaluation and communication of pluvial flood risks in urban areas. WIREs Water 2020, 7, e1401. [Google Scholar] [CrossRef] [Green Version]
- Willems, P.; Arnbjerg-Nielsen, K.; Olsson, J.; Nguyen, V.T.V. Climate change impact assessment on urban rainfall extremes and urban drainage: Methods and shortcomings. Atmos. Res. 2012, 103, 106–118. [Google Scholar] [CrossRef]
- Masson, V.; Lemonsu, A.; Hidalgo, J.; Voogt, J. Urban climates and climate change. Annu. Rev. Environ. Resour. 2020, 45, 411–444. [Google Scholar] [CrossRef]
- Kourtis, I.M.; Tsihrintzis, V.A. Adaptation of urban drainage networks to climate change: A review. Sci. Total Environ. 2021, 771, 145431. [Google Scholar] [CrossRef]
- Schanze, J. Pluvial flood risk management: An evolving and specific field: Editorial. J. Flood Risk Manag. 2018, 11, 227–229. [Google Scholar] [CrossRef]
- Falconer, R.H.; Cobby, D.; Smyth, P.; Astle, G.; Dent, J.; Golding, B. Pluvial flooding: New approaches in flood warning, mapping and risk management. J. Flood Risk Manag. 2009, 2, 198–208. [Google Scholar] [CrossRef]
- Zhou, Q.; Mikkelsen, P.S.; Halsnæs, K.; Arnbjerg-Nielsen, K. Framework for economic pluvial flood risk assessment considering climate change effects and adaptation benefits. J. Hydrol. 2012, 414–415, 539–549. [Google Scholar] [CrossRef]
- Szewrański, S.; Chruściński, J.; Kazak, J.; Świąder, M.; Tokarczyk-Dorociak, K.; Żmuda, R. Pluvial flood risk assessment tool (PFRA) for rainwater management and adaptation to climate change in newly urbanised areas. Water 2018, 10, 386. [Google Scholar] [CrossRef] [Green Version]
- El-Zein, A.; Ahmed, T.; Tonmoy, F. Geophysical and social vulnerability to floods at municipal scale under climate change: The case of an inner-city suburb of Sydney. Ecol. Indic. 2021, 121, 106988. [Google Scholar] [CrossRef]
- Apel, H.; Trepat, O.M.; Hung, N.N.; Chinh, D.T.; Merz, B.; Dung, N.V. Combined fluvial and pluvial urban flood hazard analysis: Concept development and application to Can Tho City, Mekong Delta, Vietnam. Nat. Hazards Earth Syst. Sci. 2016, 16, 941–961. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Sebastian, A. Empirical numerical simulation of precipitation events for pluvial flood management. In Proceedings of the Geo-Extreme 2021, Savannah, GA, USA, 7–10 November 2021; American Society of Civil Engineers: Reston, VA, USA; pp. 21–29. [Google Scholar]
- Bulti, D.T.; Abebe, B.G. A review of flood modeling methods for urban pluvial flood application. Model. Earth Syst. Environ. 2020, 6, 1293–1302. [Google Scholar] [CrossRef]
- Simões, N.; Ochoa-Rodríguez, S.; Wang, L.-P.; Pina, R.; Marques, A.; Onof, C.; Leitão, J. Stochastic urban pluvial flood hazard maps based upon a spatial-temporal rainfall generator. Water 2015, 7, 3396–3406. [Google Scholar] [CrossRef]
- Sun, S.; Djordjević, S.; Khu, S.-T. A general framework for flood risk-based storm sewer network design. Urban Water J. 2011, 8, 13–27. [Google Scholar] [CrossRef]
- Di Salvo, C.; Ciotoli, G.; Pennica, F.; Cavinato, G.P. Pluvial flood hazard in the city of Rome (Italy). J. Maps 2017, 13, 545–553. [Google Scholar] [CrossRef] [Green Version]
- Guerreiro, S.; Glenis, V.; Dawson, R.; Kilsby, C. Pluvial flooding in European Cities—A continental approach to urban flood modelling. Water 2017, 9, 296. [Google Scholar] [CrossRef] [Green Version]
- Pregnolato, M.; Ford, A.; Glenis, V.; Wilkinson, S.; Dawson, R. Impact of climate change on disruption to urban transport networks from pluvial flooding. J. Infrastruct. Syst. 2017, 23, 04017015. [Google Scholar] [CrossRef] [Green Version]
- Hnilica, J.; Slámová, R.; Šípek, V.; Tesař, M. Precipitation extremes derived from temporally aggregated time series and the efficiency of their correction. Hydrol. Sci. J. 2021, 66, 2249–2257. [Google Scholar] [CrossRef]
- Morbidelli, R.; Saltalippi, C.; Dari, J.; Flammini, A. A review on rainfall data resolution and its role in the hydrological practice. Water 2021, 13, 1012. [Google Scholar] [CrossRef]
- Morbidelli, R.; Saltalippi, C.; Flammini, A.; Cifrodelli, M.; Picciafuoco, T.; Corradini, C.; Casas-Castillo, M.C.; Fowler, H.J.; Wilkinson, S.M. Effect of temporal aggregation on the estimate of annual maximum rainfall depths for the design of hydraulic infrastructure systems. J. Hydrol. 2017, 554, 710–720. [Google Scholar] [CrossRef] [Green Version]
- Young, C.B.; McEnroe, B.M. Sampling adjustment factors for rainfall recorded at fixed time intervals. J. Hydrol. Eng. 2003, 8, 294–296. [Google Scholar] [CrossRef]
- Yoo, C.; Jun, C.; Park, C. Effect of rainfall temporal distribution on the conversion factor to convert the fixed-interval into true-interval rainfall. J. Hydrol. Eng. 2015, 20, 04015018. [Google Scholar] [CrossRef]
- Morbidelli, R.; García-Marín, A.P.; Mamun, A.A.; Atiqur, R.M.; Ayuso-Muñoz, J.L.; Taouti, M.B.; Baranowski, P.; Bellocchi, G.; Sangüesa-Pool, C.; Bennett, B.; et al. The history of rainfall data time-resolution in a wide variety of geographical areas. J. Hydrol. 2020, 590, 125258. [Google Scholar] [CrossRef]
- Giannelli, D. Application of Sustainable Urban Drainage Systems for the Mitigation of the Pluvial Flood Risk in the Municipality of Florence. Master’s Thesis, University of Florence, Florence, Italy, 2020. [Google Scholar]
- Rossman, L.A. Storm Water Management Model User’s Manual Version 5.1; EPA/600/R-14/413b; National Risk Management Research Laboratory, Office of Research and Development, U.S. Environmental Protection Agency: Cincinnati, OH, USA, 2015. [Google Scholar]

| Duration | Uncorrected | c50 | c95 |
|---|---|---|---|
| 15 min | 3848 | 4059 (16.5%) 1 | 4487 (28.79%) 1 |
| 30 min | 4224 | 4788 (13.35%) 1 | 4788 (13.35%) 1 |
| 45 min | 6162 | 6464 (4.84%) 1 | 6460 (4.84%) 1 |
| 60 min | 6883 | 7197 (4.56%) 1 | 7197 (4.56%) 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lompi, M.; Tamagnone, P.; Pacetti, T.; Morbidelli, R.; Caporali, E. Impacts of Rainfall Data Aggregation Time on Pluvial Flood Hazard in Urban Watersheds. Water 2022, 14, 544. https://doi.org/10.3390/w14040544
Lompi M, Tamagnone P, Pacetti T, Morbidelli R, Caporali E. Impacts of Rainfall Data Aggregation Time on Pluvial Flood Hazard in Urban Watersheds. Water. 2022; 14(4):544. https://doi.org/10.3390/w14040544
Chicago/Turabian StyleLompi, Marco, Paolo Tamagnone, Tommaso Pacetti, Renato Morbidelli, and Enrica Caporali. 2022. "Impacts of Rainfall Data Aggregation Time on Pluvial Flood Hazard in Urban Watersheds" Water 14, no. 4: 544. https://doi.org/10.3390/w14040544
APA StyleLompi, M., Tamagnone, P., Pacetti, T., Morbidelli, R., & Caporali, E. (2022). Impacts of Rainfall Data Aggregation Time on Pluvial Flood Hazard in Urban Watersheds. Water, 14(4), 544. https://doi.org/10.3390/w14040544







