Assessment of Groundwater Flow Dynamics Using MODFLOW in Shallow Aquifer System of Mahanadi Delta (East Coast), India
Abstract
:1. Introduction
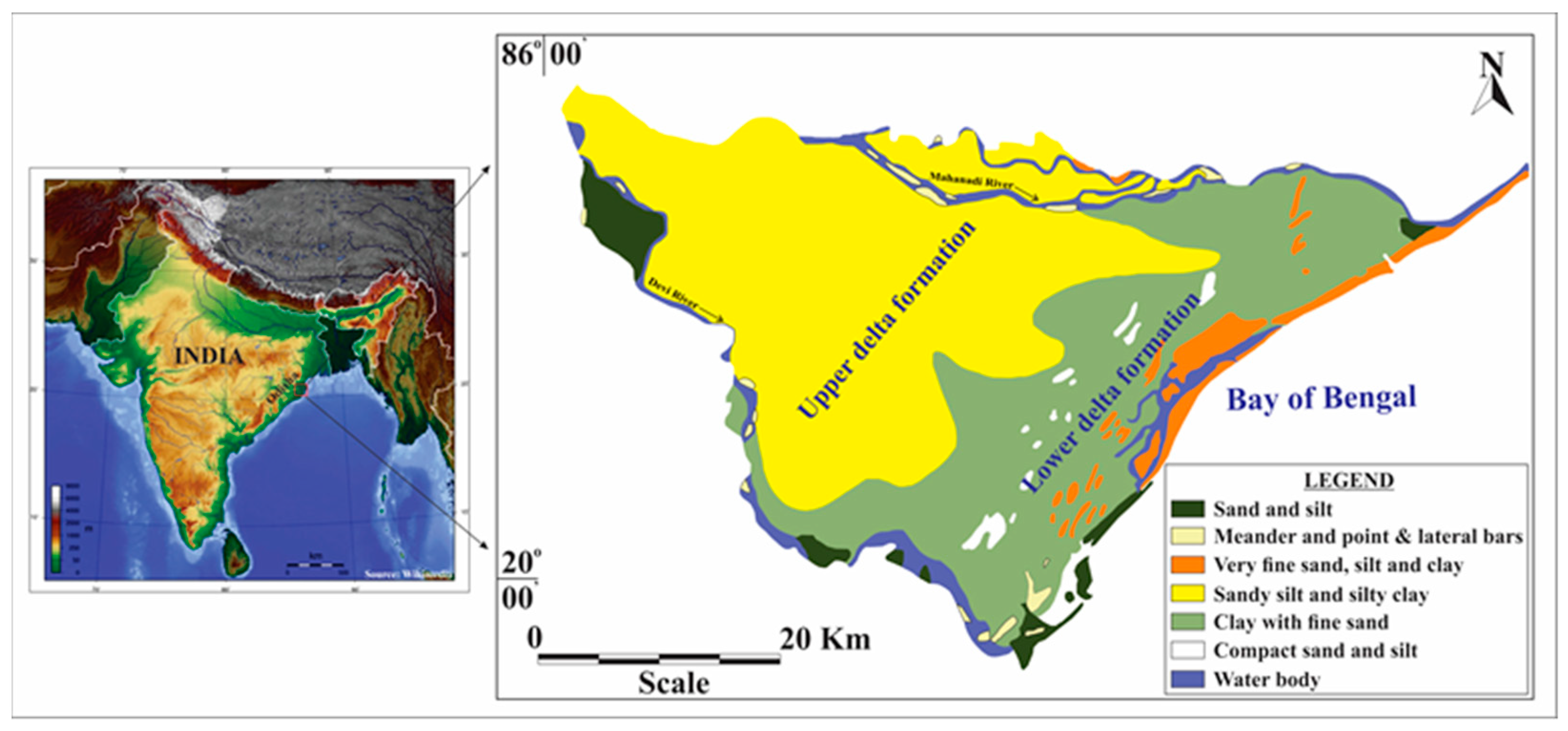
2. Study Area
3. Hydrogeology
4. Methodology
4.1. Development of the Model
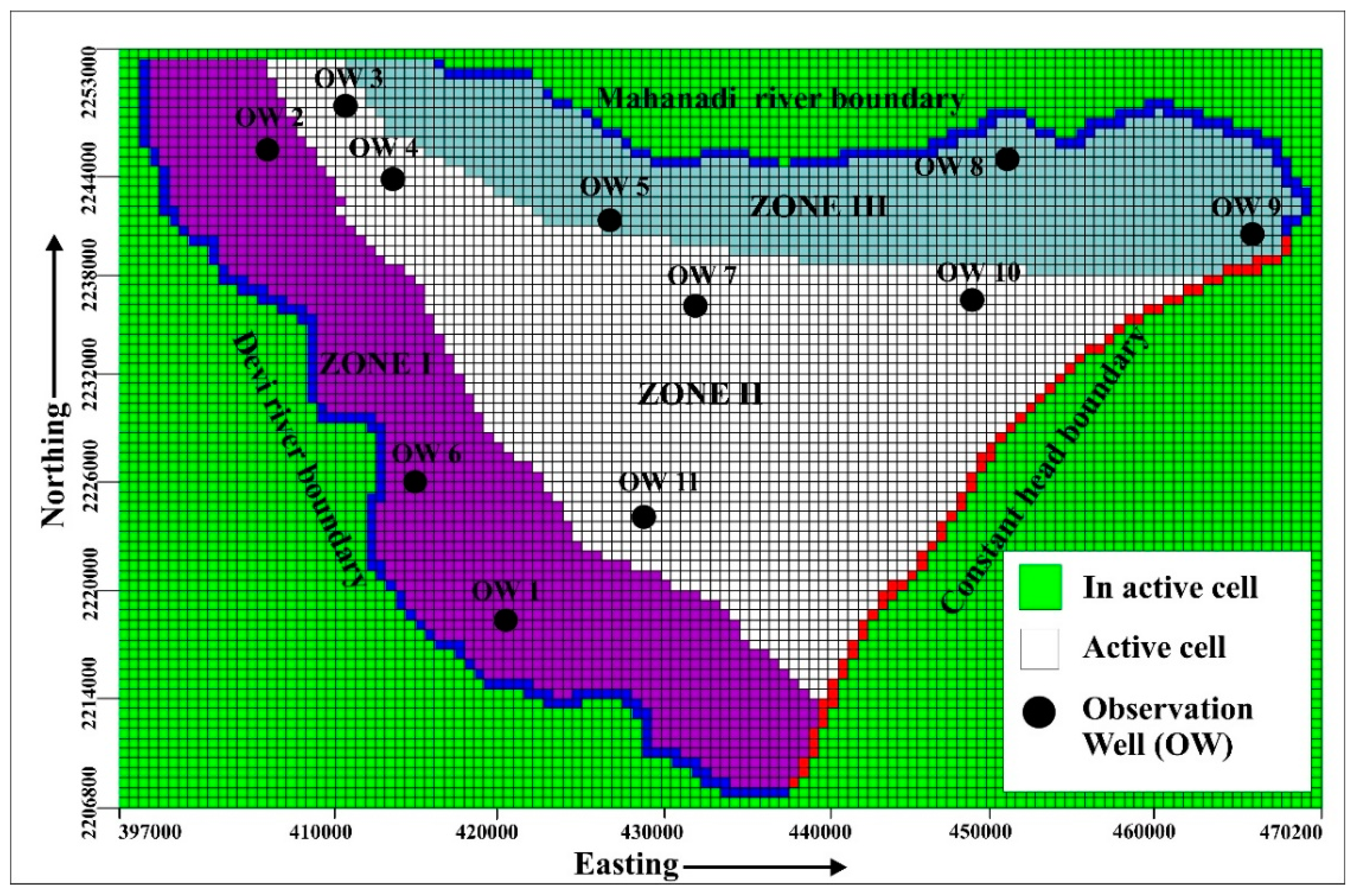
4.1.1. Discretization of the Study Area
4.1.2. Hydraulic Head Data
4.1.3. Boundary Conditions
4.2. Hydrological Parameters
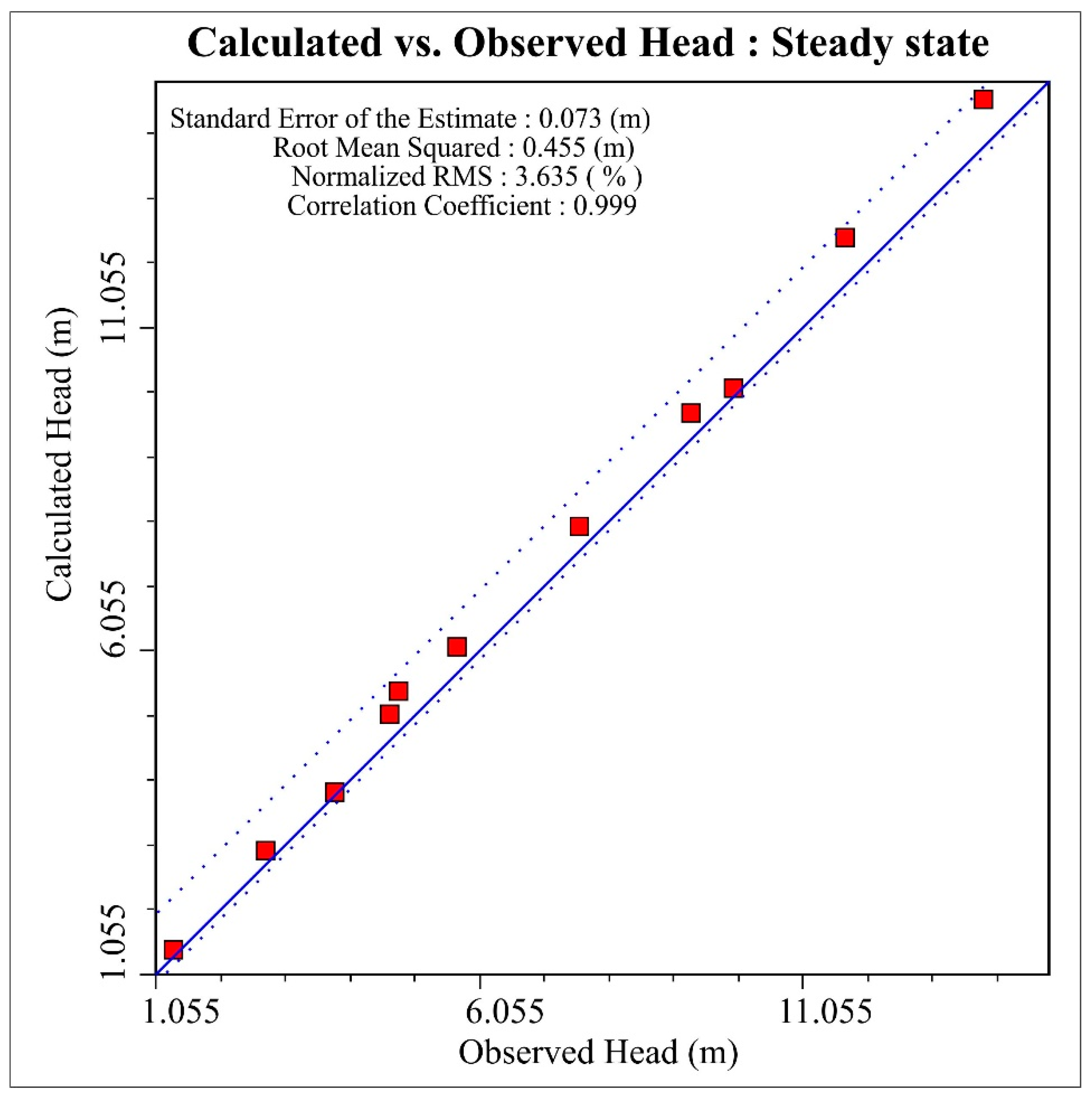
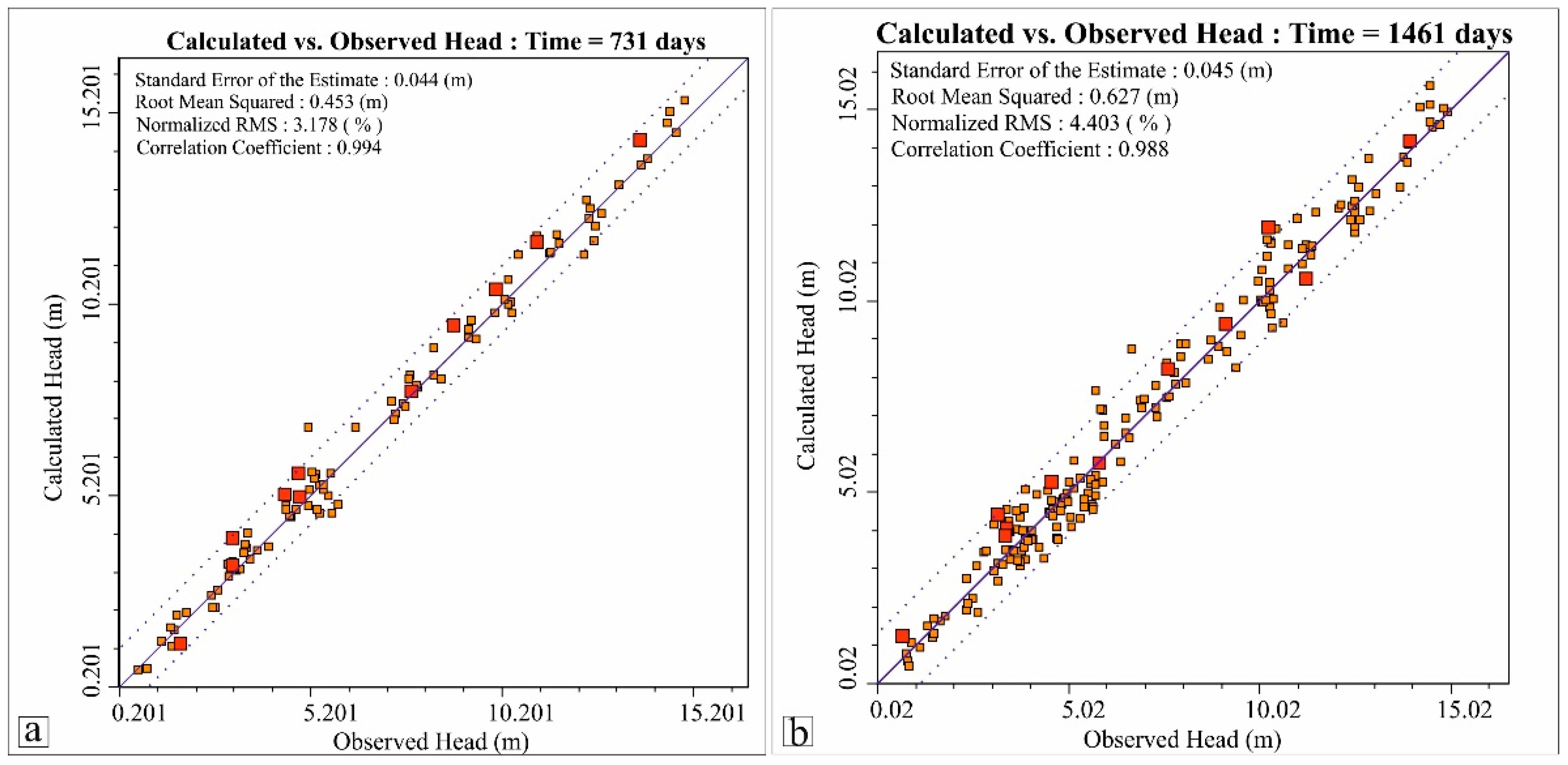
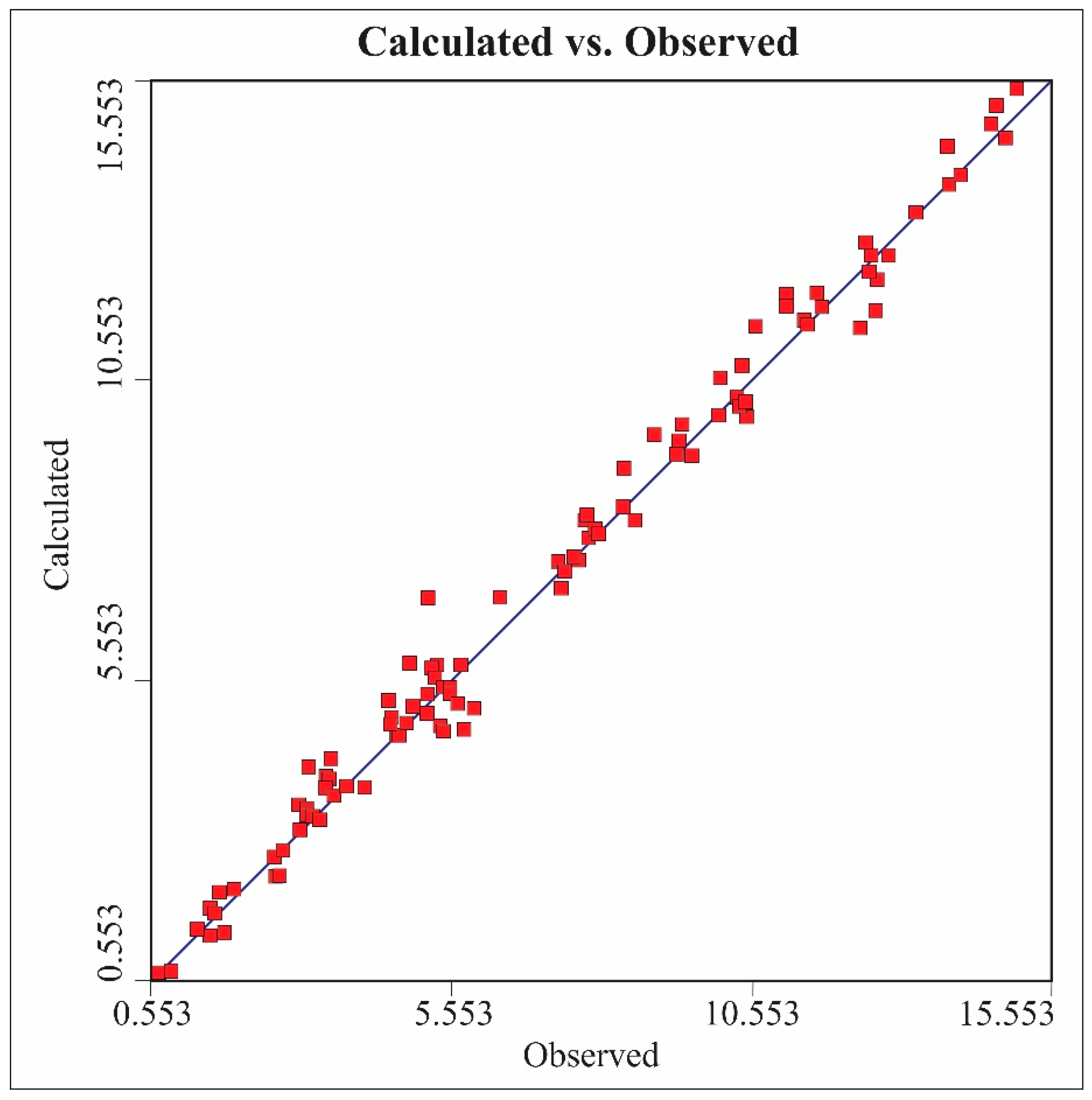
4.3. Calibration and Validation of Model
4.4. Parameter Estimation (PEST) Model
5. Results and Discussion
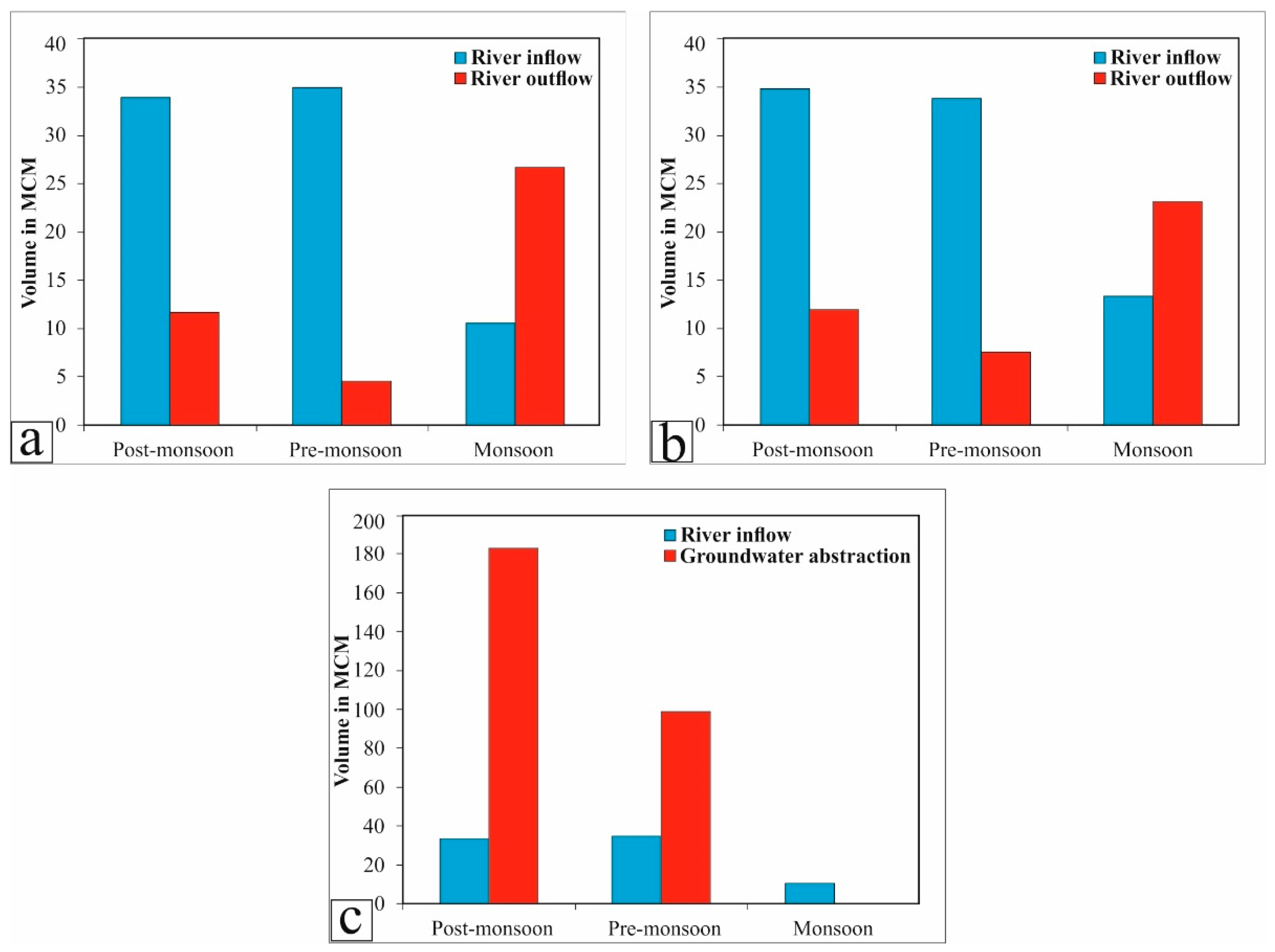
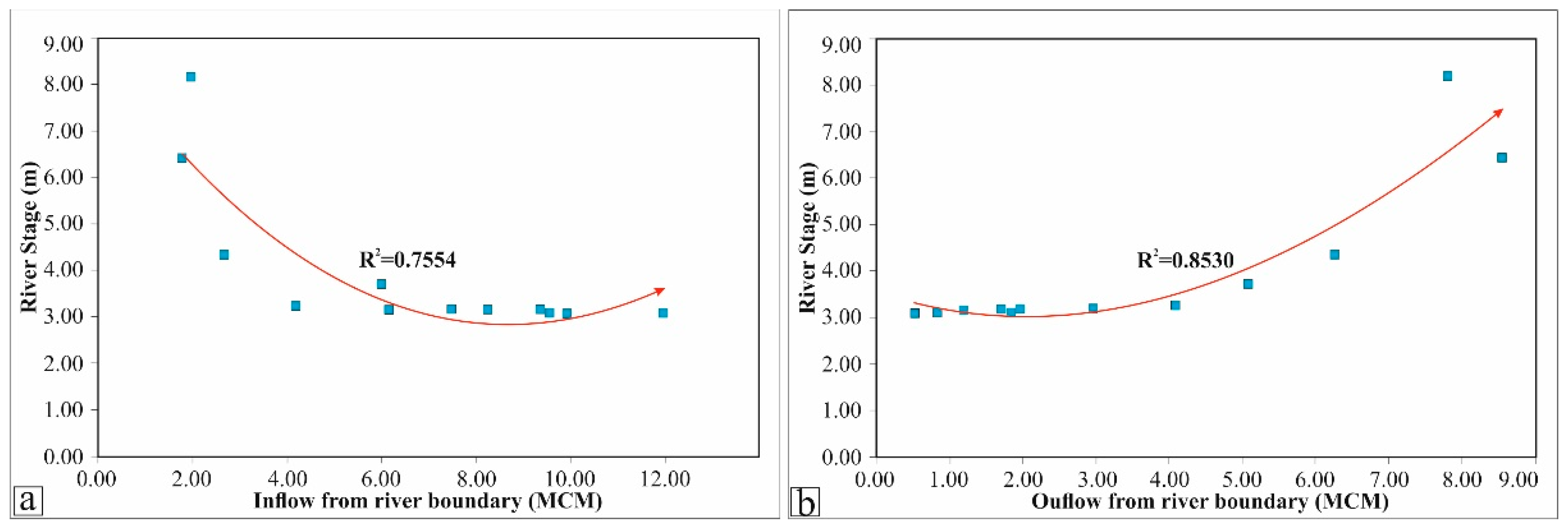
5.1. Interaction between Aquifer and River
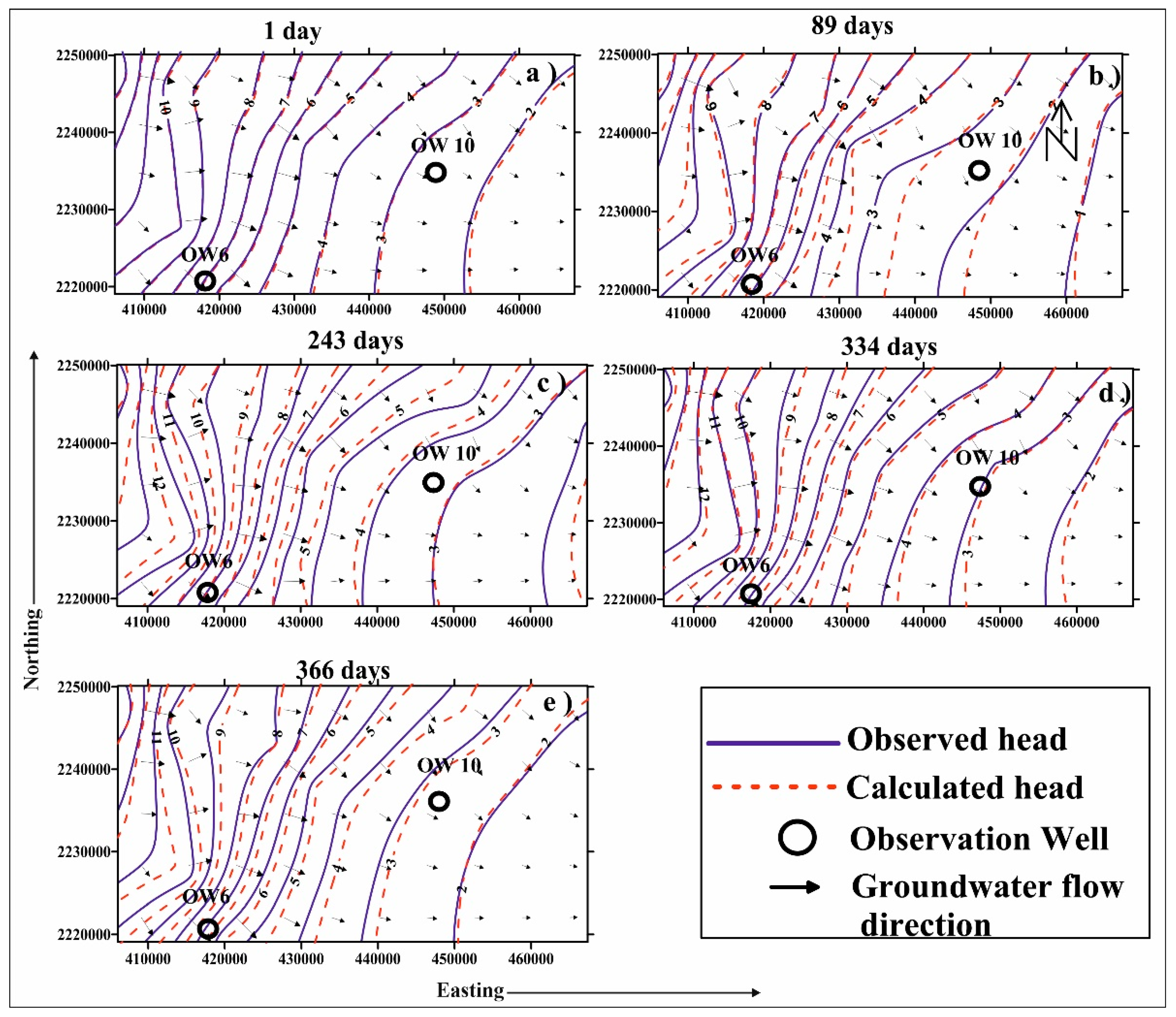
5.2. Fluctuation in Groundwater Level
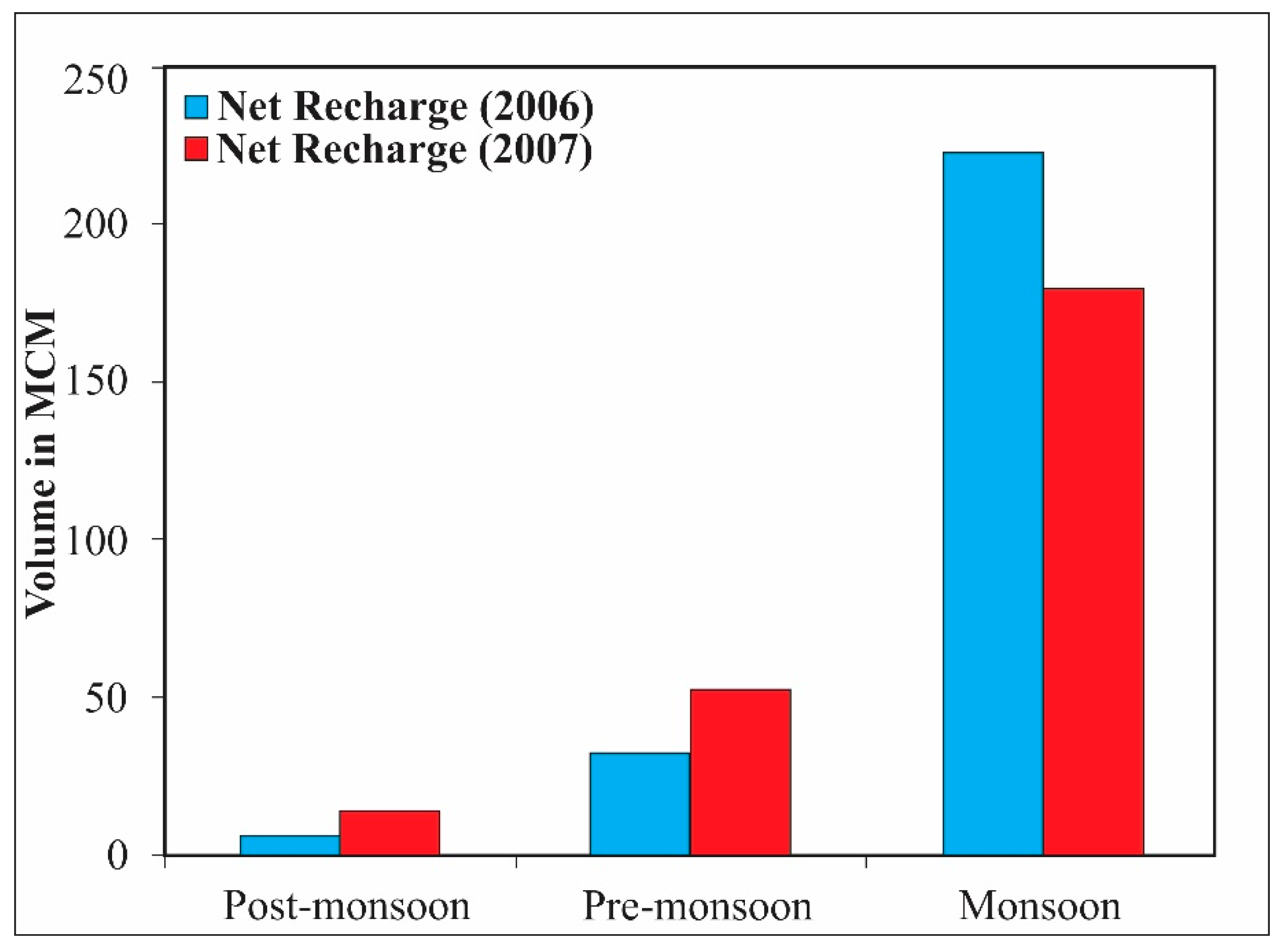
5.3. Groundwater Recharge Estimation
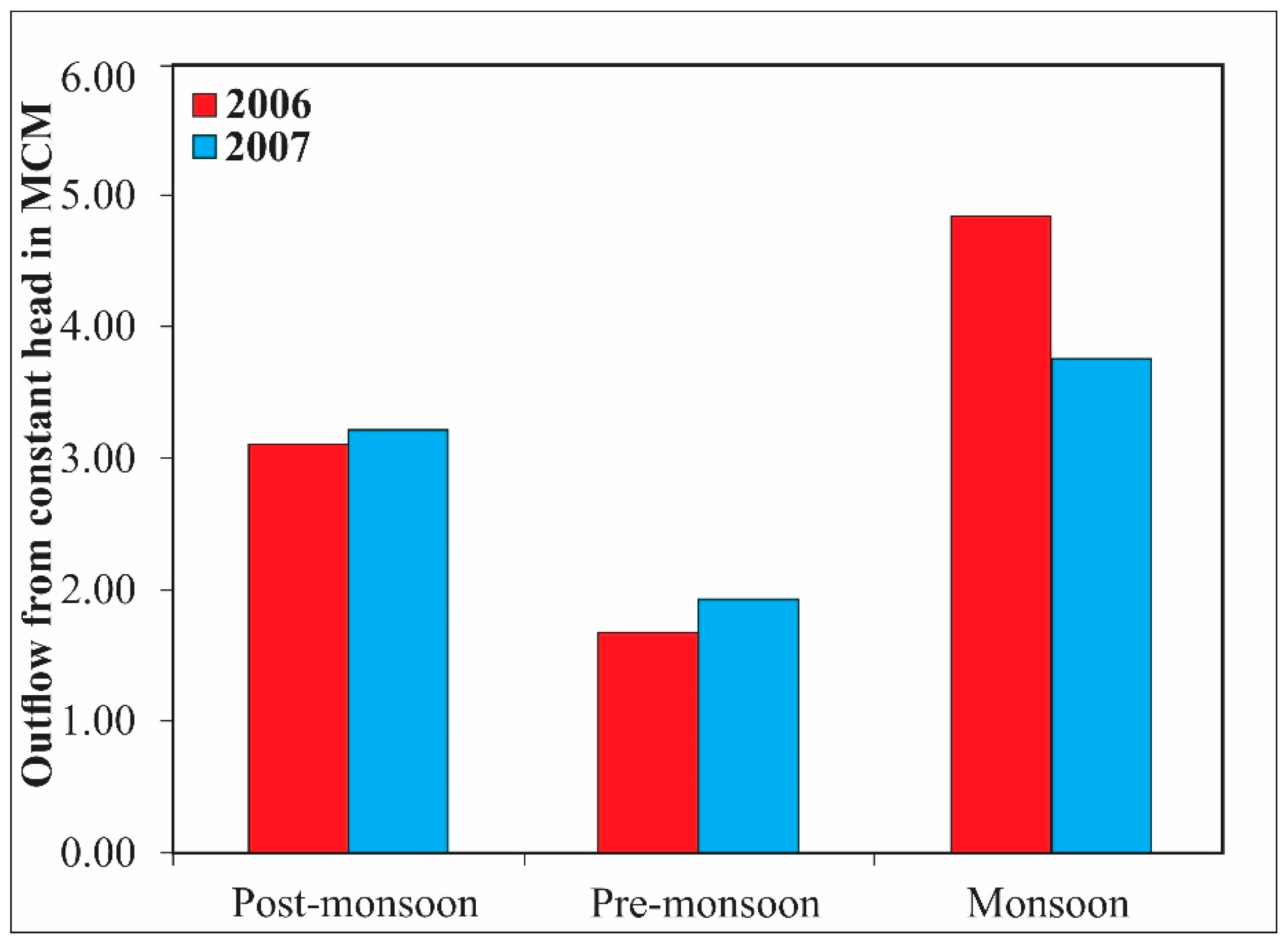
5.4. Groundwater Outflow to the Bay of Bengal
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Post, V.E.A. Fresh and saline groundwater interaction in coastal aquifers: Is our technology ready for the problems ahead? Hydrogeol. J. 2005, 13, 120–123. [Google Scholar] [CrossRef]
- Antonellini, M.; Mollema, P.; Giambastiani, B.; Bishop, K.; Caruso, L.; Minchio, A.; Pellegrini, L.; Sabia, M.; Ulazzi, E.; Gabbianelli, G. Salt water intrusion in the coastal aquifer of the southern Po Plain, Italy. Hydrogeol. J. 2008, 16, 1541–1556. [Google Scholar] [CrossRef]
- Ferguson, G.; Gleeson, T. Vulnerability of coastal aquifers to groundwater use and climate change. Nat. Clim. Chang. 2012, 2, 342–345. [Google Scholar] [CrossRef]
- Moore, W. Large groundwater inputs to coastal waters revealed by 226Ra enrichments. Nature 1996, 380, 612–614. [Google Scholar] [CrossRef]
- Trenberth, K.; Smith, L.; Qian, T.; Dai, A.; Fasullo, J. Estimates of the Global Water Budget and Its Annual Cycle Using Observational and Model Data. J. Hydrometeorol. 2007, 8, 758–769. [Google Scholar] [CrossRef]
- Schwartz, F.; Ibaraki, M. Groundwater: A Resource in Decline. Elements 2011, 7, 175–179. [Google Scholar] [CrossRef]
- Jelgersma, S.; Zijp, V.M.; Brinkman, R. Sea level rise and the coastal lowlands in the developing world. J. Coast. Res. 1993, 9, 958–972. [Google Scholar]
- Arnell, N. Climate change and global water resources. Glob. Environ. Chang. 1999, 9, 31–49. [Google Scholar] [CrossRef]
- Ranjan, R.; Shogren, J. How probability weighting affects participation in water markets. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef] [Green Version]
- Oude Essink, G.H.P.; Van Baaren, E.S.; De Louw, P.G. Effects of climate change on coastal groundwater systems: A modeling study in the Netherlands. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Singh, A.; Panda, S.N. Optimization and simulation modelling for managing the problems of water resources. Water Resour. Manag. 2013, 27, 3421–3431. [Google Scholar] [CrossRef]
- Anderson, M.P.; Woessner, W.W. Applied Groundwater Modeling: Simulation of Flow and Advective Transport; Academic Press: San Diego, CA, USA, 1992. [Google Scholar]
- Wang, H.F.; Anderson, M.P. Introduction to Groundwater Modeling: Finite Difference and Finite Element Methods; Academic Press: London, UK, 1995. [Google Scholar]
- Pinder, G.F.; Gray, W.G.; Brebbia, C.A. Finite Elements in Water Resources. In Proceedings of the First International Conference on Finite Elements in Water Resources, Princeton University, Princeton, NJ, USA, 12–16 July 1976; Pentech Press: London, UK, 1977. [Google Scholar]
- Voss, C.I. A Finite-Element Simulation Model for Saturated-Unsaturated, Fluid-Density-Dependent Ground-Water Flow with Energy Transport or Chemically-Reactive Single-Species Solute Transport; US Geological Survey: Reston, VA, USA, 1984.
- Istok, J. Groundwater Modeling by the Finite Element Method; Water Resources Monograph Series, 13; American Geophysical Union: Washington, DC, USA, 1989. [Google Scholar]
- Freeze, R.A.; Witherspoon, P.A. Theoretical analysis of regional groundwater flow: 1. Analytical and numerical solutions to the mathematical model. Water Resour. Res. 1966, 2, 641–656. [Google Scholar] [CrossRef] [Green Version]
- Pinder, G.F.; Bredehoeft, J.D. Application of the digital computer for aquifer evaluation. Water Resour. Res. 1968, 4, 1069–1093. [Google Scholar] [CrossRef]
- Trescott, P.C.; Pinder, G.F.; Larson, S.P. Finite-Difference Model for Aquifer Simulation in Two Dimensions with Results of Numerical Experiments; US Department of the Interior, Geological Survey: Reston, VA, USA, 1976.
- McDonald, M.G.; Harbaugh, A.W. A Modular Three-Dimensional Finite-Difference Ground-Water Flow Model; US Geological Survey Technical Manual of Water Resources Investigation, Book 6; USGS: Reston, VA, USA, 1988.
- Essink, G.H.O. Salt water intrusion in a three-dimensional groundwater system in the Netherlands: A numerical study. Transp. Porous Media 2001, 43, 137–158. [Google Scholar] [CrossRef]
- Bakker, M.; Essink, G.; Langevin, C. The rotating movement of three immiscible fluids—A benchmark problem. J. Hydrol. 2004, 287, 270–278. [Google Scholar] [CrossRef]
- Vandenbohede, A.; Houtte, E.; Lebbe, L. Sustainable groundwater extraction in coastal areas: A Belgian example. Environ. Geol. 2009, 57, 735–774. [Google Scholar] [CrossRef]
- Scanlon, B.; Mace, R.; Barrett, M.; Smith, B. Can we simulate regional groundwater flow in a karst system using equivalent porous media models? Case study, Barton Springs Edwards aquifer, USA. J. Hydrol. 2003, 276, 137–158. [Google Scholar] [CrossRef]
- Majumdar, P.K.; Ram, S.; Rao, P.R. Artificial recharge in multi aquifers of a mountainous watershed. J. Hydrol. Eng. 2009, 14, 215–222. [Google Scholar] [CrossRef]
- Rani, F.M.; Chen, Z.H. Numerical Modeling of Groundwater Flow in Karst Aquifer, Makeng Mining Area. Am. J. Environ. Sci. 2010, 6, 78–82. [Google Scholar] [CrossRef] [Green Version]
- Varalakshmi, V.; Venkateswara Rao, L.B.; SuriNaidu, L.; Tejaswini, M. Groundwater flow modeling of a hard rock aquifer: Case study. J. Hydrol. Eng. 2014, 19, 877–886. [Google Scholar] [CrossRef] [Green Version]
- Kashaigili, J.J.; Mashauri, D.A.; Abdo, G. Groundwater management by using mathematical modeling: Case of the Makutupora groundwater basin in Dodoma Tanzania. Botsw. J. Technol. 2003, 12, 19–24. [Google Scholar] [CrossRef]
- Rejani, R.; Jha, M.K.; Panda, S.N.; Mull, R. Simulation modeling for efficient groundwater management in Balasore coastal basin, India. Water Resour. Manag. 2008, 22, 23–50. [Google Scholar] [CrossRef]
- Rao, S.V.N.; Bhallamudi, S.M.; Thandaveswara, B.S.; Mishra, G.C. Conjunctive Use of Surface and Groundwater for Coastal and Deltaic Systems. J. Water Resour. Plan. Manag. 2004, 130, 255–267. [Google Scholar] [CrossRef] [Green Version]
- Huyakorn, P.S.; Andersen, P.F.; Mercer, J.W.; White, H.O. Saltwater intrusion in aquifers: Development and testing of a three-dimensional finite element model. Water Resour. Res. 1987, 23, 293–312. [Google Scholar] [CrossRef]
- Yeh, W.W. Review: Optimization methods for groundwater modeling and management. Hydrogeol. J. 2015, 23, 1051–1065. [Google Scholar] [CrossRef]
- Kumar, P.; Dasgupta, R.; Dhyani, S.; Kadaverugu, R.; Johnson, B.K.; Hashimoto, S.; Sahu, N.; Avtar, R.; Saito, O.; Chakraborty, S.; et al. Scenario-Based Hydrological Modeling for Designing Climate-Resilient Coastal Water Resource Management Measures: Lessons from Brahmani River, Odisha, Eastern India. Sustainability 2021, 13, 6339. [Google Scholar] [CrossRef]
- Kadaverugu, R.; Dhyani, S.; Dasgupta, R.; Kumar, P.; Hashimoto, S.; Pujari, P. Multiple values of Bhitarkanika mangroves for human well-being: Synthesis of contemporary scientific knowledge for mainstreaming ecosystem services in policy planning. J. Coast. Conserv. 2021, 25, 1–15. [Google Scholar] [CrossRef]
- CGWB; SER; BBSR. Hydrogeological Framework and Development Prospects of Jagatsinghpur District; CGWB: Odisha, India, 2013.
- Behera, A.K.; Chakrapani, G.J.; Kumar, S.; Rai, N. Identification of seawater intrusion signatures through geochemical evolution of groundwater: A case study based on coastal region of the Mahanadi delta, Bay of Bengal, India. Nat. Hazards 2019, 97, 1209–1230. [Google Scholar] [CrossRef]
- Mahalik, N.K. Mahanadi Delta, Geology, Resources and Biodiversity; AIT Alumni Assn. (India Chapter): New Delhi, India, 2000. [Google Scholar]
- Tyagi, J.V.; Kumar, S. Estimation of Rainfall Recharge in A Coastal Area Through Inverse Groundwater Modeling. In Proceedings of the International Conference on Integrated Water Resources Management for Sustainable Development, ICIWRM 2000, New Delhi, India, 19–21 December 2000; pp. 312–322. [Google Scholar]
- Nayak, S.R.; Sarangi, R.K.; Rajawat, A.S. Application of IRS-P4 OCM data to study the impact of cyclone on coastal environment of Orissa. Curr. Sci. 2001, 80, 1208–1212. [Google Scholar]
- Chhotray, V.; Few, R. Post-disaster recovery and ongoing vulnerability: Ten years after the super-cyclone of 1999 in Orissa, India. Glob. Environ. Chang. 2012, 22, 695–702. [Google Scholar] [CrossRef]
- Ghosh, S.; Raje, D.; Mujumdar, P.P. Mahanadi streamflow: Climate change impact assessment and adaptive strategies. Curr. Sci. 2010, 98, 1084–1091. [Google Scholar]
- GSI. Geological Survey of India. Kolkata, India, 2011. Available online: https://www.gsi.gov.in/webcenter/portal/OCBIS?_afrLoop=45165913799575592&_adf.ctrl-state=rdpwts8sr_1#!%40%40%3F_afrLoop%3D45165913799575592%26_adf.ctrl-state%3Drdpwts8sr_5 (accessed on 7 November 2021).
- Yidana, S.; Chegbeleh, L. The hydraulic conductivity field and groundwater flow in the unconfined aquifer system of the Keta Strip, Ghana. J. Afr. Earth Sci. 2013, 86, 45–52. [Google Scholar] [CrossRef]
- Fetter, C.W. Applied Hydrogeology; Prentice-Hall: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- Senthilkumar, M.; Elango, L. Three-dimensional mathematical model to simulate groundwater flow in the lower Palar River basin, southern India. Hydrogeol. J. 2004, 12, 197–208. [Google Scholar] [CrossRef]
- Datta, B.; Vennalakanti, H.; Dhar, A. Modeling and control of saltwater intrusion in a coastal aquifer of Andhra Pradesh, India. J. Hydroenviron. Res. 2009, 3, 148–159. [Google Scholar] [CrossRef]
- Konikow, L.F. Modeling Chloride Movement in the Alluvial Aquifer at the Rocky Mountain Arsenal, Colorado; US Government Printing Office: Washington, DC, USA, 1977.
- Luckey, R.R.; Gutentag, E.D.; Heimes, F.J.; Weeks, J.B. Digital Simulation of Ground-Water Flow in the High Plains Aquifer in Parts of Colorado, Kansas, Nebraska, New Mexico, Oklahoma, South Dakota, Texas, and Wyoming; USGS: Reston, VA, USA, 1986.
- Doherty, J. PEST–Model-Independent Parameter Estimation–User Manual Part I: PEST, SENSAN, and Global Optimisers; Watermark Numerical Computing: Corinda, Australia, 2016. [Google Scholar]
- Knowling, M.J.; Werner, A.D. Estimability of recharge through groundwater model calibration: Insights from a field-scale steady-state example. J. Hydrol. 2016, 540, 973–987. [Google Scholar] [CrossRef]
- Delottier, H.; Pryet, A.; Dupuy, A. Why Should Practitioners be Concerned about Predictive Uncertainty of Groundwater Management Models? Water Resour. Manag. 2016, 31, 61–73. [Google Scholar] [CrossRef]
- Mohanty, S.; Jha, M.K.; Kumar, A.; Jena, S.K. Hydrologic and hydrogeologic characterization of a deltaic aquifer system in Orissa, eastern India. Water Resour. Manag. 2012, 26, 1899–1928. [Google Scholar] [CrossRef]
- Sahoo, S.; Jha, M.K. Numerical groundwater-flow modeling to evaluate potential effects of pumping and recharge: Implications for sustainable groundwater management in the Mahanadi delta region. Hydrogeol. J. 2017, 25, 2489–2511. [Google Scholar] [CrossRef]
| Sl No. | Parameters | Inputs |
|---|---|---|
| 1. | Cell | |
| 1.1 | Active | White Cells (600 m × 600 m) |
| 1.2 | Inactive | Green Cells (600 m × 600 m) |
| 2. | Model Boundaries | |
| 2.1 | Constant Head | Head = 0 m (Bay of Bengal-SW to NE) |
| 2.2 | Recharge | Variable |
| 2.3 | Evapotranspiration | Rate = 1400 mm/year |
| Extinction Depth = 3.0 m | ||
| 3. | Layer | |
| 3.1 | Layer No. | 1 |
| 3.2 | Layer Type | Unconfined |
| 4. | Aquifer Parameters | |
| 4.1 | Hydraulic Conductivity (K) | Kx = Ky = 40 to 45 m/d |
| Kz = 4 to 4.5 m/d | ||
| Specific Yield (Sy) | 0.05 to 0.07 | |
| 5. | Wells | |
| 5.1 | Observation Wells | 11 nos. |
| 6. | Aquifer Stresses | Data for individual pumping wells is not available, the same has been included in net recharge |
| 7. | Simulation Period | |
| 7.1 | Steady State | 1 January 2004 (1 day) |
| 7.2 | Transient State | 2004 to 2009 |
| Zones | Horizontal Hydraulic Conductivity (Kh) in m/Day | Vertical Hydraulic Conductivity (Kv) in m/Day | Specific Yield |
|---|---|---|---|
| I | 40 | 4 | 0.05 |
| II | 42 | 4.2 | 0.06 |
| III | 45 | 4.5 | 0.07 |
| Zones | Initial Hydraulic Parameters | PEST Estimated Parameters | ||
|---|---|---|---|---|
| Hydraulic Conductivity in m/Day | Specific Yield | Hydraulic Conductivity in m/Day | Specific Yield | |
| I | 40 | 0.05 | 36.85 | 0.058 |
| II | 42 | 0.06 | 44.39 | 0.075 |
| III | 45 | 0.07 | 44.01 | 0.053 |
| Zones | Hydraulic Conductivity (K) in m/Day | Specific Yield (Sy) |
|---|---|---|
| I | 30.746 < K < 44.18 | 0.046 < Sy < 0.074 |
| II | 40.81 < K < 48.30 | 0.048 < Sy < 0.116 |
| III | 39.70 < K < 48.78 | 0.043 < Sy < 0.067 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Behera, A.K.; Pradhan, R.M.; Kumar, S.; Chakrapani, G.J.; Kumar, P. Assessment of Groundwater Flow Dynamics Using MODFLOW in Shallow Aquifer System of Mahanadi Delta (East Coast), India. Water 2022, 14, 611. https://doi.org/10.3390/w14040611
Behera AK, Pradhan RM, Kumar S, Chakrapani GJ, Kumar P. Assessment of Groundwater Flow Dynamics Using MODFLOW in Shallow Aquifer System of Mahanadi Delta (East Coast), India. Water. 2022; 14(4):611. https://doi.org/10.3390/w14040611
Chicago/Turabian StyleBehera, Ajit Kumar, Rudra Mohan Pradhan, Sudhir Kumar, Govind Joseph Chakrapani, and Pankaj Kumar. 2022. "Assessment of Groundwater Flow Dynamics Using MODFLOW in Shallow Aquifer System of Mahanadi Delta (East Coast), India" Water 14, no. 4: 611. https://doi.org/10.3390/w14040611
APA StyleBehera, A. K., Pradhan, R. M., Kumar, S., Chakrapani, G. J., & Kumar, P. (2022). Assessment of Groundwater Flow Dynamics Using MODFLOW in Shallow Aquifer System of Mahanadi Delta (East Coast), India. Water, 14(4), 611. https://doi.org/10.3390/w14040611