Managing Aquifer Recharge to Overcome Overdraft in the Lower American River, California, USA
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Hydroeconomic Model: CALVIN
2.3. Modeling Approach
2.3.1. Network Modification
2.3.2. System Analysis
3. Results and Discussion
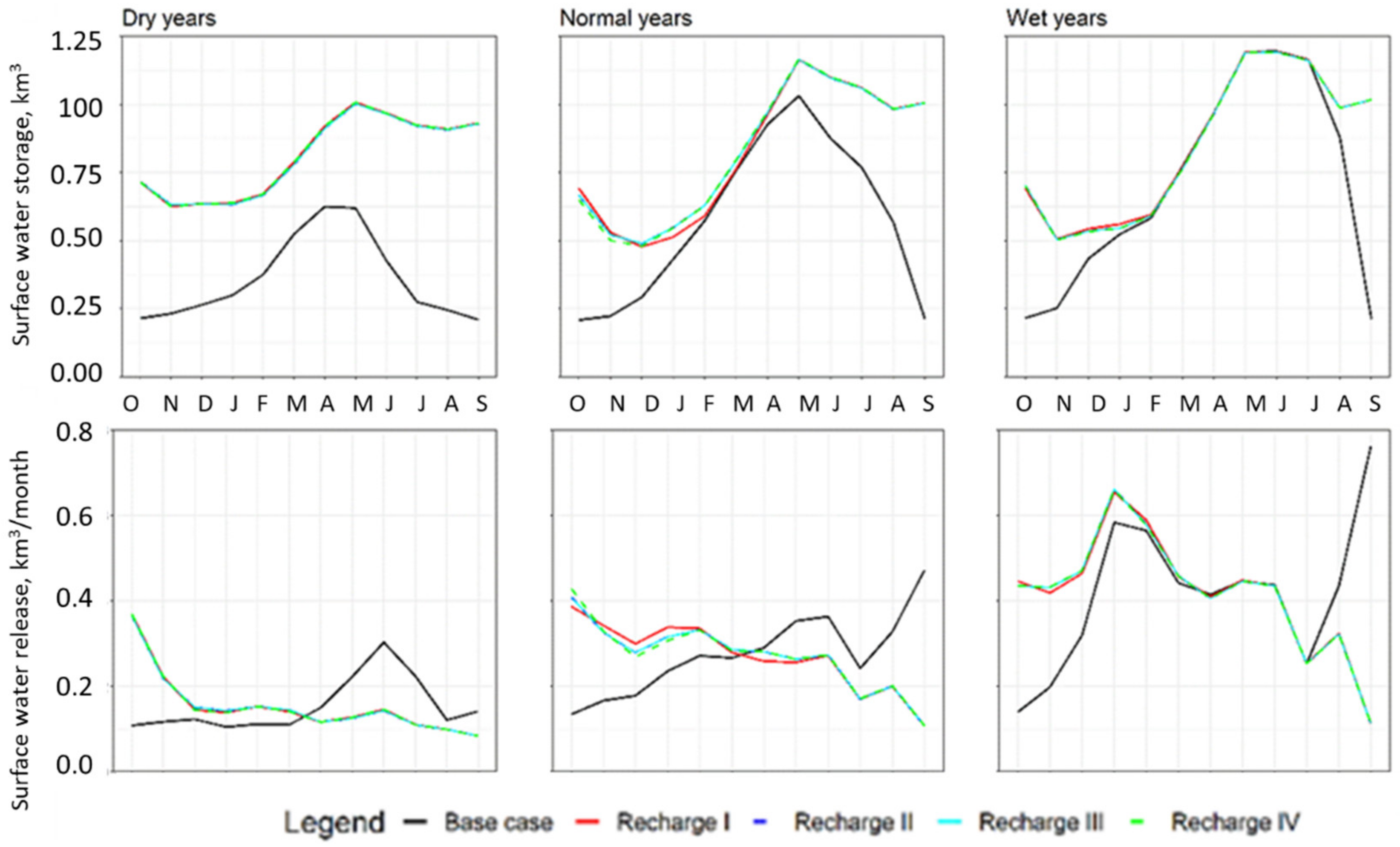
3.1. Changes in Surface Water Reservoir Operation
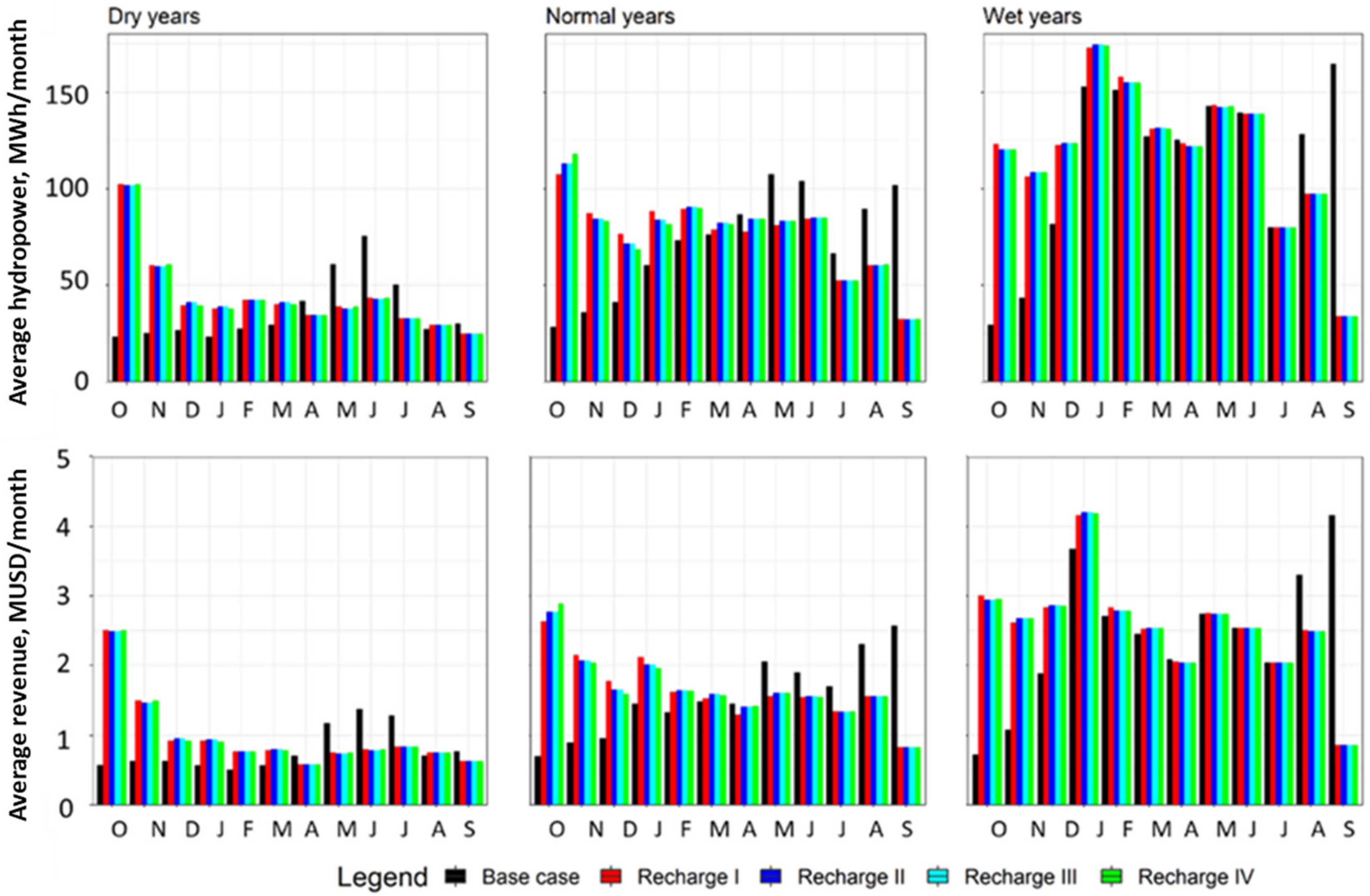
3.2. Hydropower Benefit
3.3. Artificial Recharge Facility
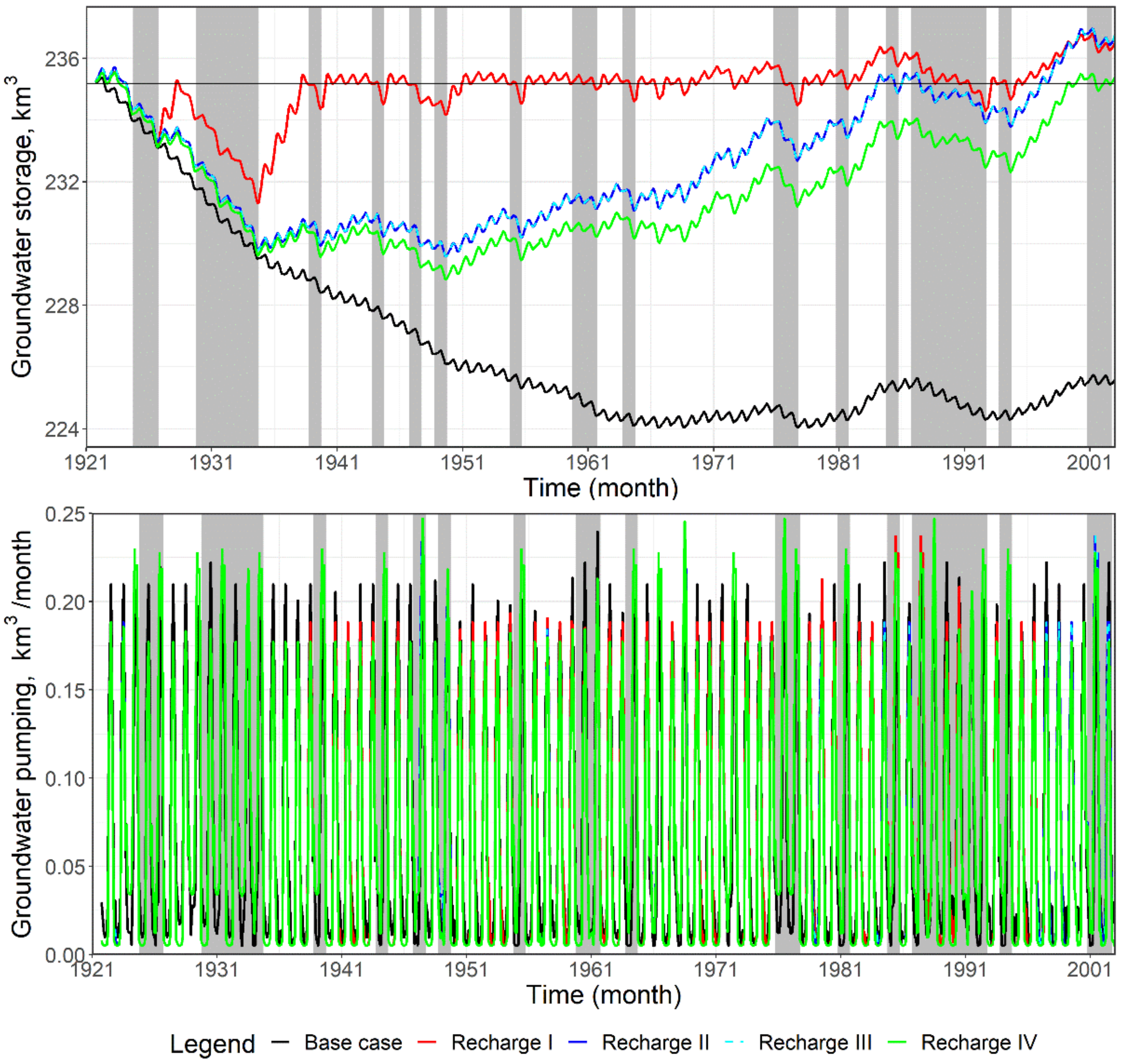
3.4. Groundwater Operation
3.5. Agricultural Water Deliveries
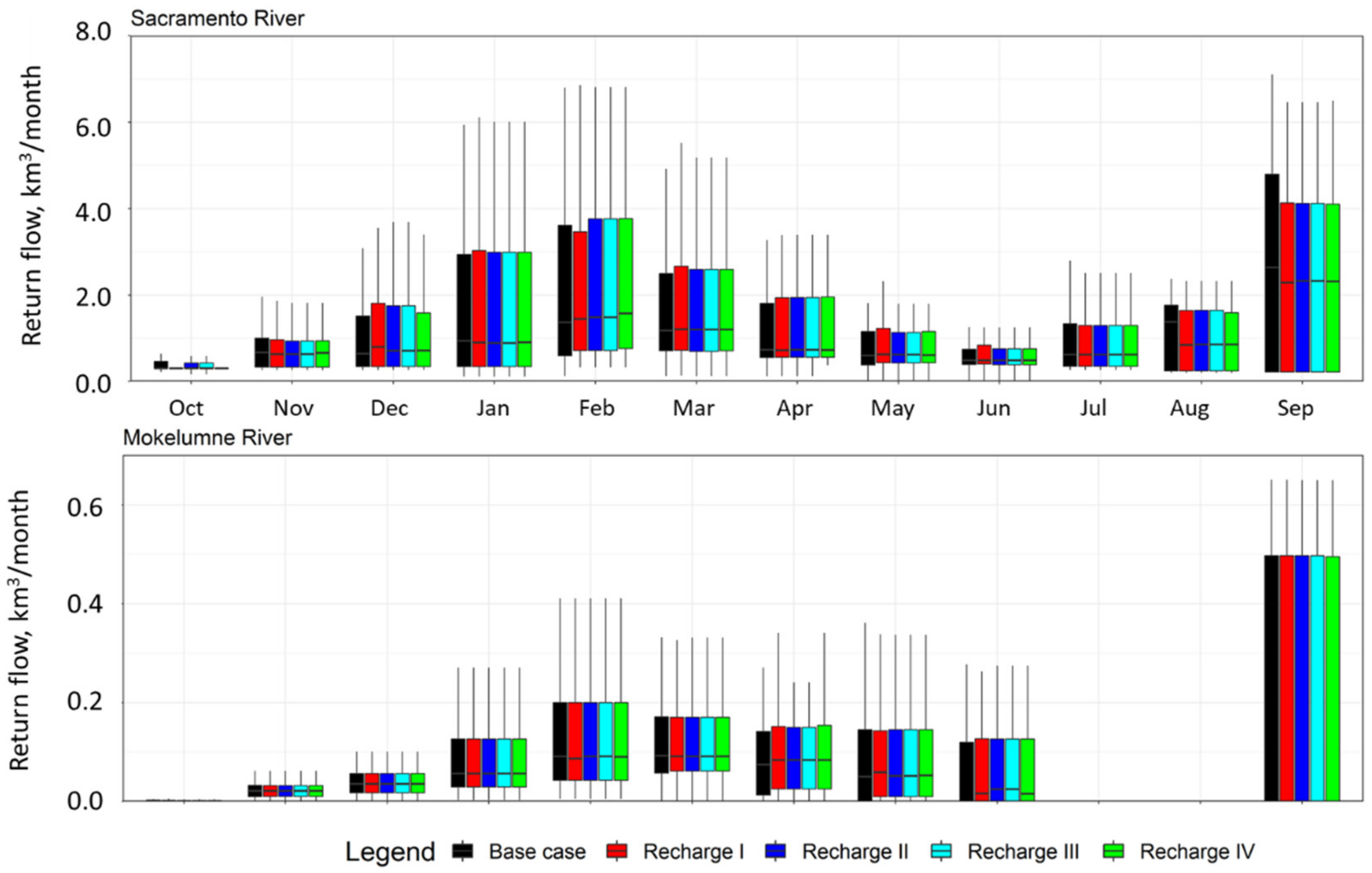
3.6. Surface Water Return Flows Draining to the Delta
3.7. Mass Balance in the Network
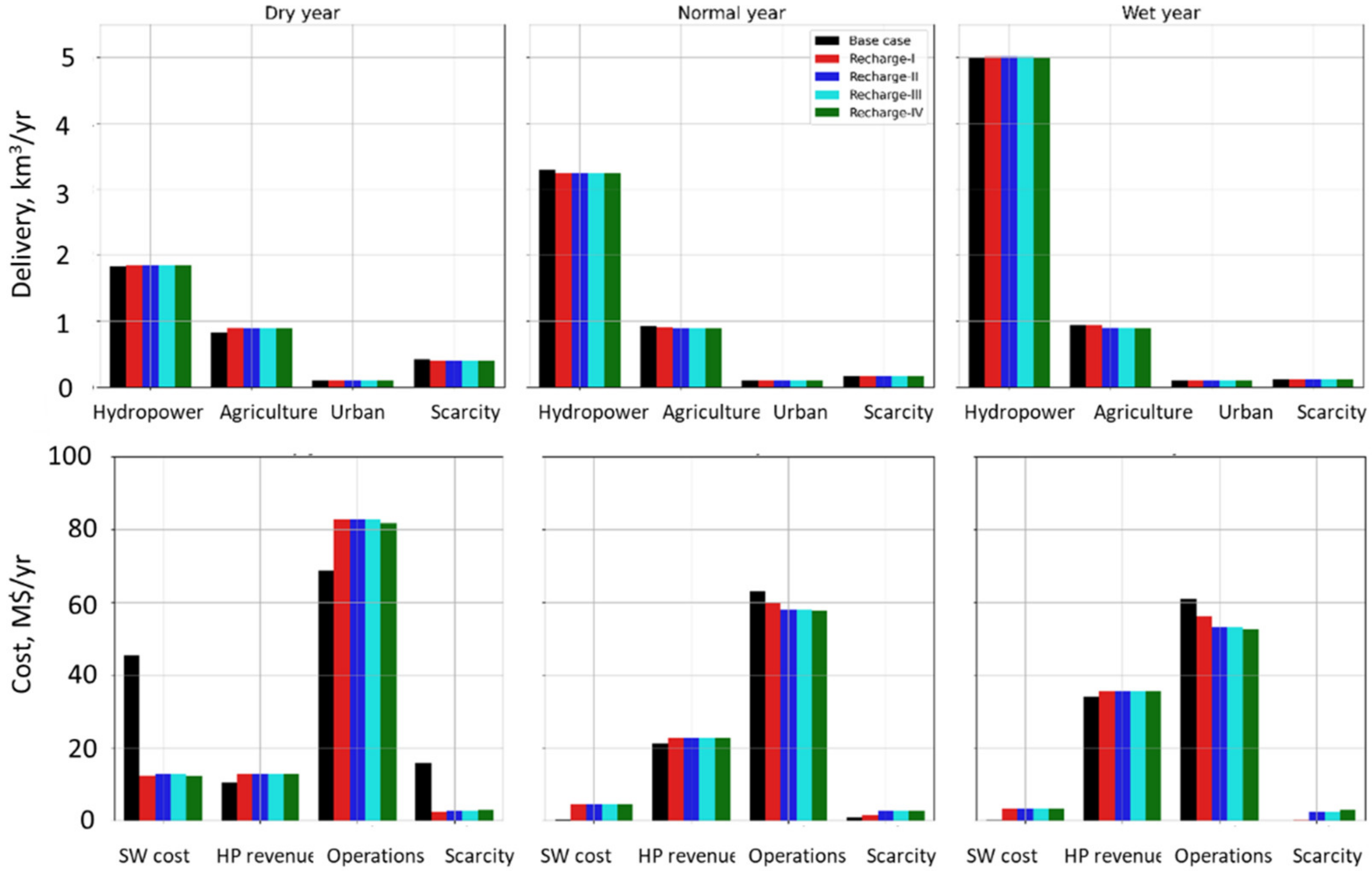
3.8. Water Delivery Cost Analysis
4. Limitations and Future Research
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Connor, R. Managing Water Under Uncertainty and Risk: The United Nations World Water Development Report 4; United Nations Educational, Scientific and Cultural Organization: Paris, France, 2012. [Google Scholar]
- Perrone, D.; Rohde, M.M. Benefits and Economic Costs of Managed Aquifer Recharge in California. San Franc. Estuary Watershed Sci. 2016, 14, 4. [Google Scholar] [CrossRef] [Green Version]
- UNESCO. Water for a Sustainable World; The United Nations World Water Development Report; United Nations Educational, Scientific and Cultural Organization: Paris, France, 2015. [Google Scholar]
- Foster, S.; Chilton, J.; Nijsten, G.-J.; Richts, A. Groundwater—A Global Focus on the ‘Local Resource’. Curr. Opin. Environ. Sustain. 2013, 5, 685–695. [Google Scholar] [CrossRef]
- Dubois, O. The State of the World’s Land and Water Resources for Food and Agriculture: Managing Systems at Risk; CAB Direct: Rome, Italy, 2011; ISBN 1-84971-327-8. [Google Scholar]
- Famiglietti, J.S.; Lo, M.; Ho, S.L.; Bethune, J.; Anderson, K.; Syed, T.H.; Swenson, S.C.; De Linage, C.R.; Rodell, M. Satellites Measure Recent Rates of Groundwater Depletion in California’s Central Valley. Geophys. Res. Lett. 2011, 38. Available online: https://agupubs.onlinelibrary.wiley.com/doi/full/10.1029/2010GL046442 (accessed on 19 September 2021). [CrossRef] [Green Version]
- Farr, T.; Jones, C.; Liu, Z. Progress Report: Subsidence in the Central Valley, California: Prepared for the California Department of Water Resources; Jet Propulsion Laboratory California Institute of Technology: Pasadena, CA, USA, 2017. [Google Scholar]
- Wada, Y.; Van Beek, L.; Bierkens, M.F. Nonsustainable Groundwater Sustaining Irrigation: A Global Assessment. Water Resour. Res. 2012, 48, 1–18. [Google Scholar] [CrossRef]
- Lund, J.; Medellin-Azuara, J.; Durand, J.; Stone, K. Lessons from California’s 2012–2016 Drought. J. Water Resour. Plan. Manag. 2018, 144, 04018067. [Google Scholar] [CrossRef] [Green Version]
- Sheffield, J.; Wood, E.F. Global Trends and Variability in Soil Moisture and Drought Characteristics, 1950–2000, from Observation-Driven Simulations of the Terrestrial Hydrologic Cycle. J. Clim. 2008, 21, 432–458. [Google Scholar] [CrossRef] [Green Version]
- Seager, R.; Ting, M.; Held, I.; Kushnir, Y.; Lu, J.; Vecchi, G.; Huang, H.-P.; Harnik, N.; Leetmaa, A.; Lau, N.-C. Model Projections of an Imminent Transition to a More Arid Climate in Southwestern North America. Science 2007, 316, 1181–1184. [Google Scholar] [CrossRef]
- Berg, N.; Hall, A. Increased Interannual Precipitation Extremes over California under Climate Change. J. Clim. 2015, 28, 6324–6334. [Google Scholar] [CrossRef]
- Dettinger, M. Climate Change, Atmospheric Rivers, and Floods in California—A Multimodel Analysis of Storm Frequency and Magnitude Change. JAWRA J. Am. Water Resour. Assoc. 2011, 47, 514–523. [Google Scholar] [CrossRef]
- Konikow, L.F. Groundwater Depletion in the United States (1900–2008); US Department of the Interior, US Geological Survey: Reston, VA, USA, 2013.
- Pierce, D.W.; Das, T.; Cayan, D.R.; Maurer, E.P.; Miller, N.L.; Bao, Y.; Kanamitsu, M.; Yoshimura, K.; Snyder, M.A.; Sloan, L.C. Probabilistic Estimates of Future Changes in California Temperature and Precipitation Using Statistical and Dynamical Downscaling. Clim. Dyn. 2013, 40, 839–856. [Google Scholar] [CrossRef] [Green Version]
- Russo, T.A.; Fisher, A.T.; Lockwood, B.S. Assessment of Managed Aquifer Recharge Site Suitability Using a GIS and Modeling. Groundwater 2015, 53, 389–400. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gleick, P.H. Impacts of California’s Ongoing Drought: Hydroelectricity Generation—2015 Update; Pacific Institute: Oakland, CA, USA, 2016. [Google Scholar]
- Dogan, M.S.; Buck, I.; Medellin-Azuara, J.; Lund, J.R. Statewide Effects of Ending Long-Term Groundwater Overdraft in California. J. Water Resour. Plan. Manag. 2019, 145, 04019035. [Google Scholar] [CrossRef]
- Nelson, T.; Hui, R.; Lund, J.; Medellín–Azuara, J. Reservoir Operating Rule Optimization for California’s Sacramento Valley. San Franc. Estuary Watershed Sci. 2016, 14, 6. [Google Scholar] [CrossRef] [Green Version]
- Chappelle, C.; Hanak, E.; Harter, T. Groundwater in California; Public Policy Institute of California: San Francisco, CA, USA, 2007. [Google Scholar]
- Escriva-Bou, A.; Gray, B.; Green, S.; Harter, T.; Howitt, R.; MacEwan, D.; Seavy, N. Water Stress and a Changing San Joaquin Valley; Public Policy Institute of California: San Francisco, CA, USA, 2017. [Google Scholar]
- Scanlon, B.R.; Reedy, R.C.; Faunt, C.C.; Pool, D.; Uhlman, K. Enhancing Drought Resilience with Conjunctive Use and Managed Aquifer Recharge in California and Arizona. Environ. Res. Lett. 2016, 11, 035013. [Google Scholar] [CrossRef] [Green Version]
- Howitt, R.; Medellín-Azuara, J.; MacEwan, D.; Lund, J.R.; Sumner, D. Economic Analysis of the 2014 Drought for California Agriculture; Center for Watershed Sciences University of California: Davis, CA, USA, 2014. [Google Scholar]
- Xiao, M.; Koppa, A.; Mekonnen, Z.; Pagán, B.R.; Zhan, S.; Cao, Q.; Aierken, A.; Lee, H.; Lettenmaier, D.P. How Much Groundwater Did California’s Central Valley Lose during the 2012–2016 Drought? Geophys. Res. Lett. 2017, 44, 4872–4879. [Google Scholar] [CrossRef]
- Hanak, E.; Lund, J.R. Adapting California’s Water Management to Climate Change. Clim. Chang. 2012, 111, 17–44. [Google Scholar] [CrossRef]
- Maendly, R. Using Flood Water for Managed Aquifer Recharge to Support Sustainable Water Resources (Flood MAR). 2018. Available online: https://water.ca.gov/programs/all-programs/flood-mar (accessed on 19 September 2021).
- Haines-Young, R.; Potschin, M. Common International Classification of Ecosystem Services (CICES, Version 4.1). Eur. Environ. Agency 2012, 33, 107. [Google Scholar]
- Ojea, E.; Martin-Ortega, J.; Chiabai, A. Defining and Classifying Ecosystem Services for Economic Valuation: The Case of Forest Water Services. Environ. Sci. Policy 2012, 19, 1–15. [Google Scholar] [CrossRef]
- Goharian, E.; Fogg, G.E. UC Water team Role of Managing Headwaters. Forestry Practices, and Reservoirs for Groundwater Management; Groundwater Resources Association: Davis, CA, USA, 2016. [Google Scholar]
- Dahlke, H.; Kocis, T. Streamflow Availability Ratings Identify Surface Water Sources for Groundwater Recharge in the Central Valley. Calif. Agric. 2018, 72, 162–169. [Google Scholar] [CrossRef] [Green Version]
- Dahlke, H.E.; LaHue, G.T.; Mautner, M.R.; Murphy, N.P.; Patterson, N.K.; Waterhouse, H.; Yang, F.; Foglia, L. Managed Aquifer Recharge as a Tool to Enhance Sustainable Groundwater Management in California: Examples from Field and Modeling Studies. In Advances in Chemical Pollution, Environmental Management and Protection; Elsevier: Amsterdam, The Netherlands, 2018; Volume 3, pp. 215–275. [Google Scholar]
- O’Geen, A.; Saal, M.; Dahlke, H.; Doll, D.; Elkins, R.; Fulton, A.; Fogg, G.; Harter, T.; Hopmans, J.; Ingels, C. Soil Suitability Index Identifies Potential Areas for Groundwater Banking on Agricultural Lands. Calif. Agric. 2015, 69, 75–84. [Google Scholar] [CrossRef] [Green Version]
- Hanak, E.; Lund, J.; Dinar, A.; Gray, B.; Howitt, R.; Mount, J.; Moyle, P.; Thompson, B. California Water Myths. Public Policy Inst.: San Francisco, CA, USA, 2009. [Google Scholar]
- Maher, K.M. Potential Use of Real-Time Information for Flood Operation Rules for Folsom Reservoir; University of California: Davis, CA, USA, 2011; ISBN 1-267-23917-4. [Google Scholar]
- Goharian, E.; Azizipour, M.; Sandoval-Soils, S.; Fogg, G.E. Surface Reservoir Reoperation for Managed Aquifer Recharge: Folsom Reservoir System. J. Water Resour. Plan. Manag. 2020, 146, 04020095. [Google Scholar] [CrossRef]
- Bienick, D. Folsom Lake Buoy Measures Water Lost to Air. Available online: https://www.kcra.com/article/folsom-lake-buoy-measures-water-lost-to-air/6425147 (accessed on 19 September 2021).
- Freeman, G.J. Looking for Recent Climatic Trends and Patterns in California’s Central Sierra. 2002. Available online: http://featherriver.org/catalog/resource/138 (accessed on 19 September 2021).
- CA DWR. USBR CalSim 3.0 Draft Report; A Water Resources System Planning Model For State Water Project (SWP) & Central Valley Project (CVP); Department of Water Resources, The California Natural Resources Agency State of California: Sacramento CA, USA, 2017; p. 625. [Google Scholar]
- Placer County. Utilities and Service Systems—Placer County, California; Draft EIR Whitehawk I & II Projects; Placer County: Auburn, CA, USA, 2018; p. 40. [Google Scholar]
- Gailey, R.M.; Lund, J.R.; Medellín-Azuara, J. Domestic Well Reliability: Evaluating Supply Interruptions from Groundwater Overdraft, Estimating Costs and Managing Economic Externalities. Hydrogeol. J. 2019, 27, 1159–1182. [Google Scholar] [CrossRef]
- Goharian, E.; Gailey, R.; Maples, S.; Sandoval-Solis, S.; Fogg, G. Maximizing Whole Watershed Storage through Optimized Reservoir Reoperation and Managed Aquifer Recharge. In Proceedings of the 20th EGU General Assembly, EGU2018, Vienna, Austria, 4–13 April 2018; p. 867. [Google Scholar]
- Maples, S.R.; Fogg, G.E.; Maxwell, R.M. Modeling Managed Aquifer Recharge Processes in a Highly Heterogeneous, Semi-Confined Aquifer System. Hydrogeol. J. 2019, 27, 2869–2888. [Google Scholar] [CrossRef] [Green Version]
- Fleckenstein, J.H.; Niswonger, R.G.; Fogg, G.E. River-aquifer Interactions, Geologic Heterogeneity, and Low-flow Management. Groundwater 2006, 44, 837–852. [Google Scholar] [CrossRef]
- Niswonger, R.G.; Fogg, G.E. Influence of Perched Groundwater on Base Flow. Water Resour. Res. 2008, 44, W03405. [Google Scholar] [CrossRef] [Green Version]
- Giuliani, M.; Li, Y.; Cominola, A.; Denaro, S.; Mason, E.; Castelletti, A. A Matlab Toolbox for Designing Multi-Objective Optimal Operations of Water Reservoir Systems. Environ. Model. Softw. 2016, 85, 293–298. [Google Scholar] [CrossRef]
- Labadie, J.W. Optimal Operation of Multireservoir Systems: State-of-the-Art Review. J. Water Resour. Plan. Manag. 2004, 130, 93–111. [Google Scholar] [CrossRef]
- Li, F.-F.; Shoemaker, C.A.; Qiu, J.; Wei, J.-H. Hierarchical Multi-Reservoir Optimization Modeling for Real-World Complexity with Application to the Three Gorges System. Environ. Model. Softw. 2015, 69, 319–329. [Google Scholar] [CrossRef] [Green Version]
- Matrosov, E.S.; Harou, J.J.; Loucks, D.P. A Computationally Efficient Open-Source Water Resource System Simulator–Application to London and the Thames Basin. Environ. Model. Softw. 2011, 26, 1599–1610. [Google Scholar] [CrossRef]
- Draper, A.J.; Jenkins, M.W.; Kirby, K.W.; Lund, J.R.; Howitt, R.E. Economic-Engineering Optimization for California Water Management. J. Water Resour. Plan. Manag. 2003, 129, 155–164. [Google Scholar] [CrossRef]
- Bartolomeo, E.S. Economic Responses to Water Scarcity in Southern California; University of California: Davis, CA, USA, 2011; ISBN 1-124-90644-4. [Google Scholar]
- Dogan, M.S. Integrated Water Operations in California: Hydropower, Overdraft, and Climate Change. Master’s Thesis, University of California, Davis, CA, USA, 2015. [Google Scholar]
- Dogan, M.S.; Fefer, M.A.; Herman, J.D.; Hart, Q.J.; Merz, J.R.; Medellín-Azuara, J.; Lund, J.R. An Open-Source Python Implementation of California’s Hydroeconomic Optimization Model. Environ. Model. Softw. 2018, 108, 8–13. [Google Scholar] [CrossRef]
- Singh, K. Central Valley Refuge Management under Non-Stationary Climatic and Management Conditions. Master’s Thesis, University of California, Davis, CA, USA, 2015. [Google Scholar]
- Zikalala, P. Groundwater Management in Central Valley California: Updating Representation of Groundwater in CALVIN Water Management Model and Study of How Groundwater Systems Change in Response to Pumping; University of California: Davis, CA, USA, 2013. [Google Scholar]
- Medellín-Azuara, J.; Mendoza-Espinosa, L.; Lund, J.; Harou, J.; Howitt, R. Virtues of Simple Hydro-Economic Optimization: Baja California, Mexico. J. Environ. Manag. 2009, 90, 3470–3478. [Google Scholar] [CrossRef] [PubMed]
- Harou, J.J.; Pulido-Velazquez, M.; Rosenberg, D.E.; Medellín-Azuara, J.; Lund, J.R.; Howitt, R.E. Hydro-Economic Models: Concepts, Design, Applications, and Future Prospects. J. Hydrol. 2009, 375, 627–643. [Google Scholar] [CrossRef] [Green Version]
- Jenkins, M.W.; Draper, A.J.; Lund, J.R.; Howitt, R.E.; Tanaka, S.K.; Ritzema, R.S.; Marques, G.F.; Msangi, S.M.; Newlin, B.D.; Van Lienden, B.J.; et al. Improving California Water Management: Optimizing Value and Flexibility; Department of Civil and Environmental Engineering, University of California: Davis, CA, USA, 2001. [Google Scholar]
- Hart, W.E. Python Optimization Modeling Objects (Pyomo). In Operations Research and Cyber-Infrastructure; Springer: Berlin/Heidelberg, Germany, 2009; pp. 3–19. [Google Scholar]
- Hart, W.E.; Laird, C.D.; Watson, J.-P.; Woodruff, D.L.; Hackebeil, G.A.; Nicholson, B.L.; Siirola, J.D. Pyomo-Optimization Modeling in Python; Springer: Berlin/Heidelberg, Germany, 2017; Volume 67, ISBN 3-319-58821-4. [Google Scholar]
- Draper, A.J. Implicit Stochastic Optimization with Limited Foresight for Reservoir Systems. Ph.D. Thesis, University of California, Davis, CA, USA, 2001. [Google Scholar]
- Arnold, W. The Economic Value of Carryover Storage in California’s Water Supply System with Limited Hydrologic Foresight. Master’s Thesis, University of California, Davis, CA, USA, 2021. [Google Scholar]
- UC Davis California Water Network. HOBBES. Available online: https://hobbes.ucdavis.edu/cwn (accessed on 18 October 2020).
- Draper, A.J. Appendix K: Irrigation Water Requirements; University of California: Davis, CA, USA, 2000. [Google Scholar]
- Davis, M.D.; Jenkins, M.W. Appendix J. Groundwater Hydrology; University of California: Davis, CA, USA, 2001. [Google Scholar]
- Dogan, M.S. Hydropower Generation Optimization in the Era of Renewables and Climate Change; University of California: Davis, CA, USA, 2019. [Google Scholar]
- Ritzema, R.S. Appendix D Hydropower in the CALVIN Model; University of California: Davis, CA, USA, 2002. [Google Scholar]
- CAISO Locational Marginal Energy Price Data. Available online: http://www.caiso.com/ (accessed on 26 February 2018).
- CA DWR Chronological Reconstructed Sacramento and San Joaquin Valley: Water Year Hydrologic Classification Indices. Available online: http://cdec.water.ca.gov/reportapp/javareports?name=WSIHIST (accessed on 15 June 2020).
- Arshad, M.; Qureshi, E.; Jakeman, A. Cost-Benefit Analysis of Farm Water Storage: Surface Storage versus Managed Aquifer Storage. In Proceedings of the 20th International Congress on Modelling and Simulation; Modelling and Simulation Society of Australia and New Zealand Inc, Adelaide, Australia, 1–6 December 2013. [Google Scholar]
- Howitt, R.E.; Ward, K.B.; Msangi, S.M. Statewide Water and Agricultural Production Model; Department of Agricultural and Resource Economics, University of California, Davis: Davis, CA, USA, 2001. [Google Scholar]
- Howitt, R.E.; Medellín-Azuara, J.; MacEwan, D.; Lund, J.R. Calibrating Disaggregate Economic Models of Agricultural Production and Water Management. Environ. Model. Softw. 2012, 38, 244–258. [Google Scholar] [CrossRef]
- Lund, J.R. Comparing Futures for the Sacramento-San Joaquin Delta; Public Policy Institute: San Franscisco, CA, USA, 2008; ISBN 1-58213-130-9. [Google Scholar]
- Dogan, M.S.; Herman, J.D.; Fefer, M. CALVIN Source Code. Available online: https://github.com/ucd-cws/calvin (accessed on 26 December 2019).
- Hart, Q.J.; Merz, J.R.; Dogan, M.S. CALVIN Network Data. Available online: https://github.com/ucd-cws/calvin-network-data (accessed on 5 January 2020).
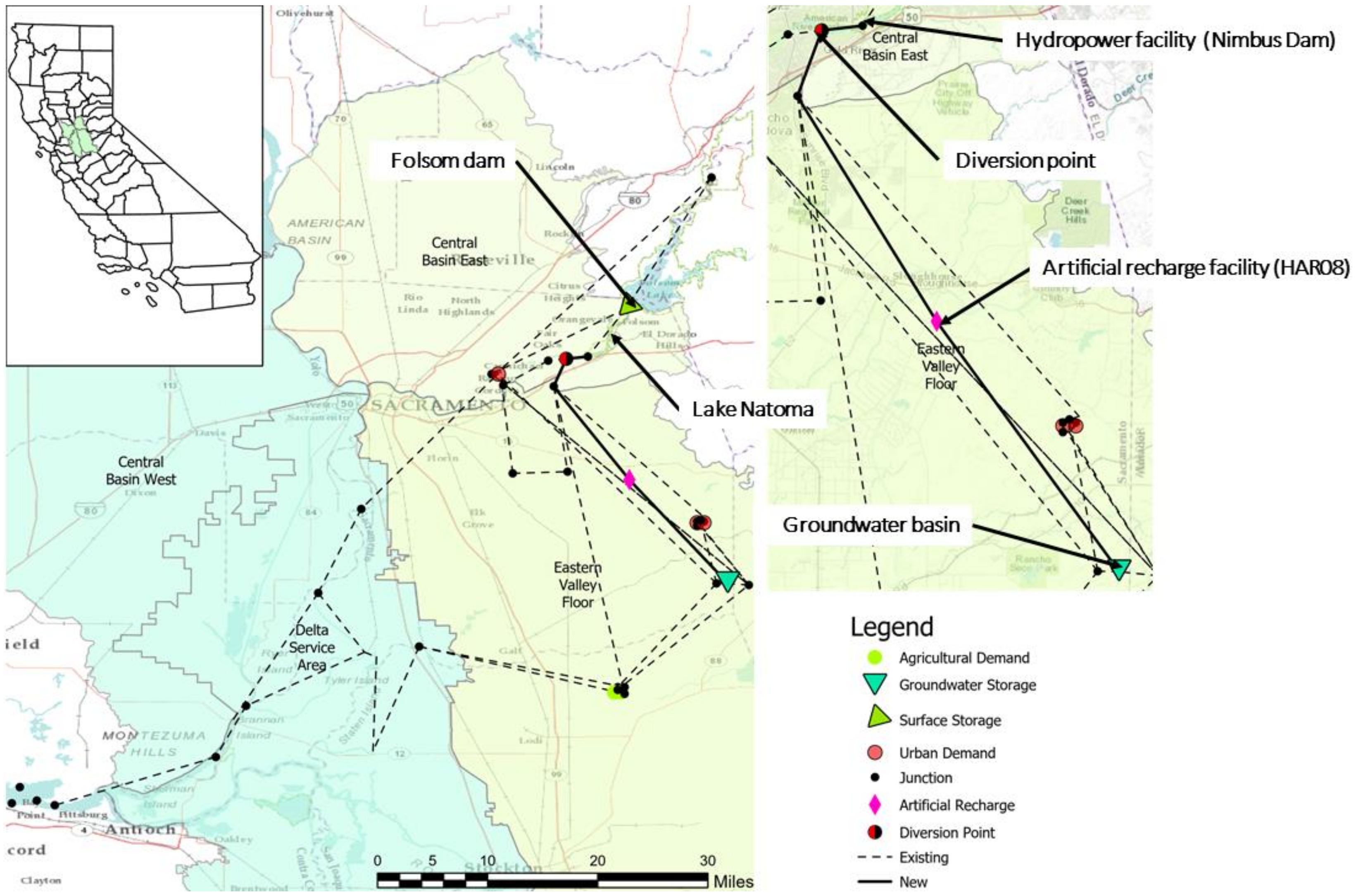
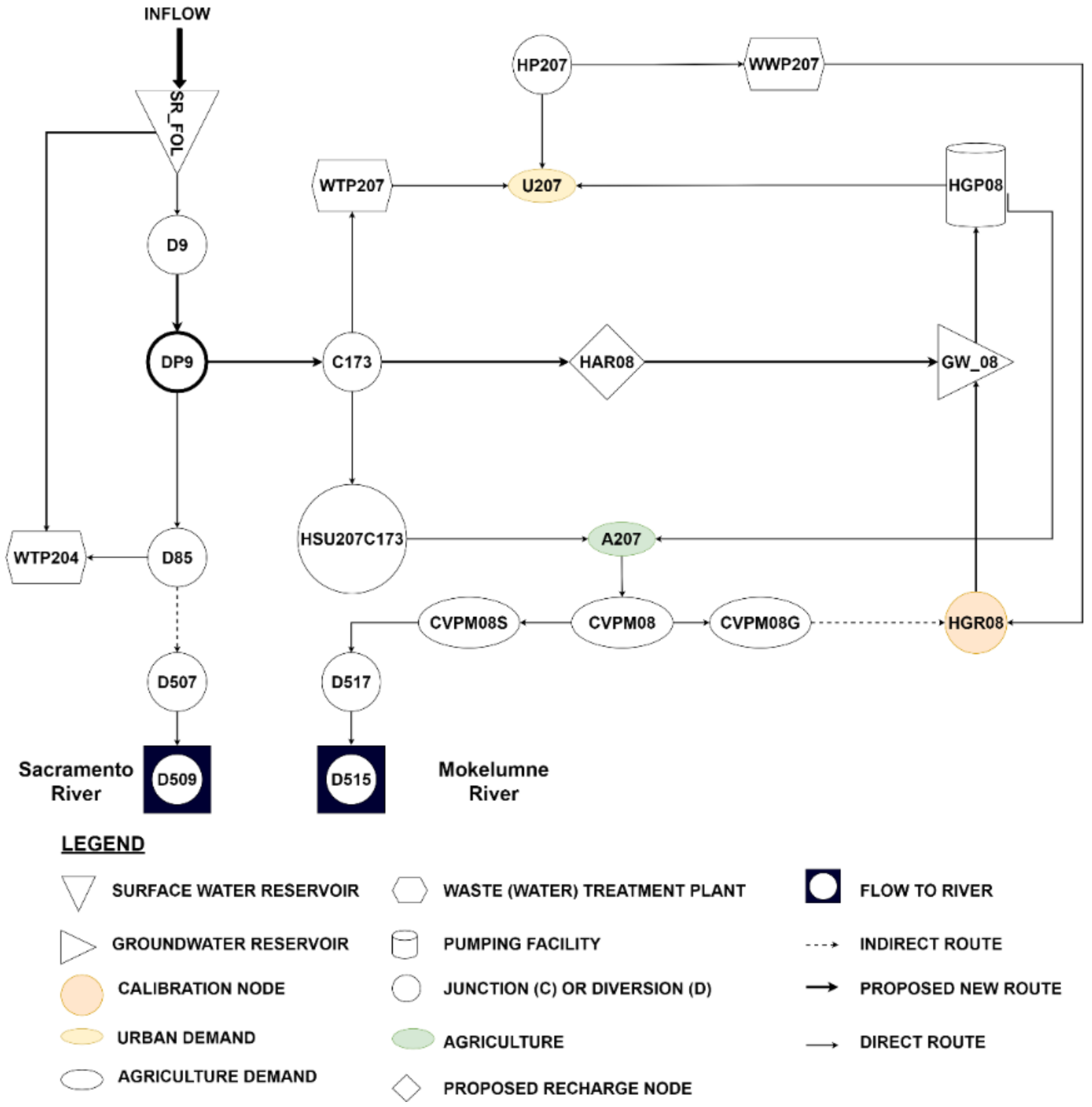

| Network configuration: Node: geographical information of water-related infrastructure such as surface water and groundwater storage, point of deliveries. Links: Spatial connection between two infrastructures. |
| Input hydrology: Surface and subsurface inflow and reservoir storage are derived from CALSIM II and C2VSIM. |
| Constraints: Facilities and capacities are based on the flood control operation. Environmental flow requirements: time series of minimum and fixed flow at certain nodes representing environmental flow requirements and wildlife refuges. Agricultural demand is simply the applied water at the farm level based on 2010 projected land use data. Urban demand is projected water usage based on the 2050 projected urban population. |
| The economic value of water: The economic value of water for agriculture comes from the Statewide Agricultural Production model, while such for urban users comes from economic demand curves for urban water use. |
| Output: Shadow values represent economic costs and benefits such as willingness to pay for water use. Such benefits also include the economic value of expanding capacities. Water deliveries to agricultural and urban sectors are provided by optimized inflow to the nodes that represent demand nodes. |
| Scenarios * | Upstream | Downstream | ||
|---|---|---|---|---|
| Upper Bound | Lower Bound | Upper Bound | Lower Bound | |
| Base case | ||||
| Recharge I | NOB | NOB | NOB | NOB |
| Recharge II | Qm | Qm | NOB | NOB |
| Recharge III | Qm | NOB | NOB | NOB |
| Recharge IV | Qm | NOB | Qm | NOB |
| Month | November | December | January | February | March |
|---|---|---|---|---|---|
| Minimum, | 3.53 | 3.18 | 5.09 | 5.88 | 36.50 |
| Average, | 41.77 | 43.58 | 44.95 | 44.20 | 50.28 |
| Maximum, | 54.42 | 54.42 | 54.42 | 54.42 | 54.42 |
| Scenarios | Dry Years | Normal Years | Wet Years | |||
|---|---|---|---|---|---|---|
| Hydropower, MWh/yr | Revenue, MUSD/yr | Hydropower, MWh/yr | Revenue, MUSD/yr | Hydropower, MWh/yr | Revenue, MUSD/yr | |
| Base case | 444.20 | 10.13 | 872.38 | 20.66 | 1365.87 | 33.43 |
| Recharge I | 529.72 | 12.68 | 918.35 | 22.28 | 1431.62 | 35.12 |
| Recharge II | 529.83 | 12.71 | 925.81 | 22.41 | 1429.34 | 35.08 |
| Recharge III | 529.83 | 12.71 | 925.81 | 22.41 | 1429.34 | 35.08 |
| Recharge IV | 529.63 | 12.68 | 923.61 | 22.33 | 1428.50 | 35.05 |
| Scenarios | Upstream, USD/m3 | Downstream, USD/m3 | ||||
|---|---|---|---|---|---|---|
| Dry | Normal | Wet | Dry | Normal | Wet | |
| Recharge I | 0.99 | 0.72 | 0.69 | 0.02 | 0.01 | <0.01 |
| Recharge II | 0.99 | 0.75 | 0.70 | 0.00 | 0.00 | 0.00 |
| Recharge III | 0.99 | 0.75 | 0.70 | 0.00 | 0.00 | 0.00 |
| Recharge IV | 0.02 | 0.01 | 0.00 | 0.99 | 0.75 | 0.72 |
| Base Case | Recharge | ||||
|---|---|---|---|---|---|
| I | II | III | IV | ||
| Ending storage, km3/yr | 225.52 | 236.49 | 236.87 | 236.87 | 235.39 |
| Long-term change, km3 | N/A | 10.98 | 11.35 | 11.35 | 9.88 |
| Annual change, km3 | N/A | 0.13 | 0.14 | 0.14 | 0.12 |
| Month | Base Case | Recharge I | Recharge II | Recharge III | Recharge IV | Target |
|---|---|---|---|---|---|---|
| October | 5.3 | 9.7 | 9.6 | 9.6 | 9.6 | 34.2 |
| November | 0.2 | 0.6 | 0.6 | 0.6 | 0.6 | 2.2 |
| December | 4.7 | 4.2 | 4.2 | 4.2 | 4.2 | 0.7 |
| January | 48.7 | 45.6 | 45.3 | 45.3 | 45.5 | 0.2 |
| February | 43.2 | 35.5 | 35.0 | 35.0 | 35.5 | 0.2 |
| March | 42.8 | 35.2 | 35.0 | 35.0 | 35.3 | 5.1 |
| April | 41.8 | 35.4 | 35.5 | 35.5 | 35.6 | 53.4 |
| May | 47.1 | 50.2 | 49.2 | 49.2 | 49.0 | 156.7 |
| June | 144.4 | 145.8 | 143.1 | 143.1 | 142.1 | 193.5 |
| July | 167.9 | 176.1 | 172.4 | 172.4 | 171.5 | 225.6 |
| August | 173.9 | 185.6 | 181.2 | 181.2 | 180.1 | 182.9 |
| September | 133.7 | 143.3 | 139.9 | 139.9 | 138.9 | 91.8 |
| Total | 853.8 | 867.4 | 851.1 | 851.1 | 847.9 | 946.4 |
| Scenario | Sacramento River | Mokelumne River | ||||
|---|---|---|---|---|---|---|
| Dry | Normal | Wet | Dry | Normal | Wet | |
| Base case | 6360 | 14780 | 35520 | 240 | 880 | 1740 |
| Recharge I | −101 (−1.6%) | −285 (−1.9%) | −560 (−1.7%) | 28 (+11.7%) | 16 (+1.8%) | 0 (0.0%) |
| Recharge II | −132 (−2.1%) | −89 (−0.6%) | −741 (−2.3%) | 28 (+12.0%) | 14 (+1.6%) | −3 (−0.2%) |
| Recharge III | −132 (−2.1%) | −89 (−0.6%) | −741 (−2.3%) | 28 (+12.0%) | 14 (+1.6%) | −3 (−0.2%) |
| Recharge IV | −113 (−1.8%) | −91 (−0.6%) | −807 (−2.5%) | 28 (+11.5%) | 14 (+1.6%) | −4 (−0.2%) |
| Scenario | Sacramento River | Mokelumne River | ||||
|---|---|---|---|---|---|---|
| Dry | Normal | Wet | Dry | Normal | Wet | |
| Base case | 0.22 | 0.03 | <0.01 | 0.17 | 0.04 | 0.01 |
| Recharge I | 0.19 | 0.03 | <0.01 | 0.14 | 0.04 | 0.01 |
| Recharge II | 0.20 | 0.03 | <0.01 | 0.14 | 0.04 | 0.01 |
| Recharge III | 0.20 | 0.03 | <0.01 | 0.14 | 0.04 | 0.01 |
| Recharge IV | 0.19 | 0.02 | <0.01 | 0.14 | 0.04 | 0.01 |
| Metrics | Dry Year | Normal Year | Wet Year |
|---|---|---|---|
| Surface water storage, km3/yr | 0.451 (125%) | 0.255 (44%) | 0.149 (21%) |
| Hydropower generation. MWh/yr | 85.6 (19%) | 53.4 (6%) | 65.8 (5%) |
| Hydropower revenue, MUSD/yr | 2.6 (25%) | 1.6 (8%) | 1.5 (5%) |
| Groundwater storage, km3/yr | 7.4 (3.3%) | 8.2 (3.6%) | 9.7 (4.3%) |
| Groundwater pumping, km3/yr | 0.216 (23%) | −0.087 (−10%) | −0.105 (−13%) |
| Agriculture Delivery, km3/yr | 0.067 (8%) | −0.011 (−1.1%) | −0.002 (−0.2%) |
| Surface water storage cost, MUSD/yr | −33.2 (−73%) | 4.1 (>100%) | 3.1 (>100%) |
| Scarcity volume, km3/yr | −0.067 (−66%) | 0.027 (>100%) | 0.045 (>100%) |
| Scarcity cost, MUSD/yr | −12.9 (−82%) | 1.6 (>100%) | 2.9 (>100%) |
| Operating cost, MUSD/yr | 13.9 (20%) | −5.5 (−9%) | −8.4 (−14%) |
| Net Benefit, MUSD/yr | 34.75 | 1.43 | 3.86 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maskey, M.L.; Dogan, M.S.; Fernandez-Bou, A.S.; Li, L.; Guzman, A.; Arnold, W.; Goharian, E.; Lund, J.R.; Medellin-Azuara, J. Managing Aquifer Recharge to Overcome Overdraft in the Lower American River, California, USA. Water 2022, 14, 966. https://doi.org/10.3390/w14060966
Maskey ML, Dogan MS, Fernandez-Bou AS, Li L, Guzman A, Arnold W, Goharian E, Lund JR, Medellin-Azuara J. Managing Aquifer Recharge to Overcome Overdraft in the Lower American River, California, USA. Water. 2022; 14(6):966. https://doi.org/10.3390/w14060966
Chicago/Turabian StyleMaskey, Mahesh L., Mustafa S. Dogan, Angel Santiago Fernandez-Bou, Liying Li, Alexander Guzman, Wyatt Arnold, Erfan Goharian, Jay R. Lund, and Josue Medellin-Azuara. 2022. "Managing Aquifer Recharge to Overcome Overdraft in the Lower American River, California, USA" Water 14, no. 6: 966. https://doi.org/10.3390/w14060966
APA StyleMaskey, M. L., Dogan, M. S., Fernandez-Bou, A. S., Li, L., Guzman, A., Arnold, W., Goharian, E., Lund, J. R., & Medellin-Azuara, J. (2022). Managing Aquifer Recharge to Overcome Overdraft in the Lower American River, California, USA. Water, 14(6), 966. https://doi.org/10.3390/w14060966







