Migration Law of LNAPLs in the Groundwater Level Fluctuation Zone Affected by Freezing and Thawing

Abstract

Freezing and thawing can cause dynamic fluctuations of the groundwater level, resulting in the migration and retention of LNAPLs. However, this process is difficult to observe visually, and a suitable simulation method for its quantitative calculation is lacking. In this study, a numerical simulation is established by coupling the HYDRUS-1D software and the TOUGH program to realize dynamic simulation of the entire process of soil temperature changes, water migration, water level fluctuation, and redistribution of LNAPLs during the freeze–thaw process. The results of the study show that the process of soil freezing and thawing causes water migration, which in turn causes groundwater level fluctuation, leading to the migration and redistribution of LNAPLs within the water level fluctuation zone. In this process, the soil particle size and porosity control the response degree and speed of the water level under freezing and thawing and the spatiotemporal distribution of LNAPLs by affecting the soil temperature, capillary force, and water migration. The migration ability of free LNAPLs is determined by their own density and viscosity; the retention of residual LNAPLs is affected by soil porosity and permeability as well as LNAPL viscosity. The results of this study can not only be used to develop a simulation method for the migration and retention mechanism of LNAPLs in cold regions but also serve as a scientific and theoretical basis for LNAPL pollution control in seasonal frozen soil regions.

1. Introduction

The exploration, development, transportation, and utilization of petroleum are often accompanied by serious groundwater and soil pollution problems. The main pollutants are petroleum hydrocarbons in the form of light nonaqueous phase liquids (LNAPLs), which are carcinogenic and teratogenic to the human body and pose a continuous threat to the ecological environment [1]. After the pollution of LNAPLs leaks on the surface, under the action of gravity and capillary force it will gradually diffuse and migrate to the deep layer of the vadose zone and its surroundings, eventually making it difficult to use groundwater resources and soil [2,3].

Seasonal frozen soil is a type of soil in which the surface layer is frozen in winter and thawed in summer. Approximately 30% of the total land area of the northern hemisphere consists of this type of soil, and there are a large amount of oil and oil fields located in these seasonal frozen soil areas which are contributing to the pollution of LNAPLs in the freeze–thaw environment [4,5]. Compared with non-frozen soil areas, seasonal frozen soil areas experience more than 100 days of surface freezing and thawing processes each year. The soil temperature during this process will transmit downward, thereby causing a large amount of moisture migration in the range above the groundwater level, which is mainly carried out in the vertical direction [6,7,8,9,10]. The drastic changes in water content and heat will become involved in the process of temperature-dependent redistribution of LNAPLs in the groundwater level fluctuation zone, and will result in more complicated migration and retention of LNAPLs [11,12,13,14,15]. Ignoring the important effects of freezing and thawing on the dynamics and distribution of LNAPLs will result in significant deviations in the assessment results of the damage, diffusion range, and remediation efficiency of the LNAPL pollution in the groundwater and soil [15,16]. This will severely restrict the rationality of LNAPL pollution prevention and control planning, control objectives, and remediation plans in seasonal frozen soil areas. Therefore, it is necessary to focus on the freeze–thaw environment and study the migration law of LNAPLs in the groundwater level fluctuation zone.

Monitoring LNAPLs in the underground environment in cold regions is difficult; for this reason, numerical simulation has become a relatively effective method [17,18,19]. Currently, scholars have established advanced research on the simulation of water and heat transfer in the freeze–thaw process, but the existing research does not consider both the freeze–thaw process and the migration and retention law of LNAPLs in the water level fluctuation zone [17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34]. There is no single piece of software that can simulate the entire process of soil temperature changes, water migration, water level fluctuation, and redistribution of LNAPLs during the freeze–thaw process [20,21,22]. And in order to solve more complicated simulation problems than the water and heat transfer under freezing and thawing, it is essential to establish a coupling model [23,24,25,26]. To study the migration of LNAPL with the change of water levels under freezing and thawing, the established model needs to couple the water and heat transfer under freezing and thawing and the dynamics of LNAPL with the water level.

In existing research, the water and heat transfer in the freezing and thawing process of the coupled model is mainly simulated by HYDRUS [23,24,25,26]. Compared with other finite element numerical codes for simulating freezing and thawing processes such as FEFlow and OpenGeoSys [27,28,29,30,31,32,33,34,35], HYDRUS is more suitable for freeze-thaw simulation in coupled models. This is because the HYDRUS model can be used for both direct problems and inverse problems when certain parameters are calibrated from observation data, which is very important for the fitting of coupled models [30]. And for soil hydrodynamics and heat conduction, HYDURS-1D is also the most satisfactory [31,32]. Ce et al. [23] developed a fully coupled numerical module and incorporated it into the Hydrus-1D software to simulate the simultaneous movement of water, steam and heat during freezing and thawing, and the simulation result restores the moisture and temperature data of the frozen site well. However, for LNAPLs in the fluctuation zone of water levels in seasonal frozen soil regions, relying solely on the HYDRUS model can only reflect the changes in the water level and temperature with freezing and thawing and does not elucidate on the migration and retention of LNAPLs during water level fluctuations.

Meanwhile, TOUGH is the most suitable numerical simulation method for studying the migration process of LNAPLs [36,37,38]. Tao et al. [39] used the T2VOC module in the TOUGH2 program and constructed a numerical model to simulate the migration and redistribution of LNAPLs after they leak from the surface. The results showed that water level fluctuation will affect the continuous migration of LNAPLs; further, the pollution level will expand in the vertical and horizontal directions until it reaches the entire water level fluctuation zone, and the structural complexity of the polluted area will increase. Yang [40] used the TMVOC module in the TOUGH program to discover that water level fluctuations lead to the mutual displacement of the water, gas, and NAPL phases in the porous medium, and the saturation of the three phases shows a complementary relationship between growth and decline. Dafny [41] used the TMVOC module to quantify the distribution, partitioning, and fate of NAPL in the vadose zone. However, because the TOUGH model has limitations in the simulation of multiphase flow in sub-zero temperature environments, this type of research can only focus on the migration of LNAPLs in the water level fluctuation zone under normal temperature environments and is not suitable for seasonal frozen soil regions [42,43,44,45].

Based on the foundation and deficiencies of related research, in this study, HYDRUS-1D, which can simulate the water and heat transfer in the freeze–thaw process [46], is coupled with the TOUGH program, which can simulate the distribution of LNAPLs with water level fluctuation. Through this coupled simulation method, under the conditions of different media and different types of LNAPLs, the migration and retention law of LNAPLs with the water level fluctuation during freeze–thaw periods is comprehensively analyzed, and the factors affecting it are evaluated. This research is expected to provide the theoretical methods and promotional basis for the numerical simulation of LNAPL migration in the water level fluctuation zone of seasonal frozen soil regions as well as serve as a reference for pollution evaluation, management, and the restoration of LNAPLs.

2. Materials and Methods

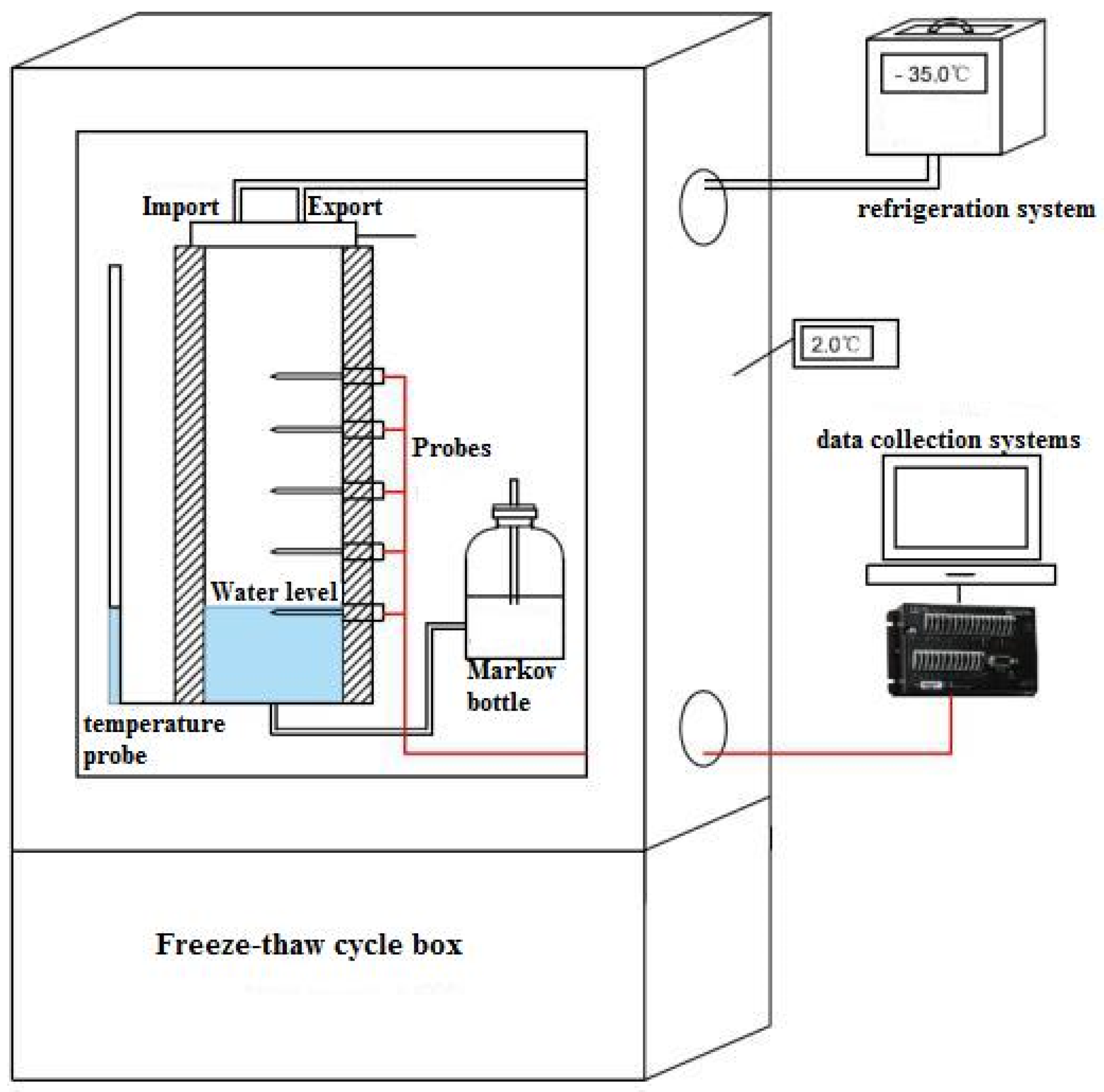
2.1. Soil Column Experiment of Water and Heat Transport

The equipment used in the experiment consists of a freeze–thaw cycle box, a refrigeration system, moisture content and temperature probes, a pressure measuring tube, and a water supply system with a constant water head. The experimental setup is shown in Figure 1.

The test soil column is a plexiglass container with a height of 30 cm, and medium sand (average particle size 0.5–0.2 mm) was selected as the representative test medium. A water supply pipe and a Markov bottle were used to supply water at a fixed head to the soil column, and the initial water level was set to 16 cm from the top of the soil.

A total of five monitoring holes were set on the wall of the column at an interval of 4 cm to monitor the soil temperature and moisture content in the soil column in real time. Each monitoring hole is equipped with a CR300 soil temperature and humidity sensor. The piezometer reading was periodically taken to obtain the dynamic data of the water level. After the start of the experiment, the piezometer is read every 10 min, and the temperature and water content are automatically monitored and outputted every 2 min through the sensor.

The experimental soil column was placed in the freeze–thaw cycle box, which adjusts the temperature around the soil column to be constant at 2 °C. The temperature control cover on the top of the soil is used to control the freezing and thawing of the soil from the top to the bottom in stages. The minimum temperature in the freezing period is −35 °C, and the temperature in the thawing period is 5 °C. The temperature control process is shown in Figure 2.

The resulting data from the soil column experiment will be used to adjust and fit the parameters in the subsequent HYDRUS-1D model. Taking the empirical value of the hydrothermal parameters in HYDRUS-1D as the initial value [46], the hydraulic parameters related to the soil hydraulic conductivity in the medium sand obtained by adjusting and fitting are shown in

Table 1. Soil hydraulic parameters.

Parameter	${\theta }_{\mathit{r}} ({\mathbf{cm}}^3/{\mathbf{cm}}^3)$	${\theta }_{\mathit{s}} ({\mathbf{cm}}^3/{\mathbf{cm}}^3)$	$\mathit{\alpha } \left({\mathbf{cm}}^{-1}\right)$	n	K (cm/s)	l
medium sand	0.040	0.300	0.094	2.05	9.72 × 10−3	0.5

, and the parameters related to the soil heat conductivity are shown in

Table 2. Soil thermodynamic parameters.

Parameter	Solid	Org.	${\mathit{D}}_{\mathit{L}} ({\mathbf{cm}}^2·{\mathbf{s}}^{-1})$	b1	b2	b3
medium sand	0.59	0.00	5.00	1.06376 × 1012	−1.12254 × 1010	2.48832 × 1011

. And for the data of the soil column experiment, please refer to Table S1 in the Supplementary Materials.

2.2. Model Method

HYDRUS-1D and TOUGH are coupled to establish a model to simulate the effect of the freeze–thaw cycle on temperature, moisture migration, water level fluctuation, and LNAPL migration and retention. The coupling process mainly considers the consistency of temperature and water level between the two codes. The simulation range of the HYDRUS-1D model is from the top of the soil column (0 cm) to 20 cm below, and the initial groundwater level is located 16 cm below the column surface. The upper and lower boundaries of the water flow are zero flux boundaries, and the upper and lower boundaries of heat transfer are temperature boundaries that change with time. Since TOUGH is not suitable for simulation at a temperature below 0 °C, the TOUGH simulation range is the area within −10 cm to −30 cm in the soil column experiment, and the soil temperature change within this depth range is consistently above 0 °C. And order to comply with the aforementioned soil column experiment and the HYDRUS-1D numerical model, the top is set as the Dirichlet boundary, with constant atmospheric pressure, no water infiltration, and zero water flux. The bottom is set as a waterproof boundary condition. The initial temperature of the topper and lower are set to 6.55 °C and 7 °C, respectively, according to the experimental results, and the temperature changes with time during the simulation. And since the heat and water migration in the freezing and thawing process are mainly reflected in the vertical direction, the boundary conditions in the coupling model are assumed to be horizontally closed [6,7,8,9,10].The left boundary (x = 0–0.05 m) and the right boundary (x = 0.85–0.90 cm) of the simulation area are both physical boundaries, which are set as zero flux boundary conditions [39].

Coupled simulation is achieved through the transfer of heat and water volume time by time between HYDRUS-1D and TOUGH, and the temperature and water content at each depth are verified by measured data. The interface for the water flux interaction of the coupled model is the layer above the water level fluctuation in the TOUGH model. In order to realize the mutual coupling of water flow, 16 cells in this layer are used as the water injection and pumping cells to control the water level changes, and the changed flux is entered into the source and sink of the cell. Figure 3 shows the water level control obtained by TOUGH. On the other hand, the interaction of heat in the coupled model is achieved jointly by each layer of cells in TOUGH. The heat source–sink items are added to each cell after the division in TOUGH, and the corresponding conversion relationship between the rate of heat addition and the temperature change at each representative layer is calculated. Thus, the coupling of water and heat between the two models is realized.

In the water and heat transfer model, The modified Richards’ equation [43] is used as the basic equation of water migration:

$$\frac{\partial \theta u\left(h\right)}{\partial t}+\frac{{\rho }_i}{{\rho }_w}\frac{\partial {\theta }_i(T)}{\partial t}=\frac{\partial }{\partial z}\left[K_{Lh}\left(h\right)\frac{\partial h}{\partial z}+K_{Lh}\left(h\right)+K_{LT}\left(h\right)\frac{\partial T}{\partial z}+K_{Vh}\left(\theta \right)\frac{\partial h}{\partial z}+K_{vT}\left(\theta \right)\frac{\partial T}{\partial z}\right]-S$$

(1)

where θ_u is the volumetric unfrozen water content (L³ L⁻³) (= θ + θ_u), θ is the volumetric liquid water content (L³ L⁻³), θ_v is the volumetric vapor content expressed as an equivalent water content (L³ L⁻³), θ_i is the volumetric ice content (L³ L⁻³), t is time (T), z is the spatial coordinate positive upward (L), ρ_i is the density of ice (M L⁻³) (931 kg m⁻³), ρ_w is the density of liquid water (M L⁻³) (approximately 1000 kg m⁻³), h is the pressure head (L), T is the temperature (K), and S is a sink term (T⁻¹) usually accounting for root water uptake. Water flow in Equation (1) is assumed to be caused by five different processes with corresponding hydraulic conductivities. The first three terms on the right-hand side of Equation (1) represent liquid flows due to a pressure head gradient (K_Lh, [LT⁻¹]), gravity, and a temperature gradient (K_LT, [L² T⁻¹ K⁻¹]), respectively. The next two terms represent vapor flows due to pressure head (K_vh, [LT⁻¹]) and temperature (K_vT, [L² T⁻¹ K⁻¹]) gradients, respectively.

The soil hydraulic conduction module uses the Van Genuchten–Mualem equation, which is generally recognized in soil water calculations. The basic equation of soil heat transfer [28] is given as follows.

$$\frac{\partial C_{p}T}{\partial t}-L_f{\rho }_i\frac{\partial {\theta }_i}{\partial t}+L_0\left(T\right)\frac{\partial {\theta }_v(T)}{\partial t}=\frac{\partial }{\partial z}\left[\lambda \left(\theta \right)\frac{\partial T}{\partial z}\right]-C_{\omega }\frac{\partial q_{l}T}{\partial z}-C_v\frac{\partial q_{v}T}{\partial z}-L_0\left(T\right)\frac{\partial q_v}{\partial z}-C_{\omega }ST$$

(2)

where the first term on the left-hand side represents changes in the energy content, and the second and third terms represent changes in the latent heat of the frozen and vapor phases, respectively. The terms on the right-hand side represent soil heat flow by conduction, convection of sensible heat with flowing water, transfer of sensible heat by diffusion of water vapor, transfer of latent heat by diffusion of water vapor, and uptake of energy associated with root water uptake, respectively. The phase change between water and ice is controlled by the generalized Clapeyron equation, which defines a relationship between the liquid pressure head and temperature when ice is present in the porous material [32]. Hence, the unfrozen water content can be derived from the liquid pressure head as a function of temperature alone when ice and pure water coexist in the soil [43]. Further, ice volume fraction is determined by the difference between initial water content and liquid water content. The volumetric heat capacity of the soil, C_p (J m⁻³ K⁻¹, M L⁻¹ T⁻² K⁻¹), in Equation (2) is defined as the sum of the volumetric heat capacities of the solid (C_n), liquid (C_w), vapor (C_v), and ice (C_i) phases multiplied by their respective volumetric fractions:

$$C_p=C_n{\theta }_n+C_w\theta +C_v{\theta }_v+C_i{\theta }_i$$

(3)

Furthermore, in Equation (2), L_o is the volumetric latent heat of vaporization of water (J m⁻³, M L⁻¹ T⁻²), L_o = L_w ρ_w, L_w is the latent heat of vaporization of water (J kg⁻¹) (=2.501 × 10⁶ − 2369.2 T [°C]), and L_f is the latent heat of freezing (J kg⁻¹, L² T⁻²) (approximately 3.34 × 10⁵ J kg⁻¹).

In the simulation of LNAPL migration and retention with water level fluctuation, the mass and energy conservation equations [37] are used as the basic governing equations of the components in the multiphase flow (i.e., water, gas, and NAPL phases). Parker’s equation [39] is used as the relative permeability coefficient equation in the multiphase flow problem. Van Genuchten’s equation [39] is used as the capillary pressure governing equation of the NAPL–water phase. Finally, the migration and flow equation of free LNAPLs in the soil medium [38] is shown in Equation (4).

$$\frac{\partial }{\partial t}\left(\phi S_N{\rho }_N\right)=-\frac{\partial }{\partial x}\left(\phi S_N{\rho }_{N}V\right)-\frac{\partial }{\partial z}\left(\phi S_N{\rho }_{N}V\right)+I$$

(4)

where ϕ is the porosity, S_N is the NAPL phase saturation, ρ_N is the NAPL phase density, and V is the Darcy flow velocity of the immiscible phase. The last term I on the right side of the equation is the source (sink) term (=ρ_NQ_N + E), Q_N is the volume of NAPL existing or leaked in the unit time, and E represents the mass exchange between phases. Such source and sink terms are not considered in this model, so I = 0.

3. Results

3.1. Law of Soil Water and Heat Transfer during Freezing and Thawing

During the freeze–thaw experiment, the water content within 4 cm of the top of the soil column changes drastically, becoming weaker with increasing depth (Figure 4(c1)). This is mainly related to the mutual transformation of the water and ice phases. During the freezing process, as shown in Figure 4(b1,c1), the upper part of the soil body freezes first, decreasing the water content. The negative temperature transfers from top to bottom and the water migrates upward, causing the water level to drop, as shown in Figure 4(d1). In the process of melting, the ice phase on the upper part of the soil melts, the water content increases, and the water moves downward, which increases the groundwater level. The HYDRUS-1D model also shows the changes of temperature, water content and water level in the medium-sand medium during the freezing and thawing process (Figure 4(a’2–d’2)), and its water and heat transfer law is consistent with the results of the soil column experiment: Moisture migration due to freezing and thawing of the upper soil is responsible for changes in the water table.

As shown in Figure 4(1,2), In the HYDRUS-1D model, the changes of soil temperature and water content at each depth are similar to the soil column experiment results. Although the water level changes stepwise, the overall trend and range of change are consistent with the soil column experiment results. In order to evaluate the accuracy of the Hydrus-1D model, two indicators, the percentage of deviation (PBIAS) and the root mean square error (RMSE), were used to quantitatively evaluate the simulation data of HYDRUS-1D for medium-sand media. The PBIAS absolute value of the water level and temperature data in the HYDRUS-1D model is less than 10%, and RMSE is within 0.6, indicating that the water level and soil temperature simulation results are good, and they are overall consistent with the experimental results and have high accuracy. Figure 5a–f show the changes in the water level and temperature obtained by the HYDRUS-1D model with different media. The response rate of soil temperature conduction and water level to the freeze–thaw process is in the order of silty clay > fine sand > medium sand > coarse sand. Compared with the other three media, the soil temperature at the middle depth level of silty clay responds more quickly to the temperature changes in the upper part of the soil. This is because the soil solid particles are arranged closer together, allowing the upper temperature to diffuse downward during the freeze–thaw process [16] and thus improving the overall heat transfer properties of the soil. Moreover, because the temperature of silty clay soil changes rapidly, the capillary force of the upper part of the soil also changes faster, and the time of drop and rise of the water level is earlier than that in the case of coarse sand, medium sand, and fine sand.

The magnitude of the water level change in different media is in the order of fine sand > silty clay > medium sand > coarse sand. For the same temperature gradient, the smaller the particle size of the soil, the better is its water holding capacity and the greater is the capillary force produced during freezing. Therefore, in the freezing process, the amount of water migration on the soil profile in the fine sand medium is greater than that in the medium sand and coarse sand, which increases the water level change.

Compared with fine sand, silty clay has smaller particles; however, owing to its lower residual moisture content and greater soil porosity, silty clay has lower capillary force generated during the freeze–thaw process. Consequently, the water migration and the water level fluctuation range on the soil profile are smaller than those in the case of fine sand. In addition, the water level change range in silty clay is larger than that in coarse sand and medium sand. The reason is similar to that for fine sand: the smaller the soil particle size, the better is the water holding capacity and the greater is the capillary force generated during freezing.

Taken together, in the same temperature gradient, the capillary force generated by the medium during the freeze–thaw process and the thermal conductivity of the medium are important factors that affect the water migration, range, and speed of the water level change.

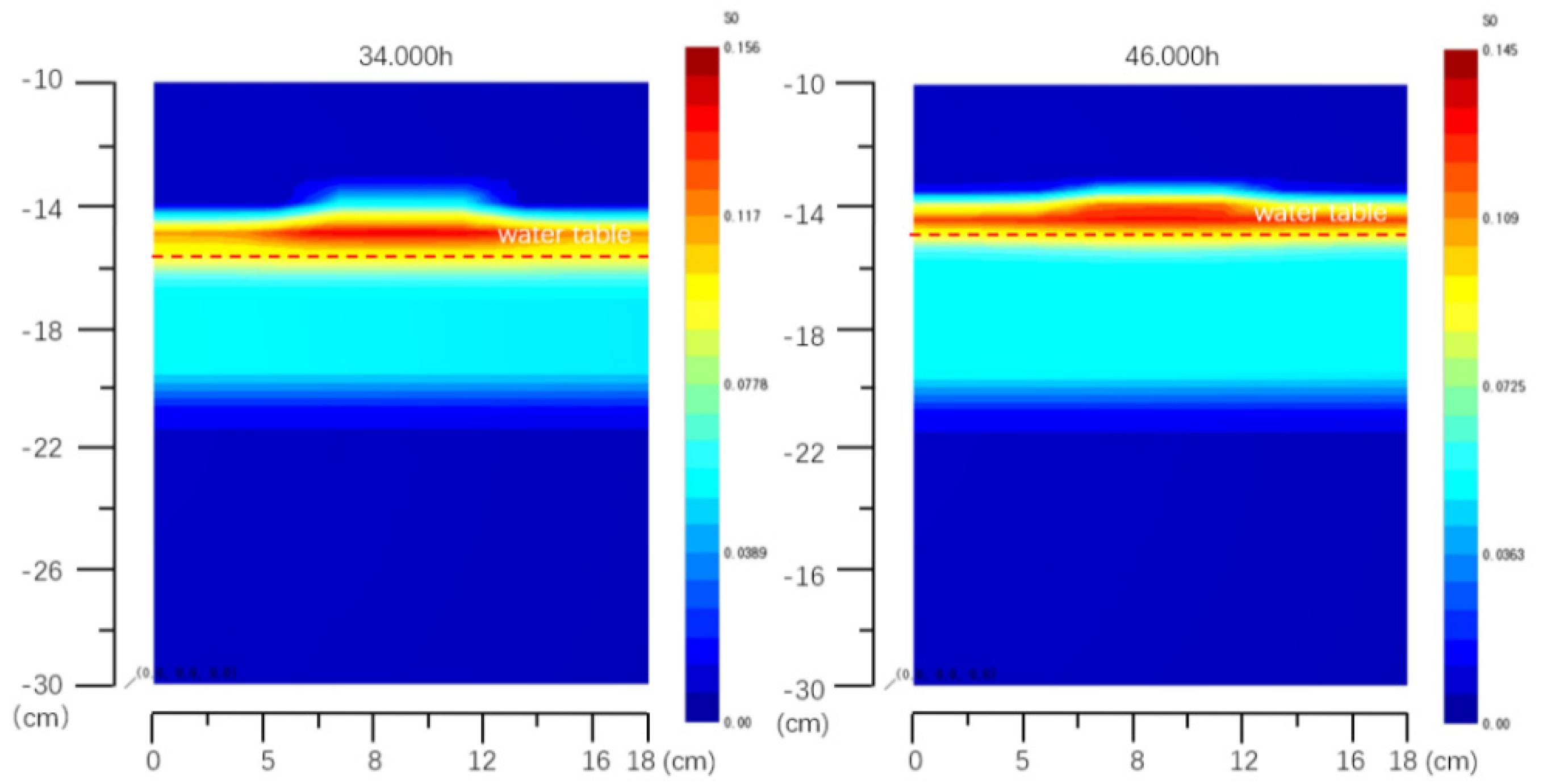
3.2. Migration and Retention Process of LNAPLs Affected by Freezing and Thawing

Figure 6 shows the migration and retention of LNAPLs with water level fluctuation (TOUGH model with toluene as the LNAPL and medium sand as the medium). The residual saturation of the LNAPL phase is 0.05; therefore, when the saturation is less than 0.05, the LNAPLs will remain under the control of capillary force and transform into a residual state. As the water level drops, the free-state LNAPLs migrate downward; simultaneously, their saturation continues to decrease and gradually expands to the entire level in the horizontal direction. When the LNAPLs drop to the lowest position with the water level, a part of the LNAPLs with saturation close to 0.05 are distributed in the descending range. This indicates that a considerable part of the free-state LNAPLs changes into the residual state and remains in the process of the water level drop. In addition, there are some LNAPLs below the water level during the water level drop. This proves that LNAPLs will preferentially displace water when the water level drops [40].

When the water level rises, the free LNAPLs also rise with the water level, and, at the same time, their saturation continues to decrease. In this process, residual LNAPLs continuously stay below the groundwater surface. Therefore, the drop and rise of the water level during the entire freeze–thaw process will cause the original LNAPLs to undergo a significant redistribution process. Furthermore, the pollution range of LNAPLs continues to expand both vertically and horizontally with decreasing water level, while the pollution range of the area above the initial water level increases as the water level increases. During the whole process, the vertical fluctuation range of the water level is approximately 3.3 cm, and the vertical pollution range caused by the migration and retention of LNAPLs is approximately 6 cm.

Taken together, the mechanism of the freeze–thaw process on the migration and retention of LNAPLs is as follows: soil temperature changes cause water phase changes, resulting in water migration, which in turn causes water level fluctuations and the migration and retention of LNAPLs within the water level fluctuation zone. The temperature at the top of the soil is the most fundamental controlling factor in this process. During the freeze–thaw cycle, when LNAPLs rose and fell with the water level, a considerable part of the LNAPLs was retained and transformed into a residual state. Therefore, the effect of retention cannot be ignored. Both migration and retention effects lead to the continuous expansion of the pollution range of LNAPLs in the water level fluctuation zone, resulting in the redistribution of LNAPLs with the water level. Therefore, compared with that in areas not affected by freeze–thaw, the pollution range of LNAPLs in the water level fluctuation zone will be larger in the seasonal frozen soil area.

3.3. Analysis of Factors Affecting the Migration of LNAPLs

After successfully simulating the migration and retention model of LNAPLs in the freeze–thaw water level fluctuation zone by combining HYDRUS-1D and TOUGH, the model is extended to different media conditions and different types of LNAPLs to study their effect on the migration and retention of LNAPLs.

Table 3. Comparison of influencing factors.

Influencing Factors		Corresponding Time of Water Level Change/h	Water Level Fluctuation Range/cm	LNAPLs Pollution Range/cm	The Speed of Migration of LNAPLs	Maximum Saturation of LNAPLs after Freeze-Thaw
Media	coarse sand	9.300	1.210	4 cm	fast	0.227
	Medium sand	7.540	3.300	6 cm	slow	0.145
	Fine sand	7.380	5.250	8 cm	Extremely slow	0.115
	Silty clay	7.510	4.250	7 cm	slow	0.195
LNAPLs	Toluene	7.540	3.300	6 cm	slow	0.145
	Chloroethane	7.540	3.300	6 cm	fast	0.134
	Ethylbenzene	7.540	3.300	6 cm	slow	0.15

shows the comparison of model results with different media conditions and different types of LNAPLs.

The response of water level and LNAPL position to temperature changes during freeze–thaw is affected by the medium condition; the response speed in different media is in the order of fine sand < silty clay < medium sand < coarse sand. This indicates that the smaller the soil particles, the smaller the porosity. That is, with closer arrangement of the soil particles, the heat conduction properties of the soil improves and the hysteresis of the soil temperature change at the middle depth of the soil decreases. As a result, water migration can quickly respond to changes in the top surface temperature of the soil during the freeze–thaw process, and the start of the fluctuation of free LNAPLs near the water level occurs earlier.

The water level fluctuation and the final pollution depth range of LNAPLs in different media are in the order of fine sand > silty clay > medium sand > coarse sand. This phenomenon should be related to the porosity of the soil. The smaller the porosity of the soil, the greater is the capillary force generated in the unsaturated zone during freezing, resulting in the increase of the amount of water migration on the soil profile as well as the ranges of water level fluctuation and LNAPL pollution.

The rate of LNAPL migration and expansion is related to the porosity, permeability, and properties of the medium. With higher porosity and permeability of the soil or lower viscosity of LNAPLs, the migration speed of LNAPLs as well as the distribution thickness of free-state LNAPLs that can move with the water level increase. Conversely, with lower soil porosity and permeability or greater viscosity of LNAPLs, the migration speed of LNAPLs in the vertical direction decreases and more LNAPLs will expand and be retained in the lateral direction. Thus, the maximum saturation of LNAPLs becomes lower at the end of the freeze–thaw process. Therefore, at the lowest water level, in the fine sand medium with the least porosity, the residual LNAPLs near the initial position have the largest retention range. Among different LNAPLs, there is less residual chloroethane in the initial position because of the lower viscosity of chloroethane.

In addition, some LNAPLs exist below the water level during the freezing period, and from the perspective of saturation, this part of the LNAPLs is not in a stagnant state. This is possibly because LNAPLs will preferentially displace water when the water level decreases [42]. In each medium, this part of LNAPLs does not have much difference in the range below the water level; however, comparing the three LNAPLs, the denser chloroethane has a wider range below the water level. Therefore, LNAPLs with high density can more easily displace water below the water level.

In the same TOUGH model, each medium is simulated at a constant temperature, only changing the non-isothermal mode to the isothermal mode. The soil temperature was constant at 22 °C, with no change in other conditions such as the water level. The results of isothermal simulation are compared with the results during the freeze–thaw process. The comparison is shown in

Table 4. Comparison of LNAPL migration status during isothermal and the freeze–thaw process.

Medium	LNAPLs Contamination Range (Isothermal/Freeze-Thaw)	Status of LNAPLs Near the Water Level	Maximum LNAPLs Saturation (Isothermal/Freeze-Thaw)
coarse sand	4.3 cm/4 cm	similar	0.137/0.127
Medium sand	6.2 cm/6 cm	similar	0.161/0.145
Fine sand	8.0 cm/8 cm	similar	0.130/0.115
Silty clay	7.0 cm/7 cm	similar	0.214/0.195

.

The migration distribution and pollution range of LNAPLs in both isothermal and non-isothermal models do not show any considerable difference. The only difference is that the maximum saturation of LNAPLs in the isothermal condition is approximately 0.01–0.02 larger than that during the freeze–thaw process; this difference is relatively small. This confirms that temperature does not directly control the migration and retention of LANPLs, but indirectly leads to the redistribution of LNAPLs by affecting water level changes.

4. Conclusions

In this study, the HYDRUS-1D software and TOUGH program were combined to successfully establish a migration and retention model of LNAPLs with water level fluctuation under the effect of the freeze–thaw cycle. This model can thus be applied to study the interaction mechanism of freezing and thawing temperature-dependent LNAPL redistribution in the water level fluctuation zone. Based on this model, the migration models under different media, LNAPLs, and temperature conditions were established. The following conclusions can be drawn:

(1)

The temperature changes during freezing and thawing is the most fundamental factor controlling the migration of LNAPLs in the water level fluctuation zone. The LNAPLs near the water level during the freeze–thaw process migrate or remain with the fluctuation of the water level. Thus, the pollution range and diffusion degree of LNAPLs in the seasonal frozen soil area are greater than those in the non-frozen soil area.

(2)

The particle size and porosity of the medium as well as LNAPL composition type are the main factors that affect the migration of LNAPLs. In general, the finer and more closely packed the medium particles, the faster is the response of soil temperature and water level changes to freezing and thawing. The smaller the porosity, the greater is the capillary force generated above the water level during the freeze–thaw process and the greater are the amount of water migration, the amplitude of the water level, and the migration and diffusion range of LNAPLs. By contrast, the composition type of LNAPLs determines their retention process and phase change.

(3)

The coupling model in this study can provide a simulation method for the analysis of the migration and retention of LNAPLs in the water level fluctuation zone of seasonal frozen soil regions. The research results on the migration and retention mechanism and the factors affecting LNAPLs can be used as a theoretical basis for LNAPL pollution evaluation and treatment in areas subjected to freeze–thaw cycles. Considering that T2VOC lacks simulation functions for chemical adsorption and microbial degradation processes, the effect of temperature on chemical and biological processes is not reflected and requires further research.