Numerical Simulation and Analysis of the Influencing Factors of Foundation Pit Dewatering under a Coupled Radial Well and Curtain
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
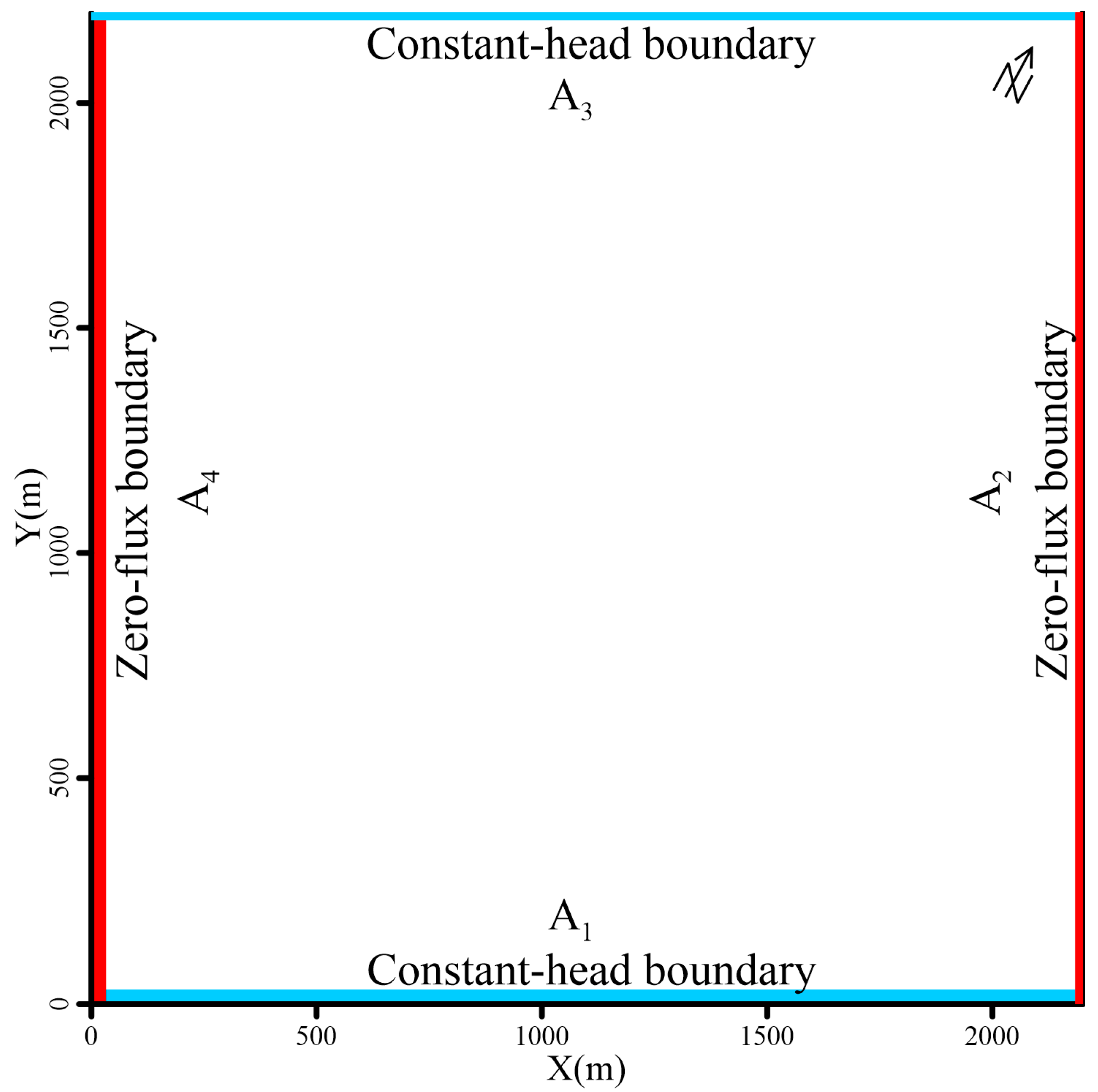
2.2. Conceptual Model
2.3. Mathematical Model
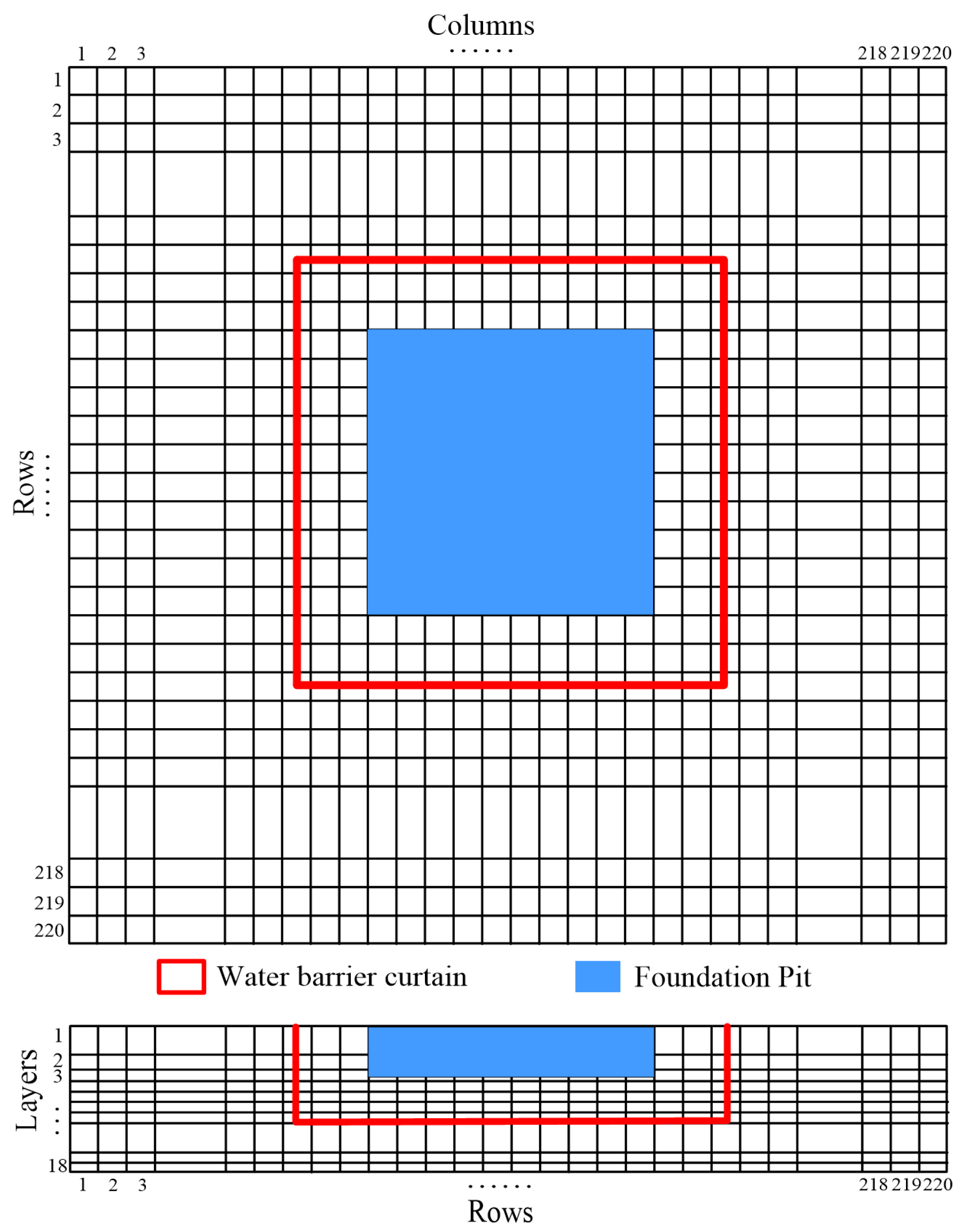
2.4. Numerical Model
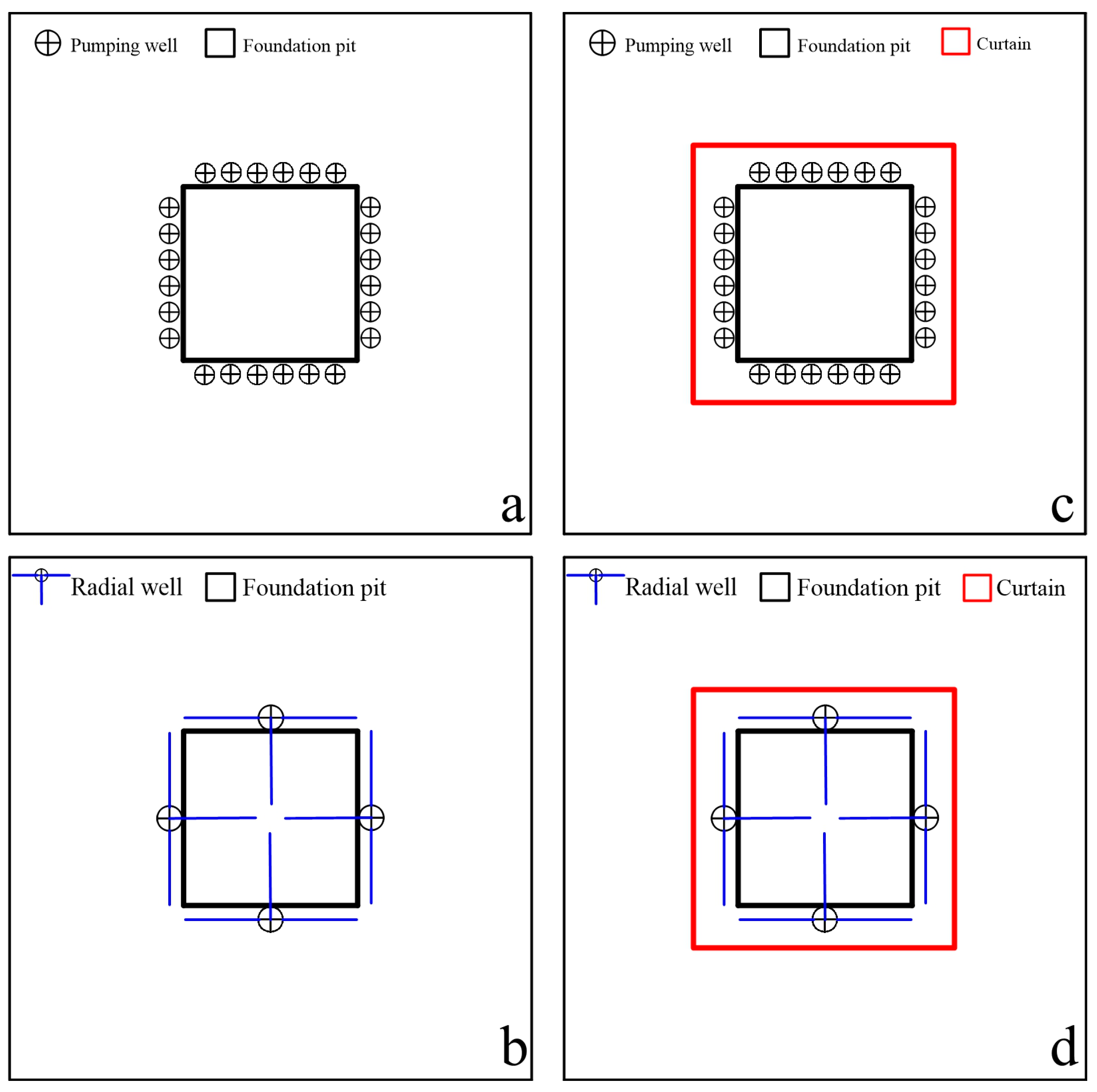
2.5. Scheme Design
2.6. Principles of Scheme Preference
3. Results and Discussion
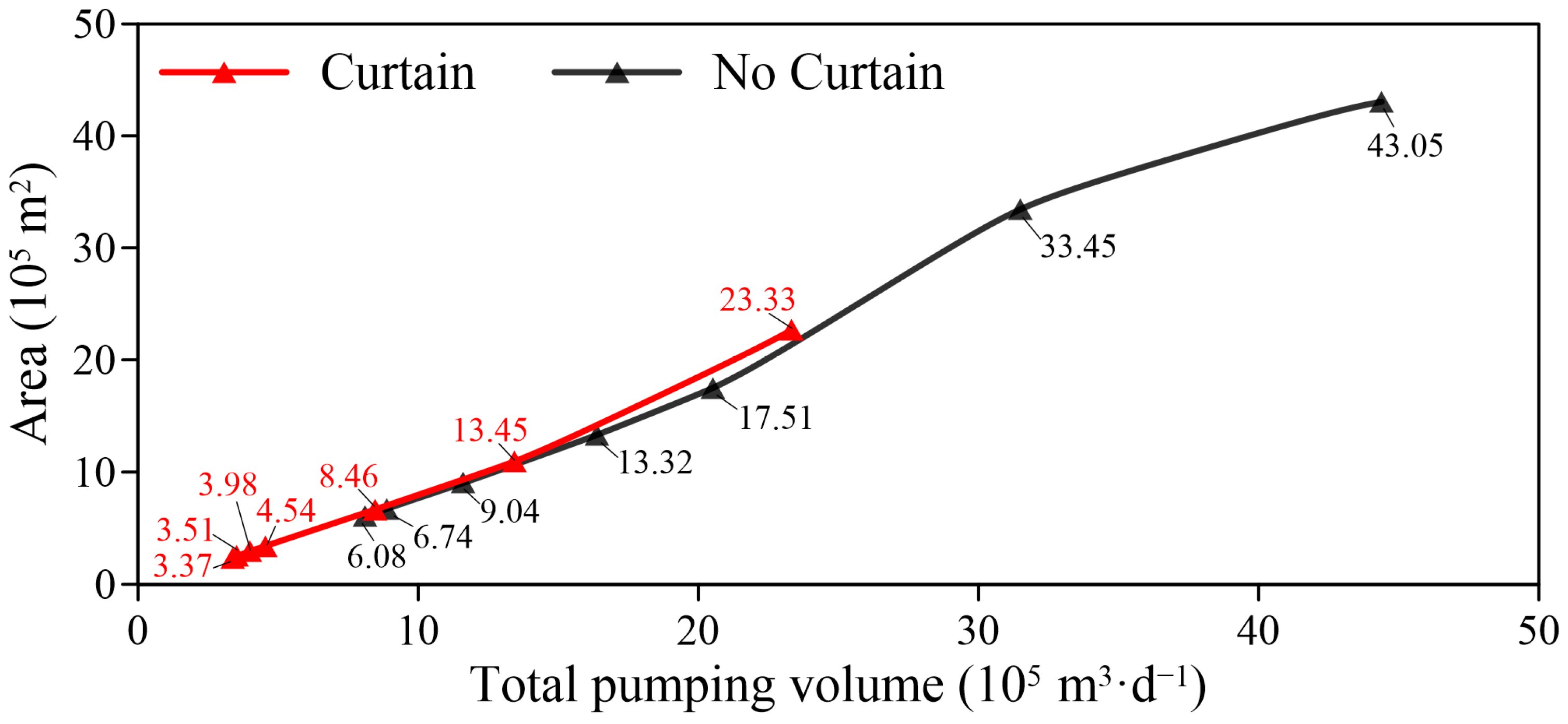
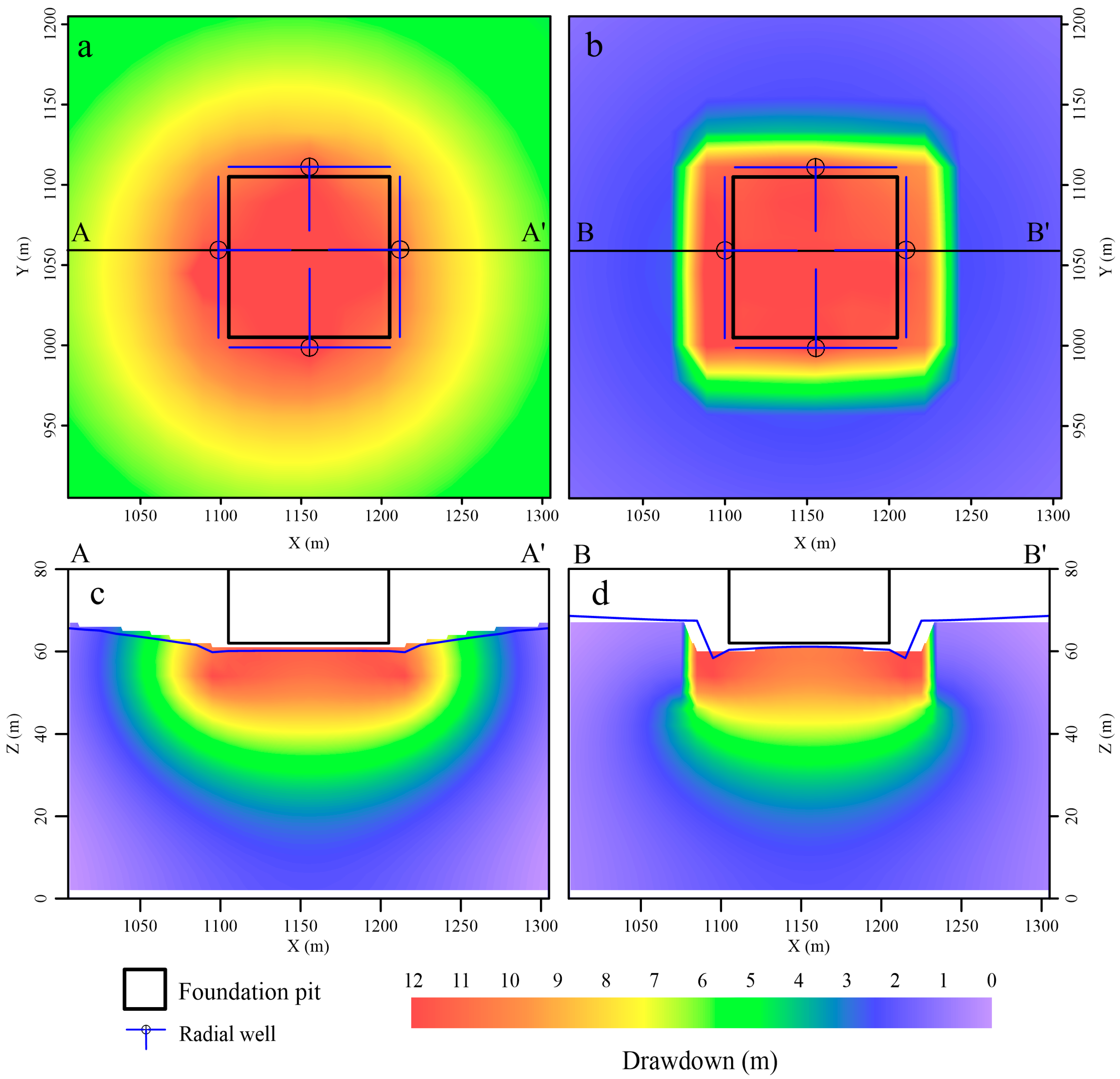
3.1. Pumping Well
3.2. Radial Well
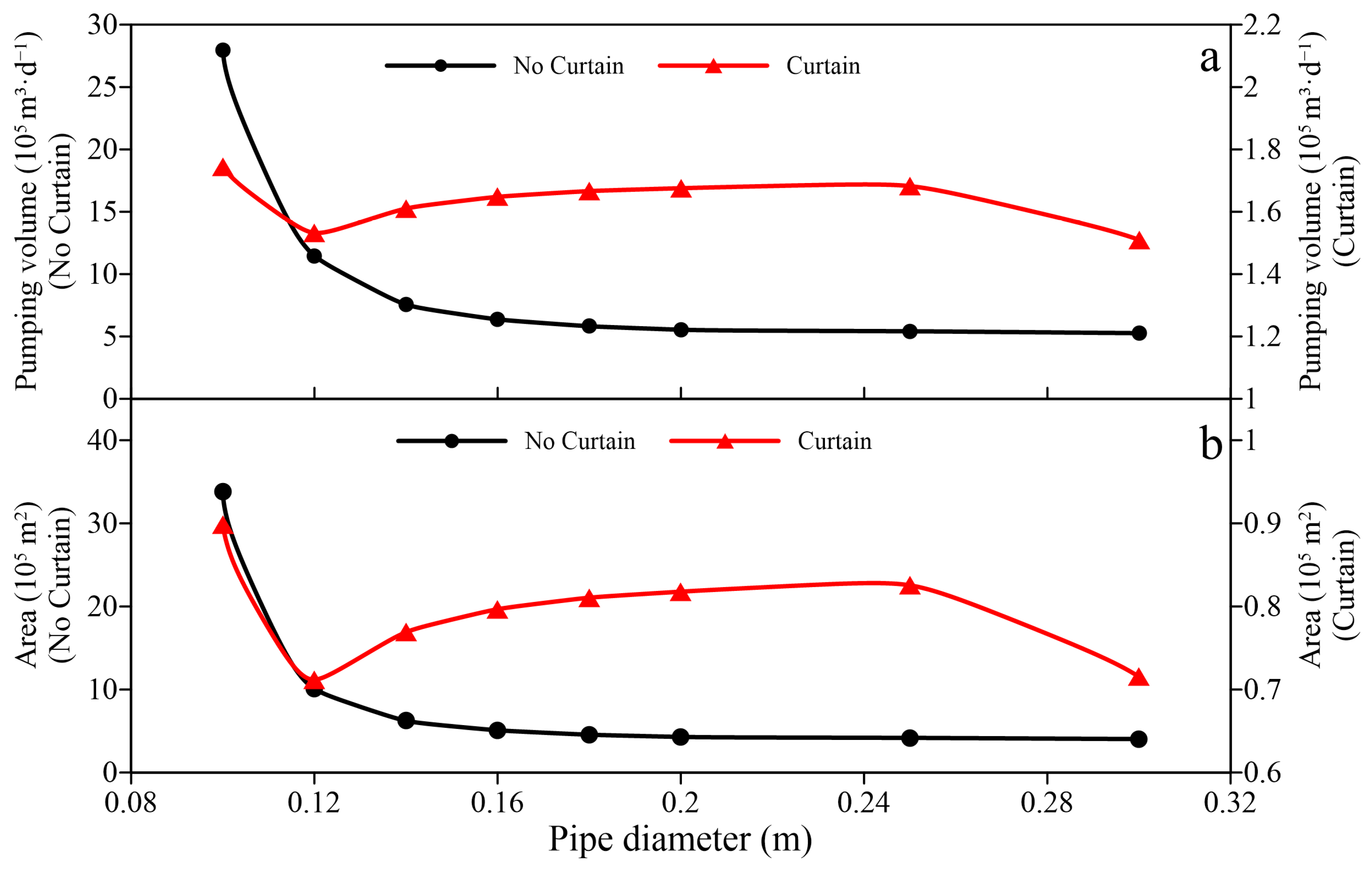
3.2.1. Diameter of the Radial Pipes
3.2.2. Conductance of the Radial Pipes
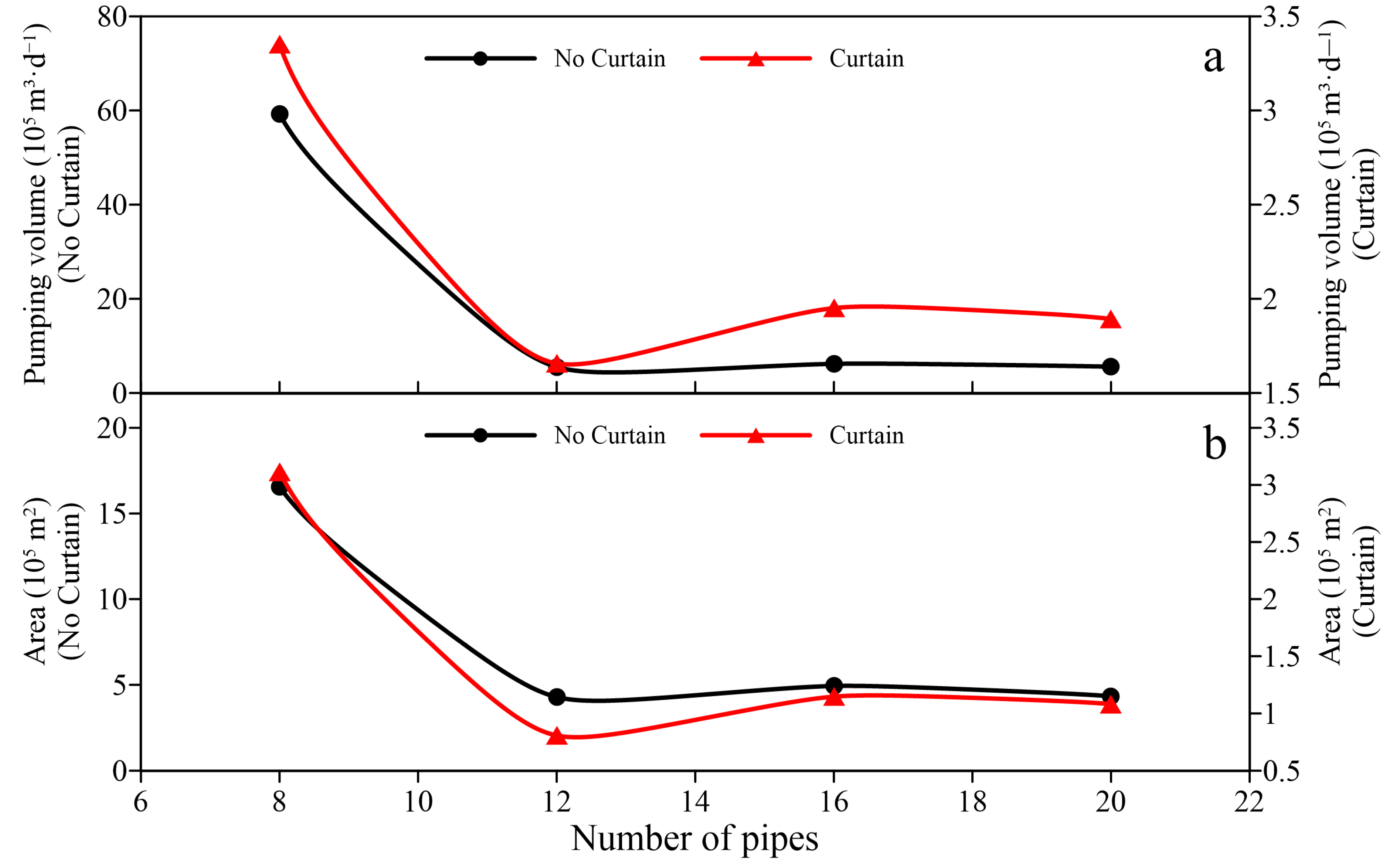
3.2.3. Number of Radial Pipes
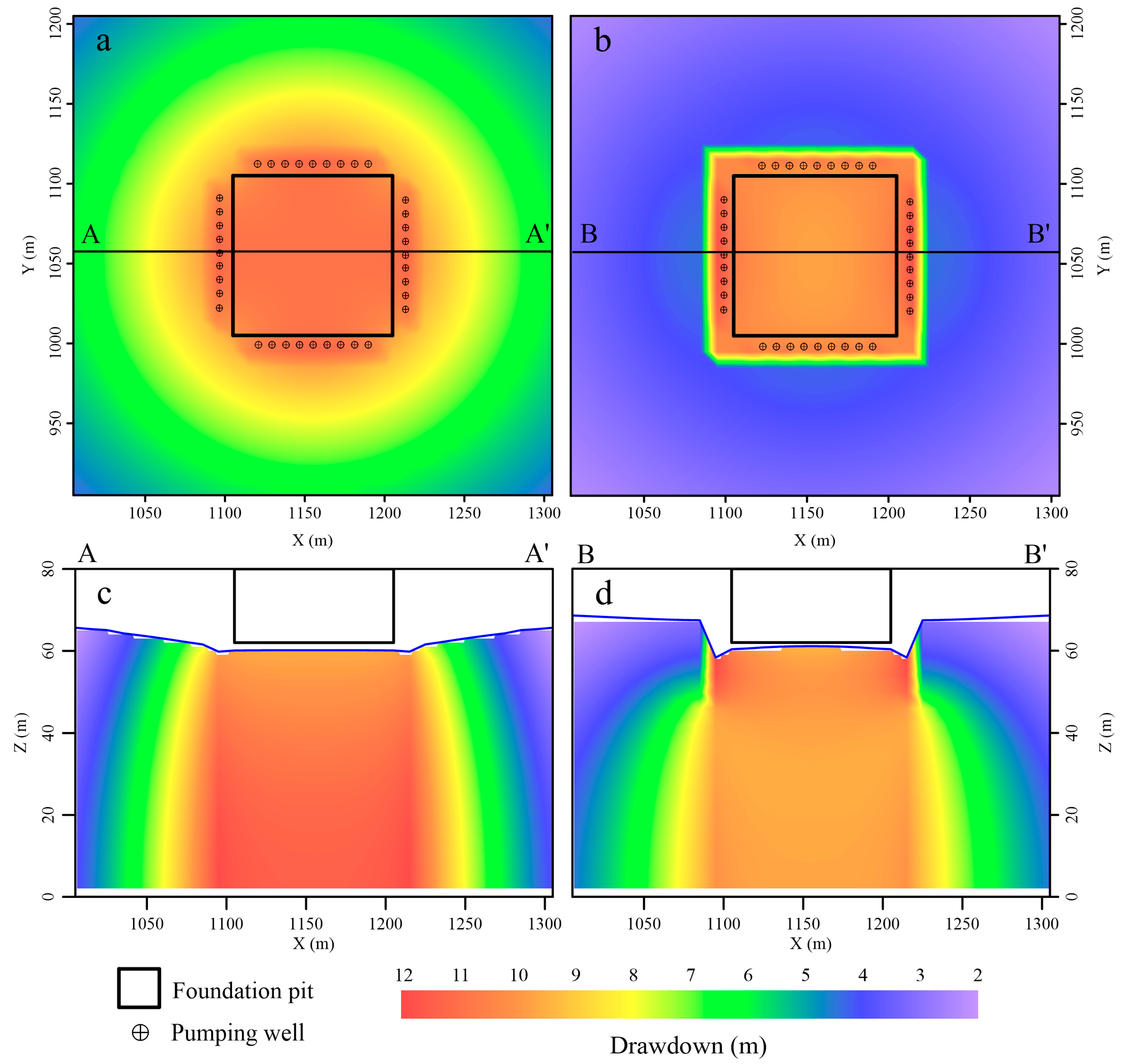
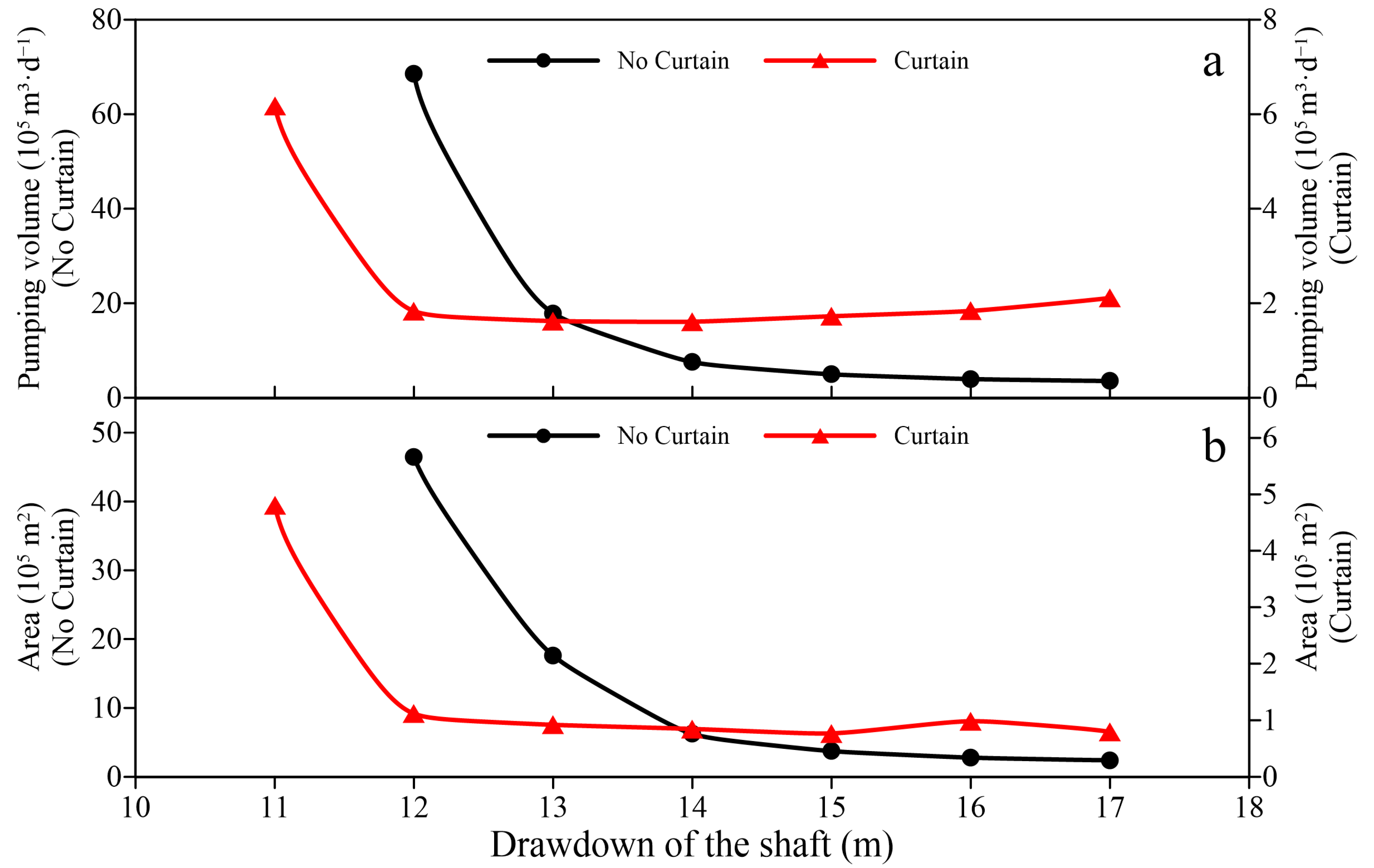
3.2.4. Drawdown of the Shaft
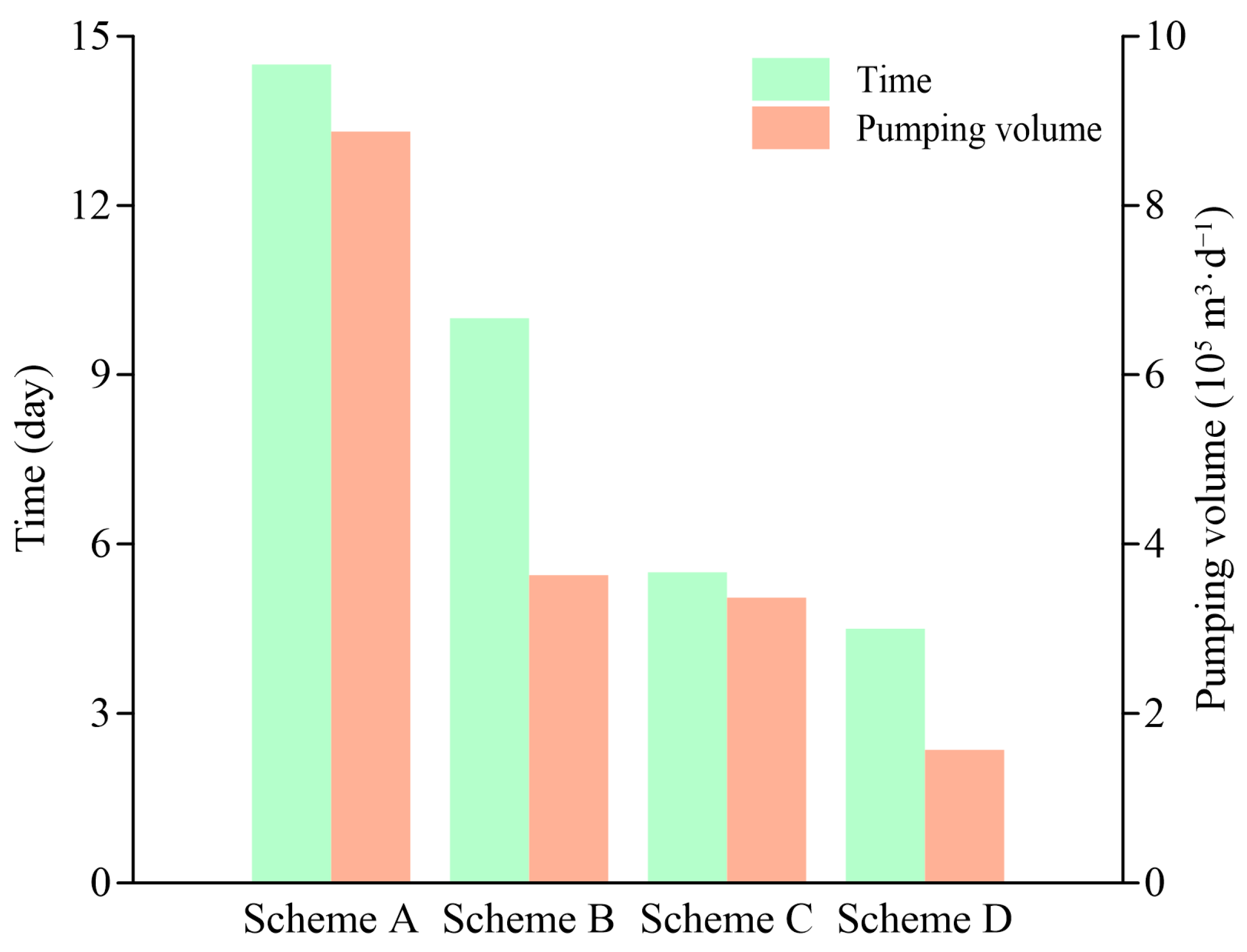
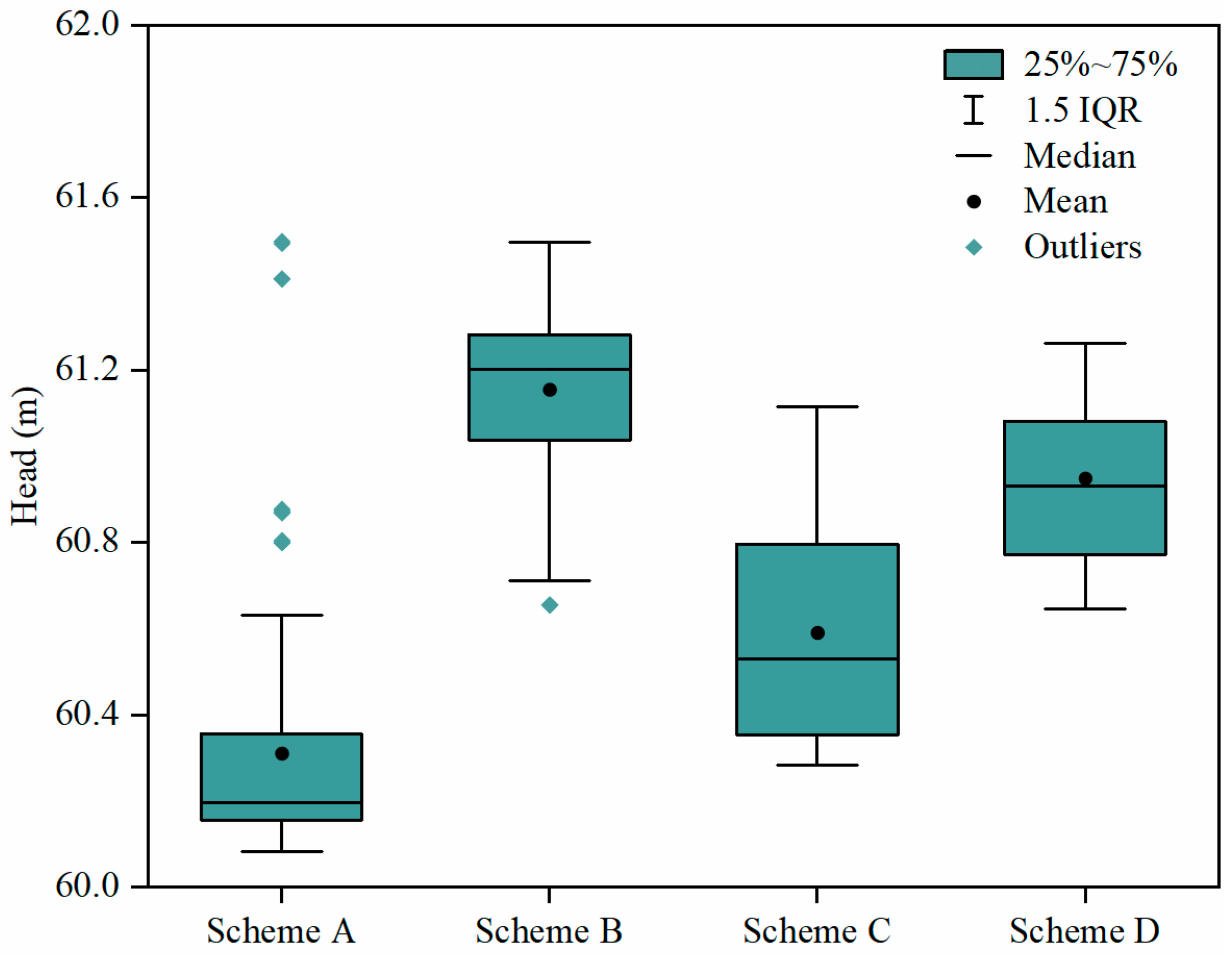
3.3. Optimal Dewatering Scheme
3.4. Land Subsidence
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- You, Y.; Yan, C.; Xu, B.; Liu, S.; Che, C. Optimization of dewatering schemes for a deep foundation pit near the Yangtze River, China. J. Rock Mech. Geotech. Eng. 2018, 10, 555–566. [Google Scholar] [CrossRef]
- Huang, Y.; Bao, Y.; Wang, Y. Analysis of geoenvironmental hazards in urban underground space development in Shanghai. Nat. Hazards 2015, 75, 2067–2079. [Google Scholar] [CrossRef]
- Wang, X.-W.; Yang, T.-L.; Xu, Y.-S.; Shen, S.-L. Evaluation of optimized depth of waterproof curtain to mitigate negative impacts during dewatering. J. Hydrol. 2019, 577, 123969. [Google Scholar] [CrossRef]
- Cao, C.; Shi, C.; Liu, L.; Liu, J. Evaluation of the effectiveness of an alternative to control groundwater inflow during a deep excavation into confined aquifers. Environ. Earth Sci. 2020, 79, 502. [Google Scholar] [CrossRef]
- Liu, L.; Lei, M.; Cao, C.; Shi, C. Dewatering Characteristics and Inflow Prediction of Deep Foundation Pits with Partial Penetrating Curtains in Sand and Gravel Strata. Water 2019, 11, 2182. [Google Scholar] [CrossRef]
- Wang, J.; Liu, X.; Liu, S.; Zhu, Y.; Pan, W.; Zhou, J. Physical model test of transparent soil on coupling effect of cut-off wall and pumping wells during foundation pit dewatering. Acta Geotech. 2018, 14, 141–162. [Google Scholar] [CrossRef]
- Hsi, J.P.; Small, J.C. Ground settlements and drawdown of the water table around an excavation. Can. Geotech. J. 1992, 29, 740–756. [Google Scholar] [CrossRef]
- Wang, X.-w.; Xu, Y.-s. Impact of the Depth of Diaphragm Wall on the Groundwater Drawdown during Foundation Dewatering Considering Anisotropic Permeability of Aquifer. Water 2021, 13, 418. [Google Scholar] [CrossRef]
- Song, L. Some Groundwater Treatment Methods During the Construction of Beijing Subway. Geotech. Investig. Surv. 2006, 19–22. [Google Scholar]
- Zhang, L.; Zhou, X.; Pan, Y.; Zeng, B.; Zhu, D.; Jiang, H. Design of Groundwater Extraction in Open Cut Foundation Pit and Simplified Calculation of Ground Subsidence due to Dewatering in Sandy Pebble Soil Strata. Adv. Civ. Eng. 2020, 2020, 1046937. [Google Scholar] [CrossRef]
- Wang, J.; Wu, Y.; Liu, X.; Yang, T.; Wang, H.; Zhu, Y. Areal subsidence under pumping well–curtain interaction in subway foundation pit dewatering: Conceptual model and numerical simulations. Environ. Earth Sci. 2016, 75, 198. [Google Scholar] [CrossRef]
- Pujades, E.; Vàzquez-Suñé, E.; Carrera, J.; Jurado, A. Dewatering of a deep excavation undertaken in a layered soil. Eng. Geol. 2014, 178, 15–27. [Google Scholar] [CrossRef]
- Wu, Y.-X.; Shen, S.-L.; Wu, H.-N.; Xu, Y.-S.; Yin, Z.-Y.; Sun, W.-J. Environmental protection using dewatering technology in a deep confined aquifer beneath a shallow aquifer. Eng. Geol. 2015, 196, 59–70. [Google Scholar] [CrossRef]
- Pujades, E.; De Simone, S.; Carrera, J.; Vázquez-Suñé, E.; Jurado, A. Settlements around pumping wells: Analysis of influential factors and a simple calculation procedure. J. Hydrol. 2017, 548, 225–236. [Google Scholar] [CrossRef]
- Liu, J.W.; Shi, C.H.; Cao, C.Y.; Lei, M.F.; Wang, Z.X. Improved analytical method for pile response due to foundation pit excavation. Comput. Geotech. 2020, 123, 103609. [Google Scholar] [CrossRef]
- Zeng, C.F.; Xue, X.L.; Zheng, G.; Xue, T.Y.; Mei, G.X. Responses of retaining wall and surrounding ground to pre-excavation dewatering in an alternated multi-aquifer-aquitard system. J. Hydrol. 2018, 559, 609–626. [Google Scholar] [CrossRef]
- Sarychikhina, O.; Glowacka, E.; Mellors, R.; Vidal, F.S. Land subsidence in the Cerro Prieto Geothermal Field, Baja California, Mexico, from 1994 to 2005. J. Volcanol. Geotherm. Res. 2011, 204, 76–90. [Google Scholar] [CrossRef]
- Xie, Z.-F.; Shen, S.-L.; Arulrajah, A.; Horpibulsuk, S. Environmentally sustainable groundwater control during dewatering with barriers: A case study in Shanghai. Undergr. Space 2021, 6, 12–23. [Google Scholar] [CrossRef]
- Zhou, N.; Vermeer, P.A.; Lou, R.; Tang, Y.; Jiang, S. Numerical simulation of deep foundation pit dewatering and optimization of controlling land subsidence. Eng. Geol. 2010, 114, 251–260. [Google Scholar] [CrossRef]
- Luo, C.Y.; Shen, S.L.; Han, J.; Ye, G.L.; Horpibulsuk, S. Hydrogeochemical environment of aquifer groundwater in Shanghai and potential hazards to underground infrastructures. Nat. Hazards 2015, 78, 753–774. [Google Scholar] [CrossRef]
- Wu, Y.X.; Shen, S.L.; Xu, Y.S.; Yin, Z.Y. Characteristics of groundwater seepage with cut-off wall in gravel aquifer. I: Field observations. Can. Geotech. J. 2015, 52, 1526–1538. [Google Scholar] [CrossRef]
- Chen, J.-J.; Zhang, L.; Zhang, J.-F.; Zhu, Y.-F.; Wang, J.-H. Field Tests, Modification, and Application of Deep Soil Mixing Method in Soft Clay. J. Geotech. Geoenvironmental Eng. 2013, 139, 24–34. [Google Scholar] [CrossRef]
- Shen, S.-L.; Wang, Z.-F.; Horpibulsuk, S.; Kim, Y.-H. Jet grouting with a newly developed technology: The Twin-Jet method. Eng. Geol. 2013, 152, 87–95. [Google Scholar] [CrossRef]
- Zhi-Feng, W.; Shui-Long, S.; Chu-Eu, H.; Yong-Hyun, K. Investigation of field-installation effects of horizontal twin-jet grouting in Shanghai soft soil deposits. Can. Geotech. J. 2013, 50, 288–297. [Google Scholar] [CrossRef]
- Yuan, C.; Hu, Z.; Zhu, Z.; Yuan, Z.; Fan, Y.; Guan, H.; Li, L.; Xiong, F. Numerical Simulation of Seepage and Deformation in Excavation of a Deep Foundation Pit under Water-Rich Fractured Intrusive Rock. Geofluids 2021, 2021, 1–10. [Google Scholar] [CrossRef]
- Ni, J.C.; Cheng, W.C.; Ge, L. A simple data reduction method for pumping tests with tidal, partial penetration, and storage effects. Soils Found. 2013, 53, 894–902. [Google Scholar] [CrossRef]
- Tan, Y.; Lu, Y.; Wang, D. Deep Excavation of the Gate of the Orient in Suzhou Stiff Clay: Composite Earth-Retaining Systems and Dewatering Plans. J. Geotech. Geoenvironmental Eng. 2018, 144, 05017009. [Google Scholar] [CrossRef]
- Shen, S.-L.; Wu, Y.-X.; Misra, A. Calculation of head difference at two sides of a cut-off barrier during excavation dewatering. Comput. Geotech. 2017, 91, 192–202. [Google Scholar] [CrossRef]
- Xu, Y.S.; Wu, H.N.; Wang, B.Z.F.; Yang, T.L. Dewatering induced subsidence during excavation in a Shanghai soft deposit. Environ. Earth Sci. 2017, 76, 351. [Google Scholar] [CrossRef]
- Zhang, Y.-Q.; Wang, J.-H.; Chen, J.-J.; Li, M.-G. Numerical study on the responses of groundwater and strata to pumping and recharge in a deep confined aquifer. J. Hydrol. 2017, 548, 342–352. [Google Scholar] [CrossRef]
- Ahmad, I.; Tayyab, M.; Zaman, M.; Anjum, M.; Dong, X. Finite-Difference Numerical Simulation of Dewatering System in a Large Deep Foundation Pit at Taunsa Barrage, Pakistan. Sustainability 2019, 11, 694. [Google Scholar] [CrossRef]
- Xu, Y.-S.; Shen, S.-L.; Ren, D.-J.; Wu, H.-N. Analysis of Factors in Land Subsidence in Shanghai: A View Based on a Strategic Environmental Assessment. Sustainability 2016, 8, 573. [Google Scholar] [CrossRef]
- Wang, J.; Liu, X.; Wu, Y.; Liu, S.; Wu, L.; Lou, R.; Lu, J.; Yin, Y. Field experiment and numerical simulation of coupling non-Darcy flow caused by curtain and pumping well in foundation pit dewatering. J. Hydrol. 2017, 549, 277–293. [Google Scholar] [CrossRef]
- Xu, Y.-S.; Yan, X.-X.; Shen, S.-L.; Zhou, A.-N. Experimental investigation on the blocking of groundwater seepage from a waterproof curtain during pumped dewatering in an excavation. Hydrogeol. J. 2019, 27, 2659–2672. [Google Scholar] [CrossRef]
- Lee, E.; Hyun, Y.; Lee, K.-K. Numerical modeling of groundwater flow into a radial collector well with horizontal arms. Geosci. J. 2011, 14, 403–414. [Google Scholar] [CrossRef]
- Zengguang, X.; Yanqing, W.; Jun, W.; Xiaoqing, Z. A model of seepage field in the tailings dam considering the chemical clogging process. Adv. Eng. Softw. 2011, 42, 426–434. [Google Scholar] [CrossRef]
- Ke, X.M.; Wang, W.; Xu, X.D.; Li, J.L.; Hu, H.Y. A saturated-unsaturated coupling model for groundwater flowing into seepage wells: A modeling study for groundwater development in river basins. Environ. Earth Sci. 2021, 80, 711. [Google Scholar] [CrossRef]
- Wang, W.; Chen, P.; Zheng, Q.Q.; Zheng, X.Y.; Lu, K.M. A modified calculation model for groundwater flowing to horizontal seepage wells. J. Earth Syst. Sci. 2013, 122, 407–418. [Google Scholar] [CrossRef]
- Ke, X.M.; Wang, W.; Li, J.L.; Sun, Q.M.; Lian, L.L.; Xu, X.D.; Lyu, Q. In-situ pumping tests and numerical simulations of seepage wells in the Yellow River valley, China. Water Supply 2021, 22, 1459–1473. [Google Scholar] [CrossRef]
- Shoemaker, W.B.; Kuniansky, E.L.; Birk, S.; Bauer, S.; Swain, E.D. Documentation of a Conduit Flow Process (CFP) for MODFLOW-2005; US Department of the Interior; US Geological Survey Reston: Reston, VA, USA, 2008; Volume 6.
- Deng, L.; Xu, B.; Yang, X.; Hu, A. Water quality and health risk assessment based on hydrochemical characteristics of tap and large-size bottled water from the main cities and towns in Guanzhong Basin, China. Environ. Earth Sci. 2021, 80, 139. [Google Scholar] [CrossRef]
- Wang, Y.-Q.; Wang, Z.-F.; Cheng, W.-C. A review on land subsidence caused by groundwater withdrawal in Xi’an, China. Bull. Eng. Geol. Environ. 2018, 78, 2851–2863. [Google Scholar] [CrossRef]
- Gong, H.; Pan, Y.; Zheng, L.; Li, X.; Zhu, L.; Zhang, C.; Huang, Z.; Li, Z.; Wang, H.; Zhou, C. Long-term groundwater storage changes and land subsidence development in the North China Plain (1971–2015). Hydrogeol. J. 2018, 26, 1417–1427. [Google Scholar] [CrossRef]
- Terzaghi, K. Principles of soil mechanics: IV Settlement and consolidation of clay. Eng. News-Rec. 1925, 95, 874–878. [Google Scholar]
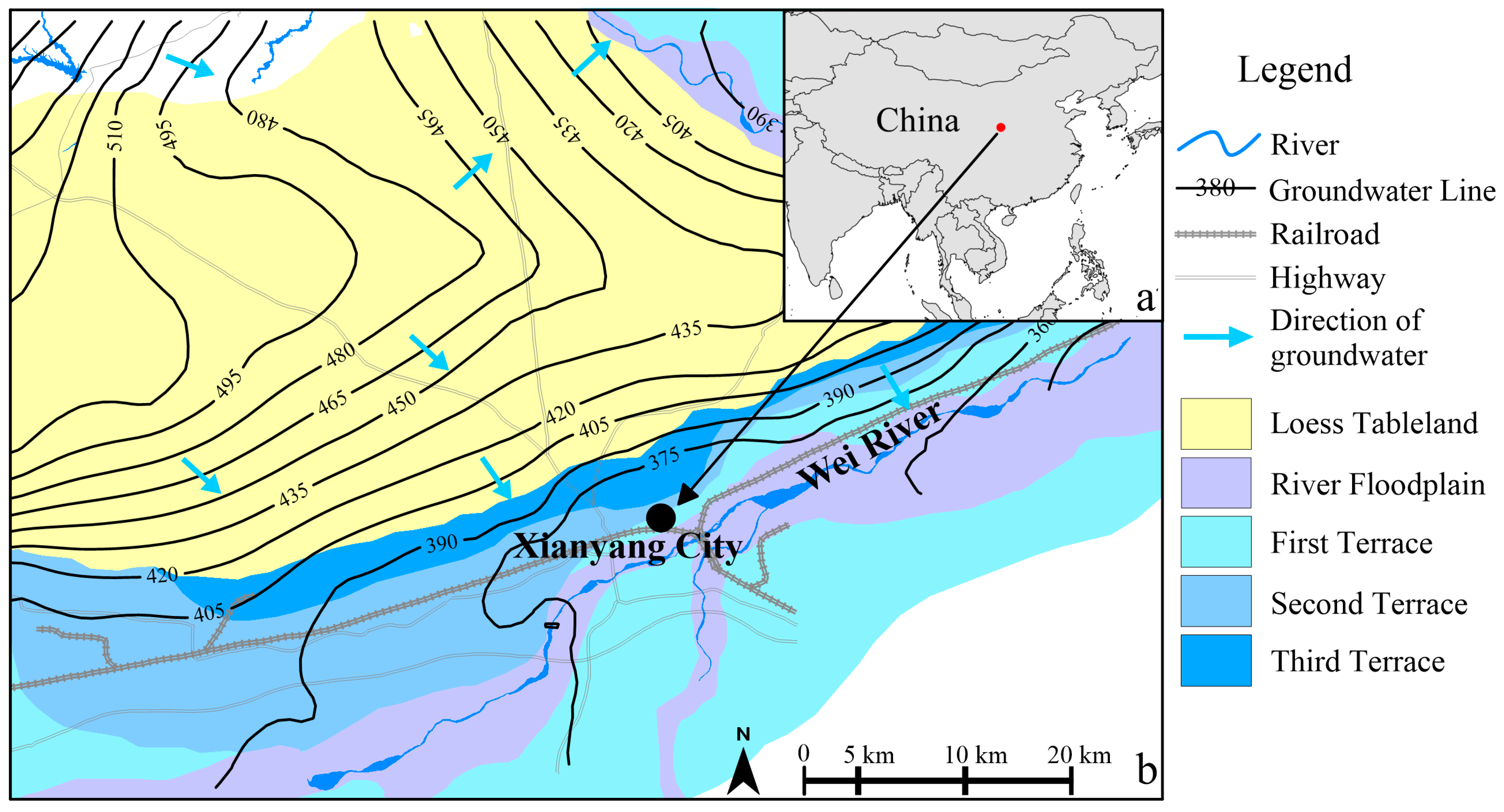



| Landform Characteristics | Hydraulic Conductivity (m·d−1) | Hydraulic Gradient | |
|---|---|---|---|
| Alluvial Plain | River Floodplain | 40–70 | 0.1–0.2% |
| First Terrace | 17–60 | ||
| Second Terrace | 13–47 | ||
| Third Terrace | 4.7–16 | ||
| Loess Tableland | 0.1–2.8 | 0.5–0.15% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, S.; Liu, P.; Wang, W.; Shi, W.; Li, Q.; Li, J.; Li, J. Numerical Simulation and Analysis of the Influencing Factors of Foundation Pit Dewatering under a Coupled Radial Well and Curtain. Water 2023, 15, 1839. https://doi.org/10.3390/w15101839
Du S, Liu P, Wang W, Shi W, Li Q, Li J, Li J. Numerical Simulation and Analysis of the Influencing Factors of Foundation Pit Dewatering under a Coupled Radial Well and Curtain. Water. 2023; 15(10):1839. https://doi.org/10.3390/w15101839
Chicago/Turabian StyleDu, Shaoshao, Peng Liu, Wei Wang, Wei Shi, Qi Li, Jianhua Li, and Jiaqi Li. 2023. "Numerical Simulation and Analysis of the Influencing Factors of Foundation Pit Dewatering under a Coupled Radial Well and Curtain" Water 15, no. 10: 1839. https://doi.org/10.3390/w15101839
APA StyleDu, S., Liu, P., Wang, W., Shi, W., Li, Q., Li, J., & Li, J. (2023). Numerical Simulation and Analysis of the Influencing Factors of Foundation Pit Dewatering under a Coupled Radial Well and Curtain. Water, 15(10), 1839. https://doi.org/10.3390/w15101839






