A Rolling Real-Time Correction Method for Minute Precipitation Forecast Based on Weather Radars
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Models
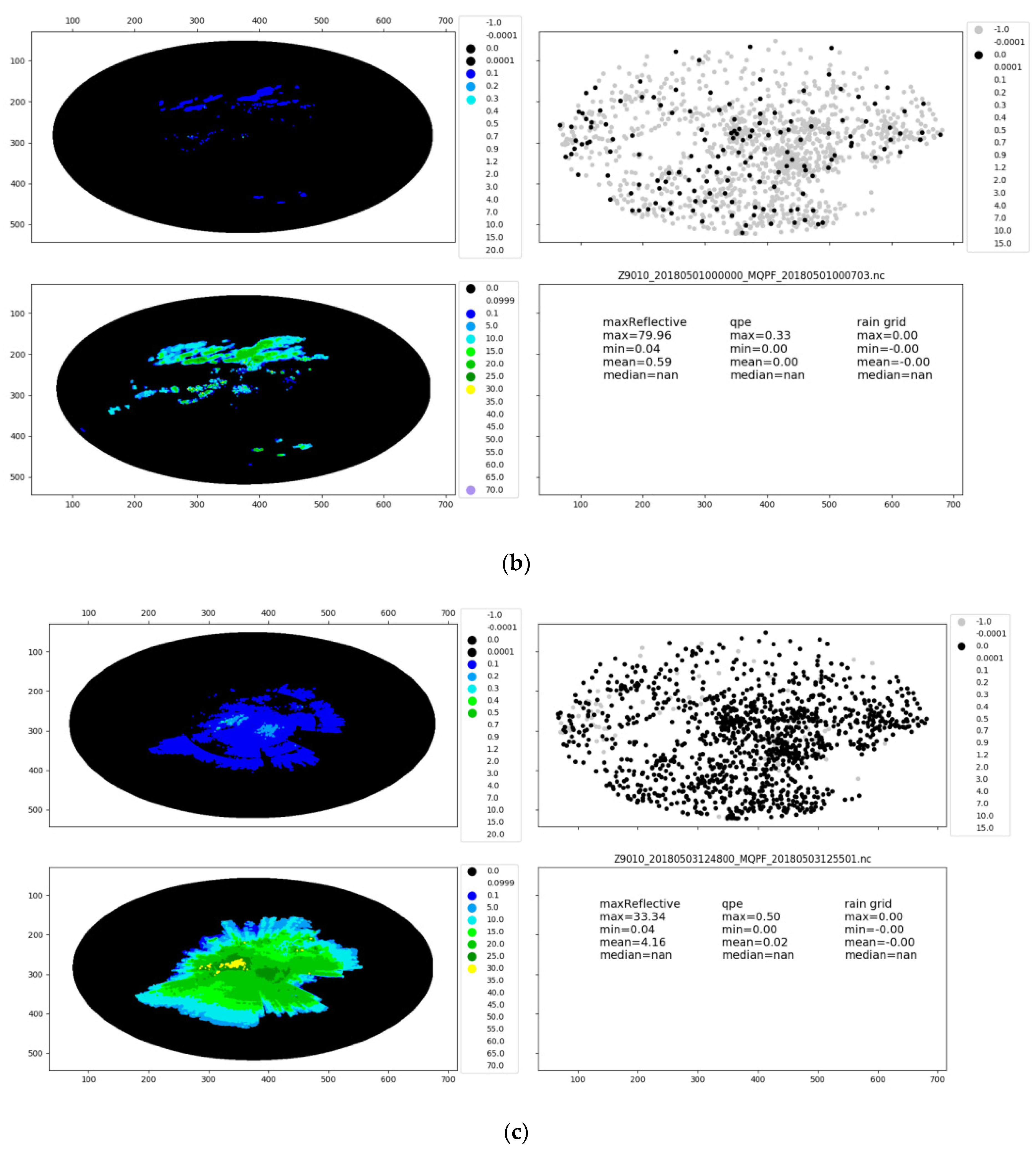
2.2.1. Radar Echo Monomer Extraction
Precipitation/Nonprecipitation Echo Monomer Recognition Technology
Radar Monomer Recognition Technology Based on Region Segmentation
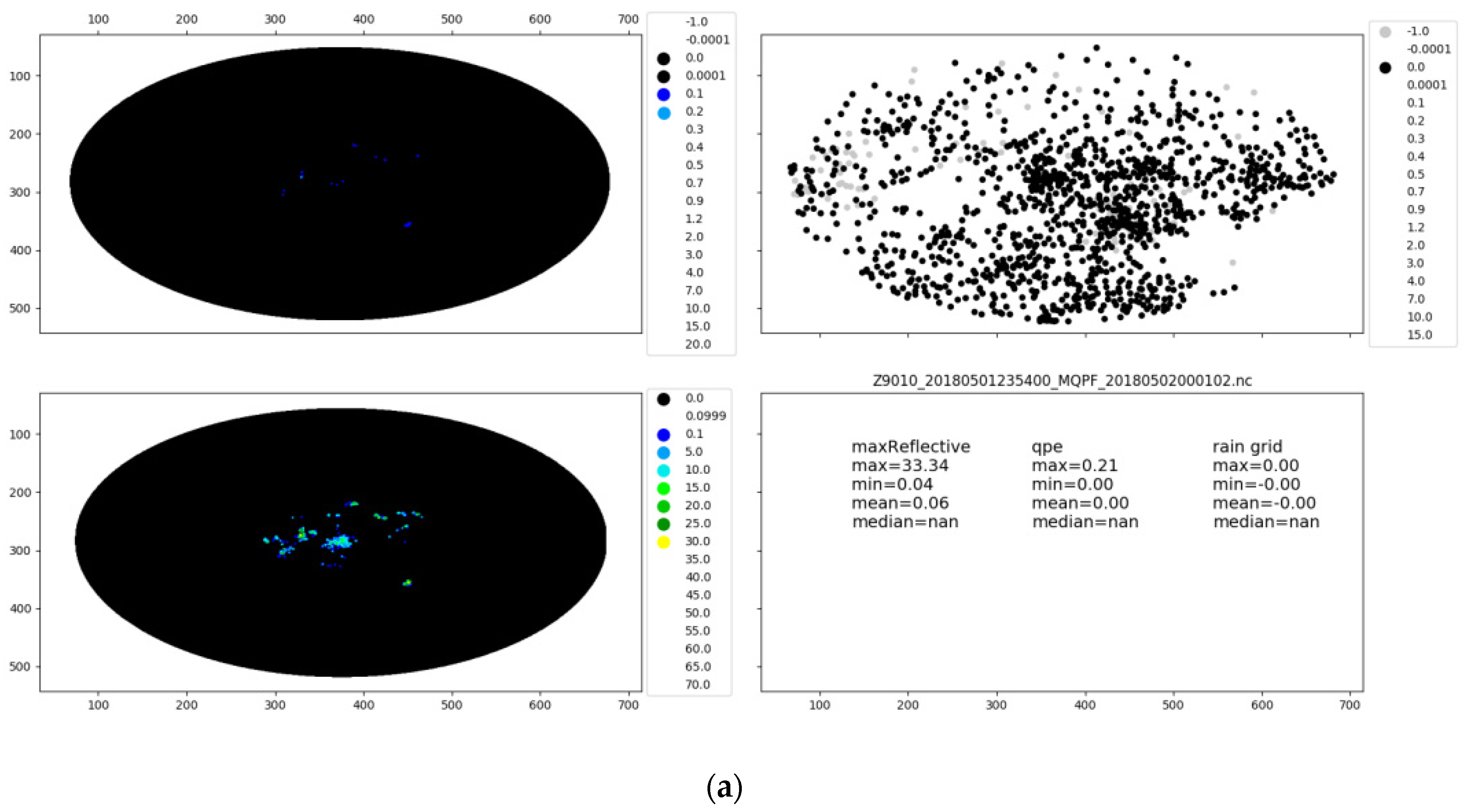
2.2.2. The Spatial Error Correction Technology Based on Linear Interpolation
- (A)
- Obtain the historical observation of minute level ground precipitation in the past 1 h through the rolling delay of 3 h through the data website service interface, and store the data every minute in a file.
- (B)
- By matching by station IDs, the minute precipitation within an hour is archived to a file. During this period, the data downloaded within hours are incomplete or the longitude and latitude information of the station cannot match.
- (C)
- According to the ground station number information obtained by the specified radar, the documents and contents are retrieved through time period, station number, and other information. Obtain an array with one row by station number and one column by minute.
- (D)
- Accumulate the data according to the station number to obtain the accumulated rainfall data in the time period corresponding to each station number.
- (A)
- Start the scheduled task every 5 min to obtain the minute precipitation observation from the past 10 min to the past 5 min. Count the latest 5 min accumulated data and the latest accumulated data in the past 2 h, create the latest data table, respectively, and store the data in the table.
- (B)
- After that, clean up the data stored in the database for more than 3 h and back up the data. The background automatically calculates the radar ground station correspondence table every hour and stores it in the dictionary configuration file.
- (C)
- Through the front-end web interface, the precipitation accumulation information of the corresponding station is obtained according to the radar number and time, and the data are saved in CSV format.
- (A)
- Based on the radar number and product time, the corresponding ground station observation is obtained through the historical observation text/real-time data web interface.
- (B)
- According to the longitude and latitude information of the ground station, the QPE on the corresponding grid point is obtained, and then the radar precipitation estimation error on the station is calculated.
- (C)
- The radar precipitation estimation error on the station is interpolated to the grid by linear interpolation algorithm to generate the radar precipitation estimation error of the grid field.
- (D)
- The grid radar precipitation estimation error is added to the radar precipitation estimation field, and finally the revised radar precipitation estimation field is obtained.
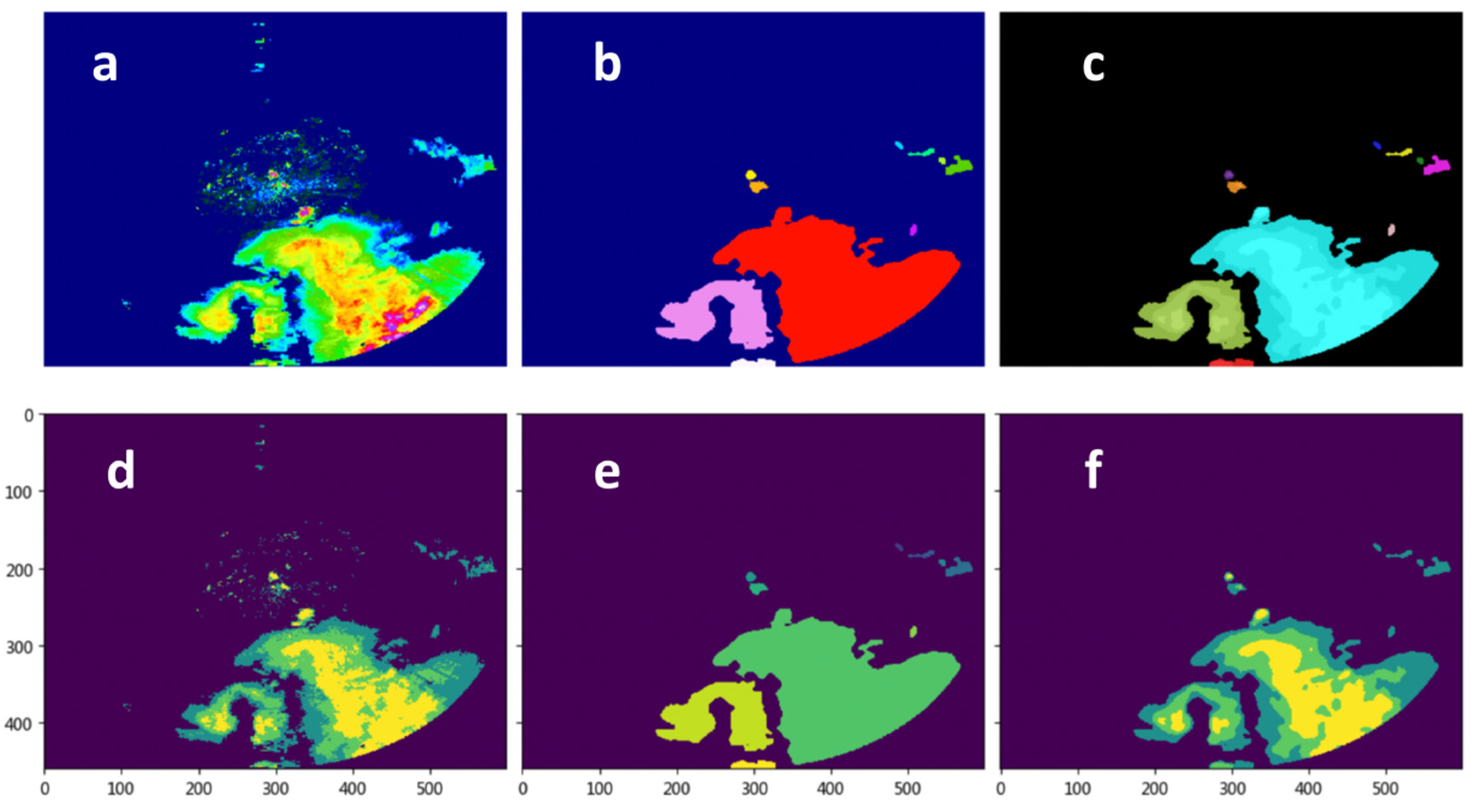
2.2.3. The Temporal Error Correction Technology Based on Linear Interpolation
- (A)
- Based on the radar ID and product time, the data of the corresponding ground station in the past 2 h and 5 min can be obtained through the historical observation text/real-time data web interface.
- (B)
- The change slope S of the number of precipitation stations in the past 2 h, the change slope A of the mean precipitation of all stations in the past 2 h, and the change slope R of the mean precipitation of stations with rainfall in the past 2 h are calculated by linear regression. Among them, S reflects the change of precipitation area, A reflects the change of regional average precipitation efficiency, and R reflects the change of precipitation intensity of precipitation clouds (Figure 7). Then, the calculation formulas of rain intensity calculation variation coefficient m and n are
- (C)
- According to the calculated regression coefficients m and n, the revised quantitative precipitation forecast (QPF) value is calculated.
2.3. Model Evaluation
3. Results
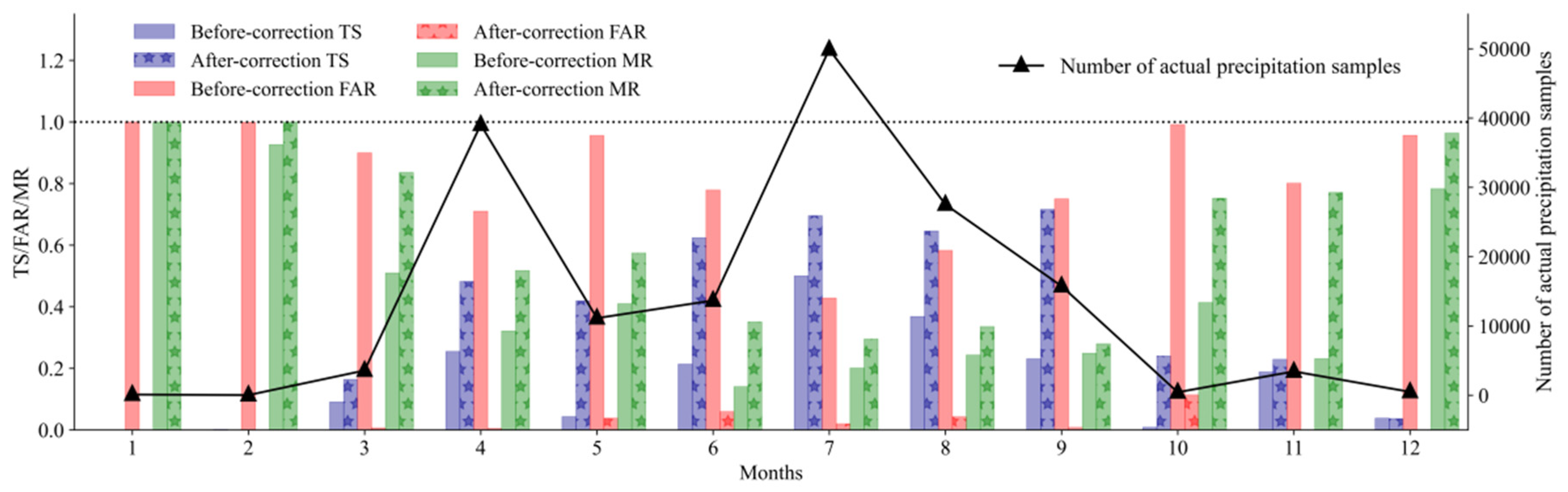
3.1. Test of the Spatial and Temporal Error Correction Results
3.2. Test of Algorithm Timeliness
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xie, X.; Tian, Y.; Wei, G. Deduction of sudden rainstorm scenarios: Integrating decision makers’ emotions, dynamic Bayesian network and DS evidence theory. Nat. Hazards 2022, 116, 2935–2955. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, J.; Liu, M.; Yin, Z.; Liu, X.; Yin, L.; Zheng, W. Remote sensing and geostatistics in urban water-resource monitoring: A review. Mar. Freshw. Res. 2023. [Google Scholar] [CrossRef]
- Tian, H.F.; Huang, N.; Niu, Z.; Qin, Y.C.; Pei, J.; Wang, J. Mapping Winter Crops in China with Multi-Source Satellite Imagery and Phenology-Based Algorithm. Remote Sens. 2019, 11, 820. [Google Scholar] [CrossRef]
- Arno, G.; Hadi, P.; Suprayogi, S.; Herumurti, S. Daily quantitative precipitation estimates use weather radar reflectivity in South Sulawesi. IOP Conf. Ser. Earth Environ. Sci. 2018, 256, 012042. [Google Scholar] [CrossRef]
- Marshall, J.S.; Palmer, W. The distribution of raindrops with size. J. Meteor. 1948, 5, 165–166. [Google Scholar] [CrossRef]
- Gilewski, P.; Nawalany, M. Inter-Comparison of Rain-Gauge, Radar, and Satellite (IMERG GPM) Precipitation Estimates Performance for Rainfall-Runoff Modeling in a Mountainous Catchment in Poland. Water 2018, 10, 1665. [Google Scholar] [CrossRef]
- Guallpa, M.; Orellana-Alvear, J.; Bendix, J. Tropical Andes Radar Precipitation Estimates Need High Temporal and Moderate Spatial Resolution. Water 2019, 11, 1038. [Google Scholar] [CrossRef]
- Zhang, J.; Howard, K.W.; Langston, C.; Kaney, B.; Qi, Y.; Tang, L.; Grams, H.; Wang, Y.; Cocks, S.; Martinaitis, S.M.; et al. Multi-Radar Multi-Sensor (MRMS) Quantitative Precipitation Estimation: Initial Operating Capabilities. Bull. Am. Meteorol. Soc. 2016, 97, 621–638. [Google Scholar] [CrossRef]
- Ware, E.C. Corrections to radar-estimated precipitation using observed rain gauge data. Master’s Thesis, Cornell University, Ithaca, NY, USA, 2005; 96p. [Google Scholar]
- Tong, Y.F.; Lai, S.T.; Tong, Y.F.; Lai, E. Applications of NWP and Nowcasting Techniques for the Warning of Rainstorms and Landslips. In Proceedings of the Tenth WMO Symposium on Education and Training, “Meteorological and Hydrological Education and Training for Disaster Prevention and Mitigation”, Nanjing, China, 18–22 September 2008. [Google Scholar]
- Ding, J.; Zhang, G.; Gao, J.; Wang, S.; Wang, K.; Xue, B.; Zhang, F.; Yang, J. Erification of the National Radar Minute Precipitation Method Applied in the Area precipitation Forecast—Taking Chaohu as an Example. J. Anhui Agric. Sci. 2021, 49, 221–225. (In Chinese) [Google Scholar] [CrossRef]
- Wu, S.; Pan, T.; Cao, J.; He, D.; Xiao, Z. Barrier–corridor effect of longitudinal range–gorge terrain on monsoons in Southwest China. Geogr. Res. 2012, 31, 1393–1406. (In Chinese) [Google Scholar] [CrossRef]
- Gu, J.; Shi, C.; Yang, P. Advances in research of the weather radar quantitative precipitation estimation. Adv. Meteorol. Sci. Technol. 2018, 8, 71–78. (In Chinese) [Google Scholar] [CrossRef]
- Feng, L.; Zhou, T.; Wu, B.; Li, T.; Luo, J.-J. Projection of future precipitation change over China with a high-resolution global atmospheric model. Adv. Atmospheric Sci. 2011, 28, 464–476. [Google Scholar] [CrossRef]
- Wong, M.C. From SWIRLS to RAPIDS: Nowcast applications development in Hong Kong. In Proceedings of the PWS Workshop on Warnings of Real-Time Hazards by Using Nowcasting Technology, Sydney, Australia, 9–13 October 2006. [Google Scholar]
- Wong, W.K.; Yeung, L.H.; Wang, Y.C.; Chen, M. Towards the blending of NWP with nowcast—Operation experience in B08FDP. In Proceedings of the WMO Symposium on Nowcasting, Whistler, BC, Canada, 30 August–4 September 2009; Volume 30, p. 24. [Google Scholar]
- Chu, Z.; Ma, Y.; Zhang, G.; Wang, Z.; Han, J.; Kou, L.; Li, N. Mitigating Spatial Discontinuity of Multi-Radar QPE Based on GPM/KuPR. Hydrology 2018, 5, 48. [Google Scholar] [CrossRef]
- Andersen, C.B.; Wright, D.B.; Thorndahl, S. Sub-Hourly to Daily Rainfall Intensity-Duration-Frequency Estimation Using Stochastic Storm Transposition and Discontinuous Radar Data. Water 2022, 14, 4013. [Google Scholar] [CrossRef]
- da Silva, E.J.R.; Alves, C.N.; Campos, P.C.D.O.; e Oliveira, R.A.A.C.; Marques, M.E.S.; Amorim, J.C.C.; Paz, I. Comparison of Rain Gauge Network and Weather Radar Data: Case Study in Angra dos Reis, Brazil. Water 2022, 14, 3944. [Google Scholar] [CrossRef]
- Yoon, S.-S.; Lee, B. Effects of Using High-Density Rain Gauge Networks and Weather Radar Data on Urban Hydrological Analyses. Water 2017, 9, 931. [Google Scholar] [CrossRef]
- Jing, G.; Luo, L.; Xiao, H.; Guo, J.; Cui, X. Application research of dual-polarization radar in quality control of automatic rain gauge. Meteorol. Mon. 2020, 46, 1189–1198. (In Chinese) [Google Scholar] [CrossRef]
- Li, X.; Zhang, W.; Huang, S.; Deng, W.; Zhou, X. Analysis of fusion test results on hourly precipitation from meteorological and hydrological stations and radar. Torrential Rain Disasters 2020, 39, 276–284. (In Chinese) [Google Scholar] [CrossRef]
- Li, M.; Qi, Y.; Zhang, Z.; Guan, X. Improving the Detection Performance of Extreme Precipitation Observations Using a Radar-Gauge Merging Algorithm. Chin. J. Atmos. Sci. 2022, 46, 1523–1542. (In Chinese) [Google Scholar] [CrossRef]
- Kim, T.-J.; Kwon, H.-H.; Lima, C. A Bayesian partial pooling approach to mean field bias correction of weather radar rainfall estimates: Application to Osungsan weather radar in South Korea. J. Hydrol. 2018, 565, 14–26. [Google Scholar] [CrossRef]
- Ozkaya, A.; Yilmaz, A.E. Analyzing radar rainfall estimate errors with three vector norms: Application to weather radar rainfall data in Muğla, Turkey. Theor. Appl. Clim. 2022, 149, 103–117. [Google Scholar] [CrossRef]
- Men, B.; Wu, Z.; Liu, H.; Tian, W.; Zhao, Y. Spatio-temporal analysis of precipitation and temperature: A case study over the Beijing–Tianjin–Hebei Region, China. Pure Appl. Geophys. 2020, 177, 3527–3541. [Google Scholar] [CrossRef]
- Ding, J.; Zhang, G.; Yang, J.; Wang, S.; Xue, B.; Du, X.; Tian, Y.; Wang, K.; Jiang, R.; Gao, J. Temporal and Spatial Characteristics of Meteorological Elements in the Vertical Direction at Airports and Hourly Airport Visibility Prediction by Artificial Intelligence Methods. Sustainability 2022, 14, 12213. [Google Scholar] [CrossRef]
- Ding, J.; Zhang, G.; Wang, S.; Xue, B.; Yang, J.; Gao, J.; Wang, K.; Jiang, R.; Zhu, X. Forecast of Hourly Airport Visibility Based on Artificial Intelligence Methods. Atmosphere 2022, 13, 75. [Google Scholar] [CrossRef]
- Cristianini, N.; Taylor, J.S. An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods; United Kingdom at the University Press: Cambridge, UK, 2000. [Google Scholar]
- Li, J.; Liu, J. Measurement for area based on connected regions arithmetic. Sci. Technol. Eng. 2008, 8, 2492–2494. (In Chinese) [Google Scholar]
- Hsu, J.; Huang, W.-R.; Liu, P.-Y.; Li, X. Validation of chirps precipitation estimates over taiwan at multiple timescales. Remote Sens. 2021, 13, 254. [Google Scholar] [CrossRef]
- Huang, W.-R.; Liu, P.-Y.; Chang, Y.-H.; Liu, C.-Y. Evaluation and Application of Satellite Precipitation Products in Studying the Summer Precipitation Variations over Taiwan. Remote Sens. 2020, 12, 347. [Google Scholar] [CrossRef]
- Yu, Z.; Wu, M.; Min, J.; Yan, Y.; Lou, X. Impacts of WRF model domain size on meiyu rainfall forecasts over Zhejiang, China. Asia-Pacific J. Atmos. Sci. 2021, 58, 265–280. [Google Scholar] [CrossRef]
- Chen, H.; Wang, Z.; Wang, H.; Sun, J.; Guo, J.; Wang, Z. Research on a New Quantitative Precipitation Estimation Method Based on CINRAD-SA Dual Polarization Radar. Meteorol. Sci. Technol. 2022, 50, 611–622. (In Chinese) [Google Scholar] [CrossRef]
- Yang, Y.; Chen, X.; Qi, Y. Classification of convective/stratiform echoes in radar reflectivity observations using a fuzzy logic algorithm. J. Geophys. Res. Atmos. 2013, 118, 1896–1905. [Google Scholar] [CrossRef]
- Bangsawan, L.; Jatmiko, R.H.; Nurjani, E. The comparison of z-r relation methods on convective and stratiform rain of quantitative precipitation estimation (QPE) in east java area. In Proceedings of the International Conference on Radioscience, Equatorial Atmospheric Science and Environment and Humanosphere Science, Online, 22–23 November 2022; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar] [CrossRef]
- Xia, Q.; Zhang, W.; Chen, H.; Lee, W.-C.; Han, L.; Ma, Y.; Liu, X. Quantification of Precipitation Using Polarimetric Radar Measurements during Several Typhoon Events in Southern China. Remote Sens. 2020, 12, 2058. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, L.; Wen, H. Performance of a Radar Mosaic Quantitative Precipitation Estimation Algorithm Based on a New Data Quality Index for the Chinese Polarimetric Radars. Remote Sens. 2020, 12, 3557. [Google Scholar] [CrossRef]
- Zhang, J.; Tang, L.; Cocks, S.; Zhang, P.; Ryzhkov, A.; Howard, K.; Langston, C.; Kaney, B. A dual-polarization radar synthetic qpe for operations. J. Hydrometeorol. 2020, 21, 2507–2521. [Google Scholar] [CrossRef]
- Peinó, E.; Bech, J.; Udina, M. Performance Assessment of GPM IMERG Products at Different Time Resolutions, Climatic Areas and Topographic Conditions in Catalonia. Remote Sens. 2022, 14, 5085. [Google Scholar] [CrossRef]
- Ren, J.; Xu, G.; Zhang, W.; Leng, L.; Xiao, Y.; Wan, R.; Wang, J. Evaluation and Improvement of FY-4A AGRI Quantitative Precipitation Estimation for Summer Precipitation over Complex Topography of Western China. Remote Sens. 2021, 13, 4366. [Google Scholar] [CrossRef]
- Xu, J.; Ma, Z.; Tang, G.; Ji, Q.; Min, X.; Wan, W.; Shi, Z. Quantitative Evaluations and Error Source Analysis of Fengyun-2-Based and GPM-Based Precipitation Products over Mainland China in Summer, 2018. Remote Sens. 2019, 11, 2992. [Google Scholar] [CrossRef]
- Shen, Y.; Hong, Z.; Pan, Y.; Yu, J.; Maguire, L. China’s 1 km Merged Gauge, Radar and Satellite Experimental Precipitation Dataset. Remote Sens. 2018, 10, 264. [Google Scholar] [CrossRef]






| Yes Observed | No Observed | The Total | |
|---|---|---|---|
| Yes forecast | NA | NB | NA + NB |
| No forecast | NC | ND | NC + ND |
| The total | NA + NC | NB + ND |
| Month | The Mean Running Time of Spatial Error Correction | The Longest Running Time of Spatial Error Correction | The Shortest Running Time of Spatial Error Correction | The Mean Running Time of Temporal Error Correction | The Longest Running Time of Temporal Error Correction | The Shortest Running Time of Temporal Error Correction |
|---|---|---|---|---|---|---|
| 1 | 4.7 | 7.8 | 2.0 | 9.8 | 15.2 | 7.7 |
| 2 | 5.4 | 9.6 | 3.0 | 11.5 | 16.7 | 9.4 |
| 3 | 5.0 | 23.6 | 1.5 | 10.8 | 34.5 | 8.0 |
| 4 | 5.2 | 56.3 | 1.5 | 10.0 | 81.8 | 3.8 |
| 5 | 6.4 | 20.1 | 1.1 | 10.6 | 37.4 | 3.7 |
| 6 | 5.0 | 8.8 | 2.0 | 9.8 | 14.4 | 7.6 |
| 7 | 4.5 | 8.9 | 1.6 | 8.6 | 16.2 | 6.1 |
| 8 | 3.9 | 7.7 | 1.8 | 7.7 | 13.0 | 5.8 |
| 9 | 3.9 | 7.5 | 1.8 | 8.0 | 12.3 | 6.4 |
| 10 | 3.8 | 7.2 | 1.8 | 8.1 | 13.1 | 6.5 |
| 11 | 4.3 | 17.6 | 0.9 | 7.9 | 24.0 | 3.4 |
| 12 | 6.3 | 17.3 | 0.2 | 12.8 | 26.0 | 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, J.; Gao, J.; Zhang, G.; Zhang, F.; Yang, J.; Wang, S.; Xue, B.; Wang, K. A Rolling Real-Time Correction Method for Minute Precipitation Forecast Based on Weather Radars. Water 2023, 15, 1872. https://doi.org/10.3390/w15101872
Ding J, Gao J, Zhang G, Zhang F, Yang J, Wang S, Xue B, Wang K. A Rolling Real-Time Correction Method for Minute Precipitation Forecast Based on Weather Radars. Water. 2023; 15(10):1872. https://doi.org/10.3390/w15101872
Chicago/Turabian StyleDing, Jin, Jinbing Gao, Guoping Zhang, Fang Zhang, Jing Yang, Shudong Wang, Bing Xue, and Kuoyin Wang. 2023. "A Rolling Real-Time Correction Method for Minute Precipitation Forecast Based on Weather Radars" Water 15, no. 10: 1872. https://doi.org/10.3390/w15101872
APA StyleDing, J., Gao, J., Zhang, G., Zhang, F., Yang, J., Wang, S., Xue, B., & Wang, K. (2023). A Rolling Real-Time Correction Method for Minute Precipitation Forecast Based on Weather Radars. Water, 15(10), 1872. https://doi.org/10.3390/w15101872






