LI-DWT- and PD-FC-MSPCNN-Based Small-Target Localization Method for Floating Garbage on Water Surfaces
Abstract
:1. Introduction
1.1. Background
1.2. Related Research
2. Materials and Methods
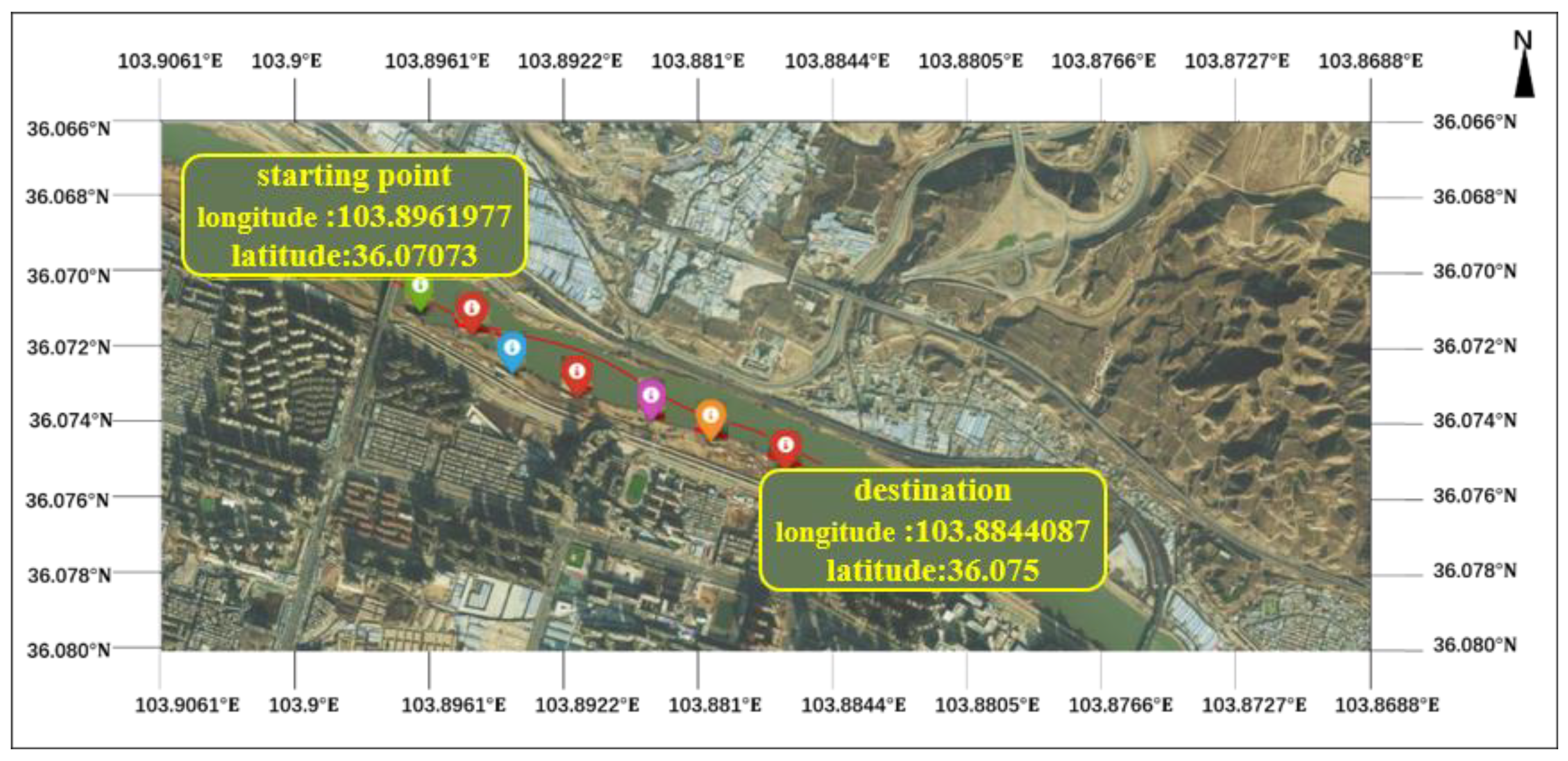
2.1. Dataset and Description
2.2. Methods
2.3. Preprocessing: LI-DWT Denoising
2.4. Segmentation: PD-FC-MSPCNN
2.5. Postprocessing: MMF
3. Results
3.1. Evaluation Indicators
- Perceived hash similarity (phash):
- Volumetric overlap error (VOE):
- Relative volume difference (RVD):
- MAE:
- Hausdorff distance (HF):
- Sensitivity (SEN):
- Time complexity (T):
- Coordinate distance error (CD):
- Overall comprehensive evaluation (OCE):
3.2. Ablation Experiments
3.3. Comparative Analysis of Split Extraction Algorithms
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LI | lateral inhibition network |
| DWT | discrete wavelet transform |
| MMF | multi-scale morphological filtering |
| FC-MSPCNN | a fire-controlled MSPCNN model |
| PD-FC-MSPCNN | parameter-designed-FC-MSPCNN |
| Faster R-CNN | faster Regions with Convolutional Neural Network |
| CA | Class Activation |
| Yolo | You Only Look Once |
| CNN | Convolutional Neural Network |
| GAN | Generative Adversarial Network |
| PCNN | Pulse Coupled Neural Network |
| SPCNN | simplified PCNN |
| SCM | spiking cortical model |
| SCHPCNN | oscillating sine–cosine pulse coupled neural network |
| HVS | Human Vision System |
| SM-ISPCNN | saliency motivated improved simplified pulse coupled neural network |
Appendix A
| Algorithm A1 A Small Target Location Method for Floating Garbage on Water Surface Based on LI-DWT and PD-FC-MSPCNN Implementation Steps | |
| Input | Color image of floating garbage on water surface, image size , normalized Otsu threshold , number of iterations , structure element . |
| Pre-processing | For: T = 2 |
| Generating high- and low-frequency component images by T times discrete wavelet transform by (1) and (2). | |
| By (3) and (4), the Gaussian low-pass filter is . | |
| For: | |
| Using (5), the Gaussian kernel is calculated, and the lateral inhibition network is introduced using (6)–(9), the lateral inhibition network is fused, and the wavelet reconstruction outputs the denoised image. | |
| End | |
| End | |
| Segmentation | For i = 1:x |
| For j = 1:y | |
| Using (21)–(23), the parameter values of PD-FCMSPCNN are calculated, including feed input, link input, internal activity, excitation state, and dynamic threshold. | |
| End | |
| End | |
| For t = 30 | |
| Using (24)–(27), the attenuation factor ,weight matrix , magnitude parameter of the dynamic threshold, and the auxiliary parameter are calculated. | |
| If | |
| Else | |
| End | |
| By (23), the dynamic threshold is calculated . | |
| End | |
| Post-processing | For |
| Set by (30) | |
| For | |
| Set by (31) | |
| End | |
| Using (32), the morphological filtering results are calculated | |
| Calculate the pixel coordinates of the segmented target (top left, bottom right and center) | |
| End | |
| Output | Image and coordinates of floating garbage segmentation results on water surface |
References
- Yang, X.; Zhao, J.; Zhao, L.; Zhang, H.; Li, L.; Ji, Z.; Ganchev, I. Detection of River Floating Garbage Based on Improved YOLOv5. Mathematics 2022, 10, 4366. [Google Scholar] [CrossRef]
- Yang, W.; Wang, R.; Li, L. Method and System for Detecting and Recognizing Floating Garbage Moving Targets on Water Surface with Big Data Based on Blockchain Technology. Adv. Multimed. 2022, 2022, 9917770. [Google Scholar] [CrossRef]
- Gladstone, R.; Moshe, Y.; Barel, A.; Shenhav, E. Distance estima-tion for marine vehicles using a monocular video camera. In Proceedings of the 2016 24th European Signal Processing Conference (EUSIPCO), Budapest, Hungary, 29 August–2 September 2016; pp. 2405–2409. [Google Scholar] [CrossRef]
- Tominaga, A.; Tang, Z.; Zhou, T. Capture method of floating garbage by using riverside concavity zone. In River Flow 2020; CRC Press: Boca Raton, FL, USA, 2020; pp. 2154–2162. [Google Scholar] [CrossRef]
- Kamilaris, A.; Prenafeta-Boldú, F.X. Deep learning in agriculture: A survey. Comput. Electron. Agric. 2018, 147, 70–90. [Google Scholar] [CrossRef] [Green Version]
- Yi, Z.; Yao, D.; Li, G.; Ai, J.; Xie, W. Detection and localization for lake floating objects based on CA-faster R-CNN. Multimed. Tools Appl. 2022, 81, 17263–17281. [Google Scholar] [CrossRef]
- van Lieshout, C.; van Oeveren, K.; van Emmerik, T.; Postma, E. Automated river plastic monitoring using deep learning and cameras. Earth Space Sci. 2020, 7, e2019EA000960. [Google Scholar] [CrossRef]
- Li, X.; Tian, M.; Kong, S.; Wu, L.; Yu, J. A modified YOLOv3 detection method for vision-based water surface garbage capture robot. Int. J. Adv. Robot. Syst. 2020, 17, 1729881420932715. [Google Scholar] [CrossRef]
- Armitage, S.; Awty-Carroll, K.; Clewley, D.; Martinez-Vicente, V. Detection and Classification of Floating Plastic Litter Using a Vessel-Mounted Video Camera and Deep Learning. Remote. Sens. 2022, 14, 3425. [Google Scholar] [CrossRef]
- Arshad, N.; Moon, K.S.; Kim, J.N. An adaptive moving ship detection and tracking based on edge information and morphological operations. In Proceedings of the International Conference on Graphic and Image Processing (ICGIP 2011), Cairo, Egypt, 1–3 October 2011; Volume 8285. [Google Scholar] [CrossRef]
- Ali, I.; Mille, J.; Tougne, L. Wood detection and tracking in videos of rivers. In Image Analysis, Proceedings of the 17th Scandinavian Conference, SCIA 2011, Ystad, Sweden, 23–25 May 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 646–655. [Google Scholar] [CrossRef] [Green Version]
- Ribeiro, M.; Damas, B.; Bernardino, A. Real-Time Ship Segmentation in Maritime Surveillance Videos Using Automatically Annotated Synthetic Datasets. Sensors 2022, 22, 8090. [Google Scholar] [CrossRef] [PubMed]
- Li, N.; Lv, X.; Li, B.; Xu, S. An improved OTSU method based on uniformity measurement for segmentation of water surface images. In Proceedings of the 2019 International Conference on Internet of Things (iThings) and IEEE Green Computing and Communications (GreenCom) and IEEE Cyber, Physical and Social Computing (CPSCom) and IEEE Smart Data (SmartData), Atlanta, GA, USA, 14–17 July 2019. [Google Scholar] [CrossRef]
- Jin, X.; Niu, P.; Liu, L. A GMM-Based Segmentation Method for the Detection of Water Surface Floats. IEEE Access 2019, 7, 119018–119025. [Google Scholar] [CrossRef]
- Dai, Y.; Wu, Y.; Zhou, F.; Barnard, K. Asymmetric contextual modulation for infrared small target detection. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2021. [Google Scholar] [CrossRef]
- Fujieda, S.; Takayama, K.; Hachisuka, T. Wavelet convolutional neural networks for texture classification. arXiv 2017, arXiv:1707.07394. [Google Scholar]
- Li, J.Y.; Zhang, R.F.; Liu, Y.H. Multi-scale image fusion enhancement Algorithm based on Wavelet Transform. Opt. Tech. 2021, 47, 217–222. [Google Scholar]
- Zhang, Q. Remote sensing image de-noising algorithm based on double discrete wavelet transform. Remote Sens. Land Resour. 2015, 27, 14–20. [Google Scholar]
- Fu, M.; Liu, H.; Yu, Y.; Chen, J.; Wang, K. DW-GAN: A discrete wavelet transform GAN for nonhomogeneous dehazing. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 203–212. [Google Scholar] [CrossRef]
- Liang, H.; Gao, J.; Qiang, N. A novel framework based on wavelet transform and principal component for face recognition under varying illumination. Appl. Intell. 2020, 51, 1762–1783. [Google Scholar] [CrossRef]
- Zhan, K.; Shi, J.; Wang, H.; Xie, Y.; Li, Q. Computational Mechanisms of Pulse-Coupled Neural Networks: A Comprehensive Review. Arch. Comput. Methods Eng. 2016, 24, 573–588. [Google Scholar] [CrossRef]
- Huang, C.; Tian, G.; Lan, Y.; Peng, Y.; Ng, E.Y.K.; Hao, Y.; Cheng, Y.; Che, W. A New Pulse Coupled Neural Network (PCNN) for Brain Medical Image Fusion Empowered by Shuffled Frog Leaping Algorithm. Front. Neurosci. 2019, 13, 210. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Li, Z.; Kang, H.; Huang, Y.; Gai, D. Medical Image Segmentation using PCNN based on Multi-feature Grey Wolf Optimizer Bionic Algorithm. J. Bionic Eng. 2021, 18, 711–720. [Google Scholar] [CrossRef]
- Panigrahy, C.; Seal, A.; Mahato, N.K. Parameter adaptive unit-linking dual-channel PCNN based infrared and visible image fusion. Neurocomputing 2022, 514, 21–38. [Google Scholar] [CrossRef]
- Guo, Y.; Gao, X.; Yang, Z.; Lian, J.; Du, S.; Zhang, H.; Ma, Y. SCM-motivated enhanced CV model for mass segmentation from coarse-to-fine in digital mammography. Multimed. Tools Appl. 2018, 77, 24333–24352. [Google Scholar] [CrossRef]
- Yang, Z.; Lian, J.; Li, S.; Guo, Y.; Ma, Y. A study of sine–cosine oscillation heterogeneous PCNN for image quantization. Soft Comput. 2019, 23, 11967–11978. [Google Scholar] [CrossRef]
- Deng, X.; Yan, C.; Ma, Y. PCNN Mechanism and its Parameter Settings. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 488–501. [Google Scholar] [CrossRef]
- Huang, Y.; Ma, Y.; Li, S.; Zhan, K. Application of heterogeneous pulse coupled neural network in image quantization. J. Electron. Imaging 2016, 25, 61603. [Google Scholar] [CrossRef]
- Lian, J.; Yang, Z.; Sun, W.; Guo, Y.; Zheng, L.; Li, J.; Shi, B.; Ma, Y. An image segmentation method of a modified SPCNN based on human visual system in medical images. Neurocomputing 2018, 333, 292–306. [Google Scholar] [CrossRef]
- Guo, Y.; Yang, Z.; Ma, Y.; Lian, J.; Zhu, L. Saliency motivated improved simplified PCNN model for object segmentation. Neurocomputing 2017, 275, 2179–2190. [Google Scholar] [CrossRef]
- Chen, C.; Liu, M.Y.; Tuzel, O.; Xiao, J. R-CNN for small object detection. In Proceedings of the Computer Vision–ACCV 2016: 13th Asian Conference on Computer Vision, Taipei, Taiwan, 20–24 November 2016; Revised Selected Papers, Part V. Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Chen, Y.; Park, S.K.; Ma, Y.; Ala, R. A new automatic parameter setting method of a simplified PCNN for image segmentation. IEEE Trans. Neural Netw. 2011, 22, 880–892. [Google Scholar] [CrossRef] [PubMed]
- Lian, J.; Yang, Z.; Sun, W.; Zheng, L.; Qi, Y.; Shi, B.; Ma, Y. A fire-controlled MSPCNN and its applications for image processing. Neurocomputing 2021, 422, 150–164. [Google Scholar] [CrossRef]









| Method | Phash | VOE | RVD | MAE | HD | SEN |
|---|---|---|---|---|---|---|
| (1) | 89.97% | 0.1389 | 0.1679 | 0.1492 | 15.03 | 0.8382 |
| (2) | 57.81% | 1.8923 | 35.1342 | 0.4220 | 144 | 0.0271 |
| (3) Ours | 95.32% | 0.0322 | 0.0323 | 0.0017 | 7.37 | 0.9432 |
| Dataset | Method | Phash | VOE | RVD | MAE | HD | SEN | T (ms) | CD |
|---|---|---|---|---|---|---|---|---|---|
| Dataset 1 | PSPNet | 91.34% | 0.0409 | 0.0426 | 0.0018 | 7.94 | 0.9283 | 107.2 | 8.63 |
| DeepLabv3+ | 92.21% | 0.0428 | 0.0438 | 0.0022 | 7.73 | 0.9290 | 84.6 | 6.88 | |
| HRNet | 91.40% | 0.0557 | 0.0585 | 0.0023 | 6.71 | 0.8954 | 166.7 | 8.50 | |
| TransUNet | 94.91% | 0.0406 | 0.0428 | 0.0018 | 7.19 | 0.9343 | 211.1 | 5.75 | |
| Ours | 95.32% | 0.0322 | 0.0323 | 0.0017 | 7.37 | 0.9432 | 163.1 | 4.38 | |
| Dataset 2 | PSPNet | 91.85% | 0.0495 | 0.0517 | 0.0017 | 7.90 | 0.9063 | 108.6 | 8.71 |
| DeepLabv3+ | 91.85% | 0.0542 | 0.0562 | 0.0018 | 7.26 | 0.9103 | 88.5 | 6.92 | |
| HRNet | 92.55% | 0.0468 | 0.0484 | 0.0016 | 7.85 | 0.9093 | 164.2 | 8.54 | |
| TransUNet | 94.16% | 0.0489 | 0.0491 | 0.0016 | 6.83 | 0.9216 | 212.3 | 5.83 | |
| Ours | 92.83% | 0.0466 | 0.0476 | 0.0015 | 7.57 | 0.9224 | 163.7 | 4.47 | |
| Dataset 3 | PSPNet | 91.71% | 0.1069 | 0.1131 | 0.0029 | 8.35 | 0.8627 | 107.9 | 8.67 |
| DeepLabv3+ | 91.71% | 0.0867 | 0.0907 | 0.0028 | 8.16 | 0.8703 | 89.3 | 6.90 | |
| HRNet | 91.82% | 0.0803 | 0.0812 | 0.0028 | 8.12 | 0.8814 | 166.2 | 8.63 | |
| TransUNet | 92.27% | 0.0711 | 0.0726 | 0.0025 | 8.06 | 0.8943 | 211.4 | 5.60 | |
| Ours | 92.31% | 0.0615 | 0.0648 | 0.0028 | 8.24 | 0.9168 | 164.0 | 4.56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ai, P.; Ma, L.; Wu, B. LI-DWT- and PD-FC-MSPCNN-Based Small-Target Localization Method for Floating Garbage on Water Surfaces. Water 2023, 15, 2302. https://doi.org/10.3390/w15122302
Ai P, Ma L, Wu B. LI-DWT- and PD-FC-MSPCNN-Based Small-Target Localization Method for Floating Garbage on Water Surfaces. Water. 2023; 15(12):2302. https://doi.org/10.3390/w15122302
Chicago/Turabian StyleAi, Ping, Long Ma, and Baijing Wu. 2023. "LI-DWT- and PD-FC-MSPCNN-Based Small-Target Localization Method for Floating Garbage on Water Surfaces" Water 15, no. 12: 2302. https://doi.org/10.3390/w15122302
APA StyleAi, P., Ma, L., & Wu, B. (2023). LI-DWT- and PD-FC-MSPCNN-Based Small-Target Localization Method for Floating Garbage on Water Surfaces. Water, 15(12), 2302. https://doi.org/10.3390/w15122302







