Contribution of Evaporation to Precipitation Changes in the Yangtze River Basin—Precipitation Recycling
Abstract
:1. Introduction
2. Materials and Methods
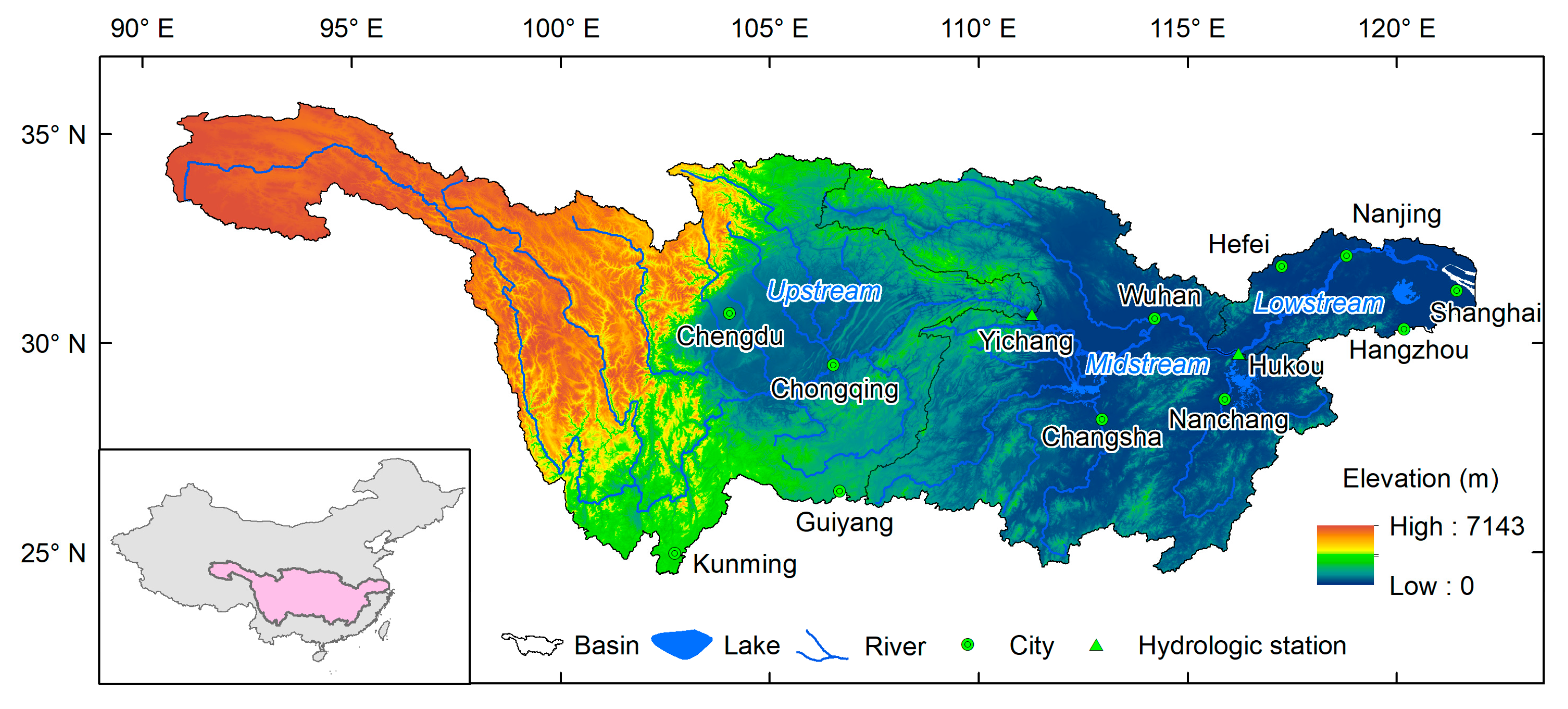
2.1. Study Area
2.2. Data
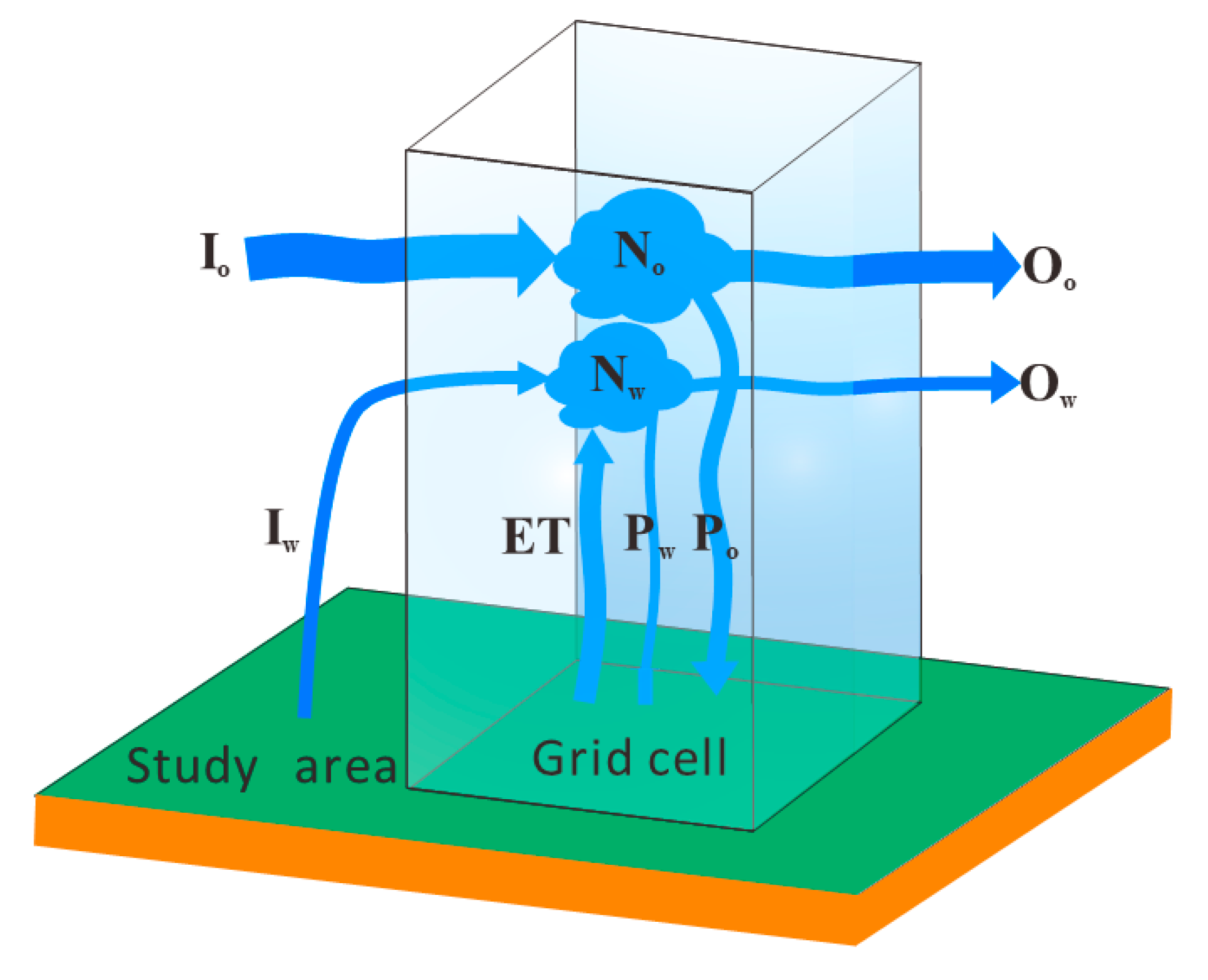
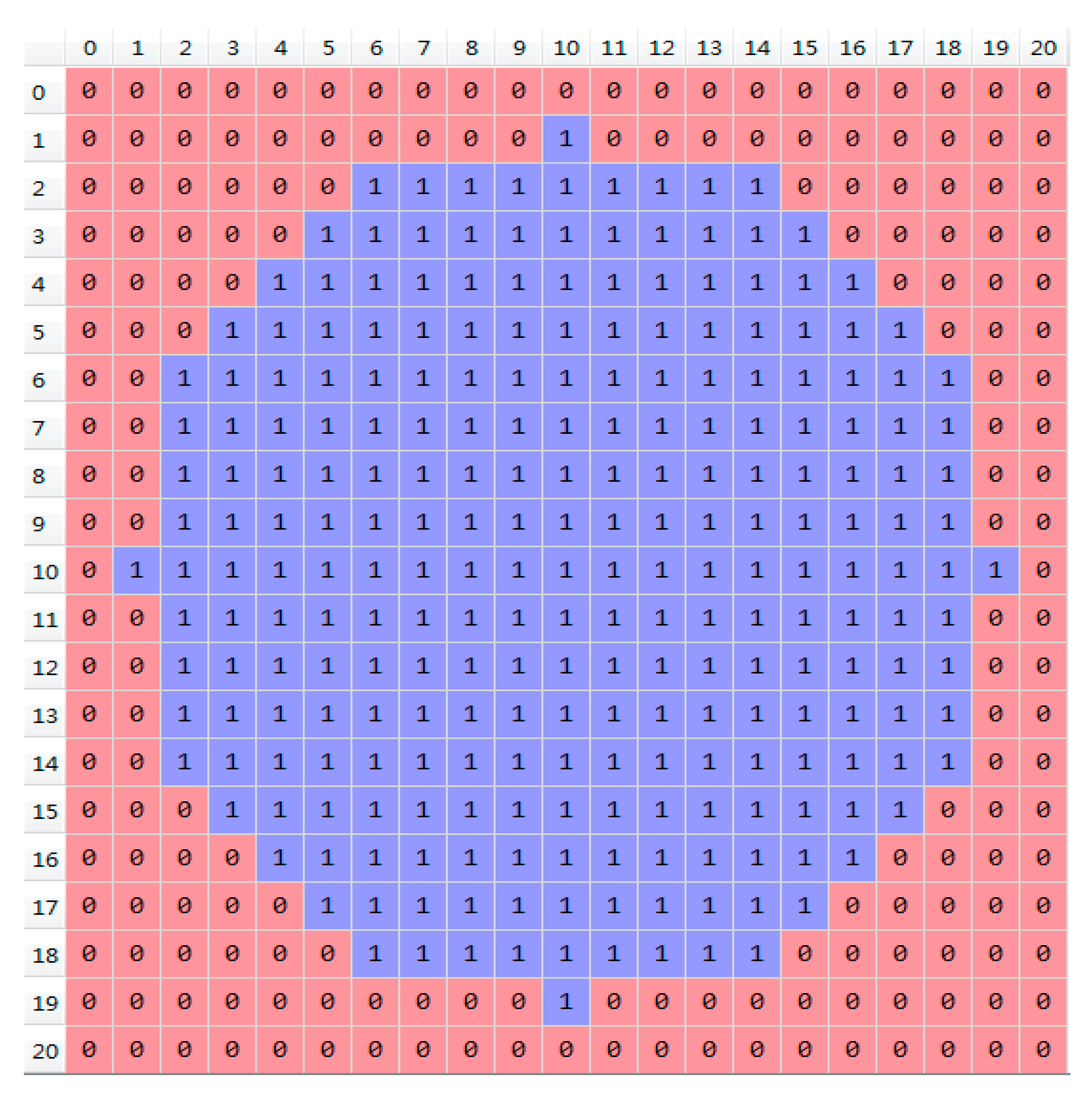
2.3. Methods
3. Results
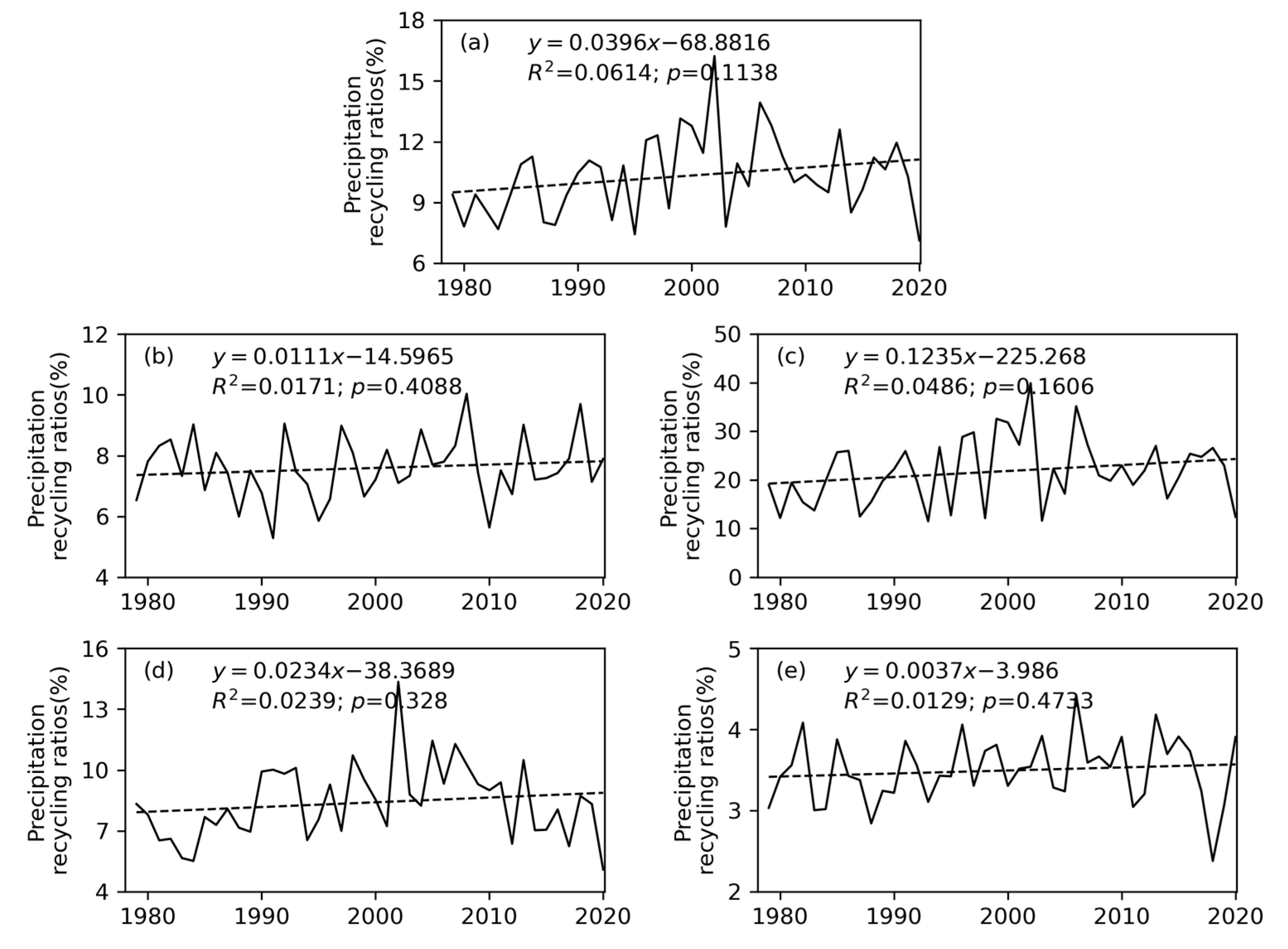
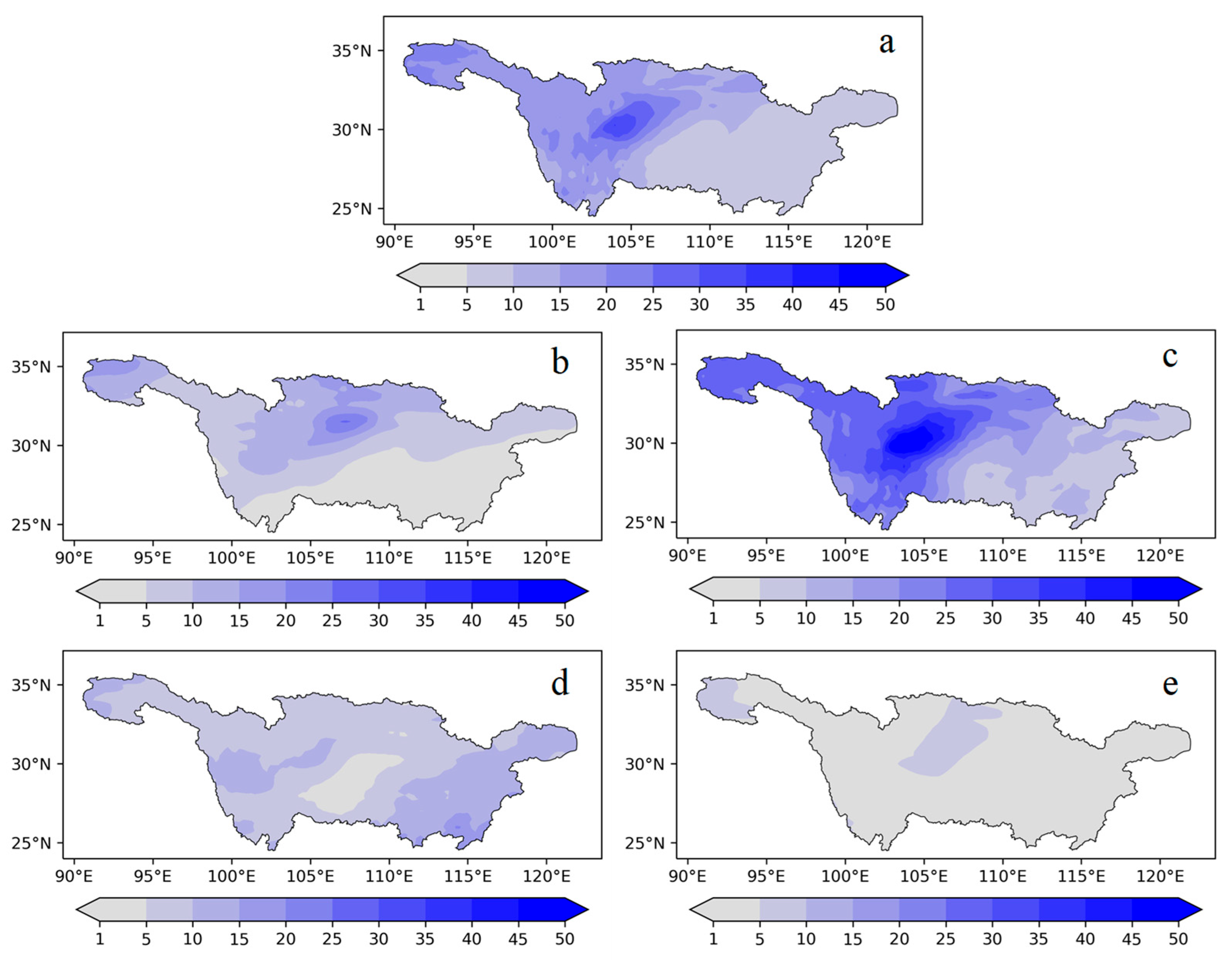
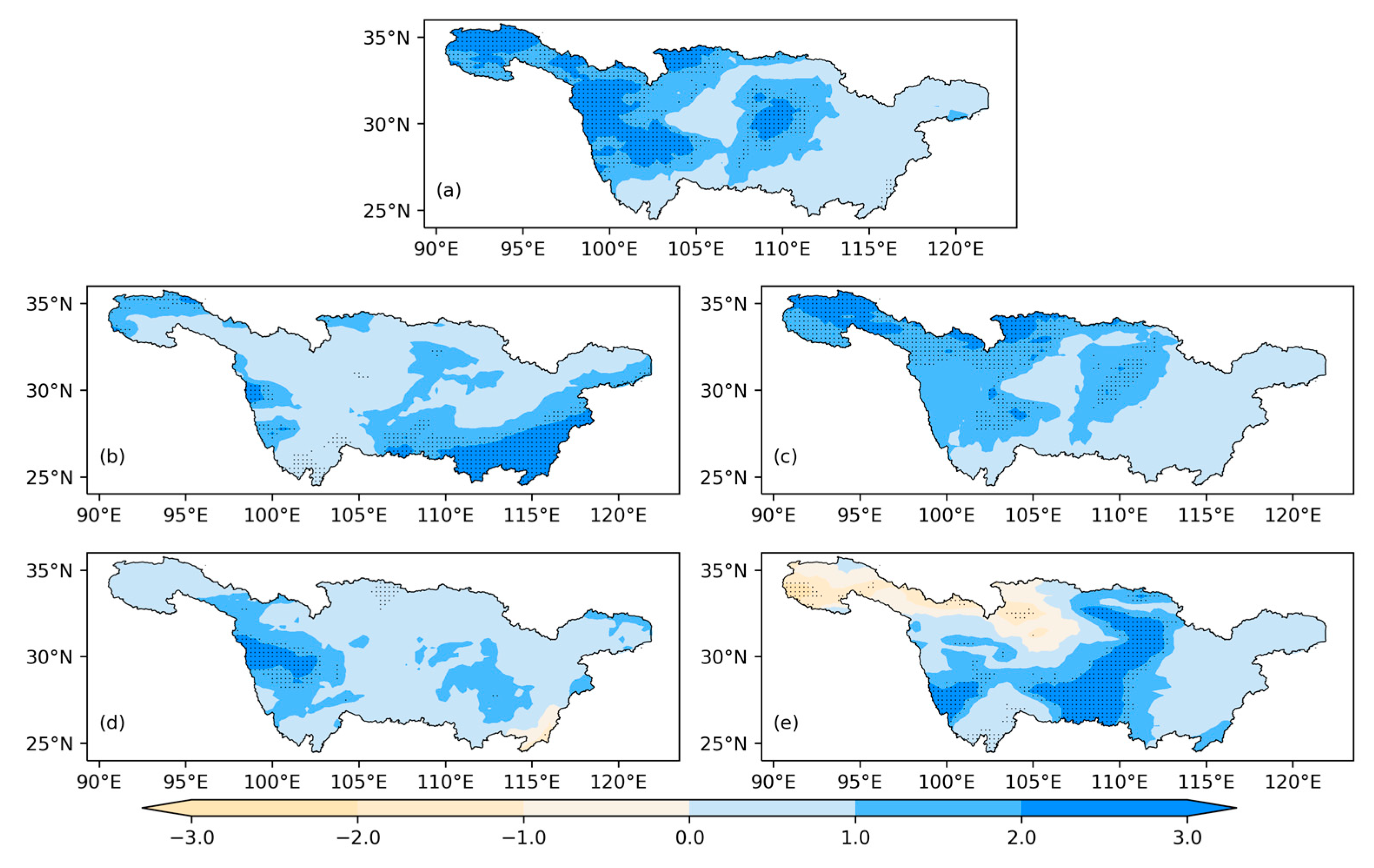
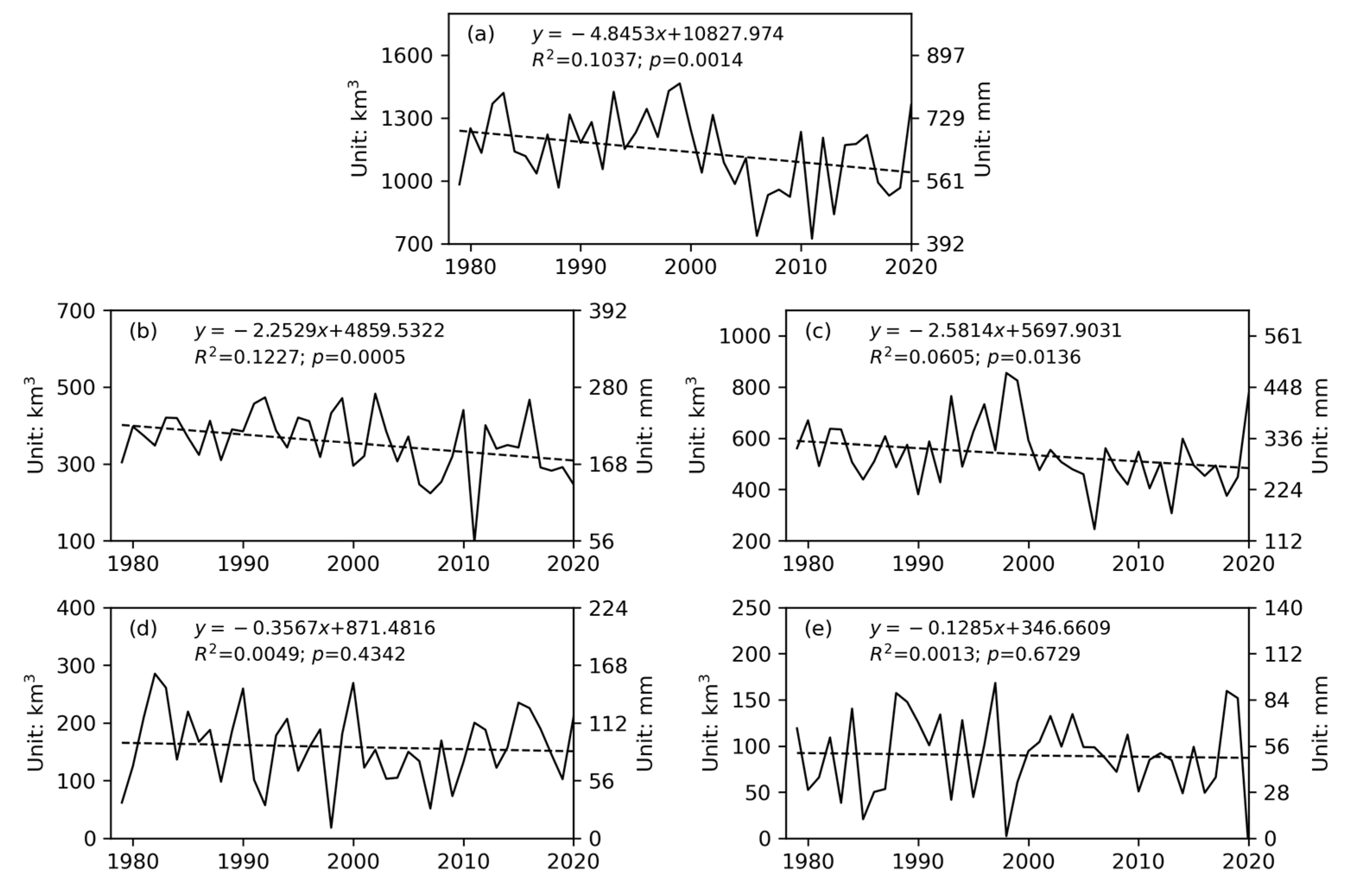
3.1. Spatiotemporal Variation of Precipitation Recycling Ratio (ρ)
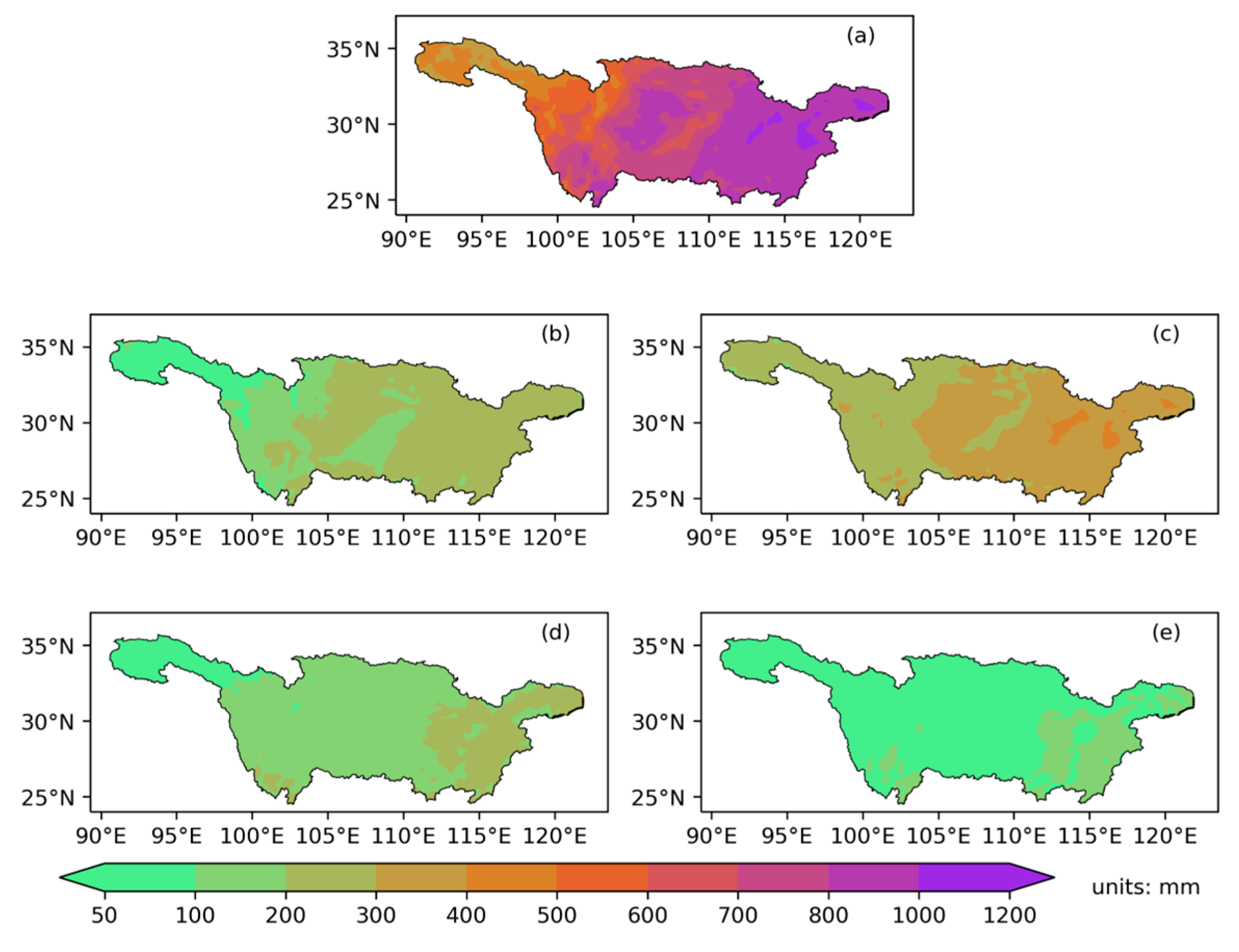
3.2. Changes in Evapotranspiration in YRB
3.3. Change of External Moisture Flux
3.4. Difference Contributions between Evaporation and External Moisture Flux to Precipitation
4. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Budyko, M.I. Climate and Life; Academic Press: New York, NY, USA; London, UK, 1974. [Google Scholar]
- Starr, V.P.; Peixoto, J.P. On the Global Balance of Water Vapor and the Hydrology of Deserts. Tellus 1958, 10, 188–194. [Google Scholar] [CrossRef] [Green Version]
- Horton, R.E. Hydrologic Interrelations between Lands and Oceans. Eos Trans. Am. Geophys. Union 1943, 24, 753–764. [Google Scholar] [CrossRef]
- McDonald, J.E. The Evaporation-Precipitation Fallacy. Weather 1962, 17, 168–177. [Google Scholar] [CrossRef]
- Dansgaard, W. Stable Isotopes in Precipitation. Tellus 1964, 16, 436–468. [Google Scholar] [CrossRef]
- Molion, L.C.B. A Climatonomic Study of the Energy and Moisture Fluxes of the Amazonas Basin with Considerations of Deforestation Effects; The University of Wisconsin-Madison: Madison, WI, USA, 1975. [Google Scholar]
- Lettau, H.; Lettau, K.; Molion, L.C.B. Amazonia’s Hydrologic Cycle and the Role of Atmospheric Recycling in Assessing Deforestation Effects. Mon. Weather Rev. 1979, 107, 227–238. [Google Scholar] [CrossRef]
- Brubaker, K.L.; Entekhabi, D.; Eagleson, P.S. Estimation of Continental Precipitation Recycling. J. Clim. 1993, 6, 1077–1089. [Google Scholar] [CrossRef]
- Burde, G.I.; Zangvil, A.; Lamb, P.J. Estimating the Role of Local Evaporation in Precipitation for a Two-Dimensional Region. J. Clim. 1996, 9, 1328–1338. [Google Scholar] [CrossRef]
- Eltahir, E.A.B.; Bras, R.L. Precipitation Recycling in the Amazon Basin. Q. J. R. Meteorol. Soc. 1994, 120, 861–880. [Google Scholar] [CrossRef]
- Gat, J.R.; Matsui, E. Atmospheric Water Balance in the Amazon Basin: An Isotopic Evapotranspiration Model. J. Geophys. Res. Atmos. 1991, 96, 13179–13188. [Google Scholar] [CrossRef]
- Craig, H.; Gordon, L. Deuterium and Oxygen 18 Variations in the Ocean and Marine Atmosphere. In Stable Isotopes in Oceanographic Studies and Paleotemperatures; Tongiorgi, E., Ed.; Laboratiorio di Geologica Nucleare: Spoleto, Italy, 1965; pp. 9–130. [Google Scholar]
- Joussaume, S.; Sadourny, R.; Jouzel, J. A General Circulation Model of Water Isotope Cycles in the Atmosphere. Nature 1984, 311, 24–29. [Google Scholar] [CrossRef]
- Cole, J.E.; Rind, D.; Webb, R.S.; Jouzel, J.; Healy, R. Climatic Controls on Interannual Variability of Precipitation Δ18O: Simulated Influence of Temperature, Precipitation Amount, and Vapor Source Region. J. Geophys. Res. Atmos. 1999, 104, 14223–14235. [Google Scholar] [CrossRef]
- Risi, C.; Bony, S.; Vimeux, F.; Frankenberg, C.; Noone, D.; Worden, J. Understanding the Sahelian Water Budget through the Isotopic Composition of Water Vapor and Precipitation. J. Geophys. Res. Atmos. 2010, 115, D24110. [Google Scholar] [CrossRef] [Green Version]
- Burde, G.I.; Zangvil, A. The Estimation of Regional Precipitation Recycling. Part II: A New Recycling Model. J. Clim. 2001, 14, 2509–2527. [Google Scholar] [CrossRef]
- Dominguez, F.; Kumar, P.; Liang, X.-Z.; Ting, M. Impact of Atmospheric Moisture Storage on Precipitation Recycling. J. Clim. 2006, 19, 1513–1530. [Google Scholar] [CrossRef]
- van der Ent, R.J.; Savenije, H.H.G.; Schaefli, B.; Steele-Dunne, S.C. Origin and Fate of Atmospheric Moisture over Continents. Water Resour. Res. 2010, 46, W09525. [Google Scholar] [CrossRef] [Green Version]
- Numaguti, A. Origin and Recycling Processes of Precipitating Water over the Eurasian Continent: Experiments Using an Atmospheric General Circulation Model. J. Geophys. Res. Atmos. 1999, 104, 1957–1972. [Google Scholar] [CrossRef]
- Bosilovich, M.G.; Schubert, S.D. Water Vapor Tracers as Diagnostics of the Regional Hydrologic Cycle. J. Hydrometeorol. 2002, 3, 149–165. [Google Scholar] [CrossRef]
- Sodemann, H.; Wernli, H.; Schwierz, C. Sources of Water Vapour Contributing to the Elbe Flood in August 2002—A Tagging Study in a Mesoscale Model. Q. J. R. Meteorol. Soc. 2009, 135, 205–223. [Google Scholar] [CrossRef]
- Knoche, H.R.; Kunstmann, H. Tracking Atmospheric Water Pathways by Direct Evaporation Tagging: A Case Study for West Africa. J. Geophys. Res. Atmos. 2013, 118, 12,345–12,358. [Google Scholar] [CrossRef]
- Dominguez, F.; Miguez-Macho, G.; Hu, H. WRF with Water Vapor Tracers: A Study of Moisture Sources for the North American Monsoon. J. Hydrometeorol. 2016, 17, 1915–1927. [Google Scholar] [CrossRef]
- Peng, H.; Mayer, B.; Norman, A.-L.; Krouse, H.R. Modelling of Hydrogen and Oxygen Isotope Compositions for Local Precipitation. Tellus B Chem. Phys. Meteorol. 2005, 57, 273. [Google Scholar] [CrossRef]
- Froehlich, K.; Kralik, M.; Papesch, W.; Rank, D.; Scheifinger, H.; Stichler, W. Deuterium Excess in Precipitation of Alpine Regions—Moisture Recycling. Isot. Environ. Health Stud. 2008, 44, 61–70. [Google Scholar] [CrossRef]
- Peng, T.-R.; Liu, K.-K.; Wang, C.-H.; Chuang, K.-H. A Water Isotope Approach to Assessing Moisture Recycling in the Island-Based Precipitation of Taiwan: A Case Study in the Western Pacific. Water Resour. Res. 2011, 47, W08507. [Google Scholar] [CrossRef]
- Liu, G.; Wang, J. A Study on Hydrologic Cycle of Land-Atmosphere System of China. Adv. Water Sci. 1997, 8, 99–107. [Google Scholar]
- Yi, L.; Tao, S. Construction and Analysis of a Precipitation Recycling Model. Adv. Water Sci. 1997, 8, 205–211. [Google Scholar]
- Kang, H.; Gu, X.; Zhu, G.; Paul, W. Precipitation Recycling in Southern and Central China. Chin. J. Atmospheric Sci. 2004, 28, 892–900. [Google Scholar]
- Kang, H.; Gu, X.; Fu, X.; Xu, X. Precipitation Recycling over the Northern China. J. Appl. Meteorol. Sci. 2005, 16, 139–147. [Google Scholar]
- Hua, L.; Zhong, L.; Ke, Z. Precipitation Recycling and Soil–Precipitation Interaction across the Arid and Semi-Arid Regions of China. Int. J. Climatol. 2016, 36, 3708–3722. [Google Scholar] [CrossRef]
- Hua, L.; Zhong, L.; Ke, Z. Characteristics of the Precipitation Recycling Ratio and Its Relationship with Regional Precipitation in China. Theor. Appl. Climatol. 2017, 127, 513–531. [Google Scholar] [CrossRef]
- Su, T.; Lu, Z.; Zhou, J.; Hou, W.; Li, Y.; Tu, G. Spatial Distribution and Seasonal Variation Characteristics of Global Atmospheric Moisture Recycling. Acta Phys. Sin. 2014, 63, 099201. [Google Scholar] [CrossRef]
- Fremme, A.; Sodemann, H. The Role of Land and Ocean Evaporation on the Variability of Precipitation in the Yangtze River Valley. Hydrol. Earth Syst. Sci. 2019, 23, 2525–2540. [Google Scholar] [CrossRef] [Green Version]
- Wu, P.; Ding, Y.; Liu, Y.; Li, X. The Characteristics of Moisture Recycling and Its Impact on Regional Precipitation against the Background of Climate Warming over Northwest China. Int. J. Climatol. 2019, 39, 5241–5255. [Google Scholar] [CrossRef]
- Li, X.; Wu, P.; Ding, Y.; Liu, Y.; Li, Q. Spatial-Temporal Variation of Precipitation Recycling over the Tibetan Plateau under Climate Warming. Atmospheric Res. 2022, 280, 106431. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhou, T. Interannual Variability of Precipitation Recycle Ratio Over the Tibetan Plateau. J. Geophys. Res. Atmos. 2021, 126, e2020JD033733. [Google Scholar] [CrossRef]
- Zhang, B.; He, Y.; Ren, Y.; Huang, B.; Peng, Y.; Wang, S.; Guan, X. The Influence of the Precipitation Recycling Process on the Shift to Heavy Precipitation over the Tibetan Plateau in the Summer. Front. Earth Sci. 2023, 11, 1078501. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 Global Reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- He, J.; Yang, K.; Tang, W.; Lu, H.; Qin, J.; Chen, Y.; Li, X. The First High-Resolution Meteorological Forcing Dataset for Land Process Studies over China. Sci. Data 2020, 7, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Qin, X.; Liu, Y.; Jin, Z.; Liu, J.; Wang, L.; Chen, J. Evaluation of Long-Term and High-Resolution Gridded Precipitation and Temperature Products in the Qilian Mountains, Qinghai–Tibet Plateau. Front. Environ. Sci. 2022, 10, 906821. [Google Scholar] [CrossRef]
- Lei, N.; Zhou, Z.; Zhuang, Q.; Chen, W.; Chalov, S.; Liu, S.; Gao, L.; Dong, G. Performance Evaluation and Improvement of CMFD’s Precipitation Products Over Shanghai City, China. Earth Space Sci. 2023, 10, e2022EA002690. [Google Scholar] [CrossRef]
- Hirsch, R.M.; Slack, J.R.; Smith, R.A. Techniques of Trend Analysis for Monthly Water Quality Data. Water Resour. Res. 1982, 18, 107–121. [Google Scholar] [CrossRef] [Green Version]
- Huntington, T.G. Evidence for Intensification of the Global Water Cycle: Review and Synthesis. J. Hydrol. 2006, 319, 83–95. [Google Scholar] [CrossRef]
- Wang, K.; Dickinson, R.E.; Wild, M.; Liang, S. Evidence for Decadal Variation in Global Terrestrial Evapotranspiration between 1982 and 2002: 1. Model Development. J. Geophys. Res. Atmos. 2010, 115, D20112. [Google Scholar] [CrossRef] [Green Version]
- Brutsaert, W.; Parlange, M.B. Hydrologic Cycle Explains the Evaporation Paradox. Nature 1998, 396, 30. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Liu, B.; Su, B.; Zhai, J.; Gemmer, M. Trends of Calculated and Simulated Actual Evaporation in the Yangtze River Basin. J. Clim. 2011, 24, 4494–4507. [Google Scholar] [CrossRef]
- Cong, Z.T.; Yang, D.W.; Ni, G.H. Does Evaporation Paradox Exist in China? Hydrol. Earth Syst. Sci. 2009, 13, 357–366. [Google Scholar] [CrossRef] [Green Version]


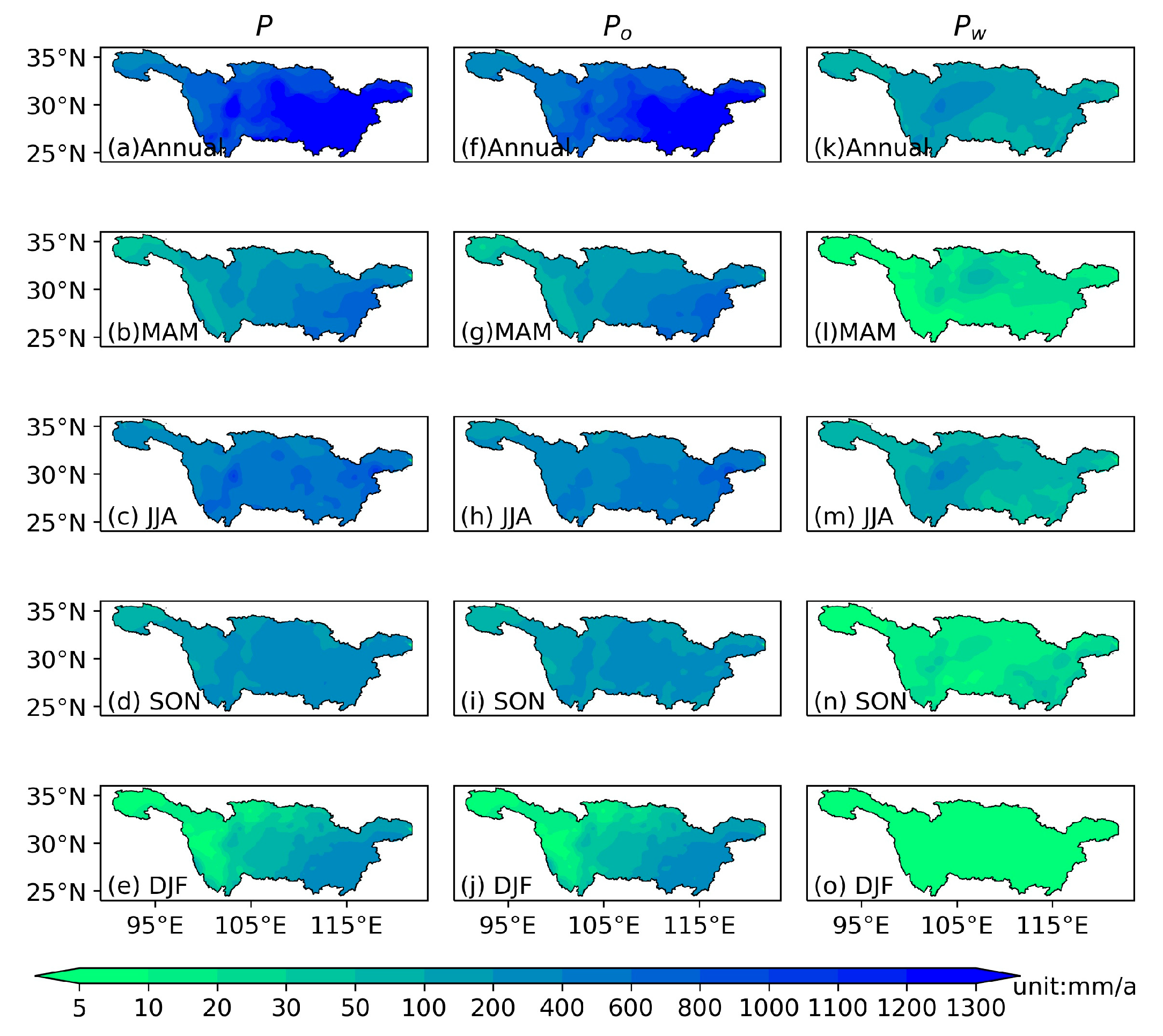
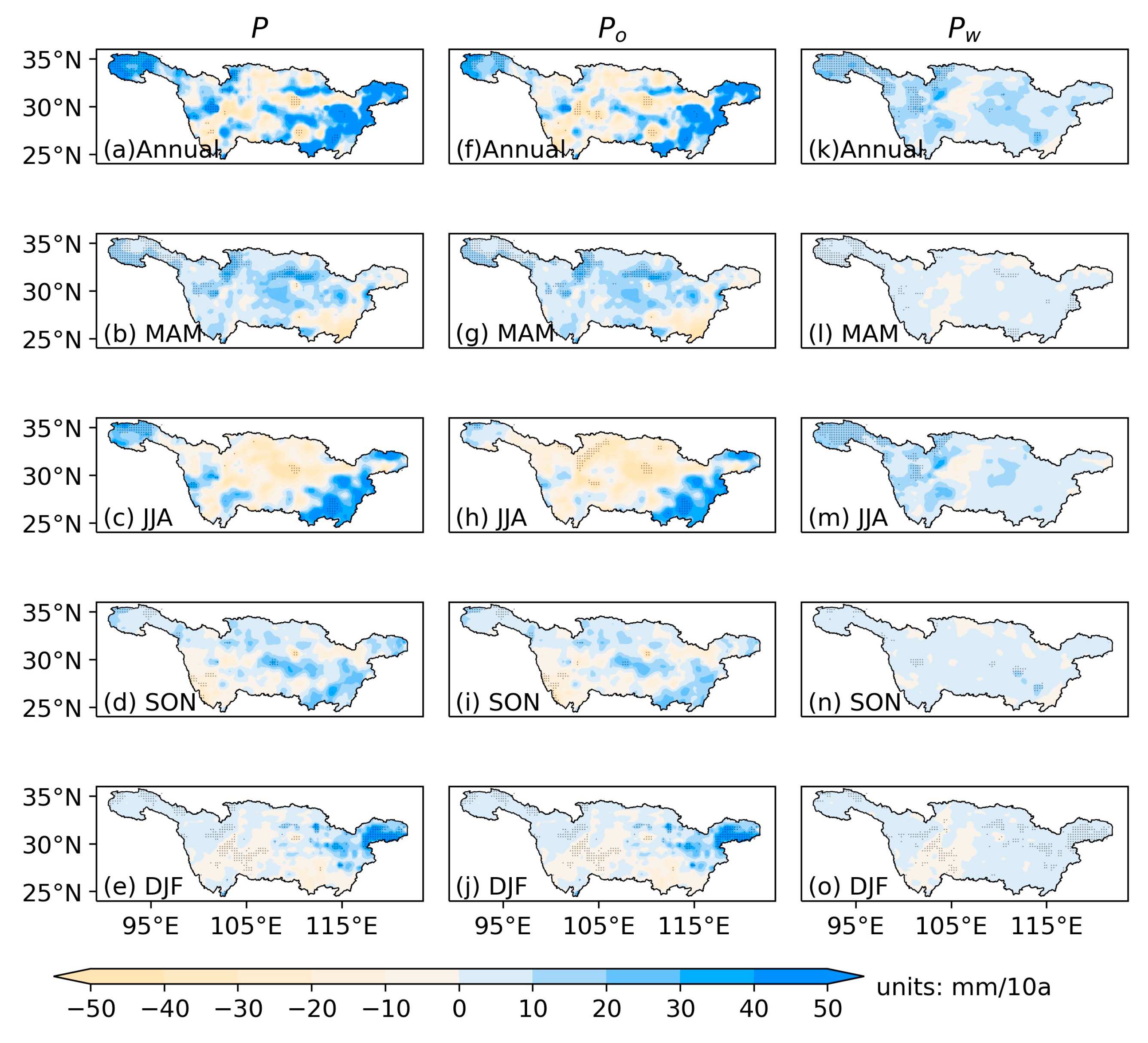
| P | Pw | Po | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | Variability | Cumulative Change (ΔP) | Mean | Variability | Cumulative Change (ΔPw) | Mean | Variability | Cumulative Change (ΔPo) | |
| Annual | 1071.5 | 11.9 | 47.4 | 141.6 | 8.2 | 32.7 | 929.9 | 3.7 | 14.7 |
| Spring | 281.1 | 6.1 | 24.2 | 19.2 | 0.6 | 2.4 | 262.0 | 5.5 | 21.9 |
| Summer | 487.7 | −0.6 | −2.2 | 100.4 | 6.2 | 24.9 | 387.2 | −6.8 | −27.1 |
| Autumn | 213.0 | 3.5 | 13.8 | 19.5 | 1.2 | 4.9 | 193.6 | 2.2 | 8.9 |
| Winter | 88.5 | −0.3 | −1.3 | 2.4 | 0.1 | 0.3 | 86.0 | −0.4 | −1.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Wu, P. Contribution of Evaporation to Precipitation Changes in the Yangtze River Basin—Precipitation Recycling. Water 2023, 15, 2407. https://doi.org/10.3390/w15132407
Li X, Wu P. Contribution of Evaporation to Precipitation Changes in the Yangtze River Basin—Precipitation Recycling. Water. 2023; 15(13):2407. https://doi.org/10.3390/w15132407
Chicago/Turabian StyleLi, Xiucang, and Ping Wu. 2023. "Contribution of Evaporation to Precipitation Changes in the Yangtze River Basin—Precipitation Recycling" Water 15, no. 13: 2407. https://doi.org/10.3390/w15132407
APA StyleLi, X., & Wu, P. (2023). Contribution of Evaporation to Precipitation Changes in the Yangtze River Basin—Precipitation Recycling. Water, 15(13), 2407. https://doi.org/10.3390/w15132407






