Evolution Characteristics of Rainfall and Runoff in the Upper Reaches of Zhang River Basin
Abstract
:1. Introduction
2. Overview of the Research Area
3. Research Methods and Data Sources
3.1. Research Methods
- (1)
- MK Trend Test
- (2)
- Cumulative departure method
- (3)
- Double mass curve
- (4)
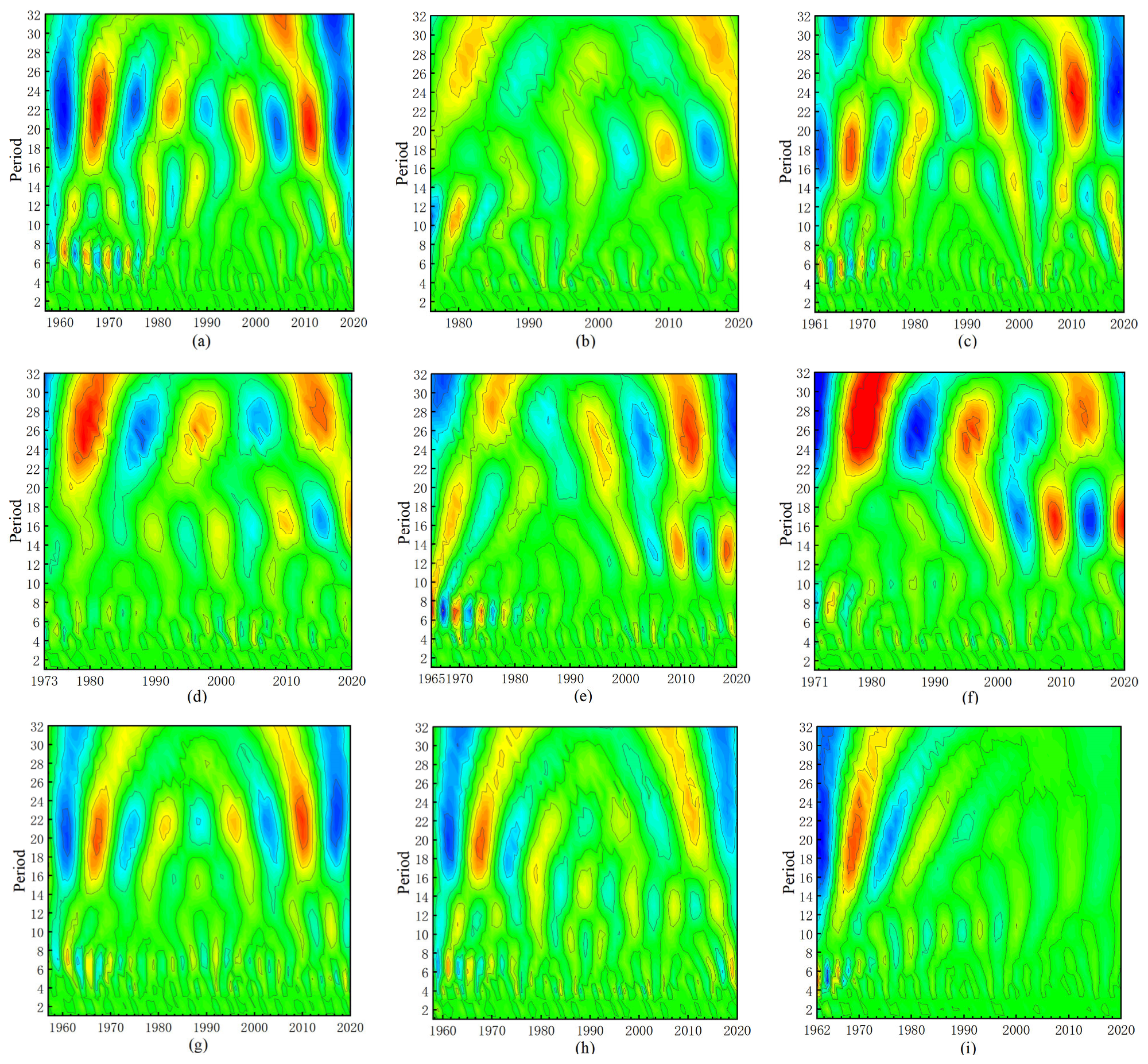
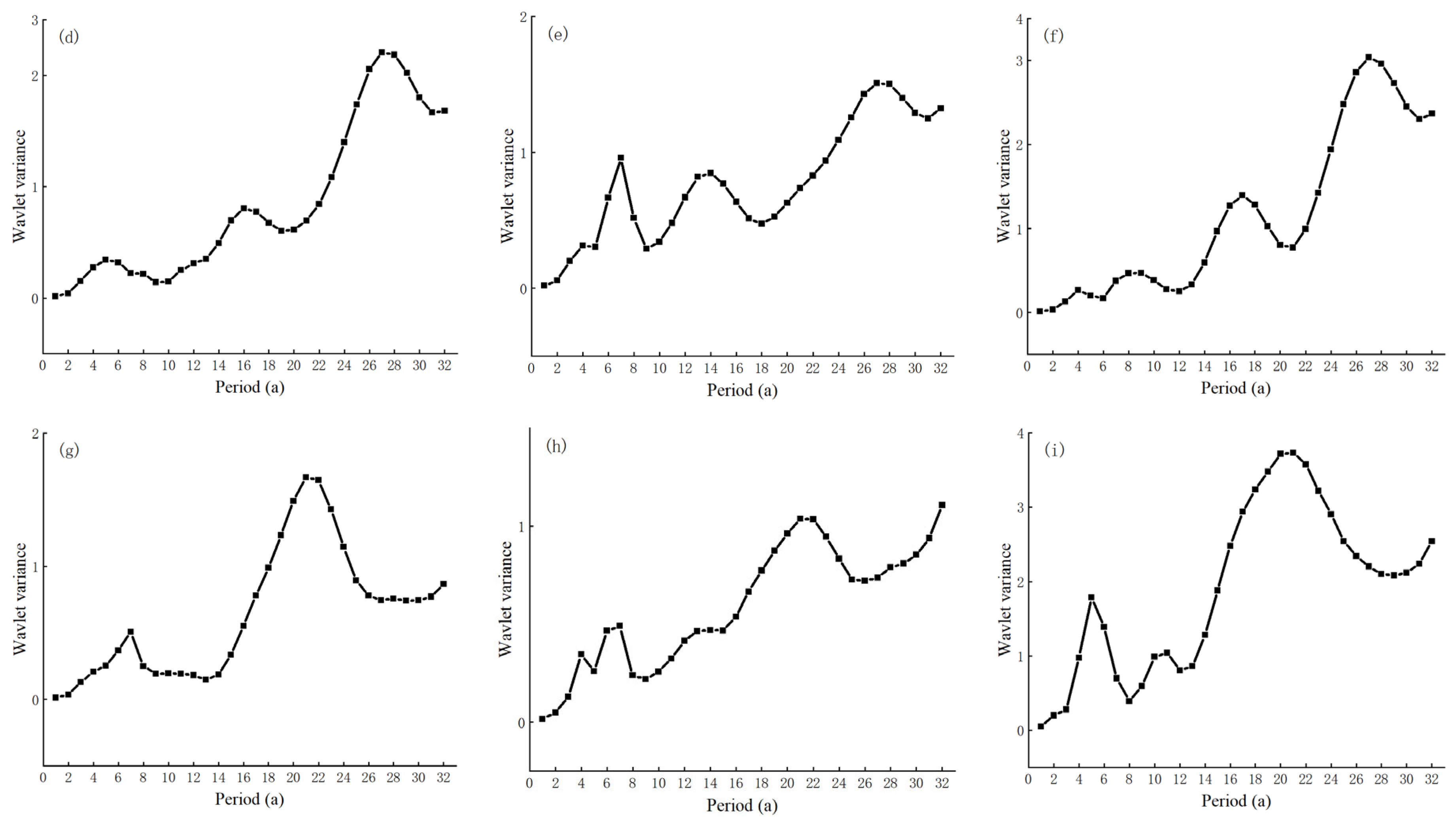
- Morlet wavelet transform
3.2. Data Sources
4. Results and Discussion
4.1. Analysis of Trend Mutability
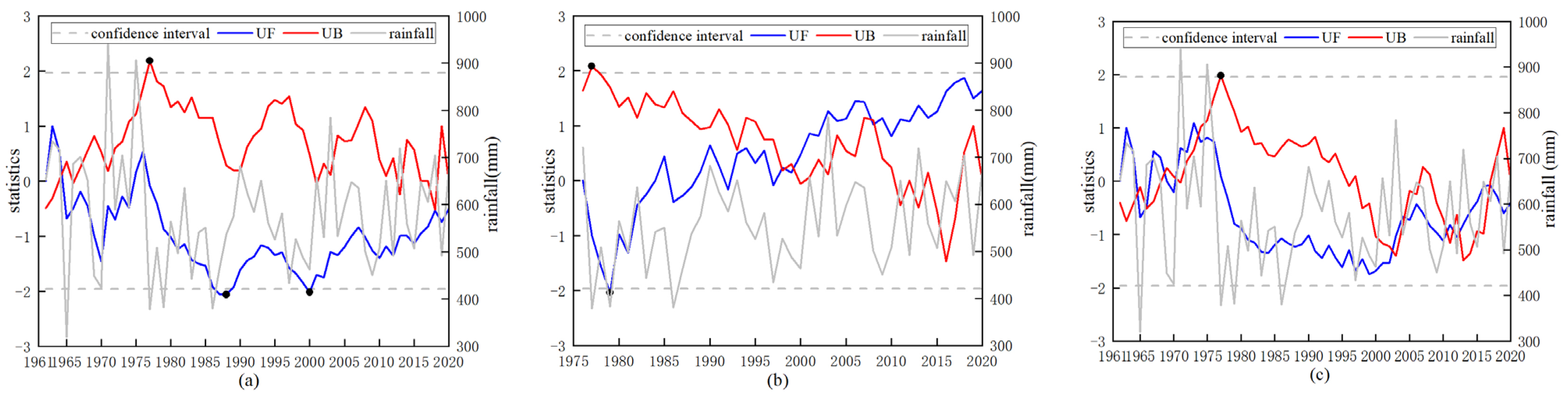
4.1.1. MK Trend Test
- (1)
- Rainfall trend analysis
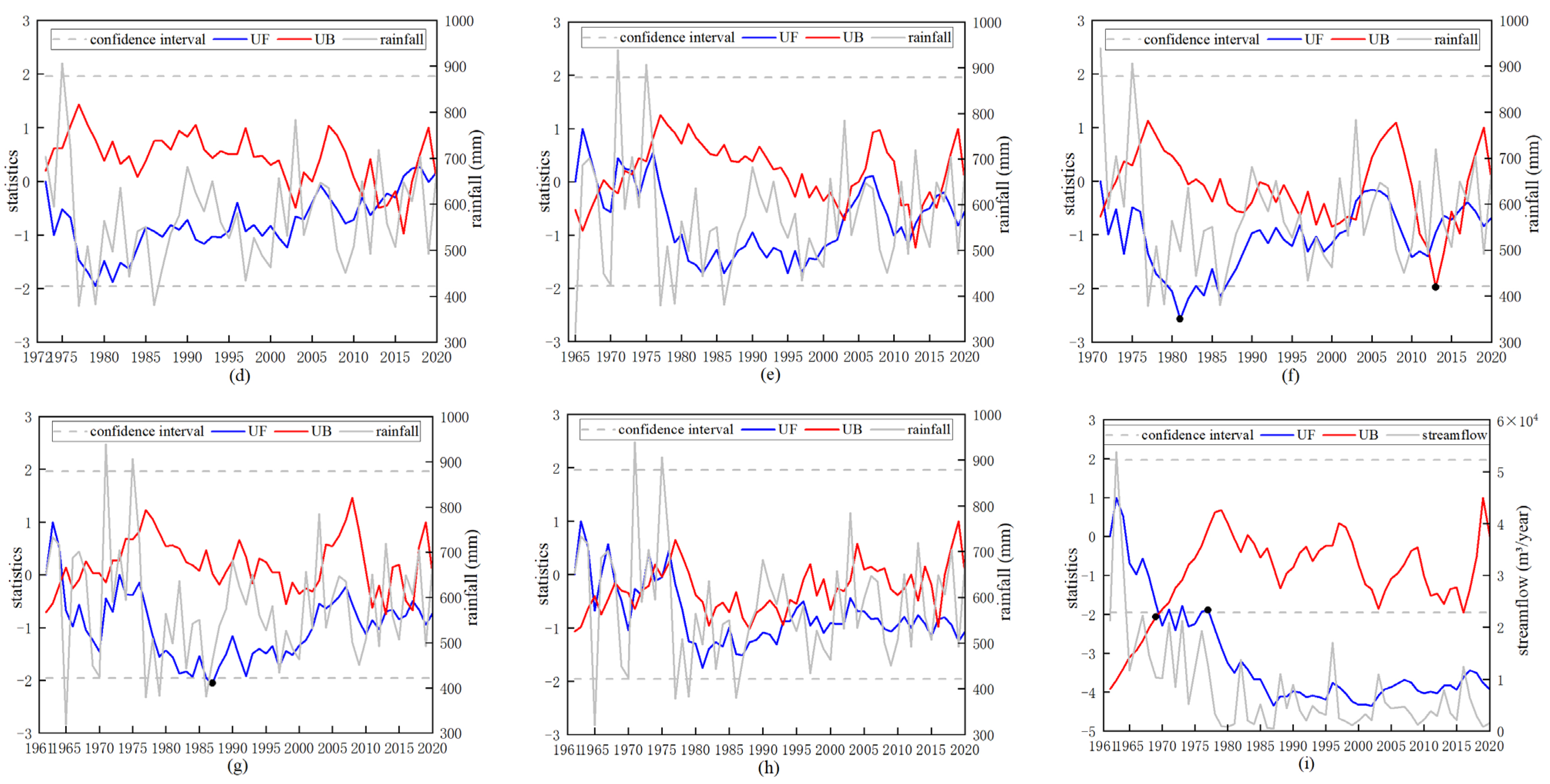
- (2)
- Runoff trend analysis
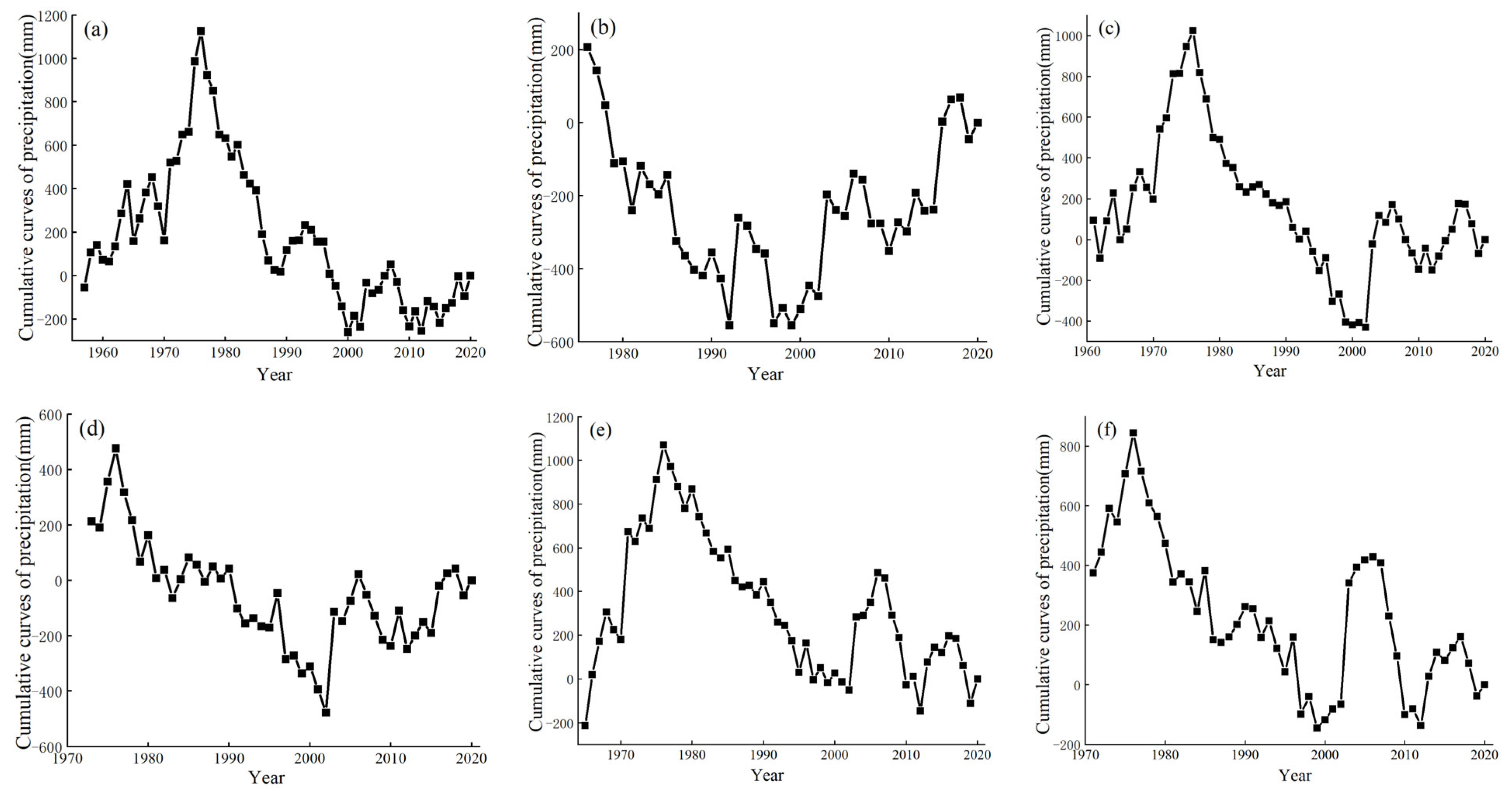
4.1.2. Cumulative Departure Method
- (1)
- Analysis of rainfall
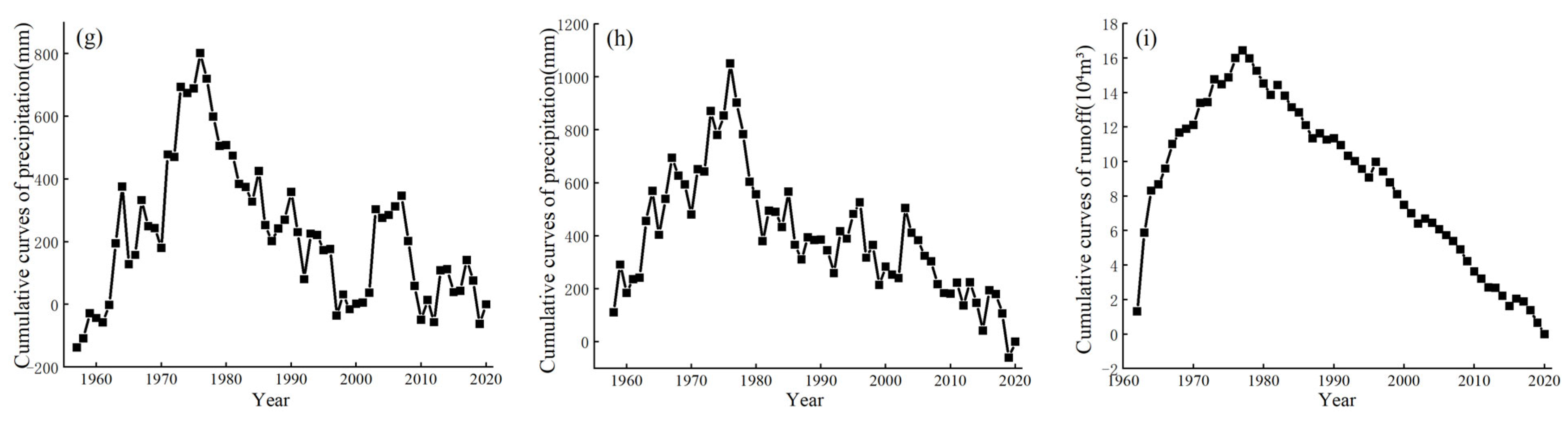
- (2)
- Analysis of runoff
4.1.3. Results of Trend Mutation
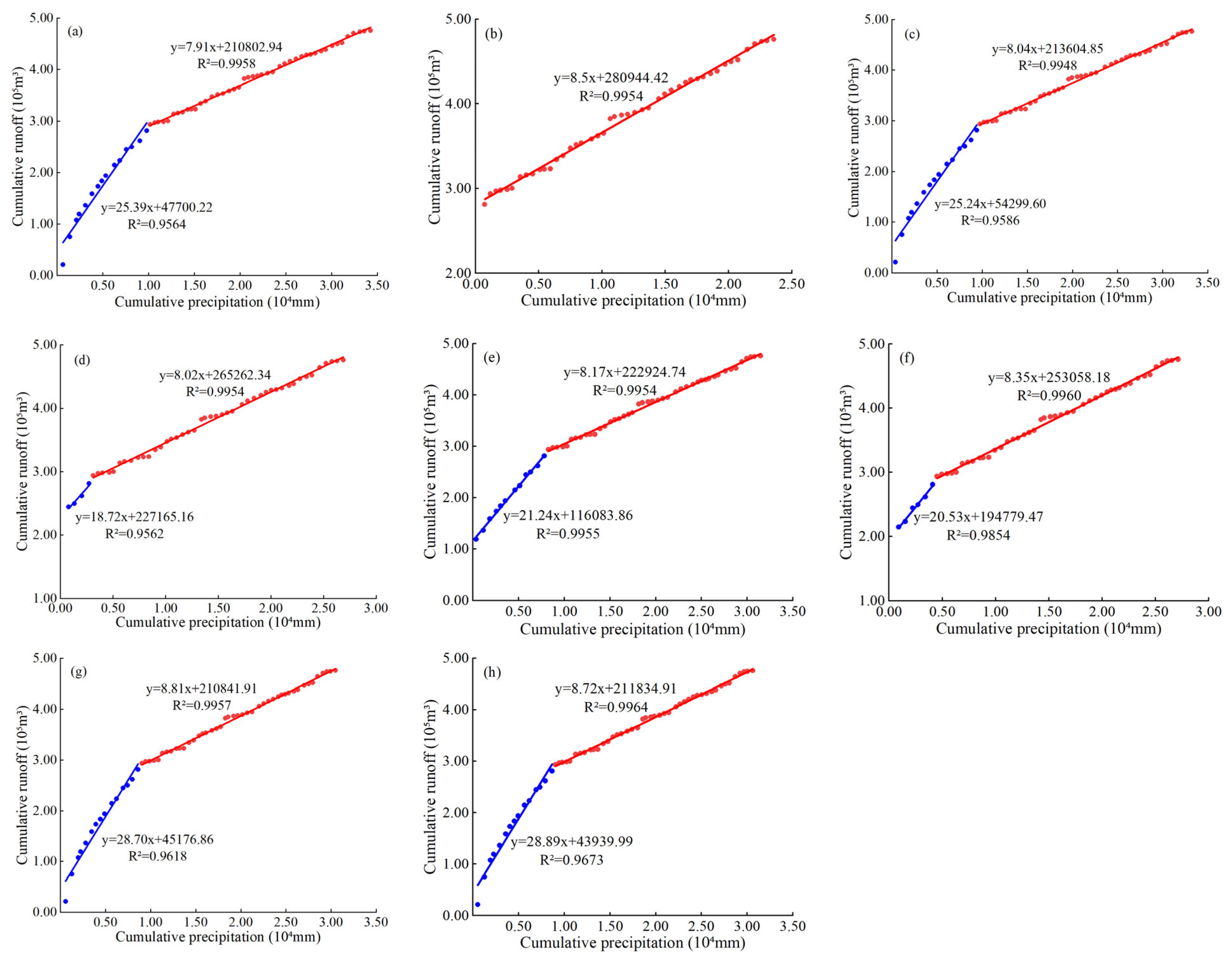
4.2. Results of Attribution Analysis
4.3. Results of Periodicity
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, G.Q.; Zhang, J.Y.; Guan, X.X.; Bao, Z.X.; Liu, Y.L.; He, R.M.; Jin, J.L.; Liu, C.S.; Chen, X. Quantifying attribution of runoff change for major rivers in China. Adv. Water Sci. 2020, 31, 313–323. [Google Scholar]
- Liu, N.; Harper, R.J.; Smettem, K.R.J.; Dell, B.; Liu, S. Responses of streamflow to vegetation and climate change in southwestern Australia. J. Hydrol. 2019, 572, 761–770. [Google Scholar] [CrossRef]
- Liu, Y.; Han, X.X.; Li, L.J. Characteristics and attribution analysis of runoff changes in the middle and upper reaches of Cao’e River from 1980 to 2018. J. Water Resour. Water Eng. 2022, 33, 53–61. [Google Scholar]
- Nyikadzino, B.; Chitakira, M.; Muchuru, S. Rainfall and runoff trend analysis in the Limpopo river basin using the Mann Kendall statistic. Phys. Chem. Earth 2020, 117, 102870. [Google Scholar] [CrossRef]
- Dan’azumi, S.; Ibrahim, U.A. Trend analysis of observed precipitation, temperature, and streamflow for Hadejia-Nguru wetlands catchment, Nigeria. Theor. Appl. Climatol. 2023, 151, 195–207. [Google Scholar] [CrossRef]
- Clavera, G.R.; Quintana, S.P.; Palazón, L.; Zabaleta, A.; Cenobio, O.; Barella, O.A.; Beguería, S. Streamflow trends of the Pyrenees using observations and multi-model approach (1980–2013). J. Hydrol. Reg. Stud. 2023, 46, 101322. [Google Scholar]
- Liu, J.P.; Wang, W.; Zhou, J.J.; Zou, X.B. The Research of Runoff Variation Characteristics of Wei River Basin. In Proceedings of the 3rd International Conference on Advances in Energy and Environmental Science, Zhuhai, China, 25–26 July 2015. [Google Scholar]
- Shen, Z.T.; Zhao, Q.; Li, X.F. Analysis of Rainfall-Runoff Variation Characteristics and Influencing Factors in the Dawen River Basin in the Past 50 Years. IOP Conf. Ser. Earth Environ. Sci. 2020, 619, 012091. [Google Scholar] [CrossRef]
- Huang, Z.Q.; Shen, K.Q.; Zhao, C.; Shan, M. Trend Analysis of Annual Runoff in Yong’an Creek Basin of Zhejiang. IOP Conf. Ser. Earth Environ. Sci. 2021, 811, 012003. [Google Scholar]
- Lu, H.X.; Ma, G.W.; Wang, X.D.; Ping, F.; Li, F.W. Effects of Abundant-and-Low-Flow Property of Annual Rainfall on Multi-Source Water Intake System Allocation. Appl. Mech. Mater. 2013, 2545, 353–356. [Google Scholar] [CrossRef]
- Li, Z.Y.; Sun, Z.L.; Sun, L.X.; Liu, J.; Xiong, W.H.; Dong, H.Y.; Zheng, H.L. Hydrological variation and hydro-sediment interrelation of the Luozha River in the Lancang River Basin. Water Supply 2022, 22, 4839–4851. [Google Scholar] [CrossRef]
- Lyu, J.Q.; Yin, S.S.; Sun, Y.T.; Wang, K.X.; Luo, P.P.; Meng, X.L. Flood Runoff Simulation under Changing Environment, Based on Multiple Satellite Data in the Jinghe River Basin of the Loess Plateau, China. Remote Sens. 2023, 15, 550. [Google Scholar] [CrossRef]
- He, B.; Miao, C.Y.; Shi, W. Trend, abrupt change, and periodicity of streamflow in the mainstream of Yellow River. Environ. Monit. Assess. 2013, 185, 6187–6199. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.L.; Zhang, W.; Wu, T. Analysis of the Periodicity of Annual Extreme Runoff at Datong Station, Yangtze River, China. Appl. Mech. Mater. 2012, 256–259, 2606–2610. [Google Scholar] [CrossRef]
- Lamborn, C.C.; Smith, W.J. Human perceptions of, and adaptations to, shifting runoff cycles: A case-study of the Yellowstone River (Montana, USA). Fisheries Research 2019, 216, 96–108. [Google Scholar] [CrossRef]
- Ji, G.X.; Wu, L.Y.; Wang, L.D.; Yan, D.; Lai, Z.Z. Attribution Analysis of Seasonal Runoff in the Source Region of the Yellow River Using Seasonal Budyko Hypothesis. Land 2021, 10, 542. [Google Scholar] [CrossRef]
- Wang, L.; Cao, H.; Li, Y.R.; Feng, B.F.; Qiu, H.; Zhang, H.R. Attribution Analysis of Runoff in the Upper Reaches of Jinsha River, China. Water 2022, 14, 2768. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, C.S.; Peng, Z.D.; Kuai, S.Y.; Zhang, S.H. Synergistic Effects of Changes in Climate and Vegetation on Basin Runoff. Water Resour. Manag. 2022, 36, 3265–3281. [Google Scholar] [CrossRef]
- Mo, C.X.; Lai, S.F.; Yang, Q.; Huang, K.K.; Lei, X.B.; Yang, L.F.; Yan, Z.W.; Jiang, C.H. A comprehensive assessment of runoff dynamics in response to climate change and human activities in a typical karst watershed, southwest China. J. Environ. Manag. 2023, 332, 117380. [Google Scholar] [CrossRef]
- Wang, H.X.; Ma, Y.C.; Yang, H.; Hong, F.T.; Guo, W.X. Quantitative evaluation of the impact of climate change and human activities on Jialing river runoff changes in the past 60 years, China. J. Water Clim. Change 2023, 14, 590–609. [Google Scholar] [CrossRef]
- Panditharathne, R.; Gunathilake, M.B.; Chathuranika, I.M.; Rathnayake, U.; Babel, M.S.; Jha, M.K. Trends and Variabilities in Rainfall and Streamflow: A Case Study of the Nilwala River Basin in Sri Lanka. Hydrology 2022, 10, 8. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, L.; Zhang, Z.; Li, J.X.; Hou, L.; Liu, J.Q.; Wang, Y.B. Research on the Hydrological Variation Law of the Dawen River, a Tributary of the Lower Yellow River. Agronomy 2022, 12, 1719. [Google Scholar] [CrossRef]
- Ji, G.X.; Gao, H.S.; Huang, J.C.; Yang, X.; Zhang, Y.L. Research on Runoff Variation Characteristics and Attribution Analysis in the Upper Yellow River Basin. J. Henan Norm. Univ. (Nat. Sci. Ed.) 2023, 01, 12–19. [Google Scholar]
- Banda, V.D.; Dzwairo, R.B.; Singh, S.K.; Kanyerere, T. Separating anthropogenic and climate contributions to streamflow variations in Rietspruit sub-basin, South Africa. Phys. Chem. Earth 2022, 127, 103200. [Google Scholar] [CrossRef]
- Wang, L.; Song, X.Y.; Li, L.J.; Zhang, L.; Liu, Y.; Li, H.Y.; Li, Y.L. Variation trend and attribution analysis of runoff in typical small watershed in gully region of the loess. Res. Soil Water Conserv. 2021, 28, 48–53+69. [Google Scholar]
- Zhang, H.Z.; Zhao, W.J. Quantitative Analysis of Annual Precipitation in Extreme Precipitation Areas. Environ. Resour. Ecol. J. 2022, 6, 90–94. [Google Scholar]
- Das, S.; Scaringi, G. River flooding in a changing climate: Rainfall-discharge trends, controlling factors, and susceptibility mapping for the Mahi catchment, Western India. Nat. Hazards 2021, 109, 2439–2459. [Google Scholar] [CrossRef]
- Talukdar, S.; Pal, S.; Shahfahad; Naikoo, M.W.; Parvez, A.; Rahman, A. Trend analysis and forecasting of streamflow using random forest in the Punarbhaba River basin. Environ. Monit. Assess. 2022, 195, 153. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.R.; He, Y.H.; Tang, Y.P.; Wang, G.Q. Research on key technologies of Haihe River Basin runoff change trend and change attribution. In Proceedings of the Future-Oriented Water Security and Sustainable Development—Proceedings of the 14th China Water Forum, Changchun, China, 25 August 2016; pp. 117–125. [Google Scholar]
- Liu, W.L.; Liu, L.N.; Wu, B. Analysis of dry runoff change characteristics and influencing factors in the lower reaches of the main stream of the Ganjiang River. Hydrology 2022, 42, 89–96. [Google Scholar]
- Pan, B.; Han, M.; Wei, F.; Tian, L.X.; Liu, Y.T.; Li, Y.L.; Wang, M. Analysis of the Variation Characteristics of Runoff and Sediment in the Yellow River within 70 Years. Water Resour. 2021, 48, 676–689. [Google Scholar] [CrossRef]
- Zhang, G.H.; Ding, W.F.; Liu, H.Y.; Liang, Y.; Xu, L.; Zhang, O.Y. Quantifying Climatic and Anthropogenic Influences on Water Discharge and Sediment Load in Xiangxi River Basin of the Three Gorges Reservoir Area. Water Resour. 2021, 48, 204–218. [Google Scholar] [CrossRef]
- Jin, S.F.; Zheng, Z.Y.; Ning, L.K. Separating variance in the runoff in Beijing’s river system under climate change and human activities. Phys. Chem. Earth 2021, 123, 103044. [Google Scholar] [CrossRef]
- Shao, Y.T.; He, Y.; Mu, X.M.; Zhao, G.J.; Gao, P.; Sun, W.Y. Contributions of climate change and human activities to runoff and sediment discharge reductions in the Jialing River, a main tributary of the upper Yangtze River, China. Theor. Appl. Climatol. 2021, 145, 1437–1450. [Google Scholar] [CrossRef]
- Qi, L.L.; Guo, Z.L.; Qi, Z.X.; Guo, J.J. Prospects of Precipitation Based on Reconstruction over the Last 2000 Years in the Qilian Mountains. Sustainability 2022, 14, 10615. [Google Scholar] [CrossRef]
- Guo, W.X.; He, N.; Ban, X.; Wang, H.X. Multi-scale variability of hydrothermal regime based on wavelet analysis—The middle reaches of the Yangtze River, China. Sci. Total Environ. 2022, 841, 156598. [Google Scholar] [CrossRef]
- Sun, N. Consistency Test of Natural Runoff Series. Shanxi Water Conserv. Sci. Technol. 2015, 04, 68–70. [Google Scholar]
- Yang, D.; Liu, H.M.; Guo, P.P.; Zheng, F.J.; Liu, Q. The change of rainfall in Liaoning Province in recent 53 years from 1956 to 2008. Resour. Environ. Arid. Reg. 2011, 25, 002. [Google Scholar]
- Lozowski, E.P.; Charlton, R.B.; Nguyen, C.D.; Wilson, J.D. The Use of Cumulative Monthly Mean Temperature Anomalies in the Analysis of Local Interannual Climate Variability. J. Clim. 1989, 2, 1059–1068. [Google Scholar] [CrossRef]
- Shu, M.Z.; Liu, L.H. Temporal and spatial variation characteristics of rainfall in the Haihe River Basin in recent 51 years. South–North Water Divers. Water Conserv. Sci. Technol. 2015, 13, 009. [Google Scholar]
- Hu, D.L.; Yan, D.H.; Song, X.S.; Zhang, M.Z.; Yu, X.; Yang, S.Y. Analysis on the changing trend of water resources in the Yangtze River Basin above Yibin. South–North Water Divers. Water Conserv. Sci. Technol. 2008, 02, 21. [Google Scholar]
- Li, L.; Wu, X.J.; Zhou, X.D.; Dong, Y.; Zhang, F.P.; Zhang, Y.N.; Liu, J. Analysis of river runoff evolution characteristics in coal mining area based on Morlet wavelet theory. Hydropower Energy Sci. 2022, 40, 37–40. [Google Scholar]


| Type | Station Name | Station Number | Longitude (E) | Latitude (N) | Time Period of Measured Data |
|---|---|---|---|---|---|
| rainfall station | Pingshun station | 53,888 | 113.26 | 36.12 | 1957–2020 |
| Lucheng station | 53,880 | 113.14 | 36.2 | 1976–2020 | |
| Huguan station | 53,885 | 113.12 | 36.07 | 1961–2020 | |
| Changzhi station | 53,882 | 113.02 | 36.04 | 1973–2020 | |
| Changzi station | 53,873 | 112.52 | 36.06 | 1965–2020 | |
| Tunliu station | 53,879 | 112.53 | 36.19 | 1971–2020 | |
| Xiangyuan station | 53,884 | 113.02 | 36.31 | 1957–2020 | |
| Licheng station | 53,878 | 113.23 | 36.31 | 1958–2020 | |
| hydrologic station | Guantai station | 36,255 | 114.08 | 36.32 | 1962–2020 |
| Type | Station Name | Mann−Kendall Trend Test | Accumulated Variance | |||
|---|---|---|---|---|---|---|
| Trend Test Statistic | Year of Mutation Point | Mutation Point Statistic | Trends | Year of Mutation Point | ||
| rainfall station | Pingshun station | −0.49 | 1977 *, 1988 *, 2000 * | +2.18, −2.06, −2.02 | decreased | 1976 |
| Lucheng station | 1.63 | 1977 *, 1979 * | +2.08, −2.04 | raised | 1992 | |
| Huguan station | −0.39 | 1977 * | +1.98 | decreased | 1976 | |
| Changzhi station | 0.18 | \ | \ | raised | 1976 | |
| Changzi station | −0.53 | \ | \ | decreased | 1976 | |
| Tunliu station | −0.66 | 1981 **, 2013 * | −2.57, −1.98 | decreased | 1976 | |
| Xiangyuan station | −0.71 | 1987 * | −2.05 | decreased | 1976 | |
| Licheng station | −1.06 | \ | \ | decreased | 1976 | |
| hydrologic station | Guantai station | −3.92 ** | 1969 *, 1977 ** | −2.29, −2.39 | decreased | 1977 |
| Rainfall Station-Hydrological Station | Period | Observed Value (m3/s) | Simulated Value (m3/s) | Runoff Variation Value (m3/s) | Rainfall | Human Activities | ||
|---|---|---|---|---|---|---|---|---|
| Variation (m3/s) | Contribution Rate (%) | Variation (m3/s) | Contribution Rate (%) | |||||
| Pingshun Station-Guantai Station | 1962–1977 | 11,034.60 | 12,049.70 | 215.85 | 83.73 | 38.79 | 132.12 | 61.21 |
| 1977–2020 | 10,818.75 | 10,950.87 | ||||||
| Huguan Station-Guantai Station | 1962–1977 | 11,034.60 | 11,748.48 | 215.85 | 105.12 | 48.70 | 110.73 | 51.30 |
| 1977–2020 | 10,818.75 | 10,929.48 | ||||||
| Changzhi Station-Guantai Station | 1973–1977 | 11,034.60 | 10,835.78 | 215.85 | 103.69 | 48.04 | 112.16 | 51.96 |
| 1977–2020 | 10,818.75 | 10,930.91 | ||||||
| Zhangzi Station-Guantai Station | 1965–1977 | 11,034.60 | 11,105.96 | 215.85 | 91.94 | 42.60 | 123.91 | 57.40 |
| 1977–2020 | 10,818.75 | 10,910.70 | ||||||
| Tunliu Station-Guantai Station | 1971–1977 | 11,034.60 | 10,899.02 | 215.85 | 82.37 | 38.16 | 133.48 | 61.84 |
| 1977–2020 | 10,818.75 | 10,901.13 | ||||||
| Xiangyuan Station- Guantai Station | 1962–1977 | 11,034.60 | 11,770.28 | 215.85 | 82.80 | 38.36 | 133.05 | 61.64 |
| 1977–2020 | 10,818.75 | 10,901.56 | ||||||
| Licheng Station-Guantai Station | 1962–1977 | 11,034.60 | 11,905.22 | 215.85 | 63.13 | 29.25 | 152.72 | 70.75 |
| 1977–2020 | 10,818.75 | 10,881.89 | ||||||
| Average | 215.85 | 87.54 | 40.55 | 128.31 | 59.46 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, L.; Wang, G.; Lei, B. Evolution Characteristics of Rainfall and Runoff in the Upper Reaches of Zhang River Basin. Water 2023, 15, 2521. https://doi.org/10.3390/w15142521
Du L, Wang G, Lei B. Evolution Characteristics of Rainfall and Runoff in the Upper Reaches of Zhang River Basin. Water. 2023; 15(14):2521. https://doi.org/10.3390/w15142521
Chicago/Turabian StyleDu, Lijuan, Guangyao Wang, and Bo Lei. 2023. "Evolution Characteristics of Rainfall and Runoff in the Upper Reaches of Zhang River Basin" Water 15, no. 14: 2521. https://doi.org/10.3390/w15142521
APA StyleDu, L., Wang, G., & Lei, B. (2023). Evolution Characteristics of Rainfall and Runoff in the Upper Reaches of Zhang River Basin. Water, 15(14), 2521. https://doi.org/10.3390/w15142521






