Real-Time Control Operation Method of Water Diversion Project Based on River Diversion Disturbance
Abstract
:1. Introduction
2. Analysis of Typical Water Diversion Disturbance Conditions
3. Materials and Methods
3.1. Integrator-Delay Model
3.2. Objective Function and Constraint
3.2.1. Disturbance Line Type (C2)
3.2.2. Disturbance Line Type (C3)
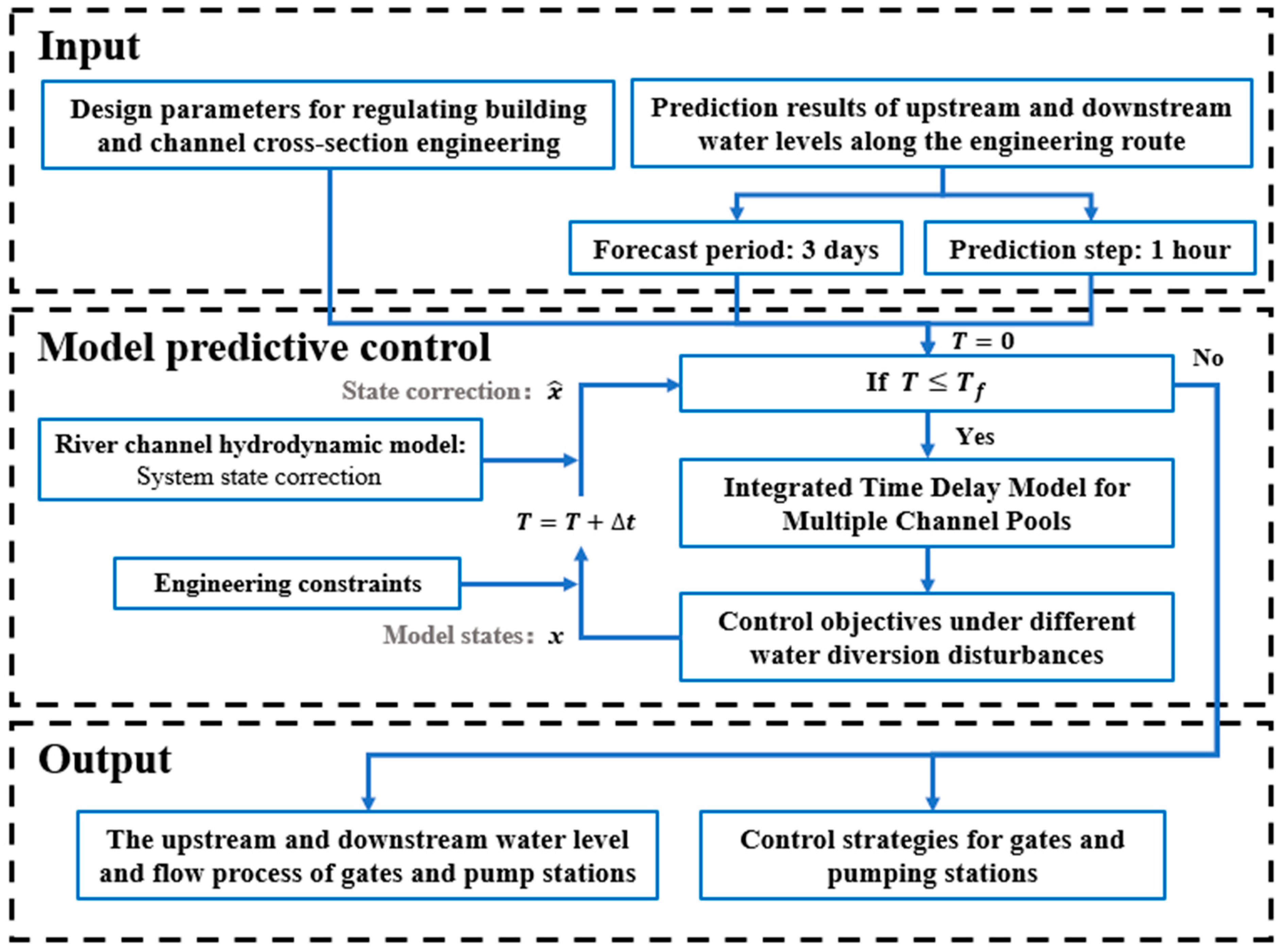
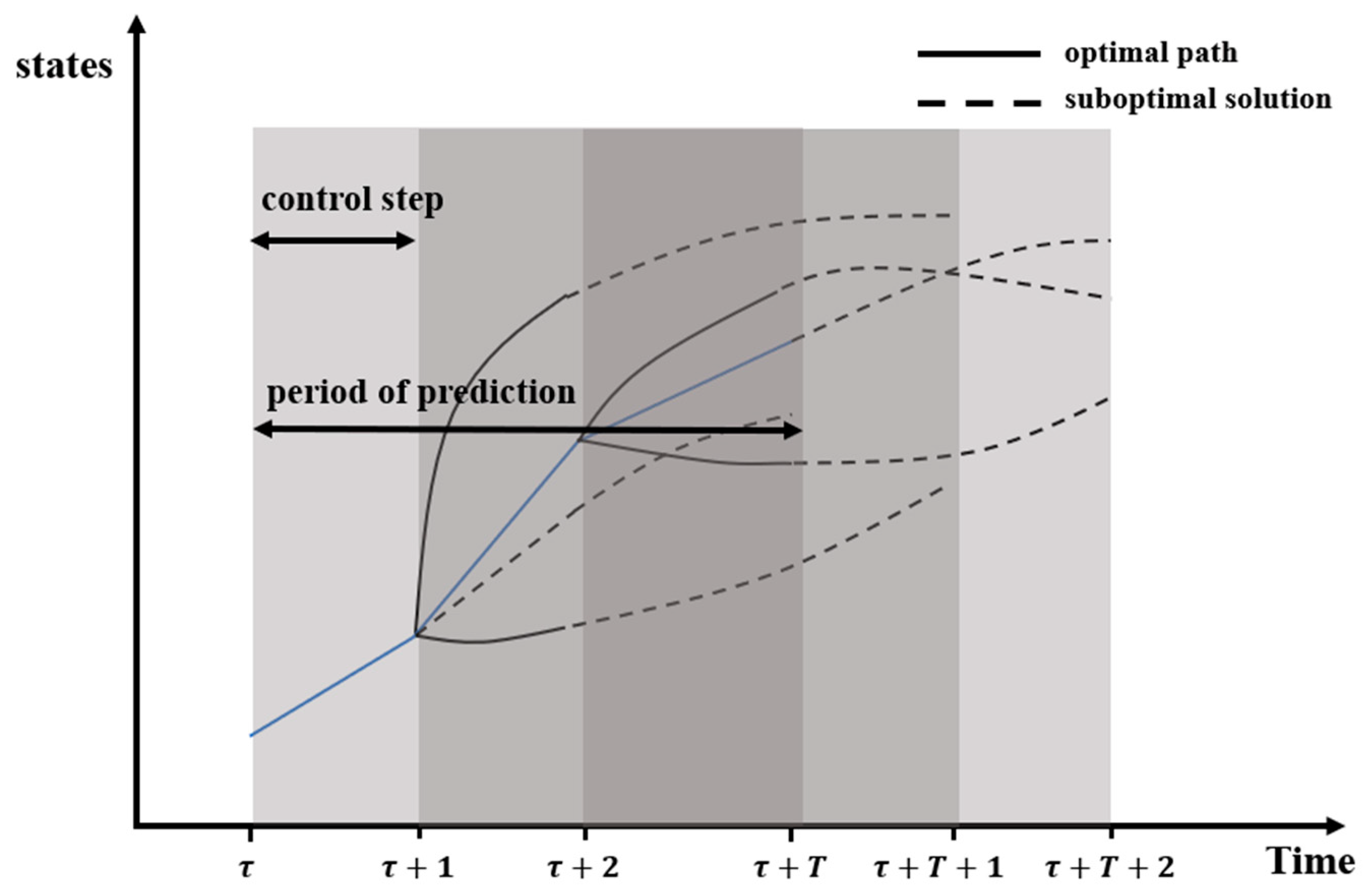
3.3. Model Predictive Control Algorithm
4. Case Study
4.1. Project Profile
4.2. Control Strategy
4.3. Test Scenario
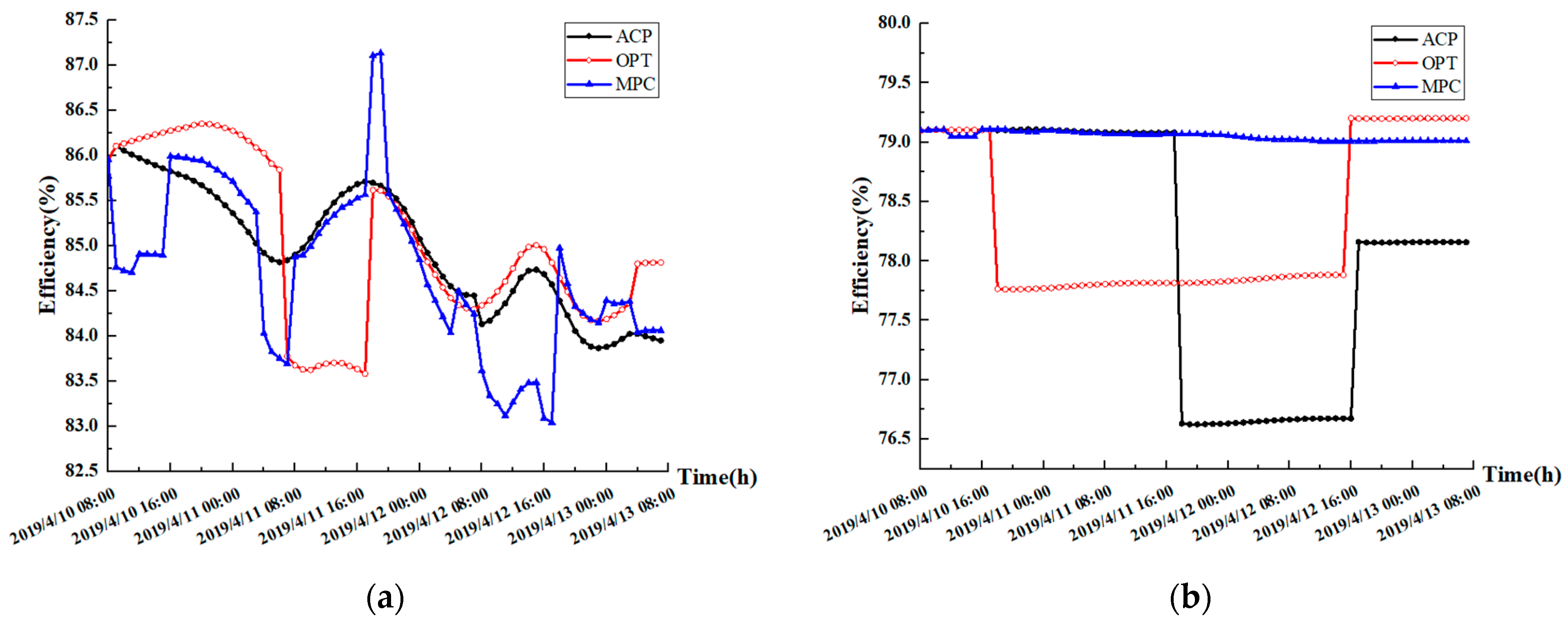
4.4. Operational Evaluation Indicators
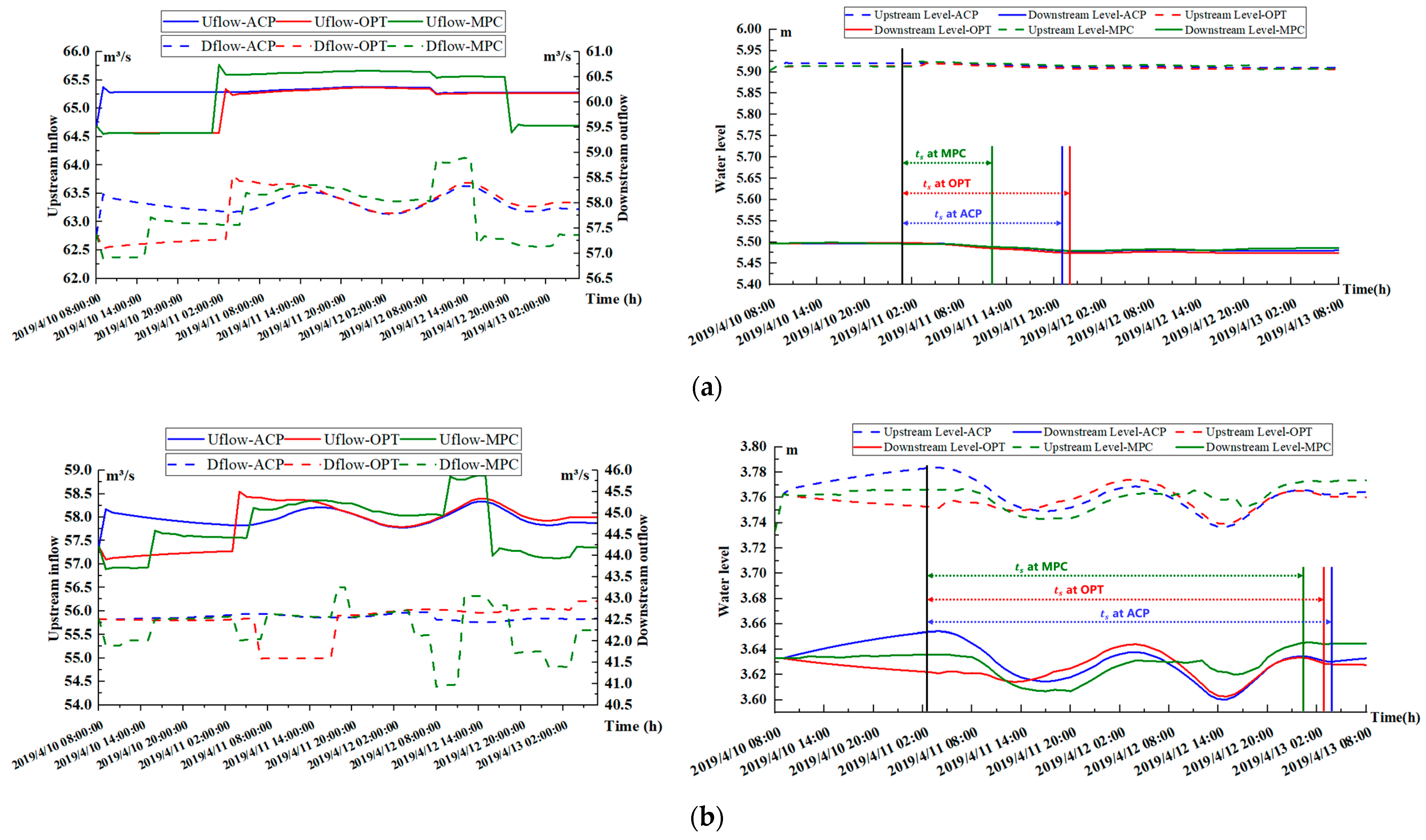
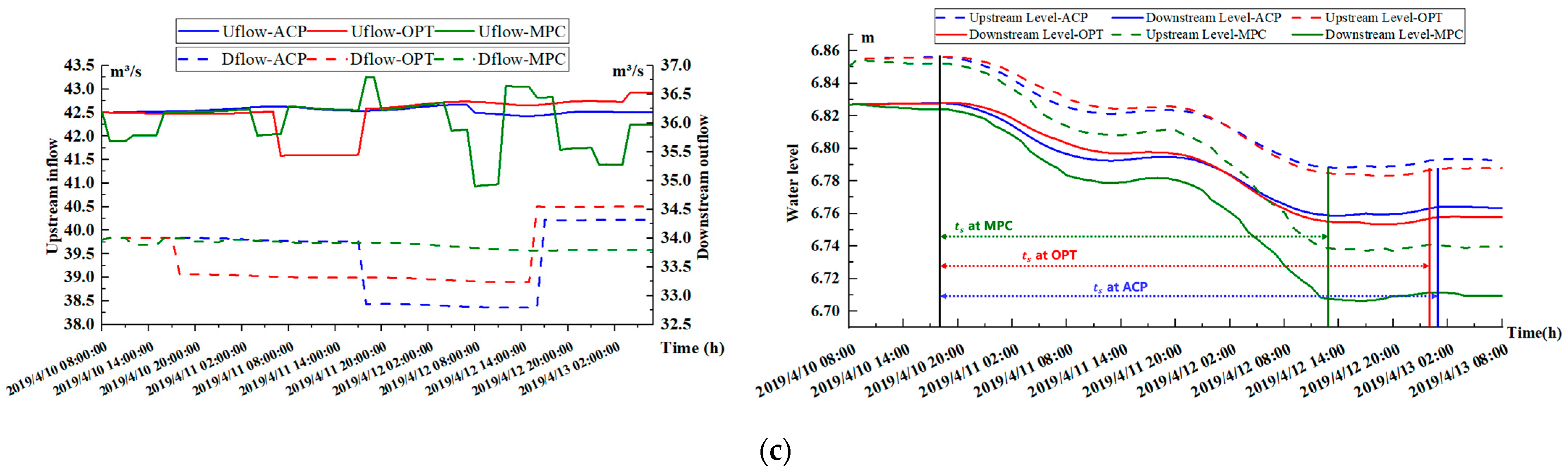
4.5. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.G.; Zhang, W.S. Modelling water quality and quantity with the influence of inter-basin water diversion projects and cascade reservoirs in the Middle-lower Hanjiang River. J. Hydrol. 2016, 541, 1348–1362. [Google Scholar] [CrossRef]
- Zhou, Y.L.; Guo, S.L. Systematic impact assessment on inter-basin water transfer projects of the Hanjiang River Basin in China. J. Hydrol. 2017, 553, 584–595. [Google Scholar] [CrossRef]
- Park, S.; Jahns, T.M. Flexible dv/dt and di/dt control method for insulated gate power switches. J. IEEE Trans. Ind. Appl. 2003, 39, 657–664. [Google Scholar] [CrossRef] [Green Version]
- Hashemy Shahdany, S.M.; Adib Majd, E.; Firoozfar, A.; Maestre, J.M. Improving operation of a main irrigation canal suffering from inflow fluctuation within a centralized model predictive control system: Case study of Roodasht Canal, Iran. J. Irrig. Drain. Eng. 2016, 142, 06016007. [Google Scholar] [CrossRef]
- Kurganov, A.; Qu, Z.; Wu, T. Well-balanced positivity preserving adaptive moving mesh central-upwind schemes for the Saint-Venant system. ESAIM Math. Model. Numer. Anal. 2022, 56, 1327–1360. [Google Scholar] [CrossRef]
- Wylie, E.B. Control of transient free-surface flow. J. Hydraul. Div. 1969, 95, 347–362. [Google Scholar] [CrossRef]
- Liu, F.; Feyen, J.; Malaterre, P.-O.; Baume, J.-P.; Kosuth, P. Development and evaluation of canal automation algorithm CLIS. J. Irrig. Drain. Eng. 1998, 124, 40–46. [Google Scholar] [CrossRef]
- Bautista, E.; Clemmens, A.J.; Strelkoff, T. Comparison of numerical procedures for gate stroking. J. Irrig. Drain. Eng. 1997, 123, 129–136. [Google Scholar] [CrossRef]
- Bautista, E.; Clemmens, A.J.; Strand, R.J. Salt River Project canal automation pilot project: Simulation tests. J. Irrig. Drain. Eng. 2006, 132, 143–152. [Google Scholar] [CrossRef] [Green Version]
- Mu, X.P.; Guo, X.C.; Li, W.X. Study on the hydraulic response sensitivity of unsteady flow in a conveyance channel to flow diversion. Hydropower J. 2010, 29, 96–101+112. (In Chinese) [Google Scholar]
- Shen, J.; Liu, Y.J. Genetic algorithm for parameter identification of water resources optimal allocation model. J. Wuhan Univ. 2002, 3, 13–16. (In Chinese) [Google Scholar]
- Li, K.B.; Shen, B.; Song, X.Y.; Hao, G.R. The application and improvement of TOPMODEL model in runoff simulation analysis in semi-humid areas. Hydraul. J. 2015, 46, 1453–1459. (In Chinese) [Google Scholar]
- Sablina, G.V.; Markova, V.A. Tuning a PID controller in a system with a delayed second-order object. Optoelectron. Instrum. Data Process. 2023, 58, 410–417. [Google Scholar] [CrossRef]
- Hashemy, S.M.; Monem, M.J.; Maestre, J.M.; Van Overloop, P.J. Application of an in-line storage strategy to improve the operational performance of main irrigation canals using model predictive control. J. Irrig. Drain. Eng. 2013, 139, 635–644. [Google Scholar] [CrossRef]
- Ooi, S.K.; Weyer, E. Control design for an irrigation channel from physical data. Control Eng. Pract. 2008, 16, 1132–1150. [Google Scholar] [CrossRef]
- Schuurmans, J. Open-channel flow model approximation for controller design. Appl. Math. Model. 1995, 19, 525–530. [Google Scholar] [CrossRef]
- Gupta, J.; van der Zaag, P. Interbasin water transfers and integrated water resources management: Where engineering, science and politics interlock. J. Phys. Chem. Earth Parts A/B/C 2008, 33, 28–40. [Google Scholar] [CrossRef]
- Vermuyten, E.; Meert, P.; Wolfs, V.; Willems, P. Model uncertainty reduction for real-time flood control by means of a flexible data assimilation approach and reduced conceptual models. J. Hydrol. 2018, 564, 490–500. [Google Scholar] [CrossRef]
- Liu, J.L.; Wang, Z.J.; Yang, Z.G.; Zhang, T. An adaptive predictive control algorithm for comprehensive dendritic canal systems. J. Irrig. Drain. Eng. 2023, 149, 04022046. [Google Scholar] [CrossRef]
- Nguyen, M.C.; Nguyen, N.T.; Bui, D.N.; Nguyen, T.L. Adaptive fuzzy Lyapunov-based model predictive control for parallel platform driving simulators. Trans. Inst. Meas. Control 2023, 45, 838–852. [Google Scholar] [CrossRef]
- Li, Z.Y.; Zhu, X.B.; Ye, Q.; Tian, S.T.; Xian, H.L. Single loop voltage control strategy based on model predictive control for NPC-UPS. J. Phys. Conf. Ser. 2023, 2418, 012045. [Google Scholar] [CrossRef]
- Zheng, H.Z.; Zhang, Z.; Wu, H.; Lei, X.H. Study on the daily optimal dispatching and economic operation of cascade pumping stations in water conveyance system. J. Hydraul. Eng. 2016, 47, 1558–1565. (In Chinese) [Google Scholar]
- Wen, X.; Li, J.Y.; Tan, Q.F.; Mao, Y.Z.; Ding, Z.Y.; Wang, H. Study on medium and long-term optimal scheduling of Jiangsu section of South-to-North Water Diversion Project. Hydropower J. 2022, 41, 65–77. (In Chinese) [Google Scholar]
- Anhui Water Conservancy and Hydropower Survey and Design Institute. Preliminary Design Report of the River Transfer Project from the Huai River; Anhui Water Conservancy and Hydropower Survey and Design Institute: Hefei, China, 2017. (In Chinese) [Google Scholar]
- Anhui Water Conservancy and Hydropower Survey and Design Institute. Feasibility Study Report of Water Transfer Project from the Yangtze River to Huai River; Anhui Water Conservancy and Hydropower Survey and Design Institute: Hefei, China, 2015. (In Chinese) [Google Scholar]
- Chen, Z.; Wang, H.; Qi, X. Pricing and Water Resource Allocation Scheme for the South-to-North Water Diversion Project in China. Water Resour Manag. 2013, 27, 1457–1472. [Google Scholar] [CrossRef]
- Liu, H.; Wang, H.; Liu, S.; Hu, C.; Ding, Y.; Zhang, J. Lattice Boltzmann method for the Saint–Venant equations. J. Hydrol. 2015, 524, 411–416. [Google Scholar] [CrossRef]
- Wang, Z.J.; Zheng, Z.L.; Xu, G.Y.; Jiang, G.Y. Optimal control of multi-cascade water conveyance channels based on linear quadratic form. Adv. Water Sci. 2018, 29, 383–389. (In Chinese) [Google Scholar]
- Kong, L.Z. Research on Normal Control and Emergency Regulation Algorithms for Large Open Channel Water Transmission Projects, D. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2019. (In Chinese). [Google Scholar]
- Kong, L.Z.; Wang, H.; Lei, X.H. Research on real-time control of open canal based on linear predictive control method. J. Hydraul. Eng. 2020, 51, 326–334. (In Chinese) [Google Scholar]
- Oh, J.; Bartos, M. Model predictive control of stormwater basins coupled with real-time data assimilation enhances flood and pollution control under uncertainty. Water Res. 2023, 235, 119825. [Google Scholar] [CrossRef]
- Tang, Y.; Zheng, G.; Zhang, S. Optimal control approaches of pumping stations to achieve energy efficiency and load shifting. Int. J. Electr. Power Energy Syst. 2014, 55, 572–580. [Google Scholar] [CrossRef]
- Sang, G.Q.; Zhang, S.H.; Zhang, L. Calculation method and application on operation efficiency of water transfer system with cascade pumping station based on time and space scale. J. Agric. Eng. 2017, 33, 67–75. [Google Scholar]
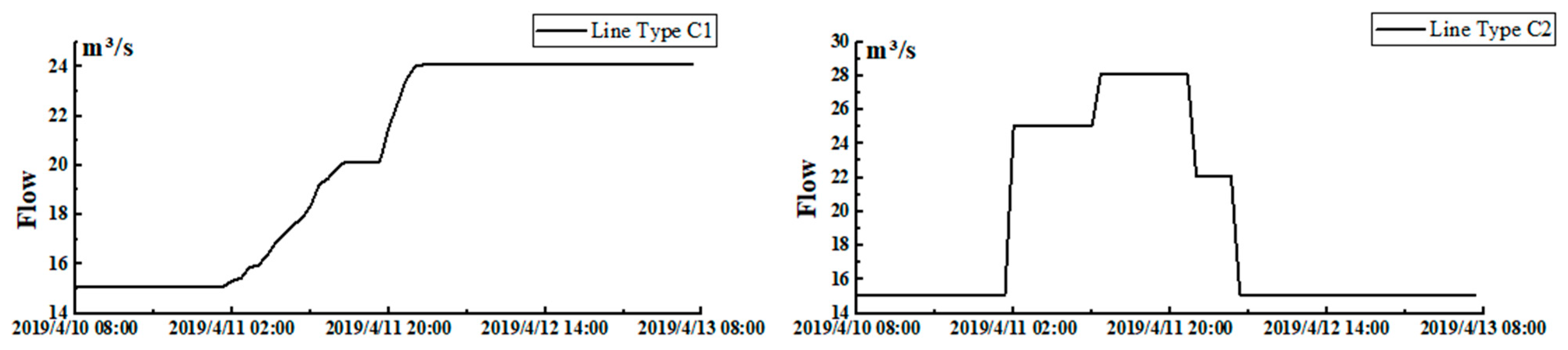
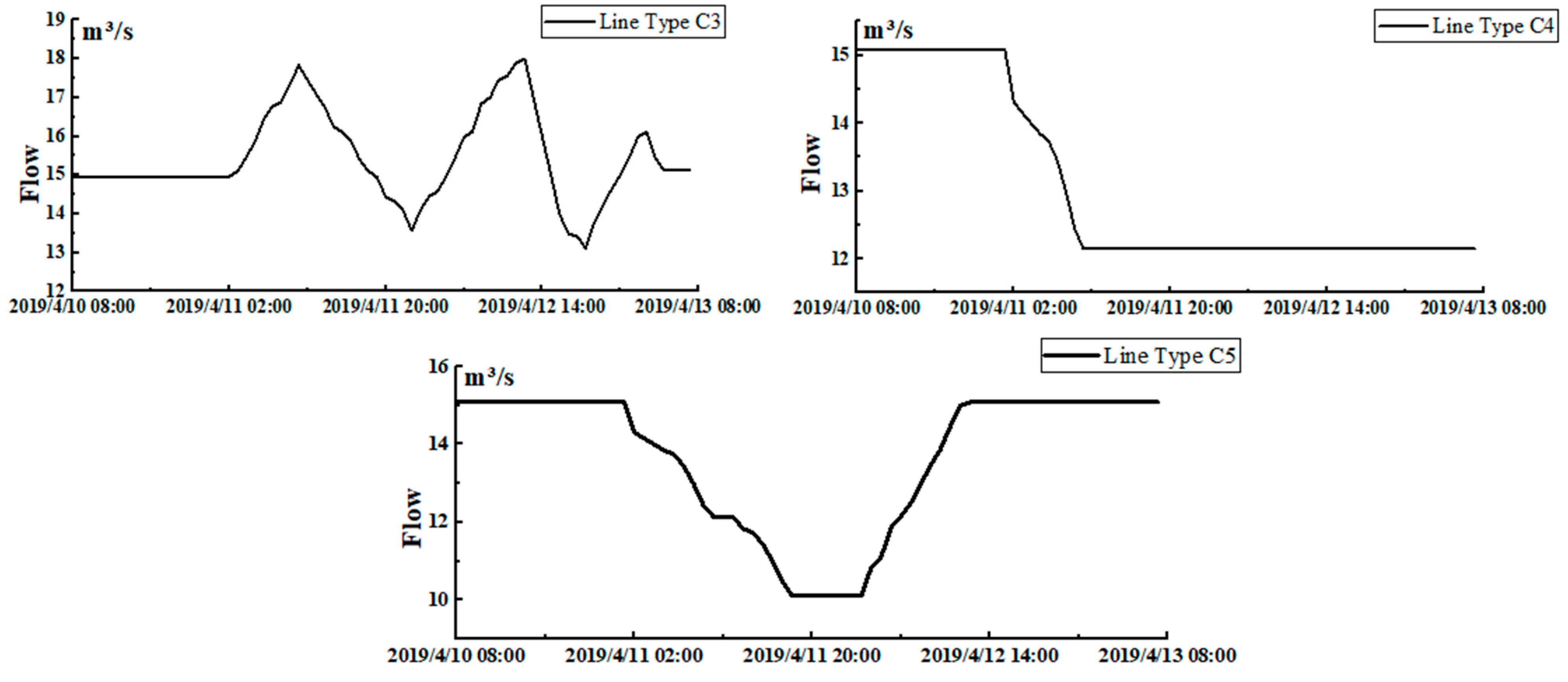


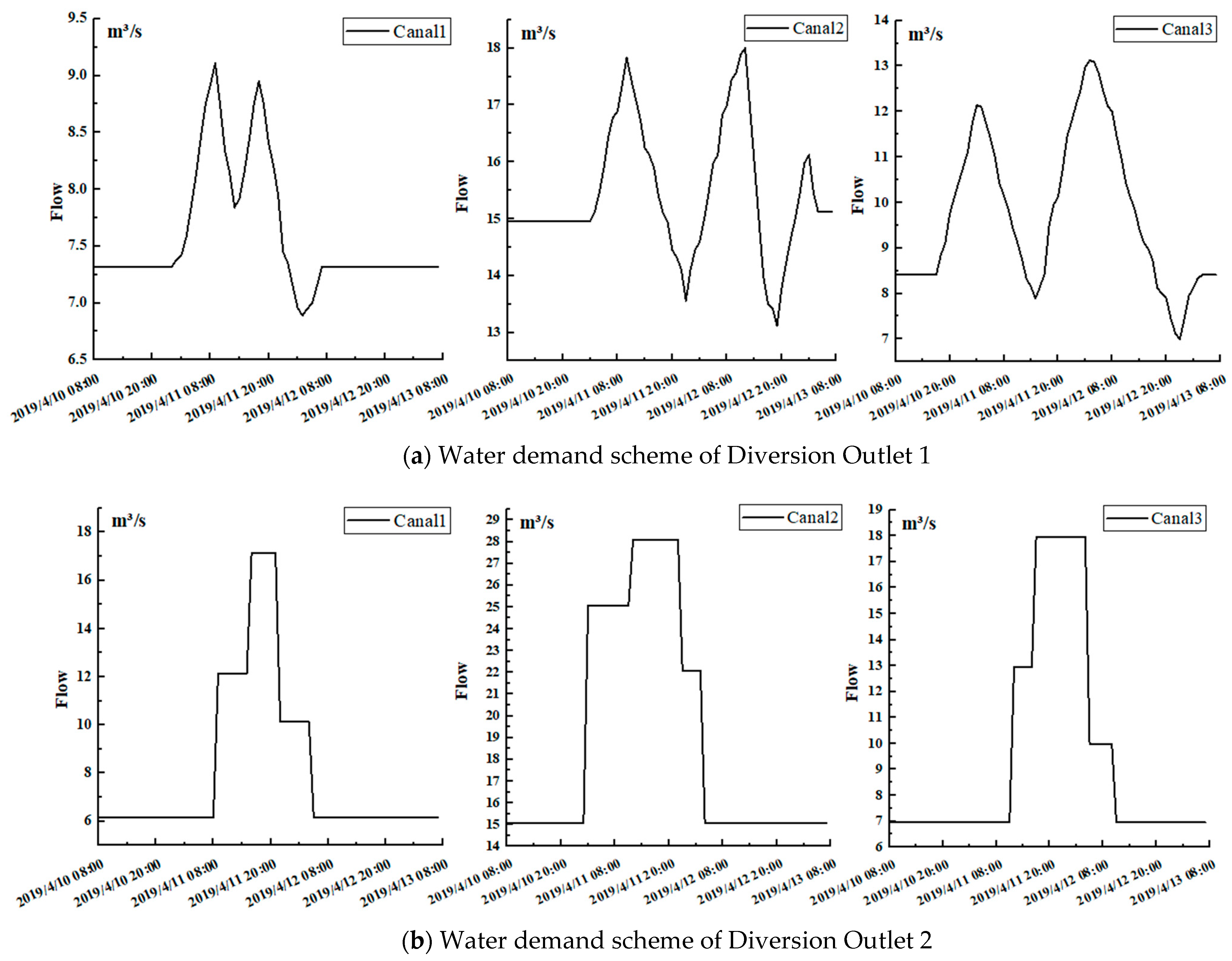

| Working Condition | Change Duration/h | Variation in Water Diversion Flow/ | Variation Rate of Water Diversion Flow/ | Channel Flow/ | The Variation in Water Diversion Accounting for the Canal Section |
|---|---|---|---|---|---|
| C1 | 17, 22 | 3, 9 | 0.0029, 0.0068 | 55, 99.5 | 5.17, 15.52 |
| C2 | 1, 1.5/ 1, 1.5 | 3, 5/6, 10 | 0.067, 0.11/0.026, 0.043 | 55, 99.5 | 10.34, 17.24/5.17, 8.62 |
| C3 | 8, 13/ 8, 21 | 1.79, 4.95/ 1.95, 6.12 | 0.0037, 0.0074/ 0.0027, 0.01 | 55, 99.5 | 3, 8.53/3.4, 10.6 |
| C4 | 6, 8 | 1.65, 2.93 | 0.0046, 0.0061 | 55, 99.5 | 2.84, 5.1 |
| C5 | 6, 11/ 4, 10 | 1.54, 4.98/ 1.54, 4.98 | 0.0043, 0.01/ 0.0054, 0.0064 | 55, 99.5 | 2.66, 8.59/2.66, 8.59 |
| Name | Target Water Level (m) | Minimum Upstream Water Level (m) | Maximum Upstream Water Level (m) | Minimum Downstream Water Level (m) | Maximum Downstream Water Level (m) | Canal Length (km) | Backwater Area | Duration of Delay (min) |
|---|---|---|---|---|---|---|---|---|
| Gate 1 | 5.17 | 5.16 | 5.18 | |||||
| Pump 1 | 3.60 | 5.80 | 6.00 | 9.40 | ||||
| Pump 2 | 5.80 | 10.7 | 17.40 | 20.80 | ||||
| Canal 1 | 20.59 | 4.061 | 68 | |||||
| Canal 2 | 18.27 | 1.424 | 29 | |||||
| Canal 3 | 27.83 | 3.484 | 50 |
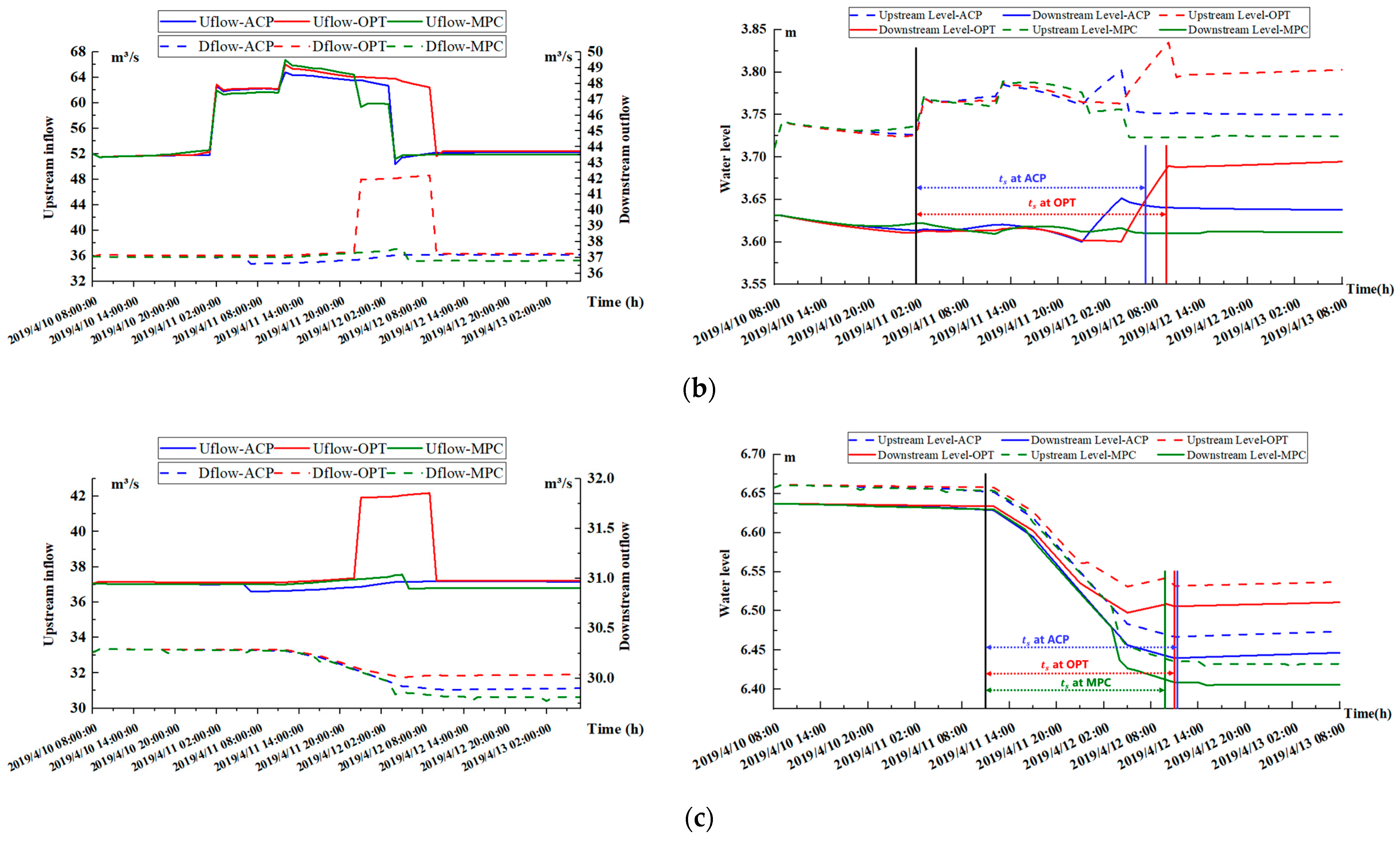
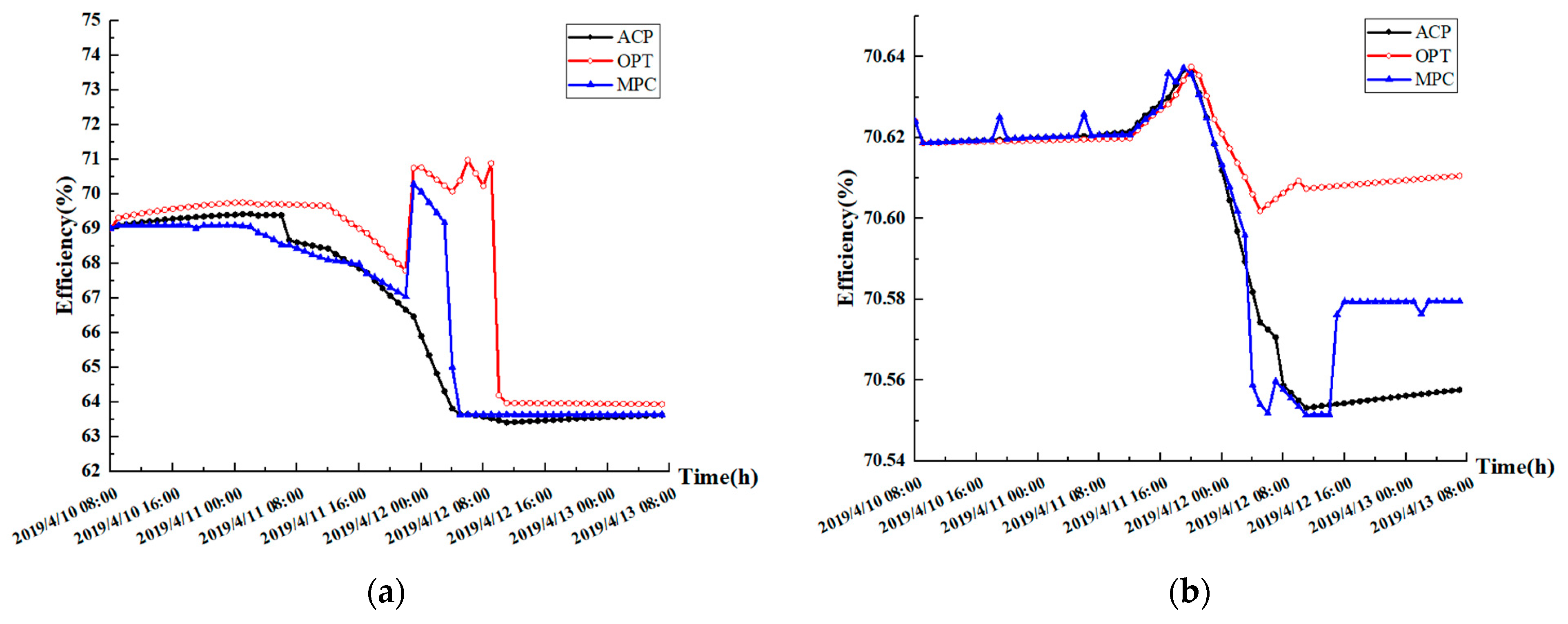
| Test Scenario | Evaluating Indicator | (%) | (h) | (%) | MAE (%) | IAE (%) | |
|---|---|---|---|---|---|---|---|
| A | ACP | Maximum | 86.10 | 54 | 80.55 | 0.004237925 | 0.002495729 |
| Average | 81.67 | 40 | 79.69 | ||||
| OPT | Maximum | 86.35 | 53 | 80.59 | 0.003429364 | 0.001884958 | |
| Average | 81.67 | 40 | 79.69 | ||||
| MPC | Maximum | 87.14 | 45 | 80.72 | 0.003203741 | 0.00165318 | |
| Average | 81.37 | 32.3 | 80.01 | ||||
| B | ACP | Maximum | 70.60 | 29 | 70.40 | 0.00315 | 0.008163 |
| Average | 68.50 | 25.7 | 69.70 | ||||
| OPT | Maximum | 75.70 | 32 | 71.60 | 0.011494 | 0.006578 | |
| Average | 69.60 | 26 | 70.10 | ||||
| MPC | Maximum | 70.60 | 23 | 70.60 | 0.016441 | 0.005329 | |
| Average | 68.60 | 11.7 | 69.70 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, P.; Wang, C.; Sun, J.; Lei, X.; Wang, H. Real-Time Control Operation Method of Water Diversion Project Based on River Diversion Disturbance. Water 2023, 15, 2793. https://doi.org/10.3390/w15152793
Jin P, Wang C, Sun J, Lei X, Wang H. Real-Time Control Operation Method of Water Diversion Project Based on River Diversion Disturbance. Water. 2023; 15(15):2793. https://doi.org/10.3390/w15152793
Chicago/Turabian StyleJin, Pengyu, Chao Wang, Jiahui Sun, Xiaohui Lei, and Hao Wang. 2023. "Real-Time Control Operation Method of Water Diversion Project Based on River Diversion Disturbance" Water 15, no. 15: 2793. https://doi.org/10.3390/w15152793





