Internal Flow Phenomena of Two-Way Contra-Rotating Axial-Flow Pump-Turbine with Various Numbers of Blades in Pump Mode
Abstract
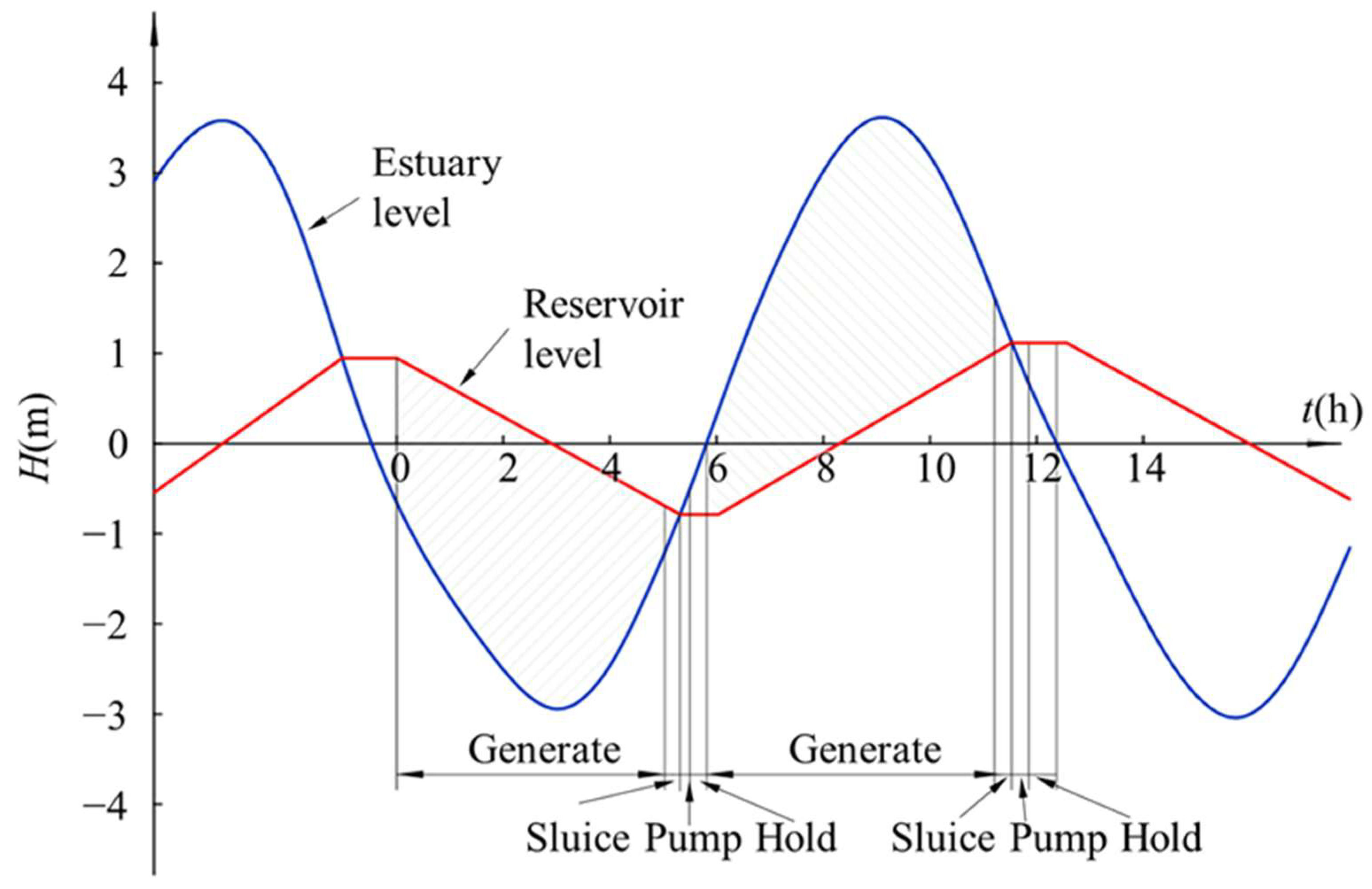
:1. Introduction
2. Materials and Methods
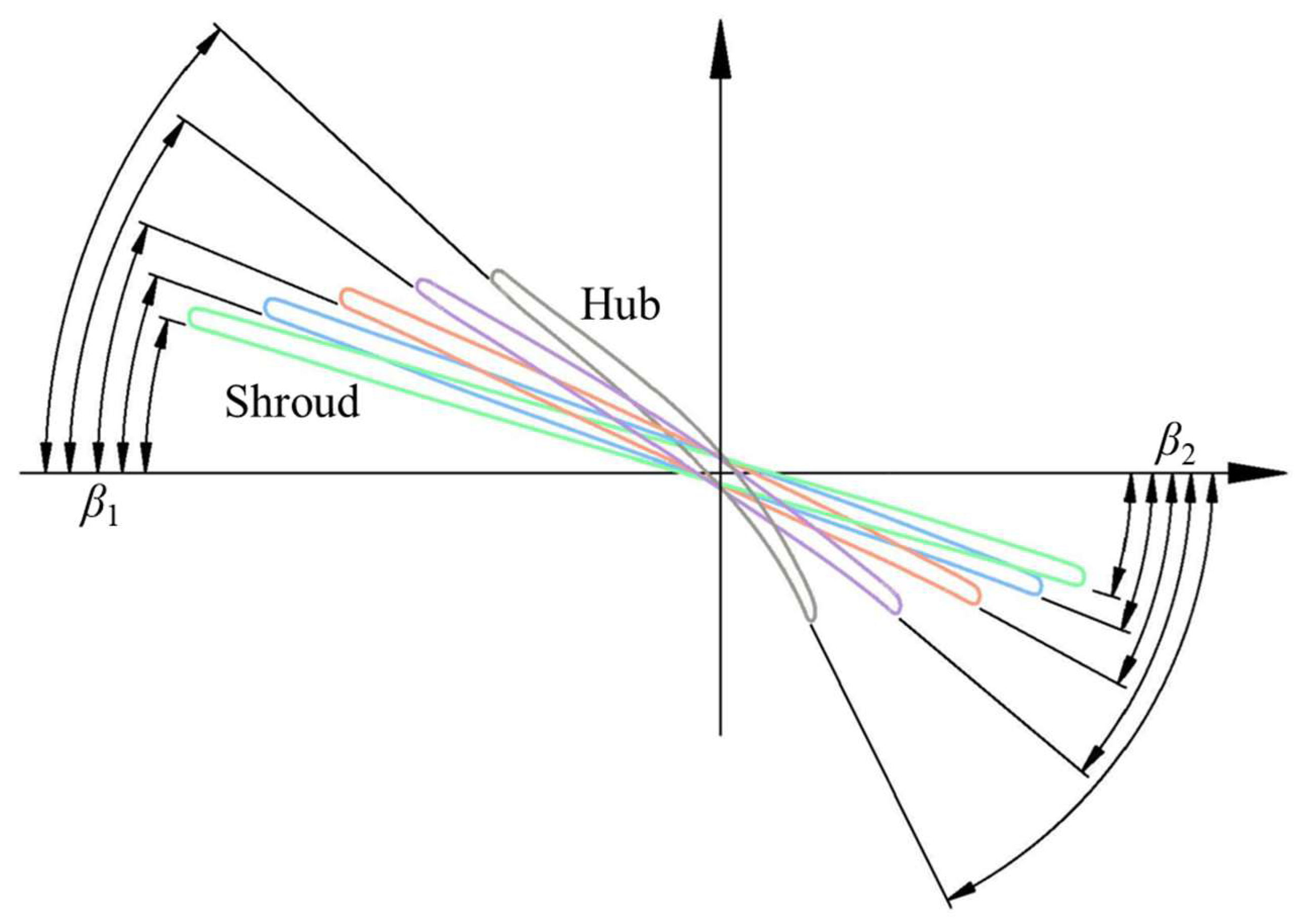
2.1. Pump Geometry
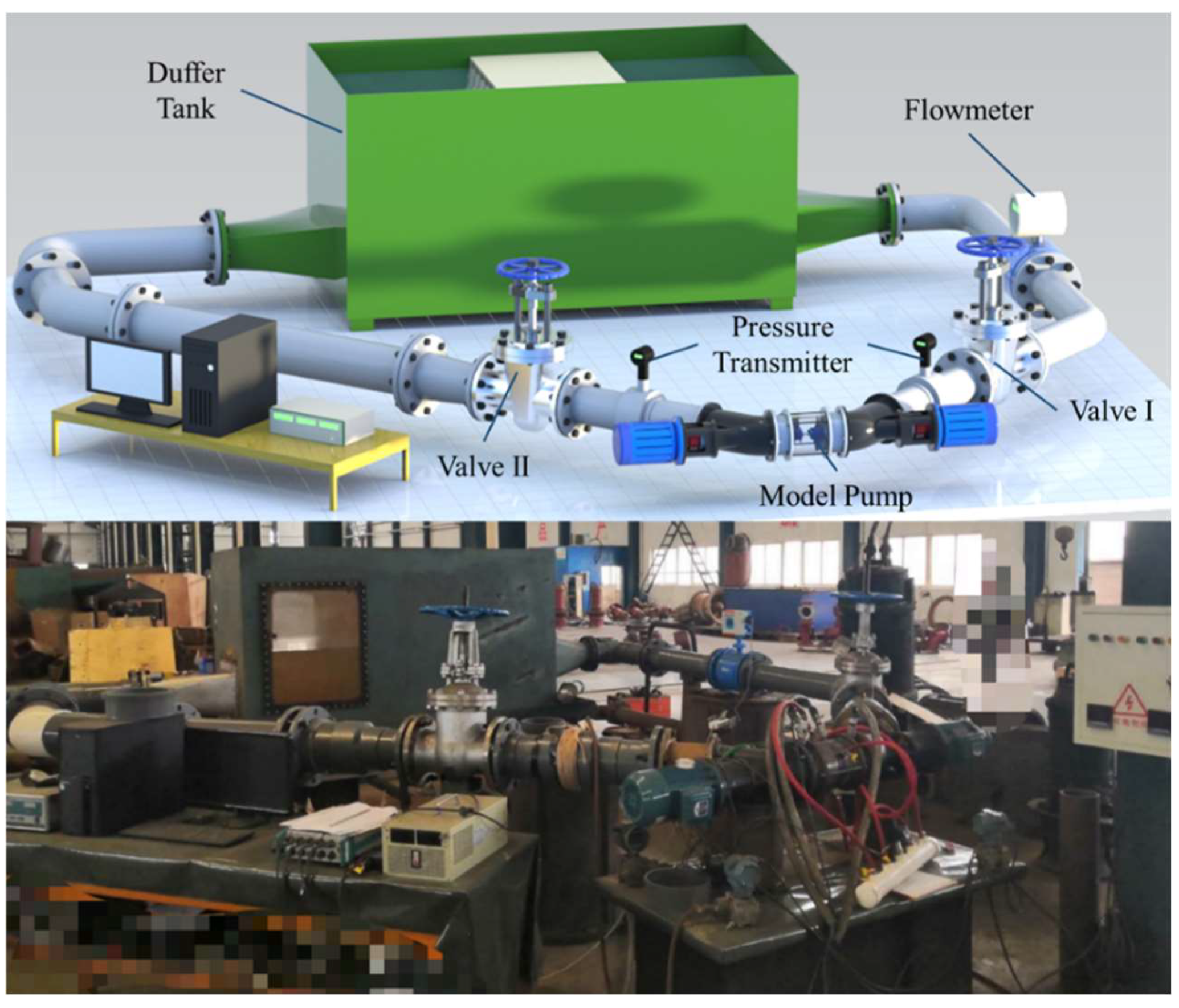
2.2. Experimental Methods
2.3. Numeral Methods
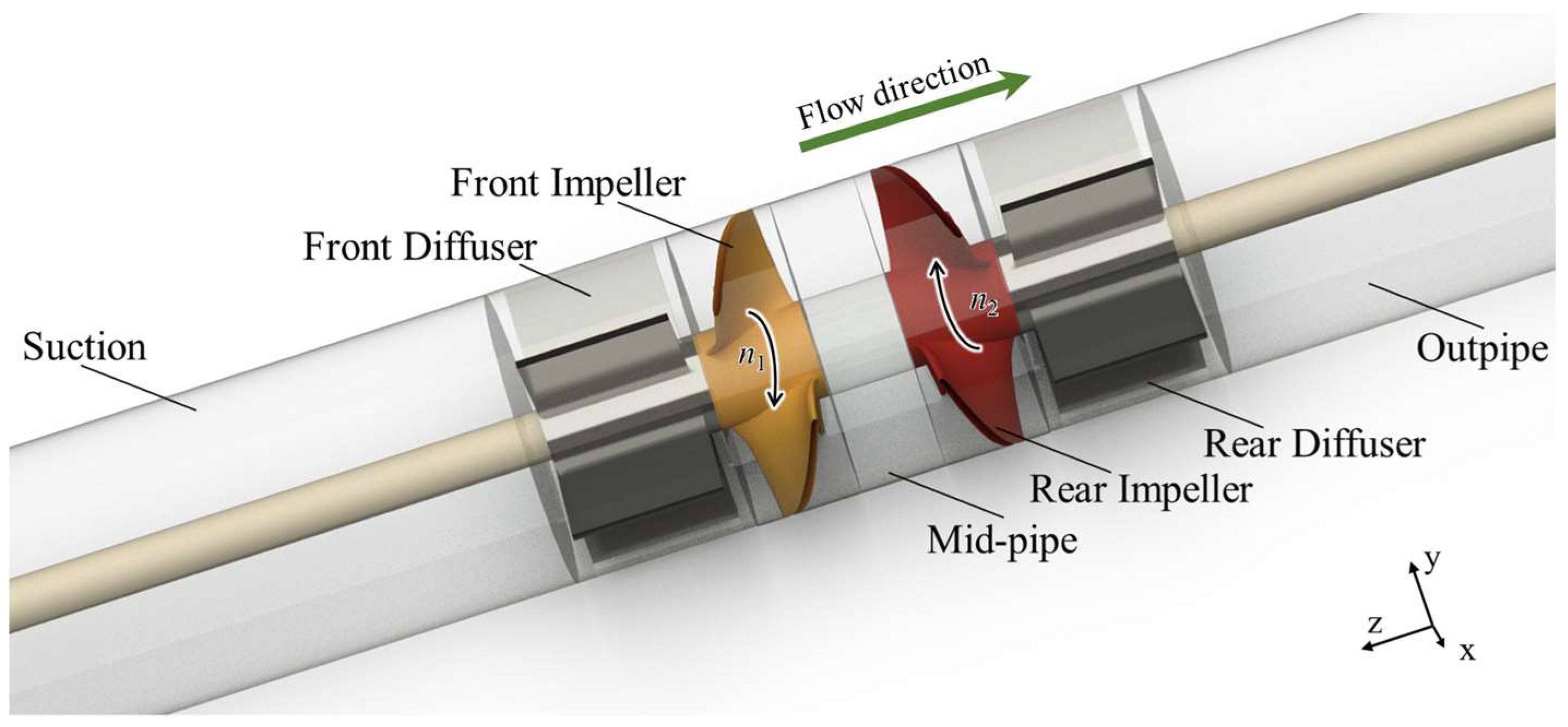
2.3.1. Hydraulic Model Components
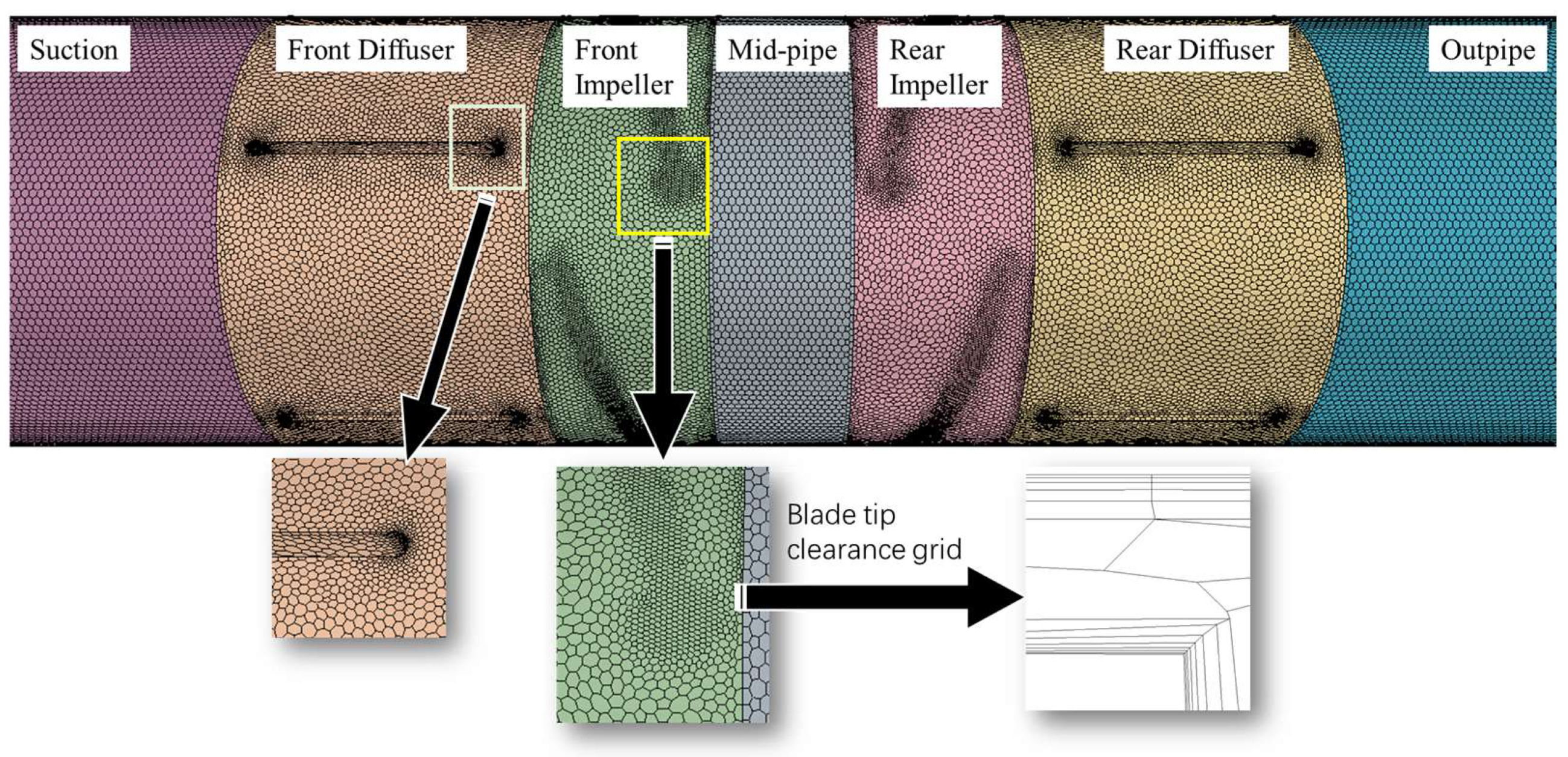
2.3.2. Meshing
2.3.3. Calculation Method and Boundary Conditions
2.3.4. Vorticity Equation
3. Results and Discussion
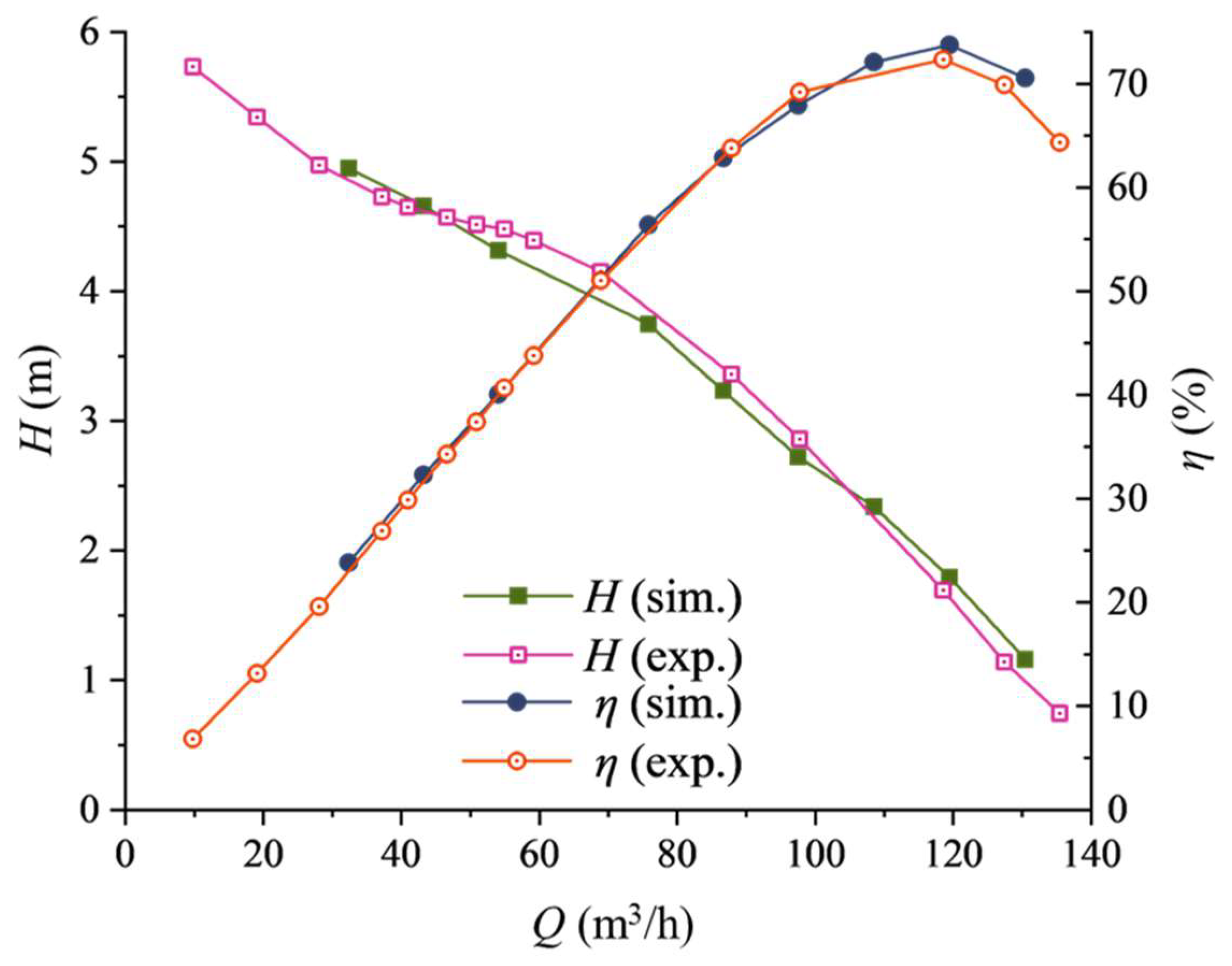
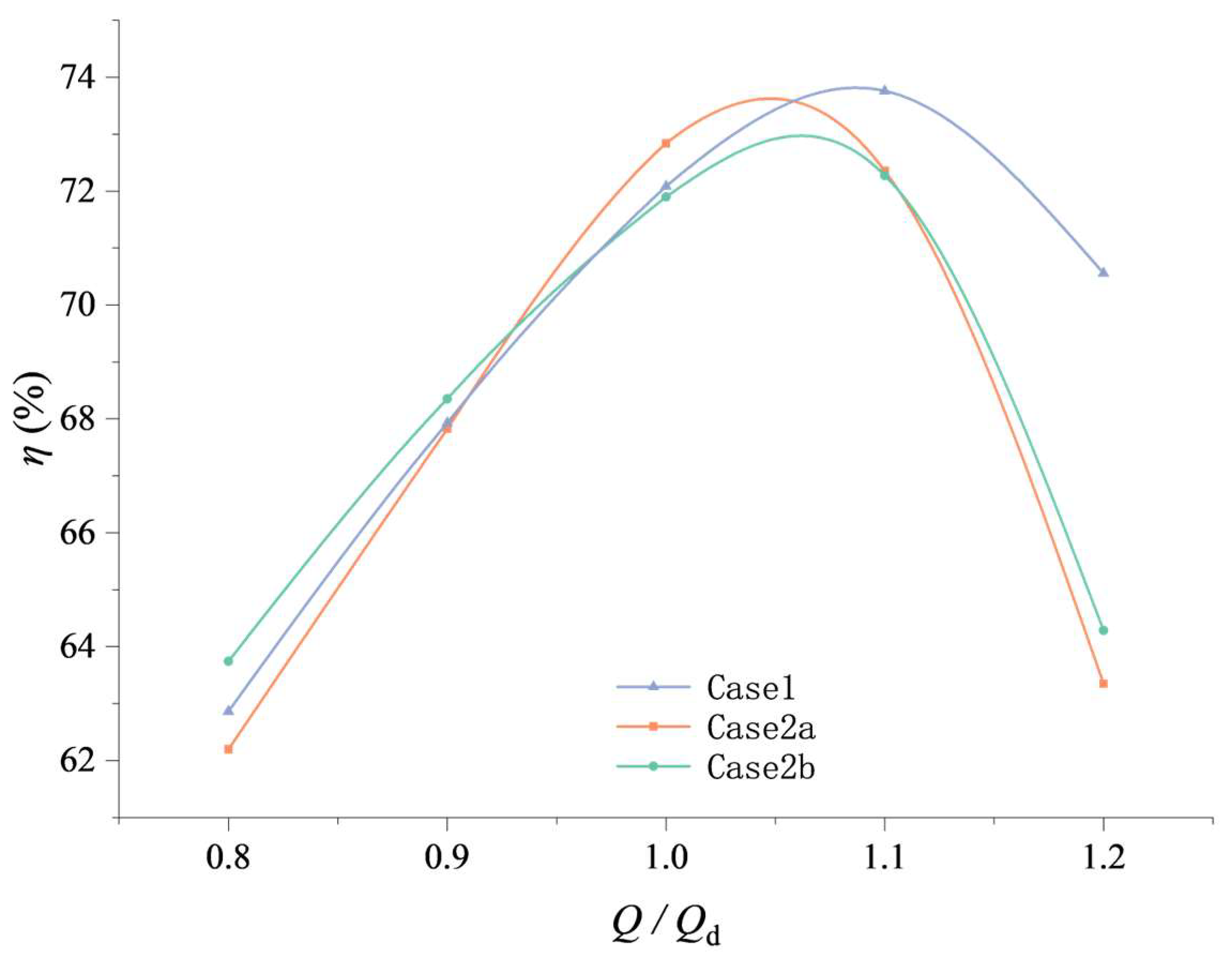
3.1. Performance Test
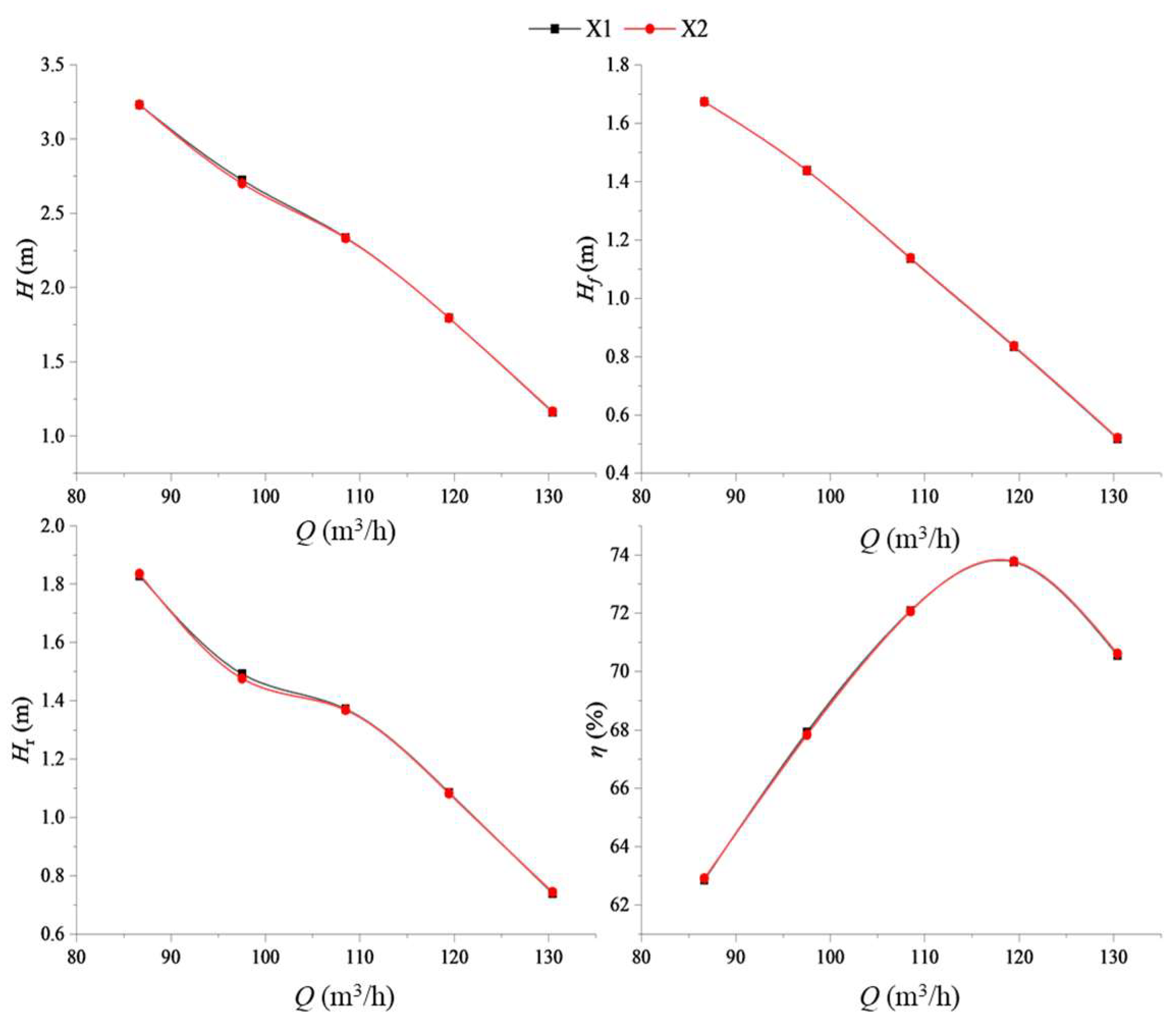
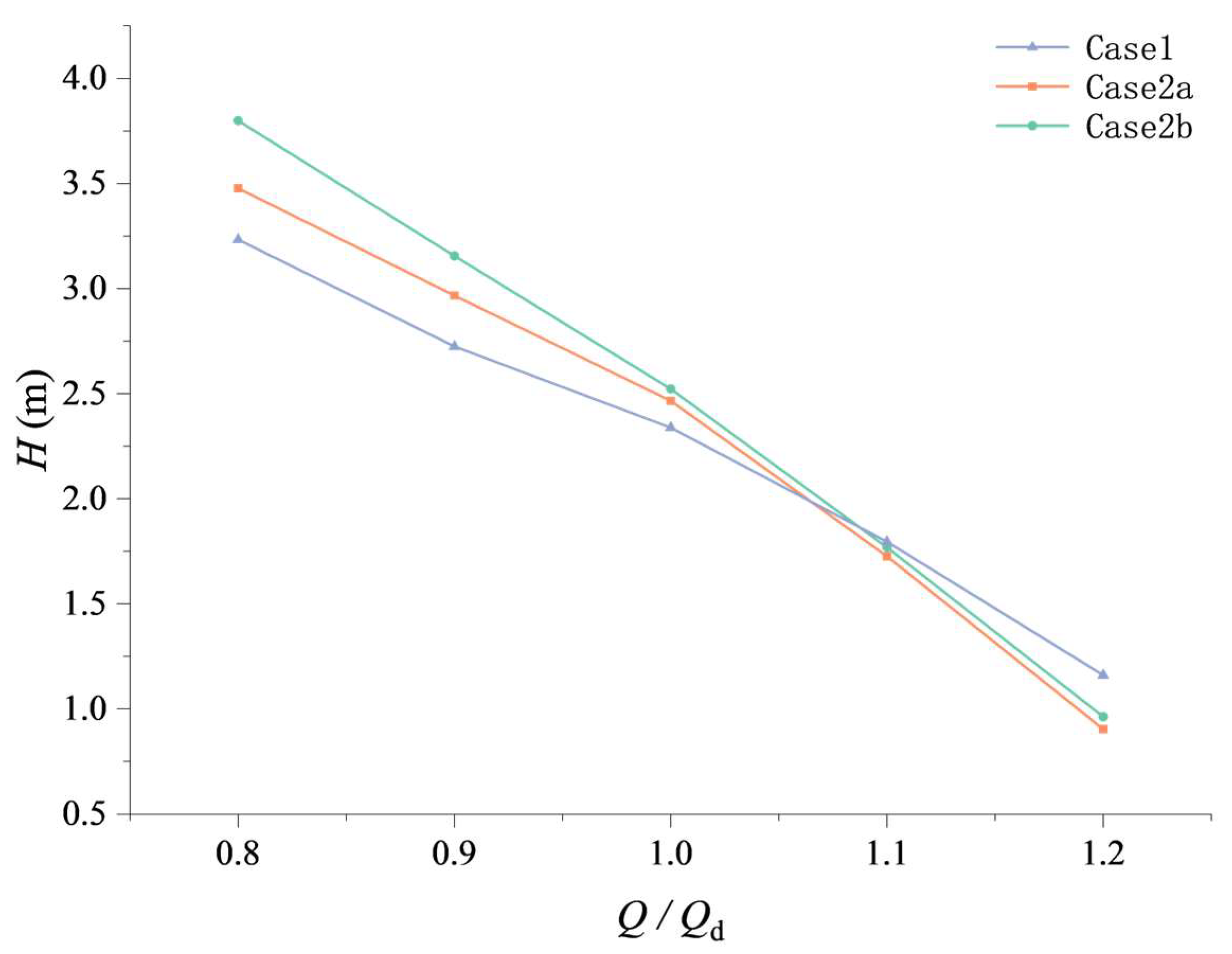
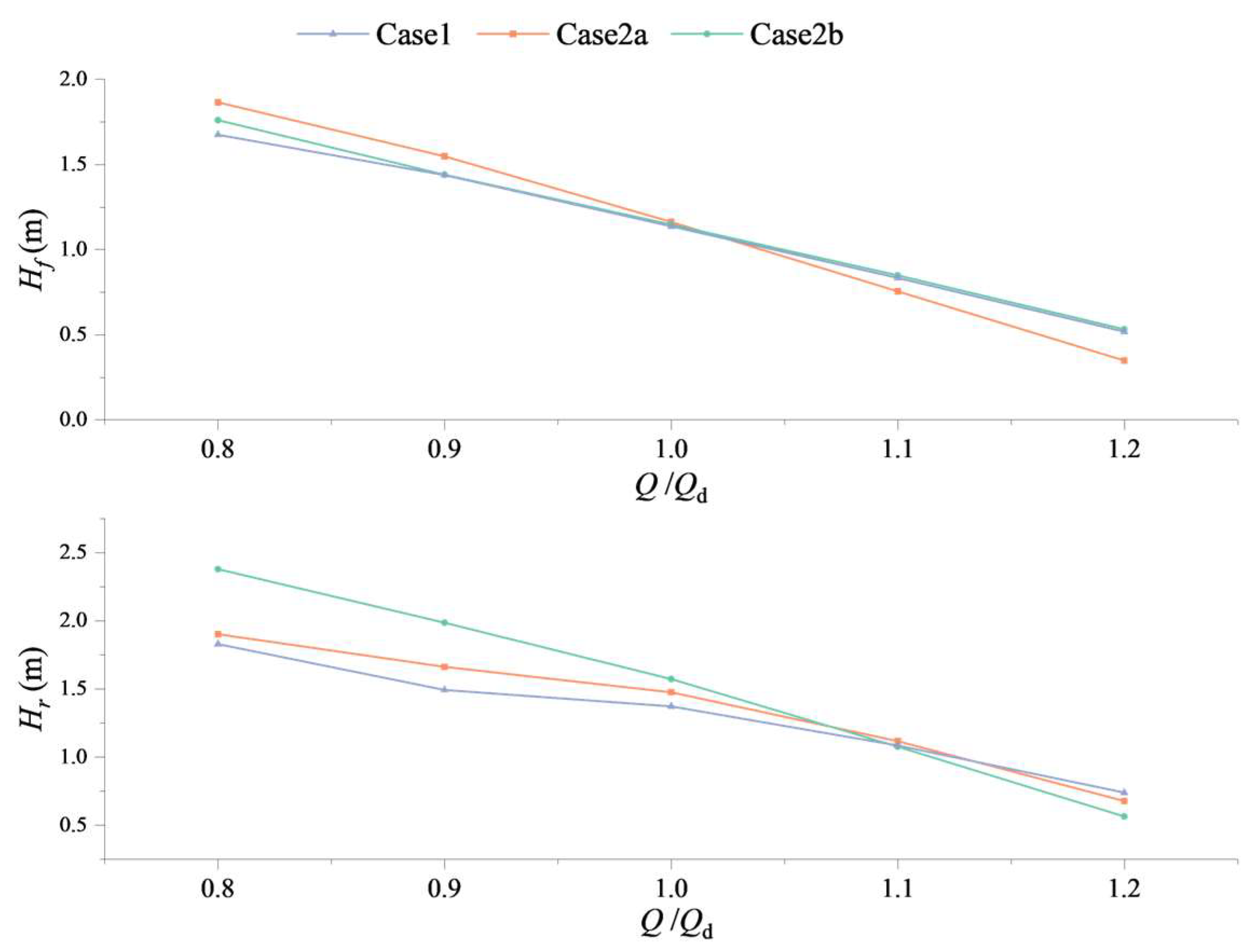
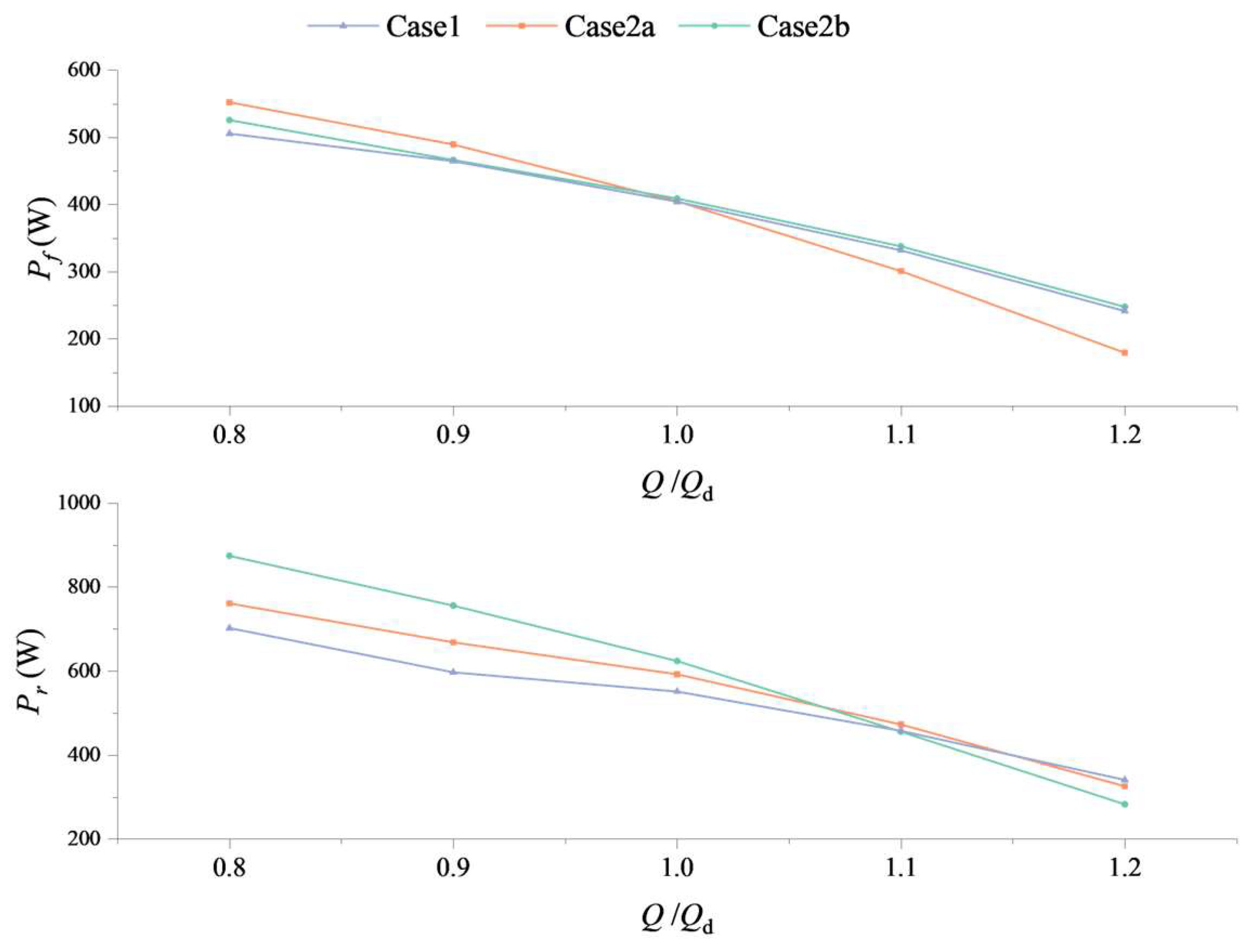
3.2. Research on the Various Numbers of Blades under Pump Mode
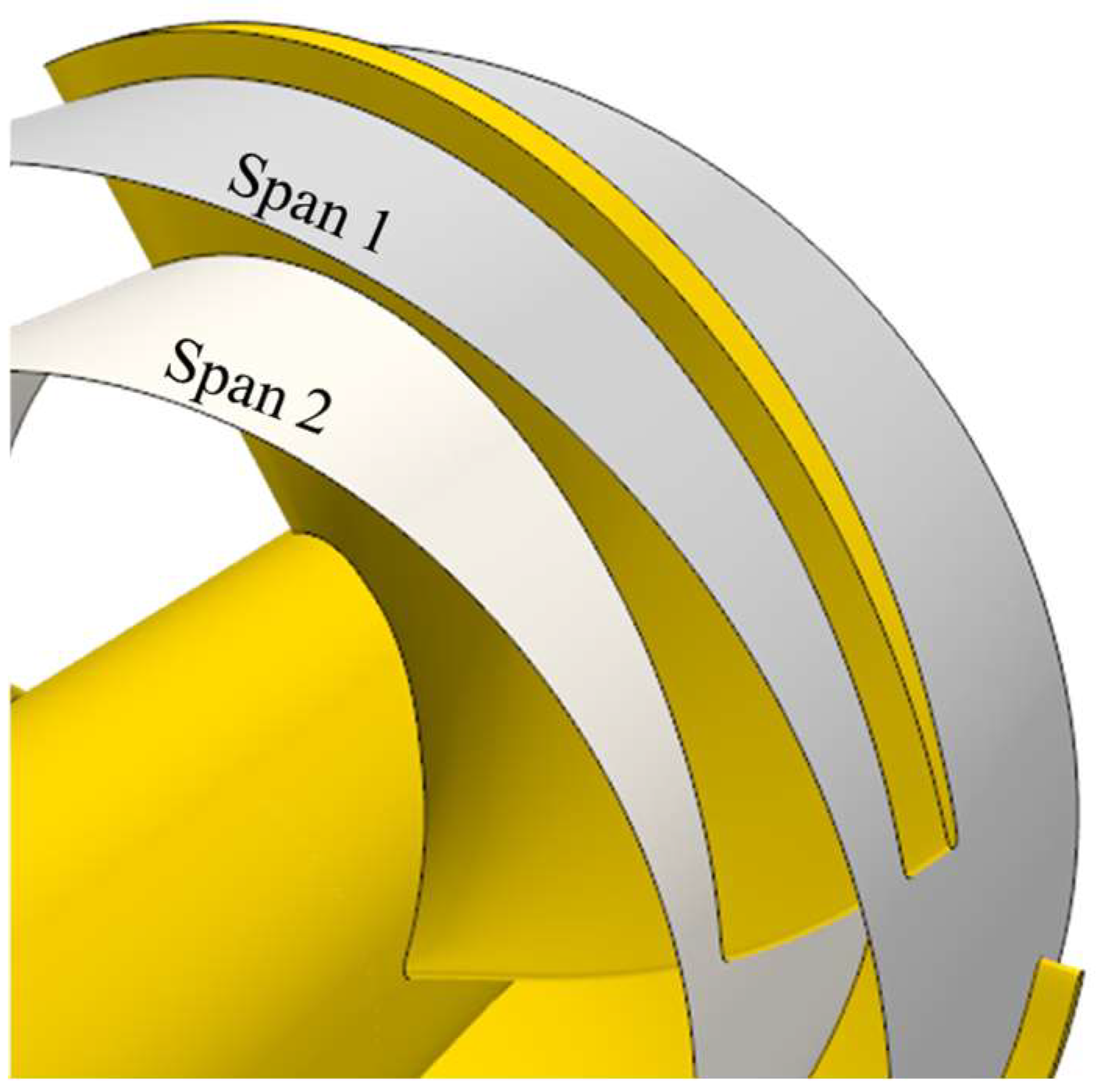
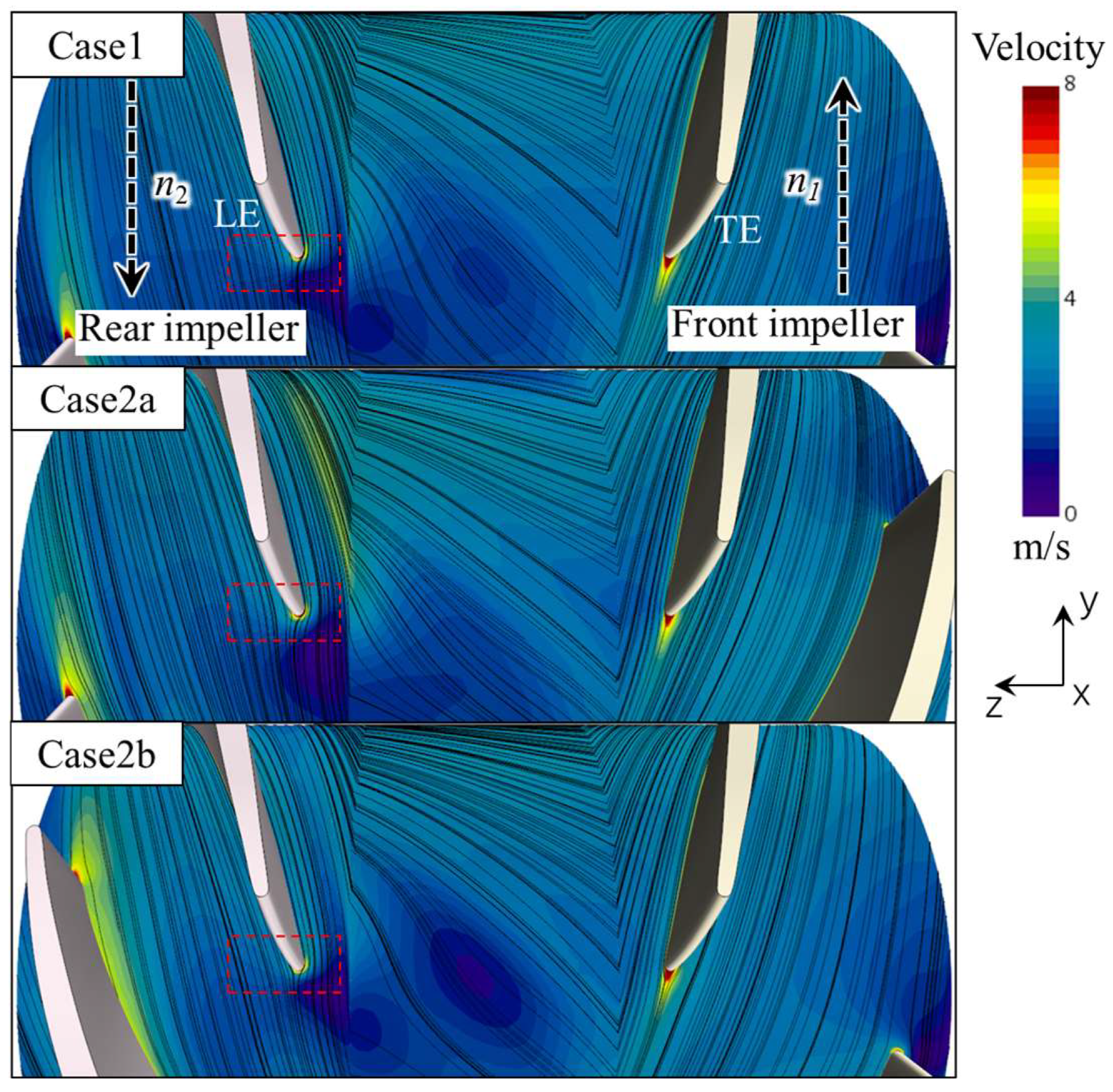
3.3. Streamline Analysis
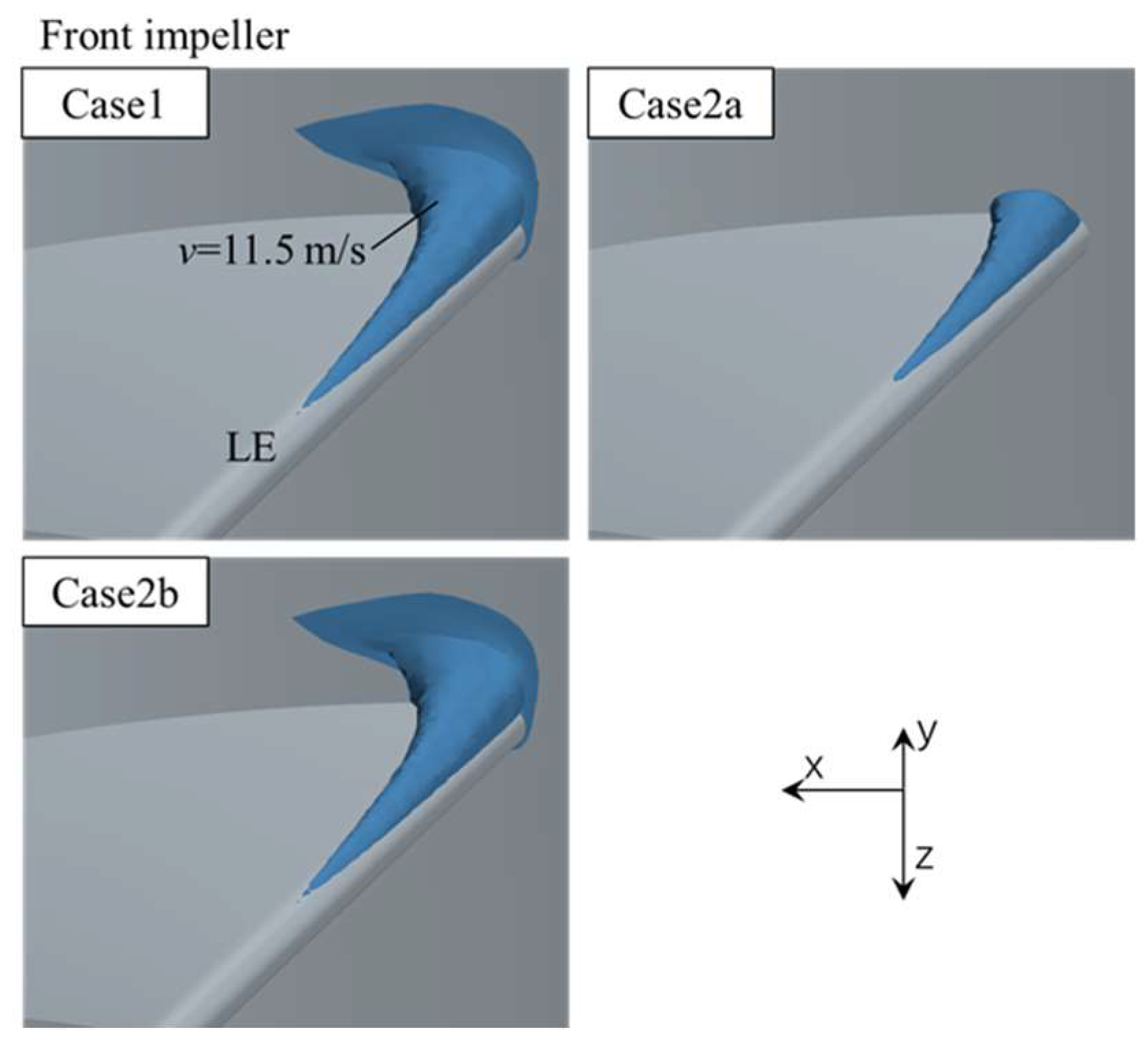
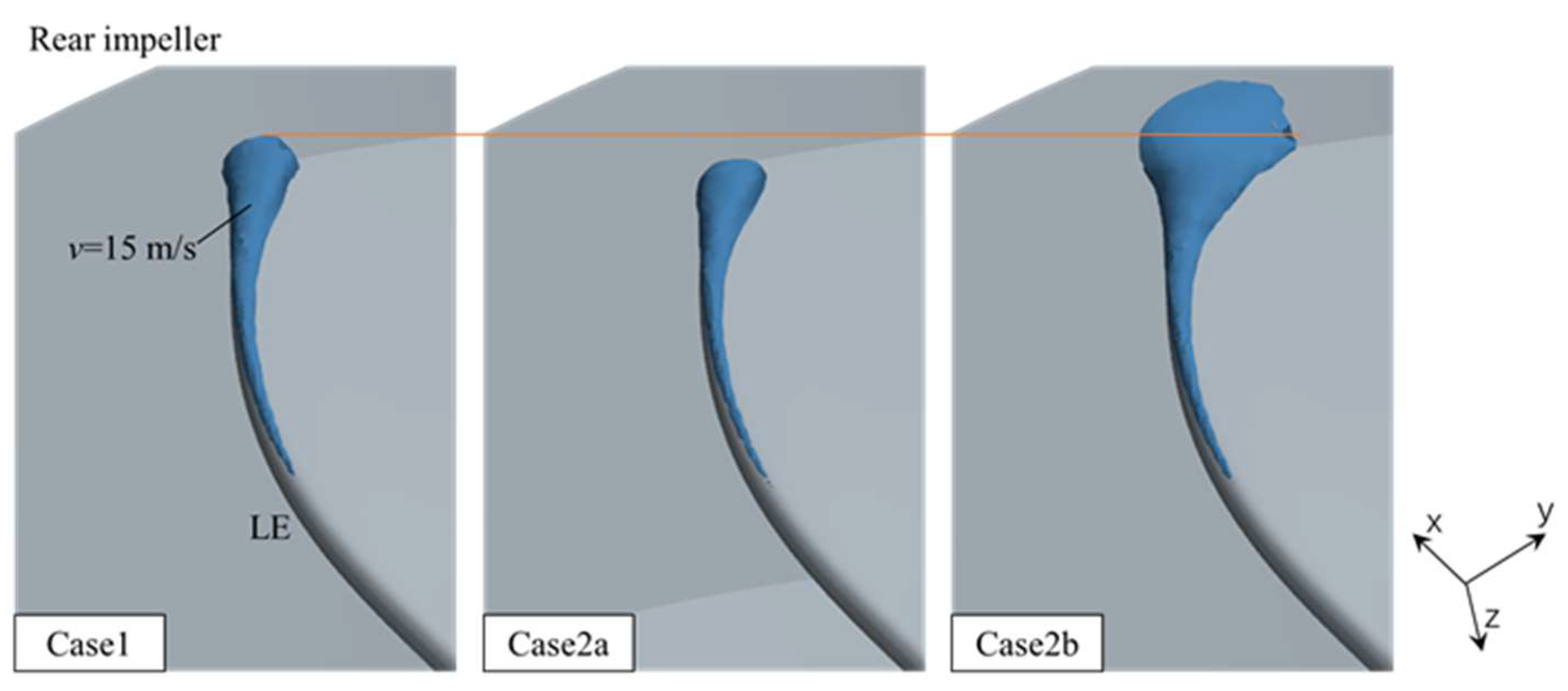
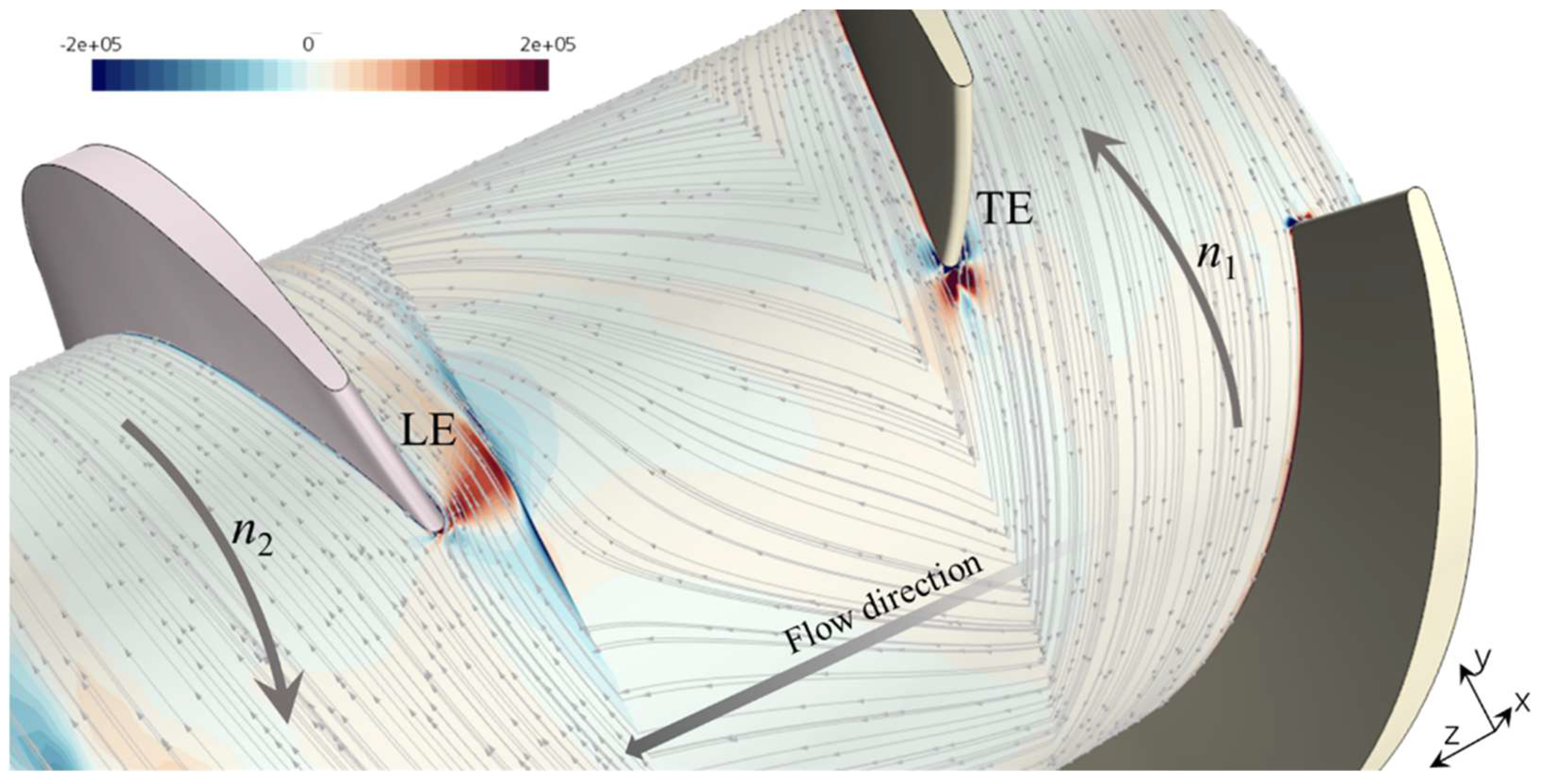
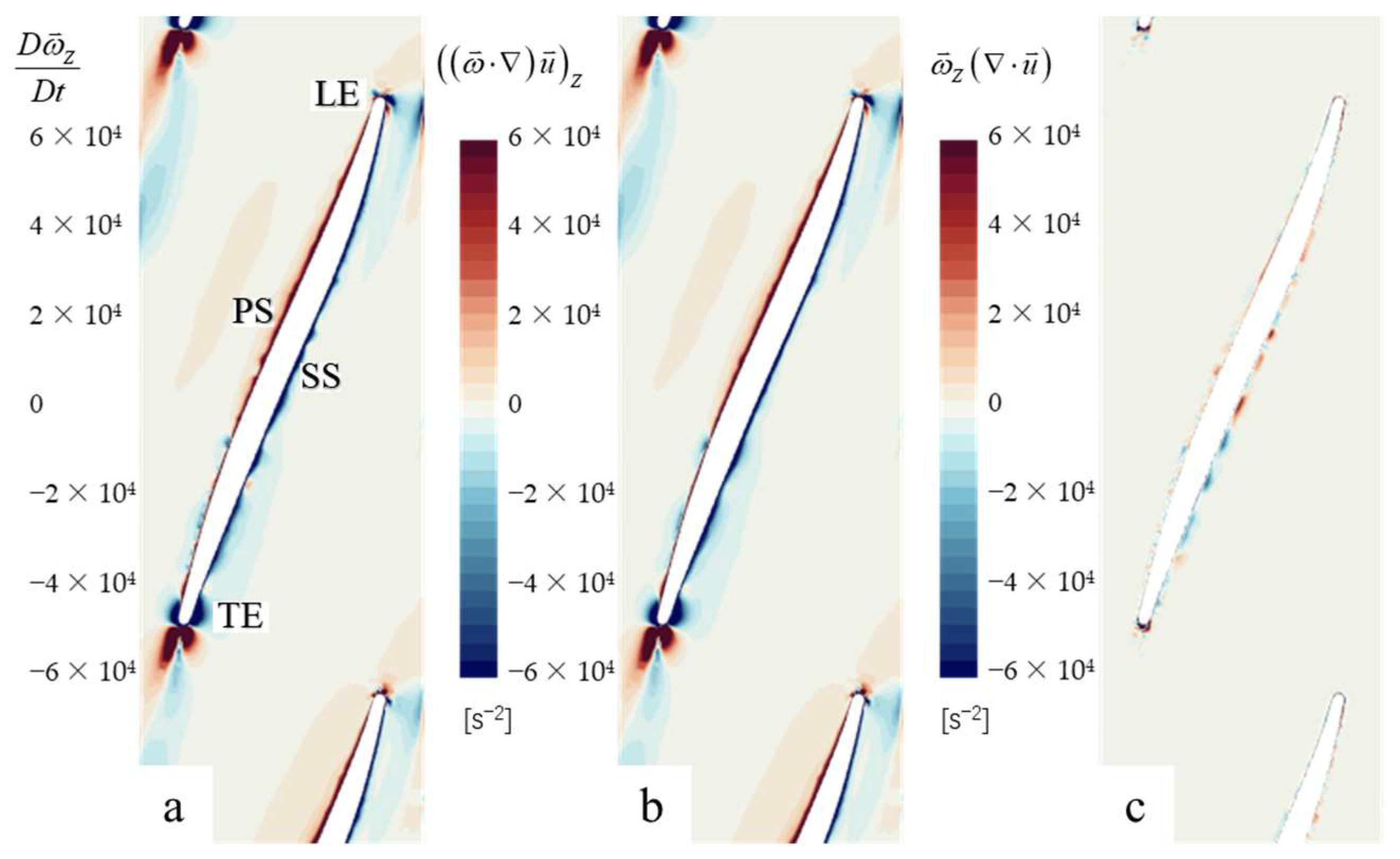
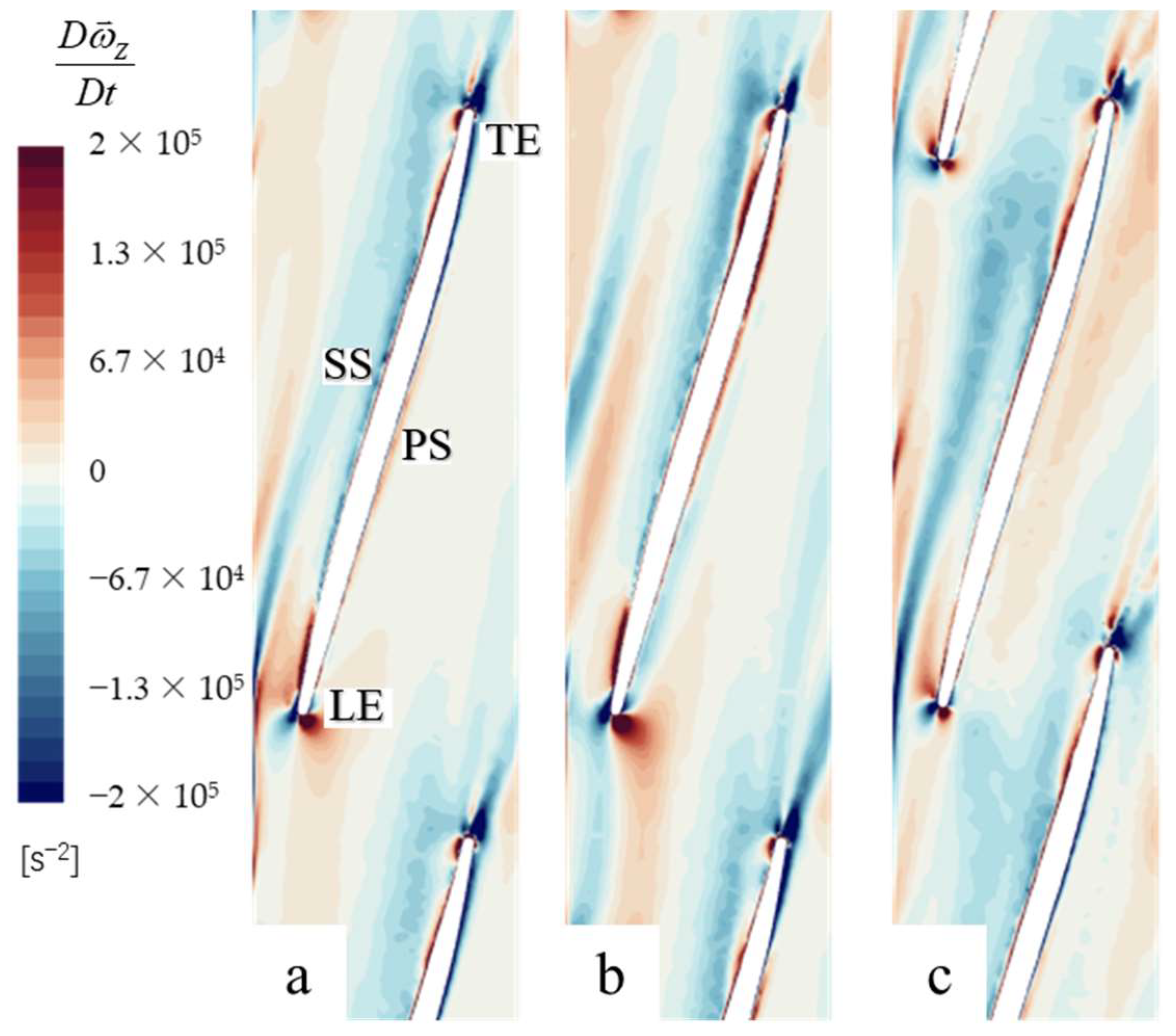
3.4. Vorticity Analysis
4. Conclusions
- An increase in the blade count of the impeller stage of a mixed-flow pump-turbine will result in a steeper Q–H curve. Increasing the blade count of the impeller stage has a greater effect on improving the head than increasing the blade count of the previous stage.
- With the increase in the number of impeller blades of a certain stage in the contra-rotating axial-flow pump, the high-efficiency point of the unit under pump mode will shift toward lower flow rates, and the high-efficiency region will also become narrower.
- Varying the number of blades will have an impact on the location of the LE water impact on the rear impeller, which in turn affects the contours of vorticity of the rear impeller near the LE.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sangiuliano, S.J. Community energy and emissions planning for tidal current turbines: A case study of the municipalities of the Southern Gulf Islands Region, British Columbia. Renew. Sustain. Energy Rev. 2017, 76, 1–8. [Google Scholar]
- Li, Y.; Lence, B.J.; Calisal, S.M. An integrated model for estimating energy cost of a tidal current turbine farm. Energy Convers. Manag. 2011, 52, 1677–1687. [Google Scholar]
- Qian, P.; Feng, B.; Liu, H.; Tian, X.; Si, Y.; Zhang, D. Review on configuration and control methods of tidal current turbines. Renew. Sustain. Energy Rev. 2019, 108, 125–139. [Google Scholar]
- Kim, K.; Ahmed, M.R.; Lee, Y. Efficiency improvement of a tidal current turbine utilizing a larger area of channel. Renew. Energy 2012, 48, 557–564. [Google Scholar]
- Charlier, R.H. A “sleeper” awakes: Tidal current power. Renew. Sustain. Energy Rev. 2003, 7, 515–529. [Google Scholar]
- Neill, S.P.; Angeloudis, A.; Robins, P.E.; Walkington, I.; Ward, S.L.; Masters, I.; Lewis, M.J.; Piano, M.; Avdis, A.; Piggot, M.D.; et al. Tidal range energy resource and optimization—Past perspectives and future challenges. Renew. Energy 2018, 127, 763–778. [Google Scholar]
- Angeloudis, A.; Falconer, R.A. Sensitivity of tidal lagoon and barrage hydrodynamic impacts and energy outputs to operational characteristics. Renew. Energy 2017, 114, 337–351. [Google Scholar]
- Prandle, D. Simple theory for designing tidal power schemes. Adv. Water Resour. 1984, 7, 21–27. [Google Scholar] [CrossRef]
- Burrows, R.; Walkington, I.; Yates, N.C.; Hedges, T.S.; Wolf, J.; Holt, J.T. The tidal range energy potential of the West Coast of the United Kingdom. Appl. Ocean. Res. 2009, 31, 229–238. [Google Scholar]
- Xia, J.; Falconer, R.A.; Lin, B. Impact of different tidal renewable energy projects on the hydrodynamic processes in the Severn Estuary, UK. Ocean. Model. 2010, 32, 86–104. [Google Scholar]
- Mackay, D.J.C.; Hafemeister, D. Sustainable Energy-Without the Hot Air. Am. J. Phys. 2010, 78, 222–223. [Google Scholar]
- Yates, N.; Walkington, I.; Burrows, R.; Wolf, J. The energy gains realisable through pumping for tidal range energy schemes. Renew. Energy 2013, 58, 79–84. [Google Scholar] [CrossRef]
- Harcourt, F.; Angeloudis, A.; Piggott, M.D. Utilising the flexible generation potential of tidal range power plants to optimise economic value. Appl. Energy 2019, 237, 873–884. [Google Scholar] [CrossRef]
- An, C.; Chen, Y.; Zhu, R.; Wang, X.; Yang, Y.; Shi, J. Internal Flow Phenomena of Two-Way Contra-Rotating Axial Flow Pump-Turbine in Pump Mode under Variable Speed. J. Appl. Fluid Mech. 2023, 16, 285–297. [Google Scholar] [CrossRef]
- Shih, T.-H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J.J.C. A new k-ϵ eddy viscosity model for high reynolds number turbulent flows. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- Rodi, W. Experience with two-layer models combining the k-epsilon model with a one-equation model near the wall. In Proceedings of the 29th Aerospace Sciences Meeting, Reno, NV, USA, 7–10 January 1991; p. 216. [Google Scholar]
- Wolfshtein, M. The velocity and temperature distribution in one-dimensional flow with turbulence augmentation and pressure gradient. Int. J. Heat Mass Transf. 1969, 12, 301–318. [Google Scholar] [CrossRef]
- Clarke, J.A.; Connor, G.; Grant, A.; Johnstone, C.; Ordonez Sanchez, S. Contra-rotating marine current turbines: Single point tethered floating system-stabilty and performance. In Proceedings of the 8th European Wave and Tidal Energy Conference, EWTEC 2009, Uppsala, Sweden, 7–11 September 2009. [Google Scholar]
- Clarke, J.A.; Connor, G.; Grant, A.; Johnstone, C. Design and testing of a contra-rotating tidal current turbine, Proceedings of the Institution of Mechanical Engineers. Part A J. Power Energy 2007, 221, 171–179. [Google Scholar] [CrossRef]
- Agostino, L.; Alfonsi, G.; Tafarojnoruz, A. Flow Pressure Behavior Downstream of Ski Jumps. Fluids 2020, 5, 14. [Google Scholar]
- Calomino, F.; Alfonsi, G.; Gaudio, R.; D’Ippolito, A.; Lauria, A.; Tafarojnoruz, A.; Artese, S. Experimental and Numerical Study of Free-Surface Flows in a Corrugated Pipe. Water 2018, 10, 638. [Google Scholar] [CrossRef]
- Mistry, C.; Pradeep, A. Effect of variation in axial spacing and rotor speed combinations on the performance of a high aspect ratio contra-rotating axial fan stage. Proc. Inst. Mech. Eng. Part A J. Power Energy 2013, 227, 138–146. [Google Scholar] [CrossRef]
- Mistry, C.; Pradeep, A. Influence of circumferential inflow distortion on the performance of a low speed, high aspect ratio contra rotating axial fan. J. Turbomach. 2014, 136, 071009. [Google Scholar] [CrossRef]
- Stuermer, A.W.; Akkermans, R.A. Validation of aerodynamic and aeroacoustic simulations of contra-rotating open rotors at low-speed flight conditions. In Proceedings of the 32nd AIAA Applied Aerodynamics Conference, Atlanta, GA, USA, 16–20 June 2014; The American Institute of Aeronautics and Astronautics: San Diego, CA, USA, 2014; pp. 16–20. [Google Scholar]
- Shih, T.-H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A New K-Epsilon Eddy Viscosity Model for High Reynolds Number Turbulent Flows: Model Development and Validation; NASA NTRS: Seattle, WA, USA, 1994. [Google Scholar]
- Jongen, T. Simulation and Modeling of Turbulent Incompressible Flows. Ph.D. Thesis, Swiss Federal Institute of Technology in Lausanne, Lausanne, Switzerland, 1998. [Google Scholar]
- Yu, Z. Numerical and Physical Investigation of Tip Leakage Vortex Cavitating Flows; Beijing Institute of Technology: Beijing, China, 2016. [Google Scholar]
- Li, X.; Chen, B.; Luo, X.; Zhu, Z. Effects of flow pattern on hydraulic performance and energy conversion characterisation in a centrifugal pump. Renew. Energy 2020, 151, 475–487. [Google Scholar] [CrossRef]
- Ali, T.; Lauria, A. Large eddy simulation of the turbulent flow field around a submerged pile within a scour hole under current condition. Coast. Eng. J. 2020, 62, 489–503. [Google Scholar]







| Design Parameters | Design Value |
|---|---|
| Flow Q (m3/h) | 108 |
| Head H (m) | 1.25 |
| Rotating speed n (r/min) | 1450 |
| Blade numbers | 3 |
| Impeller hub diameter (mm) | 48 |
| Impeller shroud diameter (mm) | 145 |
| Axial length of impeller blade outer flow line (mm) | 36 |
| Axial length of impeller blade inner flow line (mm) | 42 |
| Impeller blade thickness (mm) | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, C.; Chen, Y.; Fu, Q.; Zhu, R. Internal Flow Phenomena of Two-Way Contra-Rotating Axial-Flow Pump-Turbine with Various Numbers of Blades in Pump Mode. Water 2023, 15, 3236. https://doi.org/10.3390/w15183236
An C, Chen Y, Fu Q, Zhu R. Internal Flow Phenomena of Two-Way Contra-Rotating Axial-Flow Pump-Turbine with Various Numbers of Blades in Pump Mode. Water. 2023; 15(18):3236. https://doi.org/10.3390/w15183236
Chicago/Turabian StyleAn, Ce, Yiming Chen, Qiang Fu, and Rongsheng Zhu. 2023. "Internal Flow Phenomena of Two-Way Contra-Rotating Axial-Flow Pump-Turbine with Various Numbers of Blades in Pump Mode" Water 15, no. 18: 3236. https://doi.org/10.3390/w15183236












