A Non-Stationarity Analysis of Annual Maximum Floods: A Case Study of Campaspe River Basin, Australia
Abstract
:1. Introduction
2. Study Area and Data
3. Methodology
- (1)
- The AMF trend analysis using the MK test.
- (2)
- The AMF change point analysis using the Pettitt test.
- (3)
- The stationary and non-stationary flood frequency analysis.
3.1. AMF Trend Analysis Using MK Test
3.2. AMF Change Point Analysis Using Pettitt Test
3.3. Stationary and Non-Stationary Flood Frequency Analysis
3.3.1. Stationary Flood Frequency Analysis
3.3.2. Non-Stationary Flood Frequency Analysis
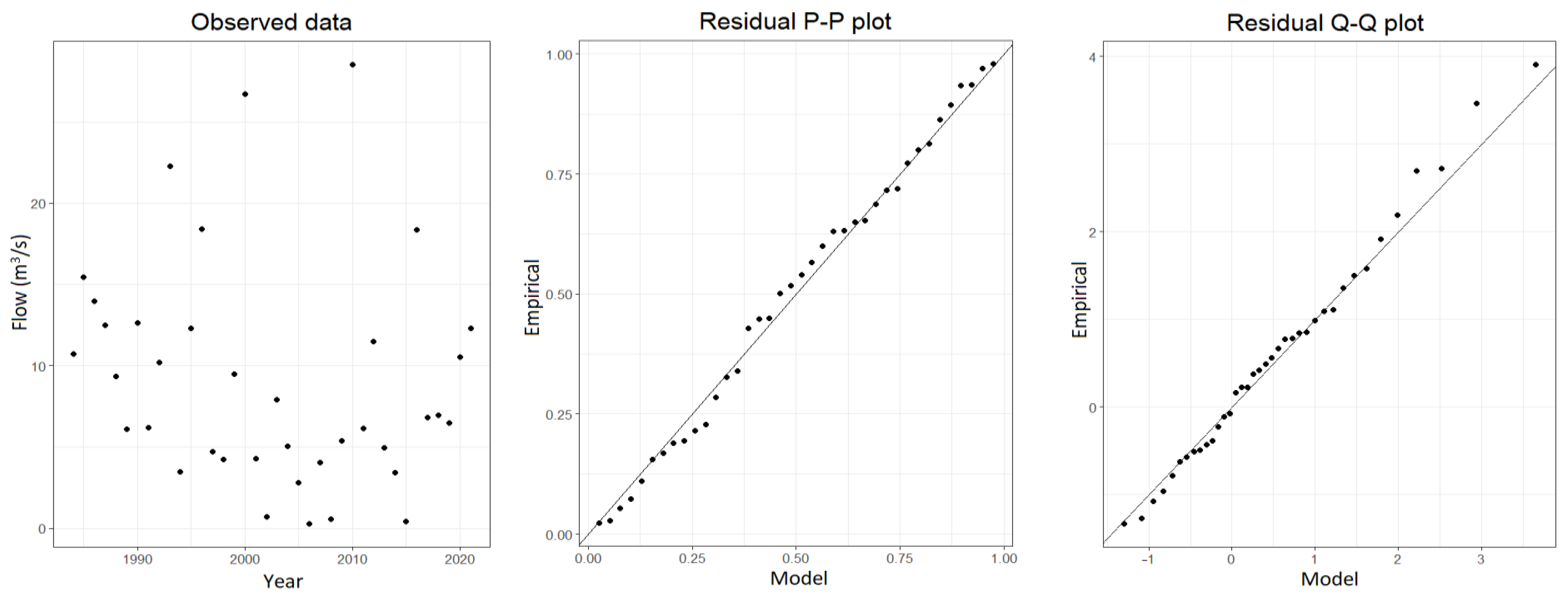
3.3.3. Model Selection Process
Statistical Methods
Graphical Methods
3.3.4. Uncertainty
4. Results and Discussion
4.1. AMF Trend Analysis
4.2. AMF Change Point Analysis
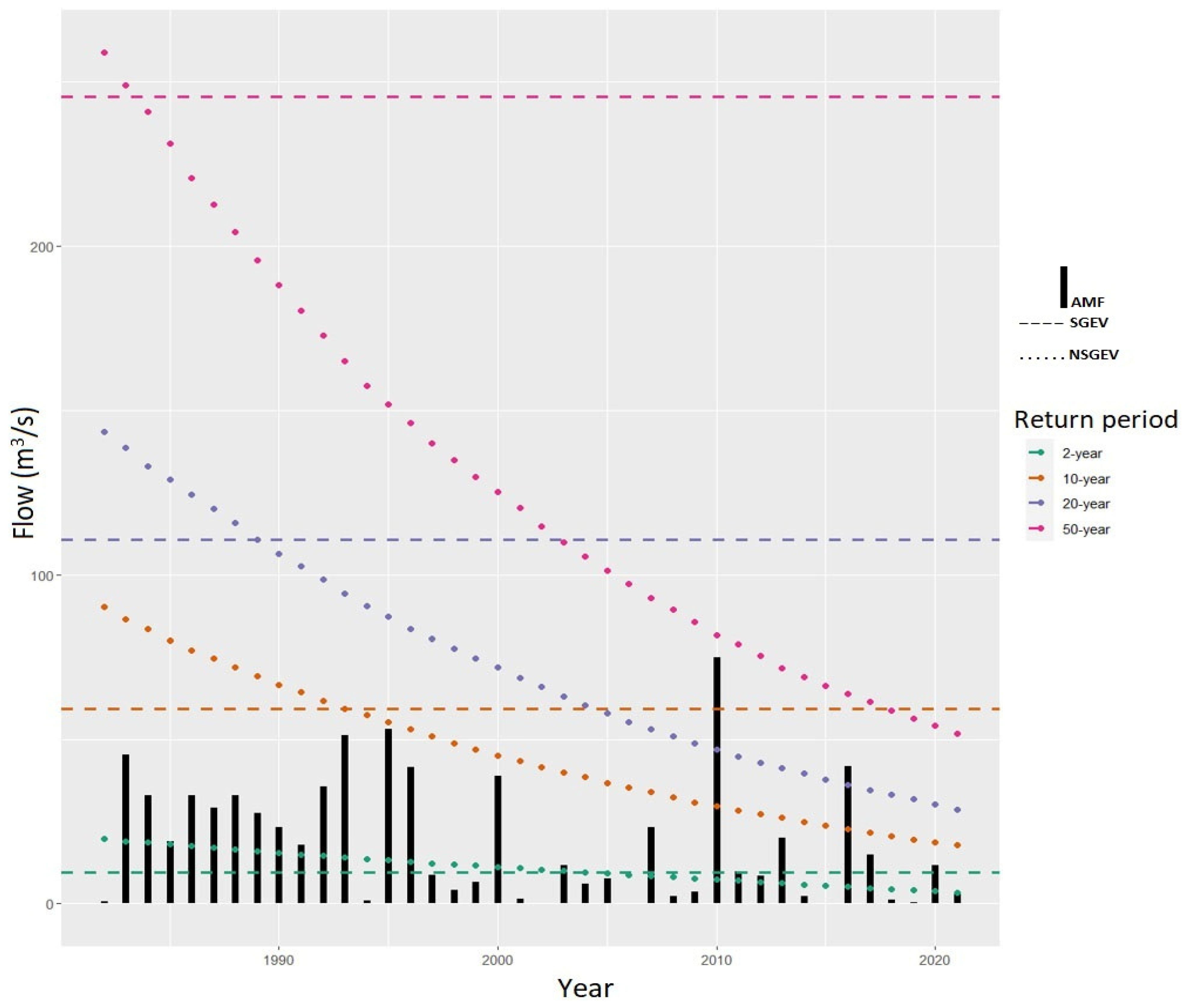
4.3. Stationary and Non-Stationary Flood Frequency Analysis
5. Conclusions
- Statistically significant decreasing trends (at 0.01 and 0.05 significance levels) in AMFs were detected regarding almost all stations in Campaspe River Basin.
- The year 1996 was identified as the statistically significant change point at almost all stations.
- Non-stationary GEV models had a time covariate that outperformed the stationary counterparts for two stations (Stations 406235 and 406250).
- The difference between the design floods of SGEV and NSGEV is particularly important for the NSGEV15 model with time-varying location and scale parameters.
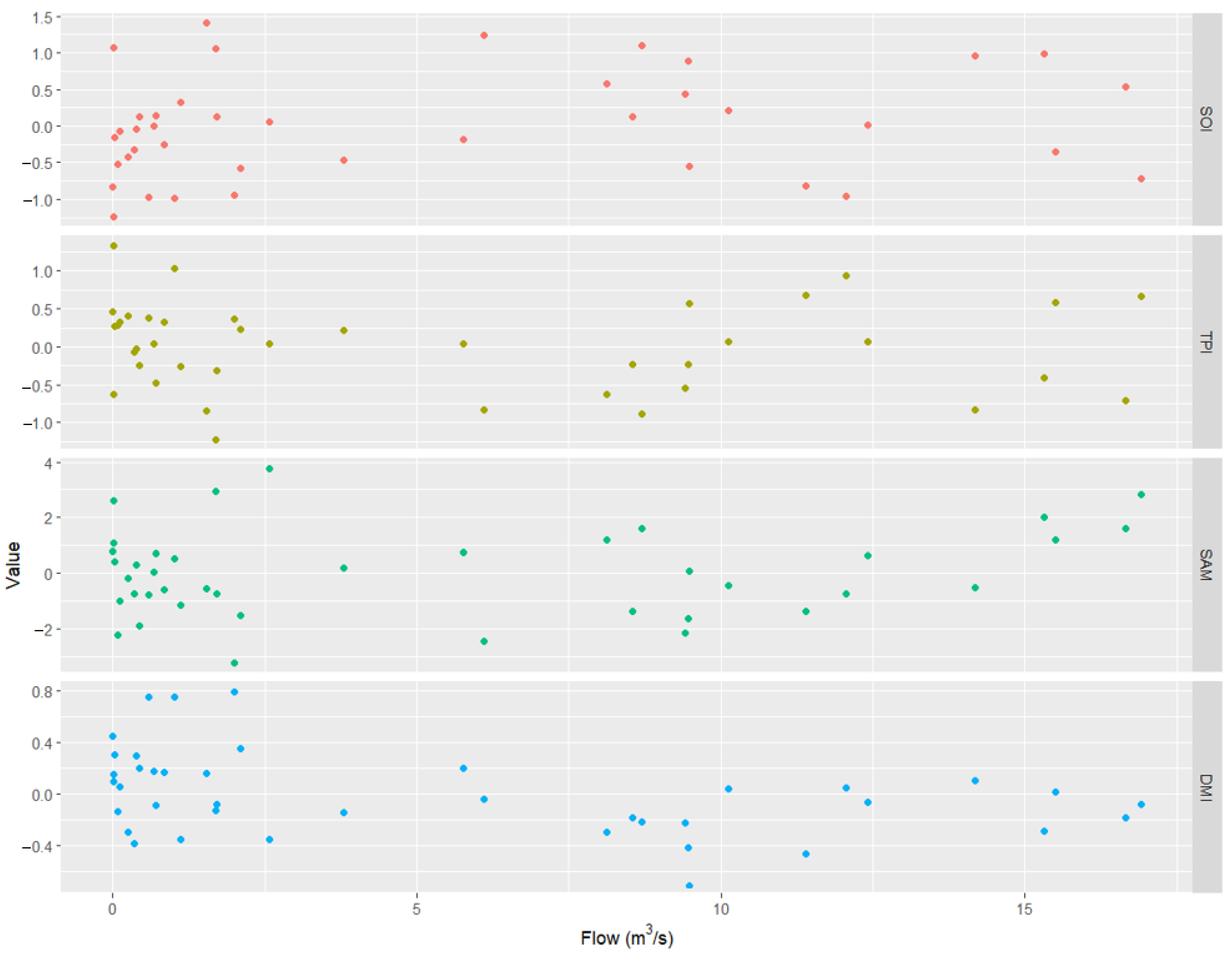
- There is not enough evidence to state that ENSO, SAM, IOD, or IPO had significant effects on AMF non-stationarity in the basin.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, M.; Papadikis, K.; Jun, C. An investigation on the non-stationarity of flood frequency across the UK. J. Hydrol. 2021, 597, 126309. [Google Scholar] [CrossRef]
- Rahman, A.S.; Rahman, A.; Zaman, M.A.; Haddad, K.; Ahsan, A.; Imteaz, M. A study on selection of probability distributions for at-site flood frequency analysis in Australia. Nat. Hazards 2013, 69, 1803–1813. [Google Scholar] [CrossRef]
- Yilmaz, A.G.; Pereira, B.J.C. Extreme rainfall non-stationarity investigation and intensity-frequency-duration relationship. ASCE J. Hydrol. Eng. 2014, 19, 1160–1172. [Google Scholar] [CrossRef]
- Wasko, C.; Westra, S.; Nathan, R.; Orr, H.G.; Villarini, G.; Herrera, R.V.; Fowler, H.J. Incorporating climate change in flood estimation guidance. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2021, 379, 20190548. [Google Scholar] [CrossRef] [PubMed]
- Khaliq, M.N.; Ouarda, T.B.M.J.; Ondo, J.-C.; Gachon, P.; Bobée, B. Frequency analysis of a sequence of dependent and/or non-stationary hydro-meteorological observations: A review. J. Hydrol. 2006, 329, 534–552. [Google Scholar] [CrossRef]
- Yilmaz, A.G.; Hossain, I.; Perera, B.J.C. Effect of climate change and variability on extreme rainfall intensity–frequency–duration relationships: A case study of Melbourne. Hydrol. Earth Syst. Sci. 2014, 18, 4065–4076. [Google Scholar] [CrossRef]
- Hesarkazzazi, S.; Arabzadeh, R.; Hajibabaei, M.; Rauch, W.; Kjeldsen, T.R.; Prosdocimi, I.; Castellarin, A.; Sitzenfrei, R. Stationary vs. non-stationary modelling of flood frequency distribution across northwest England. Hydrol. Sci. J. 2021, 66, 729–744. [Google Scholar] [CrossRef]
- Šraj, M.; Viglione, A.; Parajka, J.; Blöschl, G. The influence of non-stationarity in extreme hydrological events on flood frequency estimation. J. Hydrol. Hydromech. 2016, 64, 426–437. [Google Scholar] [CrossRef]
- Ray, L.K.; Goel, N.K. Flood Frequency Analysis of Narmada River Basin in India under Nonstationary Condition. J. Hydrol. Eng. 2019, 24, 05019018. [Google Scholar] [CrossRef]
- Singh, N.; Chinnasamy, P. Non-stationary flood frequency analysis and attribution of streamflow series: A case study of Periyar River, India. Hydrol. Sci. J. 2021, 66, 1866–1881. [Google Scholar] [CrossRef]
- Hounkpè, J.; Diekkrüger, B.; Badou, D.F.; Afouda, A.A. Non-Stationary Flood Frequency Analysis in the Ouémé River Basin, Benin Republic. Hydrology 2015, 2, 210–229. [Google Scholar] [CrossRef]
- Bossa, A.Y.; Akpaca, J.d.D.; Hounkpè, J.; Yira, Y.; Badou, D.F. Non-Stationary Flood Discharge Frequency Analysis in West Africa. GeoHazards 2023, 4, 316–327. [Google Scholar] [CrossRef]
- Anzolin, G.; Chaffe, P.L.B.; Vrugt, J.A.; AghaKouchak, A. Using climate information as covariates to improve nonstationary flood frequency analysis in Brazil. Hydrol. Sci. J. 2023, 68, 645–654. [Google Scholar] [CrossRef]
- Ishak, E.H.; Rahman, A.; Westra, S.; Sharma, A.; Kuczera, G. Evaluating the non-stationarity of Australian annual maximum flood. J. Hydrol. 2013, 494, 134–145. [Google Scholar] [CrossRef]
- Do, H.X.; Zhao, F.; Westra, S.; Leonard, M.; Gudmundsson, L.; Boulange, J.E.S.; Müller Schmied, H. Historical and future changes in global flood magnitude–evidence from a model-observation investigation. Hydrol. Earth Syst. Sci. 2020, 24, 1543–1564. [Google Scholar] [CrossRef]
- Ishak, E.; Rahman, A. Examination of Changes in Flood Data in Australia. Water 2019, 11, 1734. [Google Scholar] [CrossRef]
- Yilmaz, A.G. Climate change effects and extreme rainfall non-stationarity. ICE-Water Manag. 2017, 170, 57–65. [Google Scholar] [CrossRef]
- Han, X.; Mehrotra, R.; Sharma, A.; Rahman, A. Incorporating nonstationarity in regional flood frequency analysis procedures to account for climate change impact. J. Hydrol. 2022, 612, 128235. [Google Scholar] [CrossRef]
- Faulkner, D.; Warren, S.; Spencer, P.; Sharkey, P. Can we still predict the future from the past? Implementing non-stationary flood frequency analysis in the UK. J. Flood Risk Manag. 2020, 13, e12582. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, Y.; Wang, B.; Tan, S.; Feng, P. Nonstationary Flood Frequency Analysis Using Univariate and Bivariate Time-Varying Models Based on GAMLSS. Water 2018, 10, 819. [Google Scholar] [CrossRef]
- Goulburn-Murray Water (GMW). 2022. Available online: https://www.g-mwater.com.au/water-operations/catchments/campaspebasin (accessed on 15 December 2022).
- Murray-Darling Basin Authority (MDBA). 2022. Available online: https://www.mdba.gov.au/water-management/catchments/campaspe (accessed on 10 December 2022).
- Bureau of Meteorology (BoM). 2022. Available online: http://www.bom.gov.au/water/hrs/ (accessed on 5 October 2022).
- Yue, S.; Pilon, P.; Cavadias, G. Power of the Mann–Kendall and Spearman’s rho tests for detecting monotonic trends in hydrological series. J. Hydrol. 2002, 259, 254–271. [Google Scholar] [CrossRef]
- Laz, O.U.; Rahman, A.; Yilmaz, A.; Haddad, K. Trends in sub hourly, sub daily and daily extreme rainfall events in eastern Australia. J. Water Clim. Chang. 2014, 5, 667–675. [Google Scholar] [CrossRef]
- Wagesho, N.; Goel, N.K.; Jain, M.K. Investigation of non-stationarity in hydro-climatic variables at Rift Valley lakes basin of Ethiopia. J. Hydrol. 2012, 444–445, 113–133. [Google Scholar] [CrossRef]
- Yilmaz, A.G. The effects of climate change on historical and future extreme rainfall in Antalya, Turkey. Hydrol. Sci. J. 2015, 60, 2148–2162. [Google Scholar] [CrossRef]
- Yilmaz, A.G.; Perera, B.J.C. Spatiotemporal Trend Analysis of Extreme Rainfall Events in Victoria, Australia. Water Resour. Manag. 2015, 29, 4465–4480. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Robson, A. Detecting Trend and Other Changes in Hydrological Data; WCDMP, No. 45; WMO-TD, No. 1013; WMO: Geneva, Switzerland, 2000. [Google Scholar]
- Diop, L.; Yaseen, Z.M.; Bodian, A.; Djaman, K.; Brown, L. Trend analysis of streamflow with different time scales: A case study of the upper Senegal River. ISH J. Hydraul. Eng. 2018, 24, 105–114. [Google Scholar] [CrossRef]
- Guclu, Y.S. Improved visualization for trend analysis by comparing with classical MannKendall test and ITA. J. Hydrol. 2020, 584, 124674. [Google Scholar] [CrossRef]
- Conte, L.C.; Débora, M.B.; Fábio, M.B. Bootstrap Pettitt test for detecting change points in hydroclimatological data: Case study of Itaipu Hydroelectric Plant, Brazil. Hydrolog. Sci. J. 2019, 64, 1312–1326. [Google Scholar] [CrossRef]
- Engeland, K.; Aano, A.; Steffensen, I.; Støren, E.; Paasche, Ø. New flood frequency estimates for the largest river in Norway based on the combination of short and long time series. Hydrol. Earth Syst. Sci. 2020, 24, 5595–5619. [Google Scholar] [CrossRef]
- Park, J.-S.; Kang, H.-S.; Lee, Y.S.; Kim, M.-K. Changes in the extreme daily rainfall in South Korea. Int. J. Clim. 2010, 31, 2290–2299. [Google Scholar] [CrossRef]
- Haddad, K.; Rahman, A. Selection of the best fit flood frequency distribution and parameter estimation procedure: A case study for tasmania in australia. Stoch. Environ. Res. Risk Assess. 2011, 25, 415–428. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Y.; Yang, Y.; Gu, X.; Xiao, M. Investigating Relationships Between Australian Flooding and Large-Scale Climate Indices and Possible Mechanism. J. Geophys. Res. Atmos. 2018, 123, 8708–8723. [Google Scholar] [CrossRef]
- Johnson, F.; White, C.J.; van Dijk, A.; Ekstrom, M.; Evans, J.P.; Jakob, D.; Kiem, A.S.; Leonard, M.; Rouillard, A.; Westra, S. Natural Hazards in Australia: Floods. Clim. Chang. 2016, 139, 21–35. [Google Scholar] [CrossRef]
- Tramblay, Y.; Neppel, L.; Carreau, J.; Najib, K. Non-stationary frequency analysis of heavy rainfall events in southern France. Hydrol. Sci. J. 2013, 58, 280–294. [Google Scholar] [CrossRef]
- De Paola, F.; Giugni, M.; Pugliese, F.; Annis, A.; Nardi, F. GEV parameter estimation and stationary vs. non-stationary analysis of extreme rainfall in African test cities. Hydrology 2018, 5, 28. [Google Scholar] [CrossRef]
- Xavier, A.C.F.; Rudke, A.P.; Fujita, T.; Blain, G.C.; De Morais, M.V.B.; De Almeida, D.S.; Rafee, S.A.A.; Martins, L.D.; De Souza, R.A.F.; De Freitas, E.D.; et al. Stationary and Non-Stationary Detection of Extreme Precipitation Events and Trends of Average Precipitation from 1980 to 2010 in the Paraná River Basin, Brazil. Int. J. Climatol. 2020, 40, 1197–1212. [Google Scholar] [CrossRef]
- UK Environment Agency. Development of Interim National Guidance on Non-Stationary Fluvial Flood Frequency Estimation –R Package Nonstat User Guide. 2020. Available online: https://assets.publishing.service.gov.uk/media/6038f77de90e070555cedc22/non-stationary_fluvial_flood_frequency_estimation_-_package_user_guide.pdf (accessed on 3 March 2023).
- Dodangeh, E.; Singh, V.P.; Pham, B.T.; Yin, J.; Yang, G.; Mosavi, A. Flood frequency analysis of interconnected Rivers by copulas. Water Resour. Manag. 2020, 34, 3533–3549. [Google Scholar] [CrossRef]
- Echogdali, F.Z.; Rosine, B.K.; Ouchchen, M.; Id-Belqas, M.; Dadi, B.; Ikirri, M.; Abioui, M.; Boutaleb, S. Spatial Prediction of Flood Frequency Analysis in a Semi-Arid Zone: A Case Study from the Seyad Basin (Guelmim Region, Morocco). In Geospatial Technology for Landscape and Environmental Management; Rai, P.K., Mishra, V.N., Singh, P., Eds.; Springer: Singapore, 2022. [Google Scholar] [CrossRef]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer-Verlag Inc.: London, UK, 2001. [Google Scholar]
- Eastoe, E.M.; Tawn, J.A. Modelling non-stationary extremes with application to surface level ozone. J. R. Stat. Soc. Ser. C Appl. Stat. 2009, 58, 25–45. [Google Scholar] [CrossRef]
- Lu, H.; Bryant, R.B.; Buda, A.R.; Collick, A.S.; Folmar, G.J.; Kleinman, P.J.A. Long-term trends in climate and hydrology in an agricultural, headwater watershed of central Pennsylvania, USA. J. Hydrol. Reg. Stud. 2015, 4, 713–731. [Google Scholar] [CrossRef]
- Basarin, B.; Lukić, T.; Pavić, D.; Wilby, R.L. Trends and multi-annual variability of water temperatures in the river Danube, Serbia. Hydrol. Process. 2016, 30, 3315–3329. [Google Scholar] [CrossRef]
- Razmi, A.; Golian, S.; Zahmatkesh, Z. Non-Stationary Frequency Analysis of Extreme Water Level: Application of Annual Maximum Series and Peak-over Threshold Approaches. Water Resour. Manag. 2017, 31, 2065–2083. [Google Scholar] [CrossRef]
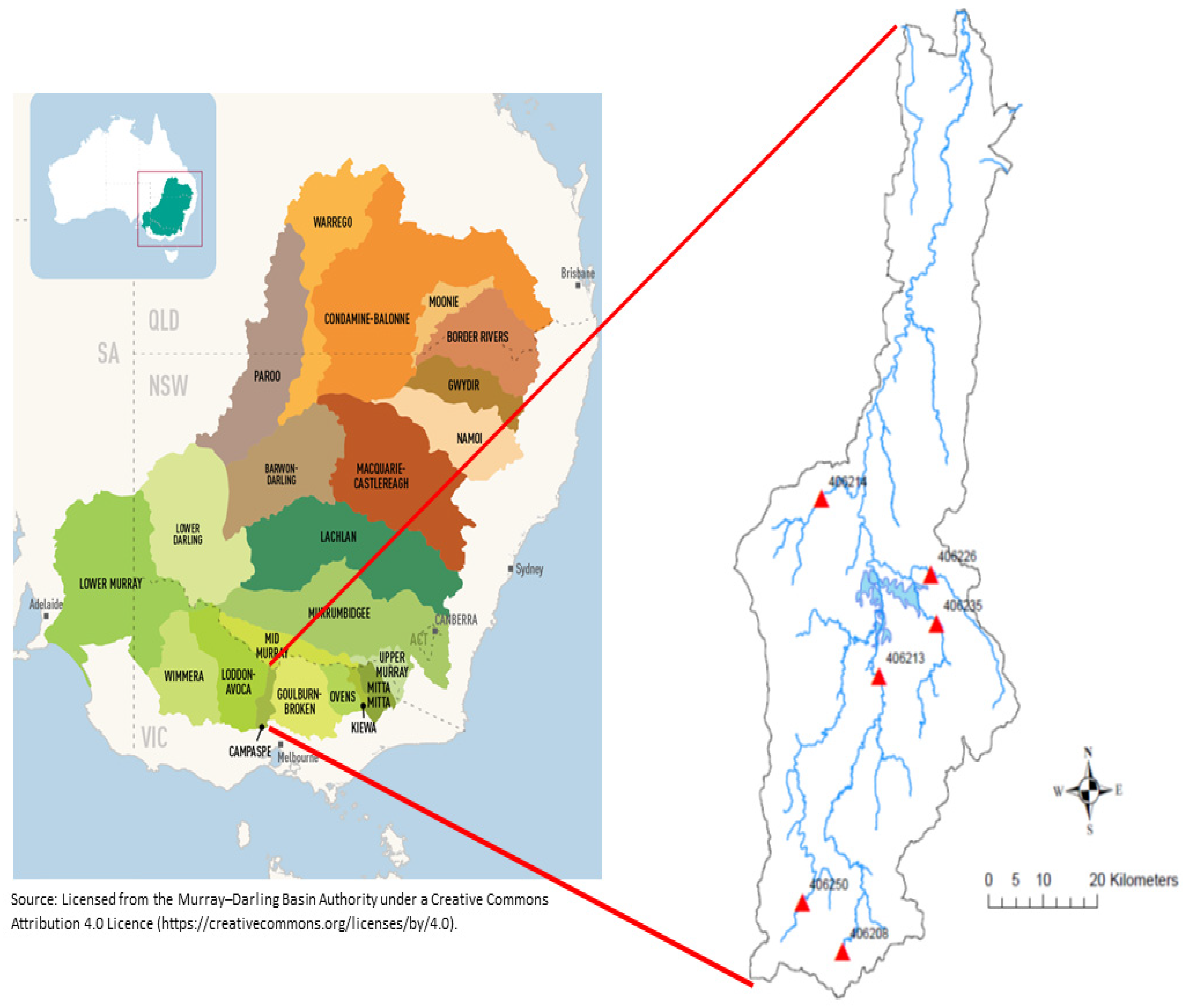

| Station Number | Sub-Basin Area (km2) | Location | Available Data Period |
|---|---|---|---|
| 406208 | 37.6 | 144.451° E, 37.388° S | 1970–2022 |
| 406213 | 633.8 | 144.539° E, 37.016° S | 1975–2022 |
| 406214 | 237 | 144.428° E, 36.774° S | 1972–2022 |
| 406226 | 171.6 | 144.650° E, 36.881° S | 1978–2022 |
| 406235 | 212.3 | 144.660° E, 36.948° S | 1980–2022 |
| 406250 | 77.5 | 144.370° E, 37.320° S | 1983–2022 |
| Model Name | Parameters of Model | ||
|---|---|---|---|
| NSGEV1 | Constant | Constant | |
| NSGEV2 | Constant | Constant | |
| NSGEV3 | Constant | Constant | |
| NSGEV4 | Constant | Constant | |
| NSGEV5 | Constant | Constant | |
| NSGEV6 | Constant | Constant | |
| NSGEV7 | Constant | Constant | |
| NSGEV8 | Constant | Constant | |
| NSGEV9 | Constant | Constant | |
| NSGEV10 | Constant | Constant | |
| NSGEV11 | Constant | ||
| NSGEV12 | Constant | ||
| NSGEV13 | Constant | ||
| NSGEV14 | Constant | ||
| NSGEV15 | Constant | ||
| Station Number | z-Score | 2-Sided p-Value | Outcome |
|---|---|---|---|
| 406208 | −3.66157 | 0.000250671 | S (0.01) |
| 406213 | −2.36704 | 0.017931094 | S (0.05) |
| 406214 | −3.66343 | 0.00024886 | S (0.01) |
| 406226 | −2.60603 | 0.009159779 | S (0.01) |
| 406235 | −2.59458 | 0.00947072 | S (0.01) |
| 406250 | −1.45834 | 0.144746587 | NS |
| Station Number | p-Value | Outcome | Year of Change |
|---|---|---|---|
| 406208 | 0.000295 | S (0.01) | 1996 |
| 406213 | 0.010492 | S (0.05) | 1996 |
| 406214 | 0.002299 | S (0.01) | 1996 |
| 406226 | 0.015921 | S (0.05) | 1996 |
| 406235 | 0.016234 | S (0.05) | 1996 |
| 406250 | 0.088723 | NS | 2000 |
| Gauge Number | Model | Shape | AIC | BIC | ||||
|---|---|---|---|---|---|---|---|---|
| 406208 | SGEV | 0.9068 | 0.4415 | 1.4555 | 226 | 231 | ||
| 406208 | NSGEV5 | 0.8803 | 0.0226 | 0.4322 | 1.4738 | 228 | 235 | |
| 406208 | NSGEV15 | 1.4105 | −0.6666 | 0.7438 | −0.6579 | 1.0779 | 225 | 233 |
| 406213 | SGEV | 12.9959 | 2.8779 | 1.0512 | 406 | 411 | ||
| 406213 | NSGEV5 | 12.6147 | 0.5300 | 2.8679 | 1.0701 | 408 | 415 | |
| 406213 | NSGEV15 | 15.3868 | −4.1344 | 3.0092 | −0.4580 | 0.8058 | 406 | 414 |
| 406214 | SGEV | 1.4513 | 1.1221 | 2.026 | 300 | 305 | ||
| 406214 | NSGEV5 | 1.2899 | 0.0499 | 1.0587 | 2.1561 | 301 | 308 | |
| 406214 | NSGEV15 | 2.3495 | −0.9221 | 1.4599 | −0.6661 | 1.3696 | 301 | 309 |
| 406226 | SGEV | 2.1333 | 1.2295 | 1.2554 | 282 | 287 | ||
| 406226 | NSGEV5 | 2.1347 | −0.0004 | 1.2300 | 1.2552 | 284 | 290 | |
| 406226 | NSGEV15 | 2.9686 | −1.2884 | 1.3622 | −0.5455 | 0.8445 | 280 | 288 |
| 406235 | SGEV | 6.1003 | 2.0935 | 0.8171 | 334 | 339 | ||
| 406235 | NSGEV5 | 6.5611 | −0.4283 | 2.1262 | 0.7407 | 335 | 342 | |
| 406235 | NSGEV15 | 7.7278 | −3.4482 | 2.1293 | −0.4784 | 0.5273 | 330 | 338 |
| 406250 | SGEV | 5.8260 | 1.5449 | 0.1154 | 249 | 253 | ||
| 406250 | NSGEV5 | 5.8056 | −1.9601 | 1.4617 | 0.1721 | 247 | 253 | |
| 406250 | NSGEV15 | 5.7582 | −2.1543 | 1.4527 | 0.1318 | 0.1695 | 248 | 256 |
| Year | NSGEV15 (2-Year) | NSGEV15 (10-Year) | NSGEV15 (20-Year) | NSGEV15 (50-Year) |
|---|---|---|---|---|
| 1982 | 19.7 | 90.2 | 143.4 | 258.8 |
| 1983 | 19.1 | 86.5 | 138.6 | 249.0 |
| 1984 | 18.6 | 83.5 | 133.0 | 241.0 |
| 1985 | 18.1 | 80.1 | 128.9 | 231.1 |
| 1986 | 17.6 | 77.2 | 124.5 | 220.8 |
| 1987 | 17.1 | 74.6 | 120.1 | 212.6 |
| 1988 | 16.5 | 72.0 | 115.7 | 204.2 |
| 1989 | 16.0 | 69.3 | 110.6 | 195.7 |
| 1990 | 15.5 | 66.5 | 106.5 | 188.2 |
| 1991 | 15.0 | 64.3 | 102.5 | 180.4 |
| 1992 | 14.5 | 61.8 | 98.5 | 172.7 |
| 1993 | 14.1 | 59.4 | 94.2 | 165.0 |
| 1994 | 13.6 | 57.3 | 90.6 | 157.6 |
| 1995 | 13.2 | 55.2 | 87.2 | 151.8 |
| 1996 | 12.8 | 53.2 | 83.4 | 146.2 |
| 1997 | 12.4 | 51.0 | 80.6 | 139.9 |
| 1998 | 12.0 | 48.9 | 77.5 | 134.8 |
| 1999 | 11.6 | 46.9 | 74.6 | 129.7 |
| 2000 | 11.2 | 45.1 | 72.0 | 125.3 |
| 2001 | 10.8 | 43.3 | 68.6 | 120.5 |
| 2002 | 10.4 | 41.7 | 66.0 | 114.8 |
| 2003 | 10.0 | 39.9 | 63.2 | 110.0 |
| 2004 | 9.7 | 38.5 | 60.5 | 105.6 |
| 2005 | 9.3 | 36.8 | 58.1 | 101.4 |
| 2006 | 8.9 | 35.4 | 55.4 | 97.4 |
| 2007 | 8.5 | 33.9 | 53.1 | 93.0 |
| 2008 | 8.1 | 32.4 | 51.0 | 89.5 |
| 2009 | 7.7 | 30.9 | 48.7 | 85.7 |
| 2010 | 7.4 | 29.6 | 46.8 | 81.8 |
| 2011 | 7.0 | 28.4 | 44.8 | 78.9 |
| 2012 | 6.6 | 27.3 | 43.0 | 75.3 |
| 2013 | 6.3 | 26.1 | 41.2 | 71.7 |
| 2014 | 5.9 | 24.9 | 39.6 | 69.0 |
| 2015 | 5.5 | 23.8 | 37.8 | 66.3 |
| 2016 | 5.2 | 22.8 | 36.1 | 63.8 |
| 2017 | 4.8 | 21.7 | 34.6 | 61.4 |
| 2018 | 4.4 | 20.5 | 33.3 | 58.7 |
| 2019 | 4.1 | 19.6 | 31.9 | 56.3 |
| 2020 | 3.8 | 18.6 | 30.3 | 54.2 |
| 2021 | 3.4 | 17.8 | 28.7 | 51.8 |
| Station 406235 | Station 406250 | |||||
|---|---|---|---|---|---|---|
| Stationary | Non-Stationary | Change (%) | Stationary | Non-Stationary | Change (%) | |
| 2-year Design Flood (m3/s) | 9.5 | 3.4 | −64 | 7.6 | 4.1 | −46 |
| 10-year Design Flood (m3/s) | 59.2 | 17.8 | −70 | 17.6 | 13.9 | −21 |
| 20-year Design Flood (m3/s) | 110.7 | 28.7 | −74 | 21.9 | 18.6 | −15 |
| 50-year Design Flood (m3/s) | 245.5 | 51.8 | −79 | 28.1 | 25.8 | −8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yilmaz, A.G.; Imteaz, M.A.; Shanableh, A.; Al-Ruzouq, R.; Atabay, S.; Haddad, K. A Non-Stationarity Analysis of Annual Maximum Floods: A Case Study of Campaspe River Basin, Australia. Water 2023, 15, 3683. https://doi.org/10.3390/w15203683
Yilmaz AG, Imteaz MA, Shanableh A, Al-Ruzouq R, Atabay S, Haddad K. A Non-Stationarity Analysis of Annual Maximum Floods: A Case Study of Campaspe River Basin, Australia. Water. 2023; 15(20):3683. https://doi.org/10.3390/w15203683
Chicago/Turabian StyleYilmaz, Abdullah Gokhan, Monzur Alam Imteaz, Abdallah Shanableh, Rami Al-Ruzouq, Serter Atabay, and Khaled Haddad. 2023. "A Non-Stationarity Analysis of Annual Maximum Floods: A Case Study of Campaspe River Basin, Australia" Water 15, no. 20: 3683. https://doi.org/10.3390/w15203683
APA StyleYilmaz, A. G., Imteaz, M. A., Shanableh, A., Al-Ruzouq, R., Atabay, S., & Haddad, K. (2023). A Non-Stationarity Analysis of Annual Maximum Floods: A Case Study of Campaspe River Basin, Australia. Water, 15(20), 3683. https://doi.org/10.3390/w15203683










