Stable Isotopes and Water Level Monitoring Integrated to Characterize Groundwater Recharge in the Pra Basin, Ghana
Abstract
:1. Introduction
2. Materials and Methods
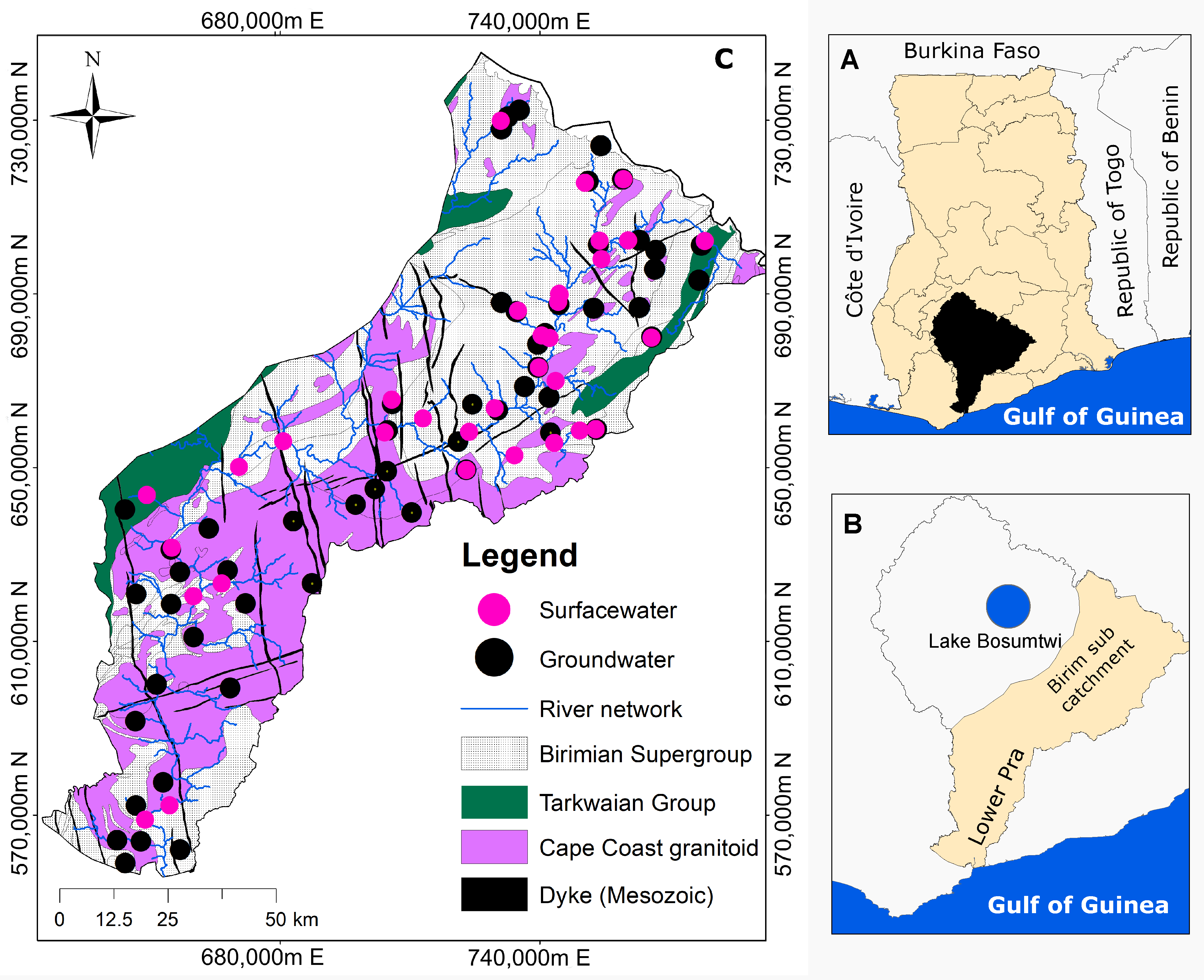
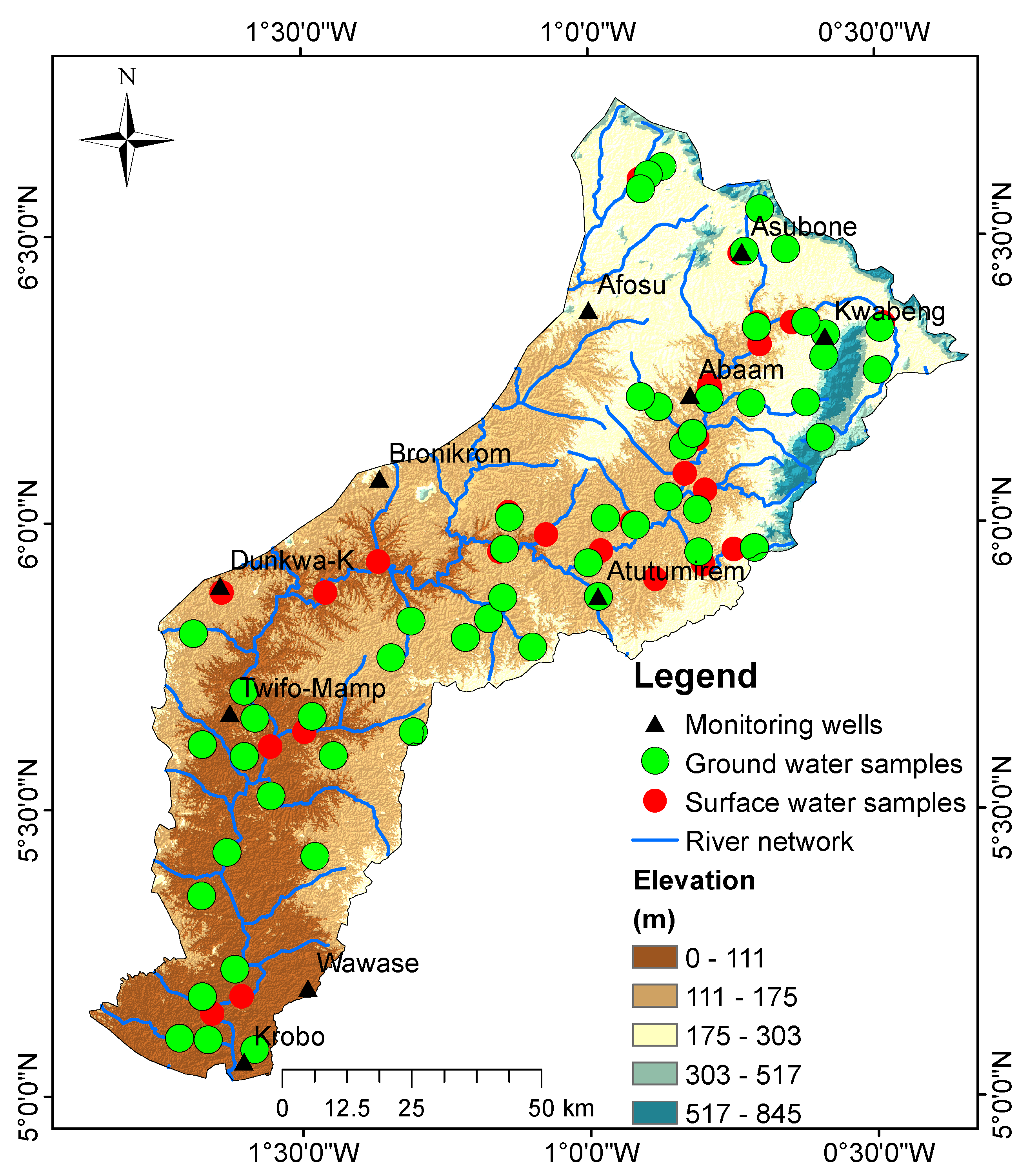
2.1. Study Area
2.2. Data Collection and Analysis
2.3. Quantification of Evaporation Losses of Sampled Water
2.4. Groundwater Recharge Estimation Using CMB Method
2.5. Groundwater Recharge Estimation Using Water Table Fluctuation Method
3. Results
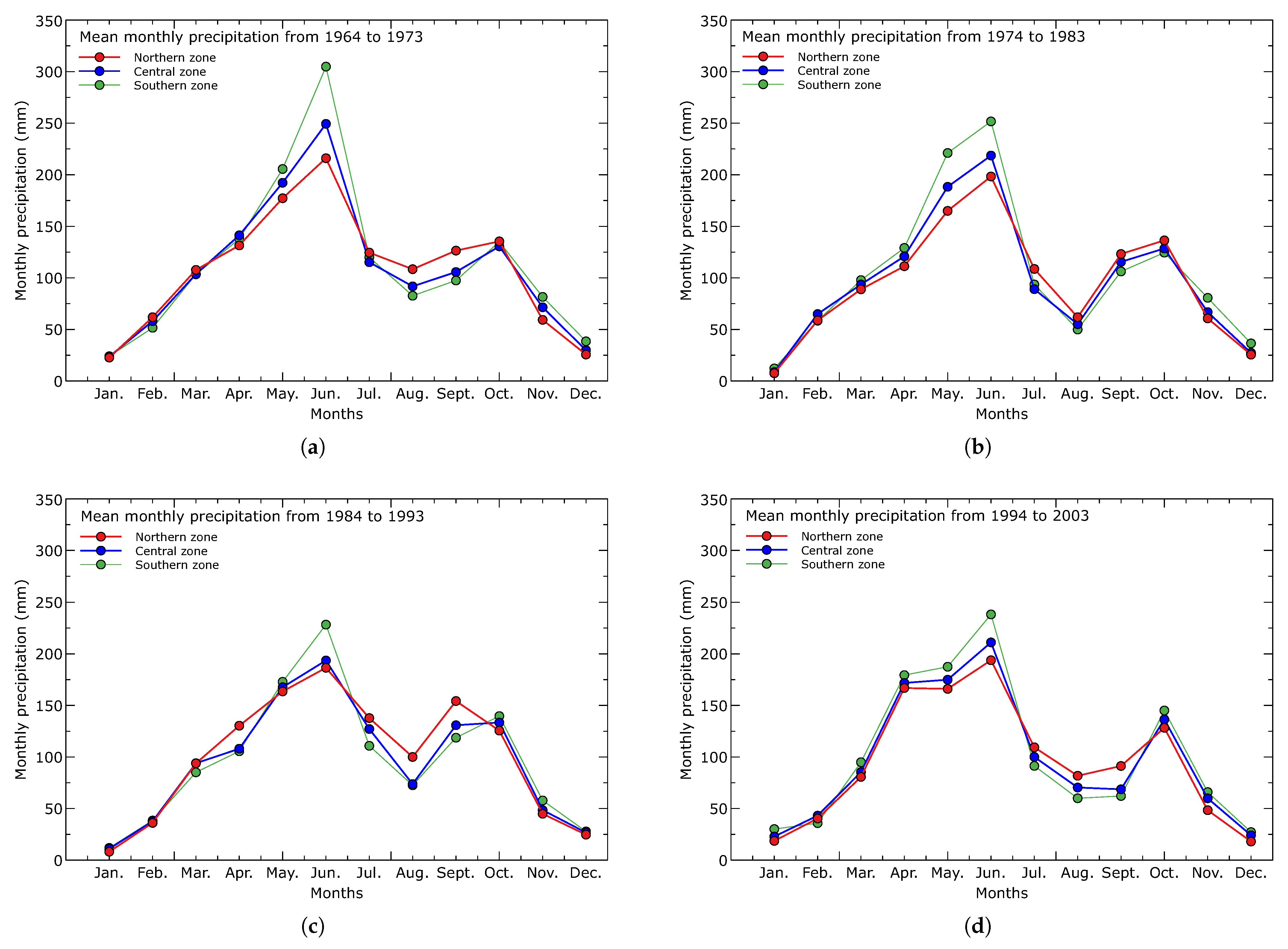
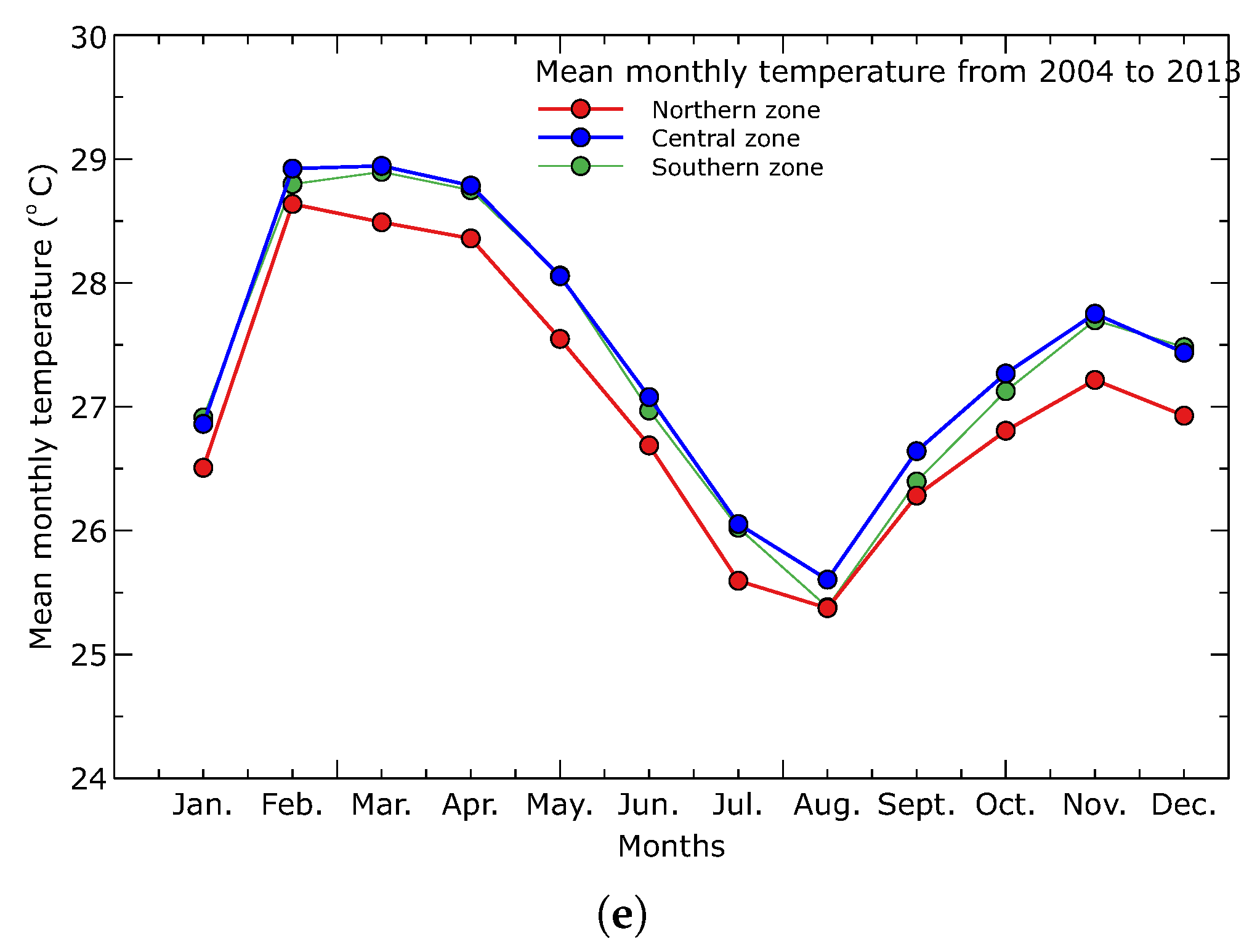
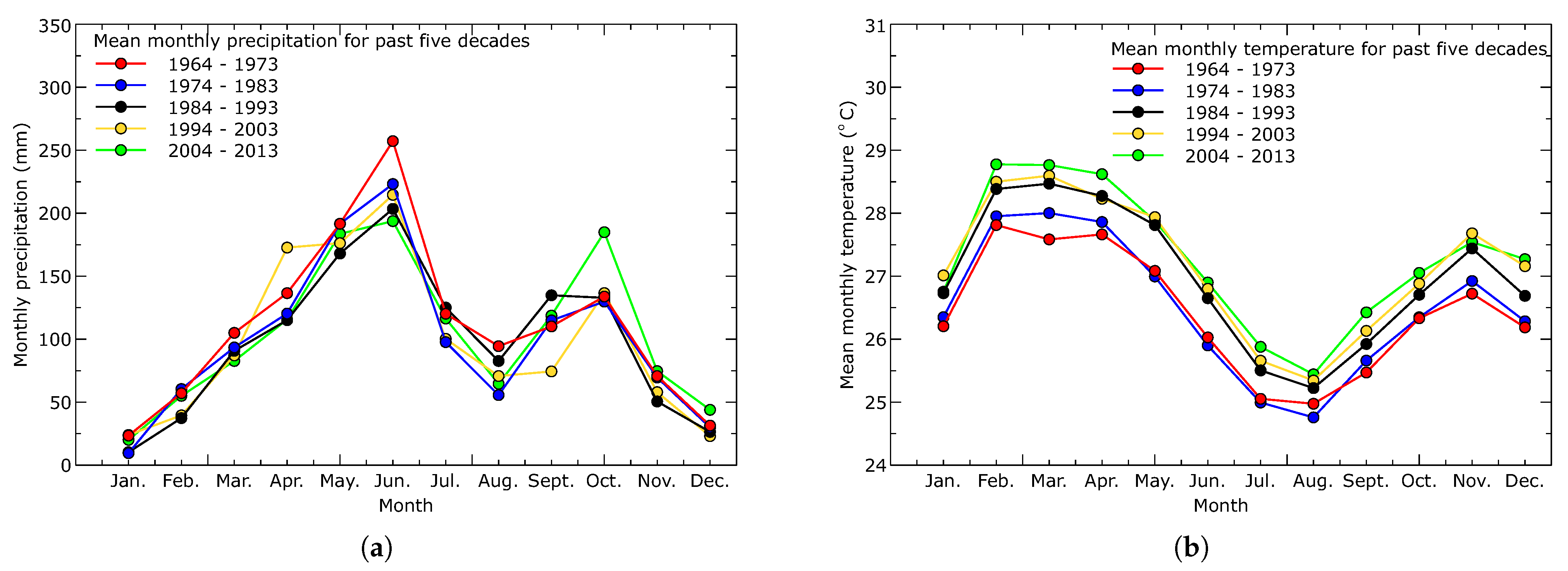
3.1. Climatology of Precipitation and Temperature in the Pra Basin
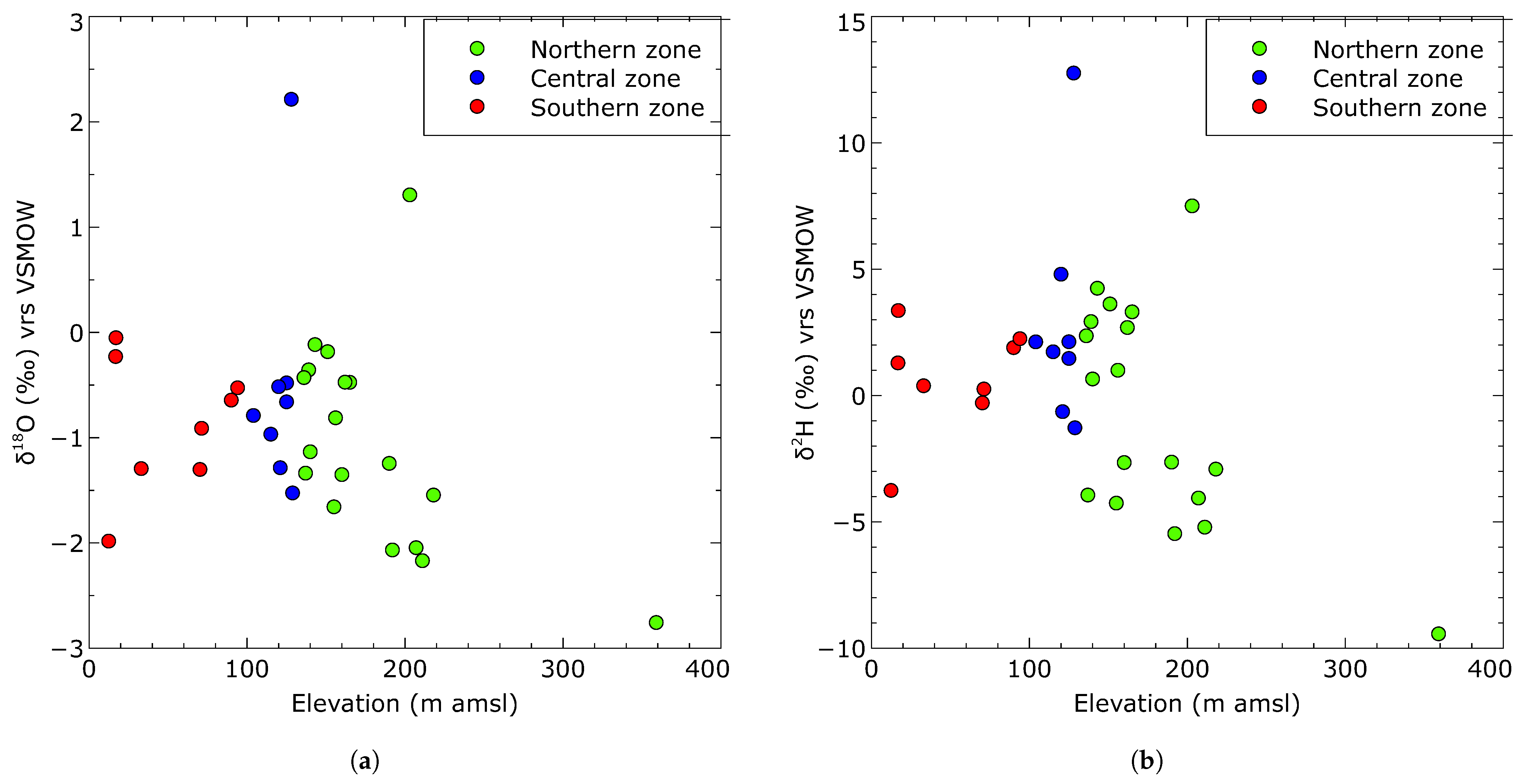
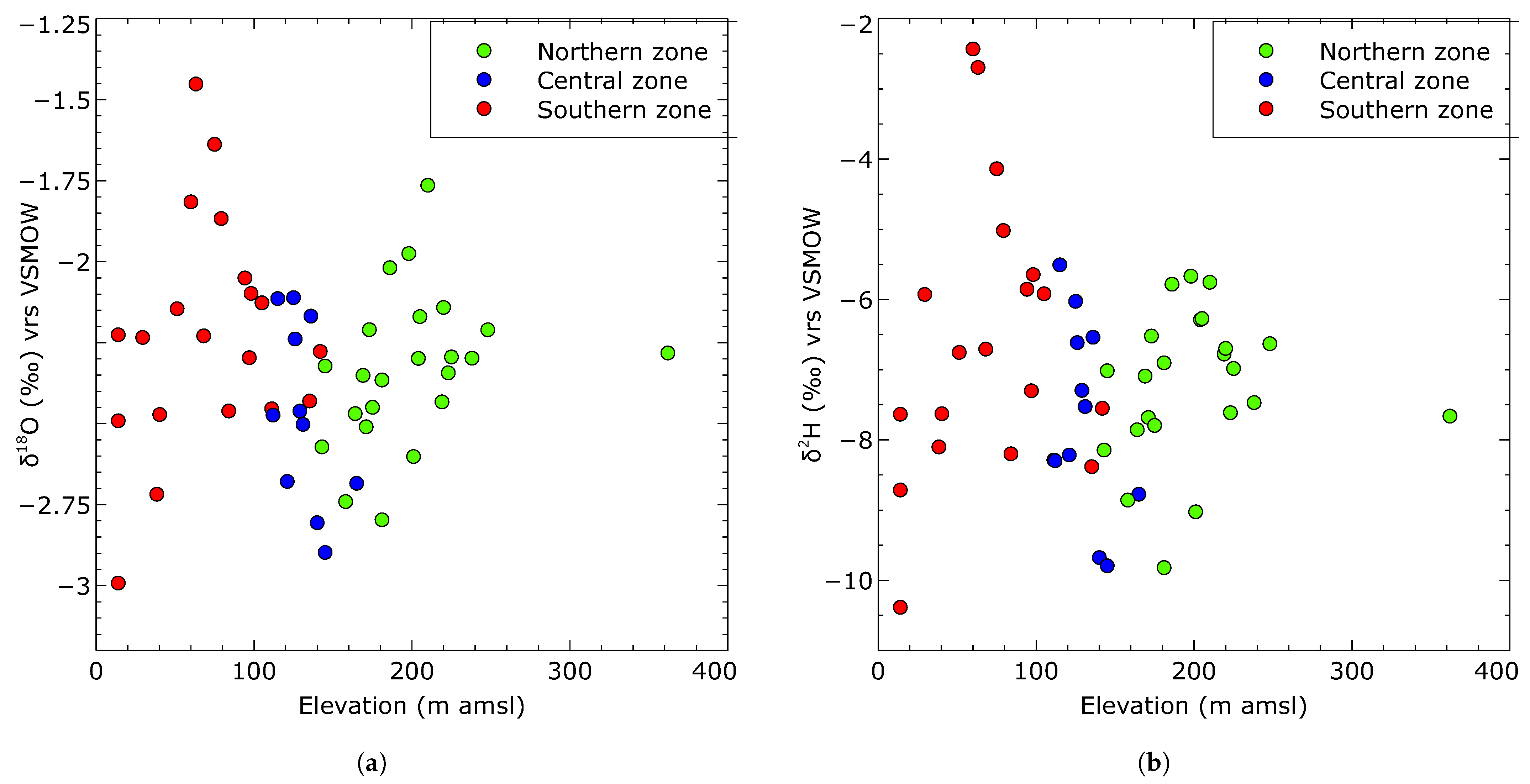
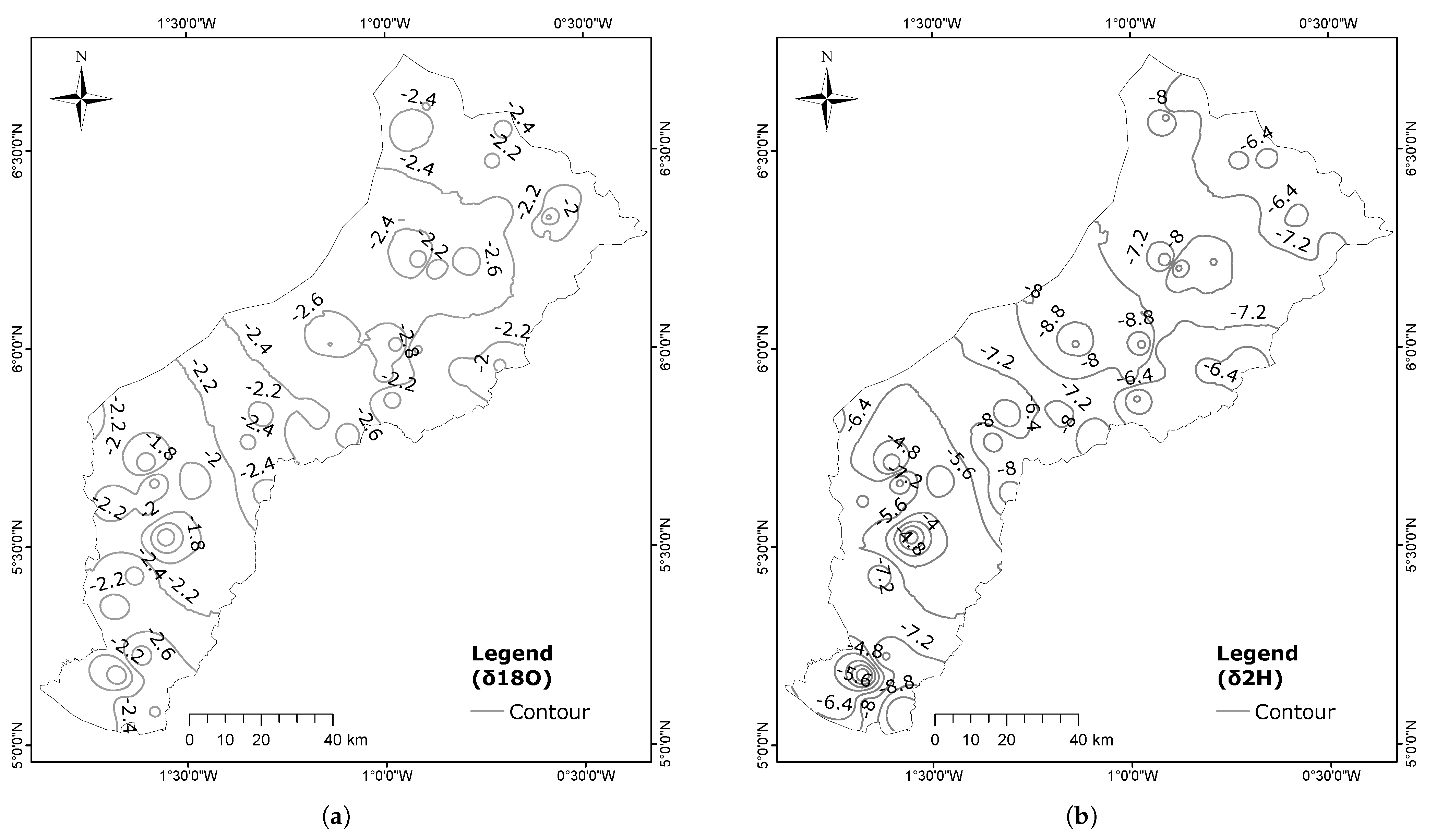
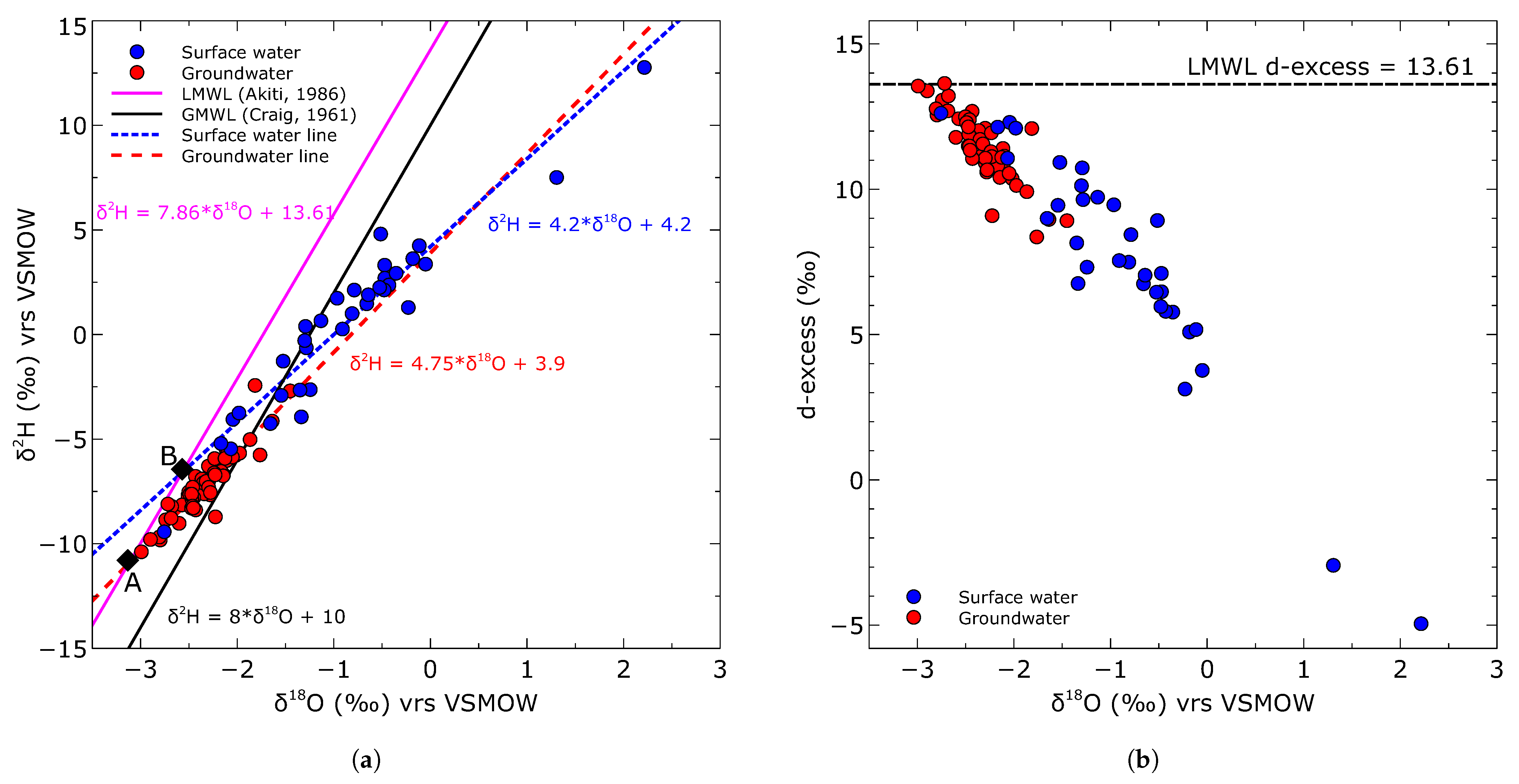
3.2. Variability in Surface Water and Groundwater and Values
3.3. Correlation between and of Water
3.4. Estimations of the Rate of Evaporation in Surface Water and Groundwater
3.5. Groundwater Recharge Estimate Using Chloride Mass Balance Method
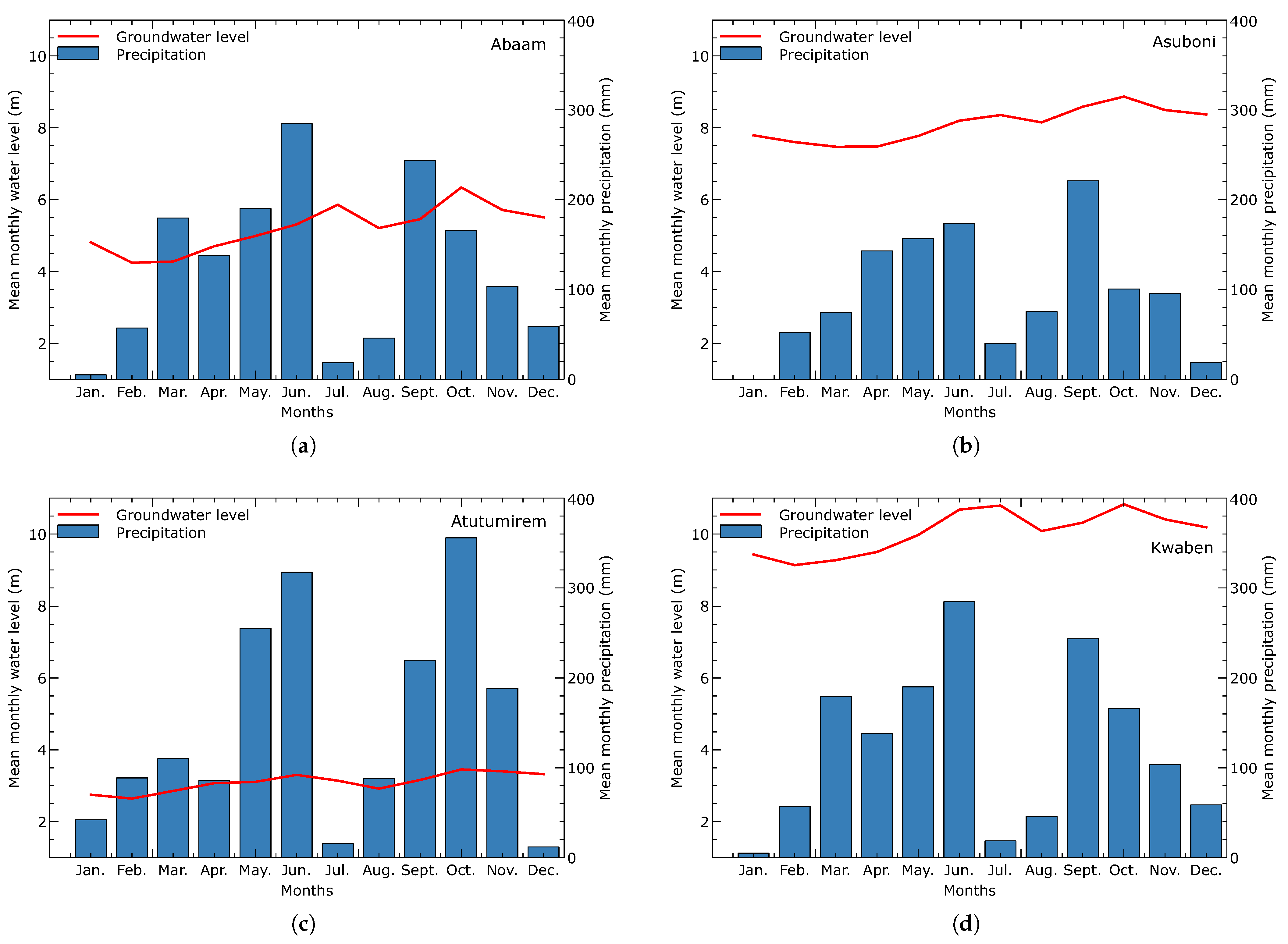
3.6. Groundwater Recharge Estimate from Water Table Fluctuation Method
4. Discussion
4.1. Regional Climatic Conditions, Present and the Past
4.2. Isotopic Characterization of the Surface Water and Groundwater
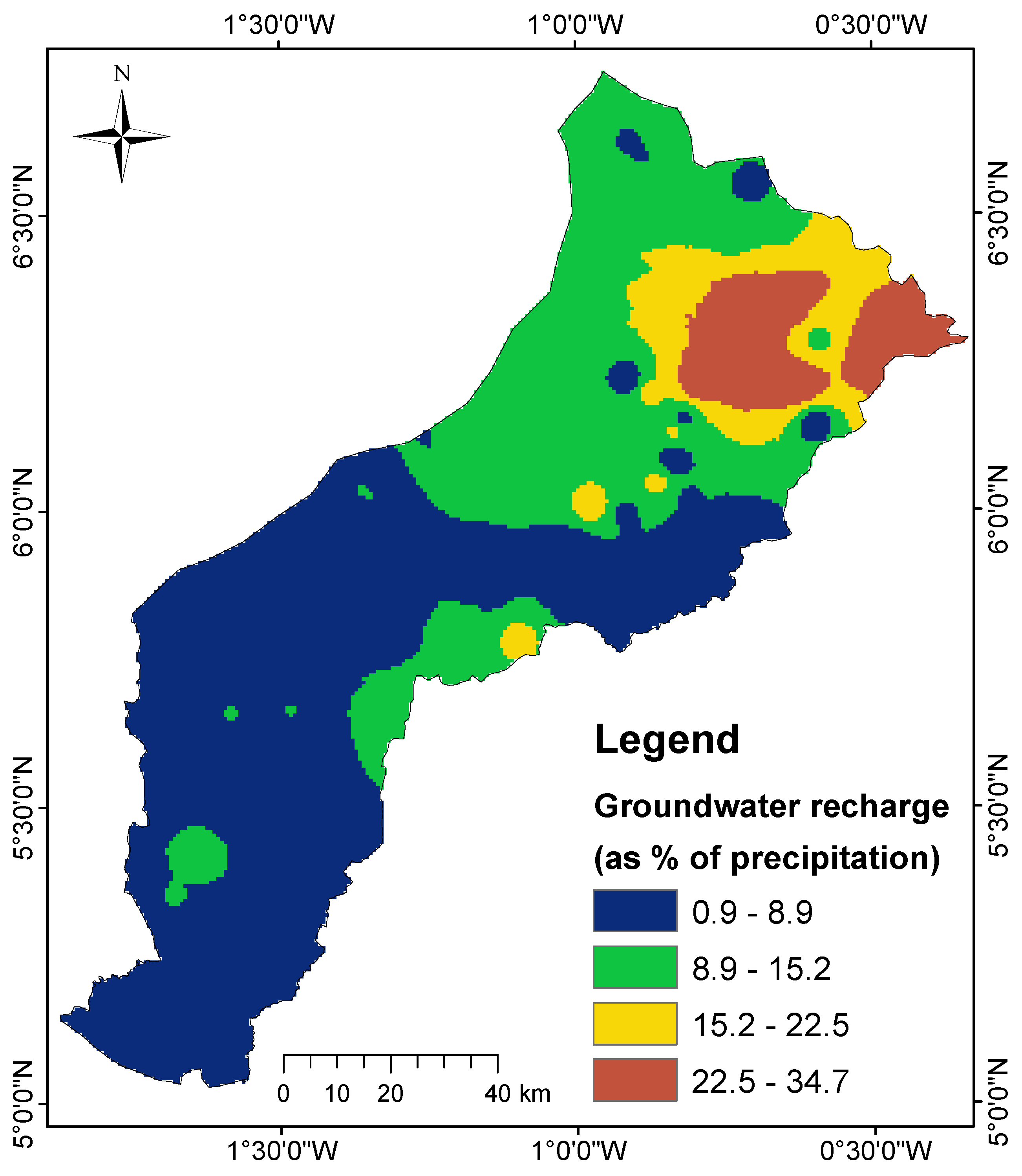
4.3. Groundwater Recharge Estimates
5. Conclusions
- The past fifty years show a temperature increase of about 1 degree Celsius. The climatology of precipitation and temperature remain unchanged; however, a gradual decrease in precipitation can be observed for the first peak of the rainy season in June.
- Surface waters have experienced relatively high levels of evaporation due to the direct effects of prevailing climatic conditions. The relatively lower evaporation rate of groundwater is attributed to the short residence time of the infiltrating water within the evaporation extinguishing depth in the vadose zone.
- Groundwater recharge from meteoric water tends to have higher concentrations of heavier isotopes relative to the LMWL. This enrichment occurs due to significant evaporation either at the land surface or during seepage through the vadose zone. The rate of evaporation of infiltrating water is likely influenced by factors such as the thickness and composition of the material between the surface and the saturated zone, as well as the high temperatures and low relative humidity prevailing in the region.
- An integrated analysis of stable isotope data and water level measurements suggests a potential hydraulic connection between surface water and groundwater. This hypothesis is supported by the fact that the isotopes of groundwater have comparatively lower values than surface water. Furthermore, the observation that the groundwater level remains constant in months with lower rainfall further supports this conclusion.
- The primary groundwater recharge area is in the northern zone, where the highest recharge occurs. The calculated recharge values show a gradual decline from the northern regions towards the southern areas of the basin.
- Groundwater recharge for the study catchment, considering the average estimate of 1.64% (WTF) and minimum annual precipitation of 1300 mm, is 228 M , which is higher than the estimated water use for the entire Pra Basin, underscoring a high potential for water supply.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Community | Northings (m) | Eastings (m) | Elevation (m) | (mg/L) | Recharge (mm) | As % of Annual Rainfall |
|---|---|---|---|---|---|---|
| Apapaw | 765,897.0 | 680,069.0 | 362.0 | 34.9 | 48.6 | 3.2 |
| Asiakwa SOS | 776,819.0 | 693,156.0 | 238.0 | 3.5 | 486.6 | 32.4 |
| Jejeti | 759,161.8 | 716,496.3 | 204.0 | 9.0 | 188.8 | 12.6 |
| Asubone | 754,144.0 | 724,194.0 | 219.0 | 18.7 | 90.8 | 6.1 |
| Kokrompe | 751,209.0 | 715,992.0 | 205.0 | 10.4 | 163.4 | 10.9 |
| Kofi dede | 735,301.0 | 732,346.0 | 225.0 | 9.2 | 184.2 | 12.3 |
| Kwahu Besease | 732,647.0 | 730,776.0 | 220.0 | 38.5 | 44.0 | 2.9 |
| Kwahu Oda | 731,178.0 | 728,046.0 | 201.0 | 7.9 | 214.0 | 14.3 |
| Kwaben | 766,831.0 | 700,042.0 | 210.0 | 6.1 | 279.7 | 18.6 |
| Akrofofo | 763,058.0 | 702,365.0 | 181.0 | 3.5 | 666.2 | 32.0 |
| Asunafo | 753,556.0 | 701,388.0 | 171.0 | 3.4 | 502.5 | 33.5 |
| Bomaa | 766,573.0 | 695,707.0 | 248.0 | 10.9 | 155.9 | 10.4 |
| Pamang | 763,069.0 | 686,882.0 | 223.0 | 3.4 | 501.5 | 33.4 |
| Kwamang | 752,530.0 | 686,709.0 | 175.0 | 4.3 | 393.3 | 26.2 |
| Okyinso | 744,419.0 | 687,559.0 | 158.0 | 3.2 | 522.3 | 32.0 |
| Akyem Abodom | 741,242.0 | 680,849.7 | 143.0 | 18.9 | 89.9 | 6.0 |
| Subi | 7395,30.0 | 678,458.8 | 164.0 | 6.7 | 251.9 | 16.8 |
| Abompe | 734,625.3 | 685,930.3 | 181.0 | 6.3 | 267.8 | 17.9 |
| Otumi | 731,175.3 | 688,002.9 | 186.0 | 34.6 | 49.0 | 3.3 |
| Kade | 739,619.2 | 673,085.2 | 132.0 | 35.0 | 48.4 | 3.2 |
| Akwatia | 742,140.6 | 666,200.2 | 169.0 | 14.2 | 119.1 | 7.9 |
| Kusi | 736,501.7 | 668,688.9 | 145.0 | 6.2 | 273.3 | 18.2 |
| Awaham | 753,138.8 | 658,835.2 | 198.0 | 49.2 | 34.4 | 2.3 |
| Kakoasi | 742,452.0 | 658,015.0 | 125.0 | 23.2 | 73.0 | 4.9 |
| Etwereso | 705,906.0 | 664,604.8 | 140.0 | 9.3 | 181.9 | 12.1 |
| Zevor | 704,904.4 | 658,538.3 | 112.0 | 16.8 | 101.0 | 6.7 |
| Lebikrom | 724,448.3 | 664,516.9 | 145.0 | 5.3 | 320.1 | 21.3 |
| Soabe | 730,327.1 | 663,168.4 | 136.0 | 15.9 | 106.9 | 7.1 |
| Oda | 721,159.6 | 655,929.2 | 121.0 | 98.0 | 17.3 | 1.2 |
| Atutumirem | 723,063.7 | 649,411.2 | 115.0 | 49.6 | 34.1 | 2.3 |
| Aprade | 710,391.5 | 639,605.4 | 165.0 | 6.0 | 284.1 | 18.9 |
| Kenie | 697,462.6 | 641,406.8 | 131.0 | 10.5 | 162.1 | 10.8 |
| Obobakrokrowa | 701,896.6 | 645,044.1 | 126.0 | 12.5 | 135.8 | 9.1 |
| Akotikrom | 704,676.7 | 649,089.0 | 129.0 | 21.5 | 78.7 | 5.2 |
| Nyamebekyere | 683,039.0 | 637,611.0 | 135.2 | 12.9 | 131.4 | 8.8 |
| Ababuom | 687,388.0 | 623,282.0 | 111.2 | 7.6 | 223.0 | 14.9 |
| Bronokrom | 656,858.0 | 561,969.0 | 14.0 | 55.0 | 30.8 | 2.1 |
| Brunokrom | 656,856.0 | 561,958.0 | 14.0 | 196.7 | 8.6 | 0.6 |
| Kotogyina | 644,148.0 | 558,902.0 | 32.5 | 87.9 | 19.3 | 1.3 |
| Abotere | 642,296.0 | 564,153.0 | 29.5 | 58.1 | 29.1 | 1.9 |
| Dompin | 647,796.3 | 563,871.1 | 14.0 | 33.9 | 50.0 | 3.3 |
| Ewiadaso | 646,686.0 | 572,168.0 | 60.0 | 27.2 | 62.4 | 4.2 |
| Nyekompoe | 652,970.0 | 577,496.0 | 38.4 | 20.7 | 82.0 | 5.5 |
| Essamang | 646,554.0 | 591,595.0 | 51.3 | 12.4 | 136.6 | 9.1 |
| Mamponso | 651,448.0 | 600,012.0 | 40.3 | 10.0 | 169.6 | 11.3 |
| Anyanasi | 654,795.0 | 618,484.0 | 68.1 | 34.2 | 49.5 | 3.3 |
| Dokoro | 646,702.0 | 620,785.0 | 97.0 | 14.2 | 119.5 | 8.0 |
| Somnyamekor | 656,844.5 | 625,862.5 | 84.0 | 12.0 | 141.3 | 9.4 |
| Breman | 654,738.0 | 631,093.0 | 75.0 | 79.5 | 21.3 | 1.4 |
| Imbrain | 636,514.0 | 642,921.0 | 141.9 | 17.5 | 96.9 | 6.5 |
| Akonfudi | 686,960.0 | 644,646.0 | 98.1 | 35.8 | 47.3 | 3.2 |
| Kenkuase | 671,977.0 | 618,658.0 | 94.2 | 19.6 | 86.6 | 5.8 |
| Okyerekrom | 667,847.0 | 626,235.0 | 79.2 | 5.1 | 334.0 | 22.3 |
| Twifo Mamp | 660,003.0 | 610,858.0 | 63.2 | 122.0 | 13.9 | 0.9 |
| Wawase | 668,444.0 | 599,214.0 | 105.0 | 13.4 | 126.5 | 8.4 |


References
- Manu, E.; De Lucia, M.; Kühn, M. Hydrochemical characterization of groundwater in the crystalline basement aquifer system in the Pra Basin (Ghana). Water 2023, 15, 1325. [Google Scholar] [CrossRef]
- Afrifa, G.Y.; Sakyi, P.A.; Chegbeleh, L.P. Estimation of groundwater recharge in sedimentary rock aquifer systems in the Oti basin of Gushiegu District, Northern Ghana. J. Afr. Earth Sci. 2017, 131, 272–283. [Google Scholar] [CrossRef]
- Yidana, S.M.; Ganyaglo, S.; Banoeng-Yakubo, B.; Akabzaa, T. A conceptual framework of groundwater flow in some crystalline aquifers in Southeastern Ghana. J. Afr. Earth Sci. 2011, 59, 185–194. [Google Scholar] [CrossRef]
- Okofo, L.B.; Martienssen, M. A three-dimensional numerical groundwater flow model to assess the feasibility of managed aquifer recharge in the Tamne River basin of Ghana. Hydrogeol. J. 2022, 30, 1071–1090. [Google Scholar] [CrossRef]
- Yidana, S.M.; Alfa, B.; Banoeng-Yakubo, B.; Obeng Addai, M. Simulation of groundwater flow in a crystalline rock aquifer system in Southern Ghana—An evaluation of the effects of increased groundwater abstraction on the aquifers using a transient groundwater flow model. Hydrol. Process. 2014, 28, 1084–1094. [Google Scholar] [CrossRef]
- Mace, R.E.; Chowdhury, A.H.; Anaya, R.; Way, S.C.T. A Numerical Groundwater Flow Model of the Upper and Middle Trinity Aquifer, Hill Country Area; Texas Water Development Board Open File Report 00-02; Texas Water Development Board: Austin, TX, USA, 2000.
- Addai, M.O.; Yidana, S.M.; Chegbeleh, L.P.; Adomako, D.; Banoeng-Yakubo, B. Groundwater recharge processes in the Nasia sub-catchment of the White Volta Basin: Analysis of porewater characteristics in the unsaturated zone. J. Afr. Earth Sci. 2016, 122, 4–14. [Google Scholar] [CrossRef]
- Obuobie, E.; Diekkrueger, B.; Reichert, B. Use of chloride mass balance method for estimating the groundwater recharge in northeastern Ghana. Int. J. River Basin Manag. 2010, 8, 245–253. [Google Scholar] [CrossRef]
- Adomako, D.; Maloszewski, P.; Stumpp, C.; Osae, S.; Akiti, T. Estimating groundwater recharge from water isotope (δ2H, δ18O) depth profiles in the Densu River basin, Ghana. Hydrol. Sci. J. 2010, 55, 1405–1416. [Google Scholar] [CrossRef]
- Gibrilla, A.; Fianko, J.R.; Ganyaglo, S.; Adomako, D.; Stigter, T.Y.; Salifu, M.; Anornu, G.; Zango, M.S.; Zakaria, N. Understanding recharge mechanisms and surface water contribution to groundwater in granitic aquifers, Ghana: Insights from stable isotopes of δ2H and δ18O. J. Afr. Earth Sci. 2022, 192, 104567. [Google Scholar] [CrossRef]
- Yidana, S. The stable isotope characteristics of groundwater in the Voltaian Basin—An evaluation of the role of meteoric recharge in the basin. J. Hydrogeol. Hydrol. Eng. 2013, 2, 2. [Google Scholar]
- Love, A.; Herczeg, A.; Armstrong, D.; Stadter, F.; Mazor, E. Groundwater flow regime within the Gambier Embayment of the Otway Basin, Australia: Evidence from hydraulics and hydrochemistry. J. Hydrol. 1993, 143, 297–338. [Google Scholar] [CrossRef]
- Davisson, M.; Smith, D.; Kenneally, J.; Rose, T. Isotope hydrology of southern Nevada groundwater: Stable isotopes and radiocarbon. Water Resour. Res. 1999, 35, 279–294. [Google Scholar] [CrossRef]
- Duah, A.A.; Akurugu, B.A.; Darko, P.K.; Manu, E.; Mainoo, P.A. Groundwater recharge and potential exploitation in the Densu basin, Southwestern Ghana. J. Afr. Earth Sci. 2021, 183, 104332. [Google Scholar] [CrossRef]
- Eriksson, E.; Khunakasem, V. Chloride concentration in groundwater, recharge rate and rate of deposition of chloride in the Israel Coastal Plain. J. Hydrol. 1969, 7, 178–197. [Google Scholar] [CrossRef]
- Marei, A.; Khayat, S.; Weise, S.; Ghannam, S.; Sbaih, M.; Geyer, S. Estimating groundwater recharge using the chloride mass-balance method in the West Bank, Palestine. Hydrol. Sci. J. 2010, 55, 780–791. [Google Scholar] [CrossRef]
- Dassi, L. Use of chloride mass balance and tritium data for estimation of groundwater recharge and renewal rate in an unconfined aquifer from North Africa: A case study from Tunisia. Environ. Earth Sci. 2010, 60, 861–871. [Google Scholar] [CrossRef]
- Gebru, T.A.; Tesfahunegn, G.B. Chloride mass balance for estimation of groundwater recharge in a semi-arid catchment of northern Ethiopia. Hydrogeol. J. 2019, 27, 363–378. [Google Scholar] [CrossRef]
- Uugulu, S.; Wanke, H. Estimation of groundwater recharge in savannah aquifers along a precipitation gradient using chloride mass balance method and environmental isotopes, Namibia. Phys. Chem. Earth Parts a/b/c 2020, 116, 102844. [Google Scholar] [CrossRef]
- Zhu, C.; Winterle, J.R.; Love, E.I. Late Pleistocene and Holocene groundwater recharge from the chloride mass balance method and chlorine-36 data. Water Resour. Res. 2003, 39, 7. [Google Scholar] [CrossRef]
- McNamara, J.P. An Assessment of the Potential for Using Water and Chloride Budgets to Estimate Groundwater Recharge in Granitic, Mountain Environments. Final Report. 2005. Available online: https://www2.deq.idaho.gov/admin/LEIA/api/document/download/4654 (accessed on 30 April 2023).
- Delin, G.N.; Healy, R.W.; Lorenz, D.L.; Nimmo, J.R. Comparison of local-to regional-scale estimates of ground-water recharge in Minnesota, USA. J. Hydrol. 2007, 334, 231–249. [Google Scholar] [CrossRef]
- Obuobie, E.; Diekkrueger, B.; Agyekum, W.; Agodzo, S. Groundwater level monitoring and recharge estimation in the White Volta River basin of Ghana. J. Afr. Earth Sci. 2012, 71, 80–86. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Healy, R.W.; Cook, P.G. Choosing appropriate techniques for quantifying groundwater recharge. Hydrogeol. J. 2002, 10, 18–39. [Google Scholar] [CrossRef]
- Healy, R.W.; Cook, P.G. Using groundwater levels to estimate recharge. Hydrogeol. J. 2002, 10, 91–109. [Google Scholar] [CrossRef]
- Risser, D.W.; Gburek, W.J.; Folmar, G.J. Comparison of Methods for Estimating Ground-Water Recharge and Base Flow at a Small Watershed Underlain by Fractured Bedrock in the Eastern United States; US Geological Survey; US Department of the Interior: Washington, DC, USA, 2005; Volume 5038.
- Water Resources Commission, W.R.C. Pra River Basin—Integrated Water Resources Management Plan. Available online: https://www.wrc-gh.org/documents/reports/ (accessed on 23 March 2023).
- Manu, E.; Vieth-Hillebrand, A.; Rach, O.; Schleicher, A.M.; Trumbull, R.; Stammeier, J.A.; Gottsche, A.; Kühn, M. Hydrochemistry and stable oxygen (δ18O) and hydrogen (δ2H) isotopic composition of surface water and groundwater and mineralogy, in the Pra Basin (Ghana) West Africa. GFZ Data Serv. 2023. [Google Scholar] [CrossRef]
- Kankam-Yeboah, K.; Obuobie, E.; Amisigo, B.; Opoku-Ankomah, Y. Impact of climate change on streamflow in selected river basins in Ghana. Hydrol. Sci. J. 2013, 58, 773–788. [Google Scholar] [CrossRef]
- Benneh, G.; Dickson, K. A New Geography of Ghana, Revised ed.; Longman: London, UK, 1995. [Google Scholar]
- Banoeng-Yakubo, B.; Yidana, S.; Ajayi, J.; Loh, Y.; Asiedu, D. Hydrogeology and groundwater resources of Ghana: A review of the hydrogeological zonation in Ghana. In Potable Water and Sanitation; Nova Science Publishers, Inc.: Hauppauge, NY, USA, 2010. [Google Scholar]
- Banoeng-Yakubo, B.; Yidana, S.M.; Nti, E. An evaluation of the genesis and suitability of groundwater for irrigation in the Volta Region, Ghana. Environ. Geol. 2009, 57, 1005–1010. [Google Scholar] [CrossRef]
- Kortatsi, B.K. Hydrochemical framework of groundwater in the Ankobra Basin, Ghana. Aquat. Geochem. 2007, 13, 41–74. [Google Scholar] [CrossRef]
- Carrier, M.A.; Lefebvre, R.; Racicot, J.; Asare, E.B. Northern Ghana hydrogeological assessment project. In Proceedings of the 33rd WEDC International Conference, Accra, Ghana, 7–11 April 2008. [Google Scholar]
- Ganyaglo, S.Y.; Banoeng-Yakubo, B.; Osae, S.; Dampare, S.B.; Fianko, J.R.; Bhuiyan, M.A. Hydrochemical and isotopic characterisation of groundwaters in the eastern region of Ghana. J. Water Resour. Prot. 2010, 2, 199. [Google Scholar] [CrossRef]
- Dapaah-Siakwan, S.; Gyau-Boakye, P. Hydrogeologic framework and borehole yields in Ghana. Hydrogeol. J. 2000, 8, 405–416. [Google Scholar] [CrossRef]
- Akiti, T. Environmental isotope study of ground water in crystalline rocks of the Accra plains (Ghana). In Proceedings of the 4th Working Meeting on Isotopes in Nature, Leipzig, Germany, 22–26 September 1986. [Google Scholar]
- Craig, H. Isotopic variations in meteoric waters. Science 1961, 133, 1702–1703. [Google Scholar] [CrossRef]
- Sheffield, J.; Goteti, G.; Wood, E.F. Development of a 50-year high-resolution global dataset of meteorological forcings for land surface modeling. J. Clim. 2006, 19, 3088–3111. [Google Scholar] [CrossRef]
- Craig, H.; Gordon, L.I. Deuterium and oxygen 18 variations in the ocean and the marine atmosphere. In Stable Isotopes in Oceanographic Studies and Paleotemperatures; Tongiorgi, E., Ed.; Consiglio Nazionale delle Richerche, Laboratorio de Geologia Nucleare: Pisa, Italy, 1965; pp. 9–130. [Google Scholar]
- Fellman, J.B.; Dogramaci, S.; Skrzypek, G.; Dodson, W.; Grierson, P.F. Hydrologic control of dissolved organic matter biogeochemistry in pools of a subtropical dryland river. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Gibson, J.; Reid, R. Stable isotope fingerprint of open-water evaporation losses and effective drainage area fluctuations in a subarctic shield watershed. J. Hydrol. 2010, 381, 142–150. [Google Scholar] [CrossRef]
- Loh, Y.S.A.; Fynn, O.F.; Manu, E.; Afrifa, G.Y.; Addai, M.O.; Akurugu, B.A.; Yidana, S.M. Groundwater-surface water interactions: Application of hydrochemical and stable isotope tracers to the lake bosumtwi area in Ghana. Environ. Earth Sci. 2022, 81, 1–15. [Google Scholar] [CrossRef]
- Dogramaci, S.; Skrzypek, G.; Dodson, W.; Grierson, P.F. Stable isotope and hydrochemical evolution of groundwater in the semi-arid Hamersley Basin of subtropical northwest Australia. J. Hydrol. 2012, 475, 281–293. [Google Scholar] [CrossRef]
- Welhan, J.; Fritz, P. Evaporation pan isotopic behavior as an index of isotopic evaporation conditions. Geochim. Cosmochim. Acta 1977, 41, 682–686. [Google Scholar] [CrossRef]
- Allison, G.; Leaney, F. Estimation of isotopic exchange parameters, using constant-feed pans. J. Hydrol. 1982, 55, 151–161. [Google Scholar] [CrossRef]
- Turner, B.F.; Gardner, L.; Sharp, W.E.; Blood, E. The geochemistry of Lake Bosumtwi, a hydrologically closed basin in the humid zone of tropical Ghana. Limnol. Oceanogr. 1996, 41, 1415–1424. [Google Scholar] [CrossRef]
- Gonfiantini, R. Environmental isotopes in lake studies. In Handbook of Environmental Isotopes Geochemistry; Fritz, P., Fontes, J.C., Eds.; Elsevier: New York, NY, USA, 1986; Volume II, pp. 113–168. [Google Scholar]
- Adsiz, C.; Skrzypek, G.; McCallum, J. The measurement of ambient air moisture stable isotope composition for the accurate estimation of evaporative losses. MethodsX 2023, 11, 102265. [Google Scholar] [CrossRef]
- Peng, T.R.; Huang, C.C.; Wang, C.H.; Liu, T.K.; Lu, W.C.; Chen, K.Y. Using oxygen, hydrogen, and tritium isotopes to assess pond water’s contribution to groundwater and local precipitation in the pediment tableland areas of northwestern Taiwan. J. Hydrol. 2012, 450, 105–116. [Google Scholar] [CrossRef]
- Dickson, K.B.; Benneh, G.; Essah, R. A New Geography of Ghana; Longman: London, UK, 1988; Volume 34. [Google Scholar]
- Sinha, B.; Sharma, S.K. Natural Ground Water Recharge Estimation Methodologies in India; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Bergesen, H.O.; Parmann, G.; Thommessen, Ø.B. United Nations Framework Convention on Climate Change (UNFCCC). In Yearbook of International Cooperation on Environment and Development 1998–99; Routledge: Boca Raton, FL, USA, 2018; pp. 73–77. [Google Scholar]
- Barnes, C.; Allison, G. Tracing of water movement in the unsaturated zone using stable isotopes of hydrogen and oxygen. J. Hydrol. 1988, 100, 143–176. [Google Scholar] [CrossRef]
- Fan, Y.; Chen, Y.; Li, X.; Li, W.; Li, Q. Characteristics of water isotopes and ice-snowmelt quantification in the Tizinafu River, north Kunlun Mountains, Central Asia. Quat. Int. 2015, 380, 116–122. [Google Scholar] [CrossRef]
- Dawson, T.E.; Mambelli, S.; Plamboeck, A.H.; Templer, P.H.; Tu, K.P. Stable isotopes in plant ecology. Annu. Rev. Ecol. Syst. 2002, 33, 507–559. [Google Scholar] [CrossRef]
- Okofo, L.B.; Adonadaga, M.G.; Martienssen, M. Groundwater age dating using multi-environmental tracers (SF6, CFC-11, CFC-12, δ18O, and δD) to investigate groundwater residence times and recharge processes in Northeastern Ghana. J. Hydrol. 2022, 610, 127821. [Google Scholar] [CrossRef]
- Manu, E.; De Lucia, M.; Kühn, M. Water–Rock Interactions Driving Groundwater Composition in the Pra Basin (Ghana) Identified by Combinatorial Inverse Geochemical Modelling. Minerals 2023, 13, 899. [Google Scholar] [CrossRef]
- Banoeng-Yakubu, B.; Yidana, S.; Ajayi, J.; Loh, Y.; Aseidu, D. Hydrogeology and groundwater resources of Ghana: A review of the hydrogeology and hydrochemistry of Ghana. In Potable Water and Sanitation; Nova Science Publishers, Inc.: Hauppauge, NY, USA, 2011; p. 142. [Google Scholar]
- Lee, J.Y.; Yi, M.J.; Hwang, D. Dependency of hydrologic responses and recharge estimates on water-level monitoring locations within a small catchment. Geosci. J. 2005, 9, 277–286. [Google Scholar] [CrossRef]


| Community | Well ID | Longitude | Latitude | Elevation (m) | Well Depth (m) | Geology |
|---|---|---|---|---|---|---|
| Abaam | PTB 20 | −0.82403 | 6.22183 | 146 | 70.8 | Meta-sediment |
| Asubone Rail | PTB 30 | −0.73244 | 6.47144 | 191 | 27.0 | Meta-sediment |
| Krobo | PTB 21 | −1.60335 | 5.06144 | 13 | 56.0 | Meta-sediment |
| Kwabeng | PTB 31 | −0.58864 | 6.32337 | 207 | 37.0 | Meta-sediment |
| Wawase | PTB 25 | −1.48185 | 5.14681 | 59 | 20.0 | Meta-sediment |
| Bronikrom | PTB 28 | −1.36528 | 6.07804 | 140 | 80.0 | Meta-sediment |
| Afosu | PTB 29 | −1.00022 | 6.37052 | 187 | 48.0 | Meta-sediment |
| Dunkwa-K | PTB 26 | −1.67817 | 5.92007 | 105 | 36.7 | Sandstone |
| Twifo-Mamp | PTB 17 | −1.62684 | 5.66945 | 88 | 28.6 | Granite |
| Atuntumirem | PTB 19 | −0.98522 | 5.87161 | 133 | 40.5 | Granite |
| Material | Range of Specific Yield |
|---|---|
| Sandy alluvium | 0.12–0.18 |
| Valley fills | 0.10–0.14 |
| Silt/clay rich alluvium | 0.05–0.12 |
| Sandstone | 0.01–0.08 |
| Limestone | 0.03 |
| Highly karstified limestone | 0.07 |
| Granite | 0.02–0.04 |
| Basalt | 0.01–0.03 |
| Laterite | 0.02–0.04 |
| Weathered phyllite, shale, schist, and associated rocks | 0.01–0.03 |
| Well Location | Aquifer Material | Specific Yield () | Δh (m) 1st Wet Season | Δh (m) 2nd Wet Season | Recharge (mm) 1st Wet Season | Recharge (mm) 2nd Wet Season | Mean Recharge (mm) | As % of Annual Rainfall |
|---|---|---|---|---|---|---|---|---|
| Abaam | Meta-sediments | 0.02 | 1.60 | 1.13 | 32.0 | 22.6 | 27.3 | 1.82 |
| Asuboni | Meta-sediments | 0.02 | 0.87 | 1.07 | 17.4 | 21.4 | 19.4 | 1.29 |
| Krobo | Meta-sediments | 0.02 | 1.85 | 0.15 | 37.0 | 3.0 | 20.0 | 1.33 |
| Kwaben | Meta-sediments | 0.02 | 3.29 | 2.12 | 65.8 | 42.4 | 54.1 | 3.60 |
| Wawaase | Meta-sediments | 0.02 | 1.24 | 0.92 | 24.8 | 18.4 | 21.6 | 1.44 |
| Bronikrom | Meta-sediments | 0.02 | 0.12 | 0.23 | 2.4 | 4.6 | 3.5 | 0.23 |
| Afosu | Meta-sediments | 0.02 | 0.85 | 0.74 | 17.0 | 14.8 | 15.9 | 1.06 |
| Dunkwa-K | Sandstone | 0.05 | 0.73 | 0.49 | 36.5 | 24.5 | 30.5 | 2.00 |
| Twifo Mamp | Granite | 0.03 | 1.47 | 0.77 | 44.1 | 23.1 | 33.6 | 2.20 |
| Atutumirem | Granite | 0.03 | 1.05 | 0.98 | 21.0 | 19.9 | 20.5 | 1.40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manu, E.; De Lucia, M.; Akiti, T.T.; Kühn, M. Stable Isotopes and Water Level Monitoring Integrated to Characterize Groundwater Recharge in the Pra Basin, Ghana. Water 2023, 15, 3760. https://doi.org/10.3390/w15213760
Manu E, De Lucia M, Akiti TT, Kühn M. Stable Isotopes and Water Level Monitoring Integrated to Characterize Groundwater Recharge in the Pra Basin, Ghana. Water. 2023; 15(21):3760. https://doi.org/10.3390/w15213760
Chicago/Turabian StyleManu, Evans, Marco De Lucia, Thomas Tetteh Akiti, and Michael Kühn. 2023. "Stable Isotopes and Water Level Monitoring Integrated to Characterize Groundwater Recharge in the Pra Basin, Ghana" Water 15, no. 21: 3760. https://doi.org/10.3390/w15213760
APA StyleManu, E., De Lucia, M., Akiti, T. T., & Kühn, M. (2023). Stable Isotopes and Water Level Monitoring Integrated to Characterize Groundwater Recharge in the Pra Basin, Ghana. Water, 15(21), 3760. https://doi.org/10.3390/w15213760








