Optimization of Dam Operation and Interaction with Groundwater: An Overview Focusing on Greece
Abstract
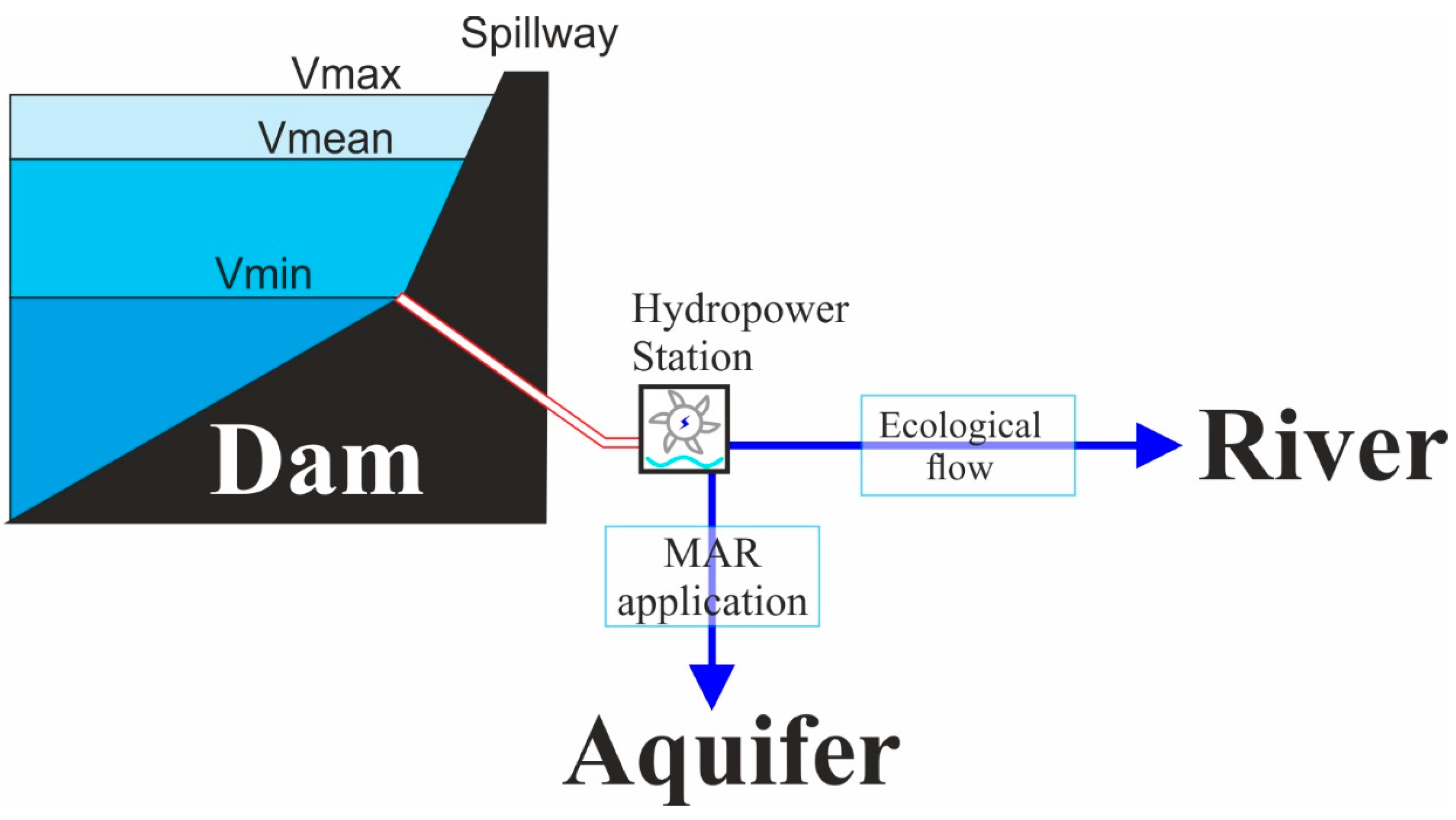
:1. Introduction
2. Hydropower in Greece
3. Water Quality in Reservoirs
- (a)
- excursioni = F2 = − 1;
- (b)
- normalized sum of excursions (nse) = ;
- (c)
- F3 = .
4. Meta-Heuristic Optimization Algorithms
4.1. Harmony Search Algorithm
4.1.1. Characteristics of the Harmony Search Algorithm
4.1.2. Single-Objective and Multi-Objective Optimization
5. Application of Meta-Heuristics Algorithms
5.1. Harmony Search Algorithm on Dams
- Striking the right equilibrium between exploration and exploitation during the quest for ideal solutions;Ithin the HSA algorithm, the management of solution diversity proves notably superior through the utilization of two sub-elements (alteration of pitch and stochastic elements) in contrast to alternative optimization methodologies;
- The harmonious interplay among the three components (harmony memory preservation, pitch adjustment, and stochastiIlements) in HSA empowers the discovery of impartial solutions;Iplementing the HSA algorithm stands out for its simplicity compared to alternative optimization techniques, largely due to its reduced sensitivity to optimization parameters.
5.2. Conceptual Model
- Tp: the time duration of pumping in hours;
- CkWh: the current price of kWh;
- ρ: the density of the pumped fluid in Kg/m3;
- g: the acceleration of gravity in m/s2;
- np: the efficiency rating of each pump;
- Qi: the pumped flow in L/s;
- si: the water level drop at the side of the borehole in meters;
- δ: the distance of the resting level from the ground surface in meters.
6. Limitations of Dam Operation and Future Challenges
- To stockpile water for agricultural, industrial, or residential consumption. The reserved water can be employed for irrigation, livestock hydration, and other water-related purposes.
- To assist in mitigating soil erosion by diminishing the speed of water flow and allowing sediment to settle within the dam-created reservoir.
- To establish diminutive lakes or leisurely ponds, offering prospects for angling and other open-air pursuits.
- To form wetlands conducive to wildlife attraction and biodiversity sustenance.
- For energy production; while larger dams typically cater to extensive hydroelectric power generation, some smaller dams can also be equipped with turbines to produce electricity on a smaller scale.
- To furnish a degree of flood control by temporarily containing excess water during intense rainfall.
- Environmental Consequences: Erecting small dams can have ecological ramifications, encompassing habitat degradation, alterations in river currents, and shifts in sediment transport, which can impact aquatic ecosystems and wildlife habitats. Additionally, dams can reduce groundwater recharge in lowlands aquifers.
- Sediment Accumulation: Small dams can trap sediment, resulting in sediment buildup within the reservoir. Over time, this can diminish storage capacity and influence downstream ecosystems.
- Maintenance and Oversight: Small dams mandate regular upkeep and oversight to guarantee their structural reliability and efficient functionality. Neglecting maintenance can escalate the risks of dam failure and associated hazards.
7. Conclusions
- -
- The are more than 235 dams in Greece with the potential to use water for MAR application;
- -
- The water quality of reservoirs is variable and should be periodically checked;
- -
- The water quality index SRDD is used in the majority of case studies in the literature;
- -
- The HSA algorithm is suggested as the most useful for hydropower generation and MAR application.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lin, N.M.; Rutten, M. Optimal Operation of a Network of Multi-purpose Reservoir: A Review. Procedia Eng. 2016, 154, 1376–1384. [Google Scholar] [CrossRef]
- Graham, E.B.; Stegen, J.C.; Huang, M.; Chen, X.; Scheibe, T.D. Subsurface biogeochemistry is a missing link between ecology and hydrology in dam-impacted river corridors. Sci. Total Environ. 2019, 657, 435–445. [Google Scholar] [CrossRef] [PubMed]
- Luo, Z.; Yong, C.; Fan, J.; Shao, M.; Wang, S.; Jin, M. Precipitation recharges the shallow groundwater of check dams in the loessial hilly and gully region of China. Sci. Total Environ. 2020, 742, 140625. [Google Scholar] [CrossRef]
- Fang, Y.; Zheng, T.; Wang, H.; Zheng, X.; Walther, M. Nitrate transport behavior behind subsurface dams under varying hydrological conditions. Sci. Total Environ. 2022, 838, 155903. [Google Scholar] [CrossRef] [PubMed]
- Fayaed, S.S.; El-Shafie, A.; Jaafar, O. Reservoir system simulation and optimization techniques. Stoch. Environ. Res. Risk Assess. 2013, 27, 1751–1772. [Google Scholar] [CrossRef]
- Busico, G.; Ntona, M.M.; Carvalho, S.C.P.; Patrikaki, O.; Voudouris, K.; Kazakis, N. Simulating future groundwater recharge in coastal and inland catchments. Water Resour. Manag. 2021, 35, 3617–3632. [Google Scholar] [CrossRef]
- Ntona, M.M.; Busico, G.; Mastrocicco, M.; Kazakis, N. Coupling SWAT and DPSIR models for groundwater management in Mediterranean catchments. J. Environ. Manag. 2023, 344, 118543. [Google Scholar] [CrossRef] [PubMed]
- Kaldellis, J.K. The contribution of small hydro power stations to the electricity generation in Greece: Technical and economic considerations. Energy Policy 2007, 35, 2187–2196. [Google Scholar] [CrossRef]
- RAE—Regulatory Authority for Energy. Available online: www.rae.gr (accessed on 1 August 2023).
- Patsialis, T.; Kougias, I.; Kazakis, N.; Theodossiou, N.; Droege, P. Supporting Renewables’ Penetration in Remote Areas through the Transformation of Non-Powered Dams. Energies 2016, 9, 1054. [Google Scholar] [CrossRef]
- YPEKA—Ministry of Environment & Energy. Available online: www.ypeka.gr (accessed on 5 August 2023).
- Kaldellis, J.K.; Katsirou, V.; Kondili, E.; Korbakis, G. Optimal sizing of small hydro power plants for maximum energy production. In Proceedings of the Eigth National Conference on the Soft Energy Resources, Thessaloniki, Greece, 7–9 April 2006. [Google Scholar]
- Patsialis, T.; Kougias, I.; Ganoulis, J.; Theodossiou, N. Irrigation dams for renewable energy production. Econom. Water Manag. Agric. 2014, 12, 270–294. [Google Scholar]
- CRES. Renewable Energy Statistics; National report for EUROSTAT; CRES: Washington, DC, USA, 2006. [Google Scholar]
- Hellenic Association of Small Hydroelectric Plants (EMSYE). Available online: http://microhydropower.gr/ (accessed on 31 October 2023).
- Droege, P. (Ed.) 100% Renewable: Energy Autonomy in Action; Routledge: London, UK, 2012. [Google Scholar]
- Alexakis, D.; Tsihrintzis, V.A.; Tsakiris, G.; Gikas, G. Suitability of Water Quality Indices for Application in Lakes in the Mediterranean. Water Resour. Manag. 2016, 30, 1621–1633. [Google Scholar] [CrossRef]
- Naveedullah, N.; Hashmi, M.Z.; Yu, C.; Shen, C.; Muhammad, N.; Shen, H.; Chen, Y. Water Quality Characterization of the Siling Reservoir (Zhejiang, China) Using Water Quality Index. Clean Soil Air Water 2016, 44, 553–562. [Google Scholar] [CrossRef]
- Fantin-Cruz, I.; Pedrollo, O.; Girard, P.; Zeilhofer, P.; Hamilton, S. Changes in river water quality caused by a diversion hydropower dam bordering the Pantanal floodplain. Hydrobiologia 2016, 768, 223–238. [Google Scholar] [CrossRef]
- Dumitran, E.; Vuta, I.; Popa, B.; Popa, F. Hydrological Variability Impact on Eutrophication in a Large Romanian Border Reservoir, Stanca–Costesti. Water 2020, 12, 3065. [Google Scholar] [CrossRef]
- UNESCO; WHO; UNEP. Water Quality Assessments—A Guide to Use of Biota, Sediments and water in Enviromental Monitoring; University Press: Cambridge, UK, 1996.
- Scott Winton, R.; Calamita, E.; Wehrli, B. Reviews and syntheses: Dams, water quality and tropical reservoir stratification. Biogeosciences 2019, 16, 1657–1671. [Google Scholar] [CrossRef]
- Azadi, F.; Ashofteh, P.S.; Loáiciga, H.A. Reservoir Water-Quality Projections under Climate-Change Conditions. Water Resour. Manag. 2019, 33, 401–421. [Google Scholar] [CrossRef]
- Ziaie, R.; Mohammadnezhad, B.; Taheriyoun, M.; Karimi, A.; Amir, S. Evaluation of Thermal Stratification and Eutrophication in Zayandeh Roud Dam Reservoir Using Two-Dimensional CE-QUAL-W2 Model. J. Environ. Eng. 2019, 145, 05019001. [Google Scholar] [CrossRef]
- Zhang, C.; Lai, S.; Gao, X.; Xu, L. Potential impacts of climate change on water quality in a shallow reservoir in China. Environ. Sci. Pollut. Res. 2015, 22, 14971–14982. [Google Scholar] [CrossRef] [PubMed]
- Friedl, G.; Wüest, A. Disrupting biogeochemical cycles—Consequences of damming. Aquat. Sci. 2002, 64, 55–65. [Google Scholar] [CrossRef]
- Gantzer, P.A.; Bryant, L.D.; Little, J.C. Controlling soluble iron and manganese in a water-supply reservoir using hypolimnetic oxygenation. Water Res. 2009, 43, 1285–1294. [Google Scholar] [CrossRef]
- Mitrakas, M.; Samaras, P.; Stylianou, S.; Kakalis, C.; Zouboulis, A. Artificial destratification of Dipotamos reservoir in Northern Greece by low energy air injection. Water Sci. Technol. Water Supply 2013, 13, 1046–1055. [Google Scholar] [CrossRef]
- Ashby, S. Impacts of hydrology and hydropower on water quality in reservoir tailwaters. WIT Trans. Ecol. Environ. 2009, 124, 1743–3541. [Google Scholar] [CrossRef]
- European Commission. Directive 2000/60/EU: European Water Framework Directive. Off. J. Eur. Communities 2000, L327, 1–73. [Google Scholar]
- Lumb, A.; Sharma, C.; Bibeault, F. A Review of Genesis and Evolution of Water Quality Index (WQI) and Some Future Directions. Water Qual. Expo. Health 2011, 3, 11–24. [Google Scholar] [CrossRef]
- Uddin, M.G.; Nash, S.; Olbert, A.I. A review of water quality index models and their use for assessing surface water quality. Ecol. Indic. 2021, 122, 107218. [Google Scholar] [CrossRef]
- Zotou, I.; Tsihrintzis, V.A.; Gikas, G.D. Comparative Assessment of Various Water Quality Indices (WQIs) in Polyphytos Reservoir-Aliakmon River, Greece. Proceedings 2018, 2, 611. [Google Scholar] [CrossRef]
- Lobato, T.C.; Hauser-Davis, R.A.; Oliveira, T.F.; Silveira, A.M.; Silva HA, N.; Tavares MR, M.; Saraiva AC, F. Construction of a novel water quality index and quality indicator for reservoir water quality evaluation: A case study in the Amazon region. J. Hydrol. 2015, 522, 674–683. [Google Scholar] [CrossRef]
- Horton, K. An index-number system for rating water quality. J. Water Pollut. Control Fed. 1965, 37, 300–306. [Google Scholar]
- Brown, R.M.; McClelland, N.I.; Deininger, R.A.; Tozer, R.G. A water quality index—Do we dare? Water Sew. Work. 1970, 117, 339–343. [Google Scholar]
- Tyagi, S.; Sharma, B.; Singh, P.; Dobhal, R. Water Quality Assessment in Terms of Water Quality Index. Am. J. Water Resour. 2013, 1, 34–38. [Google Scholar] [CrossRef]
- Cude, C.G. Oregon water quality index: A tool for evaluating water quality management effectiveness. J. Am. Water Resour. Assoc. 2001, 37, 125–137. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN′95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Dorigo, M.; Maniezzo, V.; Colorni, A. The Ant System: Optimization by a Colony of Cooperating Agents. IEEE Trans. Syst. Man Cybern. 1996, 26 Pt B, 29–41. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A New Heuristic Optimization Algorithm: Harmony Search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. Harmony Search Optimization: Application to Pipe Network Design. Int. J. Model. Simul. 2002, 22, 125–133. [Google Scholar] [CrossRef]
- Yeh, W. Reservoir Management and Operations Models: A State-of-the-Art Review. Water Resour. Res. 1985, 21, 1797–1818. [Google Scholar] [CrossRef]
- Ko, S.-K.; Fontane, D.G.; Labadie, J.W. Multiobjectwe optimization of reservoir systems operation1. JAWRA J. Am. Water Resour. Assoc. 1992, 28, 111–127. [Google Scholar] [CrossRef]
- Labadie John, W.M. ASCE, Optimal Operation of Multireservoir Systems: State-of-the-Art Review. J. Water Resour. Plan. Manag. 2004, 130, 93–111. [Google Scholar] [CrossRef]
- Chang, L.-C.; Chang, F.-J. Multi-objective evolutionary algorithm for operating parallel reservoir system. J. Hydrol. 2009, 377, 12–20. [Google Scholar] [CrossRef]
- Tospornsampan, J.; Kita, I.; Ishii, M.; Kitamura, Y. Optimization of a multiple reservoir system using a simulated annealing—A case study in the Mae Klong system, Thailand. Paddy Water Environ. 2005, 3, 137–147. [Google Scholar] [CrossRef]
- Cai, W.; Zhang, L.; Zhu, X.; Zhang, A.; Yin, J.; Wang, H. Optimized reservoir operation to balance human and environmental requirements: A case study for the Three Gorges and Gezhouba Dams, Yangtze River basin, China. Ecol. Inform. 2013, 18, 40–48. [Google Scholar] [CrossRef]
- Tospornsampan, J.; Kita, I.; Ishii, M.; Kitamura, Y. Optimization of a multiple reservoir system operation using a combination of genetic algorithm and discrete differential dynamic programming: A case study in Mae Klong system, Thailand. Paddy Water Environ. 2005, 3, 29–38. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Adib, A.; Taghian, M. Optimization of multi-reservoir operation with a new hedging rule: Application of fuzzy set theory and NSGA-II. Appl. Water Sci. 2017, 7, 3075–3086. [Google Scholar] [CrossRef]
- Chen, H.-T.; Wang, W.-C.; Chen, X.-N.; Qiu, L. Multi-objective reservoir operation using particle swarm optimization with adaptive random inertia weights. Water Sci. Eng. 2020, 13, 136–144. [Google Scholar] [CrossRef]
- Lei, X.H.; Tan, Q.F.; Wang, X.; Wang, H.; Wen, X.; Wang, C.; Zhang, J.W. Stochastic optimal operation of reservoirs based on copula functions. J. Hydrol. 2018, 557, 265–275. [Google Scholar] [CrossRef]
- Bashiri-Atrabi, H.; Qaderi, K.; Rheinheimer, D.E.; Sharifi, E. Application of Harmony Search Algorithm to Reservoir Operation Optimization. Water Resour Manag. 2015, 29, 5729–5748. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Karami, H.; Ehteram, M.; Mohd, N.S.; Mousavi, S.F.; Hin, L.S.; Kisi, O.; Farzin, S.; Kim, S.; El-Shafie, A. Optimization of Reservoir Operation using New Hybrid Algorithm. KSCE J. Civ. Eng. 2018, 22, 4668–4680. [Google Scholar] [CrossRef]
- Ehteram, M.; Karami, H.; Farzin, S. Reducing Irrigation Deficiencies Based Optimizing Model for Multi-Reservoir Systems Utilizing Spider Monkey Algorithm. Water Resour. Manag. 2018, 32, 2315–2334. [Google Scholar] [CrossRef]
- Goodarzi, E.; Ziaei, M.; Hosseinipour, E.Z. Reservoir Optimization and Simulation Modeling: A Case Study. In Introduction to Optimization Analysis in Hydrosystem Engineering; Topics in Safety, Risk, Reliability and Quality; Springer: Cham, Switzerland, 2014; Volume 25. [Google Scholar] [CrossRef]
- Malekmohammadi, B.; Zahraie, B.; Kerachian, R. A real-time operation optimization model for flood management in river-reservoir systems. Nat. Hazards 2010, 53, 459–482. [Google Scholar] [CrossRef]
- Saadat, M.; Asghari, K.A. Cooperative Use of Stochastic Dynamic Programming and Non-Linear Programming for Optimization of Reservoir Operation. KSCE J. Civ. Eng. 2018, 22, 2035–2042. [Google Scholar] [CrossRef]
- Afshar, M.H. Large scale reservoir operation by Constrained Particle Swarm Optimization algorithms. J. Hydro-Environ. Res. 2012, 6, 75–87. [Google Scholar] [CrossRef]
- Afshar, A.; Shojaei, N.; Sagharjooghifarahani, M. Multiobjective Calibration of Reservoir Water Quality Modeling Using Multiobjective Particle Swarm Optimization (MOPSO). Water Resour. Manage 2013, 27, 1931–1947. [Google Scholar] [CrossRef]
- Saber Chenari, K.; Abghari, H.; Tabari, H. Application of PSO algorithm in short-term optimization of reservoir operation. Environ. Monit Assess. 2016, 188, 667. [Google Scholar] [CrossRef] [PubMed]
- Kerachian, R.; Karamouz, M. Optimal reservoir operation considering the water quality issues: A stochastic conflict resolution approach. Water Resour. Res. 2006, 42, 12401. [Google Scholar] [CrossRef]
- Ganji, A.; Karamouz, M.; Khalili, D. Development of stochastic dynamic Nash game model for reservoir operation II. The value of players’ information availability and cooperative behaviors. Adv. Water Resour. 2007, 30, 157–168. [Google Scholar] [CrossRef]
- Li, H.; Lian, J. Multi-objective optimization of water-sedimentation-power in reservoir based on pareto-optimal solution. Trans. Tianjin Univ. 2008, 14, 282–288. [Google Scholar] [CrossRef]
- Li, F.-F.; Wei, J.-H.; Fu, X.-D.; Wan, X.-Y. An Effective Approach to Long-Term Optimal Operation of Large-Scale Reservoir Systems: Case Study of the Three Gorges System. Water Resour. Manag. 2012, 26, 4073–4090. [Google Scholar] [CrossRef]
- Bilal; Rani, D.; Pant, M.; Jain, S.K. Dynamic programming integrated particle swarm optimization algorithm for reservoir operation. Int. J. Syst. Assur. Eng. Manag. 2020, 11, 515–529. [Google Scholar] [CrossRef]
- Janga Reddy, M.; Nagesh Kumar, D. Optimal reservoir operation for irrigation of multiple crops using elitist-mutated particle swarm optimization. Hydrol. Sci. J. 2007, 52, 686–701. [Google Scholar] [CrossRef]
- Rani, D.; Srivastava, D.K. Optimal operation of Mula reservoir with combined use of dynamic programming and genetic algorithm. Sustain. Water Resour. Manag. 2016, 2, 1–12. [Google Scholar] [CrossRef]
- Kumar, N.D.; Raju Srinivasa, K.; Ashok, B. Optimal Reservoir Operation for Irrigation of Multiple Crops Using Genetic Algorithms. J. Irrig. Drain. Eng. 2006, 132, 123–139. [Google Scholar] [CrossRef]
- Jothiprakash, V.; Shanthi, G. Single Reservoir Operating Policies Using Genetic Algorithm. Water Resour. Manag. 2006, 20, 917–929. [Google Scholar] [CrossRef]
- Al-Aqeeli, Y.H.; Lee, T.S.; Abd Aziz, S. Enhanced genetic algorithm optimization model for a single reservoir operation based on hydropower generation: Case study of Mosul reservoir, northern Iraq. Springerplus 2016, 5, 797. [Google Scholar] [CrossRef] [PubMed]
- Tran, D.; Kovacs, K.; Wallander, S. Long run optimization of landscape level irrigation through managed aquifer recharge or expanded surface reservoirs. J. Hydrol. 2012, 579, 124220. [Google Scholar] [CrossRef]
- Hınçal, O.; Altan-Sakarya, A.B.; Metin Ger, A. Optimization of Multireservoir Systems by Genetic Algorithm. Water Resour. Manag. 2011, 25, 1465–1487. [Google Scholar] [CrossRef]
- Geem, Z.W. Optimal Scheduling of Multiple Dam System Using Harmony Search Algorithm. In Computational and Ambient Intelligence IWANN 2007; Lecture Notes in Computer Science; Sandoval, F., Prieto, A., Cabestany, J., Graña, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4507. [Google Scholar] [CrossRef]
- Janatrostami, S.; Kholghi, M.; Omid, B.H. Management of Reservoir Operation System Using Improved Harmony Search Algorithm. Water Soil Sci. 2010, 20, 61–71. [Google Scholar]
- Abell, R.; Thieme, M.; Brenner, B.L. Ecoregion conservation for freshwater systems, with a focus on large rivers. In Proceedings of the Second International Symposium on the Management of Large Rivers for Fisheries; Phnom Penh, Kingdom of Cambodia, 11–14 February 2003, Welcomme, R., Petr, T., Eds.; RAP Publication; FAO Regional Office for Asia and the Pacific: Bangkok, Thailand, 2004; Volume 2, pp. 1–14. [Google Scholar]
- Kougias, I.; Ho, V.; Kim, J. A Hybrid Harmony Search Optimization Algorithm: Application on Hydropower in Central Vietnam. In Conference Proceedings: Proceedings of OPT-i Conference on Engineering and Applied Sciences Optimization; National Technical University of Athens (NTUA): Athens, Greece, 2014; pp. 1046–1054, JRC88446. [Google Scholar]
- Mousavi, S.J.; Nakhaei, P.; Sadollah, A.; Kim, J.H. Optimization of hydropower storage projects using harmony search algorithm. In Harmony Search Algorithm, Proceedings of the 3rd International Conference on Harmony Search Algorithm (ICHSA 2017), Bilbao, Spain, 22–24 February 2017; Advances in Intelligent Systems and Computing; Del Ser, J., Ed.; Springer: Singapore, 2017; Volume 514. [Google Scholar] [CrossRef]
- Hassanvand, M.R.; Karami, H.; Mousavi, S. Use of multi-criteria decision-making for selecting spillway type and optimizing dimensions by applying the harmony search algorithm: Qeshlagh Dam Case Study. Lakes Reserv. Res. Manag. 2018, 24, 66–75 . [Google Scholar] [CrossRef]
- Kougias, I.; Karakatsanis, D.; Malatras, A.; Monforti-Ferrario, F.; Theodossiou, N. Renewable energy production management with a new harmony search optimization toolkit. Clean Technol. Environ. Policy 2016, 18, 2603–2612, JRC97549. [Google Scholar] [CrossRef]
- Cisty, M.; Soldanova, V. Ensemble Prediction of Stream Flows Enhanced by Harmony Search Optimization; IntechOpen: London, UK, 2018. [Google Scholar] [CrossRef]
- Azizipour, M.; Sattari, A.; Afshar, M.H.; Goharian, E.; Solis, S.S. Optimal hydropower operation of multi-reservoir systems: Hybrid cellular automata-simulated annealing approach. J. Hydroinf. 2020, 22, 1236–1257. [Google Scholar] [CrossRef]
- Shams, M.; El-Banbi, A.; Sayyouh, H. Harmony search optimization applied to reservoir engineering assisted history matching. Pet. Explor. Dev. 2020, 47, 154–160. [Google Scholar] [CrossRef]
- Acreman, M.; Dunbar, M.J. Defining environmental river flow requirements—A review. Hydrol. Earth Syst. Sci. 2005, 8, 861–876. [Google Scholar] [CrossRef]
- Dyson, M.; Bergkamp, G.; Scanlon, J. Flow: The essential of environmental flows. In Water and Nature Initiative; IUCN: Gland, Switzerland, 2003. [Google Scholar]
- Joint Ministerial Decision 12160/1999 Generating candidate selection process for issuing installation of small hydropower projects with optimal utilization of available water. Government Gazette Β’ 1552/3.8.1999.
- Brown, C.; King, J. Environmental Flow Assessment: Concepts and Method; Water Resources and Environment, Technical Note C.1.; World Bank: Washington, DC, USA, 2003. [Google Scholar]
- Kumar, A.; Schei, T.; Ahenkorah, A.; Caceres Rodriguez, R.; Devernay, J.M.; Freitas, M.; Hall, D.; Killingtveit, A.; Liu, Z. Hydropower. In IPCC Special Report on Renewable Energy Sources and Climate Change Mitigation; Edenhofer, O., Pichs Madruga, R., Sokona, Y., Seyboth, K., Matschoss, P., Kadner, S., Zwickel, T., Eickemeier, P., Hansen, G., Schlömer, S., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2011. [Google Scholar]
- Richter, B.D.; Baumgartner, J.V.; Wigington, R.; Braun, D.P. How much water does a river need? Freshw. Biol. 1997, 37, 231–249. [Google Scholar] [CrossRef]
- Richter, B.; Mathews, R.; Harrison, D.; Wigington, R. Ecologically Sustainable Water Management: Managing River Flows for Ecological Integrity. Ecol. Appl. 2003, 13, 206–224. [Google Scholar] [CrossRef]
- Tennant, D.L. Instream flow regimes for fish, wildlife, recreation and related environmental resources. Fisheries 1976, 1, 6–10. [Google Scholar] [CrossRef]
- Tharme, R.E. A Global Perspective on Environmental Flow Assessment: Emerging Trends in the Development and Application of Environmental Flow Methodologies for Rivers. River Res. Appl. 2003, 19, 397–441. [Google Scholar] [CrossRef]
- Huggins, R.A. Energy Storage; Springer Science LLC: Secaucus, NJ, USA, 2010. [Google Scholar]
- Baker, J. New technology and possible advances in energy storage. Energy Policy 2008, 36, 4368–4373. [Google Scholar] [CrossRef]
- Ross, M.; Abbey, C.; Bouffard, F.; Jos, G. Multiobjective optimization dispatch for microgridswith a high penetration of renewable generation. IEEE Trans. Sustain. Energy 2015, 6, 1306–1314. [Google Scholar] [CrossRef]
- Tant, J.; Geth, F.; Six, D.; Tant, P.; Driesen, J. Multiobjective battery storage to improve PV integration in residential distribution grids. IEEE Trans. Sustain. Energy 2013, 4, 182–191. [Google Scholar] [CrossRef]
- Official Government Gazette of the Hellenic Republic. Ministerial Decree 8295/95 (PPC-Independent Producer). Volume 2 (385). Available online: http://www.rae.gr (accessed on 4 November 2016).
- Sherif, M.; Sefelnasr, A.; Rashed, M.A.; Alshamsi, D.; Zaidi, F.; Alghafli, K.; Baig, F.; Al-Turbak, A.; Alfaifi, H.; Loni, O.; et al. A review of managed aquifer recharge potential in the Middle East and North Africa region with examples from the Kingdom of Saudi Arabia and the United Arab Emirates. Water 2023, 15, 742. [Google Scholar] [CrossRef]
- Sherif, M.M.; Ebraheem, A.M.; Al Mulla, M.M.; Shetty, A.V. New system for the assessment of annual groundwater recharge from rainfall in the United Arab Emirates. Environ. Earth Sci. 2018, 77, 412. [Google Scholar] [CrossRef]
- Hamed, Y. Climate Change and Water Resources in North Africa. Study Day on Water Resources; University of Sétif: Sétif, Algeria, 2018. Available online: http://iast.univ-setif.dz/2-non-categorise/208-conference-younes-hamed-seminaire-iast (accessed on 9 April 2018).
- Dillon, P.; Arshad, M. Managed Aquifer Recharge in Integrated Water Resource Management. In Integrated Groundwater Management; Springer: Cham, Switzerland, 2016; pp. 435–452. [Google Scholar]
- McDermott, J. When and Why Metaheuristics Researchers can Ignore “No Free Lunch” Theorems. SN Comput. Sci. 2020, 1, 60. [Google Scholar] [CrossRef]




| WQI | Mathematical Expression | Parameters | Reference |
|---|---|---|---|
| NSFWQI: National Sanitation Foundation Water Quality Index | Dissolved oxygen, temperature, pH, BOD, total solids, fecal coliforms, turbidity total phosphate, nitrates | Brown et al. [36] | |
| CCME WQI: Canadian Council of Ministers of the Environment Water Quality Index | Four quality parameters are required but not specified | Tyagi et al. [37] | |
| OWQI: Oregon Water Quality Index | pH, dissolved oxygen, faecal coliforms, BOD, chlorate, nitrates | Cude [38] | |
| SRDD: Scottish Research Development Department index | Temperature, turbidity, total solids, pH, dissolved oxygen, free and saline ammonia, total oxide, nitrogen, phosphate, BOD, Escherichia coli (E. coli) | Uddin et al. [32] |
| Variables | Restrictions | Objective Function |
|---|---|---|
|
| OR Equation (3) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karakatsanis, D.; Patsialis, T.; Kalaitzidou, K.; Kougias, I.; Ntona, M.M.; Theodossiou, N.; Kazakis, N. Optimization of Dam Operation and Interaction with Groundwater: An Overview Focusing on Greece. Water 2023, 15, 3852. https://doi.org/10.3390/w15213852
Karakatsanis D, Patsialis T, Kalaitzidou K, Kougias I, Ntona MM, Theodossiou N, Kazakis N. Optimization of Dam Operation and Interaction with Groundwater: An Overview Focusing on Greece. Water. 2023; 15(21):3852. https://doi.org/10.3390/w15213852
Chicago/Turabian StyleKarakatsanis, Diamantis, Thomas Patsialis, Kyriaki Kalaitzidou, Ioannis Kougias, Maria Margarita Ntona, Nicolaos Theodossiou, and Nerantzis Kazakis. 2023. "Optimization of Dam Operation and Interaction with Groundwater: An Overview Focusing on Greece" Water 15, no. 21: 3852. https://doi.org/10.3390/w15213852
APA StyleKarakatsanis, D., Patsialis, T., Kalaitzidou, K., Kougias, I., Ntona, M. M., Theodossiou, N., & Kazakis, N. (2023). Optimization of Dam Operation and Interaction with Groundwater: An Overview Focusing on Greece. Water, 15(21), 3852. https://doi.org/10.3390/w15213852









