Prediction Model of Residual Soil Shear Strength under Dry–Wet Cycles and Its Uncertainty
Abstract
:1. Introduction
2. Materials and Methods
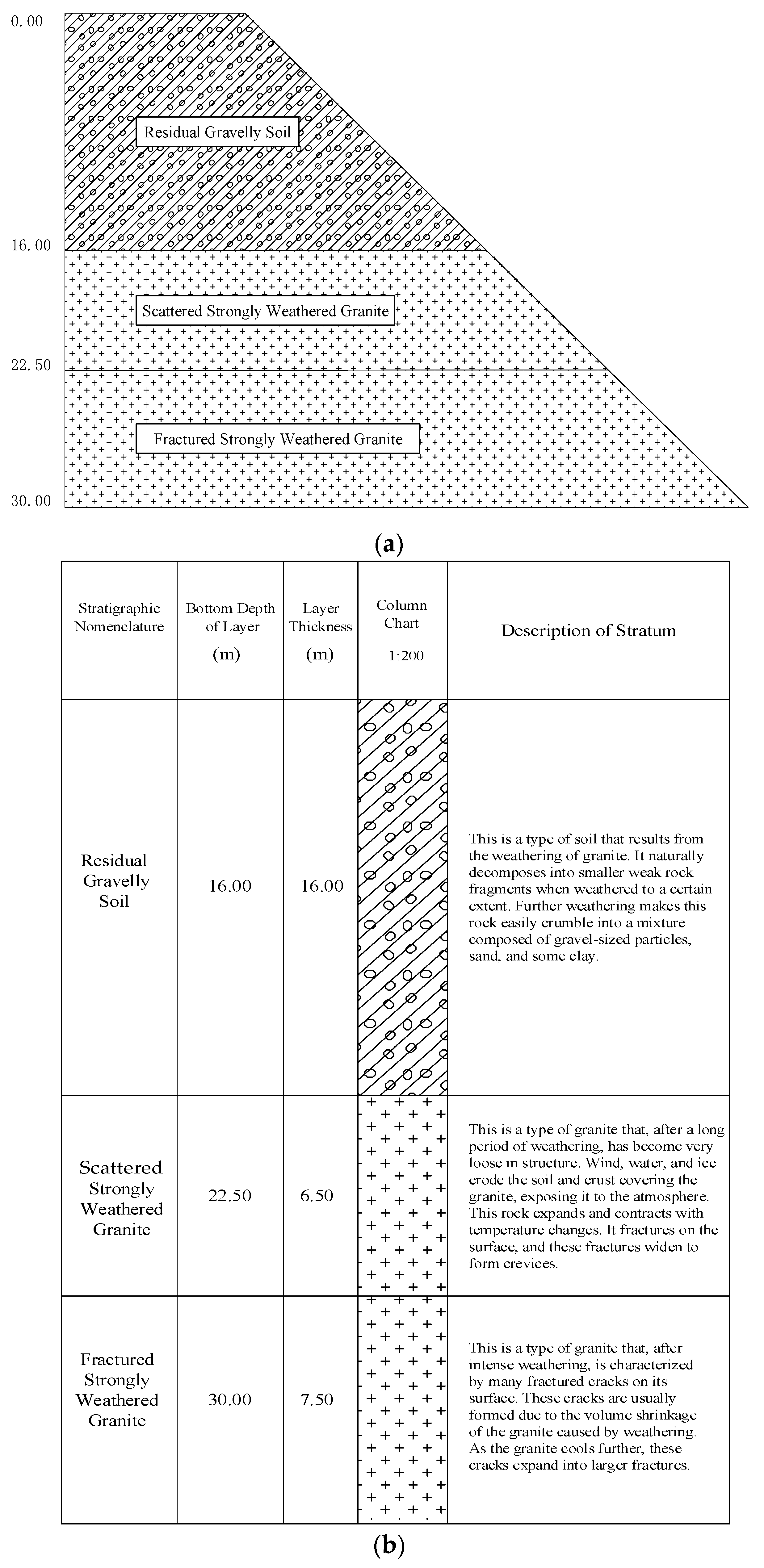
2.1. Overview of Soil Samples

2.2. Experimental Plan
2.2.1. Indoor Wet and Dry Cycle Simulation Test
- According to the physical properties of the soil samples given in Table 1 and the water content and density of the soil samples, calculate the mass of the soil when the water content reaches 12%, 20%, 25%, 30%, and 35%.
- Use an electric fan to accelerate the air-drying speed of the soil samples. Measure the quality of the soil samples every hour to detect whether the water content of the soil samples has reached the predetermined value. When the water content reaches 12%, turn off the electric fan, stop air-drying dehydration immediately, wrap the soil with plastic wrap, and seal it for 24 h to ensure that the moisture inside the soil is evenly distributed.
- Put the soil sample with an initial water content of 12% into a stacked saturation device, and use a vacuum suction device combined with a vacuum suction saturation method to perform suction saturation on the soil sample. After the soil is saturated, use step 2 of the method, using an electric fan to air-dry and dehydrate the saturated soil samples. When the water content of the soil sample reaches 20%, stop air-drying dehydration and wrap it with plastic wrap for sealed curing for 24 h. At this point, a soil sample with a water content of 20% has undergone a complete dry–wet cycle.
- According to steps 2–3, continue to perform dry–wet cycle tests on soil samples with a water content of 20% 2, 4, 6, 8, and 10 times.
- According to steps 1–3, perform indoor simulated dry–wet cycle tests on soil samples with a water content of 25%, 30%, and 35%.
2.2.2. Quick Shear Test
3. Results
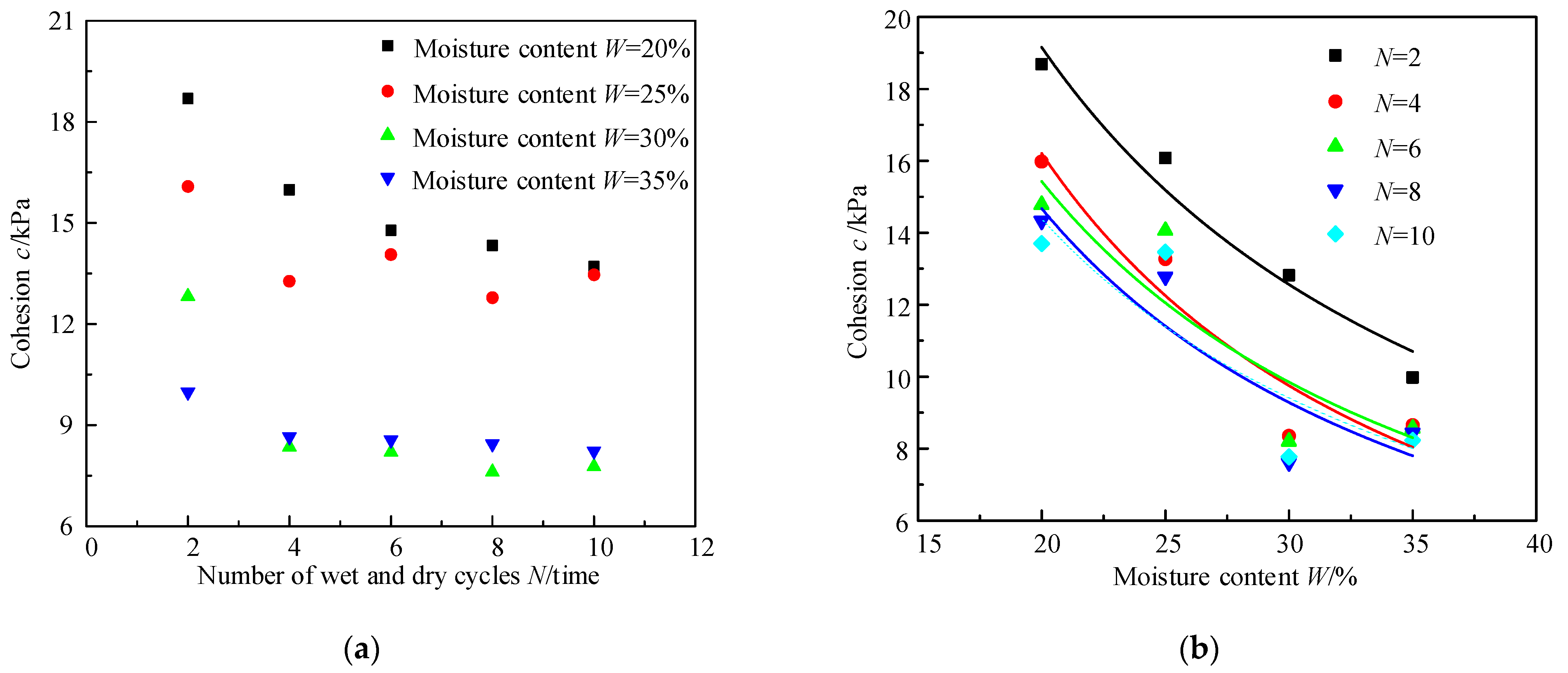
3.1. Relationship among Cohesion, Moisture Content, and Drying and Wetting Cycles of Granite Residual Soil
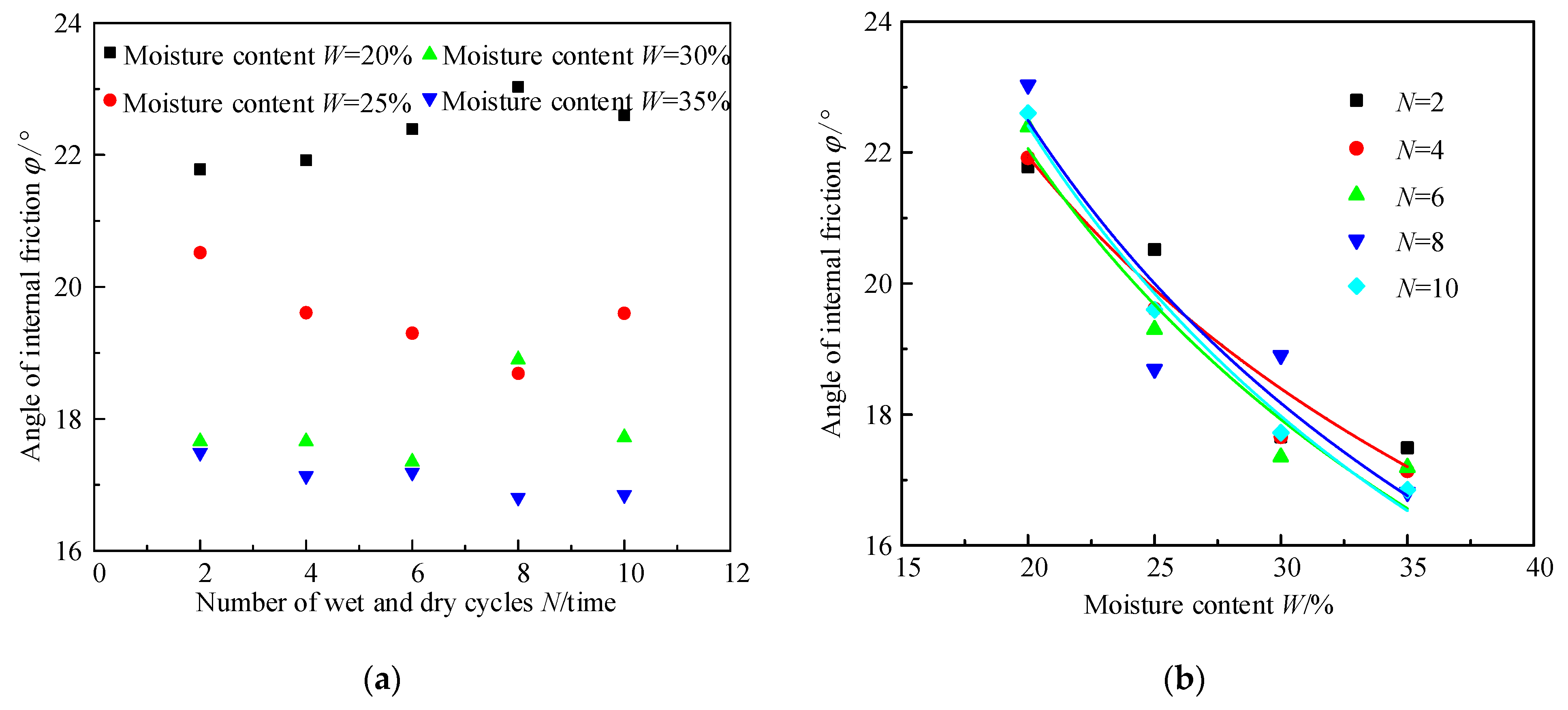
3.2. Relationship among Internal Friction Angle, Moisture Content, and Number of Drying and Wetting Cycles of Granite Residual Soil
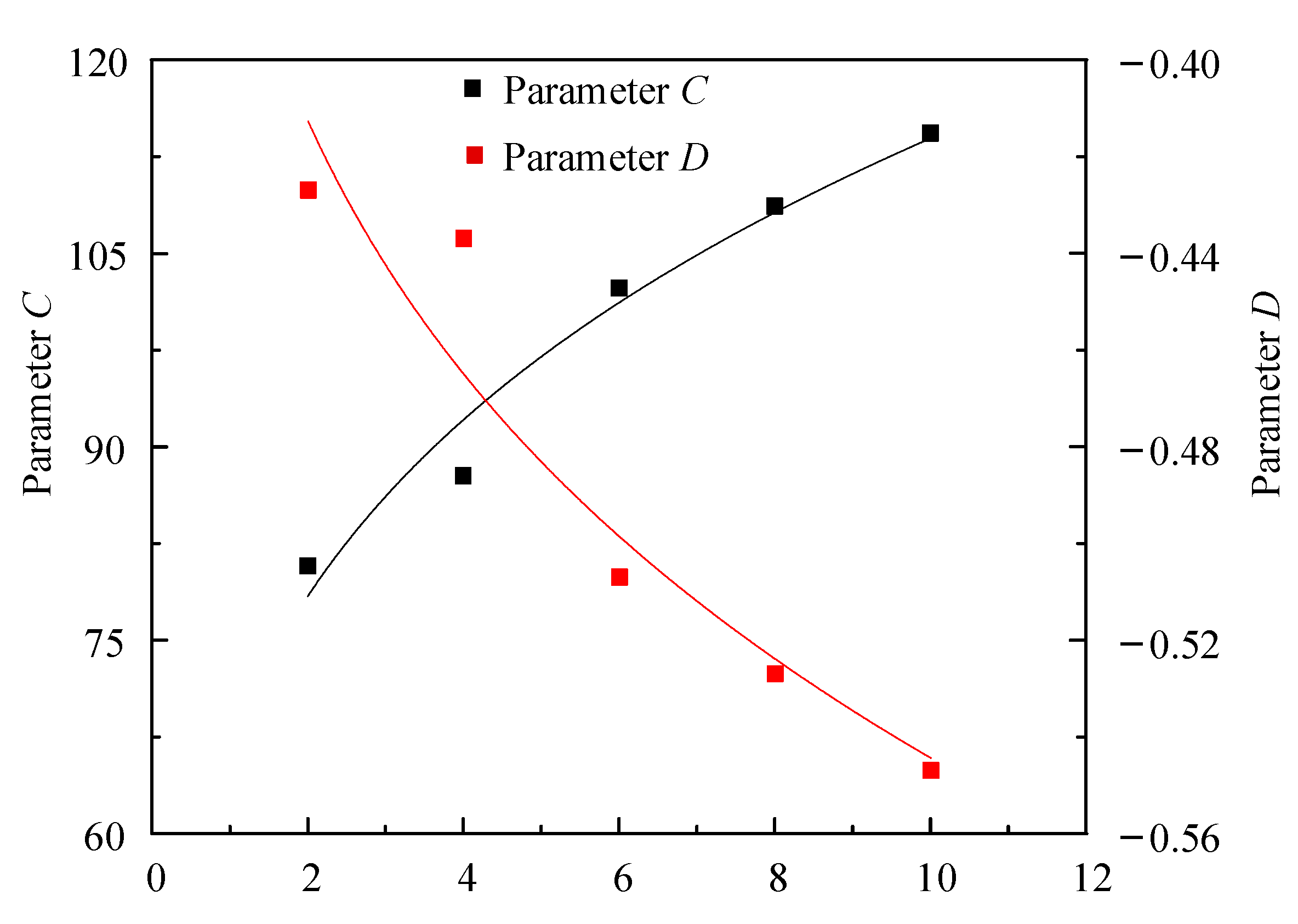
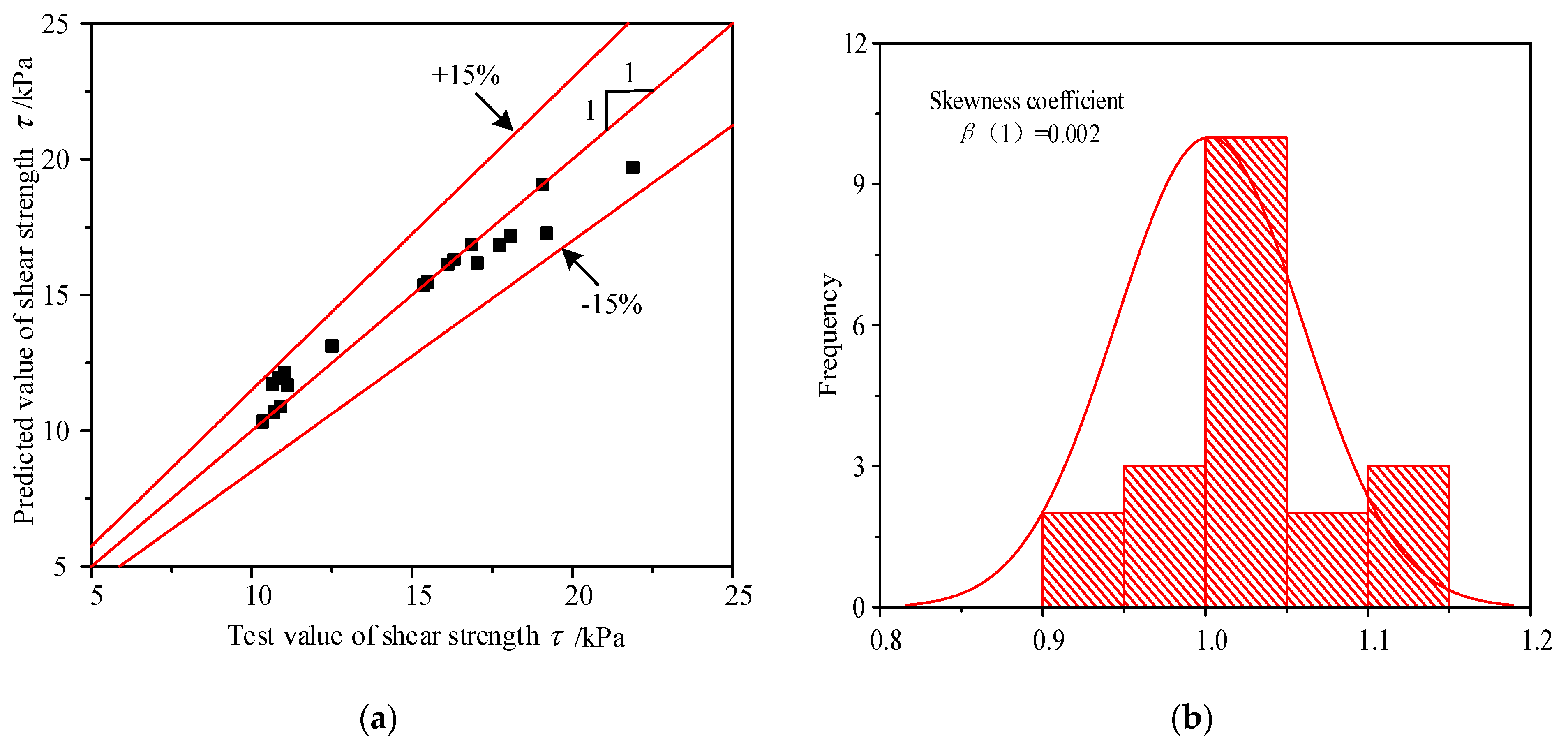
3.3. Establishment of Prediction Model of Soil Shear Strength
4. Uncertainty Analysis of Shear Strength Prediction Model
4.1. Fundamentals of Point Estimation
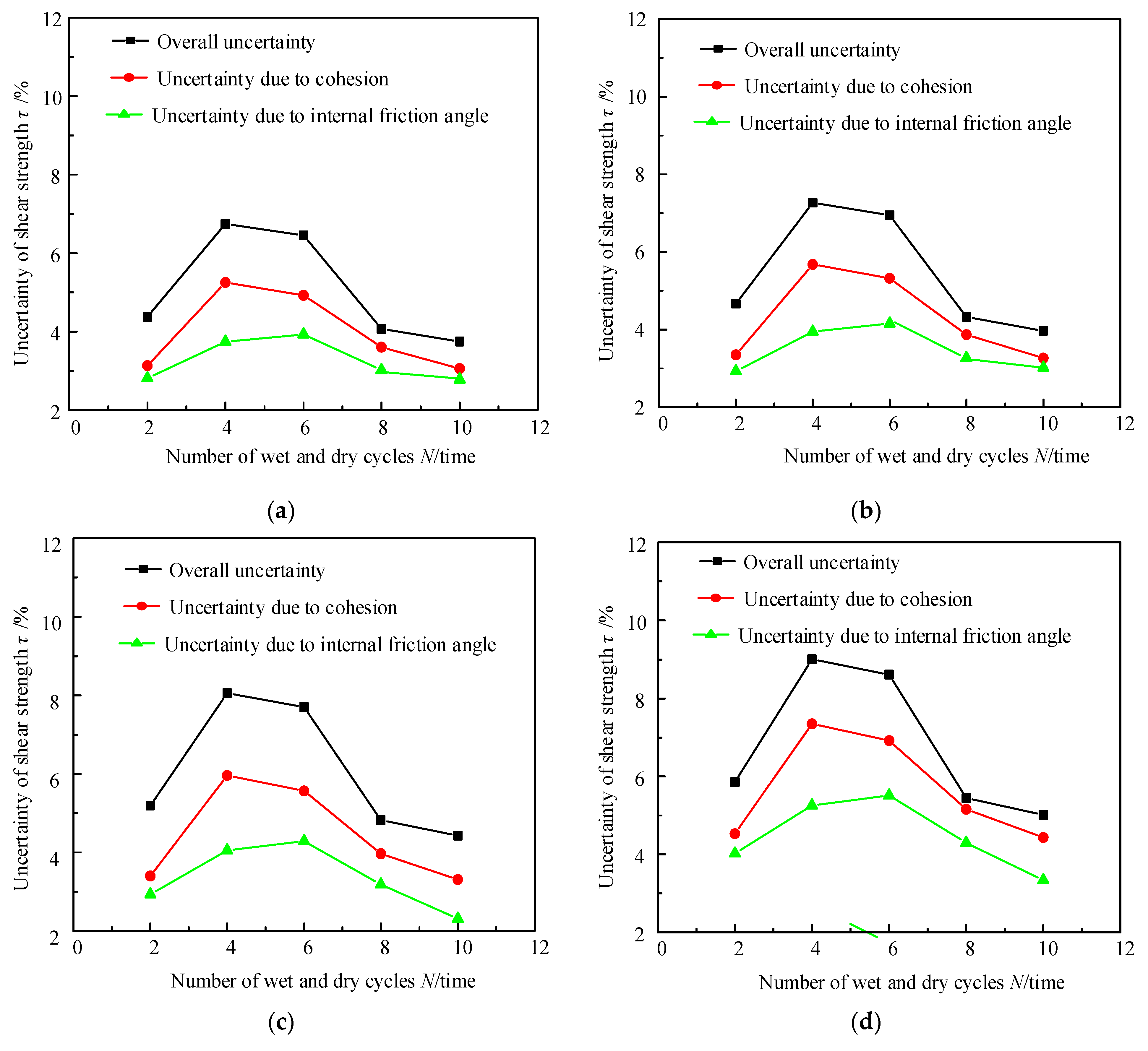
4.2. Uncertainty in Predicting Shear Strength τ
5. Conclusions
- (1)
- The cohesion c of granite residual soil decreases with an increase in the water content W, and the approximate relationship between the two satisfies the power function. The fitting parameters of the power function also satisfy a power function relationship with the number of dry–wet cycles N. A prediction formula for c considering the influence of N and W was obtained.
- (2)
- The internal friction angle φ of granite residual soil decreases with an increase in water content W, and the nonlinear relationship between the two can be described using a power function. The fitting parameters of this power function and the number of wet and dry cycles N also satisfy a power function relationship. A prediction formula for φ considering the influence of N and W was obtained.
- (3)
- A prediction formula for soil shear strength τ considering the influence of N and W was established.
- (4)
- The uncertainty of τ predicted by the formula jointly caused by the uncertainty of c and φ and the univariate uncertainty of τ predicted by only c or φ increases first and then decreases with an increase in N, and both increase with an increase in water content W.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Zhu, X.; Li, G.; Cai, Z. Failure Modes and Slope Stability of Expansive Soil Canal under Wet-Dry Cycles. Trans. Chin. Soc. Agric. Eng. 2020, 36, 159–167. [Google Scholar] [CrossRef]
- Zhang, S.; Tan, Y.; Wang, C. Research on Deformation Failure Mechanism and Stability of Slope Rock Mass Containing Multi-Weak Interlayers. Rock Soil Mech. 2014, 35, 1695–1702. [Google Scholar] [CrossRef]
- Liu, M.; Ye, J.; Oswald, J. Coarse-grained molecular simulation of the role of curing rates on the structure and strength of polyurea. Comput. Mater. Sci. 2023, 230, 112428. [Google Scholar] [CrossRef]
- Liu, M.; Oswald, J. Coarse-grained molecular modeling of the microphase structure of polyurea elastomer. Polymers 2019, 176, 1–10. [Google Scholar] [CrossRef]
- Xu, X.T.; Jian, W.B.; Wu, N.S.; Xu, X.; Liu, J. Unsaturated Seepage Characteristics of Slope under Rainfall Infiltration. Earth Sci. 2018, 43, 922–932. [Google Scholar] [CrossRef]
- Lan, Y.; Jian, W.; Luo, J. Risk Grade Evaluation of Highway Slope Water Damage Based on Grey Fixed-Weight Cluster Model. J. Fuzhou Univ. 2021, 49, 101–107. [Google Scholar] [CrossRef]
- Hu, H.; Wu, X.; Zhang, Y. Failure Mode Analysis of Granite Residual Soil Slope Based on Rainfall Landslide Simulation Test. J. Xiamen Univ. 2021, 60, 1098–1102. [Google Scholar] [CrossRef]
- Wu, J.; Yang, S. Experimental Study of Matric Suction Measurement and Its Impact on Shear Strength under Drying-Wetting Cycles for Expansive Soils. Rock Soil Mech. 2017, 38, 678–684. [Google Scholar]
- Wang, X.; Liu, N.; Li, Z. Hydro-Mechanical Behaviors of Sludge Stabilized with Magnesium Oxychloride Cement-Based Multi-Cementitious Materials under Influence of Drying-Wetting Cycles. Chin. J. Geotech. Eng. 2023, 45, 2004–2013. [Google Scholar] [CrossRef]
- Li, C.; Kong, L.; Shu, R.; An, R.; Zhang, X. Disintegration characteristics in granite residual soil and their relationship with the collapsing gully in South China. Open Geosci. 2020, 12, 1116–1126. [Google Scholar] [CrossRef]
- Tao, G.; Chen, Y.; Xiao, H.; Chen, Y.; Peng, W. Comparative analysis of soil-water characteristic curve in fractal and empirical models. Adv. Mater. Sci. Eng. 2020, 2020, 1970314. [Google Scholar] [CrossRef]
- Liu, Y.S.; Yang, T.; Zhang, X.; Zhang, Q.; Li, X.; Liu, J.; Deng, Z. Strength Deterioration of Karst Fillings under Dry–Wet Cycles: Testing and Modeling Study. Bull. Eng. Geol. Environ. 2023, 82, 339. [Google Scholar] [CrossRef]
- Wu, H.; Shao, S.; Shao, S.; Zhang, S.; Wang, Z. Variations in Dynamic Shear Modulus of Loess Exposed to Dry-Wet Cycles from Xi’an Area, China. Soil Dyn. Earthq. Eng. 2023, 173, 108126. [Google Scholar] [CrossRef]
- Wang, J.; Sun, Q.; Xue, S.; Yang, X.; Guo, H.; Geng, J. Study on the Effect of High-Temperature Dry-Wet Cycles on Argillaceous Sandstone. Bull. Eng. Geol. Environ. 2023, 82, 318. [Google Scholar] [CrossRef]
- Zheng, J.-C.; Chen, W.; Zheng, K.-R.; Gu, Y.P.; Wang, F.; Huang, Z.; Li, Y. Stability Analysis of Gravity Anchor Foundation of Layered Argillaceous Sandstone under Dry-Wet Cycles. J. Mt. Sci. 2023, 20, 1118–1130. [Google Scholar] [CrossRef]
- Goh, S.G.; Rahardjo, H.; Leong, E.C. Shear Strength of Unsaturated Soils under Multiple Drying-Wetting Cycles. J. Geotech. Geoenviron. Eng. 2014, 140, 06013001. [Google Scholar] [CrossRef]
- Ma, Q.; Wu, N.Z.; Xiao, H.L.; Li, Z.; Li, W. Effect of Bermuda Grass Root on Mechanical Properties of Soil under Dry-Wet Cycles. Bull. Eng. Geol. Environ. 2021, 80, 7083–7097. [Google Scholar] [CrossRef]
- Wu, Q.; Liu, Y.; Tang, H.; Kang, J.; Wang, L.; Li, C.; Wang, D.; Liu, Z. Experimental Study of the Influence of Wetting and Drying Cycles on the Strength of Intact Rock Samples from a Red Stratum in the Three Gorges Reservoir Area. Eng. Geol. 2023, 314, 107013. [Google Scholar] [CrossRef]
- Wang, X.; Lian, B.; Feng, W. A Nonlinear Creep Damage Model Considering the Effect of Dry-Wet Cycles of Rocks on Reservoir Bank Slopes. Water 2020, 12, 2396. [Google Scholar] [CrossRef]
- Nie, Y.; Ni, W.; Li, X.; Wang, H.; Yuan, K.; Guo, Y.; Tuo, W. The Influence of Drying-Wetting Cycles on the Suction Stress of Compacted Loess and the Associated Microscopic Mechanism. Water 2021, 13, 1809. [Google Scholar] [CrossRef]
- Yanli, Q.; Bai, M.Z.; Zhou, H.; Shi, H.; Li, P.; He, B. Study on the Mechanical Properties of Red Clay under Drying-Wetting Cycles. Adv. Mater. Sci. Eng. 2021, 2021, 8665167. [Google Scholar] [CrossRef]
- Xu, W.; Li, X.; Zhang, Y.; Zhu, H.; Zhang, W.; Xuan, C. Fine Identification and Characterization of Rock Mass Discontinuities and Its Application Using a Digital Photogrammetry System. Acta Geod. Cartogr. Sin. 2022, 51, 2093–2106. [Google Scholar] [CrossRef]
- An, R.; Kong, L.; Zhang, X.; Li, C. Effects of Dry-Wet Cycles on Three-Dimensional Pore Structure and Permeability Characteristics of Granite Residual Soil Using X-ray Micro Computed Tomography. J. Rock Mech. Geotech. Eng. 2022, 14, 851–860. [Google Scholar] [CrossRef]
- Chen, H.J.; Cui, G.Y. Probability statistical analysis of physical mechanical parameters of granite eluvial soil. J. Huazhong Univ. Sci. Technol. 2001, 29, 95–97. [Google Scholar] [CrossRef]
- Zhang, Z.; Niu, Y.; Shang, X.; Ye, P.; Zhou, R.; Gao, F. Deterioration of Physical and Mechanical Properties of Rocks by Cyclic Drying and Wetting. Geofluids 2021, 2021, 6661107. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, L.; Zhang, H. Rainfall Infiltration Process of a Rock Slope with Considering the Heterogeneity of Saturated Hydraulic Conductivity. Front. Earth Sci. 2022, 9, 804005. [Google Scholar] [CrossRef]
- Xu, Y.; Liao, X.; Li, J.; Chen, L.; Li, L. The Effects of Water Content and Dry–Wet Cycles of Weak-Interlayer Soil on Stability of Clastic Rock Slope. Geotech. Geol. Eng. 2021, 39, 3753–3760. [Google Scholar] [CrossRef]
- Wang, X.; Zhan, H.; Wang, J.; Li, P. The Stability of Tailings Dams under Dry-Wet Cycles: A Case Study in Luonan, China. Water 2018, 10, 1048. [Google Scholar] [CrossRef]
- Wen, T.; Wang, Y.; Tang, H.; Zhang, J.; Hu, M. Damage Evolution and Failure Mechanism of Red-Bed Rock under Drying–Wetting Cycles. Water 2023, 15, 2684. [Google Scholar] [CrossRef]
- Albadri, W.M.; Noor, M.J.M.; Alhani, I.J. The Relationship between the Shear Strength and Water Retention Curve of Unsaturated Sand at Different Hydraulic Phases. Acta Geotech. 2021, 16, 2821–2835. [Google Scholar] [CrossRef]
- Chen, R.; Xu, T.; Lei, W.; Zhao, Y.; Qiao, J. Impact of Multiple Drying-Wetting Cycles on Shear Behaviour of an Unsaturated Compacted Clay. Environ. Earth Sci. 2018, 77, 683. [Google Scholar] [CrossRef]
- Goh, S.G.; Rahardjo, H.; Leong, E.C. Shear Strength Equations for Unsaturated Soil under Drying and Wetting. J. Geotech. Geoenviron. Eng. 2010, 136, 594–606. [Google Scholar] [CrossRef]
- Calonico, S.; Cattaneo, M.D.; Farrell, M.H. On the effect of bias estimation on coverage accuracy in nonparametric inference. J. Am. Stat. Assoc. 2018, 113, 767–779. [Google Scholar] [CrossRef]
- Grant, E.; Finn, C.; Levine, S.; Darrell, T.; Griffiths, T. Recasting Gradient-Based Meta-Learning as Hierarchical Bayes. arXiv 2018, arXiv:1801.08930. [Google Scholar] [CrossRef]
- Zhu, Y.; Xie, M.; Zhang, K.; Li, Z. A Dam Deformation Residual Correction Method for High Arch Dams Using Phase Space Reconstruction and an Optimized Long Short-Term Memory Network. Mathematics 2023, 11, 2010. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, Z.; Gu, C.; Li, Y.; Zhang, K.; Xie, M. A Coupled Model for Dam Foundation Seepage Behavior Monitoring and Forecasting Based on Variational Mode Decomposition and Improved Temporal Convolutional Network. Struct. Control Health Monit. 2023, 2023, 3879096. [Google Scholar] [CrossRef]
- Bi, Y.; Zou, H.; Zhu, C. Dynamic monitoring of soil bulk density and infiltration rate during coal mining in sandy land with different vegetation. Int. J. Coal Sci. Technol. 2014, 1, 198–206. [Google Scholar] [CrossRef]
- GB/T 50123-2019; Standard for Geotechnical Testing Method. China Planning Press: Beijing, China, 2019.
- An, R.; Zhang, X.W.; Kong, L.W.; Gong, J.W.; Lei, X.W. Artificial ground freezing impact on shear strength and microstructure of granite residual soil under an extremely low temperature. Front. Earth Sci. 2021, 9, 935. [Google Scholar] [CrossRef]
- Kim, C.K.; Kim, T.H. Behavior of unsaturated weathered residual granite soil with initial water contents. Eng. Geol. 2010, 113, 1–10. [Google Scholar] [CrossRef]
- Zhang, X.W.; Kong, L.W.; Yin, S.; Chen, C. Engineering geology of basaltic residual soil in Leigong, Southern China. Eng. Geol. 2017, 220, 196–207. [Google Scholar] [CrossRef]
- Sayem, H.M.; Kong, L.W.; Yin, S. Effect of drying-wetting cycles on saturated shear strength of undisturbed residual soils. Am. J. Civ. Eng. 2016, 4, 159–166. [Google Scholar] [CrossRef]
- Kong, L.W.; Sayem, H.M.; Tian, H.H. Influence of drying-wetting cycles on soil-water characteristic curve of undisturbed granite residual soils and microstructure mechanism by nuclear magnetic resonance (NMR) spin-spin relaxation time (T2) relaxometry. Can. Geotech. J. 2018, 55, 208–216. [Google Scholar] [CrossRef]
- GB/T 50145-2007; Standard for Engineering Classification of Soil. China Planning Press: Beijing, China, 2007.
- Wu, N.S. Study on Classification of Granite Residual Soils. Rock Soil Mech. 2006, 27, 2299–2304. [Google Scholar] [CrossRef]
- Rosenblueth, E. Two-Point Estimates in Probabilities. Appl. Math. Model. 1981, 5, 329–335. [Google Scholar] [CrossRef]



| Moisture Content W/% | Dry Density ρd/(g/m3) | Proportion Gs | Void Ratio e | Saturation Level Sr/% |
|---|---|---|---|---|
| 23.2 | 1.56 | 2.78 | 0.71 | 86.59 |
| Number of Cycles | Cohesion c | Coefficient of Determination R2 | Internal Friction Angle φ | Coefficient of Determination R2 | ||
|---|---|---|---|---|---|---|
| A | B | C | D | |||
| 2 | 463.86 | −1.05 | 0.981 | 80.75 | −0.43 | 0.931 |
| 4 | 439.97 | −1.12 | 0.892 | 87.73 | −0.44 | 0.944 |
| 6 | 425.99 | −1.11 | 0.902 | 102.31 | −0.51 | 0.905 |
| 8 | 410.94 | −1.13 | 0.861 | 108.66 | −0.53 | 0.872 |
| 10 | 390.95 | −1.16 | 0.871 | 114.32 | −0.55 | 0.956 |
| Prediction Equation | Coefficient | Coefficient of Determination R2 | |
|---|---|---|---|
| ai | bi | ||
| A = a1Nb1 | 500.52 | −0.098 | 0.972 |
| B = a2Nb2 | −1.01 | 0.05 | 0.912 |
| C = a3Nb3 | 66.75 | 0.23 | 0.981 |
| D = a4Nb4 | −0.37 | 0.10 | 0.953 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, J.; Wang, S.; Huang, H.; Pan, F.; Wu, Y.; Gu, Y.; Zhang, Y. Prediction Model of Residual Soil Shear Strength under Dry–Wet Cycles and Its Uncertainty. Water 2023, 15, 3931. https://doi.org/10.3390/w15223931
Ding J, Wang S, Huang H, Pan F, Wu Y, Gu Y, Zhang Y. Prediction Model of Residual Soil Shear Strength under Dry–Wet Cycles and Its Uncertainty. Water. 2023; 15(22):3931. https://doi.org/10.3390/w15223931
Chicago/Turabian StyleDing, Jiefa, Shijun Wang, Haoran Huang, Fengqian Pan, Yunxing Wu, Yanchang Gu, and Yan Zhang. 2023. "Prediction Model of Residual Soil Shear Strength under Dry–Wet Cycles and Its Uncertainty" Water 15, no. 22: 3931. https://doi.org/10.3390/w15223931




