A Bayesian Network Model for Risk Management during Hydraulic Fracturing Process
Abstract
:1. Introduction
2. Methodology
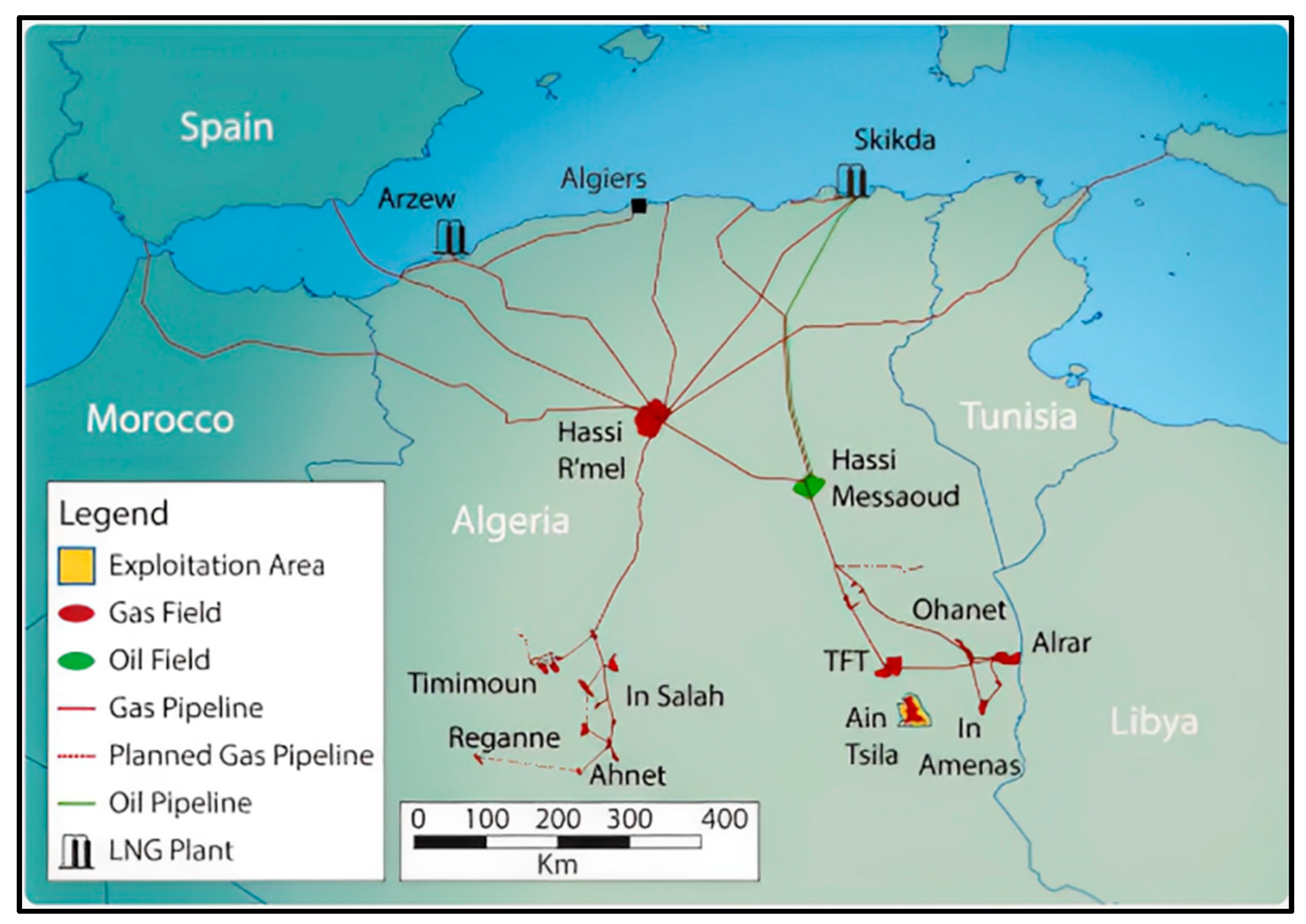
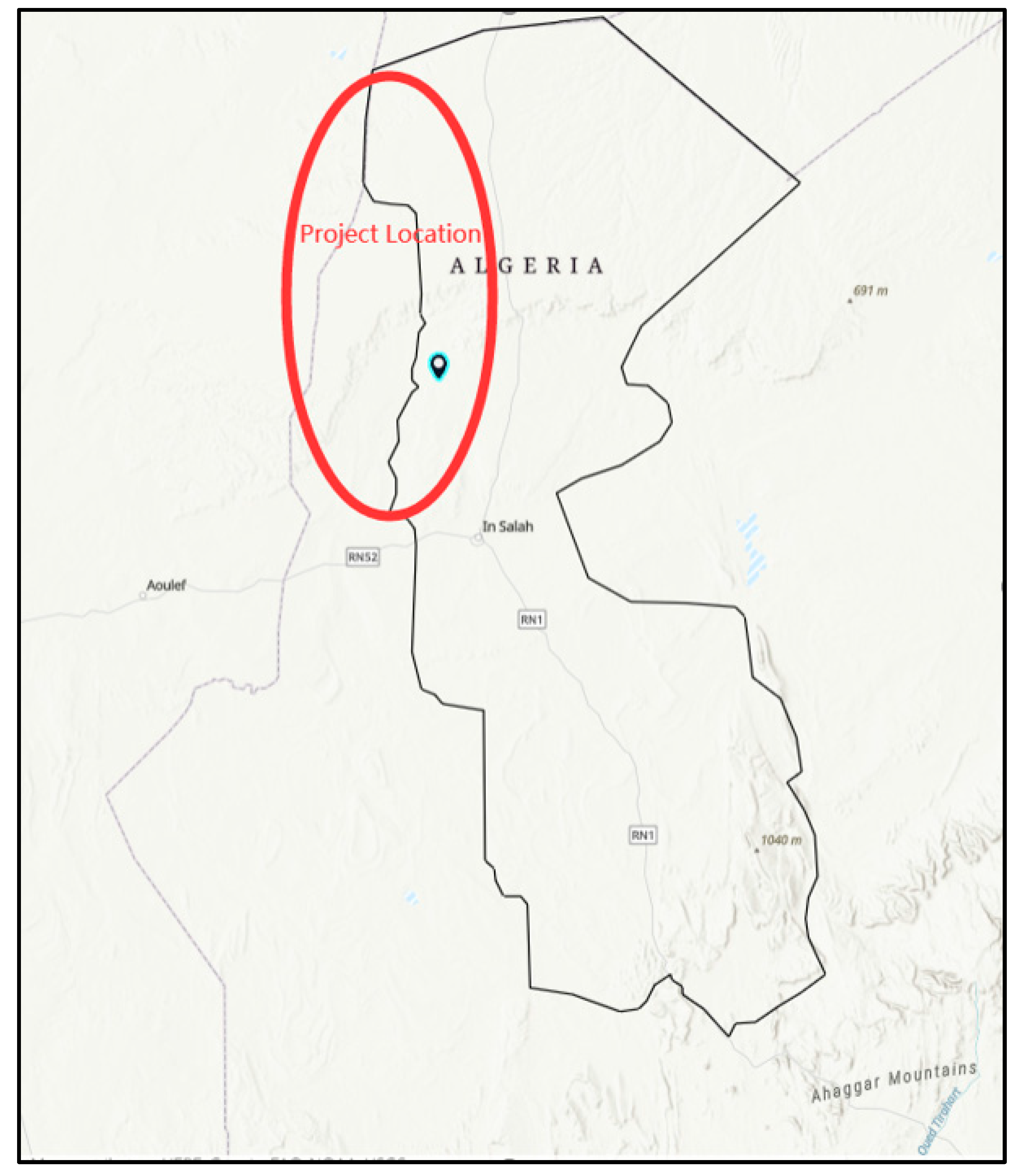
2.1. Case Study
2.2. Formulation, Hazard Identification, and Development of an Fault Tree
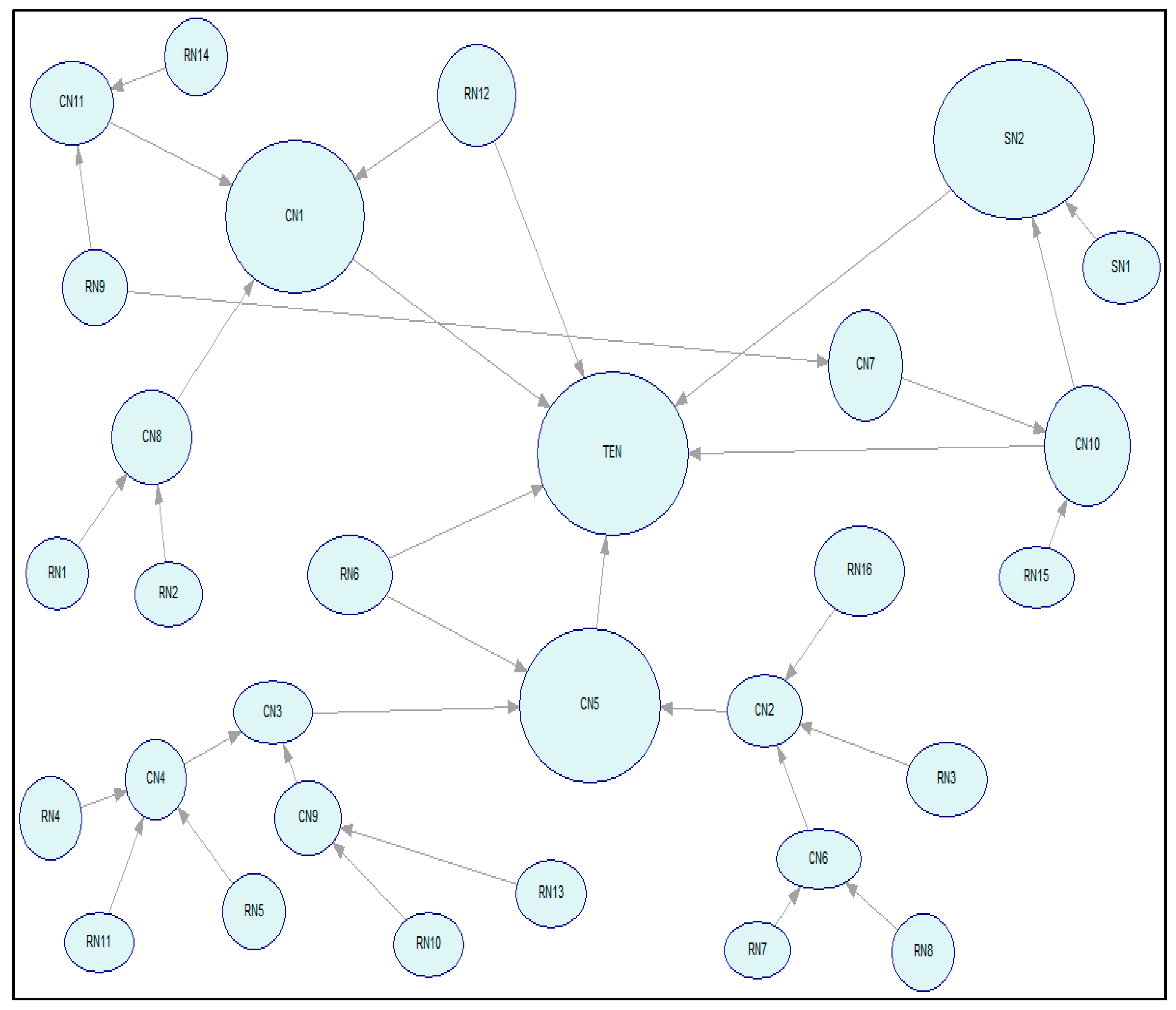
2.3. Building a BBN Model
2.4. A BBN for Hydraulic Fracturing
3. The Main Results of Bayesian Belief Networks
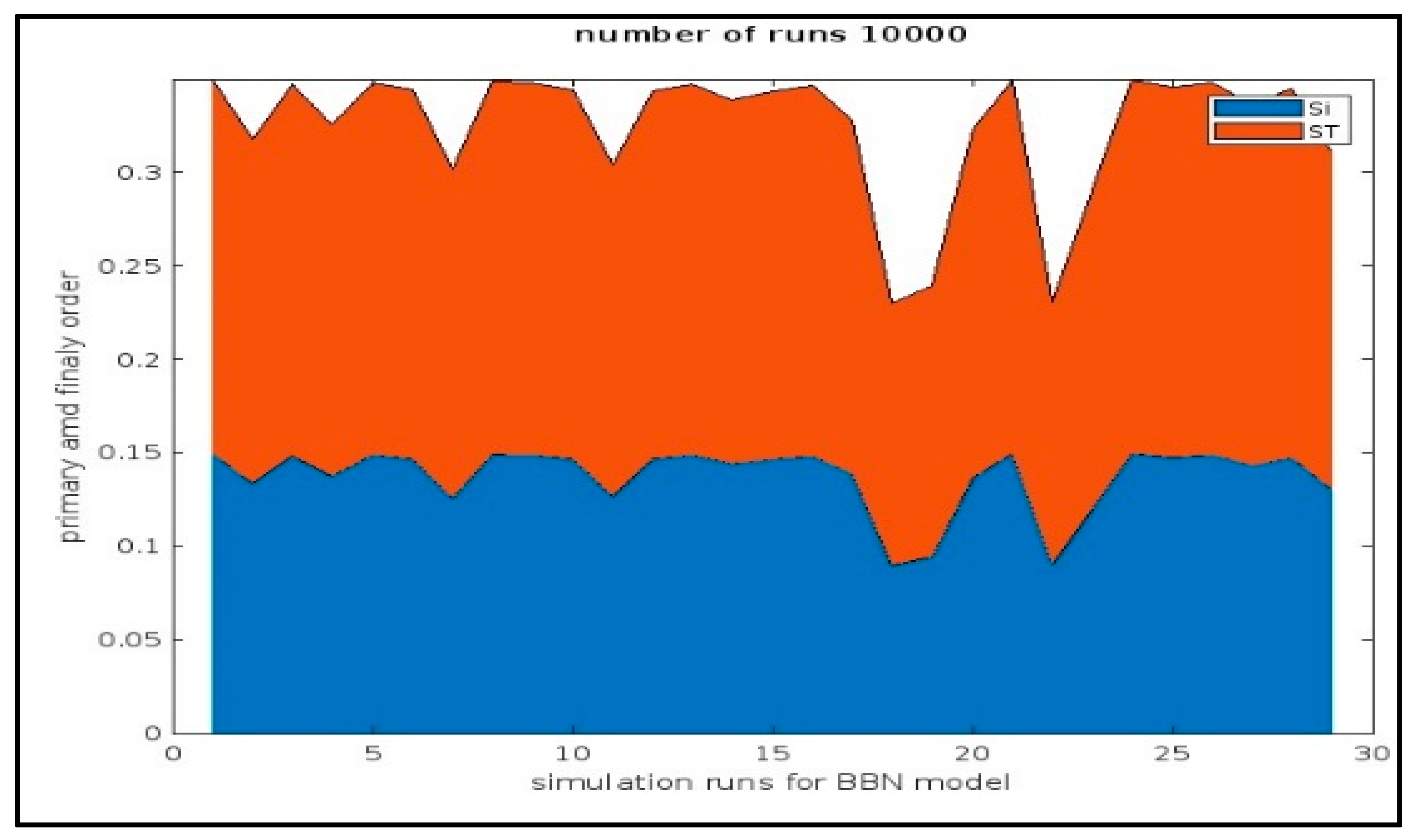
3.1. Finding Sensitivity Parameters
3.2. Calculation of Indices
4. Discussion
4.1. Analysis of the Most Important Scenarios Proposed from the BBN Framework
4.2. The Results of Sensitivity Analysis and Partial Validation
4.3. The Cost–Benefit Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Glossary
| Acronym | Term |
| BBN | Bayesian belief networks |
| CN | Consequence nodes |
| CPT | Conditional Probability Tables |
| E | The conditional expected disutility function for scenario Se |
| EBBN | Establish Bayesian belief networks |
| ET | Event tree |
| FTA | Fault tree analysis |
| FT | Fault tree |
| HAZOP | Hazard and Operability Analysis |
| HBN | Hybrid belief network |
| N, r | Matrices using the Monte Carlo approach |
| P(Se) | Probability of scenario Se |
| RN | Root nodes |
| RS(Se) | Risk Share |
| Si | Indicator of sensitivity |
| Sij | Number of summands |
| S(Ti) | Indicator of sensitivity |
| Se | Scenario exclusion |
| SN | Safety nodes |
| WSA | Weighted Sum Algorithm |
| X | Input parameter |
| X_u(S_I(u)) | The function of combinations of parent states of the value for 1, which belongs to components that fail in the system, and 0, which presents them otherwise |
| Y | Model function |
| RMSE | Root mean square error |
| MAE | Mean absolute error |
| R2 | Coefficient of determination |
References
- Forster, D.; Perks, J. Climate Impact of Potential Shale Gas Production in the EU; CE Delft: Delft, The Netherlands, 2012. [Google Scholar]
- Wang, Q.; Chen, X.; Jha, A.N.; Rogers, H. Natural gas from shale formation–the evolution, evidences and challenges of shale gas revolution in United States. Renew. Sustain. Energy Rev. 2014, 30, 1–28. [Google Scholar] [CrossRef]
- Wang, C.; Wang, F.; Du, H.; Zhang, X. Is China really ready for shale gas revolution—Re-evaluating shale gas challenges. Environ. Sci. Policy 2014, 39, 49–55. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, L.; Hu, J. Real-time risk assessment of a fracturing manifold system used for shale-gas well hydraulic fracturing activity based on a hybrid Bayesian network. J. Nat. Gas Sci. Eng. 2019, 62, 79–91. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, F.; Xue, Y.; Yao, E.; Zhang, L.; Fan, F.; Wang, R. The adsorption properties of a novel ether nanofluid for gas wetting of tight sandstone reservoir. Pet. Sci. Technol. 2019, 37, 1436–1454. [Google Scholar] [CrossRef]
- Brahim, I.B.; Addouche, S.A.; El Mhamedi, A.; Boujelbene, Y. Cluster-based WSA method to elicit expert knowledge for Bayesian reasoning—Case of parcel delivery with drone. Expert Syst. Appl. 2022, 191, 116160. [Google Scholar] [CrossRef]
- The Society of Petroleum Engineers (SPE) a 501 Petrofac Scores EPC Contract in Algeria Oil and Gas Facilities, March 13, 2019. Available online: https://jpt.spe.org/petrofac-scores-epc-contract-algeria (accessed on 10 October 2023).
- Oilman Magazine, “10 Best Performing Tips for Successful Hydraulic Fracturing”, Oilman Magazine, 27 December 2018. [Online]. Available online: https://oilmanmagazine.com/10-best-performing-tips-for-successful-hydraulic-fracturing/ (accessed on 10 October 2023).
- Gao, C.H. Scientific research and field applications of polymer flooding in heavy oil recovery. J. Pet. Explor. Prod. Technol. 2011, 1, 65–70. [Google Scholar] [CrossRef]
- Belgacem, T. Les ressources de l’Algérie. Outre-Terre, 2016; 47, 152–164. [Google Scholar]
- Zio, E.; Mustafayeva, M.; Montanaro, A. A Bayesian belief network model for the risk assessment and management of premature screen-out during hydraulic fracturing. Reliab. Eng. Syst. Saf. 2022, 218, 1080914. [Google Scholar] [CrossRef]
- Martin, C.; Gonzalez-Prida, V.; Pérès, F. Reliability assessment of a multi-redundant repairable mechatronic system. In Numerical Methods for Reliability and Safety Assessment: Multiscale and Multiphysics Systems; Springer: Cham, Switzerland, 2015; pp. 407–423. [Google Scholar]
- Wan, F.L.; Li, Z.; Zeng, P.Y. Unconventional Casing Program for Complex-Deep Well D1. In Proceedings of the International Field Exploration and Development Conference 2019; Springer: Singapore, 2020; pp. 2463–2468. [Google Scholar]
- Oduoza, C.F. Framework for sustainable risk management in the manufacturing sector. Procedia Manuf. 2020, 51, 1290–1297. [Google Scholar] [CrossRef]
- Sui, Y.; Cao, G.; Guo, T.; Zhang, Z.; Bai, Y.; Wu, J.; Yao, L. Evaluation of deep penetration of high-temperature sustained-release acid based on the reaction kinetics and conductivity of acid-etched fractures. Case Stud. Therm. Eng. 2022, 38, 102336. [Google Scholar] [CrossRef]
- Guo, T.; Chen, M. Special Issue “Petroleum Engineering: Reservoir Fracturing Technology and Numerical Simulation”. Processes 2023, 11, 233. [Google Scholar] [CrossRef]
- Du, Z.; Liang, X.; Chen, S.; Li, P.; Zhu, X.; Chen, K.; Jin, X. Domain adaptation deep learning and its TS diagnosis networks for the cross-control and cross-condition scenarios in data center HVAC systems. Energy 2023, 280, 128084. [Google Scholar] [CrossRef]
- Vairo, T.; Pettinato, M.; Reverberi, A.P.; Milazzo, M.F.; Fabiano, B. An approach towards the implementation of a reliable resilience model based on machine learning. Process Saf. Environ. Prot. 2023, 172, 632–641. [Google Scholar] [CrossRef]
- Fazelipour, W. Innovative reservoir modeling and simulation of unconventional shale gas reservoirs powered by microseismic Data. In SPE Middle East Unconventional Resources Conference and Exhibition; SPE: Kuala Lumpur, Malaysia, 2011; p. SPE-141877. [Google Scholar]
- Alqahtani, N.J.; Chung, T.; Wang, Y.D.; Armstrong, R.T.; Swietojanski, P.; Mostaghimi, P. Flow-based characterization of digital rock images using deep learning. SPE J. 2021, 26, 1800–1811. [Google Scholar] [CrossRef]
- Li, T.; Zhou, Y.; Zhao, Y.; Zhang, C.; Zhang, X. A hierarchical object oriented Bayesian network-based fault diagnosis method for building energy systems. Appl. Energy 2022, 306, 118088. [Google Scholar] [CrossRef]
- Kang, N.; Kim, J.J.; On, B.W.; Lee, I. A node resistance-based probability model for resolving duplicate named entities. Scientometrics 2020, 124, 1721–1743. [Google Scholar] [CrossRef]
- Badjadi, M.A.; Zhu, H.; Zhang, C.; Naseem, M.H. Enhancing Water Management in Shale Gas Extraction through Rectangular Pulse Hydraulic Fracturing. Sustainability 2023, 15, 10795. [Google Scholar] [CrossRef]
- Laitila, P.; Virtanen, K. Portraying probabilistic relationships of continuous nodes in Bayesian networks with ranked nodes method. Decis. Support Syst. 2022, 154, 113709. [Google Scholar] [CrossRef]
- Ren, H.J.; Wang, X.C.; Guo, Q.L.; Guo, X.X.; Zhang, R. Spatial prediction of oil and gas distribution using tree augmented Bayesian network. Comput. Geosci. 2020, 142, 104518. [Google Scholar] [CrossRef]
- Luo, Z.; Zhang, N.; Zhao, L.; Liu, H.; Luo, P.; Liu, J. Innovative encapsulating acid with release dually controlled by the concentration of hydrogen ions and temperature. Energy Fuels 2019, 33, 4976–4985. [Google Scholar] [CrossRef]
- Liu, Z.; Ma, Q.; Cai, B.; Liu, Y.; Zheng, C. Risk assessment on deepwater drilling well control based on dynamic Bayesian network. Process Saf. Environ. Prot. 2021, 149, 643–654. [Google Scholar] [CrossRef]
- Johnstone, R.L.; Hansen, A.M. Introduction to the Arctic Oil and Gas Research Centre. Arct. Rev. Law Politics 2016, 7, 107–108. [Google Scholar] [CrossRef]
- Quaglietta, E.; Punzo, V. Supporting the design of railway systems by means of a Sobol variance-based sensitivity analysis. Transp. Res. Part C Emerg. Technol. 2013, 34, 38–54. [Google Scholar] [CrossRef]
- Glen, G.; Isaacs, K. Estimating Sobol sensitivity indices using correlations. Environ. Model. Softw. 2012, 37, 157–166. [Google Scholar] [CrossRef]
- Shouche, S.; Wysk, R.A.; King, R.E.; Harrysson, O.L. Supply chain operations reference model for US based powder bed metal additive manufacturing processes. In Proceedings of the 2016 Winter Simulation Conference (WSC), Washington, DC, USA, 11–14 December 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1158–1169. [Google Scholar]
- Sibiya, Z. Developing the Shale Gas Industry in South Africa: An Analysis of the Environmental Legal Framework. Doctoral Dissertation, University of Pretoria, Pretoria, South Africa, 2014. [Google Scholar]
- Sattari, F.; Macciotta, R.; Kurian, D.; Lefsrud, L. Application of Bayesian network and artificial intelligence to reduce accident/incident rates in oil & gas companies. Saf. Sci. 2021, 133, 104981. [Google Scholar]
- Zhou, Y.; Lu, Z.; Cheng, K.; Yun, W. A Bayesian Monte Carlo-based method for efficient computation of global sensitivity indices. Mech. Syst. Signal Process. 2019, 117, 498–516. [Google Scholar] [CrossRef]
- Malozyomov, B.V.; Martyushev, N.V.; Kukartsev, V.V.; Tynchenko, V.S.; Bukhtoyarov, V.V.; Wu, X.; Tyncheko, Y.A.; Kukartsev, V.A. Overview of Methods for Enhanced Oil Recovery from Conventional and Unconventional Reservoirs. Energies 2023, 16, 4907. [Google Scholar] [CrossRef]
- Wang, B.; Fan, S.D.; Jiang, P.; Zhu, H.H.; Xiong, T.; Wei, W.; Fang, Z.L. A novel method with stacking learning of data-driven soft sensors for mud concentration in a cutter suction dredger. Sensors 2020, 20, 6075. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Wang, L.; Ma, K.; Zhang, F. Numerical Simulation of Hydraulic Fracturing and Penetration Law in Continental Shale Reservoirs. Processes 2022, 10, 2364. [Google Scholar] [CrossRef]
- Zhao, S.; Soares, C.G.; Zhu, H. A Bayesian network modelling and risk analysis on LNG carrier anchoring system. In Proceedings of the 2015 International Conference on Transportation Information and Safety (ICTIS), Wuhan, China, 25–28 June 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 432–436. [Google Scholar]
- Sakib, N.; Hossain, N.U.I. Disasters cases in oil industry and probability assessment by Bayesian network model. In Crises in Oil, Gas and Petrochemical Industries; Elsevier: Amsterdam, The Netherlands, 2023; pp. 325–348. [Google Scholar]
- Guo, Q.; Ren, H.; Yu, J.; Wang, J.; Liu, J.; Chen, N. A method of predicting oil and gas resource spatial distribution based on Bayesian network and its application. J. Pet. Sci. Eng. 2022, 208, 109267. [Google Scholar] [CrossRef]
- Iaiani, M.; Tugnoli, A.; Cozzani, V.; Reniers, G.; Yang, M. A Bayesian-network approach for assessing the probability of success of physical security attacks to offshore Oil&Gas facilities. Ocean Eng. 2023, 273, 114010. [Google Scholar]
- Dimaio, F.; Scapinello, O.; Zio, E.; Ciarapica, C.; Cincotta, S.; Crivellari, A.; Decarli, L.; Larosa, L. Accounting for safety barriers degradation in the risk assessment of oil and gas systems by multistate Bayesian networks. Reliab. Eng. Syst. Saf. 2021, 216, 107943. [Google Scholar] [CrossRef]








| Type of Risks | Description Event | Select Nodes | Nodes | State |
|---|---|---|---|---|
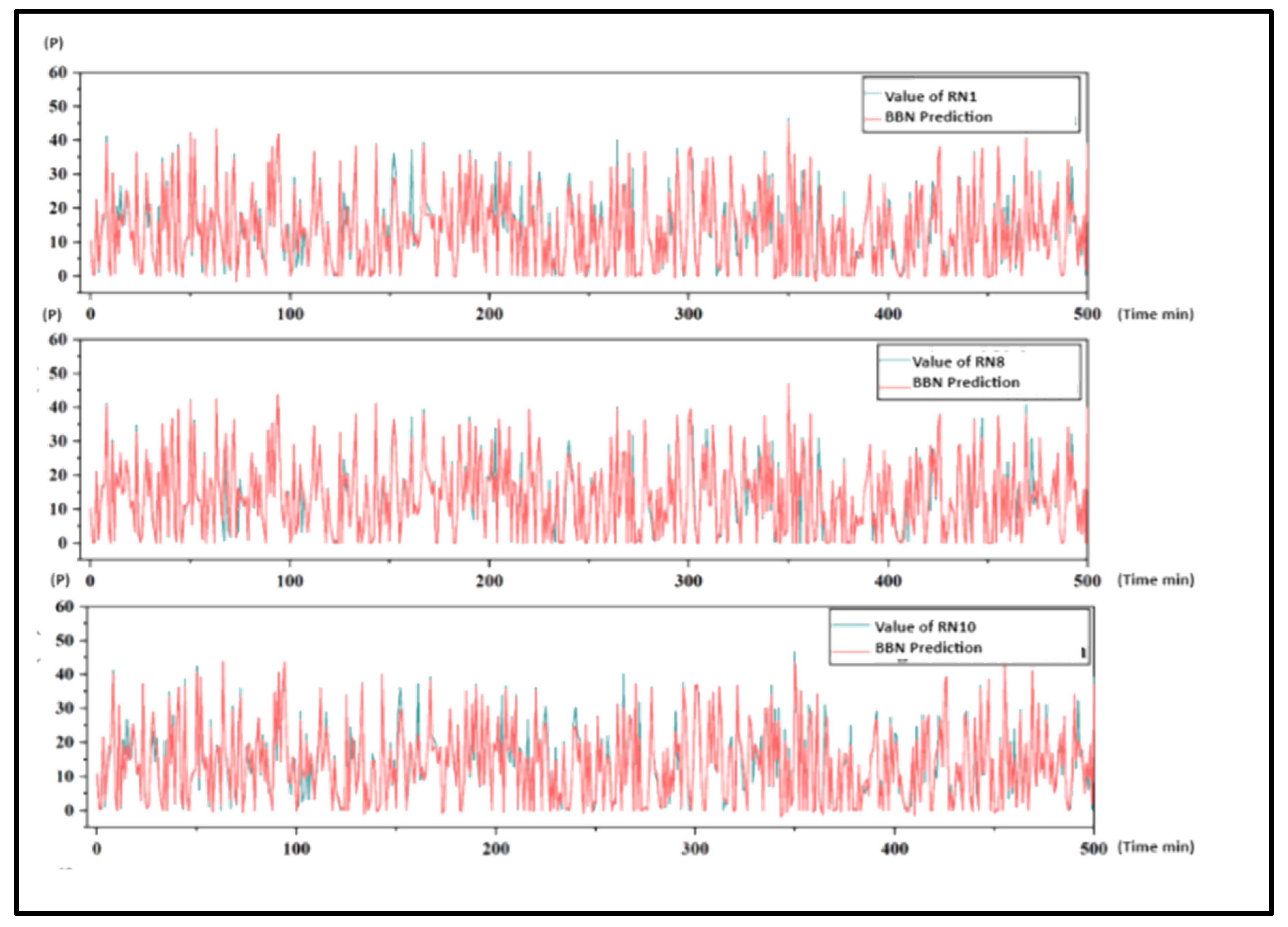
| Characteristics of the static system of the environment | Strata with high in situ stress in shale reservoirs | Root node | RN1 | Yes–no |
| High permeability zones | Root node | RN2 | Yes–no | |
| Poor physical properties | Root node | RN3 | Yes–no | |
| High temperature | Root node | RN4 | High–Med–Low | |
| Strongly heterogeneous reservoir | Root node | RN5 | Yes–no | |
| The resulting effects of the fracturing process on the well and the surrounding environment | Reservoir contamination (max treating) | Consequence node | CN1 | High–Med–Low |
| Restricting the further penetration of gels in the reservoir | Consequence node | CN2 | Yes–no | |
| Effective distance of live additive | Consequence node | CN3 | High–Med–Low | |
| Rapid acid rock reaction rate | Consequence node | CN4 | Yes–no | |
| Limited gel-etched fracture conductivity | Root node | RN6 | High–Med–Low | |
| Well production declines rapidly and fails to stabilize | Consequence node | CN5 | Yes–no | |
| Shortens the gels penetration distance | Consequence node | CN6 | Yes–no | |
| Difficult to achieve rational distribution of gels | Root node | RN7 | Yes–no | |
| Near-wellbore friction | Root node | RN8 | High–Med–Low | |
| Exceeding limitations of wellhead completion | Consequence node | CN7 | Yes–no | |
| The developments and changes that occur during the process | High pressure of the fracturing process | Root node | RN9 | High–Med–Low |
| Uncontrolled additive leak off | Consequence node | CN8 | Yes–no | |
| Errors of the well trajectory control | safety node | SN1 | Yes–no | |
| Fluid loss | Consequence node | CN9 | Yes–no | |
| Gel flow velocity in the cracks | Root node | RN10 | High–Med–Low | |
| Error gel system | safety node | SN2 | Yes–no | |
| Gel dissolving power | Root node | RN11 | High–Med–Low | |
| Gel and additive efficiency | Root node | RN12 | High–Med–Low | |
| Gels amount additive loss | Root node | RN13 | High–Med–Low | |
| Exceeding equipment loading capacity | Consequence node | CN10 | Yes–no | |
| Large injection rate | Root node | RN14 | Yes–no | |
| Uncontrolled in gels fracturing pumps | Consequence node | CN11 | High–Med–Low | |
| High pressure inside primary pipeline | Root node | RN15 | High–Med–Low | |
| Perforation friction | Root node | RN16 | High–Med–Low | |
| Failure of gels fracturing process | Top event node | TEN | Yes–no | |
| Damage in the reservoir and shortening the life of the well | Top event node | TEN | Yes–no |
| Nodes | Probability Measurement | |||||||
|---|---|---|---|---|---|---|---|---|
| CN1 | SN2 | RN2 | RN8 | RN12 | CN10 | Likelihood | EBBN | WSA |
| High | No | No | High | Low | Yes | 0.978 | 0.227 | 0.375 |
| High | No | No | Low | High | No | 0.981 | 0.341 | 0.412 |
| Low | No | Yes | Low | High | No | 0.991 | 0.369 | 0.488 |
| Low | No | Yes | Low | Low | No | 1 | 0.382 | 0.497 |
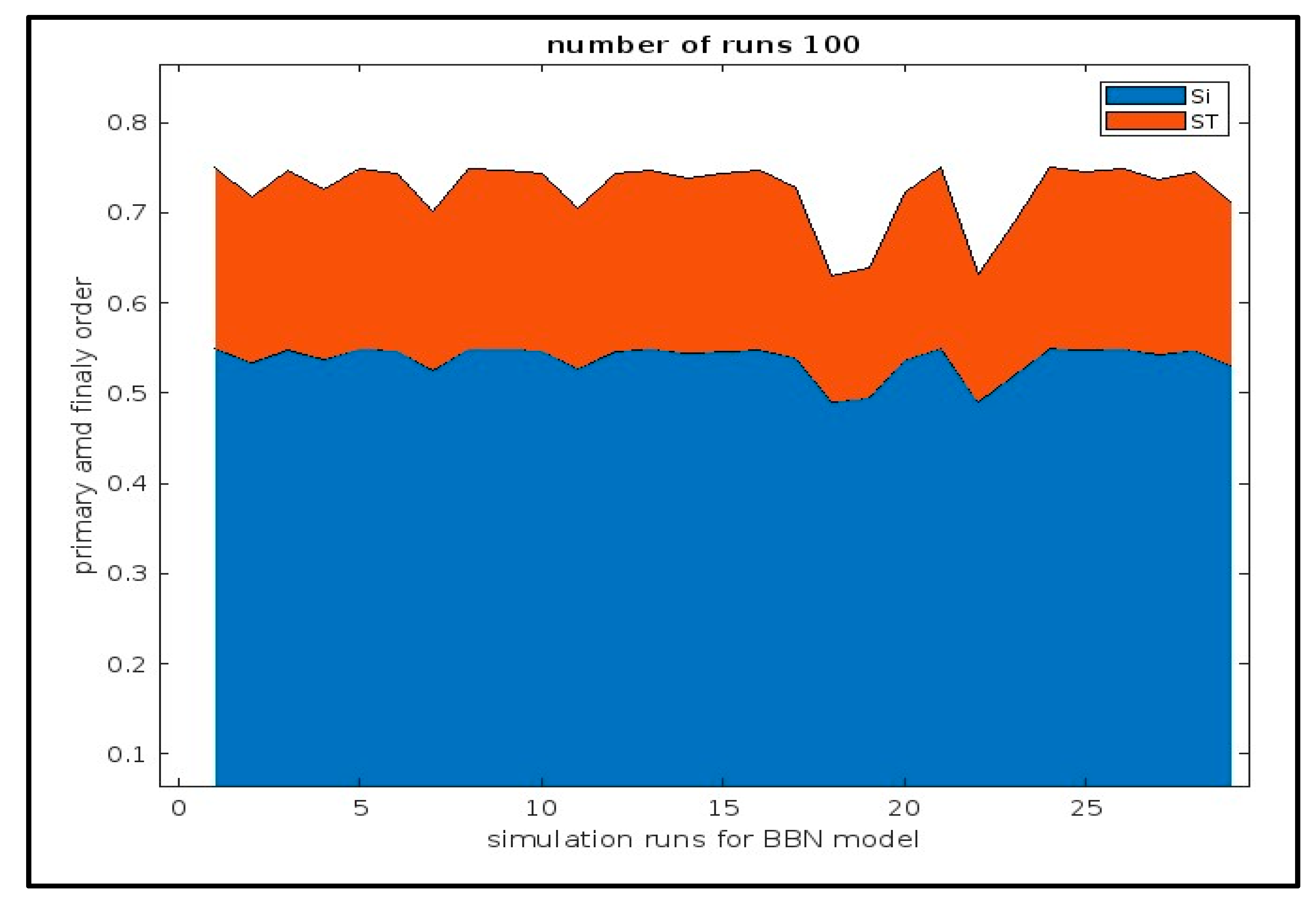
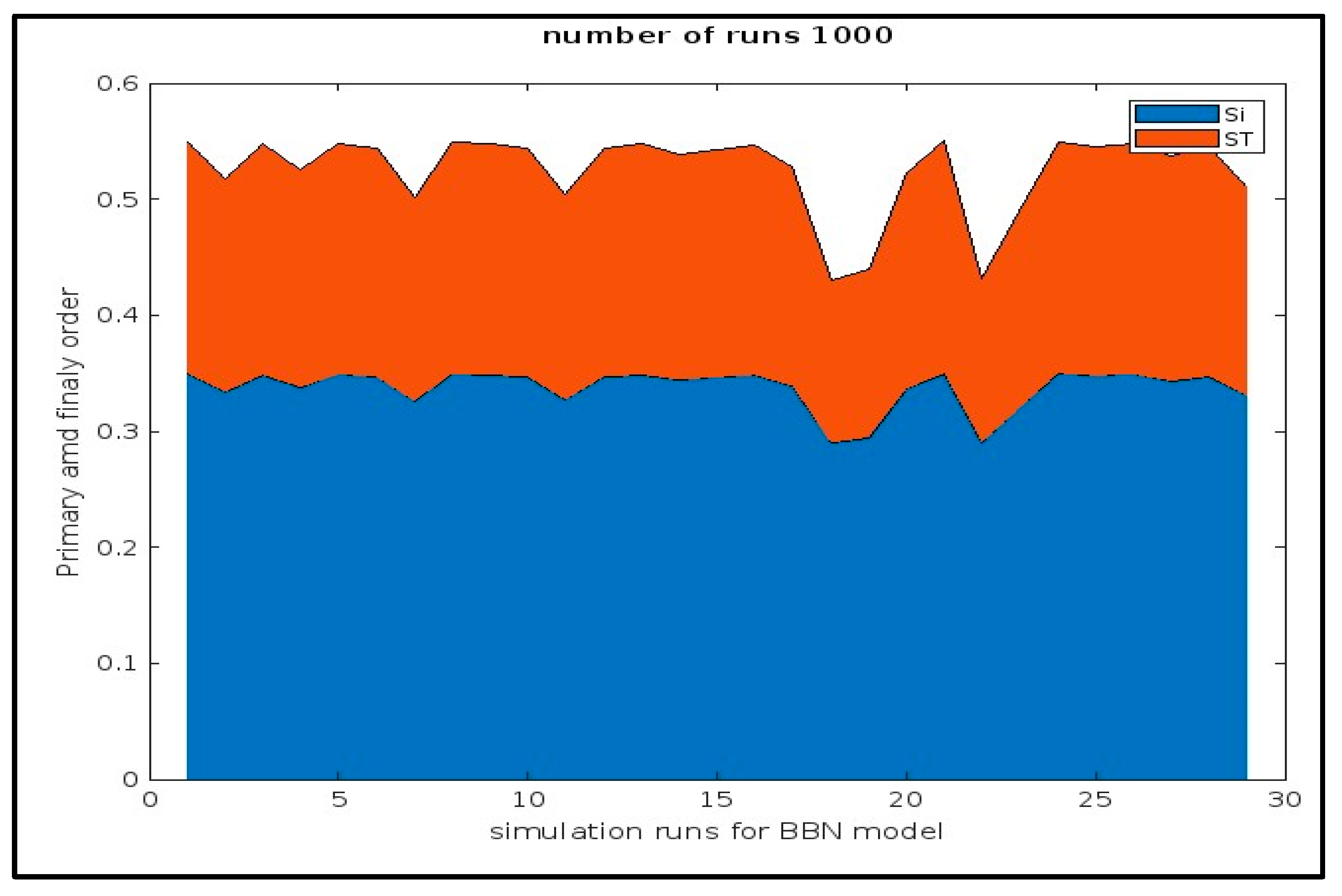
| Input Parameter BBN Model | Primary Order Index | Output Parameter BBN Model | Finally Order Index |
|---|---|---|---|
| RN1 | 0.0095 | RN1 | 0.0090 |
| RN2 | 0.1242 | RN2 | 0.1441 |
| RN3 | 0.0188 | RN3 | 0.0184 |
| RN4 | 0.0156 | RN4 | 0.0154 |
| RN5 | 0.0781 | RN5 | 0.0190 |
| CN1 | 0.1271 | CN1 | 0.1582 |
| CN2 | 0.0063 | CN2 | 0.0078 |
| CN3 | 0.0094 | CN3 | 0.0049 |
| CN4 | 0.0087 | CN4 | 0.0065 |
| RN6 | 0.0071 | RN6 | 0.0064 |
| CN5 | 0.0072 | CN5 | 0.0083 |
| CN6 | 0.0072 | CN6 | 0.0079 |
| RN7 | 0.0081 | RN7 | 0.0061 |
| RN8 | 0.1155 | RN8 | 0.1201 |
| CN7 | 0.0069 | CN7 | 0.0058 |
| RN9 | 0.0089 | RN9 | 0.0077 |
| CN8 | 0.0081 | CN8 | 0.0087 |
| SN1 | 0.0004 | SN1 | 0.0003 |
| CN9 | 0.0048 | CN9 | 0.0041 |
| RN10 | 0.0067 | RN10 | 0.0046 |
| SN2 | 0.1011 | SN2 | 0.1109 |
| RN11 | 0.0009 | RN11 | 0.0009 |
| RN12 | 0.1470 | RN12 | 0.1605 |
| RN13 | 0.0099 | RN13 | 0.0069 |
| CN10 | 0.1380 | CN10 | 0.1480 |
| RN14 | 0.0081 | RN14 | 0.0094 |
| CN11 | 0.0035 | CN11 | 0.0023 |
| RN15 | 0.0074 | RN15 | 0.0069 |
| RN16 | 0.0007 | RN16 | 0.0009 |
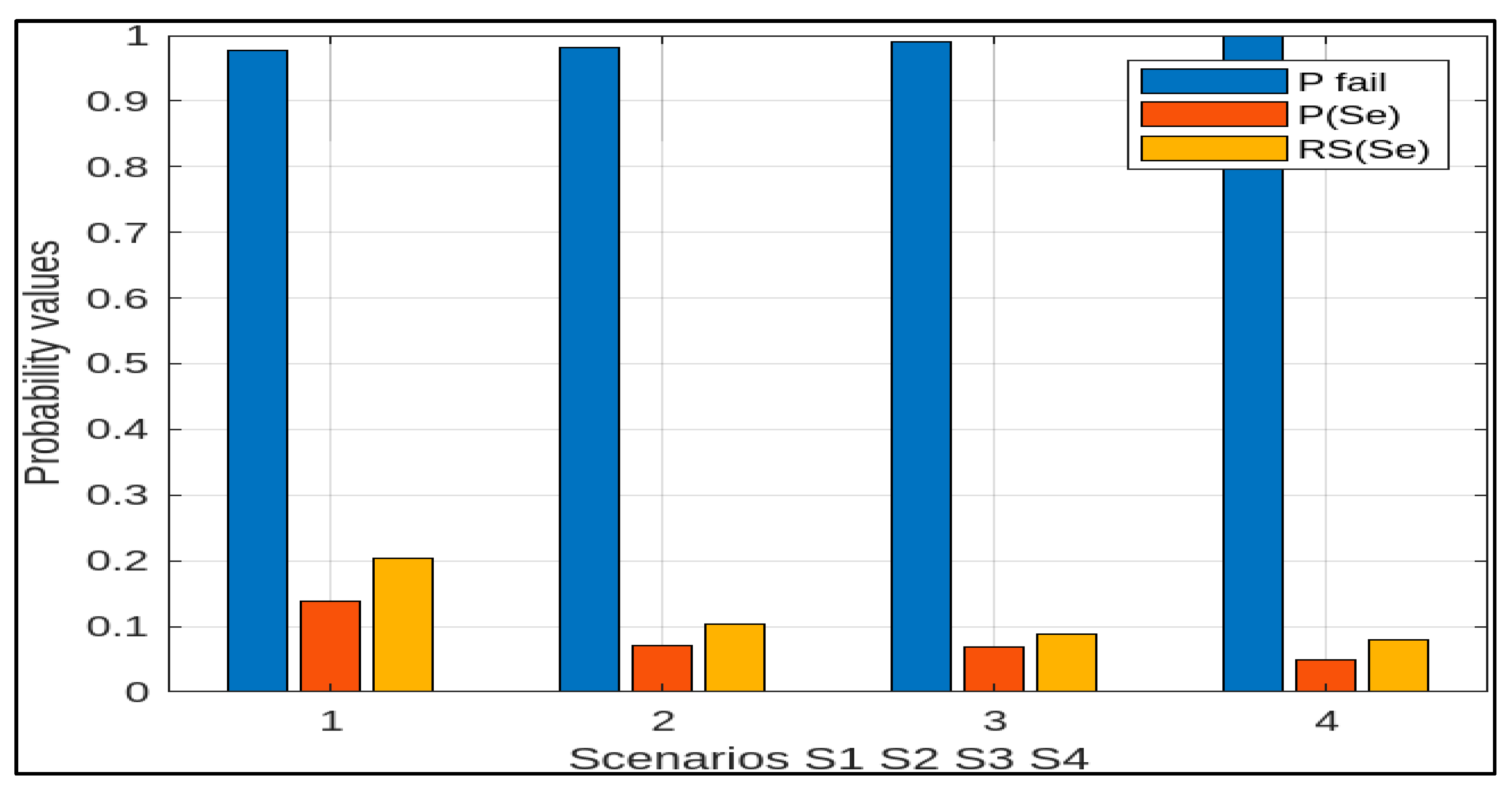
| Important Risks Scenarios from BBN | Nodes Leading Directly to Top Event | The Result Obtained of Probability Failure Hydraulic Fracturing Process, Probability of Scenario and Risks Share | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Scenarios | CN1 | SN2 | RN2 | RN8 | RN12 | CN10 | |||
| S1 | High | No | No | High | Low | Yes | 0.979 | 0.148 | 0.204 |
| S2 | High | No | No | Low | High | No | 0.971 | 0.082 | 0.103 |
| S3 | Med | No | Yes | Low | Med | No | 0.994 | 0.071 | 0.088 |
| S4 | Low | No | Yes | Low | Low | No | 1 | 0.043 | 0.079 |
| Node | Mitigation Plan | Associated Cost (USD) | Reduction in Probability of Failure |
|---|---|---|---|
| CN1 | Improved wellbore stability | 50,000 | 20% |
| SN2 | Enhanced fluid control | 30,000 | 15% |
| RN2 | Optimized pressure management | 20,000 | 10% |
| RN8 | Better reservoir characterization | 60,000 | 25% |
| RN12 | Advanced real-time monitoring | 10,000 | 12% |
| CN10 | Rigorous training of personnel | 5000 | 18% |
| Total | 175,000 | 100% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Badjadi, M.A.; Zhu, H.; Zhang, C.; Safdar, M. A Bayesian Network Model for Risk Management during Hydraulic Fracturing Process. Water 2023, 15, 4159. https://doi.org/10.3390/w15234159
Badjadi MA, Zhu H, Zhang C, Safdar M. A Bayesian Network Model for Risk Management during Hydraulic Fracturing Process. Water. 2023; 15(23):4159. https://doi.org/10.3390/w15234159
Chicago/Turabian StyleBadjadi, Mohammed Ali, Hanhua Zhu, Cunquan Zhang, and Muhammad Safdar. 2023. "A Bayesian Network Model for Risk Management during Hydraulic Fracturing Process" Water 15, no. 23: 4159. https://doi.org/10.3390/w15234159
APA StyleBadjadi, M. A., Zhu, H., Zhang, C., & Safdar, M. (2023). A Bayesian Network Model for Risk Management during Hydraulic Fracturing Process. Water, 15(23), 4159. https://doi.org/10.3390/w15234159






