A Novel Cellular Automata Framework for Modeling Depth-Averaged Solute Transport during Pluvial and Fluvial Floods
Abstract
:1. Introduction
2. Materials and Methods
2.1. Delineate Discretized Computational Cells and Decide the Neighborhood Configuration of Each Computational Cell
2.2. Determine the Variables to Express the State of Each Cell
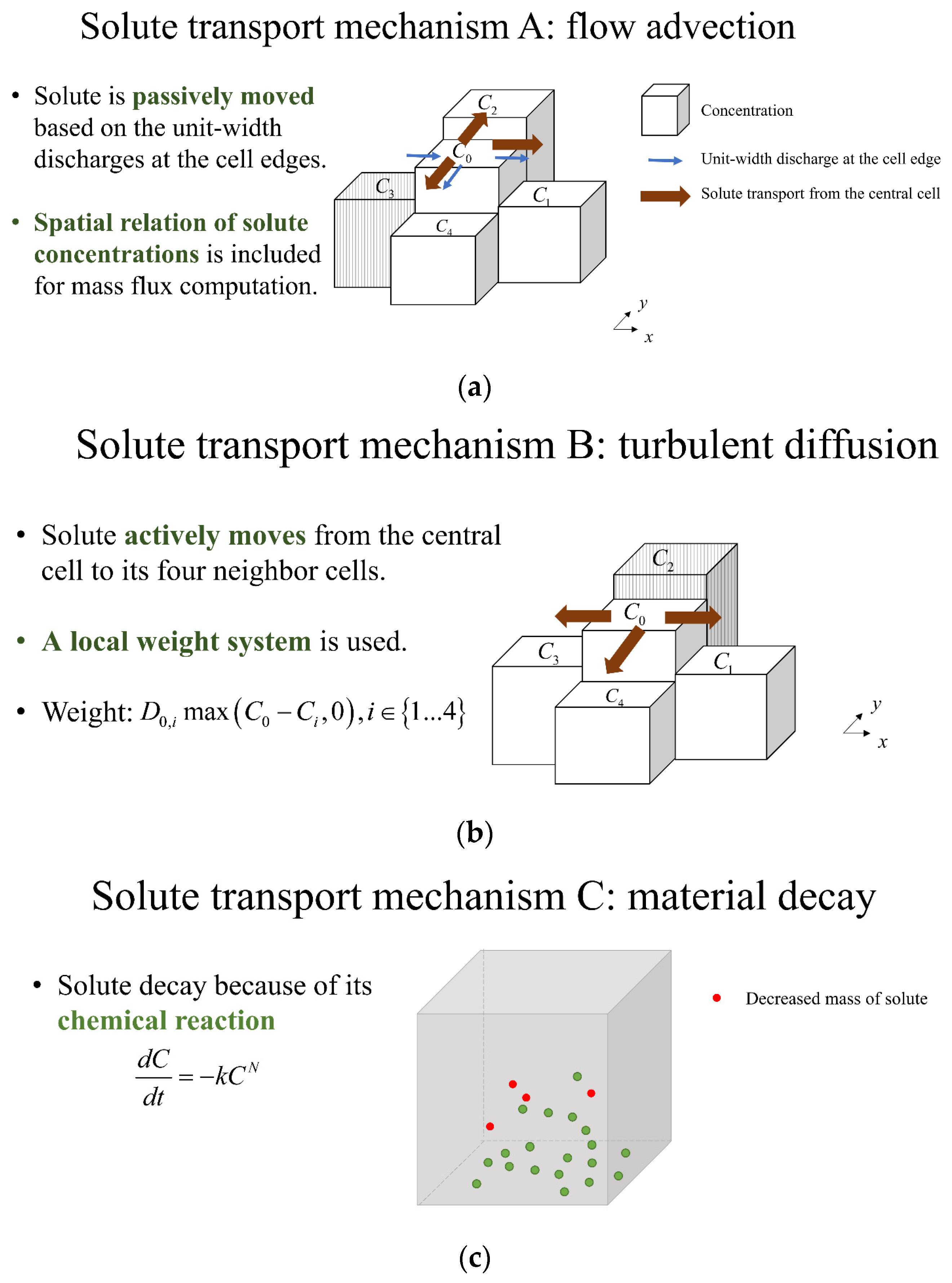
2.3. Establish a Set of Transition Rules to Advance the State of Each Cell into New Time Steps
2.3.1. Step 1: Determine the Mass of the Three Mechanisms of Each Central Cell
- Flow advection mechanism
- 2.
- Turbulent diffusion mechanism
- 3.
- Material decay mechanism
2.3.2. Step 2: Update the Solute Concentration of Each Central Cell
2.4. Adaptive Time Step and Boundary Conditions
3. Results and Discussion
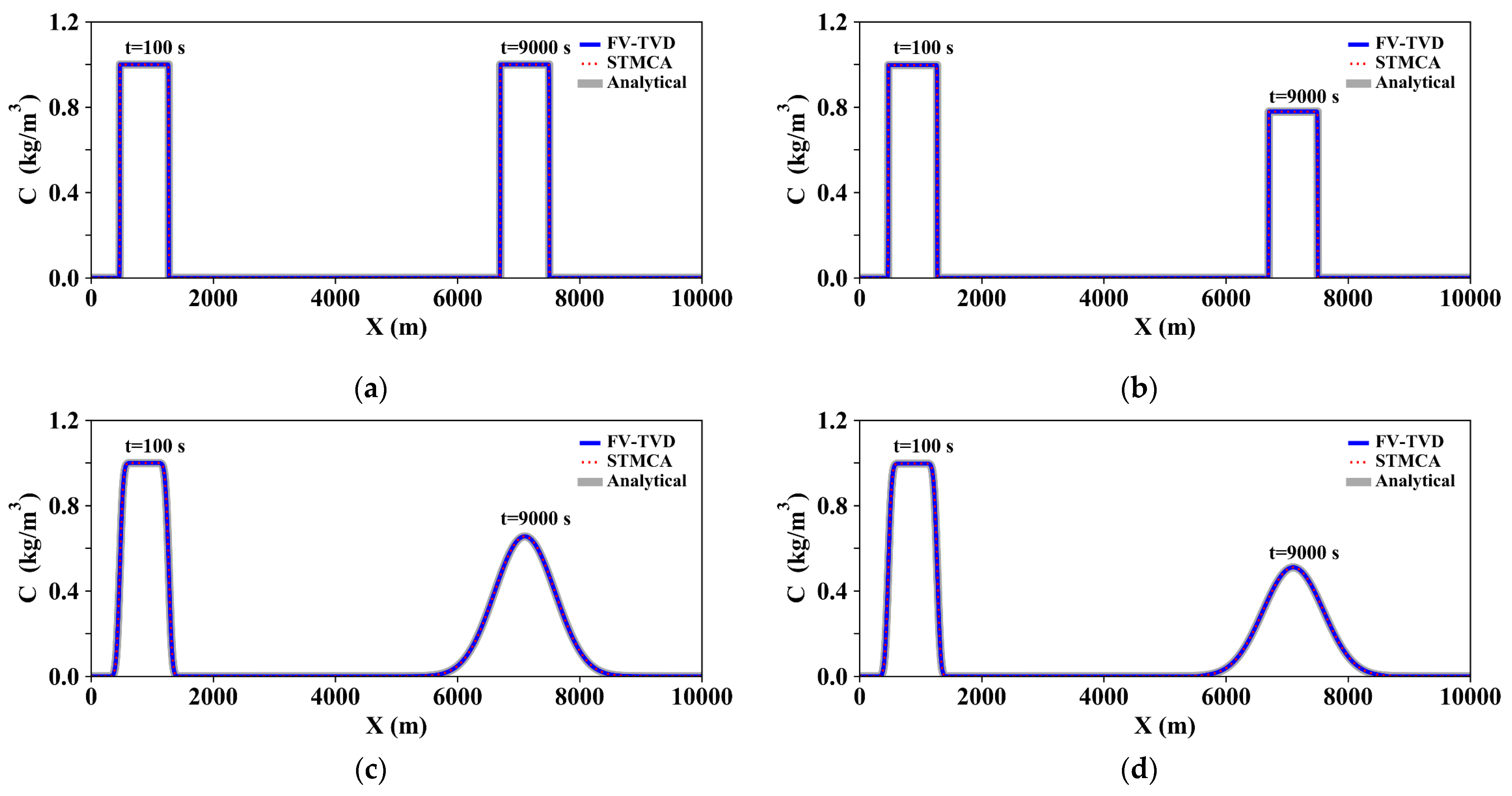
3.1. Model Verification of the STMCA Approach with Four Idealized Solute Transport Cases
3.1.1. Case 1: Solute Transport in a 2D Uniform Velocity Field (Movement of Solute with Steep Gradients in a 2D Steady Uniform Flow)
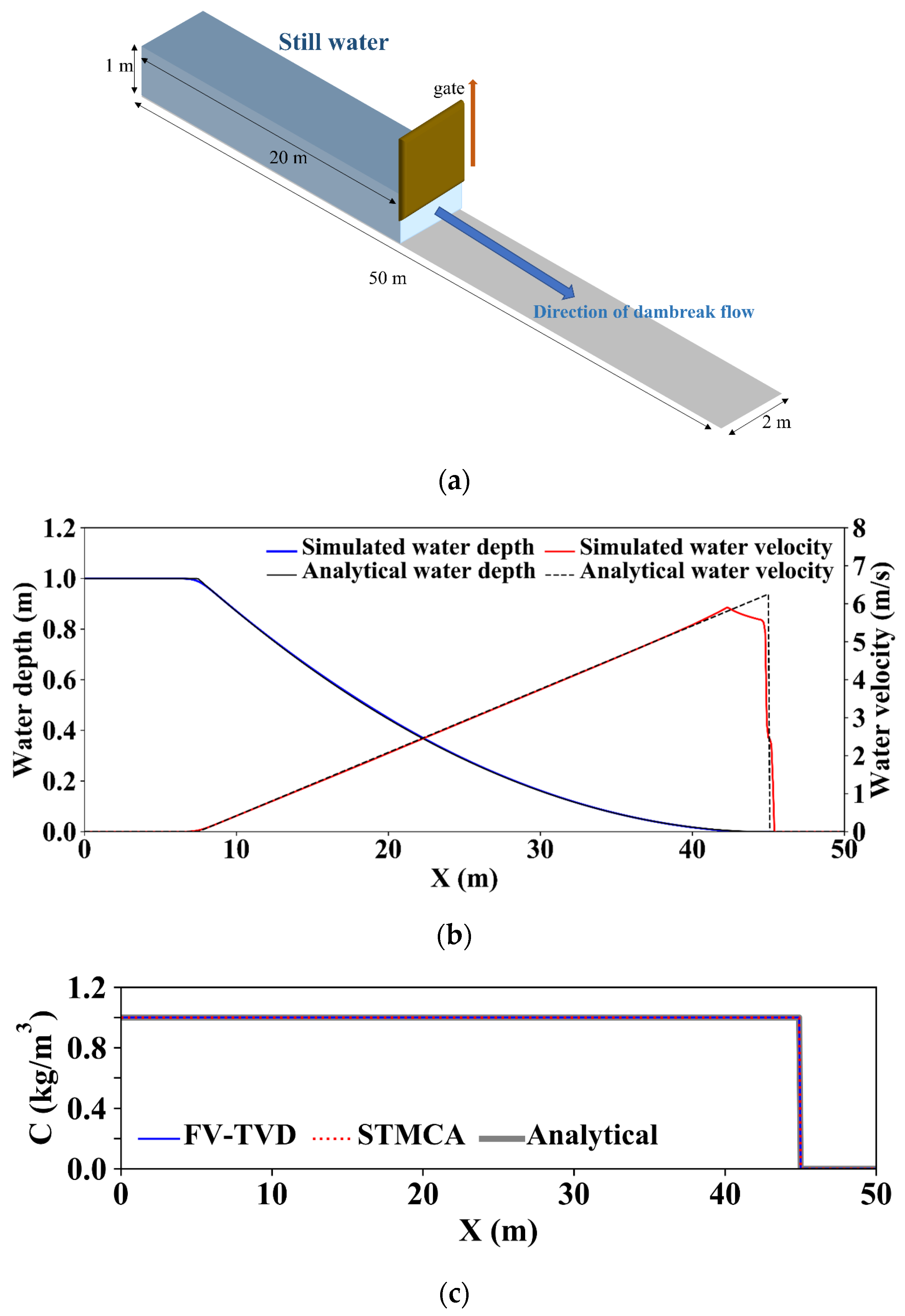
3.1.2. Case 2: Solute Transport in a 2D Dry-Bed Dam-Break Flows over a Horizontal Plate (Solute Transport in an Idealized Dry-Bed Dam-Break Flows)
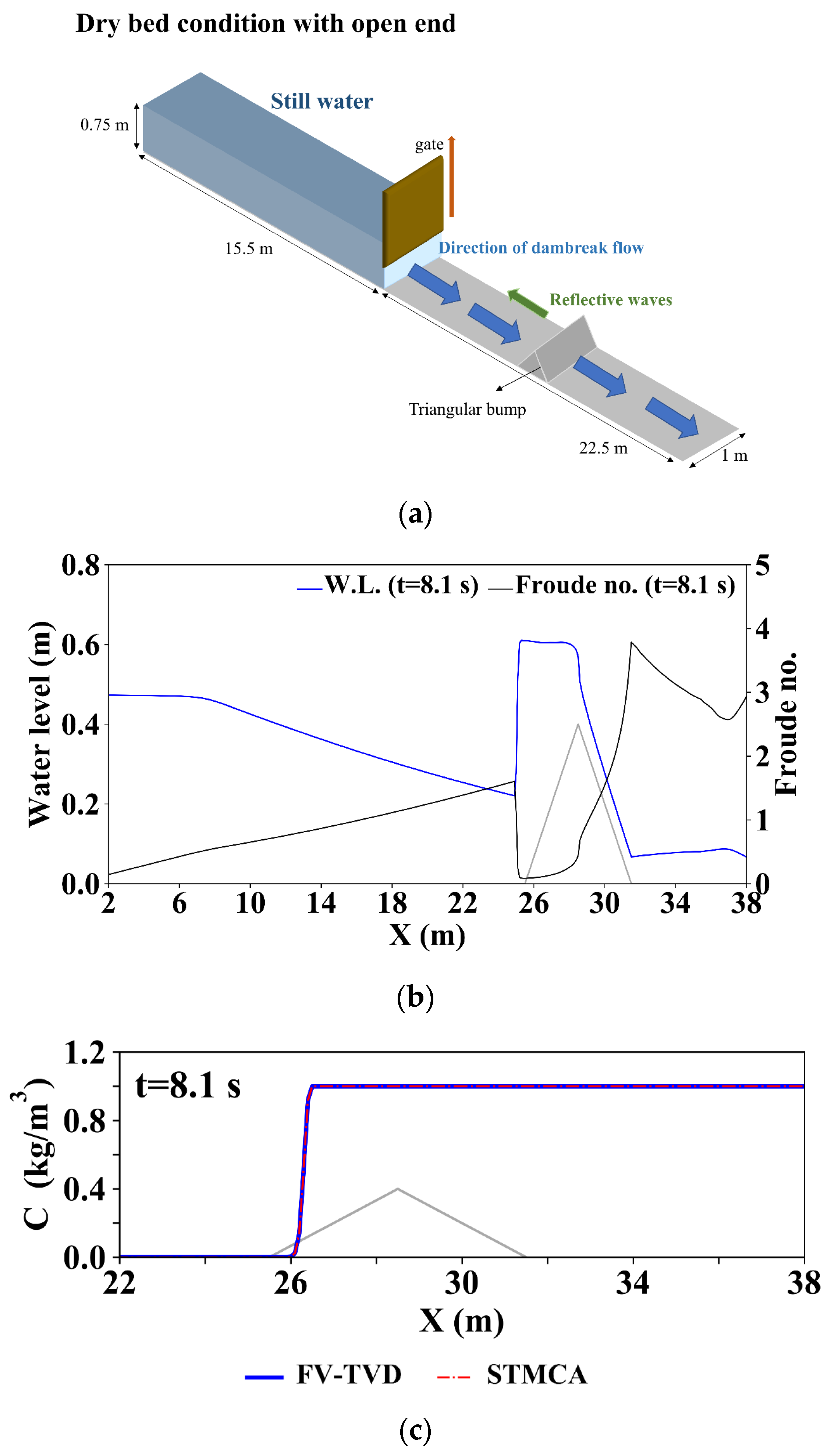
3.1.3. Case 3: Solute Transport in a 2D Dam-Break Flows over a Triangular Bump with the Dry Bed Condition and Open End (Discontinuous Solute Concentrations in a Dam-Break Flow over a Complex Terrain with the Dry Bed Condition and Open End)
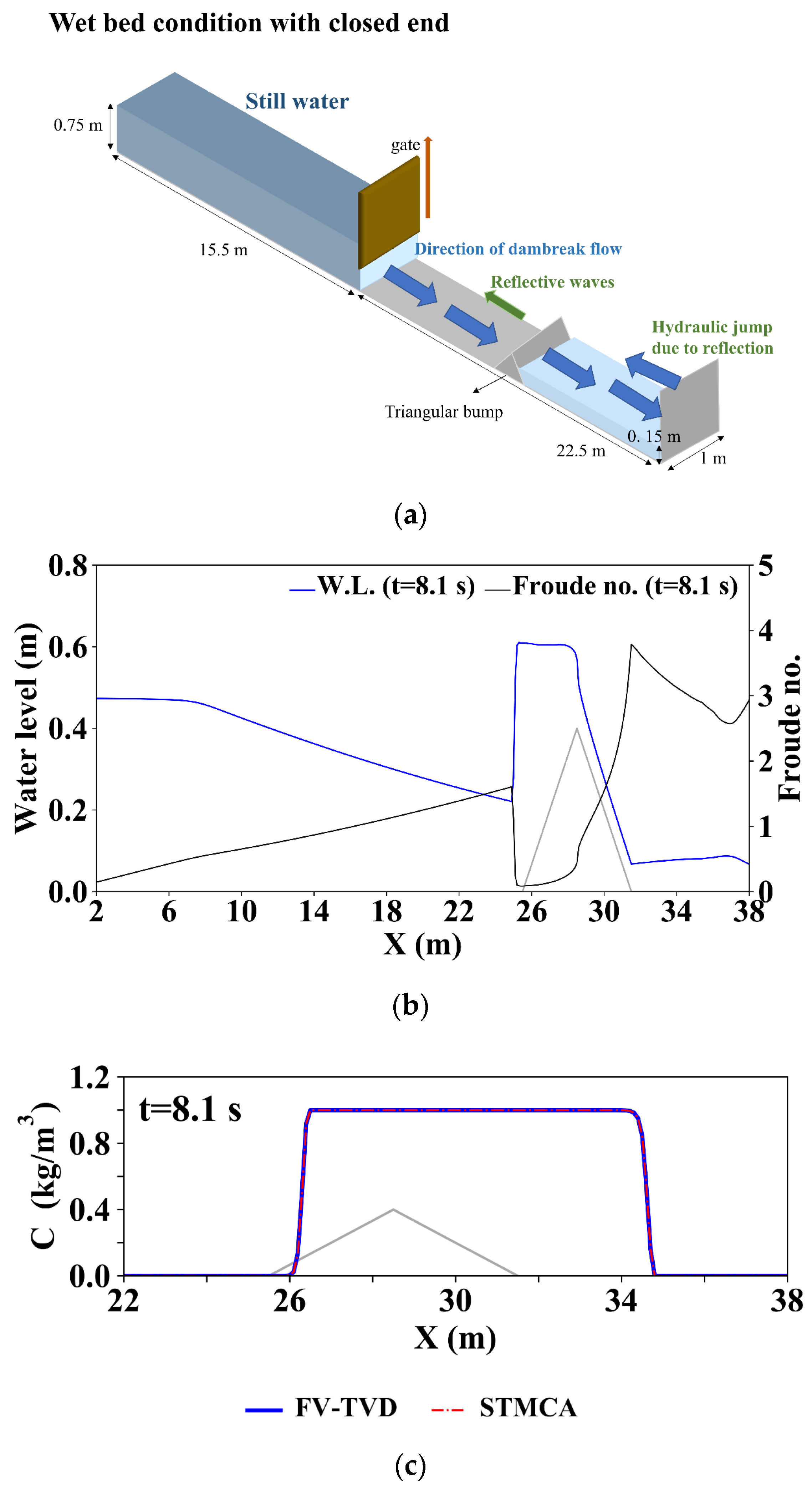
3.1.4. Case 4: Solute Transport in a 2D Dam-Break Flows over a Triangular Bump with the Wet Bed Condition and a Closed End (Discontinuous Solute Concentrations in a Dam-Break Flow over a Complex Terrain with the Wet Bed Condition and a Closed End)
3.2. Model Applications and Efficiency Assessment on a Real-Scale Terrain
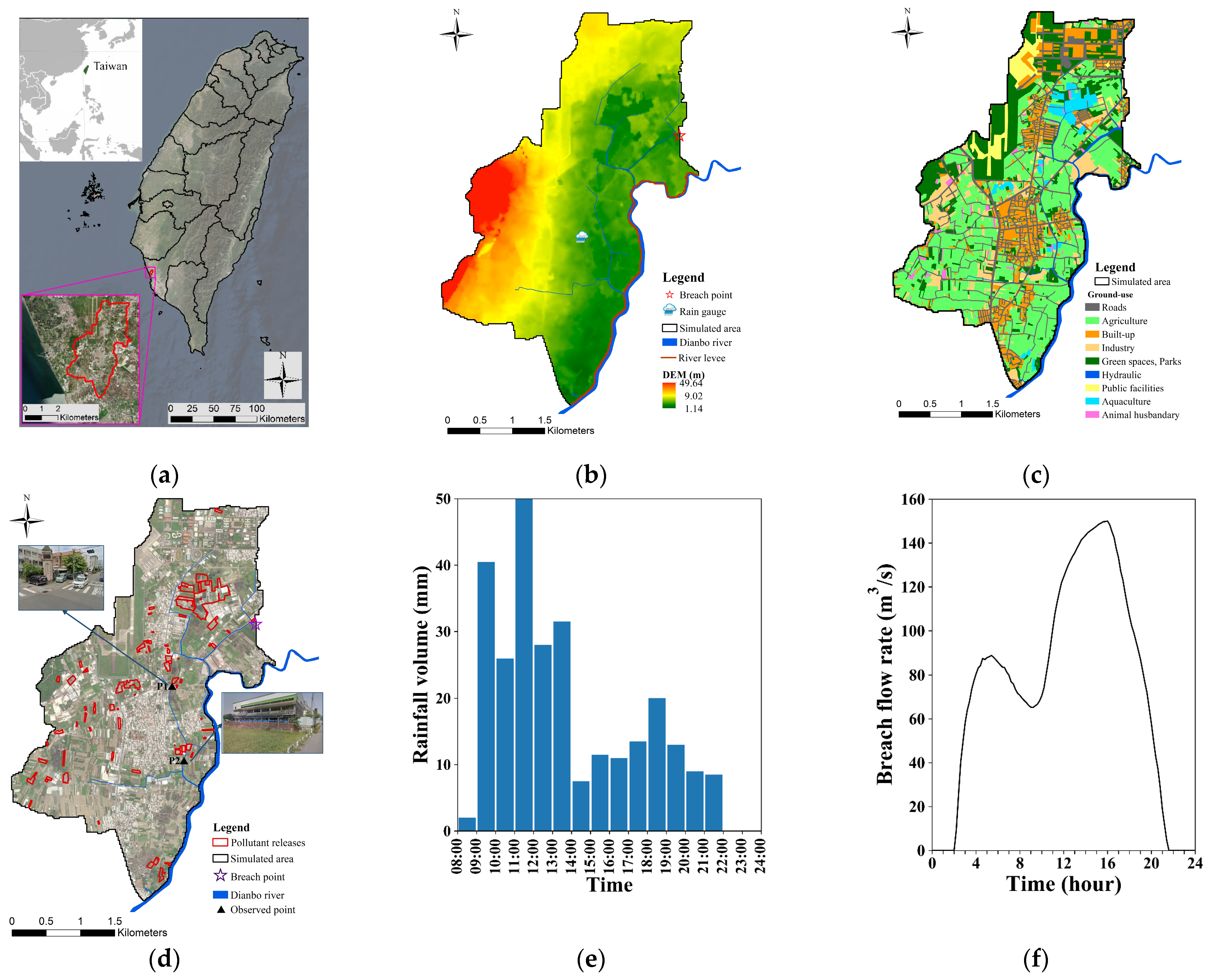
3.2.1. Study Site Delineation
3.2.2. Pluvial and Fluvial Flood Events
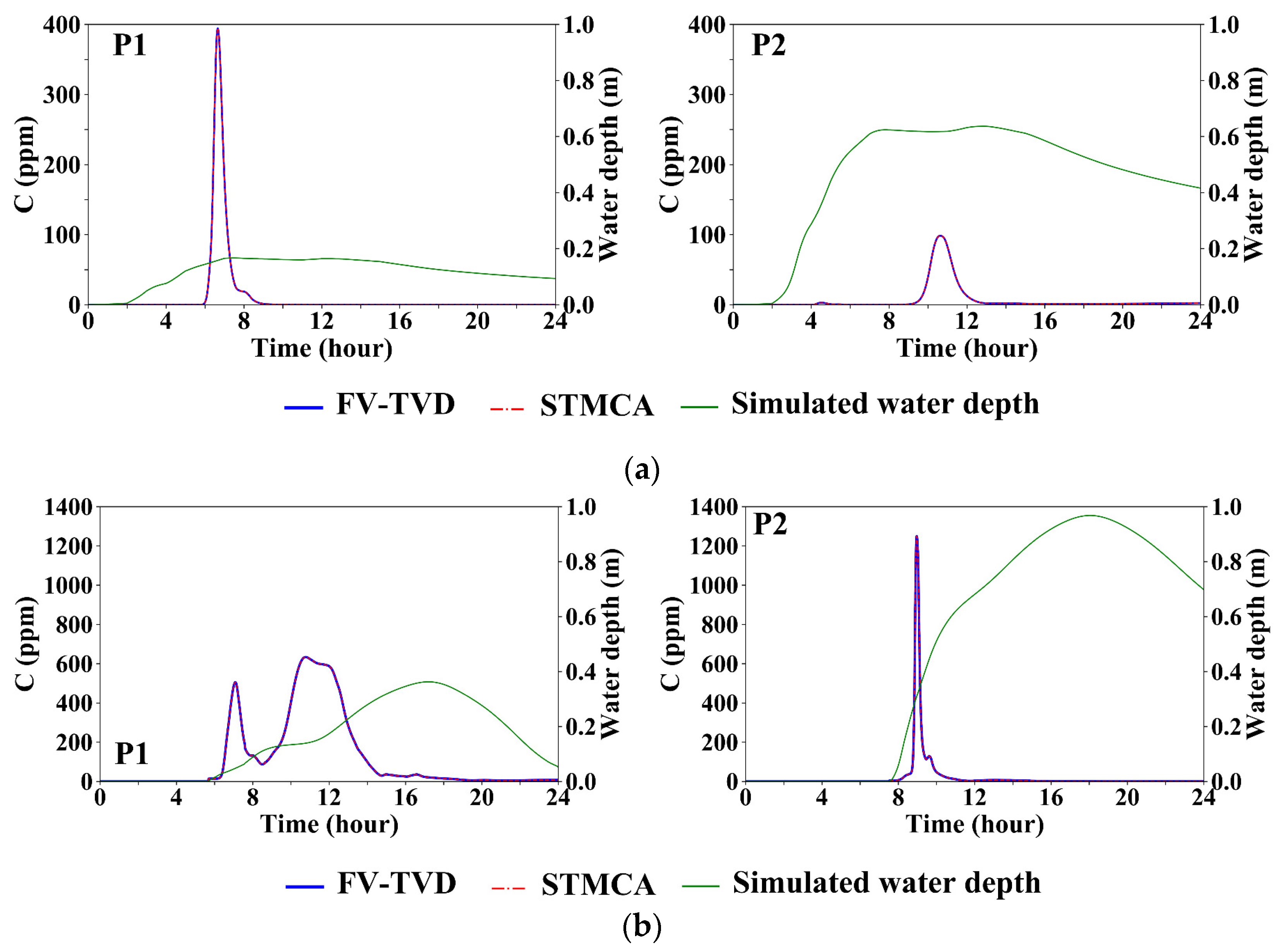
3.2.3. Accuracy Comparison
- 4.
- Simulated velocity fields
- 5.
- Simulated solute concentration fields
3.2.4. Efficiency Assessment
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Castro-Orgaz, O.; Hager, W.H. Shallow Water Hydraulics; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Liang, D.; Wang, X.; Falconer, R.A.; Bockelmann-Evans, B.N. Solving the depth-integrated solute transport equation with a TVD-MacCormack scheme. Environ. Model. Softw. 2010, 25, 1619–1629. [Google Scholar] [CrossRef]
- Kao, H.M.; Chang, T.J. Numerical modeling of dambreak-induced flood and inundation using smoothed particle hydrodynamics. J. Hydrol. 2012, 448–449, 232–244. [Google Scholar] [CrossRef]
- Martins, R.; Leandro, J.; Djordjević, S. Wetting and drying numerical treatments for the Roe Riemann scheme. J. Hydraul. Res. 2018, 56, 256–267. [Google Scholar] [CrossRef]
- Bai, F.P.; Yang, Z.H.; Zhou, W.G. Study of total variation diminishing (TVD) slope limiter in dam-break flow simulation. Water Sci. Eng. 2018, 11, 68–74. [Google Scholar] [CrossRef]
- Yu, H.L.; Chang, T.J. A hybrid shallow water solver for overland flow modelling in rural and urban areas. J. Hydrol. 2021, 598, 126262. [Google Scholar] [CrossRef]
- Zhao, J.; Liang, Q. Novel variable reconstruction and friction term discretization schemes for hydrodynamic modelling of overland flow and surface water flooding. Adv. Water Resour. 2022, 163, 104187. [Google Scholar] [CrossRef]
- Ferrari, A.; Vacondio, R.; Dazzi, S.; Mignosa, P. A 1D-2D Shallow Water Equations solver for discontinuous porosity field based on a Generalized Riemann Problem. Adv. Water Resour. 2017, 107, 233–249. [Google Scholar] [CrossRef]
- Chang, Y.S.; Chang, T.J. SPH simulations of solute transport in flows with steep velocity and concentration gradients. Water 2017, 9, 132. [Google Scholar] [CrossRef]
- Guan, Y.; Altinakar, M.S.; Krishnappan, B.G. Two-dimensional simulation of advection-dispersion in open channel flows. In Proceedings of the 5th International Conference on Hydro-Informatics, Cardfiff, UK, 1–5 July 2002; pp. 226–231. [Google Scholar]
- Yeh, G.T.; Chang, J.R. An exact peak capturing and oscillation-free scheme to solve advection-dispersion transport equations. Water Resour. Res. 1992, 28, 2937–2951. [Google Scholar] [CrossRef]
- Lee, M.E.; Seo, I.W. Analysis of pollutant transport in the Han River with tidal current using a 2D finite element model. J. Hydro-Environ. Res. 2007, 1, 30–42. [Google Scholar] [CrossRef]
- Ginzburg, I.; Roux, L.; Silva, G. Local boundary reflections in lattice Boltzmann schemes: Spurious boundary layers and their impact on the velocity, diffusion and dispersion. C. R. Mec. 2015, 343, 518–532. [Google Scholar] [CrossRef]
- Wang, H.; Cater, J.; Liu, H.; Ding, X.; Huang, W. A lattice Boltzmann model for solute transport in open channel flow. J. Hydrol. 2018, 556, 419–426. [Google Scholar] [CrossRef]
- Murillo, J.; García-Navarro, P.; Burguete, J. Analysis of a second-order upwind method for the simulation of solute transport in 2D shallow water flow. Int. J. Numer. Meth. Fluids 2008, 56, 661–686. [Google Scholar] [CrossRef]
- Burguete, B.; García-Navarro, P.; Murillo, J. Preserving bounded and conservative solutions of transport in one-dimensional shallow-water flow with upwind numerical schemes: Application to fertigation and solute transport in rivers. Int. J. Numer. Meth. Fluids 2008, 56, 1731–1764. [Google Scholar] [CrossRef]
- Liang, Q. A well-balanced and non-negative numerical scheme for solving the integrated shallow water and solute transport equations. Commun. Comput. Phys. 2010, 7, 1049–1075. [Google Scholar] [CrossRef]
- Zhang, L.; Liang, Q.; Wang, Y.; Yin, J. A robust coupled model for solute transport driven by severe flow conditions. J. Hydro-Environ. Res. 2015, 9, 49–60. [Google Scholar] [CrossRef]
- Morales-Hernánez, M.; Murillo, J.; García-Navarro, P. Diffusion-dispersion numerical discretization for solute transport in 2D transient shallow flows. Environ. Fluid Mech. 2019, 19, 1217–1234. [Google Scholar] [CrossRef]
- Lin, L.; Liu, Z. TVDal: Total variation diminishing scheme with alternating limiters to balance numerical compression and diffusion. Ocean Model. 2019, 134, 42–50. [Google Scholar] [CrossRef]
- Herrera, P.A.; Massabó, M.; Beckie, R.D. A meshless method to simulate solute transport in heterogeneous porous media. Adv. Water Resour. 2009, 32, 413–429. [Google Scholar] [CrossRef]
- Park, I.; Seo, I.W. Modeling non-Fickian pollutant mixing in open channel flows using two-dimensional particle dispersion model. Adv. Water Resour. 2018, 111, 105–120. [Google Scholar] [CrossRef]
- Sämann, R.; Graf, T.; Neuweiler, I. Modeling of contaminant transport during an urban pluvial flood event-the importance of surface flow. J. Hydrol. 2019, 568, 301–310. [Google Scholar] [CrossRef]
- Liu, W.; Hou, Q.; Lian, J.; Zhang, A.; Dang, J. Coastal pollutant transport modeling using smoothed particle hydrodynamics with diffusive flux. Adv. Water Resour. 2020, 146, 103764. [Google Scholar] [CrossRef]
- Hou, J.; Liang, Q.; Li, Z.; Wang, S.; Hinkelmann, R. Numerical error control for second-order explicit TVD scheme with limiters in advection simulation. Comput. Math. Appl. 2015, 70, 2197–2209. [Google Scholar] [CrossRef]
- Wolfram, S. Cellular automata as models of complexity. Nature 1984, 311, 419–424. [Google Scholar] [CrossRef]
- Chang, T.J.; Yu, H.L.; Wang, C.H.; Chen, A.S. Overland-gully-sewer (2D-1D-1D) urban inundation modeling based on cellular automata framework. J. Hydrol. 2021, 603, 127001. [Google Scholar] [CrossRef]
- Hadeler, K.P.; Müller, J. Cellular Automata: Analysis and Applications; Springer: Cham, Germany, 2017. [Google Scholar]
- Dottori, F.; Todini, E. Developments of a flood inundation model based on the cellular automata approach: Testing different methods to improve model performance. Phys. Chem. Earth Parts ABC 2011, 36, 266–280. [Google Scholar] [CrossRef]
- Ghimire, B.; Chen, A.S.; Guidolin, M.; Keedwell, E.C.; Djordjević, S.; Savić, D.A. Formulation of a fast 2D urban pluvial flood model using a cellular automata approach. J. Hydroinformatics 2013, 15, 676. [Google Scholar] [CrossRef]
- Guidolin, M.; Chen, A.S.; Ghimire, B.; Keedwell, E.C.; Djordjević, S.; Savić, D.A. A weighted cellular automata 2D inundation model for rapid flood analysis. Environ. Model. Softw. 2016, 84, 378–394. [Google Scholar] [CrossRef]
- Chang, T.J.; Yu, H.L.; Wang, C.H.; Chen, A.S. Dynamic-wave cellular automata framework for shallow water flow modeling. J. Hydrol. 2022, 613, 128449. [Google Scholar] [CrossRef]
- Milašinović, M.; Ranđelović, A.; Jaćimović, N.; Prodanović, D. Coupled groundwater hydrodynamic and pollution transport modelling using Cellular Automata approach. J. Hydrol. 2019, 576, 652–666. [Google Scholar] [CrossRef]
- Yu, H.L.; Chang, T.J. Modeling particulate matter concentration in indoor environment with cellular automata framework. Build Environ. 2022, 214, 108898. [Google Scholar] [CrossRef]
- Toro, E.F. Shock-Capturing Methods for Free-Surface Shallow Flows; John Wiley: New York, NY, USA, 2001. [Google Scholar]
- Tian, L.; Gu, S.; Wu, Y.; Wu, H.; Zhang, C. Numerical investigation of pollutant transport in a realistic terrain with the SPH-SWE method. Front. Environ. Sci. 2022, 10, 889526. [Google Scholar] [CrossRef]
- Zhou, J.G.; Causon, D.M.; Mingham, C.G.; Ingram, D.M. Numerical prediction of dam-break flows in general geometries with complex bed topography. J. Hydrau. Eng. ASCE 2004, 130, 332–340. [Google Scholar] [CrossRef]
- Chang, T.J.; Kao, H.M.; Chang, K.H.; Hsu, M.H. Numerical simulation of shallow-water dam break flows in open channels using smoothed particle hydrodynamics. J. Hydrol. 2011, 408, 78–90. [Google Scholar] [CrossRef]
- Craggs, R.J.; Zwart, A.; Nagels, J.W.; Davies-Colley, R.J. Modelling sunlight disinfection in a high rate pond. Ecol. Eng. 2004, 22, 113–122. [Google Scholar] [CrossRef]
- Falconer, R.A.; Chen, Y. An improved representation of flooding and drying and wind stress effects in a two-dimensional tidal numerical model. Proc. Inst. Civ. Eng. 1991, 91, 659–678. [Google Scholar] [CrossRef]
- Chopard, B. Cellular Automata Modeling of Physical Systems. In Encyclopedia of Complexity and Systems Science, 1st ed.; Meyers, R.A., Ed.; Springer: Greer, SC, USA, 2009; pp. 856–892. [Google Scholar]


| Case | Scenario | The STMCA Approach | The FV-TVD Approach |
|---|---|---|---|
| Case 1 | D = 0 m2/s | 0.03166 | 0.03166 |
| D = 0 m2/s with the material decay | 0.03166 | 0.03166 | |
| D = 10 m2/s | 0.00248 | 0.00248 | |
| D = 10 m2/s with the material decay | 0.00248 | 0.00248 | |
| Case 2 | - | <0.00001 | <0.00001 |
| Flood | The Run Time of the FV-TVD Approach (s) (1) | The Run Time of the STMCA Approach (s) (2) | The Efficiency Enhancement of the STMCA Approach (%) (3) = (1)/(2) |
|---|---|---|---|
| Pluvial | 1949 | 673 | 289.6% |
| Fluvial | 19,565 | 5954 | 328.6% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.-H.; Yu, H.-L.; Chang, T.-J. A Novel Cellular Automata Framework for Modeling Depth-Averaged Solute Transport during Pluvial and Fluvial Floods. Water 2024, 16, 129. https://doi.org/10.3390/w16010129
Wang C-H, Yu H-L, Chang T-J. A Novel Cellular Automata Framework for Modeling Depth-Averaged Solute Transport during Pluvial and Fluvial Floods. Water. 2024; 16(1):129. https://doi.org/10.3390/w16010129
Chicago/Turabian StyleWang, Chia-Ho, Hsiang-Lin Yu, and Tsang-Jung Chang. 2024. "A Novel Cellular Automata Framework for Modeling Depth-Averaged Solute Transport during Pluvial and Fluvial Floods" Water 16, no. 1: 129. https://doi.org/10.3390/w16010129
APA StyleWang, C.-H., Yu, H.-L., & Chang, T.-J. (2024). A Novel Cellular Automata Framework for Modeling Depth-Averaged Solute Transport during Pluvial and Fluvial Floods. Water, 16(1), 129. https://doi.org/10.3390/w16010129





