Inter-Comparison of Multiple Gridded Precipitation Datasets over Different Climates at Global Scale
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Availability
2.1.1. Global Precipitation Datasets
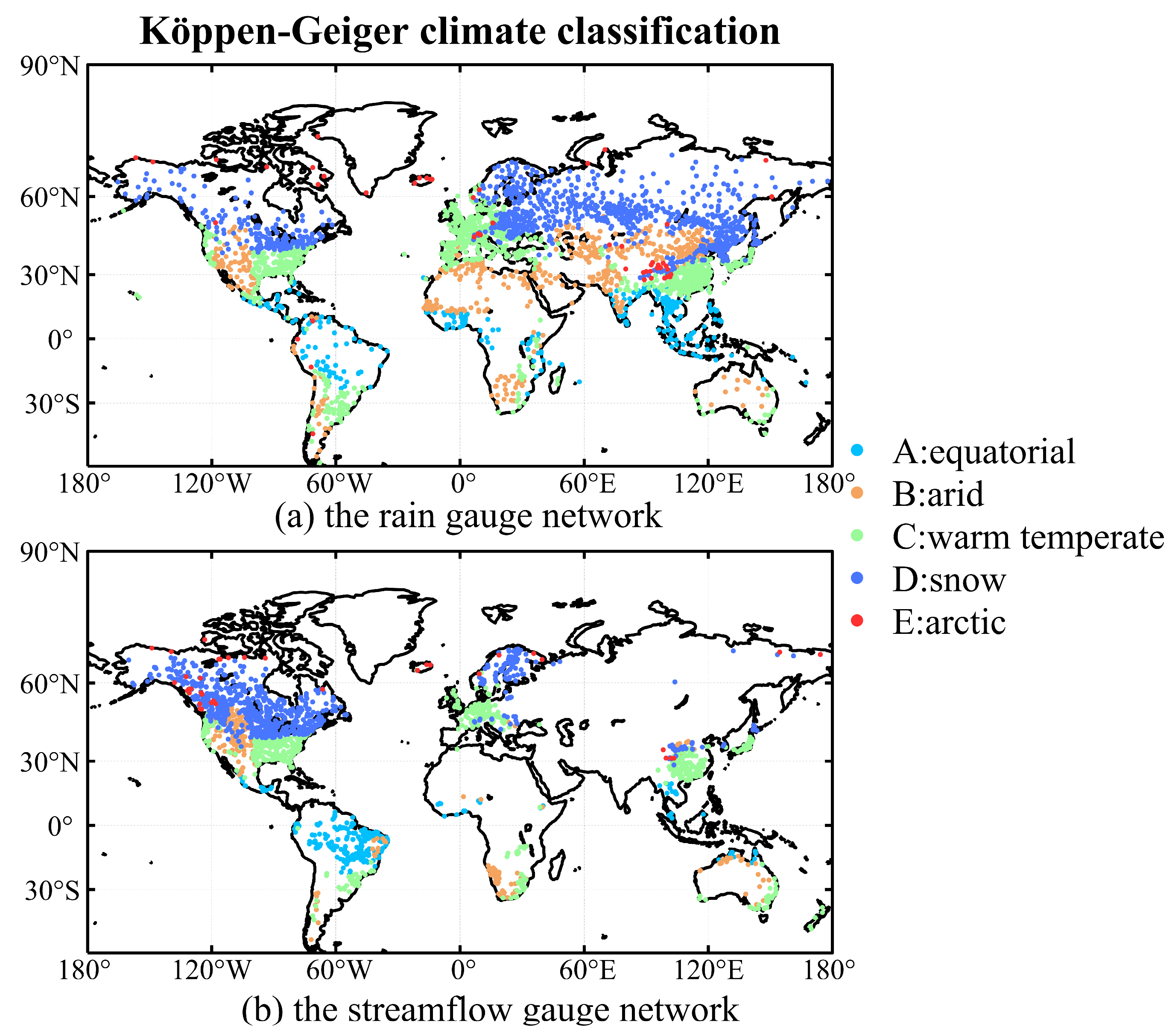
2.1.2. Rain Gauge Observations
2.1.3. Other Meteorological Data
2.1.4. Observed Streamflow
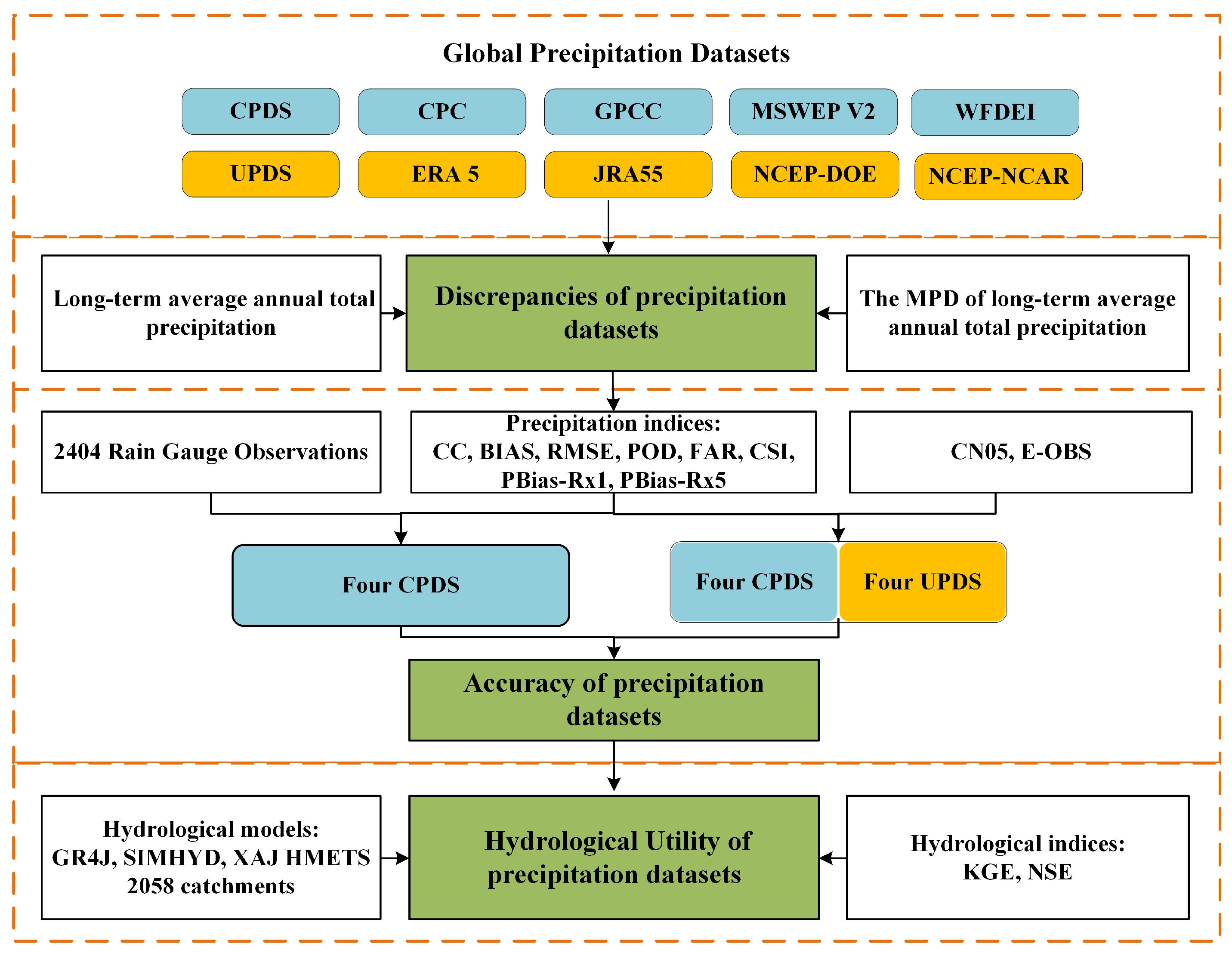
2.2. Methodology
- (1)
- The four UPDs were first evaluated on a daily timescale by comparing them with data from 2404 rain gauges worldwide.
- (2)
- The performance of the four UPDs and four CPDs (see Table 1) was then evaluated on a daily timescale using two high-resolution gridded gauge-interpolated datasets in China (i.e., CN05) and Europe (i.e., E-OBS).
- (3)
- The hydrological utility of eight precipitation datasets was subsequently assessed through hydrological modeling for 2058 catchments worldwide on a daily timescale.
2.2.1. Hydrological Models and Calibration
| Model | Snow Module | Simulated Processes (Number of Parameters) | References |
|---|---|---|---|
| GR4J | CemaNeige | Flow routing (1) Snow modeling (2) Vertical budget (3) | Perrin et al. [62,76] |
| SIMHYD | CemaNeige | Flow routing (1) Snow modeling (2) Vertical budget (8) | Chiew et al. [66,67] |
| XAJ | CemaNeige | Flow routing (7) Snow modeling (2) Vertical budget (8) | Zhao et al. [68,69] |
| HMETS | HMETS | Evapotranspiration (1) Flow routing (4) Snow modeling (10) Vertical budget (6) | Martel et al. [71] and Chen et al. [72] |
2.2.2. Statistical Analysis Methods
3. Results
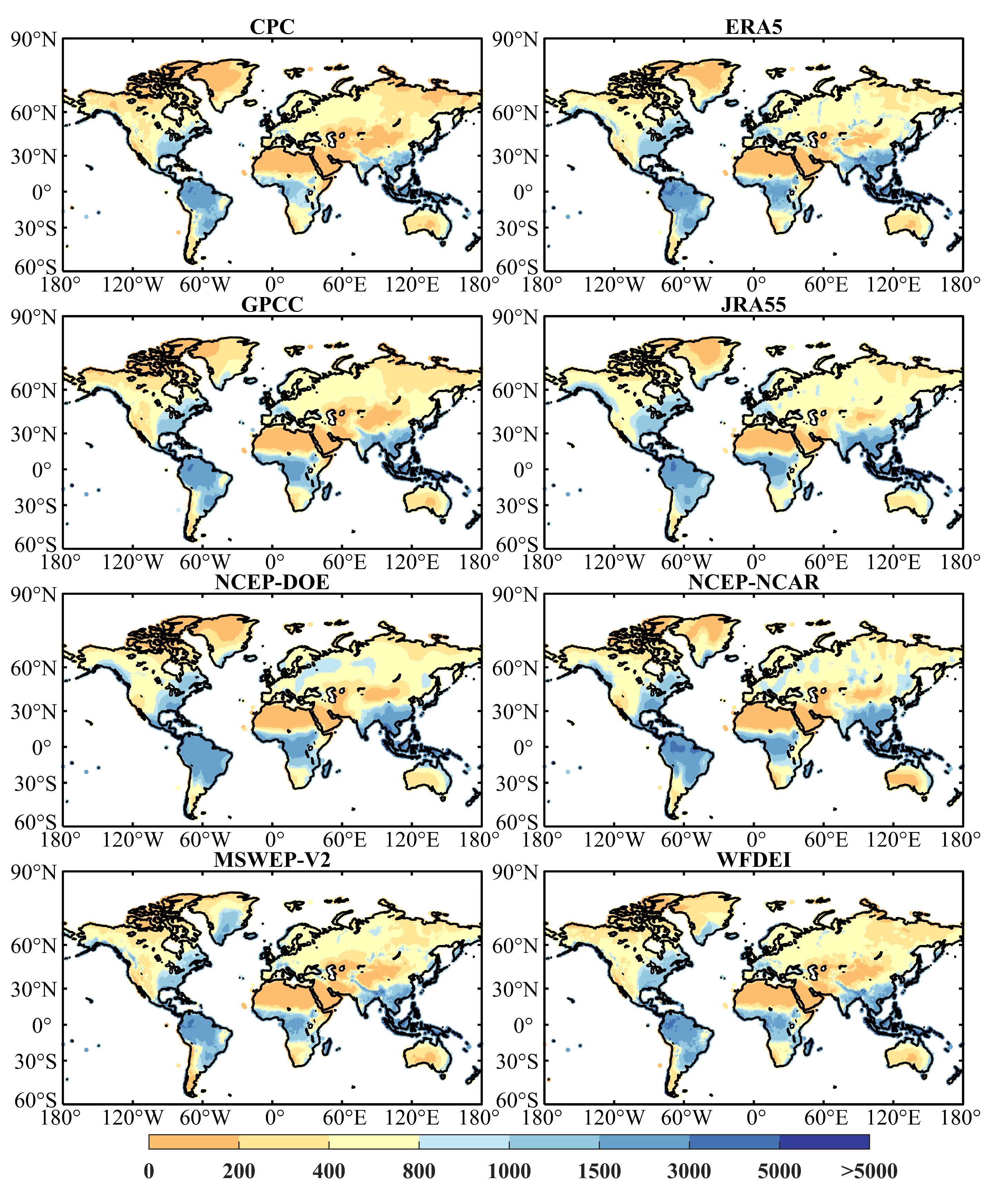
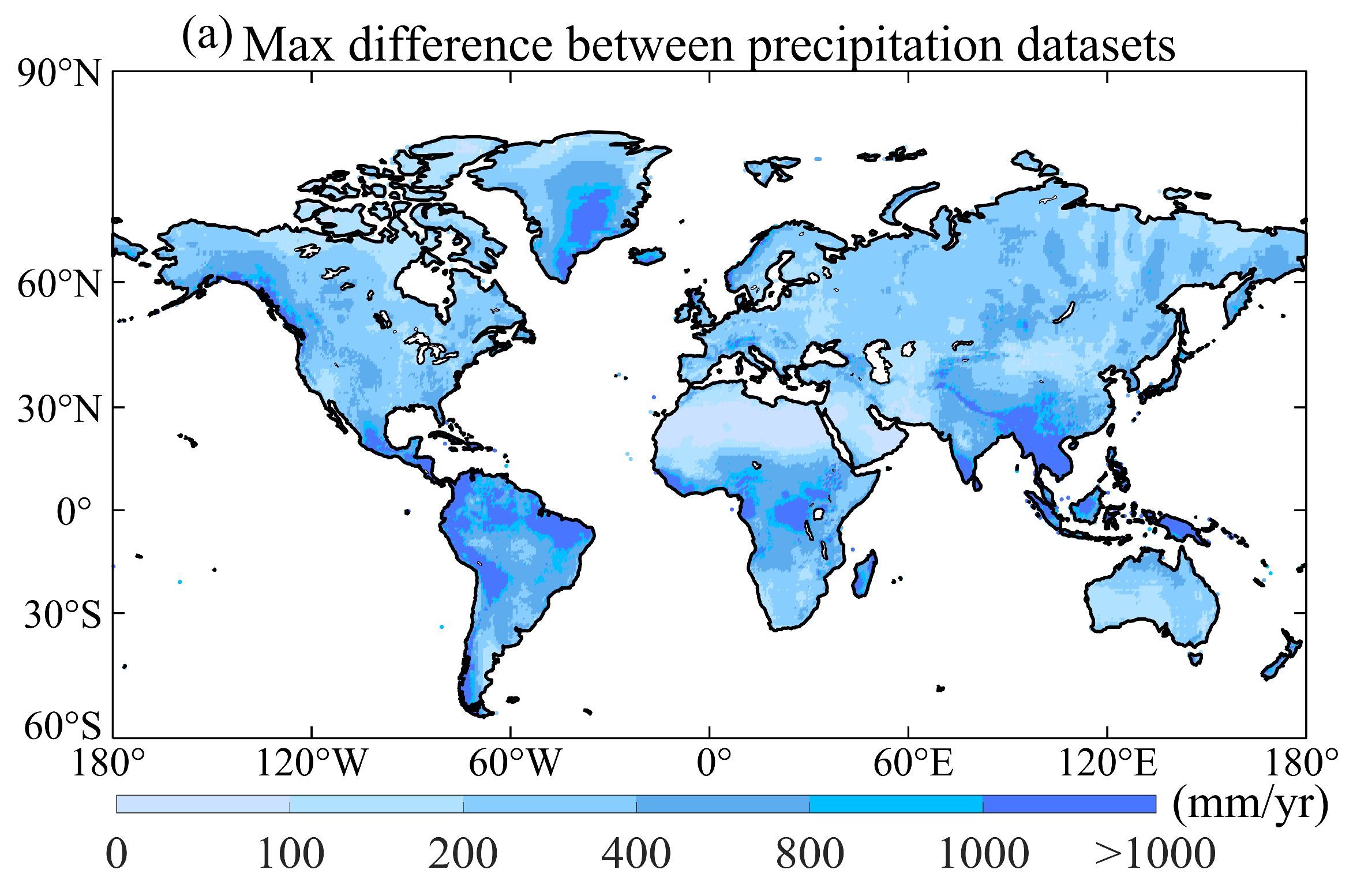
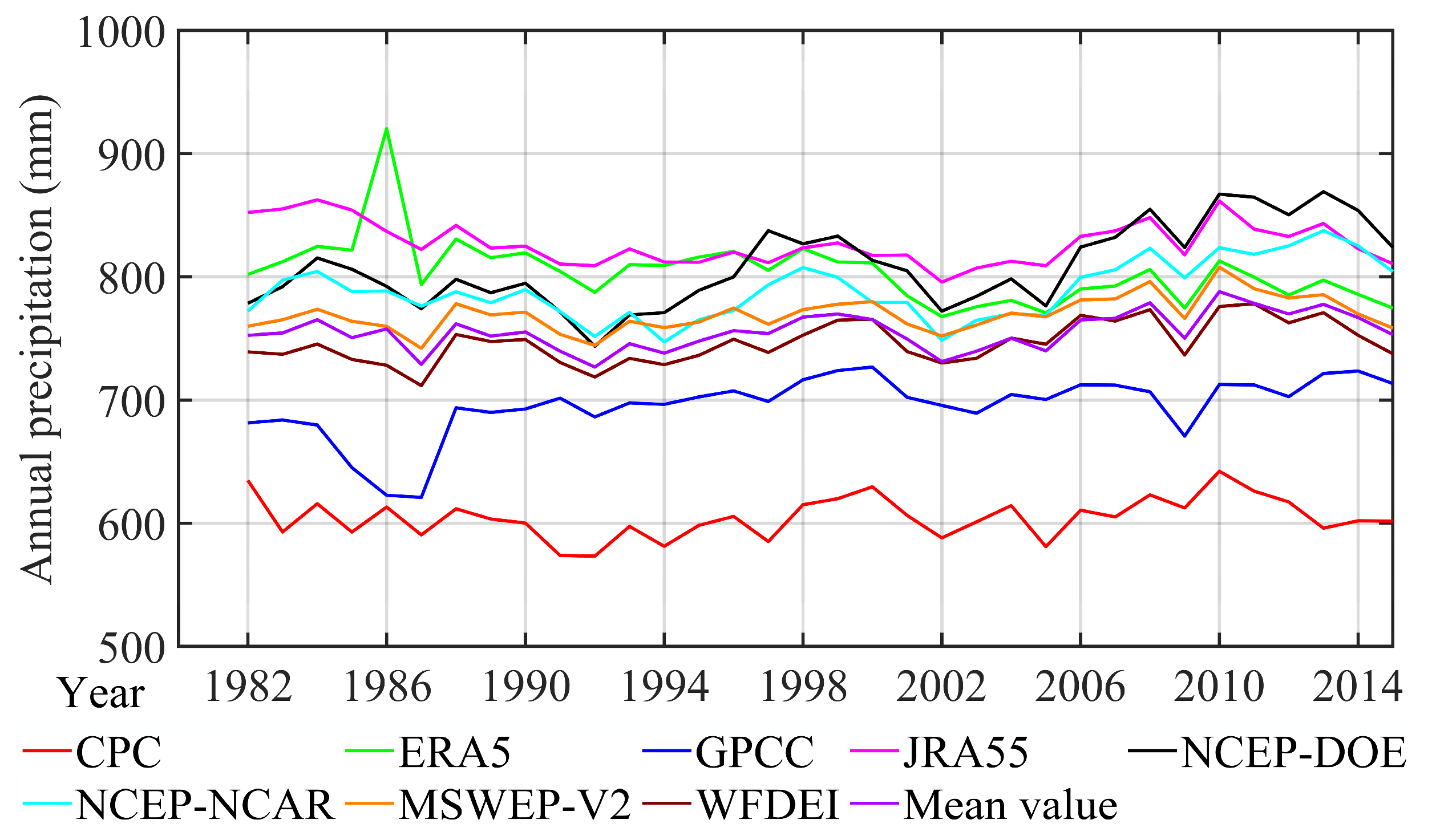
3.1. Discrepancies in Annual Precipitation
3.2. Evaluation of the Precipitation Datasets’ Performance Based on Ground Precipitation Observations
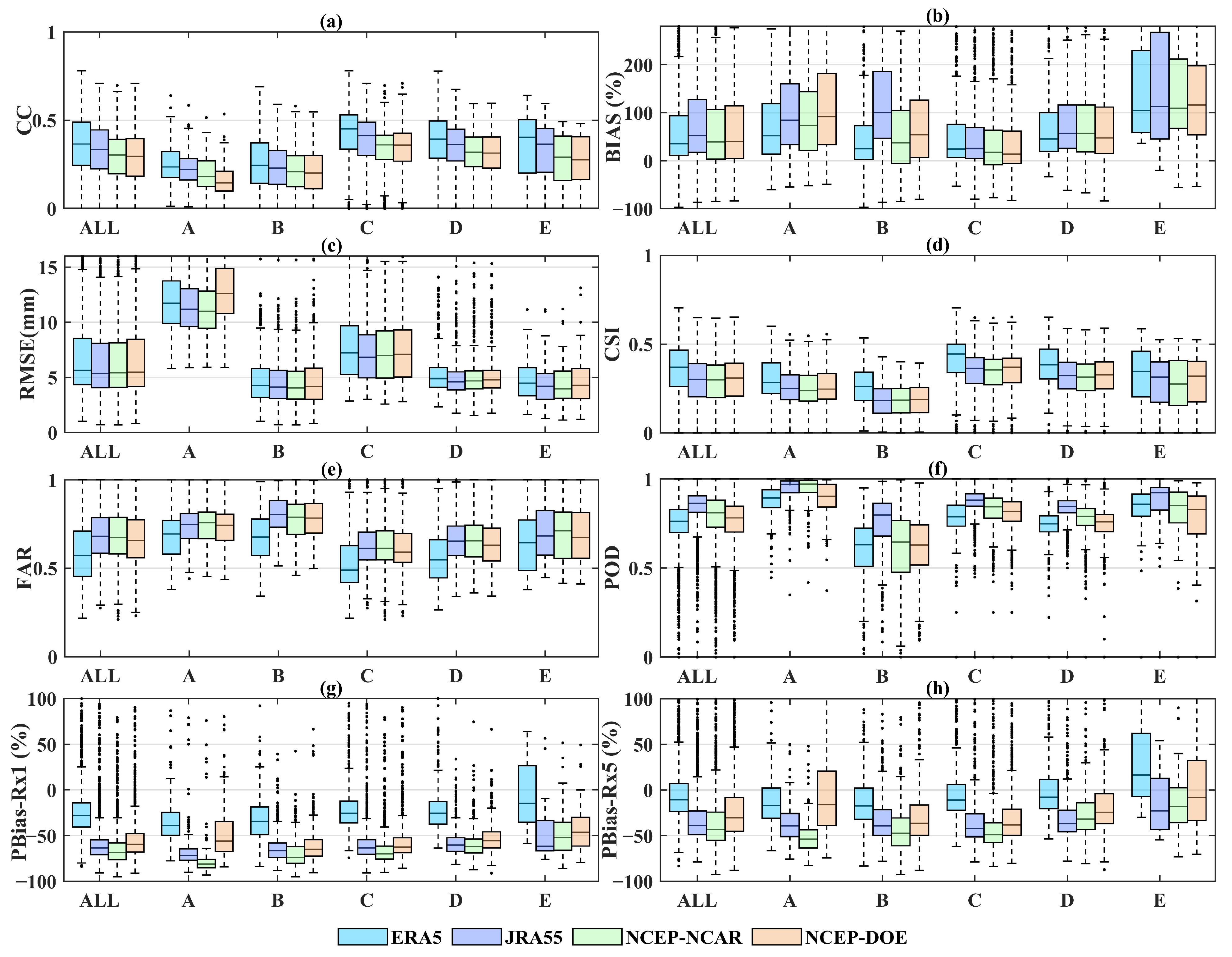
3.2.1. The Performance of the Four UPDs Using Gauge Observations
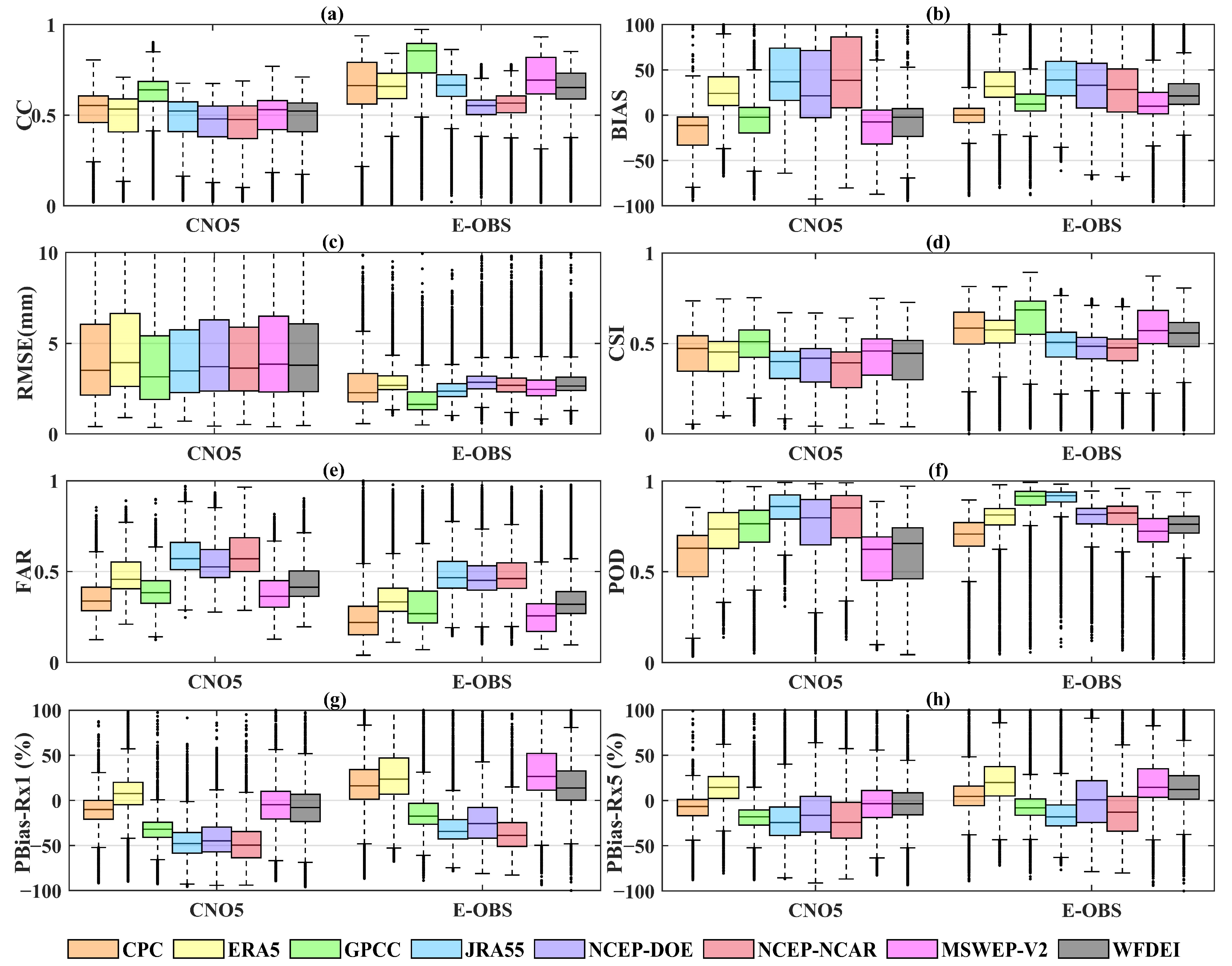
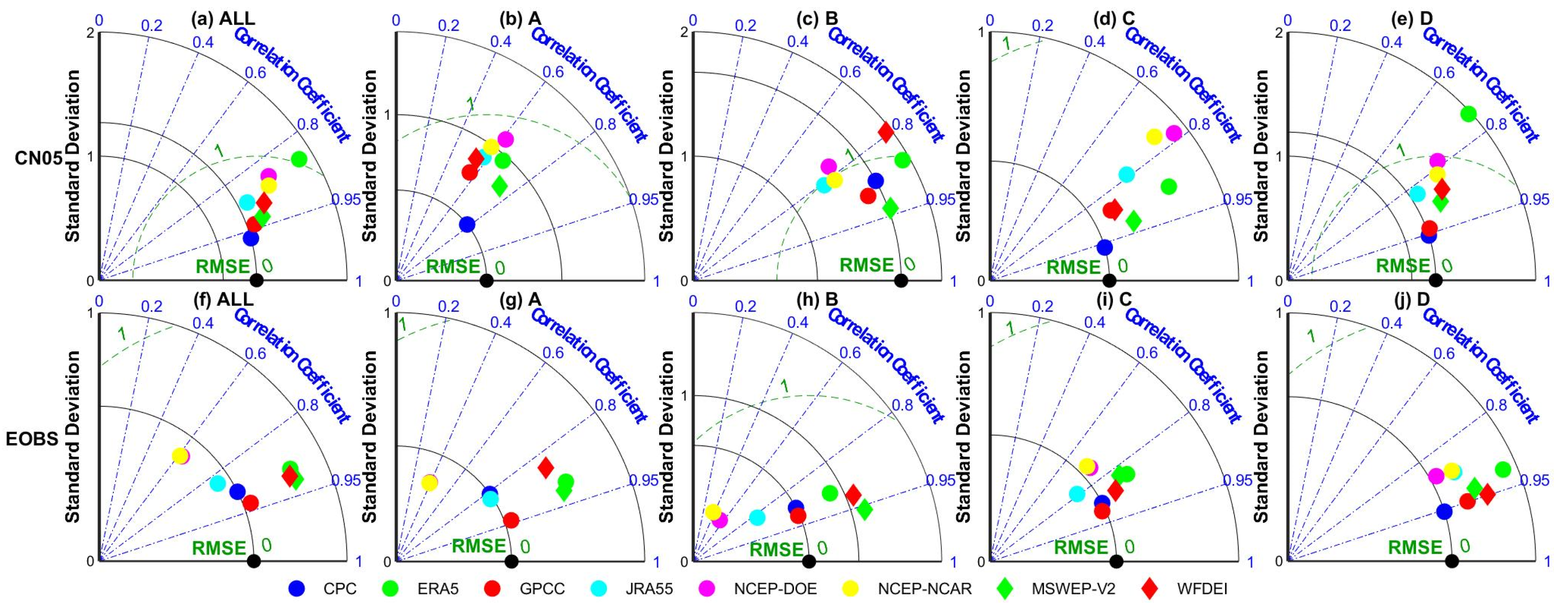
3.2.2. Performance Evaluation Using Two Gridded Gauge-Interpolated Datasets
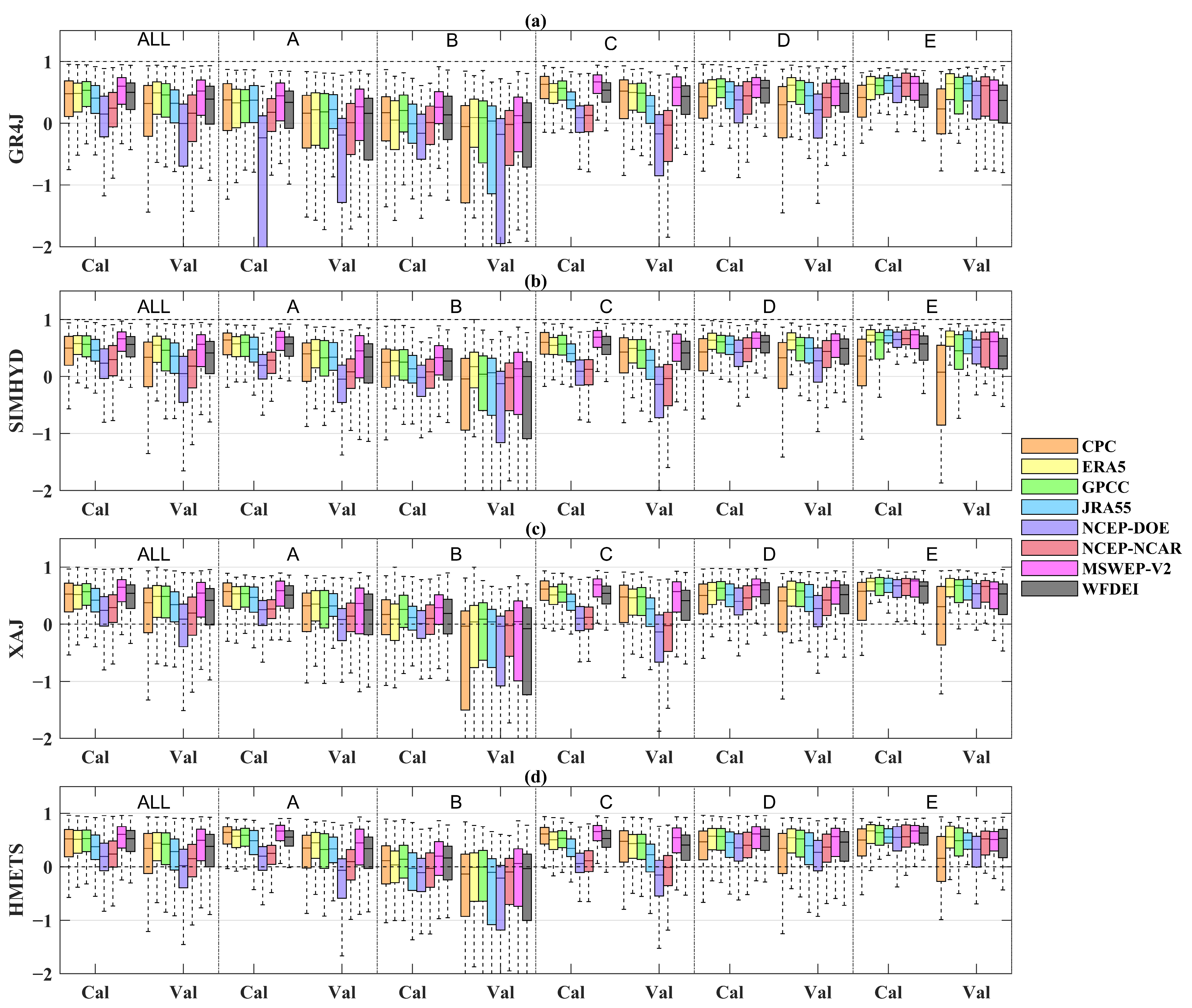
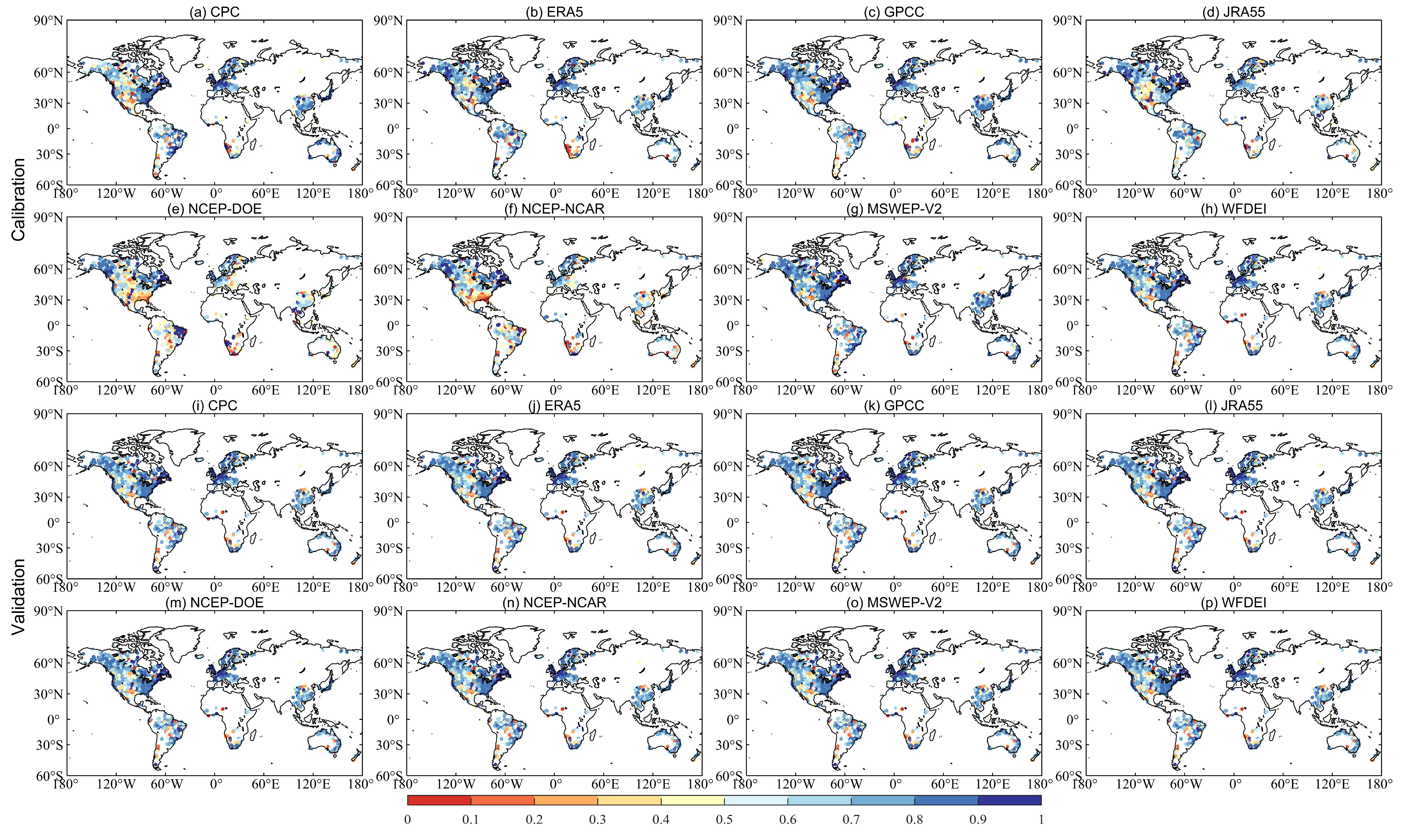
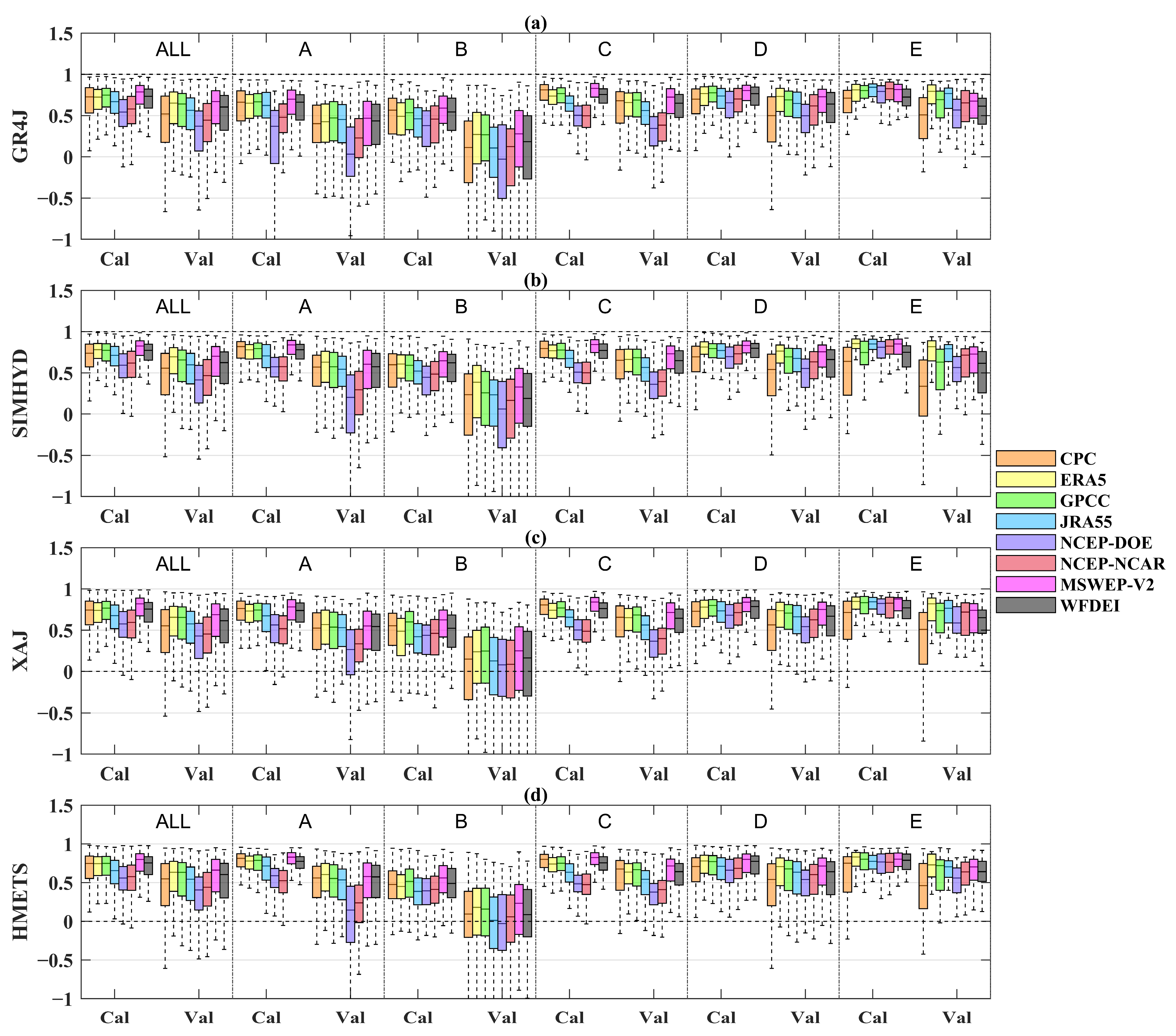
3.3. Evaluation of Precipitation Datasets’ Performance Based on Hydrological Modeling
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Precipitation | |
| CPC | Climate Precipitation Center dataset |
| GPCC | Global Precipitation Climatology Center dataset |
| ERA5 | European Centre for Medium-Range Weather Forecast Reanalysis 5 |
| NCEP–NCAR | National Centers for Environmental Prediction–National Center for Atmosphere Research |
| NCEP–DOE | National Centers for Environmental Prediction–Department of Energy |
| JRA55 | Japanese 55-year ReAnalysis |
| WFDEI | WATCH forcing data methodology is applied to ERA-Interim dataset |
| MSWEP V2 | Multi-source weighted-ensemble precipitation V2 |
| UPDs | Uncorrected precipitation datasets |
| CPDs | Corrected precipitation datasets |
| Köppen–Geiger climate classification | |
| A | Equatorial |
| B | Arid |
| C | Warm temperate |
| D | Snow |
| E | Arctic |
| Other Data | |
| CN05 | A high-quality gridded daily observation dataset over China |
| E-OBS | European high-resolution gridded dataset |
| GRDC | Global Runoff Data Centre |
| Hydrological model | |
| GR4J | Génie Rural à 4 Paramètres Journalier model |
| SIMHYD | Simple lumped conceptual daily rainfall-runoff model |
| XAJ | Xinanjiang model |
| HMETS | Hydrological model of École de Technologie supérieure model |
| Criteria | |
| KGE | Kling–Gupta efficiency |
| NSE | Nash–Sutcliffe Efficiency |
| MPD | Maximum Percentage Difference |
| CC | Correlation coefficient |
| BIAS | Relative bias |
| RMSE | Root mean squared error |
| POD | Probability of Detection |
| FAR | False Alarm Ratio |
| CSI | Critical Success Index |
| Rx1 | annual maximum 1-day precipitation amount |
| Rx5 | annual maximum 5-day precipitation amount |
| Others | |
| ITCZ | Intertropical Convergence Zone |
Appendix A


References
- Douglas-Mankin, K.R.; Srinivasan, R.; Arnold, J.G. Soil and Water Assessment Tool (SWAT) Model: Current Developments and Applications. Trans. ASABE 2010, 53, 1423–1431. [Google Scholar] [CrossRef]
- Nijssen, B.; O’Donnell, G.M.; Lettenmaier, D.P.; Lohmann, D.; Wood, E.F. Predicting the Discharge of Global Rivers. J. Climate 2001, 14, 3307–3323. [Google Scholar] [CrossRef]
- Wei, Z.; He, X.; Zhang, Y.; Pan, M.; Sheffield, J.; Peng, L.; Yamazaki, D.; Moiz, A.; Liu, Y.; Ikeuchi, K. Identification of uncertainty sources in quasi-global discharge and inundation simulations using satellite-based precipitation products. J. Hydrol. 2020, 589, 125180. [Google Scholar] [CrossRef]
- Ahmed, K.; Shahid, S.; Ali, R.O.; Bin Harun, S.; Wang, X.-j. Evaluation of the performance of gridded precipitation products over Balochistan Province, Pakistan. Desalin. Water Treat. 2017, 79, 73–86. [Google Scholar] [CrossRef]
- Chen, H.; Yong, B.; Shen, Y.; Liu, J.; Hong, Y.; Zhang, J. Comparison analysis of six purely satellite-derived global precipitation estimates. J. Hydrol. 2020, 581, 124376. [Google Scholar] [CrossRef]
- Schneider, U.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Ziese, M.; Rudolf, B. GPCC’s new land surface precipitation climatology based on quality-controlled in situ data and its role in quantifying the global water cycle. Theor. Appl. Climatol. 2014, 115, 15–40. [Google Scholar] [CrossRef]
- Weedon, G.P.; Balsamo, G.; Bellouin, N.; Gomes, S.; Best, M.J.; Viterbo, P. The WFDEI meteorological forcing data set: WATCH Forcing Data methodology applied to ERA-Interim reanalysis data. Water Resour. Res. 2014, 50, 7505–7514. [Google Scholar] [CrossRef]
- Beck, H.E.; Vergopolan, N.; Pan, M.; Levizzani, V.; van Dijk, A.I.J.M.; Weedon, G.P.; Brocca, L.; Pappenberger, F.; Huffman, G.J.; Wood, E.F. Global-scale evaluation of 22 precipitation datasets using gauge observations and hydrological modeling. Hydrol. Earth Syst. Sci. 2017, 21, 6201–6217. [Google Scholar] [CrossRef]
- Chen, M.; Shi, W.; Xie, P.; Silva, V.B.S.; Kousky, V.E.; Wayne Higgins, R.; Janowiak, J.E. Assessing objective techniques for gauge-based analyses of global daily precipitation. J. Geophys. Res. 2008, 113, D04110. [Google Scholar] [CrossRef]
- Sawunyama, T.; Hughes, D.A. Application of satellite-derived rainfall estimates to extend water resource simulation modelling in South Africa. Water Sa 2018, 34, 1–10. [Google Scholar] [CrossRef]
- Gao, Z.; Tang, G.; Jing, W.; Hou, Z.; Yang, J.; Sun, J. Evaluation of Multiple Satellite, Reanalysis, and Merged Precipitation Products for Hydrological Modeling in the Data-Scarce Tributaries of the Pearl River Basin, China. Remote Sens. 2023, 15, 5349. [Google Scholar] [CrossRef]
- Sun, Q.; Miao, C.; Duan, Q.; Ashouri, H.; Sorooshian, S.; Hsu, K.L. A Review of Global Precipitation Data Sets: Data Sources, Estimation, and Intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef]
- Lei, H.; Zhao, H.; Ao, T. A two-step merging strategy for incorporating multi-source precipitation products and gauge observations using machine learning classification and regression over China. Hydrol. Earth Syst. Sci. 2022, 26, 2969–2995. [Google Scholar] [CrossRef]
- Schamm, K.; Ziese, M.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Schneider, U.; Schröder, M.; Stender, P. Global gridded precipitation over land: A description of the new GPCC First Guess Daily product. Earth Syst. Sci. Data Discuss. 2013, 6, 435–464. [Google Scholar] [CrossRef]
- Beck, H.E.; Pan, M.; Roy, T.; Weedon, G.P.; Pappenberger, F.; van Dijk, A.I.J.M.; Huffman, G.J.; Adler, R.F.; Wood, E.F. Daily evaluation of 26 precipitation datasets using Stage-IV gauge-radar data for the CONUS. Hydrol. Earth Syst. Sci. 2019, 23, 207–224. [Google Scholar] [CrossRef]
- Shen, Z.; Yong, B.; Gourley, J.; Qi, W.; Lu, D.; Liu, J.; Ren, L.; Hong, Y.; Zhang, J.-y. Recent global performance of the Climate Hazards group Infrared Precipitation (CHIRP) with Stations (CHIRPS). J. Hydrol. 2020, 591, 125284. [Google Scholar] [CrossRef]
- Ashouri, H.; Hsu, K.; Sorooshian, S.; Braithwaite, D.; Knapp, K.; Cecil, L.; Nelson, B.; Prat, O. PERSIANN-CDR: Daily Precipitation Climate Data Record from Multisatellite Observations for Hydrological and Climate Studies. Bull. Am. Meteorol. Soc. 2014, 96, 69–83. [Google Scholar] [CrossRef]
- Huffman, G.; Adler, R.; Bolvin, D.; Gu, G.; Nelkin, E.; Bowman, K.; Hong, Y.; Stocker, E.; Wolff, D. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Kobayashi, S.; Ota, Y.; Harada, Y.; Ebita, A.; Moriya, M.; Onoda, H.; Onogi, K.; Kamahori, H.; Kobayashi, C.; Endo, H.; et al. The JRA-55 Reanalysis: General Specifications and Basic Characteristics. J. Meteorol. Soc. Jpn. Ser. II 2015, 93, 5–48. [Google Scholar] [CrossRef]
- Beck, H.E.; Van Dijk, A.I.; Levizzani, V.; Schellekens, J.; Gonzalez Miralles, D.; Martens, B.; De Roo, A. MSWEP: 3-hourly 0.25 global gridded precipitation (1979–2015) by merging gauge, satellite, and reanalysis data. Hydrol. Earth Syst. Sci. 2017, 21, 589–615. [Google Scholar] [CrossRef]
- Xie, P.; Janowiak, J.; Arkin, P.; Adler, R.; Gruber, A.; Ferraro, R.; Huffman, G.; Curtis, S. GPCP Pentad Precipitation Analyses: An Experimental Dataset Based on Gauge Observations and Satellite Estimates. J. Clim. 2003, 16, 2197–2214. [Google Scholar] [CrossRef]
- Duan, Z.; Liu, J.; Tuo, Y.; Chiogna, G.; Disse, M. Evaluation of eight high spatial resolution gridded precipitation products in Adige Basin (Italy) at multiple temporal and spatial scales. Sci. Total Environ. 2016, 573, 1536–1553. [Google Scholar] [CrossRef] [PubMed]
- Tuo, Y.; Duan, Z.; Disse, M.; Chiogna, G. Evaluation of precipitation input for SWAT modeling in Alpine catchment: A case study in the Adige river basin (Italy). Sci. Total Environ. 2016, 573, 66–82. [Google Scholar] [CrossRef]
- Chen, H.; Yong, B.; Kirstetter, P.-E.; Wang, L.; Hong, Y. Global component analysis of errors in three satellite-only global precipitation estimates. Hydrol. Earth Syst. Sci. 2021, 25, 3087–3104. [Google Scholar] [CrossRef]
- Gebremichael, M.; Hirpa, F.A.; Hopson, T. Evaluation of High-Resolution Satellite Precipitation Products over Very Complex Terrain in Ethiopia. J. Appl. Meteorol. Climatol. 2010, 49, 1044–1051. [Google Scholar] [CrossRef]
- Bumke, K.; König-Langlo, G.; Kinzel, J.; Schröder, M. HOAPS and ERA-Interim precipitation over the sea: Validation against shipboard in situ measurements. Atmos. Meas. Tech. 2016, 9, 2409–2423. [Google Scholar] [CrossRef]
- Alijanian, M.; Rakhshandehroo, G.R.; Mishra, A.K.; Dehghani, M. Evaluation of satellite rainfall climatology using CMORPH, PERSIANN-CDR, PERSIANN, TRMM, MSWEP over Iran. Int. J. Climatol. 2017, 37, 4896–4914. [Google Scholar] [CrossRef]
- Hu, X.; Zhou, Z.; Xiong, H.; Gao, Q.; Cao, X.; Yang, X. Inter-comparison of global precipitation data products at the river basin scale. Hydro Res. 2023, 55, 1–16. [Google Scholar] [CrossRef]
- Rivoire, P.; Martius, O.; Naveau, P. A Comparison of Moderate and Extreme ERA-5 Daily Precipitation With Two Observational Data Sets. Earth Space Sci. 2021, 8, e2020EA001633. [Google Scholar] [CrossRef]
- Chen, Y.; Hu, D.; Liu, M.; Shasha, W.; Yufei, D. Spatio-temporal accuracy evaluation of three high-resolution satellite precipitation products in China area. Atmos. Res. 2020, 241, 104952. [Google Scholar] [CrossRef]
- Iqbal, J.; Khan, N.; Shahid, S.; Ullah, S. Evaluation of gridded dataset in estimating extreme precipitations indices in Pakistan. Acta Geophys. 2024, 72, 1–16. [Google Scholar] [CrossRef]
- Lu, J.; Wang, K.; Wu, G.; Mao, Y. Evaluation of Multi-Source Datasets in Characterizing Spatio-Temporal Characteristics of Extreme Precipitation from 2001 to 2019 in China. J. Hydrometeorol. 2024, 25, 515–539. [Google Scholar] [CrossRef]
- Pan, M.; Li, H.; Wood, E. Assessing the skill of satellite-based precipitation estimates in hydrologic applications. Water Resour. Res. 2010, 46, 1–10. [Google Scholar] [CrossRef]
- Martens, B.; Miralles, D.G.; Lievens, H.; van der Schalie, R.; de Jeu, R.A.M.; Fernández-Prieto, D.; Beck, H.E.; Dorigo, W.A.; Verhoest, N.E.C. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 2017, 10, 1903–1925. [Google Scholar] [CrossRef]
- Gebremichael, M.; Bitew, M.M.; Ghebremichael, L.T.; Bayissa, Y.A. Evaluation of High-Resolution Satellite Rainfall Products through Streamflow Simulation in a Hydrological Modeling of a Small Mountainous Watershed in Ethiopia. J. Hydrometeorol. 2012, 13, 338–350. [Google Scholar] [CrossRef]
- Collischonn, B.; Collischonn, W.; Tucci, C.E.M. Daily hydrological modeling in the Amazon basin using TRMM rainfall estimates. J. Hydrol. 2008, 360, 207–216. [Google Scholar] [CrossRef]
- Falck, A.S.; Maggioni, V.; Tomasella, J.; Vila, D.A.; Diniz, F.L.R. Propagation of satellite precipitation uncertainties through a distributed hydrologic model: A case study in the Tocantins–Araguaia basin in Brazil. J. Hydrol. 2015, 527, 943–957. [Google Scholar] [CrossRef]
- Alexopoulos, M.J.; Müller-Thomy, H.; Nistahl, P.; Šraj, M.; Bezak, N. Validation of precipitation reanalysis products for rainfall-runoff modelling in Slovenia. Hydrol. Earth Syst. Sci. 2023, 27, 2559–2578. [Google Scholar] [CrossRef]
- Sabbaghi, M.; Shahnazari, A.; Soleimanian, E. Evaluation of high-resolution precipitation products (CMORPH-CRT, PERSIANN, and TRMM-3B42RT) and their performances as inputs to the hydrological model. Model. Earth Syst. Environ. 2024, 10, 1–17. [Google Scholar] [CrossRef]
- Maggioni, V.; Meyers, P.C.; Robinson, M.D. A review of merged high-resolution satellite precipitation product accuracy during the Tropical Rainfall Measuring Mission (TRMM) era. J. Hydrometeorol. 2016, 17, 1101–1117. [Google Scholar] [CrossRef]
- Chen, J.; Li, Z.; Li, L.; Wang, J.; Qi, W.; Xu, C.-Y.; Kim, J.-S. Evaluation of Multi-Satellite Precipitation Datasets and Their Error Propagation in Hydrological Modeling in a Monsoon-Prone Region. Remote Sens. 2020, 12, 3550. [Google Scholar] [CrossRef]
- Tang, G.; Zeng, Z.; Long, D.; Guo, X.; Yong, B.; Zhang, W.; Hong, Y. Statistical and Hydrological Comparisons between TRMM and GPM. J. Hydrometeorol. 2016, 17, 121–137. [Google Scholar] [CrossRef]
- Xiang, Y.; Chen, J.; Li, L.; Peng, T.; Yin, Z. Evaluation of Eight Global Precipitation Datasets in Hydrological Modeling. Remote Sens. 2021, 13, 2831. [Google Scholar] [CrossRef]
- Jiang, Q.; Li, W.; Fan, Z.; He, X.; Sun, W.; Chen, S.; Wen, J.; Gao, J.; Wang, J. Evaluation of the ERA5 reanalysis precipitation dataset over Chinese Mainland. J. Hydrol. 2021, 595, 125660. [Google Scholar] [CrossRef]
- Cantoni, E.; Tramblay, Y.; Grimaldi, S.; Salamon, P.; Dakhlaoui, H.; Dezetter, A.; Thiemig, V. Hydrological performance of the ERA5 reanalysis for flood modeling in Tunisia with the LISFLOOD and GR4J models. J. Hydrol. Reg. Stud. 2022, 42, 101169. [Google Scholar] [CrossRef]
- Araghi, A.; Adamowski, J.F. Assessment of 30 gridded precipitation datasets over different climates on a country scale. Earth Sci. Inform. 2024, 17, 1301–1313. [Google Scholar] [CrossRef]
- Fekete, B.M.; Vörösmarty, C.J.; Roads, J.O.; Willmott, C.J. Uncertainties in Precipitation and Their Impacts on Runoff Estimates. J. Climate 2004, 17, 294–304. [Google Scholar] [CrossRef]
- Voisin, N.; Wood, A.W.; Lettenmaier, D.P. Evaluation of Precipitation Products for Global Hydrological Prediction. J. Hydrometeorol. 2008, 9, 388–407. [Google Scholar] [CrossRef]
- Gebrechorkos, S.H.; Leyland, J.; Dadson, S.J.; Cohen, S.; Slater, L.; Wortmann, M.; Ashworth, P.J.; Bennett, G.L.; Boothroyd, R.; Cloke, H.; et al. Global scale evaluation of precipitation datasets for hydrological modelling. Hydrol. Earth Syst. Sci. Discuss. 2023, 2023, 1–33. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-Year Reanalysis Project. Bull. Am. Meteorol. Soc. 1996, 77, 437–472. [Google Scholar] [CrossRef]
- Kanamitsu, M.; Ebisuzaki, W.; Woollen, J.; Yang, S.-K.; Hnilo, J.J.; Fiorino, M.; Potter, G.L. NCEP–DOE AMIP-II Reanalysis (R-2). Bull. Am. Meteorol. Soc. 2002, 83, 1631–1644. [Google Scholar] [CrossRef]
- Du, Y.; Wang, D.; Zhu, J.; Lin, Z.; Zhong, Y. Intercomparison of multiple high-resolution precipitation products over China: Climatology and extremes. Atmos. Res. 2022, 278, 106342. [Google Scholar] [CrossRef]
- Qi, W.-y.; Chen, J.; Li, L.; Xu, C.-Y.; Li, J.; Xiang, Y.; Zhang, S. Regionalization of catchment hydrological model parameters for global water resources simulations. Hydro Res. 2022, 53, 441–466. [Google Scholar] [CrossRef]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World Map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Wu, J.; Gao, X.-J. A gridded daily observation dataset over China region and comparison with the other datasets. Chin. J. Geophys. Chin. Ed. 2013, 56, 1102–1111. (In Chinese) [Google Scholar]
- Haylock, M.R.; Hofstra, N.; Klein Tank, A.M.G.; Klok, E.J.; Jones, P.D.; New, M. A European daily high-resolution gridded data set of surface temperature and precipitation for 1950–2006. J. Geophys. Res. 2008, 113, D20119. [Google Scholar] [CrossRef]
- Yang, J. The thin plate spline robust point matching (TPS-RPM) algorithm: A revisit. Pattern Recogn. Lett. 2011, 32, 910–918. [Google Scholar] [CrossRef]
- Burek, P.; Smilovic, M. The use of GRDC gauging stations for calibrating large-scale hydrological models. Earth Syst. Sci. Data 2023, 15, 5617–5629. [Google Scholar] [CrossRef]
- Arsenault, R.; Bazile, R.; Ouellet Dallaire, C.; Brissette, F. CANOPEX: A Canadian hydrometeorological watershed database. Hydrol. Process 2016, 30, 2734–2736. [Google Scholar] [CrossRef]
- Gong, L.; Halldin, S.; Xu, C.Y. Global-scale river routing-an efficient time-delay algorithm based on HydroSHEDS high-resolution hydrography. Hydrol. Process 2011, 25, 1114–1128. [Google Scholar] [CrossRef]
- Perrin, C.; Michel, C.; Andréassian, V. Improvement of a parsimonious model for streamflow simulation. J. Hydrol. 2003, 279, 275–289. [Google Scholar] [CrossRef]
- Zeng, L.; Xiong, L.; Liu, D.; Chen, J.; Kim, J.-S. Improving Parameter Transferability of GR4J Model under Changing Environments Considering Nonstationarity. Water 2019, 11, 2029. [Google Scholar] [CrossRef]
- Valéry, A.; Andréassian, V.; Perrin, C. ‘As simple as possible but not simpler’: What is useful in a temperature-based snow-accounting routine? Part 1—Comparison of six snow accounting routines on 380 catchments. J. Hydrol. 2014, 517, 1166–1175. [Google Scholar] [CrossRef]
- Qi, W.-y.; Chen, J.; Li, L.; Xu, C.-Y.; Xiang, Y.-h.; Zhang, S.-b.; Wang, H.-M. Impact of the number of donor catchments and the efficiency threshold on regionalization performance of hydrological models. J. Hydrol. 2021, 601, 126680. [Google Scholar] [CrossRef]
- Chiew, F.H. Lumped Conceptual Rainfall-Runoff Models and Simple Water Balance Methods: Overview and Applications in Ungauged and Data Limited Regions. Geogr. Compass. 2010, 4, 206–225. [Google Scholar] [CrossRef]
- Chiew, F.H.; Peel, M.C.; Western, A.W. Application and testing of the simple rainfall-runoff model SIMHYD. In Mathematical Models of Small Watershed Hydrology and Applications; Singh, V.P., Frevert, D., Eds.; Water Resources Publications: Littleton, CO, USA, 2002; pp. 335–367. [Google Scholar]
- Zhao, R.-J.; Zuang, Y.; Fang, L.; Liu, X.; Zhang, Q. The Xinanjiang model. In Proceedings of the Oxford Symposium, 15–18 April 1980. Hydrological Forecasting Proceedings Oxford Symposium, IASH 129; International Association of Hydrological Science: Oxfordshire, UK, 1980; pp. 351–356. [Google Scholar]
- Zhao, R.-J. The Xinanjiang model applied in China. J. Hydrol. 1992, 135, 371–381. [Google Scholar]
- Chen, Y.; Shi, P.; Qu, S.; Ji, X.; Zhao, L.; Gou, J.; Mou, S. Integrating XAJ Model with GIUH Based on Nash Model for Rainfall-Runoff Modelling. Water 2019, 11, 772. [Google Scholar] [CrossRef]
- Martel, J.-L.; Demeester, K.; Brissette, F.P.; Arsenault, R.; Poulin, A. HMET: A simple and efficient hydrology model for teaching hydrological modelling, flow forecasting and climate change impacts. Int. J. Eng. Educ. 2017, 33, 1307–1316. [Google Scholar]
- Chen, J.; Brissette, F.P.; Poulin, A.; Leconte, R. Overall uncertainty study of the hydrological impacts of climate change for a Canadian watershed. Water Resour. Res. 2011, 47, W12509. [Google Scholar] [CrossRef]
- Duan, Q.; Gupta, V.K.; Sorooshian, S. Shuffled complex evolution approach for effective and efficient global minimization. J. Optim. Theory Appl. 1993, 76, 501–521. [Google Scholar] [CrossRef]
- Qi, W.; Chen, J.; Xu, C.; Wan, Y. Finding the Optimal Multimodel Averaging Method for Global Hydrological Simulations. Remote Sens. 2021, 13, 2574. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Perrin, C.; Littlewood, I. A comparative assessment of two rainfall-runoff modelling approaches: GR4J and IHACRES. In Proceedings of the Liblice Conference, IHP-V, Technical Documents in Hydrology n. Liblice, Czech Republic, 22–24 September 1998; Elias, V., Littlewood, I.G., Eds.; UNESCO: Paris, France, 2000; pp. 191–201. [Google Scholar]
- Zhang, H.; Loaiciga, H.; Du, Q.; Sauter, T. Comprehensive Evaluation of Global Precipitation Products and Their Accuracy in Drought Detection in Mainland China. J. Hydrometeorol. 2023, 24, 1907–1937. [Google Scholar] [CrossRef]
- Peng, F.; Zhao, S.; Chen, C.; Cong, D.; Wang, Y.; Hongda, O. Evaluation and comparison of the precipitation detection ability of multiple satellite products in a typical agriculture area of China. Atmos. Res. 2019, 236, 104814. [Google Scholar] [CrossRef]
- Guo, Y.; Yan, X.; Song, S. Spatiotemporal variability of extreme precipitation in east of northwest China and associated large-scale circulation factors. Environ. Sci. Pollut. Res. 2024, 31, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Vis, M.; Knight, R.; Pool, S.; Wolfe, W.; Seibert, J. Model Calibration Criteria for Estimating Ecological Flow Characteristics. Water 2015, 7, 2358–2381. [Google Scholar] [CrossRef]
- Cherchi, A.; Ambrizzi, T.; Behera, S.; Freitas, A.C.V.; Morioka, Y.; Zhou, T. The Response of Subtropical Highs to Climate Change. Curr. Clim. Chang. Rep. 2018, 4, 371–382. [Google Scholar] [CrossRef]
- Svoma, B.; Krahenbuhl, D.; Bush, C.; Malloy, J.; White, J.; Wagner, M.; Pace, M.; DeBiasse, K.; Selover, N.; Balling, R.; et al. Expansion of the northern hemisphere subtropical high pressure belt: Trends and linkages to precipitation and drought. Phys. Geogr. 2013, 34, 174–187. [Google Scholar] [CrossRef]
- Gehne, M.; Hamill, T.M.; Kiladis, G.N.; Trenberth, K.E. Comparison of Global Precipitation Estimates across a Range of Temporal and Spatial Scales. J. Clim. 2016, 29, 7773–7795. [Google Scholar] [CrossRef]
- Islam, S.U.; Déry, S.J. Evaluating uncertainties in modelling the snow hydrology of the Fraser River Basin, British Columbia, Canada. Hydrol. Earth Syst. Sci. 2017, 21, 1827–1847. [Google Scholar] [CrossRef]
- Cattani, E.; Merino, A.; Levizzani, V. Evaluation of Monthly Satellite-Derived Precipitation Products over East Africa. J. Hydrometeorol. 2016, 17, 2555–2573. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, W.; Huai, B.; Wang, Y.; Ji, K.; Yang, X.; Du, W.; Qin, X.; Wang, L. Comparison and evaluation of the performance of reanalysis datasets for compound extreme temperature and precipitation events in the Qilian Mountains. Atmos. Res. 2024, 304, 107375. [Google Scholar] [CrossRef]
- Pfeifroth, U.; Müller, R.; Ahrens, B. Evaluation of Satellite-Based and Reanalysis Precipitation Data in the Tropical Pacific. J. Appl. Meteorol. Climatol. 2013, 52, 634–644. [Google Scholar] [CrossRef]
- Blarzino, G.; Castanet, L.; Luini, L.; Capsoni, C.; Martellucci, A. Development of a new global rainfall rate model based on ERA40, TRMM, GPCC and GPCP products. In Proceedings of the Antennas and Propagation, 2009, EuCAP 2009, 3rd European Conference, Berlin, Germany, 23–27 March 2009. [Google Scholar]
- Widén-Nilsson, E.; Halldin, S.; Xu, C.-y. Global water-balance modelling with WASMOD-M: Parameter estimation and regionalisation. J. Hydrol. 2007, 340, 105–118. [Google Scholar] [CrossRef]
- Beck, H.E.; van Dijk, A.I.J.M.; de Roo, A.; Miralles, D.G.; McVicar, T.R.; Schellekens, J.; Bruijnzeel, L.A. Global-scale regionalization of hydrologic model parameters. Water Resour. Res. 2016, 52, 3599–3622. [Google Scholar] [CrossRef]
- Ghebrehiwot, A.A.; Kozlov, D.V. Hydrological modelling for ungauged basins of arid and semi-arid regions: Review. Vestnik MGSU 2019, 14, 1023–1036. [Google Scholar] [CrossRef]
- Peña-Arancibia, J.L.; van Dijk, A.I.J.M.; Mulligan, M.; Bruijnzeel, L.A. The role of climatic and terrain attributes in estimating baseflow recession in tropical catchments. Hydrol. Earth Syst. Sci. 2010, 14, 2193–2205. [Google Scholar] [CrossRef]
- Behrangi, A.; Wen, Y. On the Spatial and Temporal Sampling Errors of Remotely Sensed Precipitation Products. Remote Sens. 2017, 9, 1127. [Google Scholar] [CrossRef]
- Xu, C.-Y.; Chen, H.; Guo, S. Hydrological Modeling in a Changing Environment: Issues and Challenges. J. Water Resour. Res. 2013, 2, 85–95. [Google Scholar] [CrossRef]



| Datasets | Temporal Resolution | Spatial Resolution | Data Source | Category | Period | Reference | Download |
|---|---|---|---|---|---|---|---|
| CPC | Daily | 0.5° | Gauged-based | CPDs | 1979–present | Chen et al. [9] | https://psl.noaa.gov/data/gridded/data.cpc.globalprecip.html, accessed on 1 April 2024 |
| GPCC | Daily | 0.25° | Gauged-based | CPDs | 1981–2016 | Schneider et al. [6] | https://psl.noaa.gov/data/gridded/data.gpcc.html, accessed on 1 April 2024 |
| ERA5 | Daily | 0.5° | Reanalysis | UPDs | 1950–present | Hersbach et al. [50] | https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-complete?tab=form, accessed on 1 April 2024 |
| NCEP–NCAR | Daily | 1.875° | Reanalysis | UPDs | 1948–present | Kalnay et al. [51] | https://psl.noaa.gov/data/gridded/data.ncep.reanalysis.html, accessed on 1 April 2022 |
| NCEP–DOE | Daily | 1.875° | Reanalysis | UPDs | 1979–present | Kanamitsu et al. [52] | https://www.cpc.ncep.noaa.gov/products/wesley/reanalysis2/, accessed on 1 April 2022 |
| MSWEP V2 | Daily | 0.1° | Satellite-gauge- reanalysis | CPPs | 1979–present | Beck et al. [8] | https://gloh2o.org/mswep/, accessed on 1 April 2024 |
| JRA55 | Daily | 1.25° | Reanalysis | UPDs | 1958–present | Kobayashi et al. [19] | https://jra.kishou.go.jp/JRA-55/index_en.html, accessed on 1 April 2024 |
| WFDEI | Daily | 0.5° | Reanalysis | CPPs | 1979–2016 | Weedon et al. [7] | https://rda.ucar.edu/datasets/ds314.2/, accessed on 1 April 2024 |
| Criteria | Unit | Formula | Perfect Value | |
|---|---|---|---|---|
| Precipitation indices | Maximum Percentage Difference (MPD) | % | 0 | |
| Correlation Coefficient (CC) | NA | 1 | ||
| Relative Bias (BIAS) | % | 0 | ||
| Root Mean Square Error (RMSE) | mm | 0 | ||
| Critical Success Index (CSI) | NA | 1 | ||
| False Alarm Ratio (FAR) | NA | 0 | ||
| Probability of Detection (POD) | NA | 1 | ||
| PBias-Rx1 | % | 0 | ||
| PBias-Rx5 | % | 0 | ||
| Hydrological indices | Kling-Gupta Efficiency (KGE) | NA | 1 | |
| Nash-Sutcliffe Efficiency (NSE) | NA | 1 |
| Climate Type | All (n = 2058) | A: Equatorial (n = 248) | B: Arid (n = 217) | C: Warm Temperate (n = 665) | D: Snow (n = 885) | E: Arctic (n = 43) | |
|---|---|---|---|---|---|---|---|
| GR4J | CPC | 0.73 | 0.66 | 0.57 | 0.81 | 0.70 | 0.71 |
| ERA5 | 0.72 | 0.65 | 0.49 | 0.74 | 0.77 | 0.81 | |
| GPCC | 0.75 | 0.67 | 0.53 | 0.77 | 0.78 | 0.80 | |
| JRA55 | 0.67 | 0.62 | 0.46 | 0.65 | 0.74 | 0.84 | |
| NCEP–DOE | 0.54 | 0.37 | 0.38 | 0.50 | 0.65 | 0.79 | |
| NCEP–NCAR | 0.58 | 0.48 | 0.46 | 0.50 | 0.70 | 0.83 | |
| MSWEP V2 | 0.79 | 0.70 | 0.59 | 0.83 | 0.80 | 0.82 | |
| WFDEI | 0.73 | 0.66 | 0.54 | 0.76 | 0.76 | 0.72 | |
| SIMHYD | CPC | 0.74 | 0.82 | 0.60 | 0.80 | 0.69 | 0.64 |
| ERA5 | 0.78 | 0.78 | 0.61 | 0.77 | 0.81 | 0.85 | |
| GPCC | 0.77 | 0.79 | 0.59 | 0.78 | 0.79 | 0.75 | |
| JRA55 | 0.71 | 0.71 | 0.52 | 0.68 | 0.77 | 0.85 | |
| NCEP–DOE | 0.59 | 0.57 | 0.45 | 0.51 | 0.70 | 0.81 | |
| NCEP–NCAR | 0.62 | 0.58 | 0.48 | 0.50 | 0.73 | 0.82 | |
| MSWEP V2 | 0.83 | 0.84 | 0.65 | 0.84 | 0.83 | 0.85 | |
| WFDEI | 0.77 | 0.78 | 0.62 | 0.77 | 0.80 | 0.75 | |
| XAJ | CPC | 0.74 | 0.76 | 0.55 | 0.80 | 0.73 | 0.71 |
| ERA5 | 0.74 | 0.73 | 0.49 | 0.74 | 0.78 | 0.85 | |
| GPCC | 0.77 | 0.74 | 0.60 | 0.77 | 0.80 | 0.83 | |
| JRA55 | 0.68 | 0.67 | 0.42 | 0.66 | 0.73 | 0.84 | |
| NCEP–DOE | 0.57 | 0.56 | 0.44 | 0.50 | 0.68 | 0.82 | |
| NCEP–NCAR | 0.59 | 0.52 | 0.46 | 0.49 | 0.71 | 0.83 | |
| MSWEP V2 | 0.82 | 0.78 | 0.62 | 0.84 | 0.84 | 0.88 | |
| WFDEI | 0.75 | 0.74 | 0.52 | 0.76 | 0.79 | 0.77 | |
| HMETS | CPC | 0.75 | 0.81 | 0.48 | 0.80 | 0.71 | 0.75 |
| ERA5 | 0.75 | 0.78 | 0.45 | 0.74 | 0.78 | 0.83 | |
| GPCC | 0.75 | 0.79 | 0.52 | 0.75 | 0.77 | 0.80 | |
| JRA55 | 0.65 | 0.72 | 0.39 | 0.63 | 0.71 | 0.78 | |
| NCEP–DOE | 0.56 | 0.59 | 0.39 | 0.48 | 0.66 | 0.77 | |
| NCEP–NCAR | 0.58 | 0.52 | 0.41 | 0.47 | 0.68 | 0.76 | |
| MSWEP V2 | 0.80 | 0.83 | 0.56 | 0.82 | 0.80 | 0.80 | |
| WFDEI | 0.75 | 0.78 | 0.49 | 0.76 | 0.78 | 0.79 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, W.; Wang, S.; Chen, J. Inter-Comparison of Multiple Gridded Precipitation Datasets over Different Climates at Global Scale. Water 2024, 16, 1553. https://doi.org/10.3390/w16111553
Qi W, Wang S, Chen J. Inter-Comparison of Multiple Gridded Precipitation Datasets over Different Climates at Global Scale. Water. 2024; 16(11):1553. https://doi.org/10.3390/w16111553
Chicago/Turabian StyleQi, Wenyan, Shuhong Wang, and Jianlong Chen. 2024. "Inter-Comparison of Multiple Gridded Precipitation Datasets over Different Climates at Global Scale" Water 16, no. 11: 1553. https://doi.org/10.3390/w16111553
APA StyleQi, W., Wang, S., & Chen, J. (2024). Inter-Comparison of Multiple Gridded Precipitation Datasets over Different Climates at Global Scale. Water, 16(11), 1553. https://doi.org/10.3390/w16111553





