Reflection of Daily, Seasonal and Interannual Variations in Run-Off of a Small River in the Water Isotopic Composition (δ2H, δ18O): A Case of the Ala-Archa Mountain River Basin with Glaciation (Kyrgyzstan, Central Asia)
Abstract
:1. Introduction
- −
- Several factors that influence the formation of the water runoff, including one previously unknown component.
- −
- A correlation between runoff components and their distribution over time.
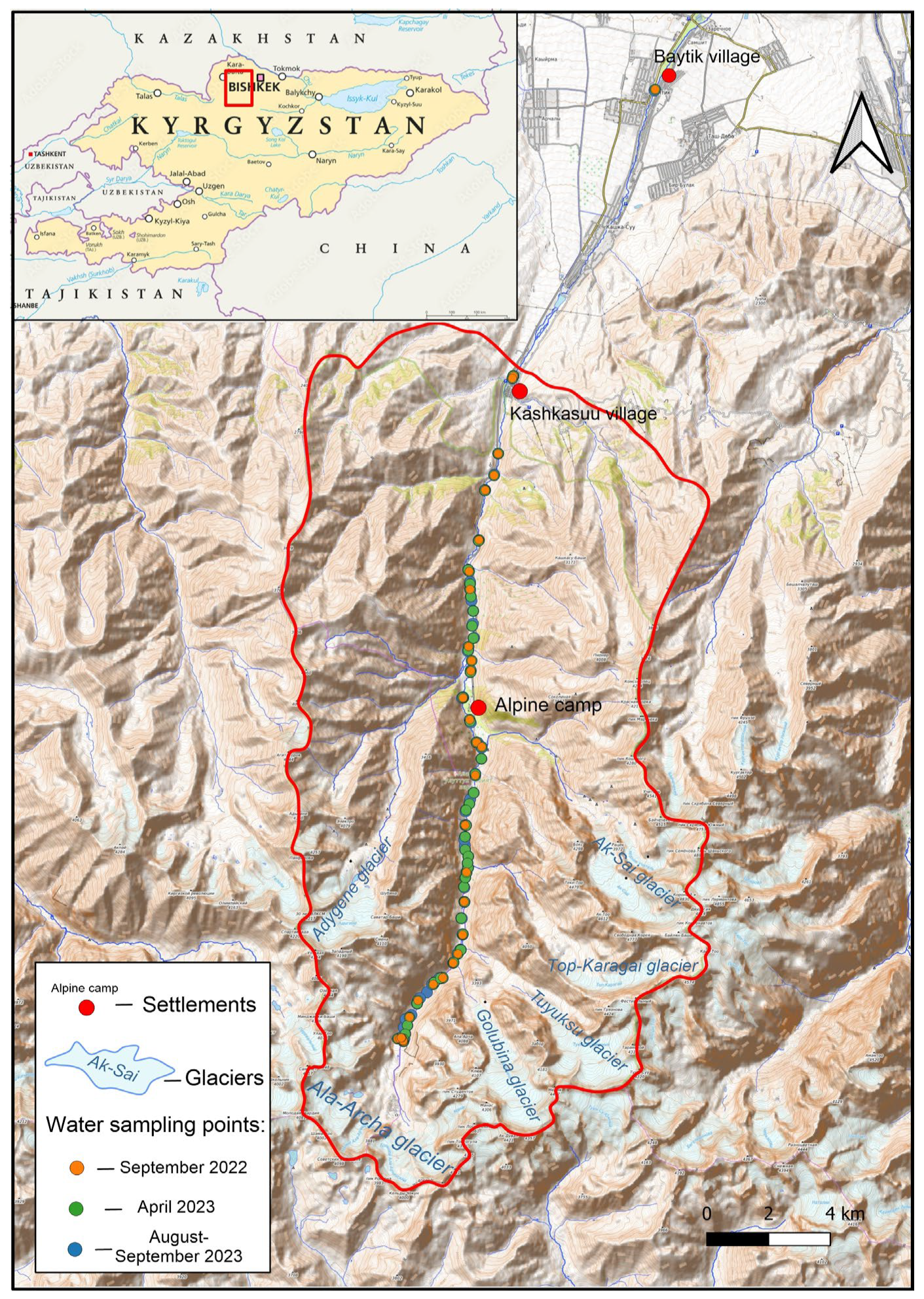
2. Research Area
- −
- Atmospheric precipitation in the form of rain;
- −
- Glacial meltwater and snowmelt;
- −
- Groundwater.
3. Materials and Methods
4. Results
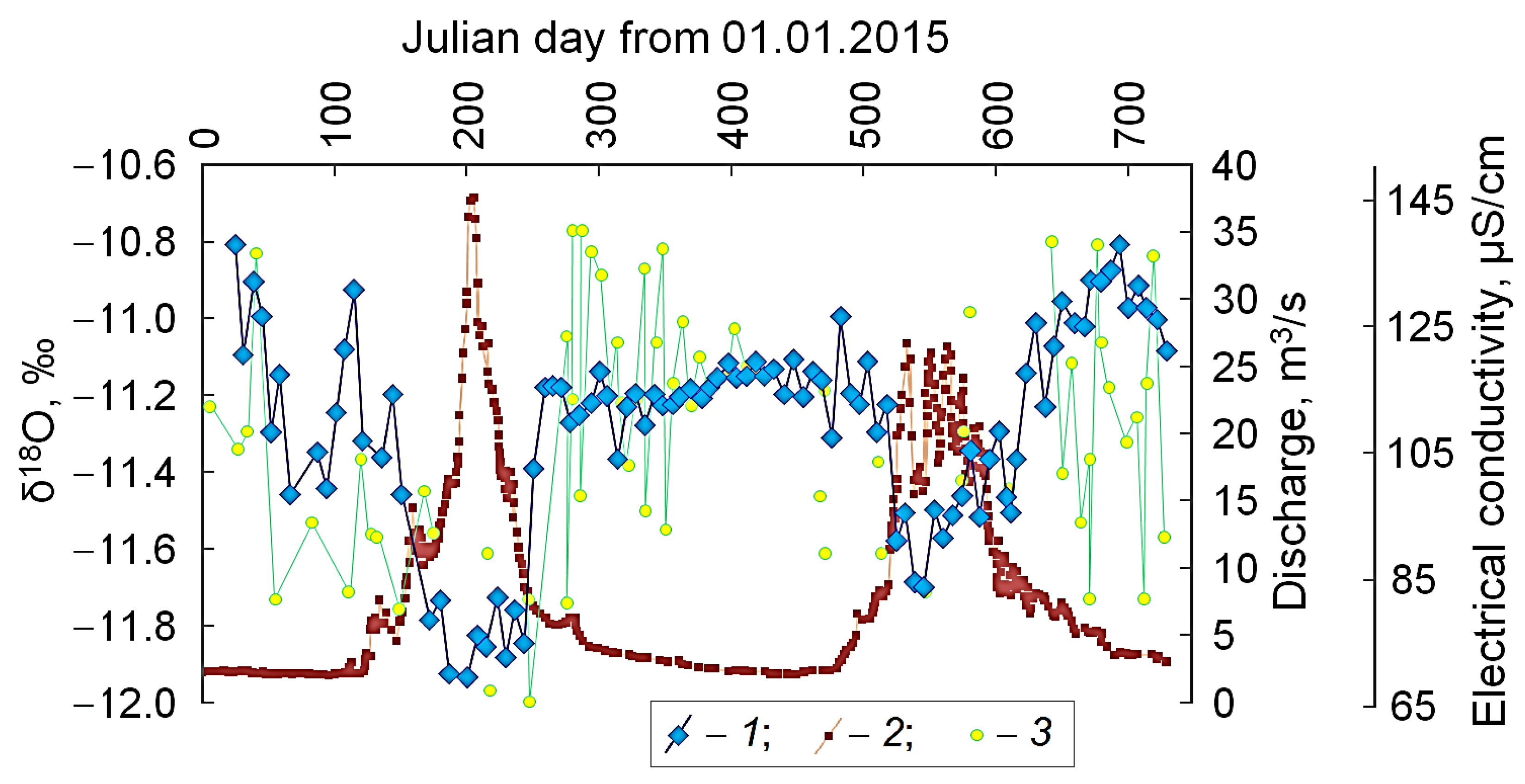
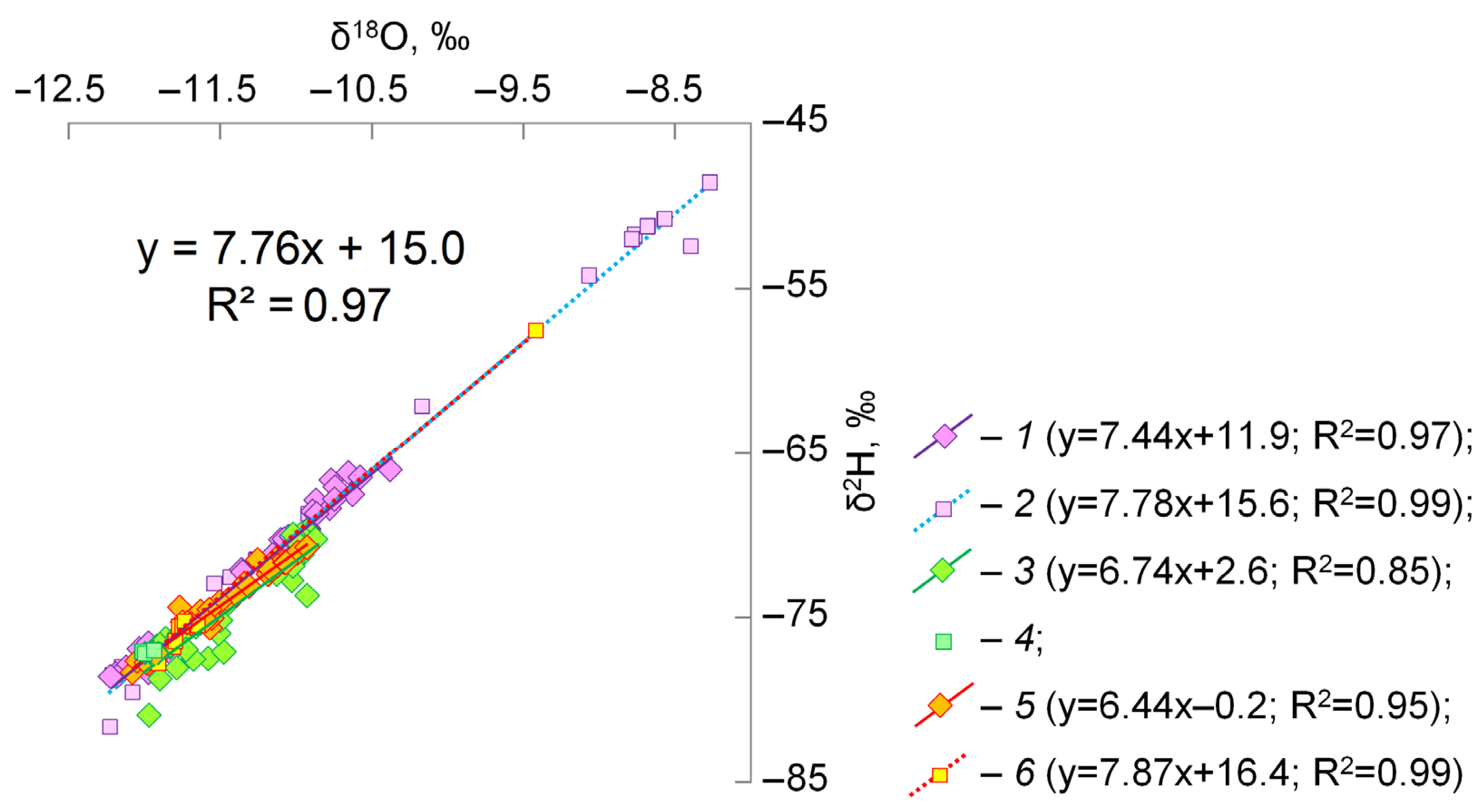
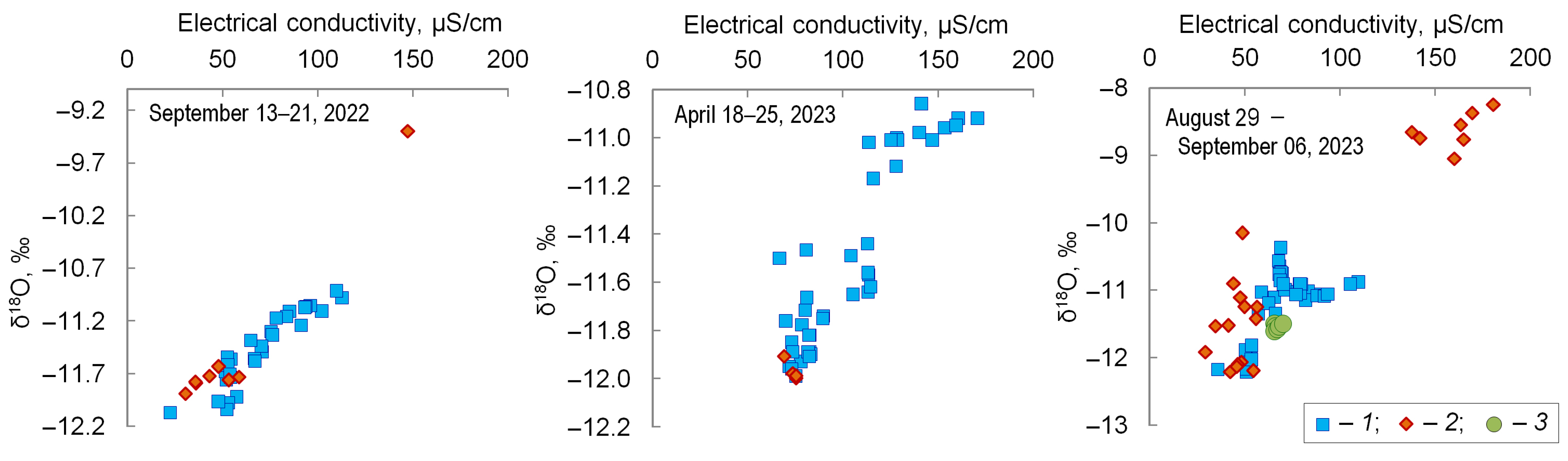
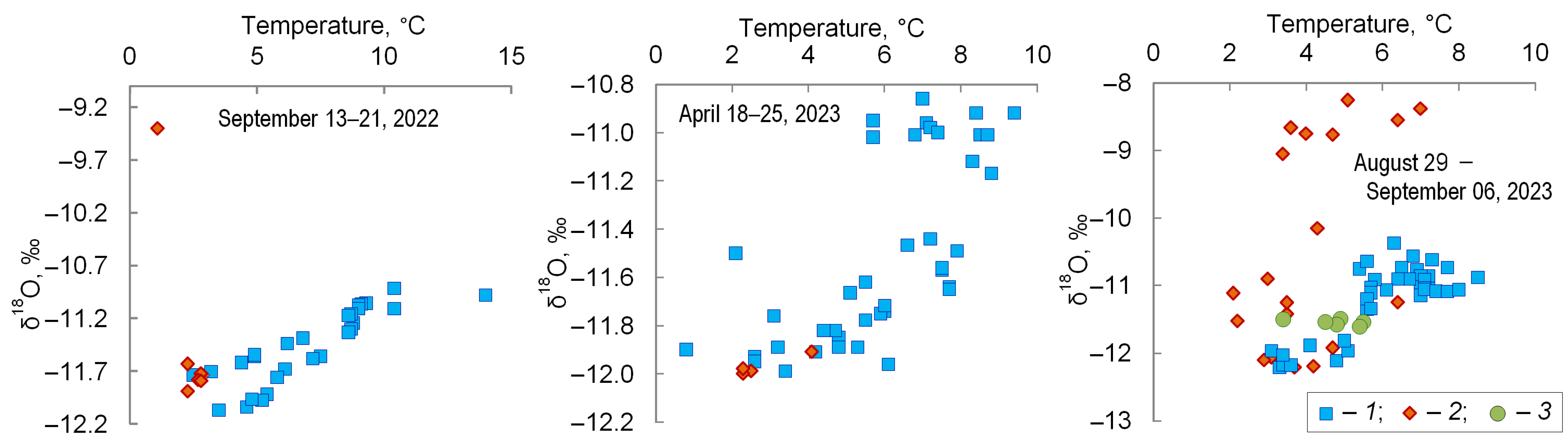
4.1. Daily Observations
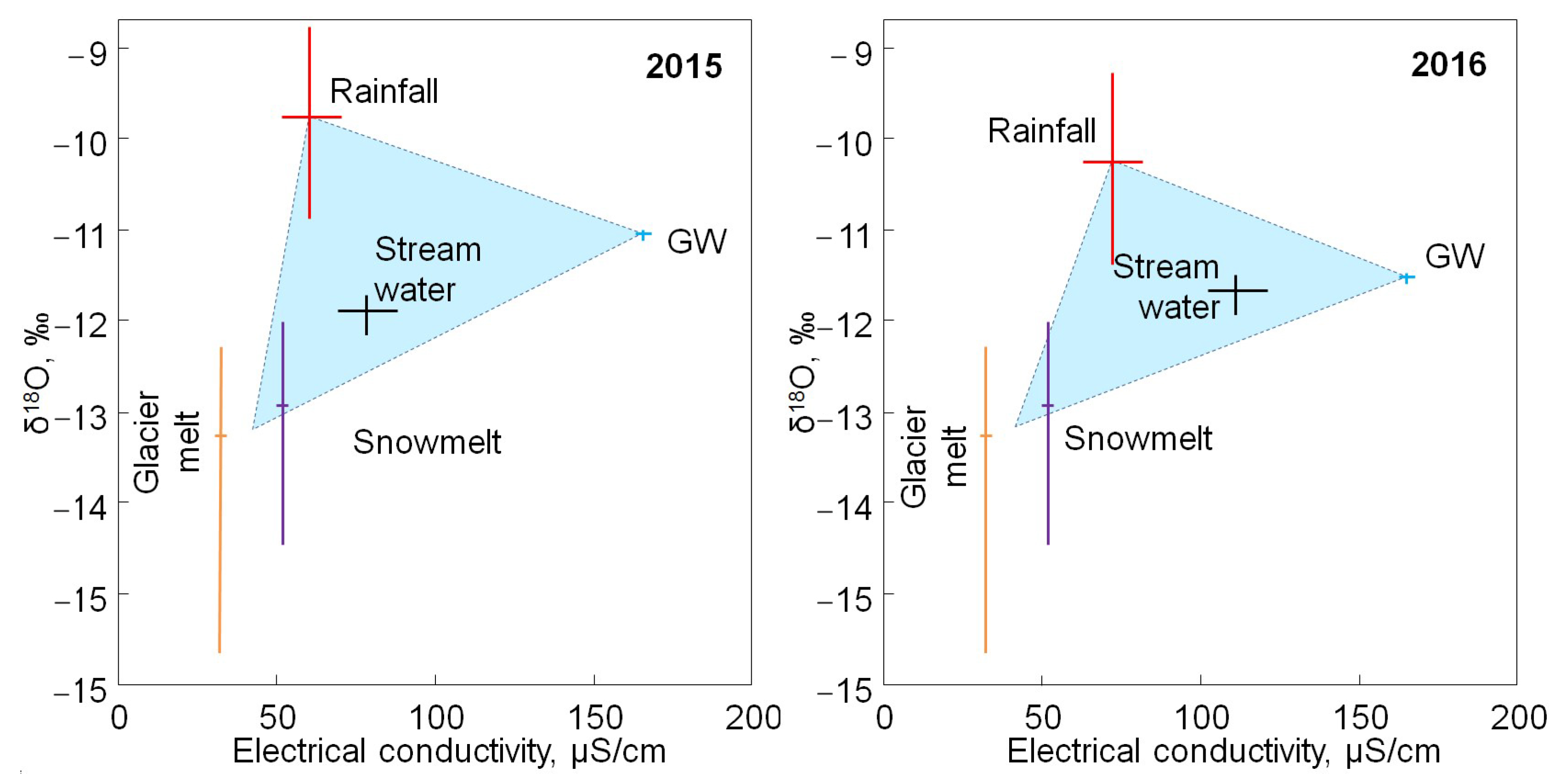
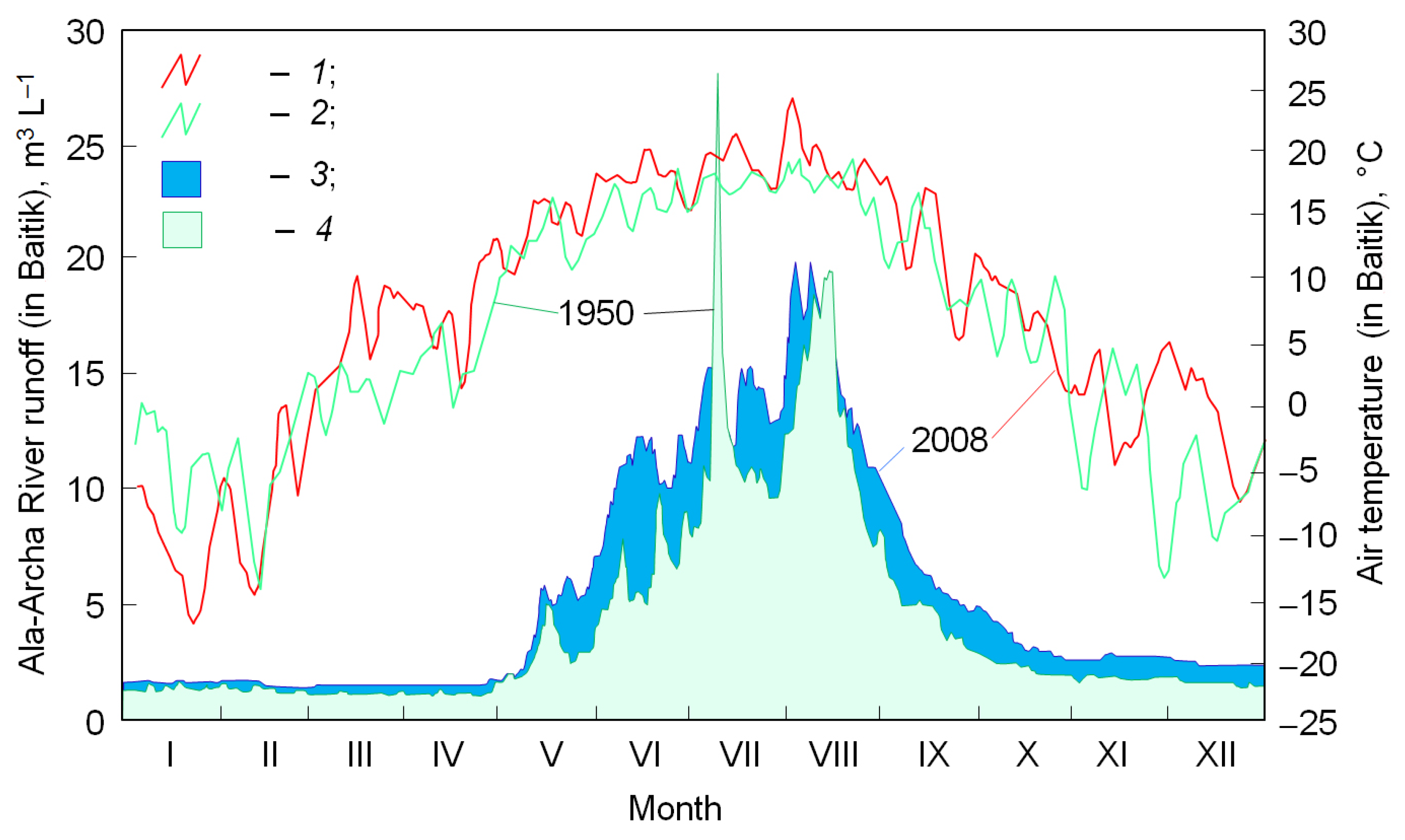
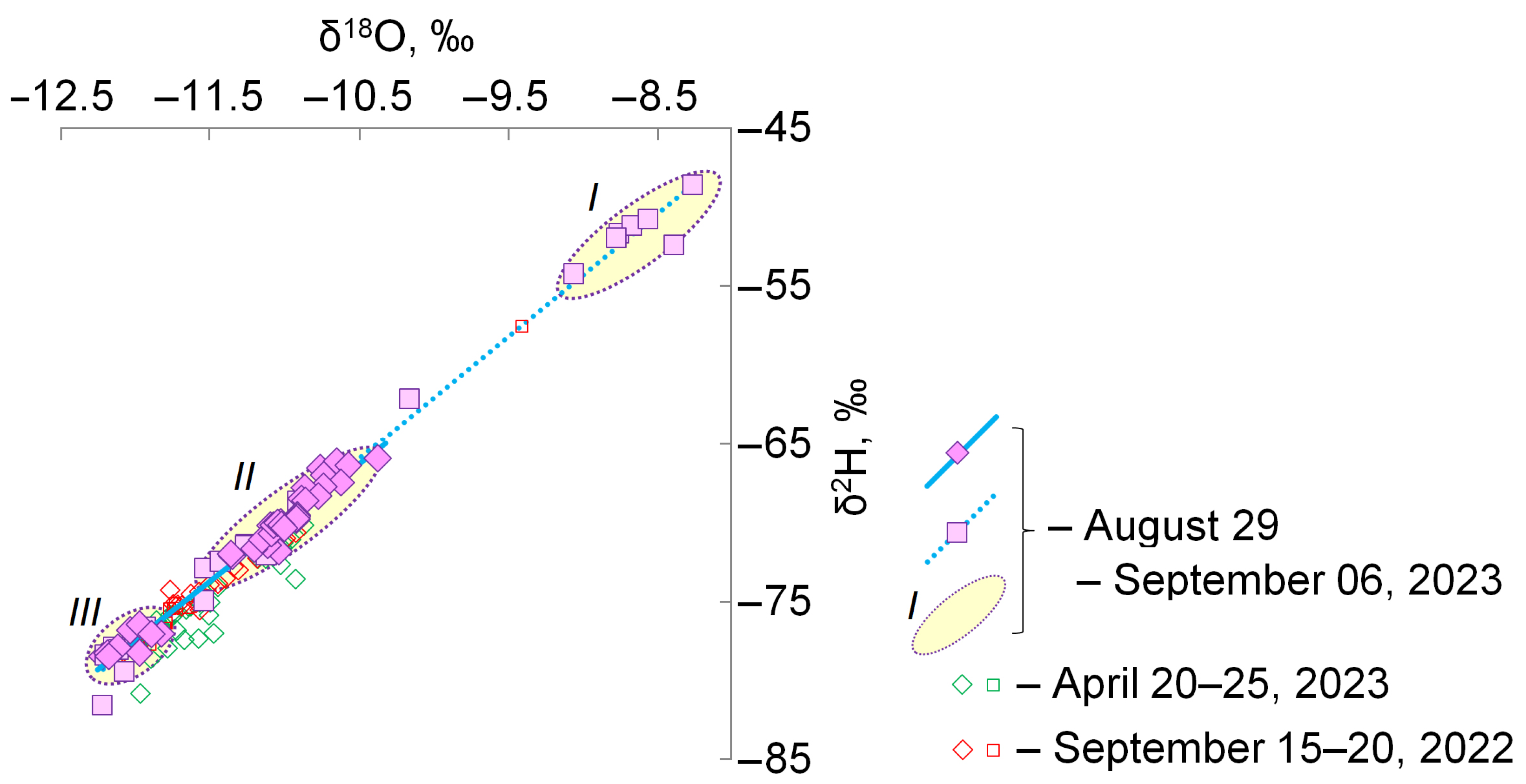
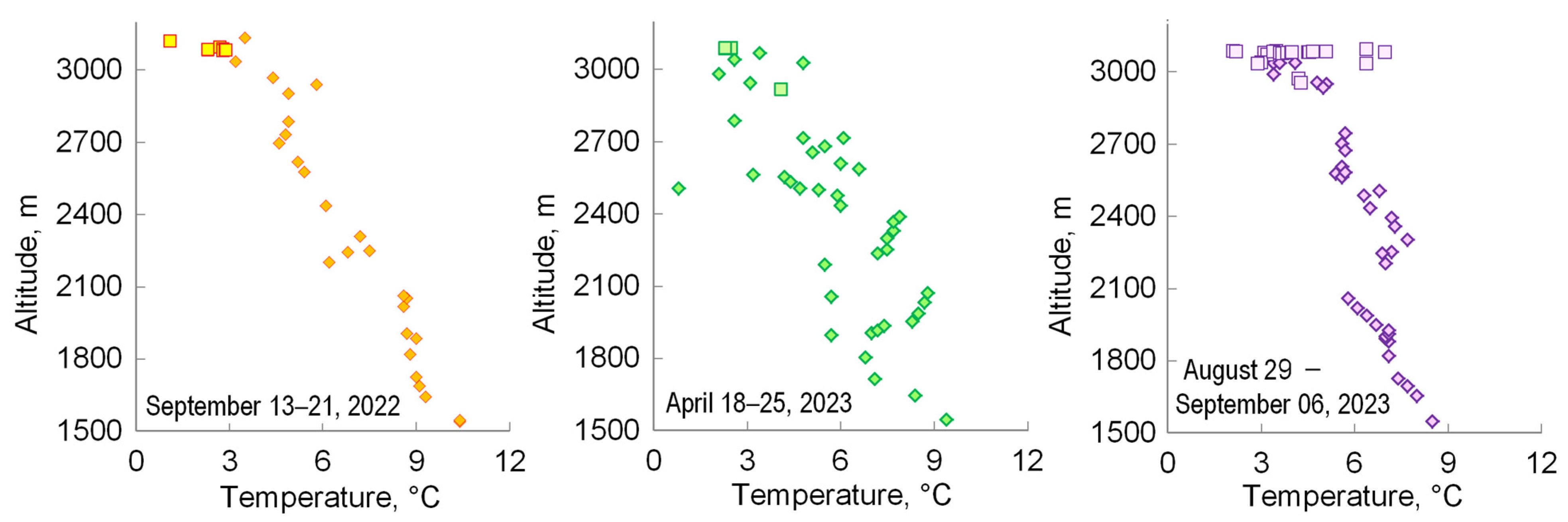
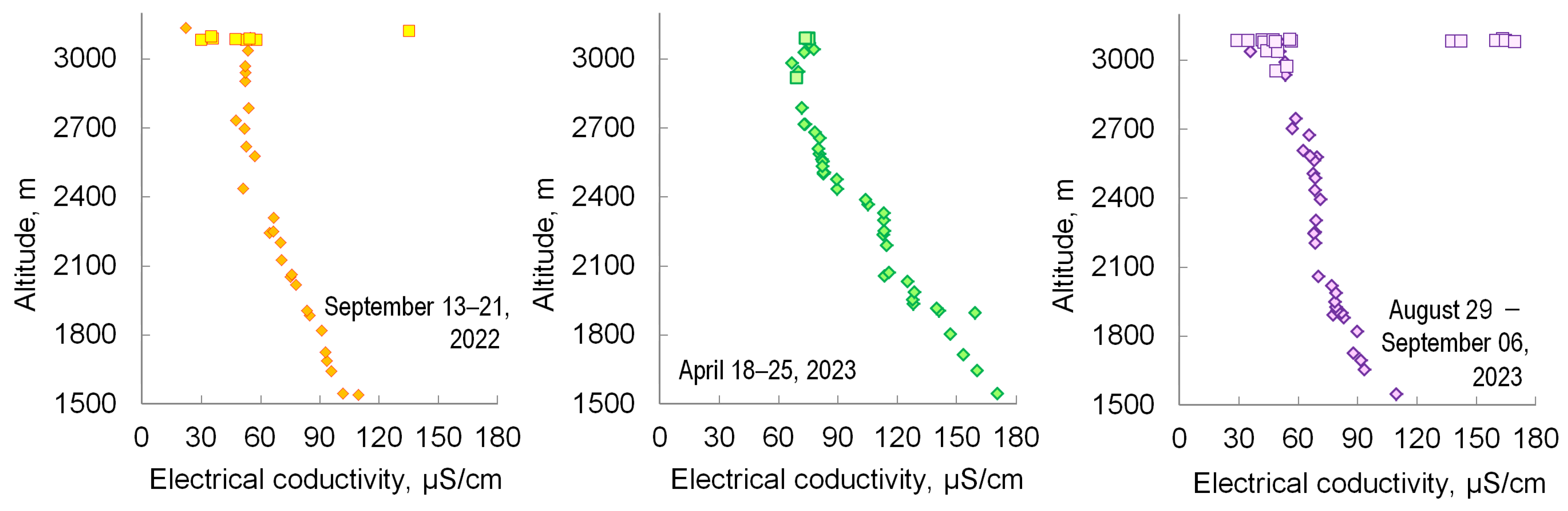
4.2. Seasonal and Inter-Annual Variations
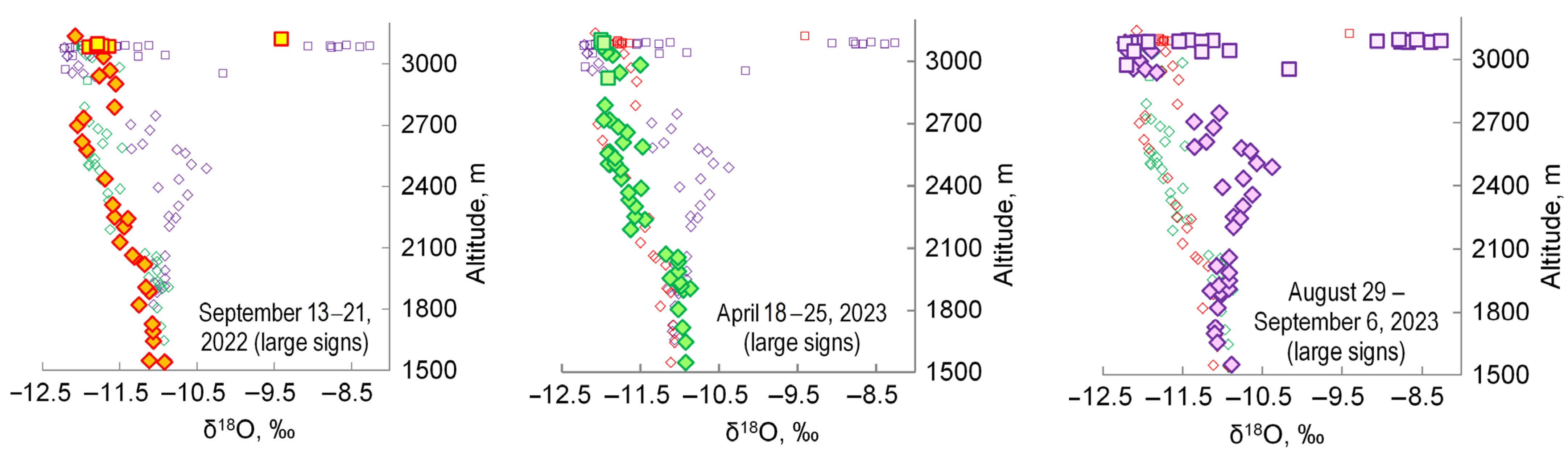
- The least populated area with relatively isotopically heavy compositions of water from δ18O = −8.26‰ and δ2H = −48.6‰ to δ18O = −9.06‰ and δ2H = −54.3‰ is represented exclusively by water from the diffuse runoff in the glaciation zone above 3000 m (Figure 10), which contradicts the assumption about the progressive depletion of the isotopic composition of precipitation with increasing elevations of the terrain, as all other samples in the altitude interval 1500–3000 m demonstrate a more depleted isotope composition of hydrogen and oxygen.
- The most populated region with a relatively depleted isotope composition of water ranging from δ18O = −10.37‰ and δ2H = −66.1‰ to δ18O = −11.53‰ and δ2H = −73.0‰ is generally represented by the river water from the main channel in the lower and middle reaches and partially by the diffuse runoff in the upper part of the basin due to small tributary inflow in the main stream of the Ala-Archa River (Figure 10).
- Water with the most depleted isotope composition from δ18O = −11.90‰ and δ2H = −77.2‰ to δ18O = −12.07‰ and δ2H = −79.6‰ is only found in the glaciation zone (above altitude 2900 m, Figure 10), and these samples were taken from the main channel (where the main flow of the Ala-Archa River acquires a tree-like and multi-branch structure) and from the diffuse runoff.
5. Discussion
5.1. Anomaly in the Isotopic Composition of the River Water
- Freezing of rainwater in the cold clastic rock massif in late spring or early summer (the composition of summer rain at the “Alpine camp” point at an altitude of 2100 m reaches δ18O = −0.06‰, Table 1).
- Detection of ice formed in one of the previous warmer climatic periods and subsequently buried under the massif of clastic sediments.
5.2. Variations in the Isotopic Composition of Water in the Main Stream of the Ala-Archa River
6. Conclusions
- Meltwater from modern glaciation and seasonal snows.
- An anomalous component associated with the melting of buried ice at altitudes above 3000 m was not previously identified.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guse, B.; Pfannerstill, M.; Gafurov, A.; Fohrer, N.; Gupta, H. Demasking the integrated information of discharge—Advancing sensitivity analysis to consider different hydrological components and their rates of change. Water Resour. Res. 2016, 52, 8724–8743. [Google Scholar] [CrossRef]
- Nearing, G.S.; Gupta, H.V. The quantity and quality of information in hydrologic models. Water Resour. Res. 2015, 51, 524–538. [Google Scholar] [CrossRef]
- Rets, E.P.; Popovnin, V.V.; Toropov, P.A.; Smirnov, A.M.; Tokarev, I.V.; Chizhova, J.N.; Budantseva, N.A.; Vasil’chuk, Y.K.; Kireeva, M.B.; Ekaykin, A.A.; et al. Djankuat Glacier Station in the North Caucasus, Russia: A Database of complex glaciological, hydrological, meteorological observations and stable isotopes sampling results during 2007–2017. Earth Syst. Sci. Data Discuss. 2019, 11, 1463–1481. [Google Scholar] [CrossRef]
- Reusser, D.; Blume, T.; Schaefli, B.; Zehe, E. Analysing the temporal dynamics of model performance for hydrological models. Hydrol. Earth Syst. Sci. 2009, 13, 999–1018. [Google Scholar] [CrossRef]
- Hingray, B.; Schaefli, B.; Mezghani, A.; Hamdi, Y. Signature-based model calibration for hydrological prediction in mesoscale Alpine catchments. Hydrol. Sci. J. 2010, 55, 1002–1016. [Google Scholar] [CrossRef]
- Schaefli, B.; Hingray, B.; Niggli, M.; Musy, A. A conceptual glacio-hydrological model for high mountainous catchments. Hydrol. Earth Syst. Sci. 2005, 9, 95–109. [Google Scholar] [CrossRef]
- Soulsby, C.; Birkel, C.; Geris, J.; Dick, J.; Tunaley, C.; Tetzlaff, D. Stream water age distributions controlled by storage dynamics and nonlinear hydrologic connectivity: Modeling with high-resolution isotope data. Water Resour. Res. 2015, 51, 7759–7776. [Google Scholar] [CrossRef] [PubMed]
- Richter, B.D.; Baumgartner, J.V.; Powell, J.; Braun, D.P. A method for assessing hydrologic alteration within ecosystems. Conserv. Biol. 1996, 10, 1163–1174. [Google Scholar] [CrossRef]
- Fovet, O.; Ruiz, L.; Hrachowitz, M.; Faucheux, M.; Gascuel-Odoux, C. Hydrological hysteresis and its value for assessing process consistency in catchment conceptual models. Hydrol. Earth Syst. Sci. 2015, 19, 105–123. [Google Scholar] [CrossRef]
- Gupta, H.V.; Wagener, T.; Liu, Y.Q. Reconciling theory with observations: Elements of a diagnostic approach to model evaluation. Hydrol. Process. 2008, 22, 3802–3813. [Google Scholar] [CrossRef]
- Hrachowitz, M.; Savenije, H.; Bogaard, T.A.; Tetzlaff, D.; Soulsby, C. What can flux tracking teach us about water age distribution patterns and their temporal dynamics? Hydrol. Earth Syst. Sci. 2013, 17, 533–564. [Google Scholar] [CrossRef]
- Sivapalan, M.; Blöschl, G.; Zhang, L.; Vertessy, R. Downward approach to hydrological prediction. Hydrol. Process. 2003, 17, 2101–2111. [Google Scholar] [CrossRef]
- Boyle, D.P.; Gupta, H.V.; Sorooshian, S. Toward improved calibration of hydrologic models: Combining the strengths of manual and automatic methods. Water Resour. Res. 2000, 36, 3663–3674. [Google Scholar] [CrossRef]
- Hay, L.E.; Leavesley, G.H.; Clark, M.P.; Markstrom, S.L.; Viger, R.J.; Umemoto, M. Step wise, multiple objective calibration of a hydrologic model for a snowmelt dominated basin. J. Am. Water Resour. Assoc. 2006, 42, 877–890. [Google Scholar] [CrossRef]
- Willems, P. Parsimonious rainfall-runoff model construction supported by time series processing and validation of hydrological extremes—Part 1: Step-wise model-structure identification and calibration approach. J. Hydrol. 2014, 510, 578–590. [Google Scholar] [CrossRef]
- Jothityangkoon, C.; Sivapalan, M.; Farmer, D.L. Process controls of water balance variability in a large semi-arid catchment: Downward approach to hydrological model development. J. Hydrol. 2001, 254, 174–198. [Google Scholar] [CrossRef]
- Liucci, L.; Valigi, D.; Casadei, S. A new application of flow duration curve (FDC) in designing run-of-river power plants. Water Resour. Manag. 2014, 28, 881–895. [Google Scholar] [CrossRef]
- Luo, Y.; Arnold, J.; Allen, P.; Chen, X. Baseflow simulation using SWAT model in an inland river basin in Tianshan Mountains, Northwest China. Hydrol. Earth Syst. Sci. 2012, 16, 1259–1267. [Google Scholar] [CrossRef]
- Ye, S.; Yaeger, M.; Coopersmith, E.; Cheng, L.; Sivapalan, M. Exploring the physical controls of regional patterns of flow duration curves-Part 2: Role of seasonality, the regime curve, and associated process controls. Hydrol. Earth Syst. Sci. 2012, 16, 4447–4465. [Google Scholar] [CrossRef]
- Coxon, G.; Freer, J.; Wagener, T.; Odoni, N.A.; Clark, M. Diagnostic evaluation of multiple hypotheses of hydrological behaviour in a limits-of-acceptability framework for 24 UK catchments. Hydrol. Process. 2014, 28, 6135–6150. [Google Scholar] [CrossRef]
- Shafii, M.; Tolson, B.A. Optimizing hydrological consistency by incorporating hydrological signatures into model calibration objectives. Water Resour. Res. 2015, 51, 3796–3814. [Google Scholar] [CrossRef]
- Finger, D.; Vis, M.; Huss, M.; Seibert, J. The value of multiple data set calibration versus model complexity for improving the performance of hydrological models in mountain catchments. Water Resour. Res. 2015, 51, 1939–1958. [Google Scholar] [CrossRef]
- Tarasova, L.; Knoche, M.; Dietrich, J.; Merz, R. Effects of input discretization, model complexity, and calibration strategy on model performance in a data-scarce glacierized catchment in Central Asia. Water Resour. Res. 2016, 52, 4674–4699. [Google Scholar] [CrossRef]
- Singh, S.K.; Bardossy, A. Calibration of hydrological models on hydrologically unusual events. Adv. Water Resour. 2012, 38, 81–91. [Google Scholar] [CrossRef]
- Duethmann, D.; Zimmer, J.; Gafurov, A.; Guntner, A.; Kriegel, D.; Merz, B.; Vorogushyn, S. Evaluation of areal precipitation estimates based on downscaled reanalysis and station data by hydrological modelling. Hydrol. Earth Syst. Sci. 2013, 17, 2415–2434. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Wanders, N.; Lutz, A.F.; Shea, J.M.; Bierkens, M.F.P. Reconciling high-altitude precipitation in the upper Indus basin with glacier mass balances and runoff. Hydrol. Earth Syst. Sci. 2015, 19, 4673–4687. [Google Scholar] [CrossRef]
- Pfannerstill, M.; Guse, B.; Fohrer, N. Smart low flow signature metrics for an improved overall performance evaluation of hydrological models. J. Hydrol. 2014, 510, 447–458. [Google Scholar] [CrossRef]
- Razavi, S.; Tolson, B.A. An efficient framework for hydrologic model calibration on long data periods. Water Resour. Res. 2013, 49, 8418–8431. [Google Scholar] [CrossRef]
- Konz, M.; Seibert, J. On the value of glacier mass balances for hydrological model calibration. J. Hydrol. 2010, 385, 238–246. [Google Scholar] [CrossRef]
- Le Lay, M.; Saulnier, G.M.; Galle, S.; Seguis, L.; Metadier, M.; Peugeot, C. Model representation of the Sudanian hydrological processes: Application on the Donga catchment (Benin). J. Hydrol. 2008, 363, 32–41. [Google Scholar] [CrossRef]
- Madsen, H. Automatic calibration of a conceptual rainfall-runoff model using multiple objectives. J. Hydrol. 2000, 235, 276–288. [Google Scholar] [CrossRef]
- Seibert, J.; McDonnell, J.J. On the dialog between experimentalist and modeler in catchment hydrology: Use of soft data for multicriteria model calibration. Water Resour. Res. 2002, 38, 1241. [Google Scholar] [CrossRef]
- Efstratiadis, A.; Koutsoyiannis, D. One decade of multi-objective calibration approaches in hydrological modelling: A review. Hydrol. Sci. J. 2010, 55, 58–78. [Google Scholar] [CrossRef]
- Parajka, J.; Naeimi, V.; Bloschl, G.; Komma, J. Matching ERS scatterometer based soil moisture patterns with simulations of a conceptual dual layer hydrologic model over Austria. Hydrol. Earth Syst. Sci. 2009, 13, 259–271. [Google Scholar] [CrossRef]
- Seibert, J. Multi-dataset calibration of a conceptual runoff model using a genetic algorithm. Hydrol. Earth Syst. Sci. 2000, 4, 215–224. [Google Scholar] [CrossRef]
- Gafurov, A.; Lüdtke, S.; Unger-Shayesteh, K.; Vorogushyn, S.; Schöne, T.; Schmidt, S.; Kalashnikova, O.; Merz, B. MODSNOW-Tool: An operational tool for daily snow cover monitoring using MODIS data. Environ. Earth Sci. 2016, 75, 1078. [Google Scholar] [CrossRef]
- Parajka, J.; Blöschl, G. The value of MODIS snow cover data in validating and calibrating conceptual hydrologic models. J. Hydrol. 2008, 358, 240–258. [Google Scholar] [CrossRef]
- Parajka, J.; Blöschl, G. Spatio-temporal combination of MODIS images-Potential for snow cover mapping. Water Resour. Res. 2008, 44, W03406. [Google Scholar] [CrossRef]
- Duethmann, D.; Peters, J.; Blume, T.; Vorogushyn, S.; Güntner, A. The value of satellite- derived snow cover images for calibrating a hydrological model in snow-dominated catchments in Central Asia. Water Resour. Res. 2014, 50, 2002–2021. [Google Scholar] [CrossRef]
- Peters, J.; Bolch, T.; Gafurov, A.; Prechtel, N. Snow cover distribution in the Aksu Catchment (Central Tien Shan) 1986–2013 based on AVHRR and MODIS data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 5361–5375. [Google Scholar] [CrossRef]
- Zhou, H.; Aizen, E.; Aizen, V. Deriving long term snow cover extent dataset from AVHRR and MODIS data: Central Asia case study. Remote Sens. Environ. 2013, 136, 146–162. [Google Scholar] [CrossRef]
- Huss, M. Extrapolating glacier mass balance to the mountain-range scale: The European Alps 1900–2100. Cryosphere 2012, 6, 713–727. [Google Scholar] [CrossRef]
- Aizen, V.B.; Kuzmichenok, V.A.; Surazakov, A.B.; Aizen, E.M. Glacier changes in the Tien Shan as determined from topographic and remotely sensed data. Glob. Planet. Chang. 2007, 56, 328–340. [Google Scholar] [CrossRef]
- Shangguan, D.H.; Bolch, T.; Ding, Y.J.; Krohnert, M.; Pieczonka, T.; Wetzel, H.U.; Liu, S.Y. Mass changes of Southern and Northern Inylchek Glacier, Central Tian Shan, Kyrgyzstan, during similar to 1975 and 2007 derived from remote sensing data. Cryosphere 2015, 9, 703–717. [Google Scholar] [CrossRef]
- Kääb, A.; Berthier, E.; Nuth, C.; Gardelle, J.; Arnaud, Y. Contrasting patterns of early twenty first-century glacier mass change in the Himalayas. Nature 2012, 488, 495–498. [Google Scholar] [CrossRef] [PubMed]
- Schaefli, B.; Huss, M. Integrating point glacier mass balance observations into hydrologic model identification. Hydrol. Earth Syst. Sci. 2011, 15, 1227–1241. [Google Scholar] [CrossRef]
- Mayr, E.; Hagg, W.; Mayer, C.; Braun, L. Calibrating a spatially distributed conceptual hydrological model using runoff, annual mass balance and winter mass balance. J. Hydrol. 2013, 478, 40–49. [Google Scholar] [CrossRef]
- Hamlet, A.F.; Mote, P.W.; Clark, M.P.; Lettenmaier, D.P. Effects of temperature and precipitation variability on snowpack trends in the western United States. J. Clim. 2005, 18, 4545–4561. [Google Scholar] [CrossRef]
- Farinotti, D.; Longuevergne, L.; Moholdt, G.; Duethmann, D.; Mölg, T.; Bolch, T.; Vorogushyn, S.; Güntner, A. Substantial glacier mass loss in the Tien Shan over the past 50 years. Nat. Geosci. 2015, 8, 716–722. [Google Scholar] [CrossRef]
- Chiogna, G.; Rolle, M.; Bellin, A.; Cirpka, O.A. Helicity and flow topology in three dimensional anisotropic porous media. Adv. Water Resour. 2014, 73, 134–143. [Google Scholar] [CrossRef]
- Dahlke, H.E.; Lyon, S.W.; Jansson, P.; Karlin, T.; Rosqvist, G. Isotopic investigation of runoff generation in a glacierized catchment in northern Sweden. Hydrol. Process. 2014, 28, 1383–1398. [Google Scholar] [CrossRef]
- Klaus, J.; McDonnell, J.J. Hydrograph separation using stable isotopes: Review and evaluation. J. Hydrol. 2013, 505, 47–64. [Google Scholar] [CrossRef]
- Li, X.G.; Williams, M.W. Snowmelt runoff modelling in an arid mountain watershed, Tarim Basin, China. Hydrol. Process. 2008, 22, 3931–3940. [Google Scholar] [CrossRef]
- Sun, Y.; Du, W.; Fu, P.; Wang, Q.; Li, J.; Ge, X.; Zhang, Q.; Zhu, C.; Ren, L.; Xu, W.; et al. Primary and secondary aerosols in Beijing in winter: Sources, variations and processes. Atmos. Chem. Phys. 2016, 16, 8309–8329. [Google Scholar] [CrossRef]
- Pu, T.; Qin, D.H.; Kang, S.C.; Niu, H.W.; He, Y.Q.; Wang, S.J. Water isotopes and hydrograph separation in different glacial catchments in the southeast margin of the Tibetan Plateau. Hydrol. Process. 2017, 31, 3810–3826. [Google Scholar] [CrossRef]
- Engel, M.; Penna, D.; Bertoldi, G.; Dell’Agnese, A.; Soulsby, C.; Comiti, F. Identifying run-off contributions during melt-induced run-off events in a glacierized alpine catchment. Hydrol. Process. 2016, 30, 343–364. [Google Scholar] [CrossRef]
- He, Z.H.; Parajka, J.; Tian, F.Q.; Blöschl, G. Estimating degree-day factors from MODIS for snowmelt runoff modeling. Hydrol. Earth Syst. Sci. 2014, 18, 4773–4789. [Google Scholar] [CrossRef]
- He, Z.H.; Tian, F.Q.; Gupta, H.V.; Hu, H.C.; Hu, H.P. Diagnostic calibration of a hydrological model in a mountain area by hydrograph partitioning. Hydrol. Earth Syst. Sci. 2015, 19, 1807–1826. [Google Scholar] [CrossRef]
- Joerin, C.; Iorgulescu, I.; Musy, A.; Beven, K.J. Uncertainty in hydrograph separations based on geochemical mixing models. J. Hydrol. 2002, 255, 90–106. [Google Scholar] [CrossRef]
- Rahman, K.; Besacier-Monbertrand, A.L.; Castella, E.; Lods-Crizet, B.; Ilg, C.; Beguin, O. Quantification of the daily dynamics of streamflow components in a small alpine watershed in Switzerland using end member mixing analysis. Environ. Earth Sci. 2015, 74, 4927. [Google Scholar] [CrossRef]
- Ala-aho, P.; Tetzlaff, D.; McNamara, J.P.; Laudon, H.; Soulsby, C. Using isotopes to constrain water flux and age estimates in snow-influenced catchments using the STARR (Spatially distributed Tracer-Aided Rainfall-Runoff) model. Hydrol. Earth Syst. Sci. 2017, 21, 5089–5110. [Google Scholar] [CrossRef]
- Bantcev, D.; Ganyushkin, D.; Terekhov, A.; Ekaykin, A.; Tokarev, I.; Chistyakov, K. Isotopic Composition of Glacier Ice and Meltwater in the Arid Parts of the Altai Mountains (Central Asia). Water 2022, 14, 252. [Google Scholar] [CrossRef]
- Birkel, C.; Dunn, S.M.; Tetzlaff, D.; Soulsby, C. Assessing the value of high-resolution isotope tracer data in the stepwise development of a lumped conceptual rainfall-runoff model. Hydrol. Process. 2010, 24, 2335–2348. [Google Scholar] [CrossRef]
- Soulsby, C.; Tetzlaff, D. Towards simple approaches for mean residence time estimation in ungauged basins using tracers and soil distributions. J. Hydrol. 2008, 363, 60–74. [Google Scholar] [CrossRef]
- van Huijgevoort, M.H.J.; Tetzlaff, D.; Sutanudjaja, E.H.; Soulsby, C. Using high resolution tracer data to constrain water storage, flux and age estimates in a spatially distributed rainfall-runoff model. Hydrol. Process. 2016, 30, 4761–4778. [Google Scholar] [CrossRef]
- Gudkov, A.V.; Tokarev, I.V.; Tolstikhin, I.N. The formation and balance of the atmospheric precipitations, surface water, and groundwater on the southern slopes of the Khibiny massif (based on data on the isotopic composition of oxygen and hydrogen). Water Resour. 2021, 48, 124–132. [Google Scholar] [CrossRef]
- Seibert, J.; Rodhe, A.; Bishop, K. Simulating interactions between saturated and unsaturated storage in a conceptual runoff model. Hydrol. Process. 2003, 17, 379–390. [Google Scholar] [CrossRef]
- Weiler, M.; McGlynn, B.L.; McGuire, K.J.; McDonnell, J.J. How does rainfall become runoff? A combined tracer and runoff transfer function approach. Water Resour. Res. 2003, 39, 1315. [Google Scholar] [CrossRef]
- Stadnyk, T.; St Amour, N.; Kouwen, N.; Edwards, T.W.D.; Pietroniro, A.; Gibson, J.J. A groundwater separation study in boreal wetland terrain: The WATFLOOD hydrological model compared with stable isotope tracers. Isotopes Environ. Health Stud. 2005, 41, 49–68. [Google Scholar] [CrossRef]
- Dunn, S.M.; Bacon, J.R. Assessing the value of Cl- and delta O-18 data in modelling the hydrological behaviour of a small upland catchment in northeast Scotland. Hydrol. Res. 2008, 39, 337–358. [Google Scholar] [CrossRef]
- Stadnyk, T.A.; Delavau, C.; Kouwen, N.; Edwards, T.W.D. Towards hydrological model calibration and validation: Simulation of stable water isotopes using the isoWATFLOOD model. Hydrol. Process. 2013, 27, 3791–3810. [Google Scholar] [CrossRef]
- Capell, R.; Tetzlaff, D.; Soulsby, C. Can time domain and source area tracers reduce uncertainty in rainfall-runoff models in larger heterogeneous catchments? Water Resour. Res. 2012, 48, W09544. [Google Scholar] [CrossRef]
- Tetzlaff, D.; Buttle, J.; Carey, S.K.; van Huijgevoort, M.H.J.; Laudon, H.; McNamara, J.P.; Mitchell, C.P.J.; Spence, C.; Gabor, R.S.; Soulsby, C. A preliminary assessment of water partitioning and ecohydrological coupling in northern headwaters using stable isotopes and conceptual runoff models. Hydrol. Process. 2015, 29, 5153–5173. [Google Scholar] [CrossRef] [PubMed]
- Penna, D.; Engel, M.; Bertoldi, G.; Comiti, F. Towards a tracer-based conceptualization of meltwater dynamics and streamflow response in a glacierized catchment. Hydrol. Earth Syst. Sci. 2017, 21, 23–41. [Google Scholar] [CrossRef]
- Maurya, A.S.; Shah, M.; Deshpande, R.D.; Bhardwaj, R.M.; Prasad, A.; Gupta, S.K. Hydrograph separation and precipitation source identification using stable water isotopes and conductivity: River Ganga at Himalayan foothills. Hydrol. Process. 2011, 25, 1521–1530. [Google Scholar] [CrossRef]
- He, Z.H.; Hu, H.C.; Tian, F.Q.; Ni, G.H.; Hu, Q.F. Correcting the TRMM rainfall product for hydrological modelling in sparsely-gauged mountainous basins. Hydrol. Sci. J. 2017, 62, 306–318. [Google Scholar] [CrossRef]
- He, Z.; Vorogushyn, S.; Unger-Shayesteh, K.; Gafurov, A.; Kalashnikova, O.; Omorova, E.; Merz, B. The value of hydrograph partitioning curves for calibrating hydrological models in glacierized basins. Water Resour. Res. 2018, 54, 2336–2361. [Google Scholar] [CrossRef]
- He, Z.; Unger-Shayesteh, K.; Vorogushyn, S.; Weise, S.M.; Duethmann, D.; Kalashnikova, O.; Gafurov, A.; Merz, B. Comparing Bayesian and traditional end-member mixing approaches for hydrograph separation in a glacierized basin. Hydrol. Earth Syst. Sci. 2020, 24, 3289–3309. [Google Scholar] [CrossRef]
- Stahl, K.; Moore, R.D.; Shea, J.M.; Hutchinson, D.; Cannon, A.J. Coupled modelling of glacier and streamflow response to future climate scenarios. Water Resour. Res. 2008, 44, W02422. [Google Scholar] [CrossRef]
- Shamov, V.V.; Tokarev, I.V.; Mikhaylik, T.A.; Kozachek, A.V. Dynamics of isotopic composition (2H, 18O) of waters of small river basins of the southern Sikhote-Alin in summer-autumn period. Hydrosphere Hazard. Process. Phenom. 2022, 4, 202–215. (In Russian) [Google Scholar]
- Aizen, V.B.; Aizen, E.M.; Melack, J.M. Climate, snow cover, glaciers, and runoff in the Tien-Shan, Central-Asia. Water Resour. Bull. 1995, 31, 1113–1129. [Google Scholar] [CrossRef]
- Aizen, V.B.; Aizen, E.M.; Melack, J.M. Precipitation, melt and runoff in the northern Tien Shan. J. Hydrol. 1996, 186, 229–251. [Google Scholar] [CrossRef]
- Aizen, V.B.; Mayewski, P.A.; Aizen, E.M.; Joswiak, D.R.; Surazakov, A.B.; Kaspari, S.; Grigholm, B.; Krachler, M.; Handley, M.; Finaev, A. Stable-isotope and trace element time series from Fedchenko glacier (pamirs) snow/firn cores. J. Glaciol. 2009, 55, 275–291. [Google Scholar] [CrossRef]
- Mikhalenko, V.N.; Kutuzov, S.S.; Lavrentiev, I.I.; Toropov, P.A.; Vladimirova, D.O.; Abramov, A.A.; Matskovsky, V.V. Glacioclimatological investigations of the Institute of Geography, RAS, in the crater of Eastern Summit of Mt. Elbrus in 2020. Ice Snow 2021, 61, 149–160. [Google Scholar] [CrossRef]
- Hoelzle, M.; Azisov, E.; Barandun, M.; Huss, M.; Farinotti, D.; Gafurov, A.; Hagg, W.; Kenzhebaev, R.; Kronenberg, M.; Machguth, H.; et al. Re-establishing glacier monitoring in Kyrgyzstan and Uzbekistan, Central Asia. Geosci. Instrum. Methods Data Syst. 2017, 6, 397. [Google Scholar] [CrossRef]
- Aizen, V.; Aizen, E.; Glazirin, G.; Loaiciga, H.A. Simulation of daily runoff in Central Asian alpine watersheds. J. Hydrol. 2000, 238, 15–34. [Google Scholar] [CrossRef]
- Kuzmichenok, V.A. Probabilistic assessment of possible evolution of glaciers and runoff of Kyrgyzstan under projected climate changes. Mater. Glaciol. Stud. 2009, 107, 10–24. [Google Scholar]
- Allen, S.T.; Kirchner, J.W.; Goldsmith, G.R. Predicting spatial patterns in precipitation isotope (δ2H and δ18O) seasonality using sinusoidal isoscapes. Geophys. Res. Lett. 2018, 45, 4859–4868. [Google Scholar] [CrossRef]
- Dalai, T.K.; Bhattacharya, S.K.; Krishnaswami, S. Stable isotopes in the source waters of the Yamuna and its tributaries: Seasonal and altitudinal variations and relation to major cations. Hydrol. Process. 2002, 16, 3345–3364. [Google Scholar] [CrossRef]
- Mark, B.G.; McKenzie, J.M. Tracing increasing tropical Andean glacier melt with stable isotopes in water. Environ. Sci. Technol. 2007, 41, 6955–6960. [Google Scholar] [CrossRef]
- Ohlanders, N.; Rodriguez, M.; McPhee, J. Stable water isotope variation in a Central Andean watershed dominated by glacier and snowmelt. Hydrol. Earth Syst. Sci. 2013, 17, 1035–1050. [Google Scholar] [CrossRef]
- Payne, B.R.; Leontiadis, J.; Dimitroulas, C. A study of the Kalamos springs in Greece with environmental isotopes. Water Resour. Res. 1978, 14, 653–658. [Google Scholar] [CrossRef]
- Vasil’chuk, Y.; Chizhova, J.; Frolova, N.; Budantseva, N.; Kireeva, M.; Oleynikov, A.; Tokarev, I.; Rets, E.; Vasil’chuk, A. A variation of stable isotope composition of snow with altitude on the Elbrus mountain, Central Caucasus. Geogr. Environ. Sustain. 2020, 13, 172–182. [Google Scholar] [CrossRef]
- Lorenz, J.M.; Tarbox, L.; Buck, B.; Qi, H.; Coplen, T.B. Biscayne aquifer drinking water (USGS45): A new isotopic reference material for δ2H and δ18O measurements of water. Rapid Commun. Mass Spectrom. 2014, 28, 2031–2034. [Google Scholar] [CrossRef] [PubMed]
- Coplen, T.B.; Qi, H.; Tarbox, L.; Lorenz, J.; Buck, B. USGS46 Greenland Ice Core Water—A New Isotopic Reference Material for δ2H and δ18O Measurements of Water. Geostand. Geoanalytical Res. 2013, 38, 153–157. [Google Scholar] [CrossRef]
- Kalashnikova, O.Y.; Esenaman Uulu, M.; Usubaliev, R.A. The impact of climate change on the runoff and glaciers of the Ala-Archa river basin for the period 1915–2018. Sci. New Technol. Innov. Kyrg. 2019, 4, 36–41. (In Russian) [Google Scholar]
- Tokarev, I.V.; Polyakov, V.A.; Samsonova, A.A.; Shilo, V.A.; Tolstikhin, G.M.; Nurbaev, T.N.; Zhakeev, B.I.; Shabunin, A.G.; Alekhina, V.M. Study of Conditions of Formation of Water Balance of Toktogul Reservoir by Isotopic Composition of Water (δ2H, δ18O); Study of Formation Factors and Assessment of the Impact of Reservoirs of the Lower Naryn Cascade of HPPs on the Quality of Water Resources of the Naryn River Basin by Isotopic Methods (Based on the Results of ISTC Project KR-1430, 2007–2010); National Academy of Sciences of the Kyrgyz Republic: Bishkek, Kyrgyzstan, 2010; pp. 56–84. (In Russian) [Google Scholar]



| Variable | δ18O, ‰ | Electrical Conductivity (EC), μS/cm | ||||
|---|---|---|---|---|---|---|
| Sample Number | Mean | Range | Sample Number | Mean | Range | |
| Precipitation at Baitik 1 | 36 | −11.21 | −20.99...1.51 | 14 | 69.9 | 26.6–99.6 |
| Streamflow at Baitik | 158 | −11.32 | −12.37...−10.82 | 25 | 114.7 | 81.0–139.3 |
| Precipitation at Alpine camp 2 | 43 | −11.41 | −22.82...−0.06 | 23 | 68.3 | 21.3–102.0 |
| Streamflow at Alpine camp | 184 | −11.73 | −12.90...−10.94 | 78 | 108.7 | 66.7–137.1 |
| Groundwater | 14 | −11.17 | −11.70...−10.61 | 12 | 126.8 | 69.6–167.2 |
| Snowmelt | 45 | −13.98 | −24.24...−10.53 | 7 | 28.4 | 11.0–55.1 |
| Glacier melt | 17 | −13.46 | −15.66...−12.33 | 3 | 32.1 | 30.1–33.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tokarev, I.; Yakovlev, E.; Erokhin, S.; Tuzova, T.; Druzhinin, S.; Puchkov, A. Reflection of Daily, Seasonal and Interannual Variations in Run-Off of a Small River in the Water Isotopic Composition (δ2H, δ18O): A Case of the Ala-Archa Mountain River Basin with Glaciation (Kyrgyzstan, Central Asia). Water 2024, 16, 1632. https://doi.org/10.3390/w16111632
Tokarev I, Yakovlev E, Erokhin S, Tuzova T, Druzhinin S, Puchkov A. Reflection of Daily, Seasonal and Interannual Variations in Run-Off of a Small River in the Water Isotopic Composition (δ2H, δ18O): A Case of the Ala-Archa Mountain River Basin with Glaciation (Kyrgyzstan, Central Asia). Water. 2024; 16(11):1632. https://doi.org/10.3390/w16111632
Chicago/Turabian StyleTokarev, Igor, Evgeny Yakovlev, Sergey Erokhin, Tamara Tuzova, Sergey Druzhinin, and Andrey Puchkov. 2024. "Reflection of Daily, Seasonal and Interannual Variations in Run-Off of a Small River in the Water Isotopic Composition (δ2H, δ18O): A Case of the Ala-Archa Mountain River Basin with Glaciation (Kyrgyzstan, Central Asia)" Water 16, no. 11: 1632. https://doi.org/10.3390/w16111632
APA StyleTokarev, I., Yakovlev, E., Erokhin, S., Tuzova, T., Druzhinin, S., & Puchkov, A. (2024). Reflection of Daily, Seasonal and Interannual Variations in Run-Off of a Small River in the Water Isotopic Composition (δ2H, δ18O): A Case of the Ala-Archa Mountain River Basin with Glaciation (Kyrgyzstan, Central Asia). Water, 16(11), 1632. https://doi.org/10.3390/w16111632






