A Study on the Transient Characteristics of the Power-Off Transition Process of a Double-Volute Centrifugal Pump
Abstract
1. Introduction
2. Numerical Methodology
2.1. Three-Dimensional Modeling of Centrifugal Pump
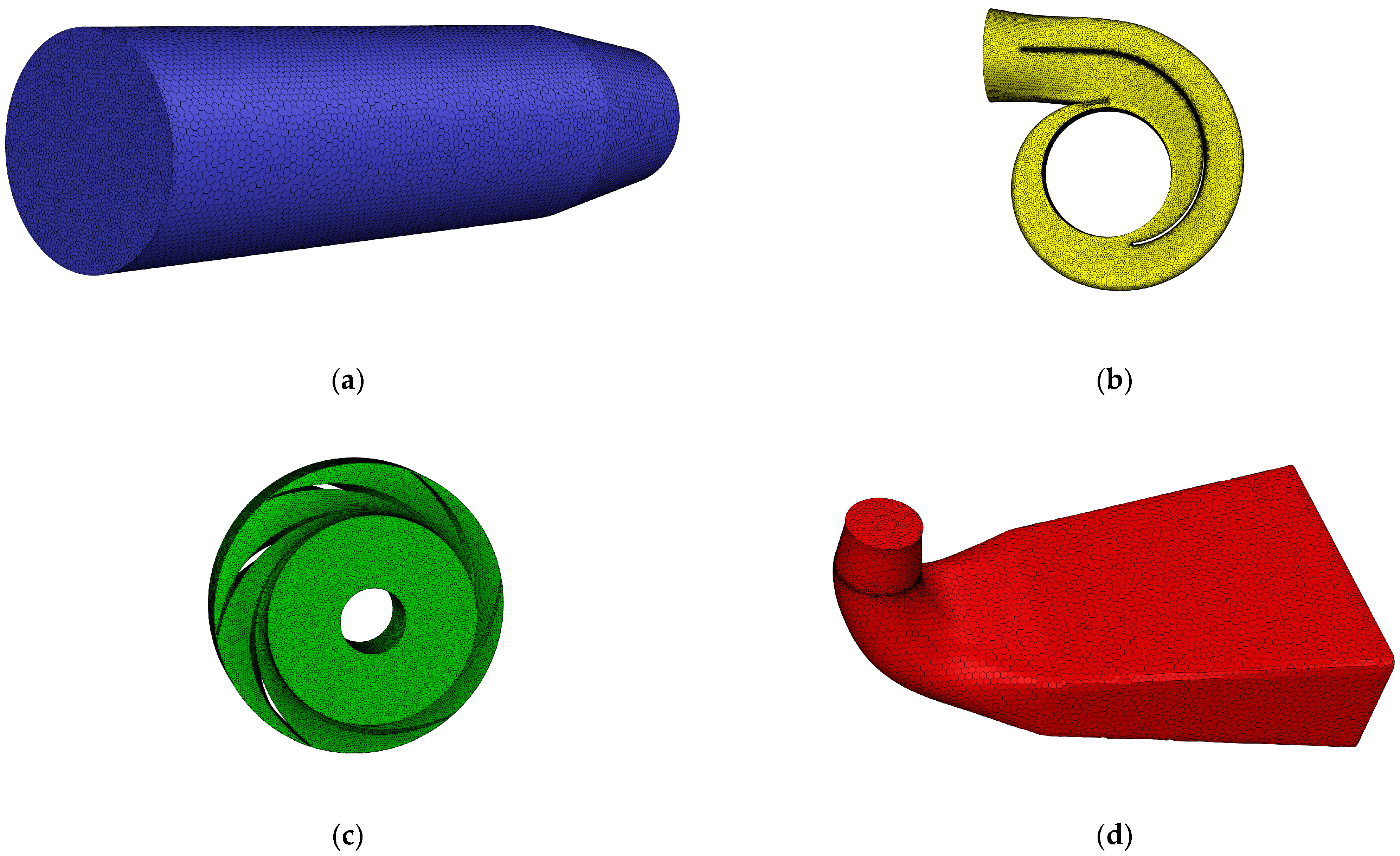
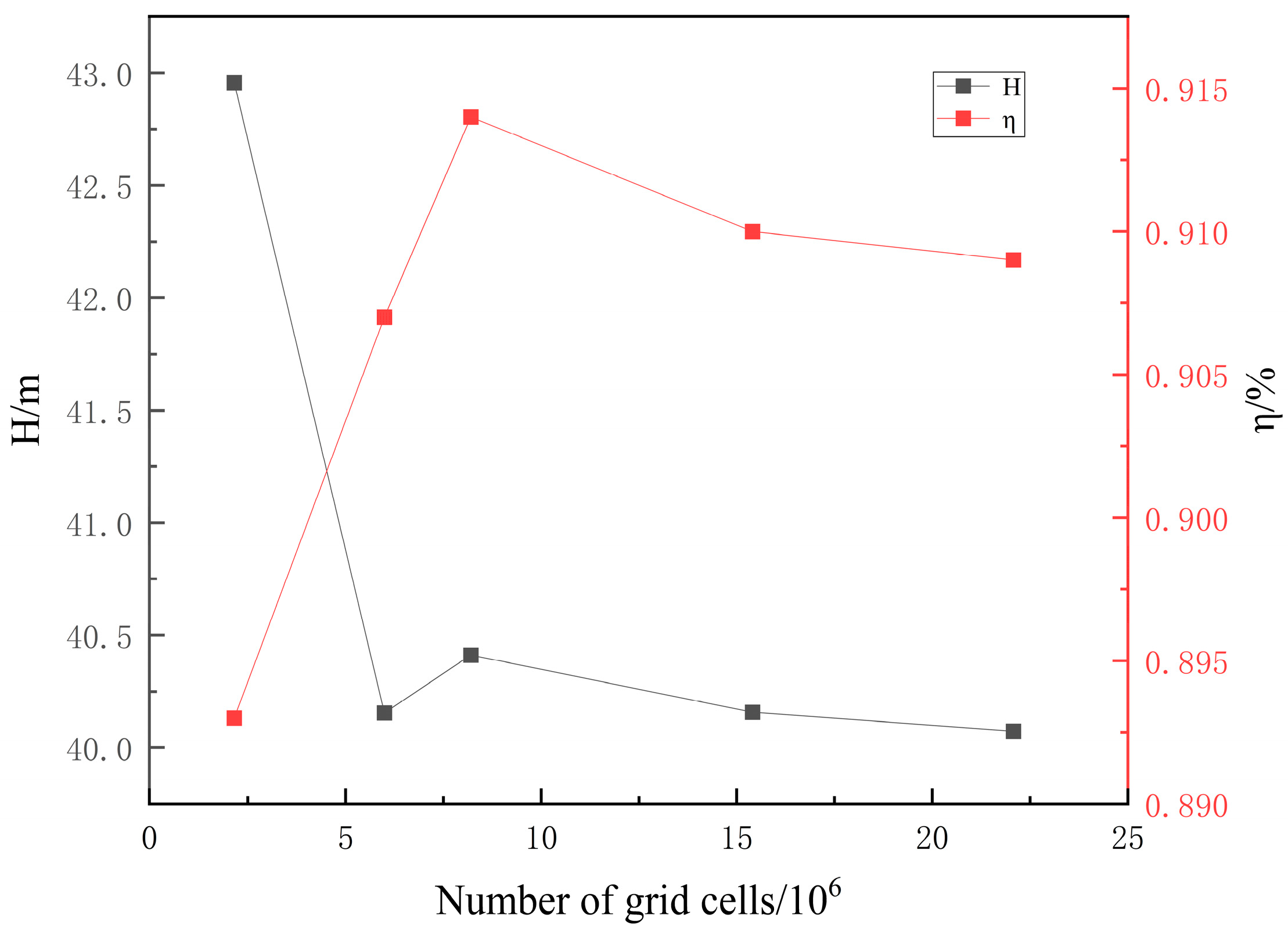
2.2. Mesh Generation
2.3. Setting of Boundary Conditions
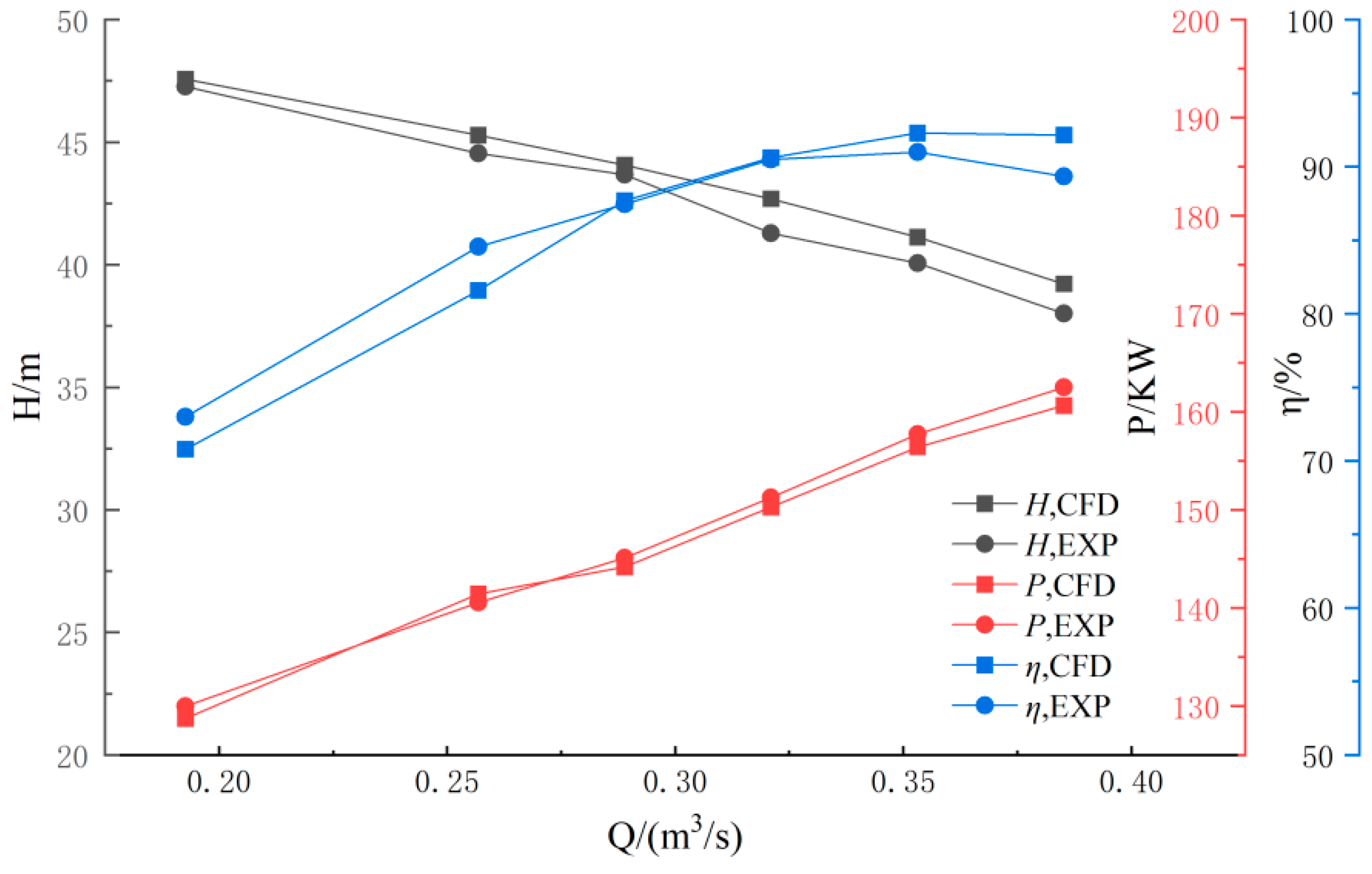
2.4. Validation of Numerical Methods
3. Results
3.1. Variation of External Characteristics
3.2. Evolution of Internal Flow
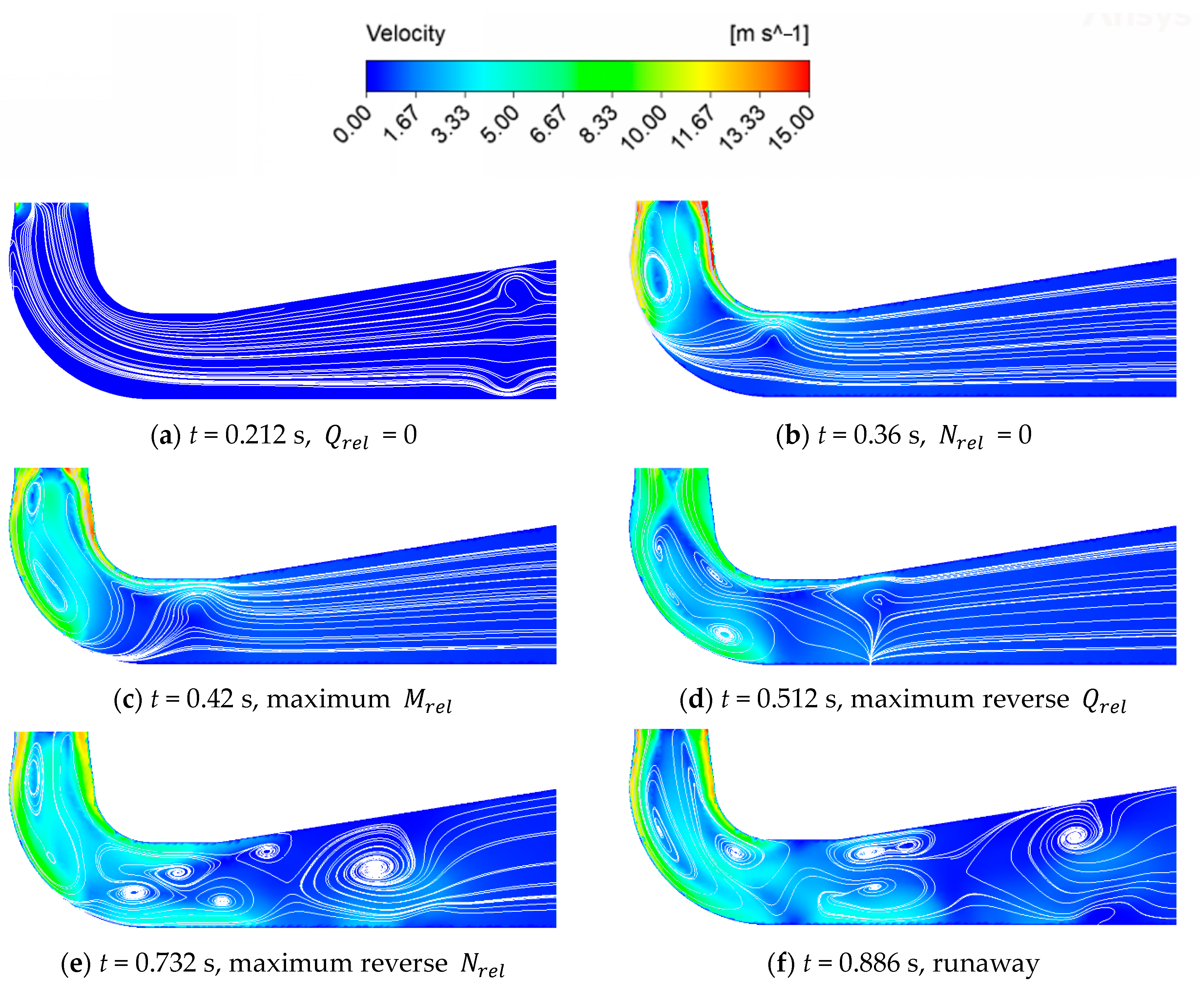
3.2.1. Flow State of Intake Pipe
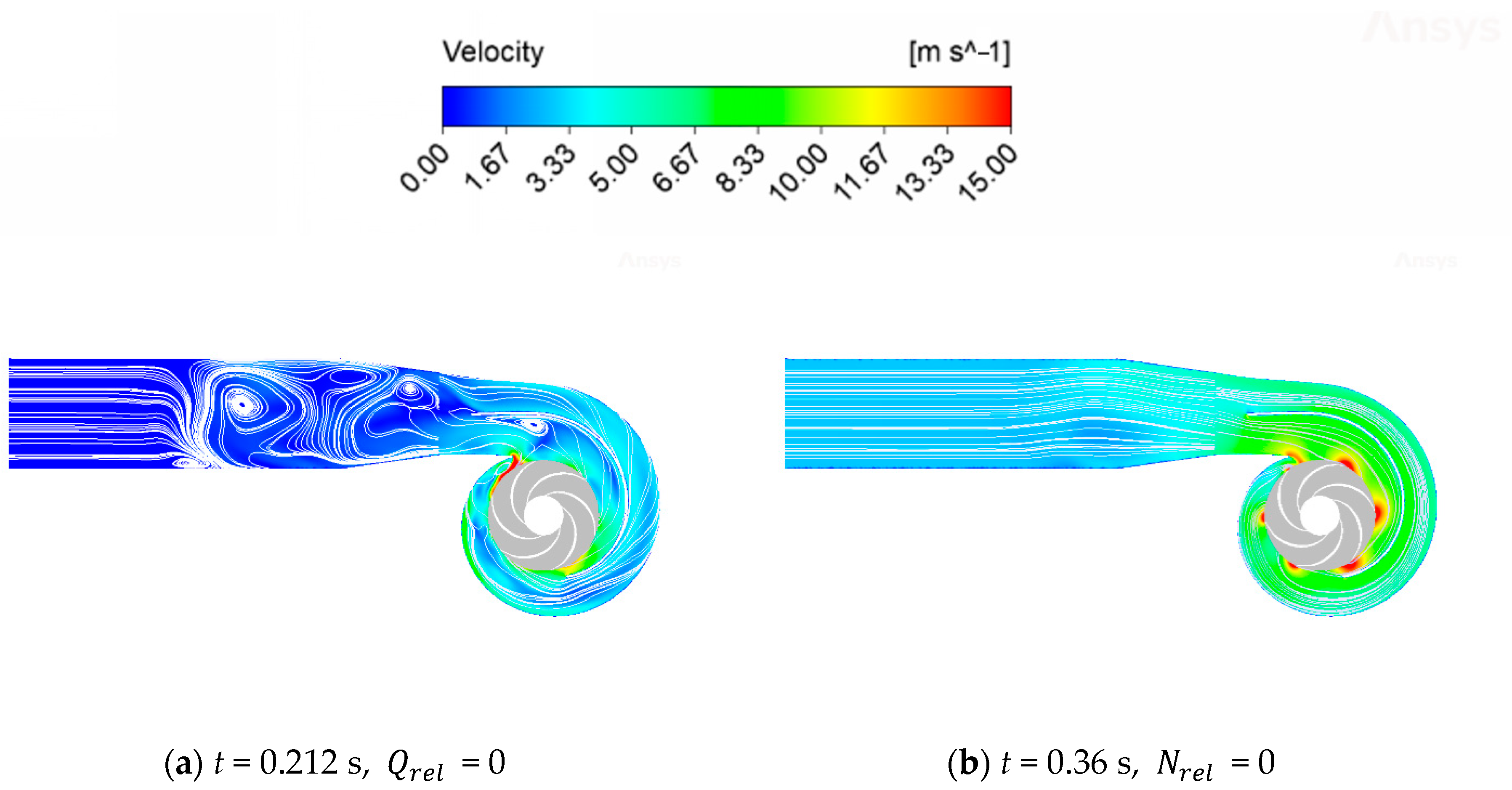
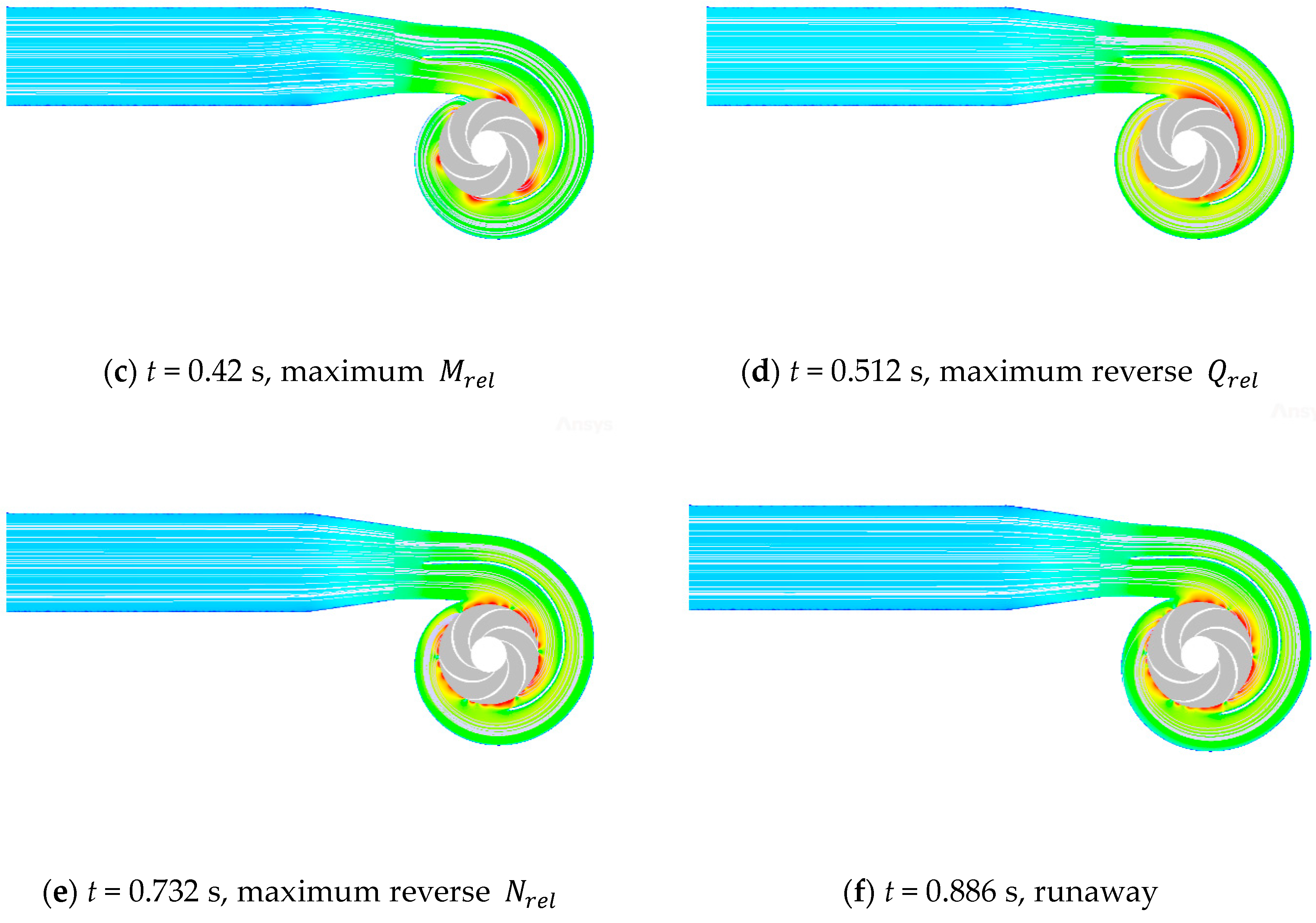
3.2.2. Flow State of Double Volute and Outlet
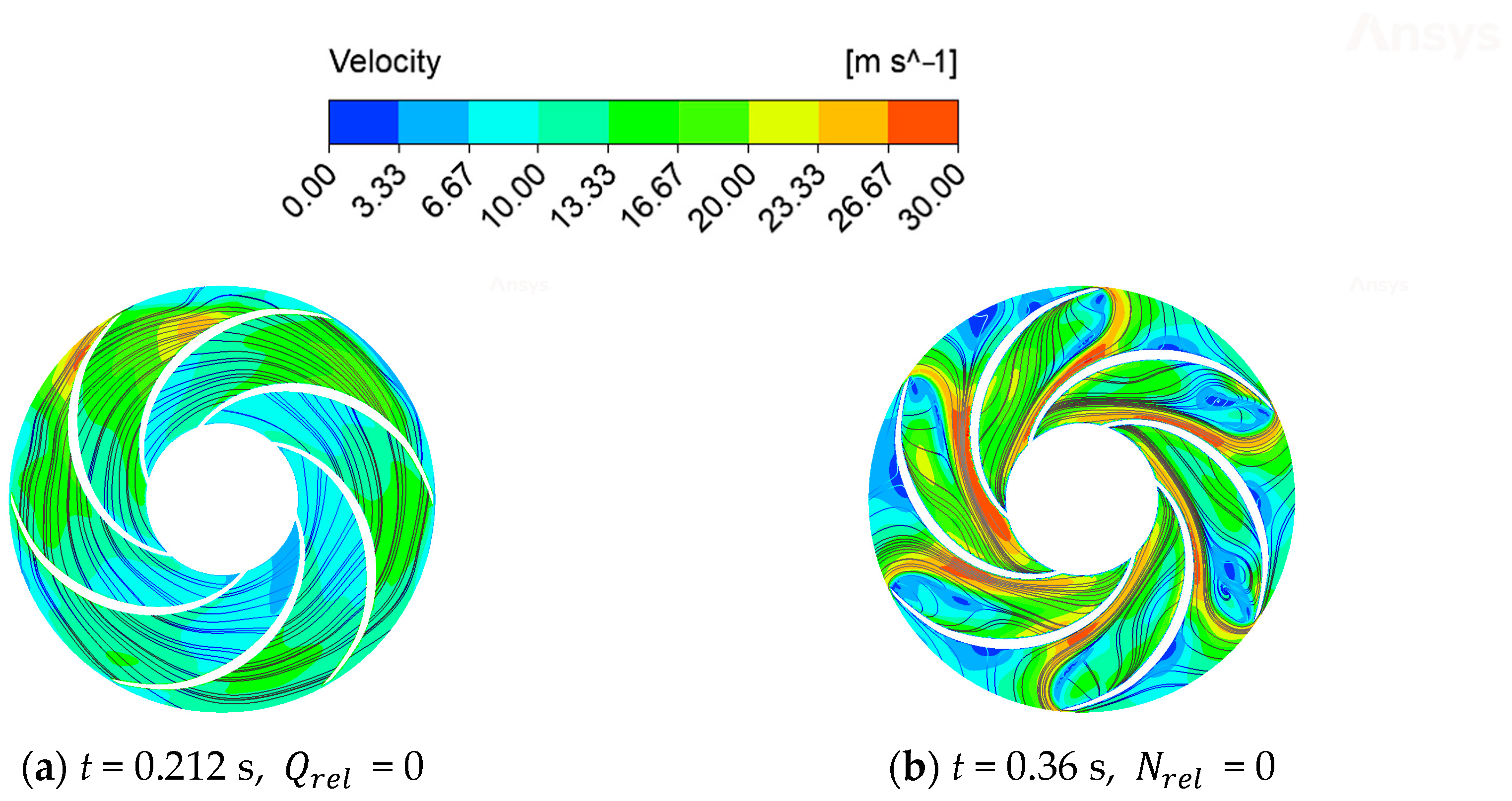
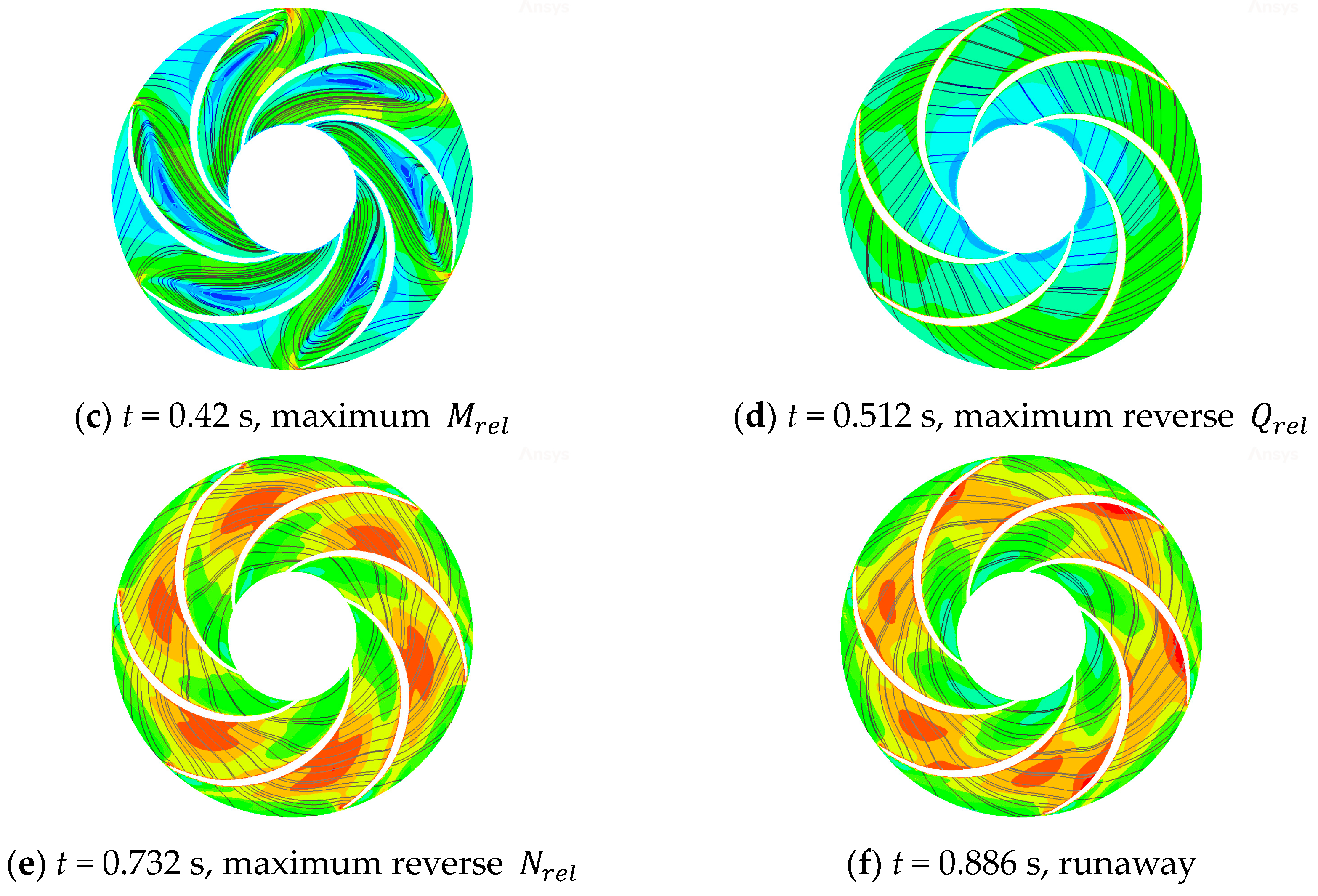
3.2.3. Flow State of Impeller
4. Conclusions
- (1)
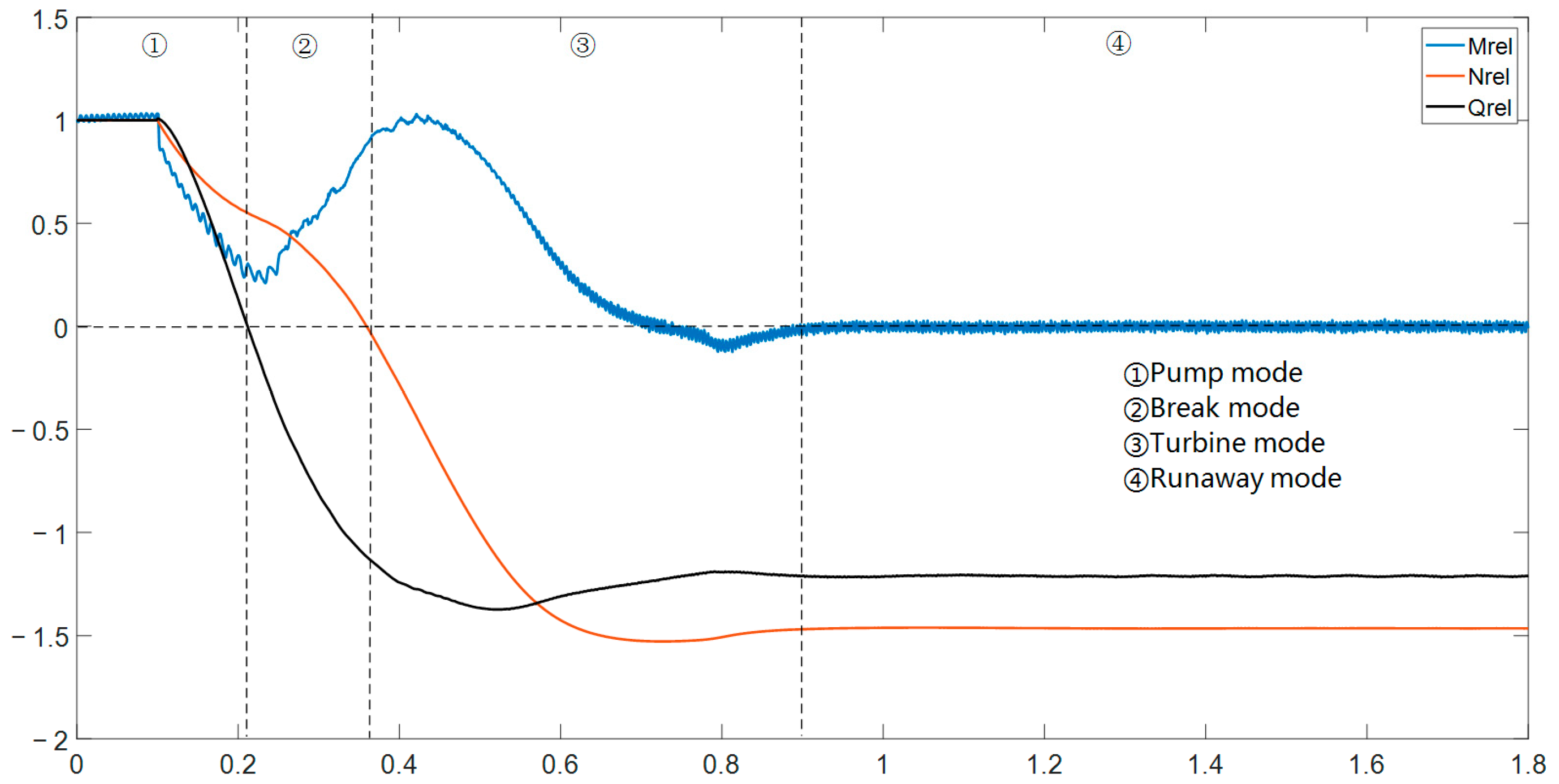
- After the double-volute centrifugal pump is powered off, it experienced four different modes, namely pump mode, braking mode, turbine mode, and runaway mode. The impeller torque, flow rate, and speed of the centrifugal pump underwent drastic changes after power failure and finally became stable under runaway mode. The absolute values of the runaway speed and the runaway flow rate are 1.465 times and 1.21 times the initial values, respectively.
- (2)
- Due to the huge change in the direction of speed and flow rate in the process of power failure, the flow regime inside the whole centrifugal pump became very complicated, and a large number of unstable flows of secondary flow, reflux, and flow separation were produced in the flow runner. Through the analysis of the flow field in the intake pipe area, the impeller area, the double-volute area, and the outlet diffusion section, we can see the change process of the generation, development, and disappearance of the vortex at each position of the centrifugal pump. We can also see the change and development process of the internal speed gradient of the centrifugal pump.
- (3)
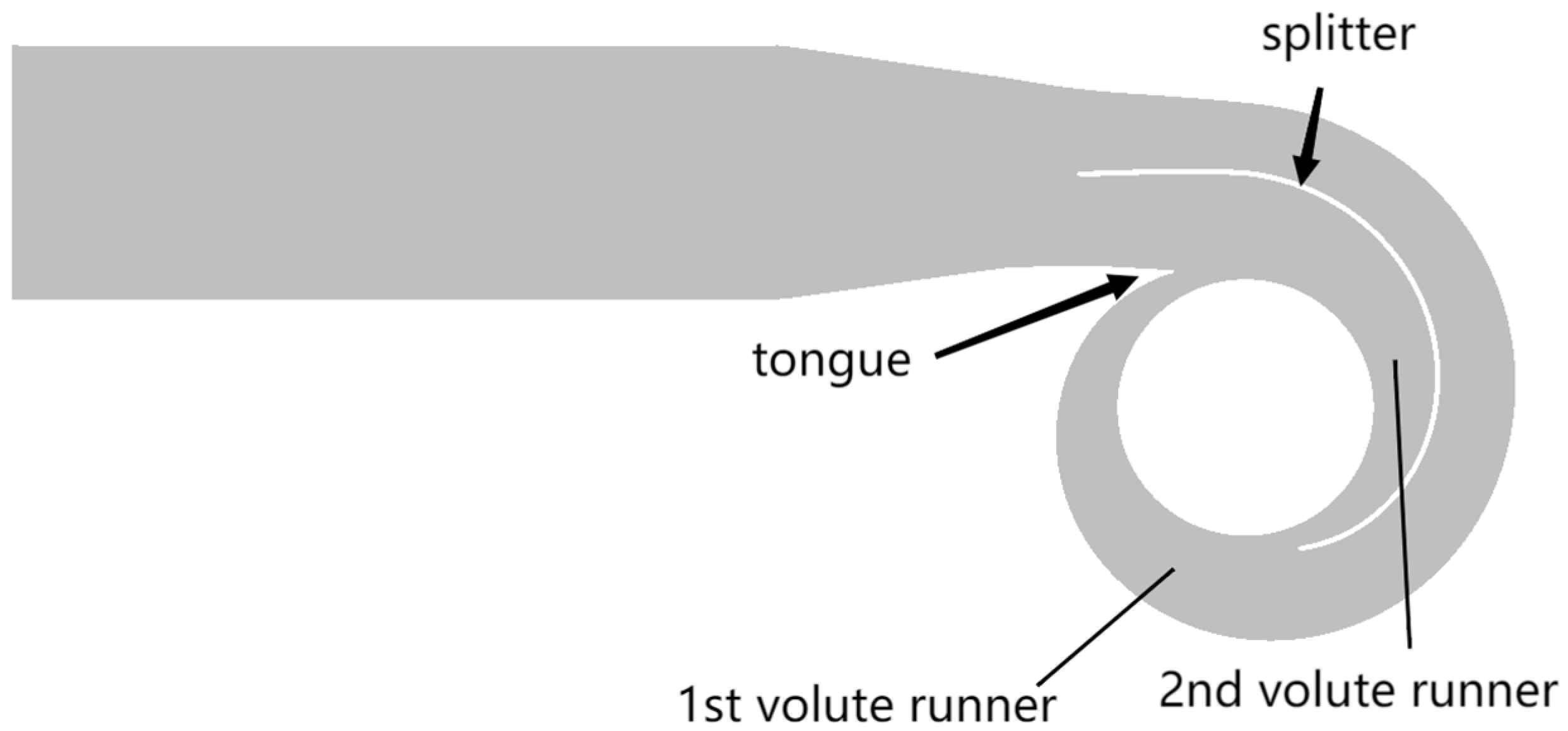
- For the double-volute centrifugal pump, not only the dynamic and static interference of the tongue, but also the dynamic and static interference at the splitter will cause certain changes in the internal flow regime of the centrifugal pump. Because the second volute runner is shorter and narrower than the first volute runner, the high-speed area located in the second volute runner will be larger than that of the first volute runner.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, X.; Yuan, S.; Zhang, J. Effects of spiral volute type on performance of high specific speed centrifugal pump. J. Drain. Irrig. Mach. Eng. 2017, 35, 25–31. [Google Scholar]
- Zhang, Z.; Wang, F.; Yao, Z.; Xiao, R. Effect of Double-Volute Casing on Impeller Radial Force for a Large Double-Suction Centrifugal Pump. In Fluids Engineering Division Summer Meeting; American Society of Mechanical Engineers: New York, NY, USA, 2015; Volume 57212, p. V001T33A016. [Google Scholar]
- Li, Q.; Zhang, R.; Xu, H. Effects of volute structure on energy performance and rotor operational stability of molten salt pumps. J. Appl. Fluid Mech. 2023, 16, 1615–1626. [Google Scholar]
- Shim, H.S.; Kim, K.Y. Numerical investigation on hydrodynamic characteristics of a centrifugal pump with a double volute at off-design conditions. Int. J. Fluid Mach. Syst. 2017, 10, 218–226. [Google Scholar] [CrossRef]
- Shim, H.S.; Afzal, A.; Kim, K.Y.; Jeong, H.S. Three-objective optimization of a centrifugal pump with double volute to minimize radial thrust at off-design conditions. Proc. Inst. Mech. Eng. Part A J. Power Energy 2016, 230, 598–615. [Google Scholar] [CrossRef]
- Khalifa, A.E.; Al-Qutub, A.M.; Ben-Mansour, R. Study of pressure fluctuations and induced vibration at blade-passing frequencies of a double volute pump. Arab. J. Sci. Eng. 2011, 36, 1333–1345. [Google Scholar] [CrossRef]
- Xiao, R.; Lu, T.; Wang, F. Influence of rib structure in double-volute centrifugal pumps on the impeller radial force. Nongye Jixie Xuebao (Trans. Chin. Soc. Agric. Mach.) 2011, 42, 85–88. [Google Scholar]
- Yang, J.; Zhou, R.; Chen, H.; Yu, T. Transient flow characteristics and pressure pulsation characteristics at splitter of double-volute centrifugal pump during startup. J. Jiangsu Univ. (Nat. Sci. Ed.) 2021, 42, 278–283. [Google Scholar]
- Yang, M.; Min, S.M.; Wang, F.J. Numerical simulation of pressure fluctuation and radial force in a double volute pump. Trans. Chin. Soc. Agric. Mach. 2009, 40, 83–88. [Google Scholar]
- Tsukamoto, H.; Ohashi, H. Transient Characteristics of a Centrifugal Pump During Starting Period. J. Fluids Eng. 1982, 104, 6–13. [Google Scholar] [CrossRef]
- Tsukamoto, H.; Matsunaga, S.; Yoneda, H.; Hata, S. Transient Characteristics of a Centrifugal Pump During Stopping Period. J. Fluids Eng. 1986, 108, 392–399. [Google Scholar] [CrossRef]
- Chalghoum, I.; Elaoud, S.; Akrout, M.; Taieb, E.H. Transient behavior of a centrifugal pump during starting period. Appl. Acoust. 2016, 109, 82–89. [Google Scholar] [CrossRef]
- Tanaka, T.; Takatsu, N. Transient Characteristics of a Centrifugal Pump at Rapid Startup; IOP Publishing Ltd.: Bristol, UK, 2019; Volume 240, p. 052016. [Google Scholar]
- Zhou, D.; Zhong, L.; Zheng, Y.; Mao, Y. Numerical simulation of transient flow in axial-flow pump unit model during runaway caused from power failure. J. Drain. Irrig. Mach. Eng./Paiguan Jixie Gongcheng Xuebao 2012, 30, 401–406. [Google Scholar]
- Wang, W.; Guo, H.; Zhang, C.; Shen, J.; Pei, J.; Yuan, S. Transient characteristics of PAT in micro pumped hydro energy storage during abnormal shutdown process. Renew. Energy 2023, 209, 401–412. [Google Scholar] [CrossRef]
- Wang, W.; Guo, H.; Zhang, C.; Shen, J.; Pei, J.; Yuan, S. Experimental investigation on pressure fluctuation characteristics of a mixed-flow pump as turbine at turbine and runaway conditions. J. Energy Storage 2022, 55, 105562. [Google Scholar] [CrossRef]
- Feng, J.; Ge, Z.; Zhang, Y.; Zhu, G.; Wu, G.; Lu, J.; Luo, X. Numerical investigation on characteristics of transient process in centrifugal pumps during power failure. Renew. Energy 2021, 170, 267–276. [Google Scholar] [CrossRef]
- Dong, W.; Fan, X.; Dong, Y.; He, F. Transient Internal Flow Characteristics of Centrifugal Pump During Rapid Start-Up. Iran. J. Sci. Technol. Trans. Mech. Eng. 2023. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Zhu, Z.C.; Cui, B.L.; Li, Y.; Tao, R.H. Numerical simulation of unsteady flow in centrifugal pump during stopping period. J. Eng. Thermophys. 2012, 33, 2096–2099. [Google Scholar]
- Kan, K.; Zheng, Y.; Chen, H.; Zhou, D.; Dai, J.; Binama, M.; Yu, A. Numerical simulation of transient flow in a shaft extension tubular pump unit during runaway process caused by power failure. Renew. Energy 2020, 154, 1153–1164. [Google Scholar] [CrossRef]
- Walseth, E.C.; Nielsen, T.K.; Svingen, B. Measuring the dynamic characteristics of a low specific speed pump—Turbine model. Energies 2016, 9, 199. [Google Scholar] [CrossRef]
- Ye, C.; Tang, Y.; An, D.; Wang, F.; Zheng, Y.; van Esch, B.P.M. Investigation on stall characteristics of marine centrifugal pump considering transition effect. Ocean Eng. 2023, 280, 114823. [Google Scholar] [CrossRef]
- Kan, K.; Xu, Z.; Chen, H.; Xu, H.; Zheng, Y.; Zhou, D.; Muhirwa, A.; Maxime, B. Energy loss mechanisms of transition from pump mode to turbine mode of an axial-flow pump under bidirectional conditions. Energy 2022, 257, 124630. [Google Scholar] [CrossRef]
- Wang, G.; Wang, B.; Wen, J.; Tian, R.; Niu, Z.; Liu, X. Experimental study on the hydraulic characteristics of inertia tank after the failure of pump power. Ann. Nucl. Energy 2021, 151, 107885. [Google Scholar] [CrossRef]
- Yang, F.; Liu, C.; Tang, F.P.; Zhou, J.R. Experimental Study on Runaway Characteristics of Pump System; IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2013; Volume 52, p. 022021. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Mao, J.Y.; Yuan, S.Q.; Pei, J.; Zhang, J.F.; Wang, W.J. Applications of Different Turbulence Models in Simulations of a Large Annular Volute-Type Pump with the Diffuser; IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2014; Volume 22, p. 022019. [Google Scholar]
- Fu, S.; Zheng, Y.; Kan, K.; Chen, H.; Han, X.; Liang, X.; Liu, H.; Tian, X. Numerical simulation and experimental study of transient characteristics in an axial flow pump during start-up. Renew. Energy 2020, 146, 1879–1887. [Google Scholar] [CrossRef]
- IEC 60193; Hydraulic Turbines, Storage Pumps and Pump-Turbines-Model Acceptance Tests. IEC: Geneva, Switzerland, 2019.



| Parameter Name | Numerical Value |
|---|---|
| Design flow rate, Qd (m3/s) | 0.321 |
| Design head, Hd (m) | 40.3 |
| Design rotational speed, Nd (r/min) | 1480 |
| Specific speed, ns | 191.3 |
| Impeller inlet diameter, D1 (mm) | 283.7 |
| Impeller outlet diameter, D2 (mm) | 399.8 |
| Number of impeller blades, Z1 | 6 |
| Component Name | Intake Pipe | Impeller | Double Volute | Outlet Pipe |
|---|---|---|---|---|
| Number of grid cells | 921,713 | 3,571,714 | 3,563,816 | 145,405 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, L.; Ren, Z.; Wang, Z.; Zhou, W.; Li, S.; Dai, J.; Yang, C.; Dang, M. A Study on the Transient Characteristics of the Power-Off Transition Process of a Double-Volute Centrifugal Pump. Water 2024, 16, 1707. https://doi.org/10.3390/w16121707
Lu L, Ren Z, Wang Z, Zhou W, Li S, Dai J, Yang C, Dang M. A Study on the Transient Characteristics of the Power-Off Transition Process of a Double-Volute Centrifugal Pump. Water. 2024; 16(12):1707. https://doi.org/10.3390/w16121707
Chicago/Turabian StyleLu, Lifeng, Ziwei Ren, Zhongzan Wang, Wenjie Zhou, Siwei Li, Jin Dai, Chunxia Yang, and Mengfan Dang. 2024. "A Study on the Transient Characteristics of the Power-Off Transition Process of a Double-Volute Centrifugal Pump" Water 16, no. 12: 1707. https://doi.org/10.3390/w16121707
APA StyleLu, L., Ren, Z., Wang, Z., Zhou, W., Li, S., Dai, J., Yang, C., & Dang, M. (2024). A Study on the Transient Characteristics of the Power-Off Transition Process of a Double-Volute Centrifugal Pump. Water, 16(12), 1707. https://doi.org/10.3390/w16121707






