Dam Deformation Prediction Model Based on Multi-Scale Adaptive Kernel Ensemble
Abstract
1. Introduction
2. The Measured Data of the Dam Are Decomposed and Denoised
2.1. The CEEDMAN Method Is Employed for Decomposing Dam Data and Noise Reduction Purposes
- (1)
- Gaussian white noise is added to the signal (dam deformation) y(t) to obtain a new signal , and the new signal is decomposed by EMD to obtain the first-order intrinsic mode component C1.
- (2)
- By integrating and averaging the obtained multiple modal components, the first intrinsic mode function (IMF) in the CEEMDAN decomposition process is obtained:
- (3)
- The residual signal is obtained by subtracting the IMF from the original signal:
- (4)
- A new signal is obtained by adding positive and negative pairs of Gaussian white noise to . The new signal is used as a carrier to perform EMD decomposition to obtain the first-order modal component . The second intrinsic modal component of CEEMDAN decomposition can be obtained:
- (5)
- By subtracting IMF2 from the above residuals, the quadratic residuals are obtained:
- (6)
- Repeat the above steps until the residual signal is a monotone function. At this time, the number of intrinsic mode components obtained is K, and the original signal is decomposed as follows:where is the ith eigenmode component obtained after EMD decomposition; The i th eigenmode component obtained by CEEMDAN decomposition is ; is a Gaussian white noise signal satisfying a standard normal distribution; is the number of times of adding white noise; is the signal-to-noise ratio of the noise relative to the original sequence; is the signal to be decomposed; and is the final residual.
CEEMDAN Computational Efficiency Analysis
2.2. Sample Entropy (SE)
- (1)
- The modal decomposition residual is processed into a time series with a length of N. According to the sequence number, the m-dimensional vector sequence is formed, {, …, }. Among them, , . These vectors represent continuous x values starting at the i th point [32].
- (2)
- Define the distance between vectors and as the absolute value of the maximum difference between their corresponding elements. That is,
- (3)
- For a given , count the number of () for which the distance between and is less than or equal to r, and denote it as . For , it is defined as
2.3. Partial Autocorrelation Function (PACF)
3. Construction of Kernel Extreme Learning Machine Model Based on Global Search Strategy to Optimize Whale Algorithm
3.1. The Global Search Whale Optimization Algorithm (GSWOA)
3.2. Kernel Extreme Learning Machine (KELM) Algorithm
3.3. The Specific Steps of GSWOA Optimizing KELM Model
4. Combined Forecasting Modeling
- (1)
- Data preprocessing: Standardize the monitoring point data to eliminate unit differences and reduce the impact of outliers.
- (2)
- CEEMDAN decomposition is performed on the processed data: The white noise level is configured, the noisy signal is augmented, and then the IMFs and residuals are extracted by EMD iteration. Ensemble averaging is performed to ensure the stability of the obtained IMFs.
- (3)
- Sample entropy optimization of decomposition data: The number of effective IMFs is determined by sample entropy to verify the integrity of the decomposition process.
- (4)
- PACF analysis of each IMF component: PACF is used to analyze the correlation between each IMF and historical data and select the appropriate feature vector for the model.
- (5)
- Optimization based on GSWOA: GSWOA is used to optimize the kernel function parameters and regularization coefficients of KELM. The optimization is to determine the optimal parameter set.
- (6)
- Parameterization of KELM model: The parameters optimized by GSWOA are applied to the KELM model, and the prediction model is finally established.
- (7)
- Model evaluation and verification: The prediction accuracy of the model is evaluated and verified on the test data set using statistical indicators such as mean square error (MSE) and determination coefficient (R2).
5. Case Analysis
5.1. Data Preprocessing: Constructing Model Feature Factors
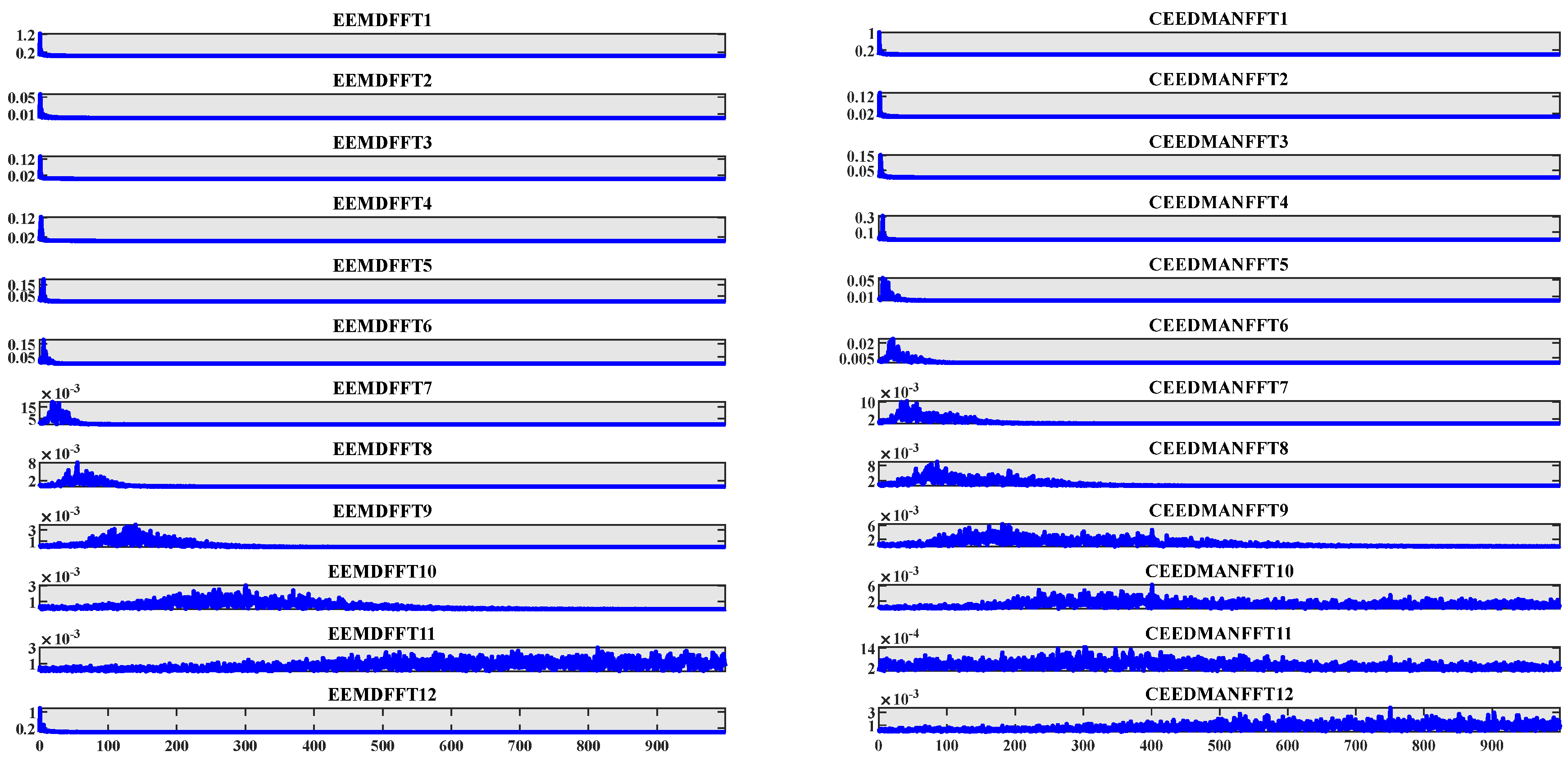
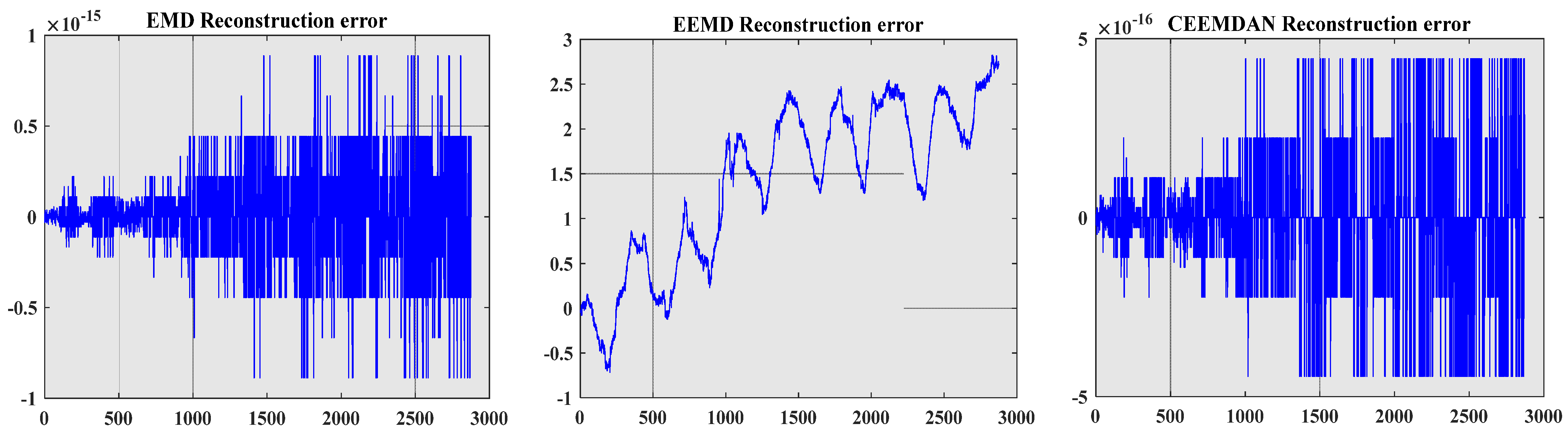
5.2. Comparative Analysis of Decomposition and Reconstruction Techniques
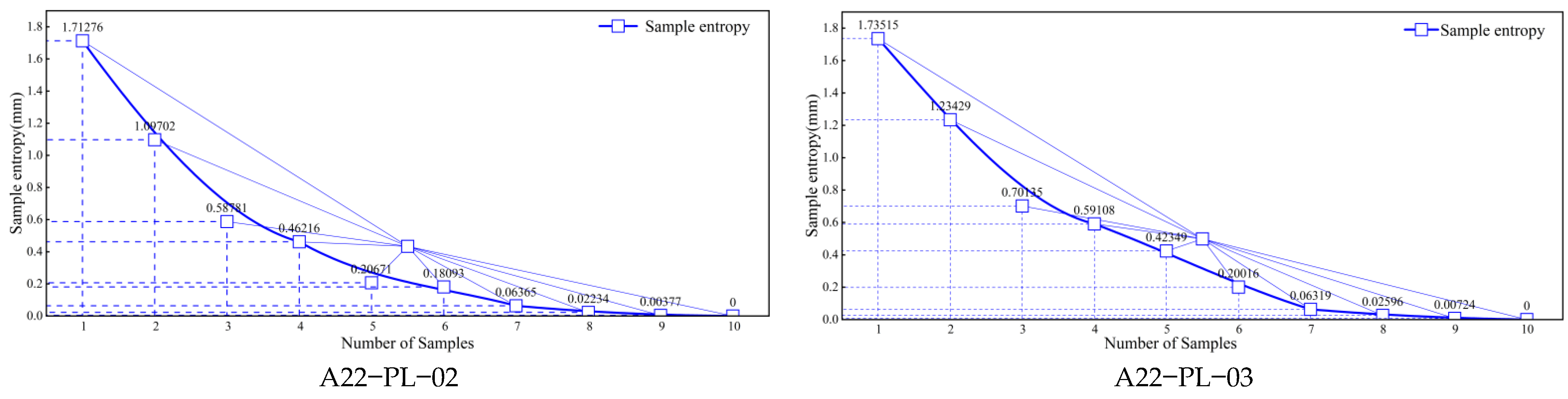
5.3. Analysis of the Results of Sample Entropy and CEEMDAN
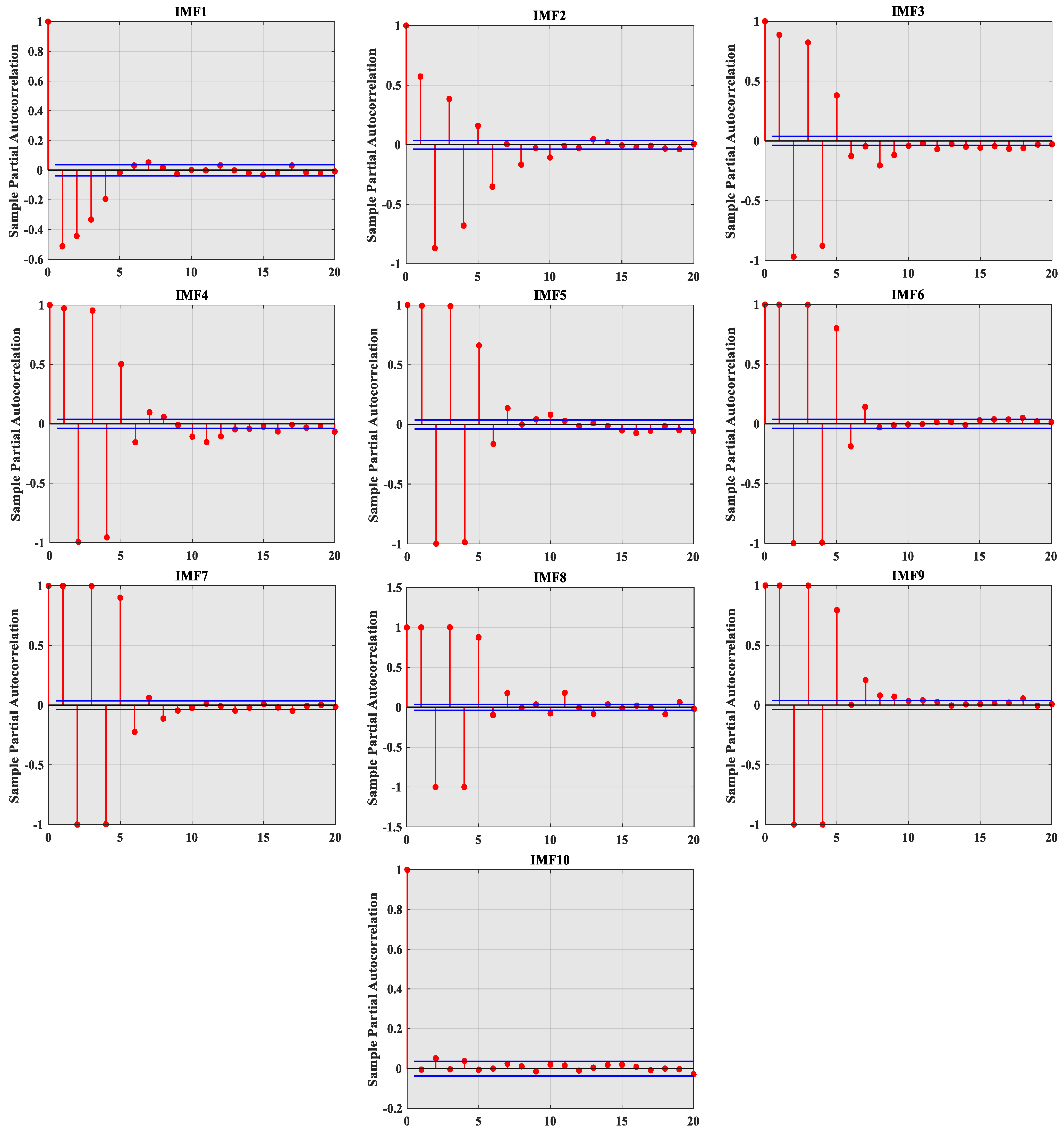
5.4. The Final Model Input Variables Are Determined by PACF Analysis
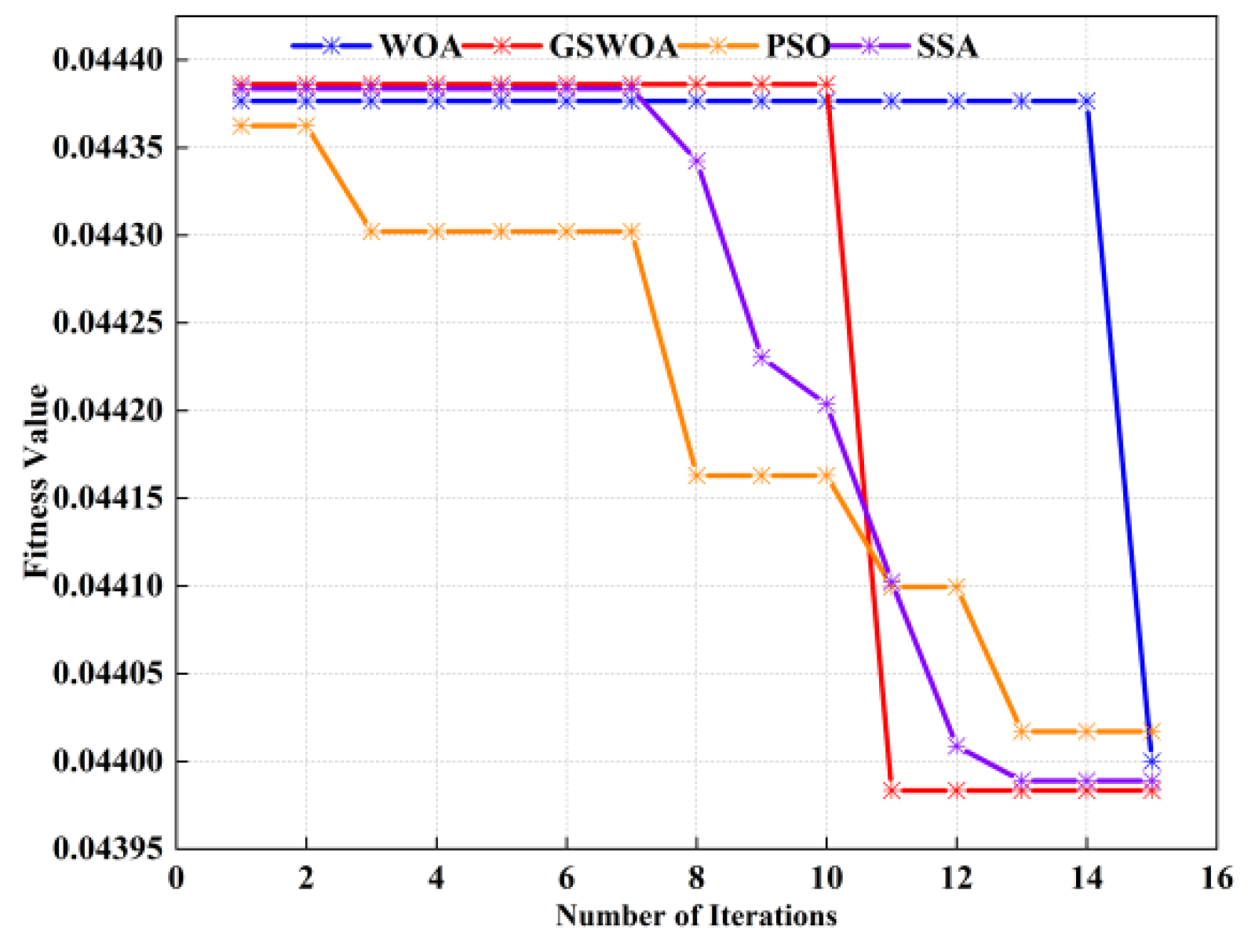
5.5. Selection of Kernel Functions and Comparative Analysis of GSWOA-KELM Models
5.6. Evaluate the Robustness and Computational Efficiency of the KELM Model
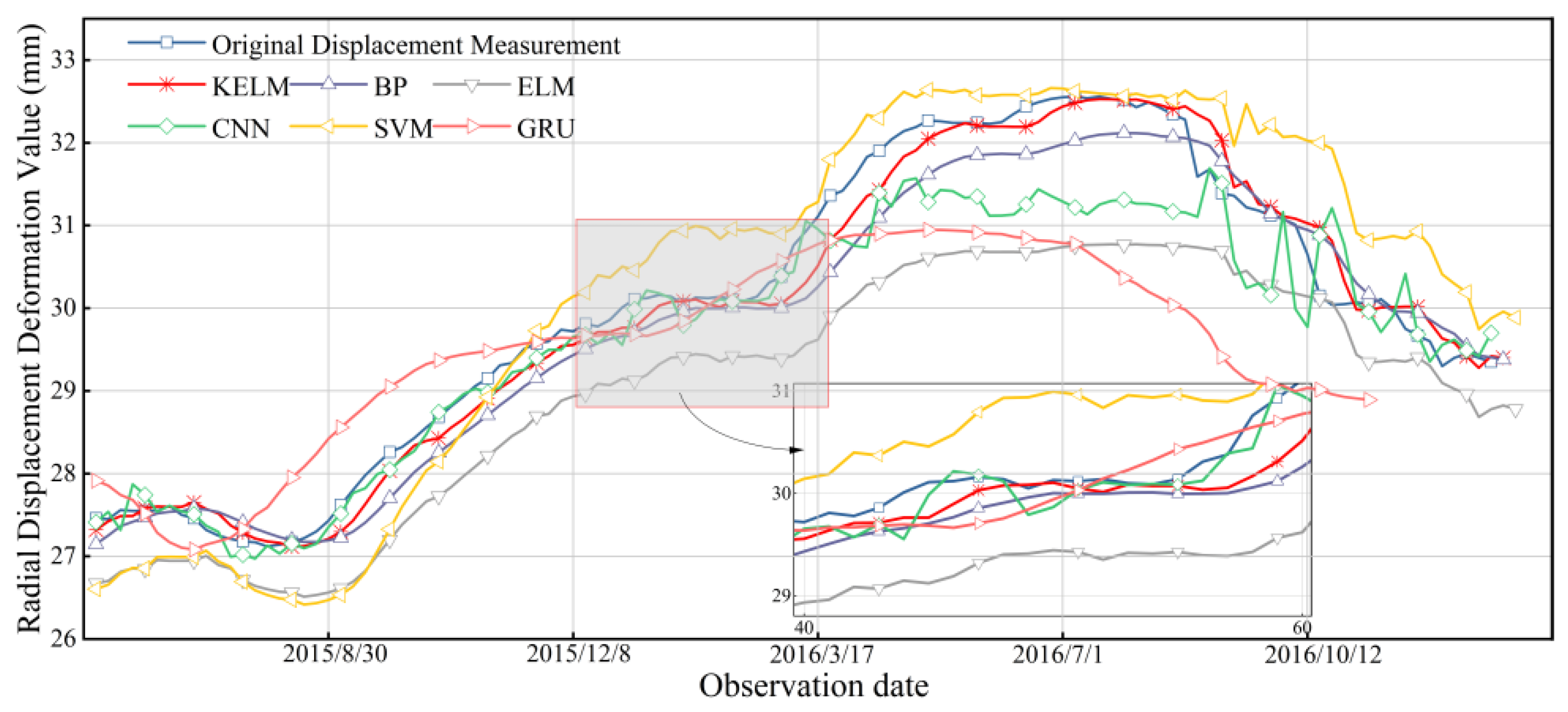
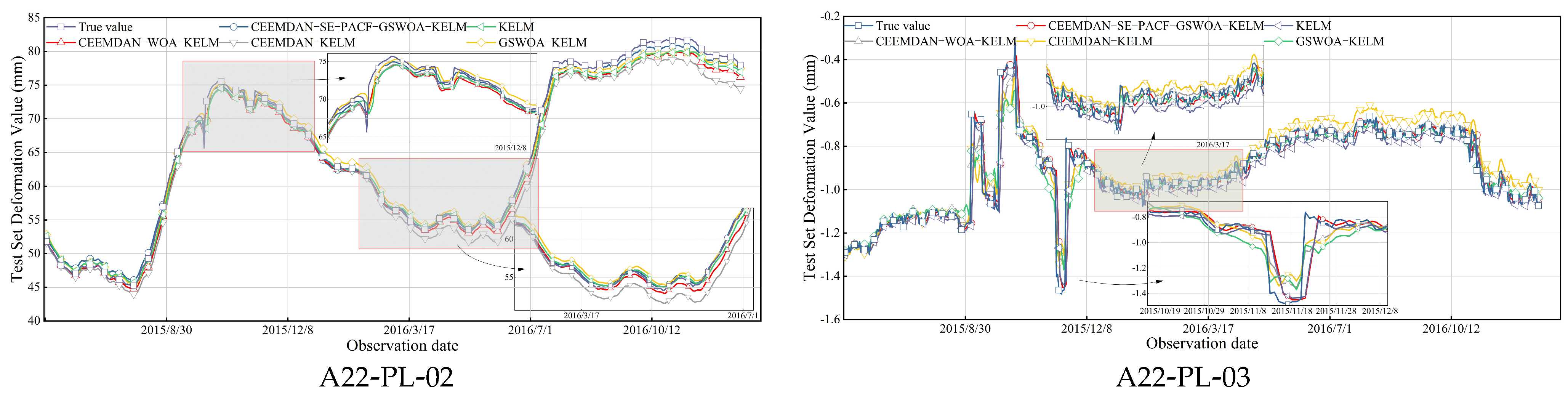
5.7. Deformation Prediction Results and Comparative Analysis
6. Conclusions
- (1)
- The CEEMDAN-SE-PACF-GSWOA-KELM model proposed in this paper has higher prediction accuracy than other models. In order to solve the nonlinear characteristics of the original data of the dam, this paper compares the CEEMDAN and EEMD methods and uses the reconstruction error and signal-to-noise ratio index. The results show that the CEEMDAN decomposition method is superior to EEMD in accurately decomposing dam signals, thereby improving the reliability of engineering decision-making in practical applications.
- (2)
- Effective management and maintenance of dams require reliable engineering decisions, including robust maintenance plans and monitoring strategies. In order to improve the accuracy of CEEMDAN decomposition, in this paper, SE and PACF are integrated into the CEEMDAN decomposition process, which is beneficial to filter noise more effectively and improve the quality of decomposition results. In addition, SE and PACF methods help to identify prominent signal features, thereby identifying and capturing key components and trends in the signal. Through the analysis of sample entropy and autocorrelation function, the frequency components and time series characteristics of the signal can be accurately determined so as to provide a more reliable basis for subsequent analysis and modeling work.
- (3)
- In order to construct a more effective prediction model, the GSWOA algorithm is used to optimize the parameters of the KELM model. At the same time, the effectiveness of the GSWOA algorithm is compared with the traditional algorithm, and the superior convergence characteristics of the GSWOA algorithm are revealed. In addition, in the final prediction comparison analysis, the prediction performance of the WOA-KELM and GSWOA-KELM models is juxtaposed, which shows the ability of the GSWOA algorithm to optimize the parameters of the KELM model and obtains better prediction results.
- (4)
- This paper aims to verify the robustness and computational efficiency of the KELM model by comparing it with several traditional prediction models. Through comparative analysis, the advantages of the KELM model are summarized as follows: a. Compared with the BP model, the KELM model usually avoids the local optimal problem by randomly initializing the feature weights, thereby reducing the possibility of converging to the suboptimal solution. b. Compared with the ELM model, the KELM model shows greater flexibility in random weight initialization between the input layer and the hidden layer, ensuring more consistent prediction performance. c. Compared with the SVM model, the KELM model has higher efficiency in dealing with high-dimensional data, because it does not need to explicitly calculate the kernel function or construct the kernel matrix. Therefore, compared with other traditional models, the robustness and computational efficiency of the KELM model have been verified to varying degrees.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gu, C.; Su, H.; Liu, H. Review of Research on Risk Analysis and Management of Dam Service. J. Water Resour. 2018, 49, 26–35. [Google Scholar] [CrossRef]
- Wu, Z. Theory and Method of Dam and Dam Foundation Safety Monitoring and Its Application. Jiangsu Sci. Technol. Inform. 2005, 12, 1–6. [Google Scholar]
- Huang, S. Analysis of Dam Deformation Monitoring Based on Statistical-Stepwise Regression Model. Water Resour. Sci. Econ. 2023, 29, 1–8. [Google Scholar]
- Su, H.; Li, X.; Yang, B.; Wen, Z. Wavelet Support Vector Machine-Based Prediction Model of Dam Deformation. Mech. Syst. Signal Process. 2018, 110, 412–427. [Google Scholar] [CrossRef]
- Xing, Y.; Chen, Y.; Huang, S.; Wang, P.; Xiang, Y. Research on Dam Deformation Prediction Model Based on Optimized SVM. Processes 2022, 10, 1842. [Google Scholar] [CrossRef]
- Ren, Q.; Li, M.; Song, L.; Liu, H. An Optimized Combination Prediction Model for Concrete Dam Deformation Considering Quantitative Evaluation and Hysteresis Correction. Adv. Eng. Inform. 2020, 46, 101154. [Google Scholar] [CrossRef]
- Wei, B.; Chen, L.; Li, H.; Yuan, D.; Wang, G. Optimized Prediction Model for Concrete Dam Displacement Based on Signal Residual Amendment. Appl. Math. Modell. 2020, 78, 20–36. [Google Scholar] [CrossRef]
- Dai, B.; Gu, H.; Zhu, Y.; Chen, S.; Rodriguez, E.F. On the Use of an Improved Artificial Fish Swarm Algorithm-Backpropagation Neural Network for Predicting Dam Deformation Behavior. Complexity 2020, 2020, 5463893. [Google Scholar] [CrossRef]
- Kang, F.; Liu, J.; Li, J.; Li, S. Concrete Dam Deformation Prediction Model for Health Monitoring Based on Extreme Learning Machine. Struct. Control Health Monit. 2017, 24, e1997. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, W.; Li, Y.; Wen, L.; Sun, X. AF-OS-ELM-MVE: A New Online Sequential Extreme Learning Machine of Dam Safety Monitoring Model for Structure Deformation Estimation. Adv. Eng. Inform. 2024, 60, 102345. [Google Scholar] [CrossRef]
- Cao, E.; Bao, T.; Liu, Y.; Li, H.; Yuan, R.; Hu, S. A Data Enhancement-Based Quadratic Imputation Framework for Consecutive Missing Values Considering Spatiotemporal Characteristics of Dam Deformation. J. Civ. Struct. Health Monit. 2024, 14, 431–447. [Google Scholar] [CrossRef]
- Ou, B.; Wu, B.; Yuan, J.; Li, S. Concrete Dam Deformation Prediction Model Based on LSTM. Adv. Water Resour. Hydropower Sci. Technol. 2022, 42, 21–26. [Google Scholar]
- Cai, S.; Gao, H.; Zhang, J.; Peng, M. A Self-Attention-LSTM Method for Dam Deformation Prediction Based on CEEMDAN Optimization. Appl. Soft Comput. 2024, 159, 111615. [Google Scholar] [CrossRef]
- Cao, E.; Bao, T.; Yuan, R.; Hu, S. Hierarchical Prediction of Dam Deformation Based on Hybrid Temporal Network and Load-Oriented Residual Correction. Eng. Struct. 2024, 308, 117949. [Google Scholar] [CrossRef]
- Zhang, C.; Fu, S.; Ou, B.; Liu, Z.; Hu, M. Prediction of Dam Deformation Using SSA-LSTM Model Based on Empirical Mode Decomposition Method and Wavelet Threshold Noise Reduction. Water 2022, 14, 3380. [Google Scholar] [CrossRef]
- Wei, Y.; Li, Q.; Hu, Y.; Wang, Y.; Zhu, X.; Tan, Y.; Liu, C.; Pei, L. Deformation Prediction Model Based on an Improved CNN + LSTM Model for the First Impoundment of Super-High Arch Dams. J. Civil Struct. Health Monit. 2023, 13, 431–442. [Google Scholar] [CrossRef]
- Zhang, S.; Zheng, D.; Liu, Y. Deformation Prediction System of Concrete Dam Based on IVM-SCSO-RF. Water 2022, 14, 3739. [Google Scholar] [CrossRef]
- Liu, M.; Wen, Z.; Zhou, R.; Su, H. Bayesian Optimization and Ensemble Learning Algorithm Combined Method for Deformation Prediction of Concrete Dam. Structures 2023, 54, 981–993. [Google Scholar] [CrossRef]
- Lin, C.; Zou, Y.; Lai, X.; Wang, X.; Su, Y. Variation Trend Prediction of Dam Displacement in the Short-Term Using a Hybrid Model Based on Clustering Methods. Appl. Sci. 2023, 13, 10827. [Google Scholar] [CrossRef]
- Xu, B.; Chen, Z.; Wang, X.; Bu, J.; Zhu, Z.; Zhang, H.; Wang, S.; Lu, J. Combined Prediction Model of Concrete Arch Dam Displacement Based on Cluster Analysis Considering Signal Residual Correction. Mech. Syst. Signal Process. 2023, 203, 110721. [Google Scholar] [CrossRef]
- Tang, Y.; Yang, M.; Li, B.; Guo, J.; Chen, Y. A Two-Stage Dam Deformation Prediction Model Based on Deep Learning. China’s Rural. Water Conserv. Hydropower 2024, 16, 225–230+237. [Google Scholar]
- Cao, E.; Bao, T.; Gu, C.; Li, H.; Liu, Y.; Hu, S. A Novel Hybrid Decomposition—Ensemble Prediction Model for Dam Deformation. Appl. Sci. 2020, 10, 5700. [Google Scholar] [CrossRef]
- Jiang, P.; Qi, H.; Li, T. Application of IF-KELM Model in Deformation Prediction of Concrete Arch Dam. Hydropower 2023, 49, 96–100. [Google Scholar]
- Zhou, L.; Xu, C.; Yuan, Z.; Lu, T. Dam Deformation Prediction Based on CEEMDAN-PSR-KELM. Peoples Yellow River 2019, 41, 138–141+145. [Google Scholar] [CrossRef]
- Xu, G.; Lu, Y.; Jing, Z.; Wu, C.; Zhang, Q. IEALL: Dam Deformation Prediction Model Based on Combination Model Method. Appl. Sci. 2023, 13, 5160. [Google Scholar] [CrossRef]
- Wu, Z.H.; Huang, N.E. Ensemble Empirical Mode Decomposition: A Noise Assisted Data Analysis Method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A Complete Ensemble Empirical Mode Decomposition with Adaptive Noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011. [Google Scholar]
- Qin, Z.; Chen, H.; Chang, J. Signal-to-Noise Ratio Enhancement Based on Empirical Mode Decomposition in Phase-Sensitive Optical Time Domain Reflectometry Systems. Sensors 2017, 17, 1870. [Google Scholar] [CrossRef]
- Dang, J.; Li, J.; Jia, R.; Fan, P. Noise Reduction of Hydropower Unit Vibration Signals Based on EMD Continuous Geometric Distribution. J. Hydropower Gener. 2020, 39, 46–54. [Google Scholar] [CrossRef]
- Zhao, H.; Hua, H.; Wang, H.; Yue, Y. Short-Term Wind Power Interval Prediction Based on LCD-SE-IWOA-KELM. Electr. Meas. Instrum. 2020, 57, 77–83. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological Time-Series Analysis Using Approximate Entropy and Sample Entropy. Am. J. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef]
- Weiß, C.H.; Aleksandrov, B.; Faymonville, M.; Jentsch, C. Partial Autocorrelation Diagnostics for Count Time Series. Entropy 2023, 25, 105. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Wen, Z.; Su, H. Deformation Prediction Based on Denoising Techniques and Ensemble Learning Algorithms for Concrete Dams. Expert Syst. Appl. 2024, 238 Pt C, 122022. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Oliva, D.; Abd El Aziz, M.; Hassanien, A.E. Parameter Estimation of Photovoltaic Cells Using an Improved Chaotic Whale Optimization Algorithm. Appl. Energy 2017, 200, 141–154. [Google Scholar] [CrossRef]
- Liu, L.; Bai, K.; Dan, Z.; Zhang, S.; Liu, Z. A Whale Optimization Algorithm for Global Search Strategy. Small Microcomput. Syst. 2020, 41, 1820–1825. [Google Scholar]
- Yang, T.; Li, W.; Huang, Z.; Peng, L.; Yang, J. Short-Term Prediction of Wind Power Generation Based on VMD-GSWOA-LSTM Model. AIP Adv. 2023, 13, 085215. [Google Scholar] [CrossRef]
- Liu, X.; Kang, F.; Ma, C.; Li, H. Concrete Arch Dam Behavior Prediction Using Kernel-Extreme Learning Machines Considering Thermal Effect. J. Civil Struct. Health Monit. 2021, 11, 283–299. [Google Scholar] [CrossRef]
- Ou, B.; Zhang, C.; Xu, B.; Fu, S.; Liu, Z.; Wang, K. Innovative Approach to Dam Deformation Analysis: Integration of VMD, Fractal Theory, and WOA-DELM. Struct. Control Health Monit. 2024, 1710019. [Google Scholar] [CrossRef]




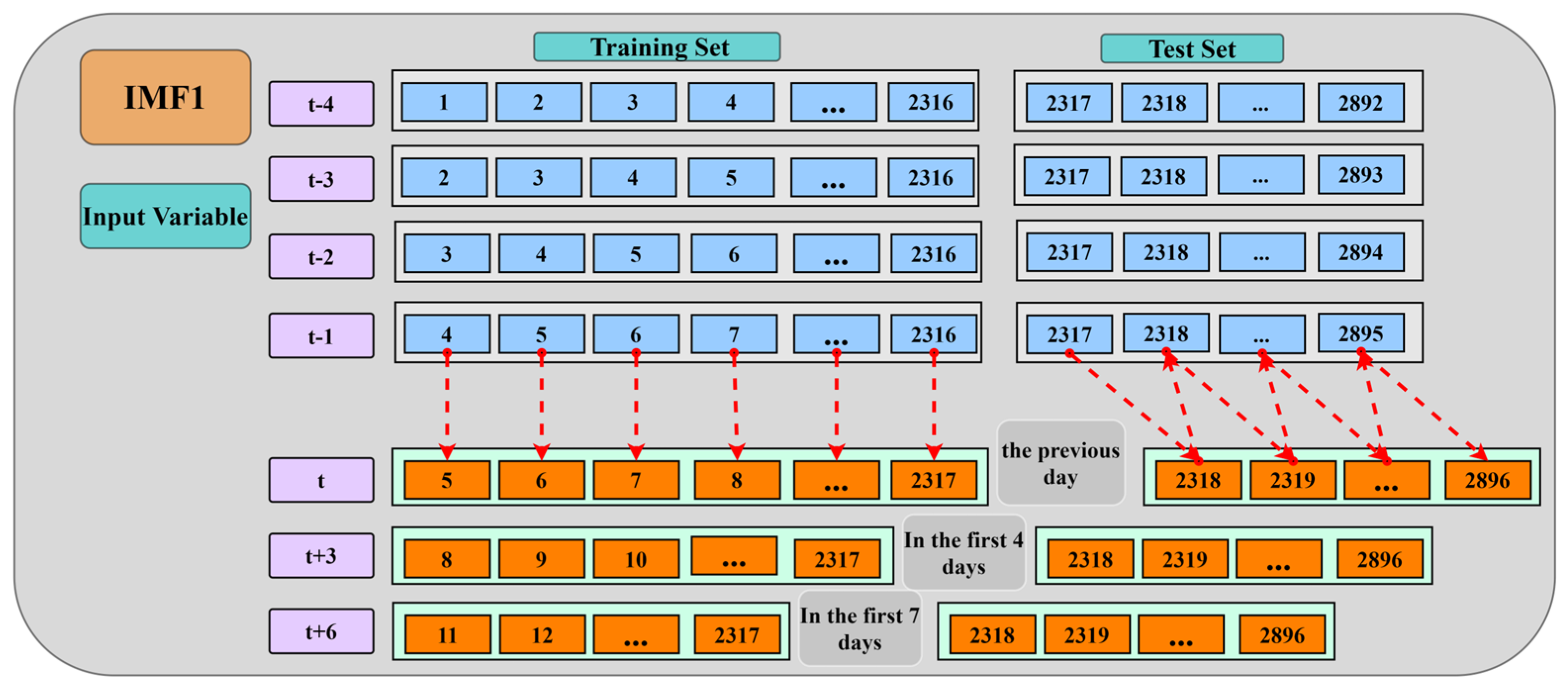


| Modal Component | Number of Inputs | Input Variable |
|---|---|---|
| IMF1 | 4 | |
| IMF2 | 8 | |
| IMF3 | 7 | |
| IMF4 | 10 | |
| IMF5 | 7 | |
| IMF6 | 7 | |
| IMF7 | 8 | |
| IMF8 | 8 | |
| IMF9 | 6 | |
| IMF10 | 1 |
| algorithm parameters | GSWOA | WOA | PSO | SSA |
| whale population = 15 | whale population = 15 | Population size = 15 | population size = 15 | |
| dimensional = 2 | dimensional = 2 | inertia weight w = 0.8 | proportion of investigators = 20% | |
| lower limit LB = [0, 1] | lower limit LB = [0, 1] | iteration speed range = [−5 × 102, 5 × 102] | percentage of discoverers = 70% | |
| upper limit UB = [1, 1000] | upper limit UB = [1, 1000] | study factor c1, c2 = 1.5 | proportion of participants = 10% | |
| iterations MaxI = 15 | iterations MaxI = 15 | iterations MaxI = 15 | iterations MaxI = 15 |
| Model | RMSE/mm | MSE/mm2 | R2 | MAE/mm |
|---|---|---|---|---|
| KELM | 0.1730 | 0.0299 | 0.9905 | 0.1243 |
| BP | 0.3437 | 0.1181 | 0.9626 | 0.2873 |
| ELM | 1.0239 | 1.0484 | 0.6718 | 0.9367 |
| CNN | 0.6073 | 0.3688 | 0.8818 | 0.4216 |
| SVM | 0.6543 | 0.4164 | 0.8697 | 0.5743 |
| GRU | 0.9479 | 0.8986 | 0.6467 | 0.8179 |
| Model | Average Execution Time/s |
|---|---|
| KELM | 4.31 |
| BP | 9.45 |
| ELM | 10.01 |
| CNN | 58.72 |
| SVM | 6.45 |
| GRU | 50.87 |
| Monitoring Point | Model | RMSE/mm | MSE/mm2 | R2 | MAE/mm |
|---|---|---|---|---|---|
| A22-PL-02 | CEEMDAN-SE-PACF-GSWOA-KELM | 0.6437 | 0.4144 | 0.9970 | 0.4476 |
| CEEMDAN-WOA-KELM | 1.2429 | 1.5447 | 0.9287 | 0.9999 | |
| GSWOA-KELM | 0.9777 | 0.9558 | 0.9491 | 0.8178 | |
| CEEMDAN-KELM | 1.9285 | 3.7190 | 0.8533 | 1.5885 | |
| KELM | 1.0472 | 1.0967 | 0.9321 | 0.8684 | |
| A22-PL-03 | CEEMDAN-SE-PACF-GSWOA-KELM | 0.0427 | 0.0018 | 0.9334 | 0.0288 |
| CEEMDAN-WOA-KELM | 0.0588 | 0.0031 | 0.9131 | 0.0303 | |
| GSWOA-KELM | 0.0699 | 0.0049 | 0.8638 | 0.0561 | |
| CEEMDAN-KELM | 0.0628 | 0.0043 | 0.8195 | 0.0502 | |
| KELM | 0.0717 | 0.0051 | 0.8568 | 0.0644 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, B.; Wang, Z.; Fu, S.; Chen, D.; Yin, T.; Gao, L.; Zhao, D.; Ou, B. Dam Deformation Prediction Model Based on Multi-Scale Adaptive Kernel Ensemble. Water 2024, 16, 1766. https://doi.org/10.3390/w16131766
Zhou B, Wang Z, Fu S, Chen D, Yin T, Gao L, Zhao D, Ou B. Dam Deformation Prediction Model Based on Multi-Scale Adaptive Kernel Ensemble. Water. 2024; 16(13):1766. https://doi.org/10.3390/w16131766
Chicago/Turabian StyleZhou, Bin, Zixuan Wang, Shuyan Fu, Dehui Chen, Tao Yin, Lanlan Gao, Dingzhu Zhao, and Bin Ou. 2024. "Dam Deformation Prediction Model Based on Multi-Scale Adaptive Kernel Ensemble" Water 16, no. 13: 1766. https://doi.org/10.3390/w16131766
APA StyleZhou, B., Wang, Z., Fu, S., Chen, D., Yin, T., Gao, L., Zhao, D., & Ou, B. (2024). Dam Deformation Prediction Model Based on Multi-Scale Adaptive Kernel Ensemble. Water, 16(13), 1766. https://doi.org/10.3390/w16131766








