Hydroelectric Unit Vibration Signal Feature Extraction Based on IMF Energy Moment and SDAE
Abstract
:1. Introduction
2. Integrating Multidimensional Information Features for State Recognition of Hydroelectric Units
2.1. IMF Energy Moment Feature Extraction Based on CEEMD
2.1.1. Complementary Ensemble Empirical Mode Decomposition
2.1.2. IMF Energy Moment
- Perform CEEMD processing on vibration signals to obtain n-order IMF components, and calculate the energy moments of each order of IMF component:
- 2.
- Calculate the total energy:
- 3.
- Normalize the energy moments of the IMF components and establish the feature vector :
2.2. Feature Extraction Based on Stacked Denoising Autoencoder
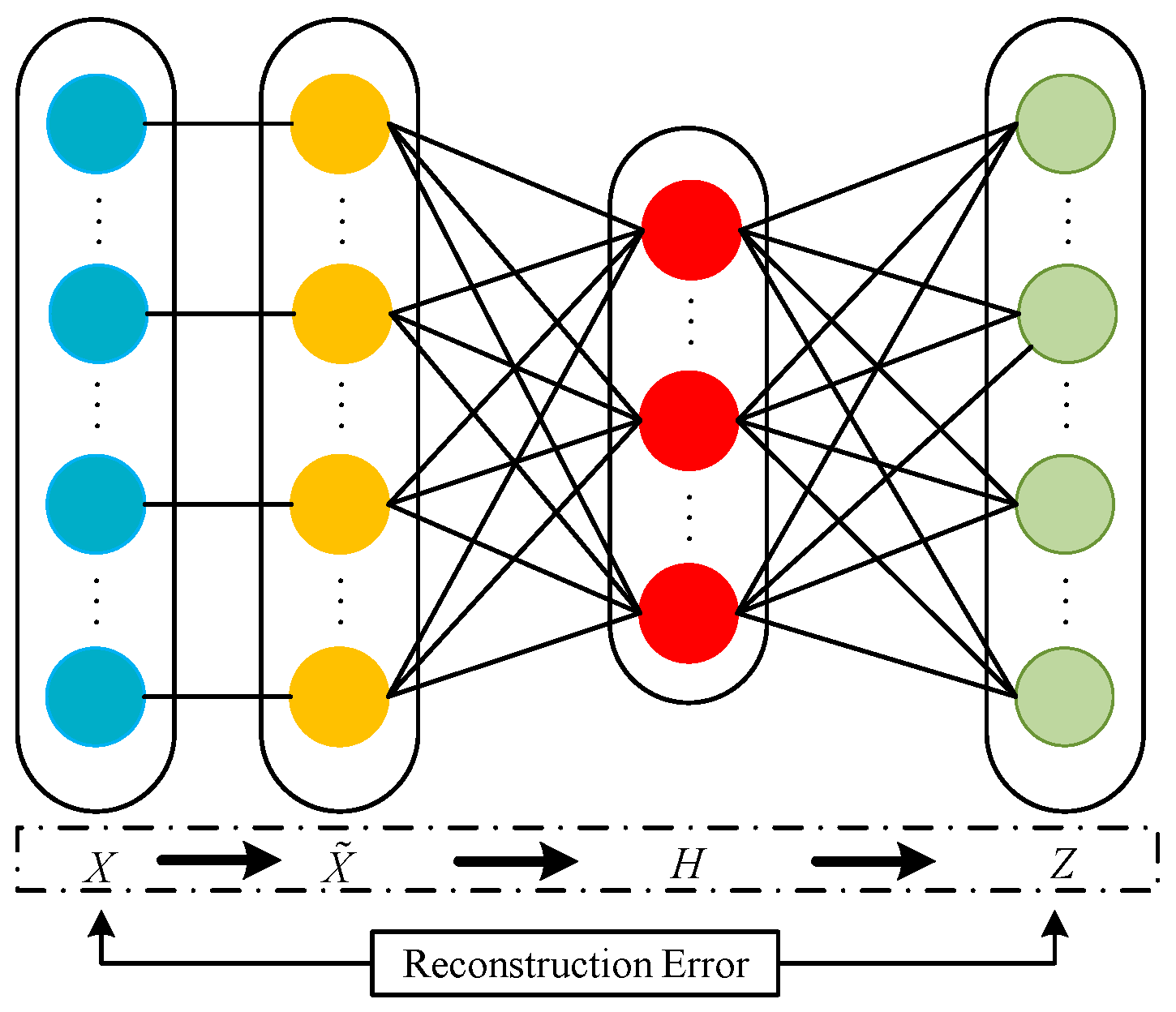
2.2.1. Autoencoder
2.2.2. Denoising Autoencoder
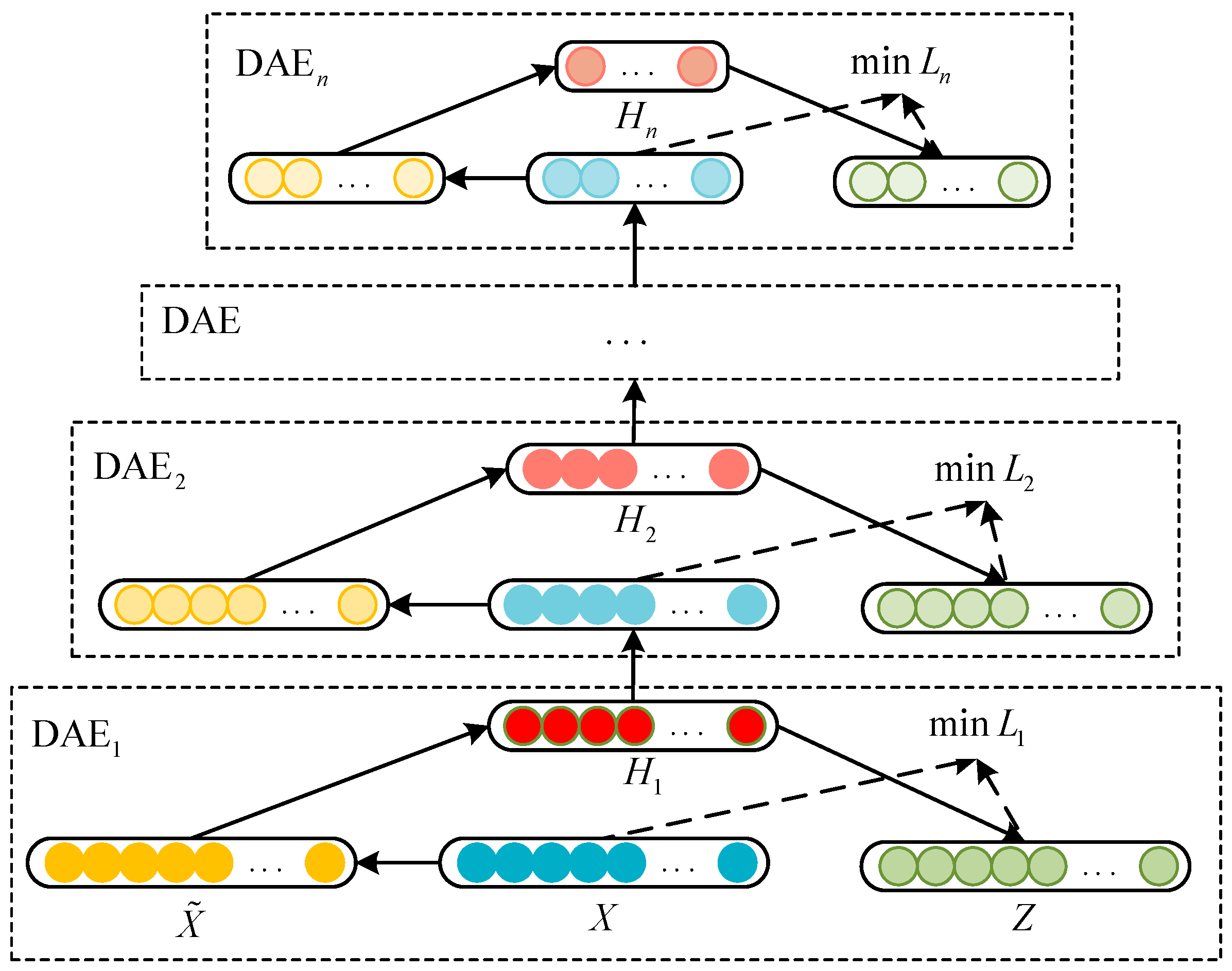
2.2.3. Construction of Stacked Noise Reduction Autoencoder Model
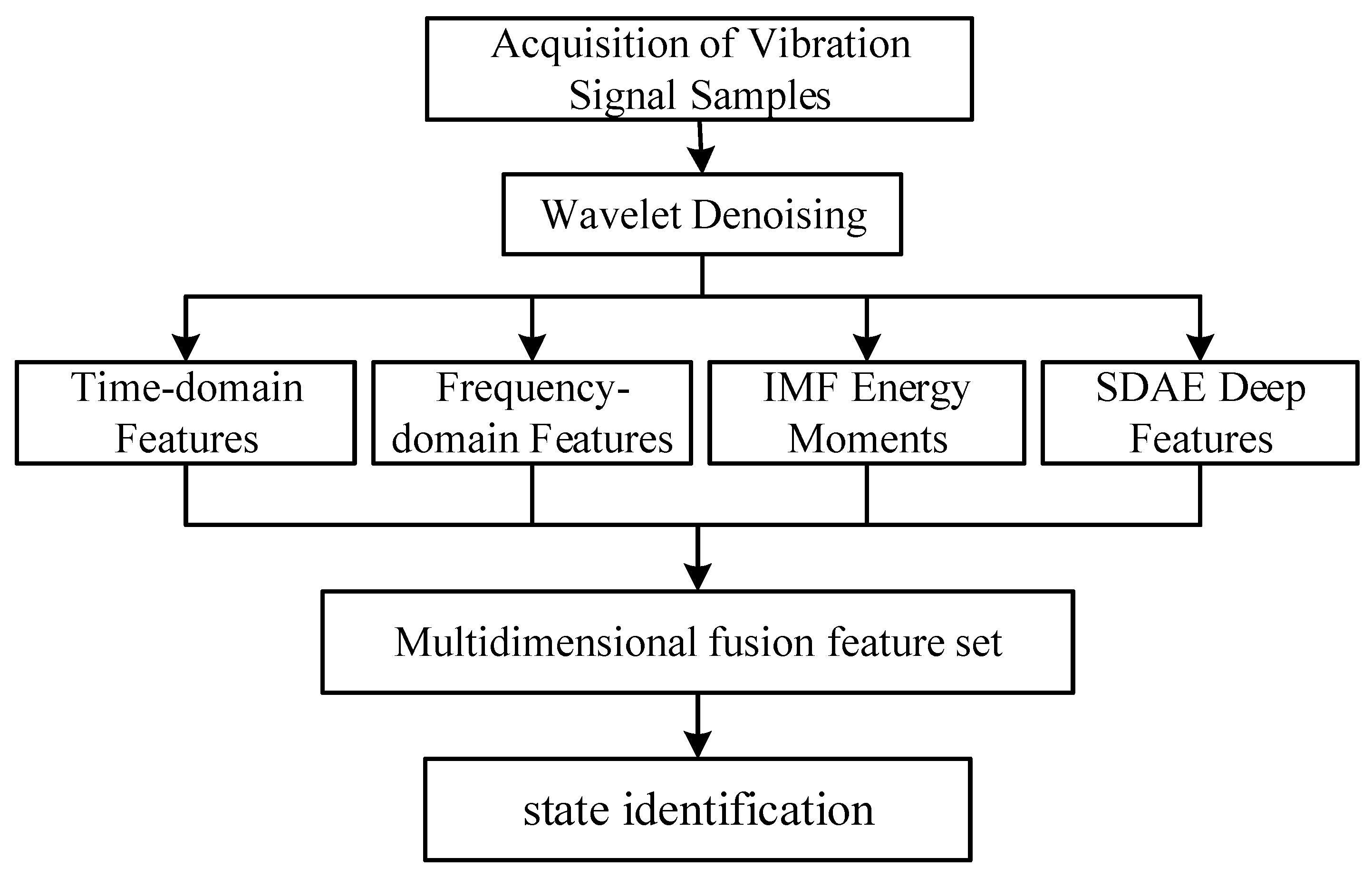
2.3. Hydropower Unit State Recognition Method Based on Multidimensional Information Fusion Features
- Based on the wavelet threshold denoising method, the vibration signal of hydroelectric units is preprocessed. The “db8” wavelet function is selected with three decomposition layers, and the number of decomposition layers is selected as three layers.
- Extract the time–domain features, frequency–domain features, IMF energy moments and SDAE deep features from the noise-canceled signal to construct a multidimensional fusion feature vector of the vibration signal.
- Learn and diagnose pattern categories based on the extracted multidimensional fusion feature vectors.
3. Verification and Analysis
3.1. Time–Domain and Frequency–Domain Feature Extraction
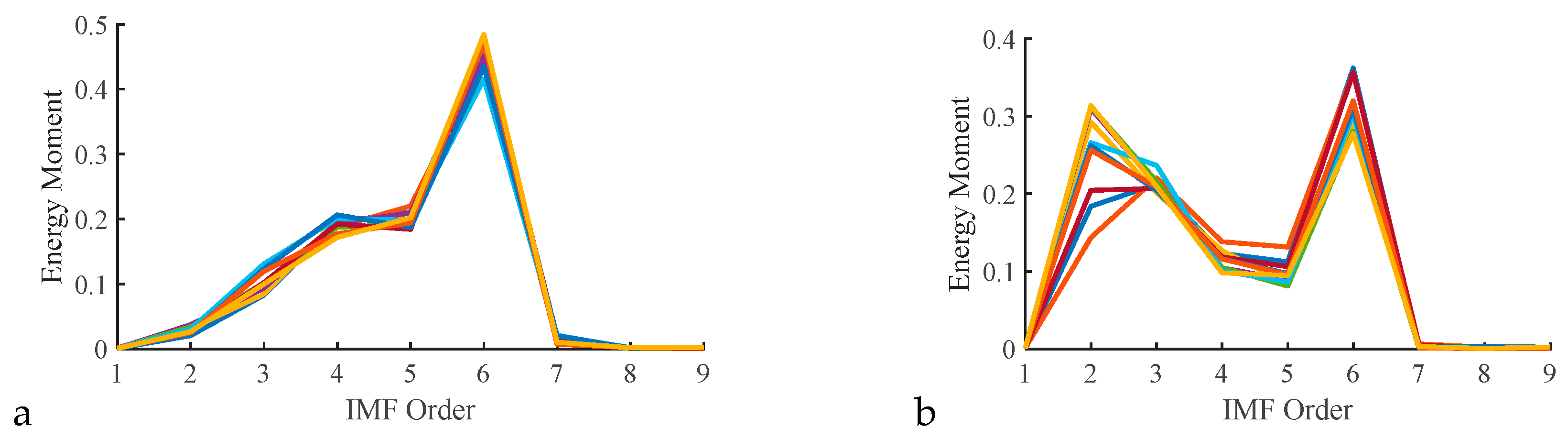
3.2. IMF Energy Moment Feature Extraction
3.3. SDAE Feature Extraction
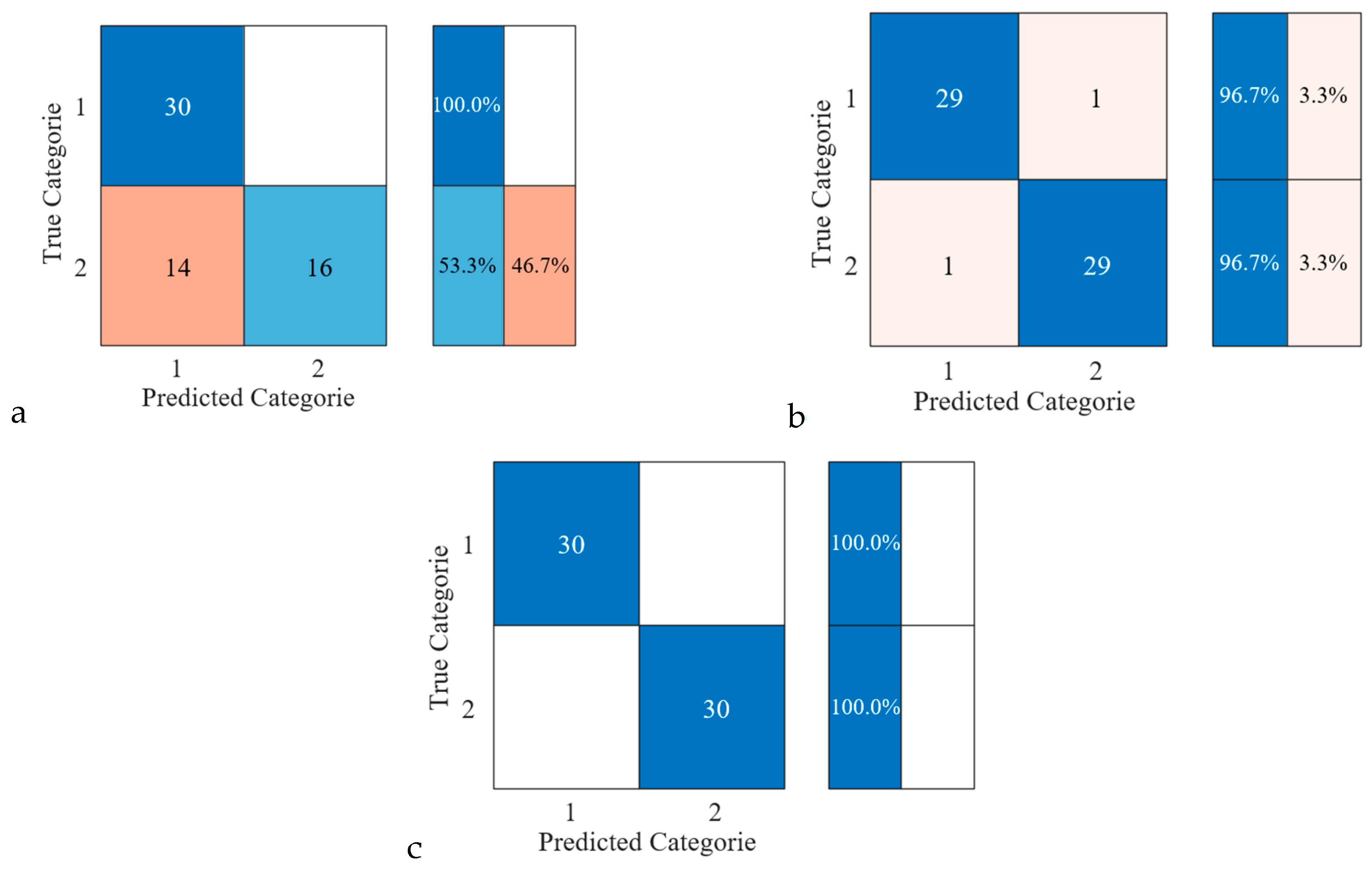
3.4. Multidimensional Information Fusion Feature Effectiveness Analysis
4. Discussion
5. Conclusions
- Combining the advantages of CEEMD’s non–smooth signal-processing capability and anti–modal aliasing and the reduction of the influence of residual noise, extract the IMF components of the signal and compute the energy moment features. This effectively supplements the multidimensional feature matrix for a more comprehensive characterization of vibration signals.
- Constructing an SDAE model to adaptively mine robust deep features from vibration signal samples, and using t–SNE to reduce dimensionality and visualize SDAE feature data, it is shown that the self-extracted features of the SDAE can effectively represent different states of equipment, breaking through the limitations of traditional feature extraction relying on expert experience and prior knowledge and effectively improving the generalization ability of model feature learning.
- According to the proposed multidimensional information fusion feature matrix, the BPNN equipment state recognition accuracy is 100%, which is 23.33% and 3.33% higher than the BPNN recognition accuracy based on traditional time, frequency and SDAE features, respectively. By comparing the effectiveness of the BPNN and SVM in identifying unit state types based on traditional time–domain and frequency–domain features, it is proven that the multidimensional fusion feature matrix constructed by supplementing IMF energy moments and SDAE deep features can more comprehensively mine signal information, achieve the multidimensional complementarity of feature attributes, help to accurately distinguish equipment state types and provide support for subsequent state recognition and trend prediction.
- With the development of sensor technology and the Internet of Things, it becomes more convenient to obtain multi-mode data. In the follow–up research, we can try to integrate various signals such as vibration, acoustics and temperature to comprehensively capture the operating state of the equipment and improve the accuracy and robustness of fault diagnosis.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kumar, K.; Saini, R. A review on operation and maintenance of hydropower plants. Sustain. Energy Technol. Assess. 2022, 49, 101704. [Google Scholar] [CrossRef]
- Li, X.; Xu, Z.; Wang, Y. PSO–MCKD–MFFResnet based fault diagnosis algorithm for hydropower units. Math. Biosci. Eng. 2023, 20, 14117–14135. [Google Scholar]
- Jia, L.; Zeng, Y.; Liu, X.; Huang, W.; Xiao, W. Testing and Numerical Analysis of Abnormal Pressure Pulsations in Francis Turbines. Energies 2024, 17, 237. [Google Scholar]
- Siddique, M.F.; Ahmad, Z.; Ullah, N.; Kim, J. A Hybrid Deep Learning Approach: Integrating Short–Time Fourier Transform and Continuous Wavelet Transform for Improved Pipeline Leak Detection. Sensors 2023, 23, 8079. [Google Scholar] [PubMed]
- Syed, S.H.; Muralidharan, V. Feature extraction using Discrete Wavelet Transform for fault classification of planetary gearbox–A comparative study. Appl. Acoust. 2022, 188, 108572. [Google Scholar]
- Sarangi, S.; Biswal, C.; Sahu, B.K.; Samanta, I.S.; Rout, P.K. Fault detection technique using time–varying filter–EMD and differential–CUSUM for LVDC microgrid system. Electr. Power Syst. Res. 2023, 219, 109254. [Google Scholar]
- Zhang, Q.; Deng, L. An intelligent fault diagnosis method of rolling bearings based on short–time Fourier transform and convolutional neural network. J. Fail. Anal. Prev. 2023, 23, 795–811. [Google Scholar] [CrossRef]
- Lu, Y.; Li, P. A Novel Fault Diagnosis Method for Motor Bearing Based on DTCWT and AFSO–KELM. Shock Vib. 2021, 2021, 2108457. [Google Scholar] [CrossRef]
- Bin, G.; Gao, J.; Li, X.; Dhillon, B. Early fault diagnosis of rotating machinery based on wavelet packets—Empirical mode decomposition feature extraction and neural network. Mech. Syst. Signal Process. 2012, 27, 696–711. [Google Scholar] [CrossRef]
- Sahu, P.K.; Rai, R.N. Fault diagnosis of rolling bearing based on an improved denoising technique using complete ensemble empirical mode decomposition and adaptive thresholding method. J. Vib. Eng. Technol. 2023, 11, 513–535. [Google Scholar] [CrossRef]
- Hou, Y.; Ma, J.; Wang, J.; Li, T.; Chen, Z. Enhanced generative adversarial networks for bearing imbalanced fault diagnosis of rotating machinery. Appl. Intell. 2023, 53, 25201–25215. [Google Scholar] [CrossRef]
- Dao, F.; Zeng, Y.; Qian, J. Fault diagnosis of hydro-turbine via the incorporation of bayesian algorithm optimized CNN–LSTM neural network. Energy 2024, 290, 130326. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, Y.; Cheng, C.; Peng, Z. A hybrid classification autoencoder for semi-supervised fault diagnosis in rotating ma-chinery. Mech. Syst. Signal Process. 2021, 149, 107327. [Google Scholar] [CrossRef]
- Almuqren, L.; Aljameel, S.S.; Alqahtani, H.; Alotaibi, S.S.; Hamza, M.A.; Salama, A.S. A White Shark Equilibrium Optimizer with a Hybrid Deep–Learning–Based Cybersecurity Solution for a Smart City Environment. Sensors 2023, 23, 7370. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Berrouche, Y.; Zimroz, R.; Vashishtha, G.; Chauhan, S.; Gandhi, C.; Tang, H.; Xiang, J. Non−parametric Ensemble Empirical Mode Decomposition for extracting weak features to identify bearing defects. Measurement 2023, 211, 112615. [Google Scholar] [CrossRef]
- Lobato, T.H.G.; da Silva, R.R.; da Costa, E.S.; Mesquita, A.L.A. An integrated approach to rotating machinery fault diagnosis using, EEMD, SVM, and augmented data. J. Vib. Eng. Technol. 2020, 8, 403–408. [Google Scholar] [CrossRef]
- Bendjama, H. Feature extraction based on vibration signal decomposition for fault diagnosis of rolling bearings. Int. J. Adv. Manuf. Technol. 2024, 130, 821–836. [Google Scholar] [CrossRef]
- Pang, Y.; Gao, J.-W. Fault Diagnosis Method of Rolling Bearings Based on ICEEMDAN Energy Moment and HHO–KLEM. Noise Vib. Control 2023, 43, 142–148. [Google Scholar]
- Jang, J.-G.; Noh, C.-M.; Kim, S.-S.; Shin, S.-C.; Lee, S.-S.; Lee, J.-C. Vibration data feature extraction and deep learning–based preprocessing method for highly accurate motor fault diagnosis. J. Comput. Des. Eng. 2023, 10, 204–220. [Google Scholar] [CrossRef]
- Neelakandan, S.; Reddy, N.V.R.; Ghfar, A.A.; Pandey, S.; Kiran, S.; Arasu, P.T. Internet of things with nanomaterials–based predictive model for wastewater treatment using stacked sparse denoising auto–encoder. Water Reuse 2023, 13, 233–249. [Google Scholar] [CrossRef]
- Jorkesh, S.; Gholaminejad, A.; Poshtan, J. Induction motors fault diagnosis using a stacked sparse auto–encoder deep neural network. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2023, 237, 359–369. [Google Scholar] [CrossRef]
- Key, S.; Ko, C.-S.; Song, K.-J.; Nam, S.-R. Fast detection of current transformer saturation using stacked denoising autoencoders. Energies 2023, 16, 1528. [Google Scholar] [CrossRef]




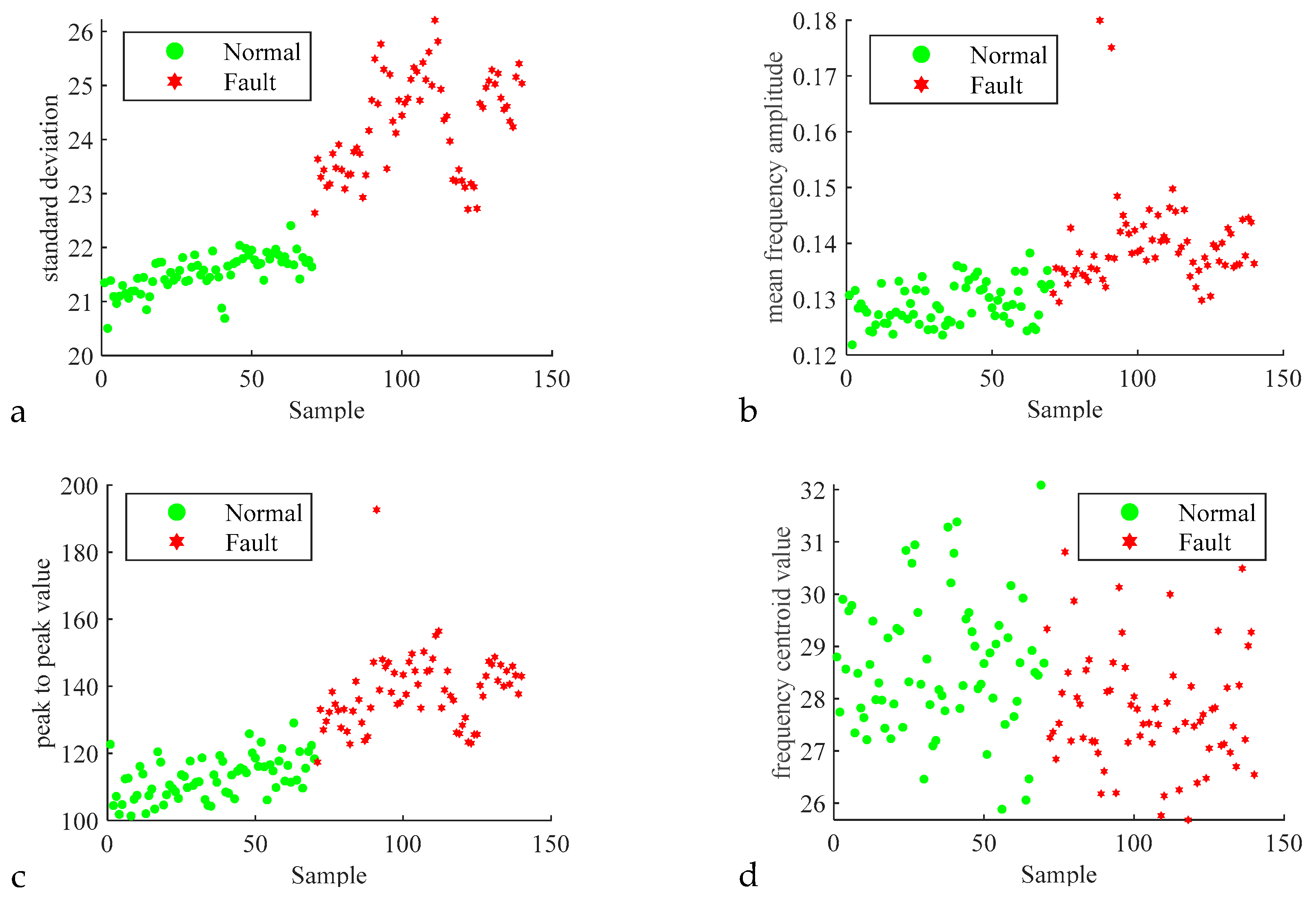





| Feature Name | Time–Domain Feature | Feature Name | Frequency–Domain Feature |
|---|---|---|---|
| standard deviation | mean frequency amplitude | ||
| peak-to-peak value | frequency centroid value | ||
| kurtosis | frequency standard deviation |
| State | Sample ID | T1 | T2 | T3 | F1 | F2 | F3 |
|---|---|---|---|---|---|---|---|
| Normal | 90 | 22.131 | 117.754 | 2.564 | 0.132 | 28.900 | 34.700 |
| Fault | 190 | 26.582 | 155.945 | 2.871 | 0.152 | 28.490 | 31.775 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, D.; Kong, L.; Yao, B.; Huang, T.; Deng, X.; Xiao, Z. Hydroelectric Unit Vibration Signal Feature Extraction Based on IMF Energy Moment and SDAE. Water 2024, 16, 1956. https://doi.org/10.3390/w16141956
Liu D, Kong L, Yao B, Huang T, Deng X, Xiao Z. Hydroelectric Unit Vibration Signal Feature Extraction Based on IMF Energy Moment and SDAE. Water. 2024; 16(14):1956. https://doi.org/10.3390/w16141956
Chicago/Turabian StyleLiu, Dong, Lijun Kong, Bing Yao, Tangming Huang, Xiaoqin Deng, and Zhihuai Xiao. 2024. "Hydroelectric Unit Vibration Signal Feature Extraction Based on IMF Energy Moment and SDAE" Water 16, no. 14: 1956. https://doi.org/10.3390/w16141956
APA StyleLiu, D., Kong, L., Yao, B., Huang, T., Deng, X., & Xiao, Z. (2024). Hydroelectric Unit Vibration Signal Feature Extraction Based on IMF Energy Moment and SDAE. Water, 16(14), 1956. https://doi.org/10.3390/w16141956







