Refined Reservoir Routing (RRR) and Its Application to Atmospheric Carbon Dioxide Balance
Abstract
What is more I loved, and still do love, mathematics for itself as not allowing room for hypocrisy or vagueness, my two pet aversions.Stendhal [1] (p. 111).
1. Introduction
- Its “lumping” in a systems approach is direct, because its concentration varies slowly, while that of atmospheric water varies dramatically with time, geographic location, and altitude.
- As we will see below, there is controversy about the atmospheric CO2 budget, reflecting incomplete understanding and quantification of the processes, which the simple RRR framework may shed light on.
- Exporting a methodological framework developed in hydrology to the study of climate may be beneficial to both hydrology and climatology and may demonstrate the potential and usefulness of hydrology in climate research.
2. Theoretical Analysis
2.1. System Components and Determination of Their Temporal Evolution
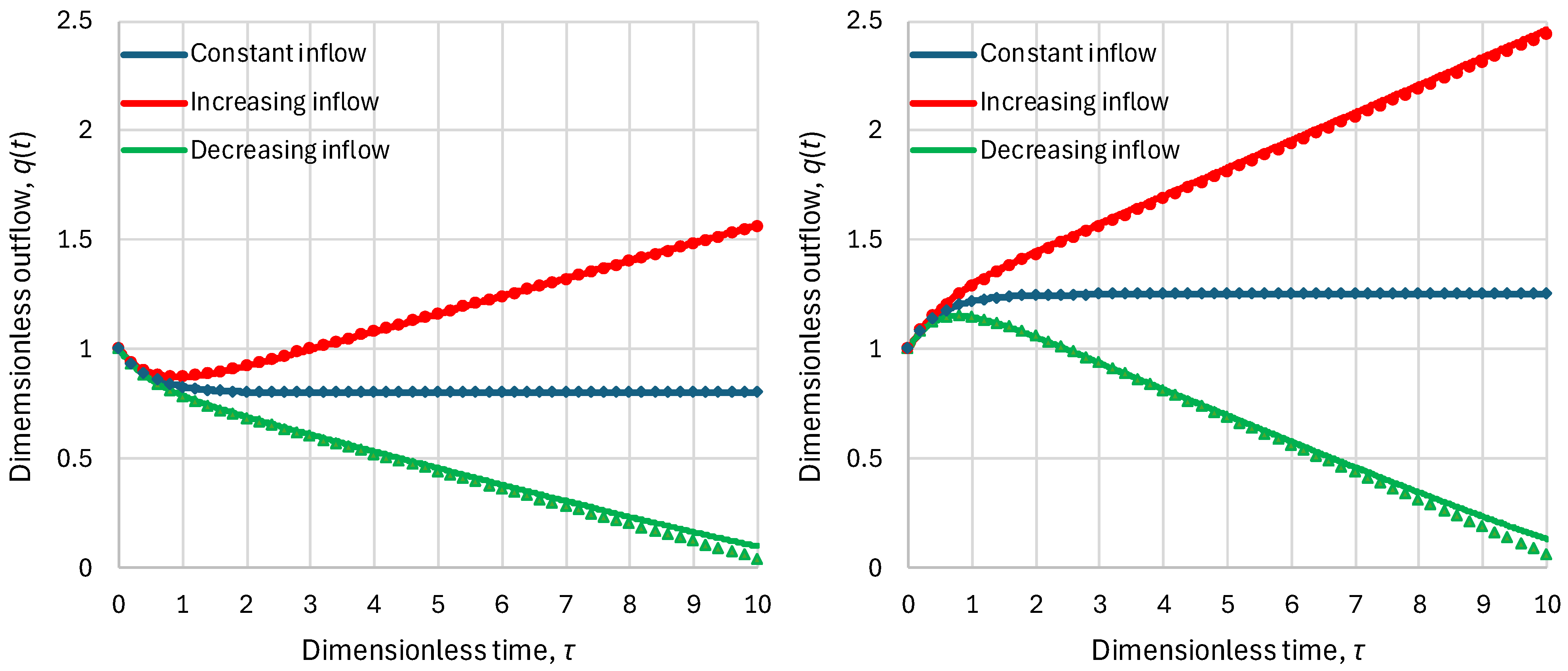
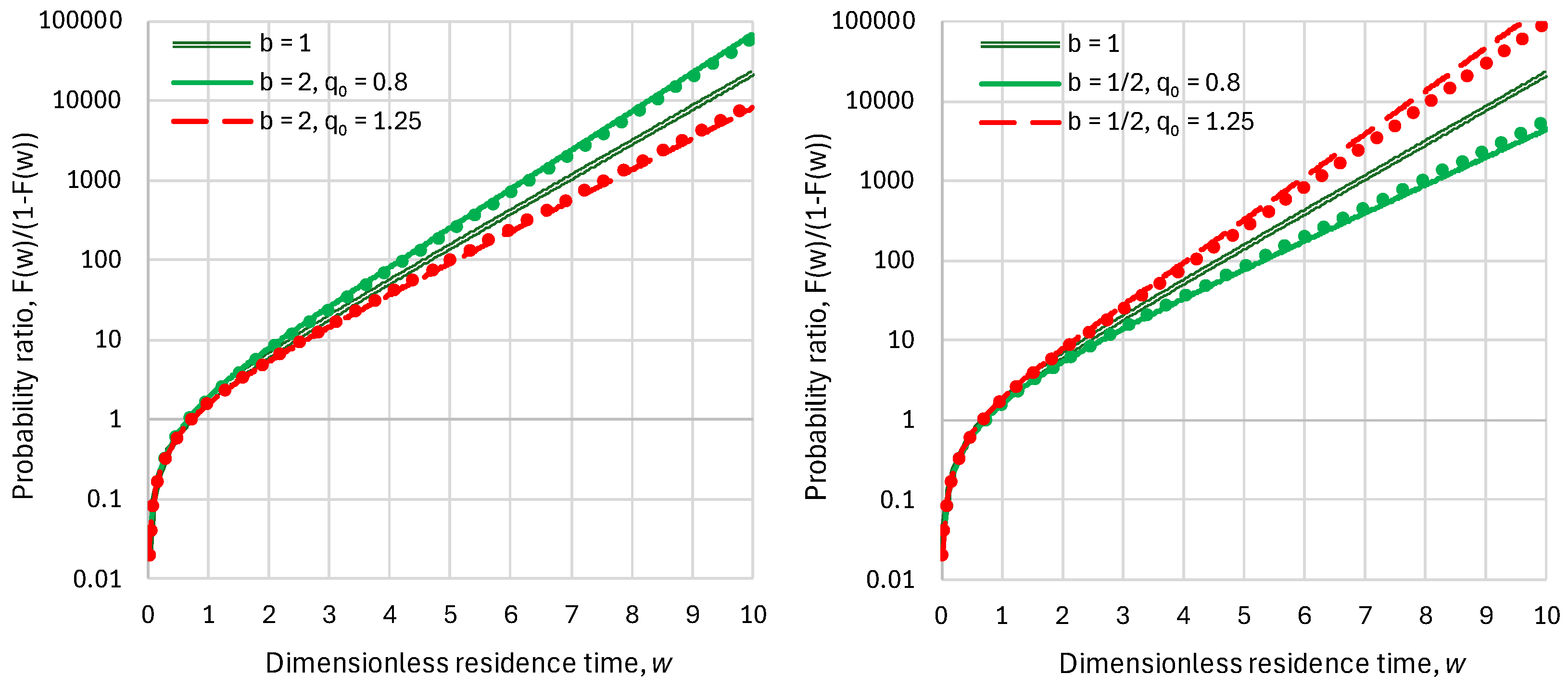
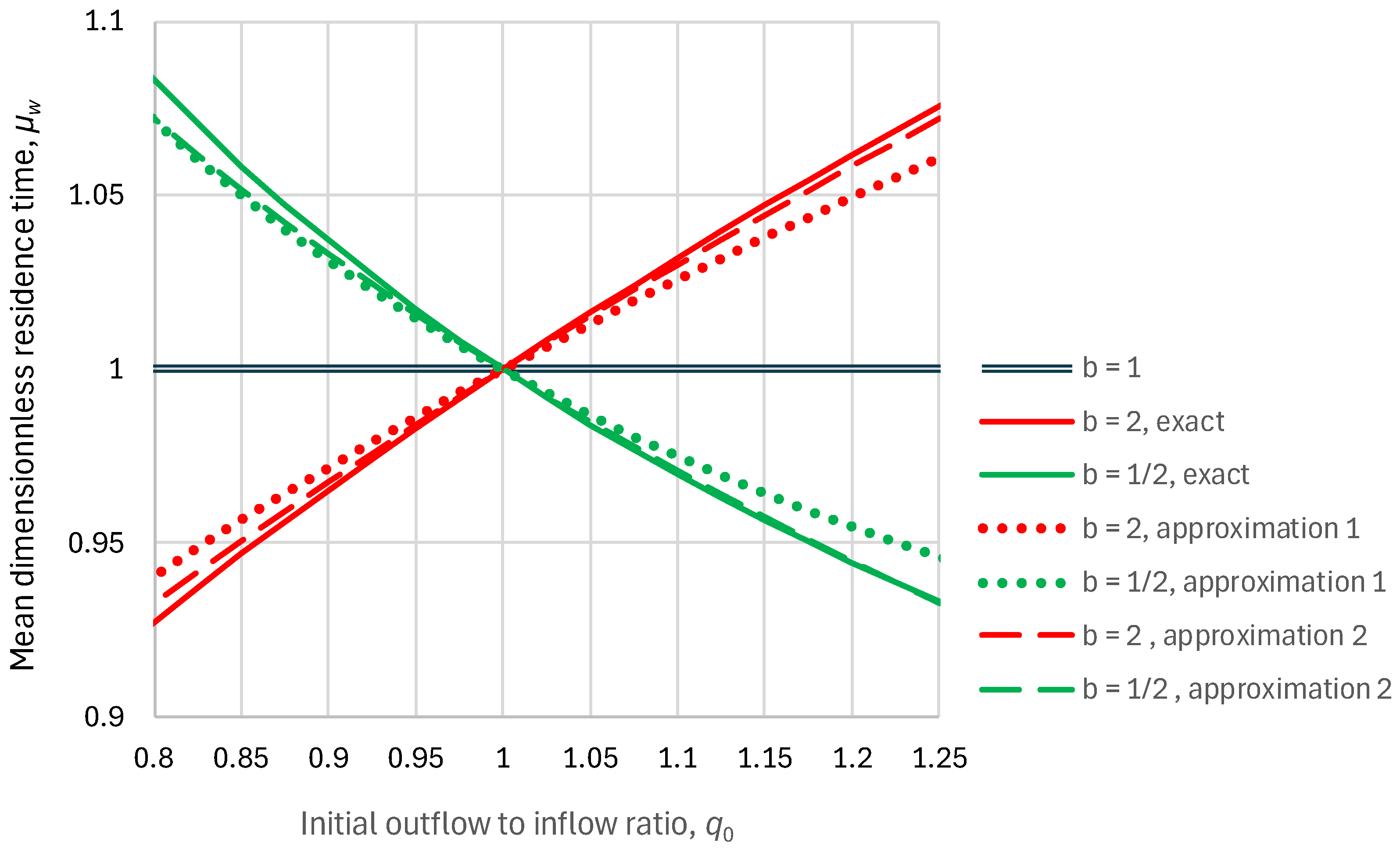
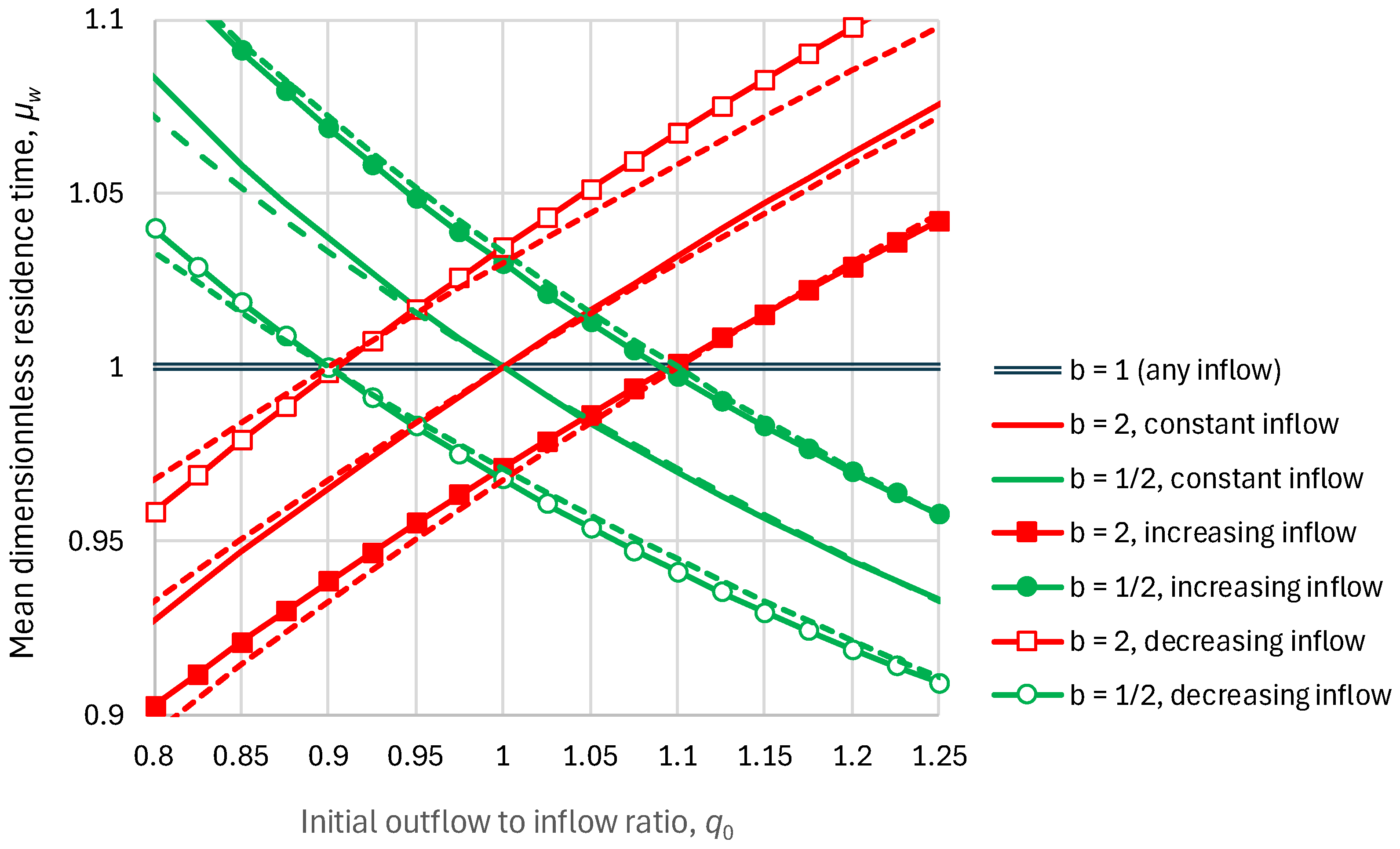
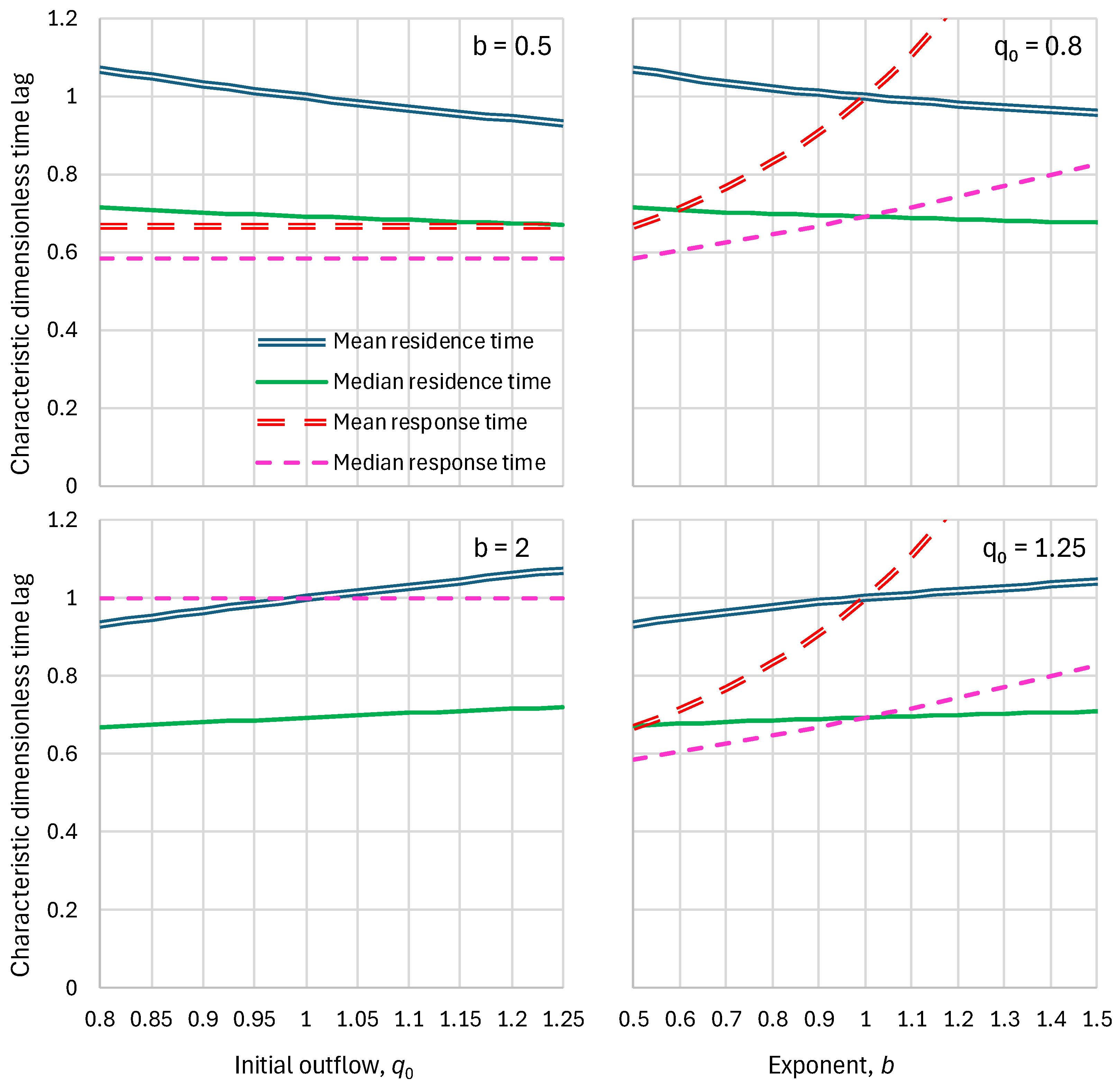
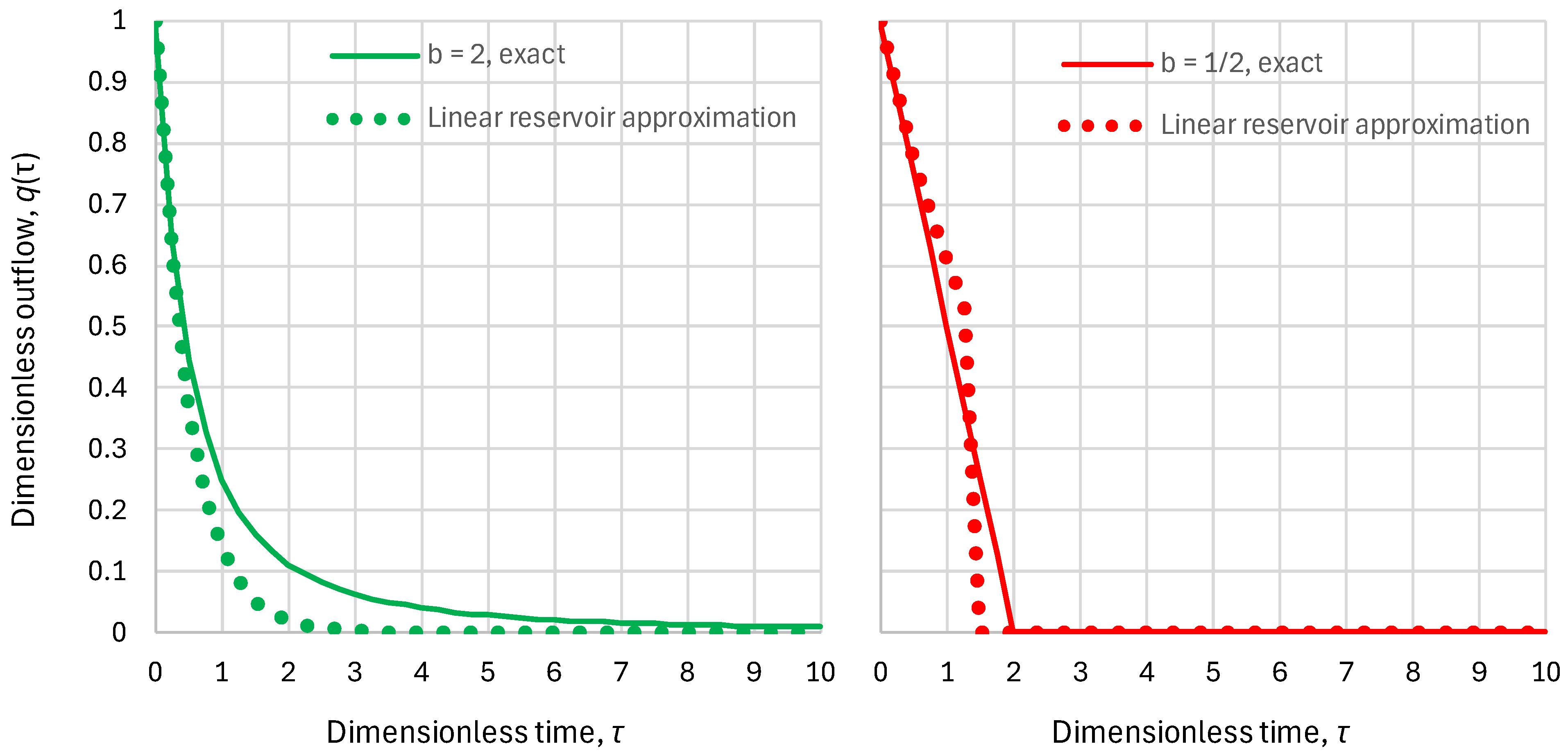
2.2. Residence Time
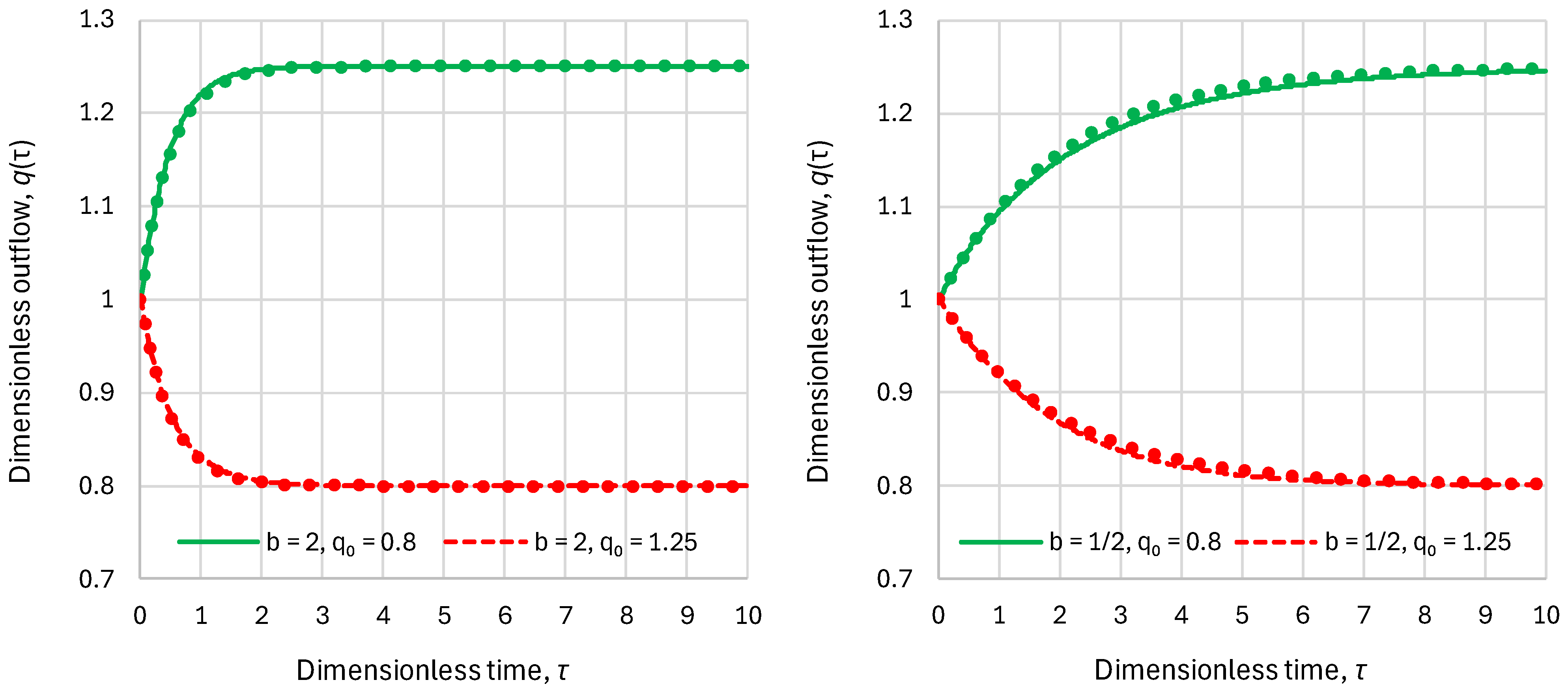
- Linear reservoir (in which ), any inflow:
- Superlinear benchmark reservoir, , constant inflow:
- Sublinear benchmark reservoir, , constant inflow:
2.3. Response Time
2.4. Parameters and Their Estimation
3. Carbon Cycle: A Summary of the Established Approach
3.1. Concepts and Terminology
Lifetime is a general term used for various time scales characterizing the rate of processes affecting the concentration of trace gases. The following lifetimes may be distinguished:[…] Response time or adjustment time (Ta) is the time scale characterizing the decay of an instantaneous pulse input into the reservoir. The term adjustment time is also used to characterize the adjustment of the mass of a reservoir following a step change in the source strength. Half-life or decay constant is used to quantify a first-order exponential decay process. […]The term lifetime is sometimes used, for simplicity, as a surrogate for adjustment time.In simple cases, where the global removal of the compound is directly proportional to the total mass of the reservoir, the adjustment time equals the turnover time: T = Ta.[…]Turnover time (T) (also called global atmospheric lifetime) is the ratio of the mass M of a reservoir (e.g., a gaseous compound in the atmosphere) and the total rate of removal S from the reservoir: T = M/S.[…]Response time or adjustment time In the context of climate variations, the response time or adjustment time is the time needed for the climate system or its components to re-equilibrate to a new state, following a forcing resulting from external processes. It is very different for various components of the climate system. The response time of the troposphere is relatively short, from days to weeks, whereas the stratosphere reaches equilibrium on a time scale of typically a few months. […] In the context of lifetimes, response time or adjustment time (Ta) is the time scale characterizing the decay of an instantaneous pulse input into the reservoir.
The concept of a single, characteristic atmospheric lifetime is not applicable to CO2.[31] (p. 473)
No single lifetime can be given [for CO2]. The impulse response function for CO2 from Joos et al. (2013) [42] has been used.[31] (p. 737)
3.2. Separate Treatment of CO2 Depending on Its Origin
Simulations with climate–carbon cycle models show multi-millennial lifetime of the anthropogenic CO2 in the atmosphere.[31] (p. 435)
This delay between a peak in emissions and a decrease in concentration is a manifestation of the very long lifetime of CO2 in the atmosphere; part of the CO2 emitted by humans remains in the atmosphere for centuries to millennia.[32] (p. 642 FAQ 4.2)
When considering the fate of anthropogenic CO2, the emission into the atmosphere can be considered as a series of consecutive pulse inputs.
The largest fraction of the CO2 recovery will take place on time scales of centuries, as CO2 invades the ocean, but a significant fraction of the fossil fuel CO2, ranging in published models in the literature from 20–60%, remains airborne for a thousand years or longer.
The models agree that 20–35% of the CO2 remains in the atmosphere after equilibration with the ocean (2–20 centuries).
Estimates for how long carbon dioxide (CO2) lasts in the atmosphere […] are often intentionally vague, ranging anywhere from hundreds to thousands of years. […] As it stands, says [Ed] Boyle, human-generated carbon dioxide is expected to continue warming the planet for tens of thousands of years [46].Once [carbon dioxide is] added to the atmosphere, it hangs around, for a long time: between 300 to 1000 years. Thus, as humans change the atmosphere by emitting carbon dioxide, those changes will endure on the timescale of many human lives [47].
3.3. Modeling Approach
Carbon dioxide (CO2) is an extreme example. Its turnover time is only about 4 years because of the rapid exchange between the atmosphere and the ocean and terrestrial biota. However, a large part of that CO2 is returned to the atmosphere within a few years. The adjustment time of CO2 in the atmosphere is determined from the rates of removal of carbon by a range of processes with time scales from months to hundreds of thousands of years. As a result, 15 to 40% of an emitted CO2 pulse will remain in the atmosphere longer than 1000 years, 10 to 25% will remain about ten thousand years, and the rest will be removed over several hundred thousand years.
4. RRR Application to the Atmospheric Component of the Carbon Cycle
4.1. Data
- From mass of C to mass of CO2, we multiply by 44/12 = 3.67 kg CO2/kg C (where 44 and 12 are the molecular masses of CO2 and C).
- From atmospheric CO2 concentration in ppm to total atmospheric mass in Gt CO2, we multiply by 7.8 Gt CO2/ppm CO2.
4.2. Premises of the Application
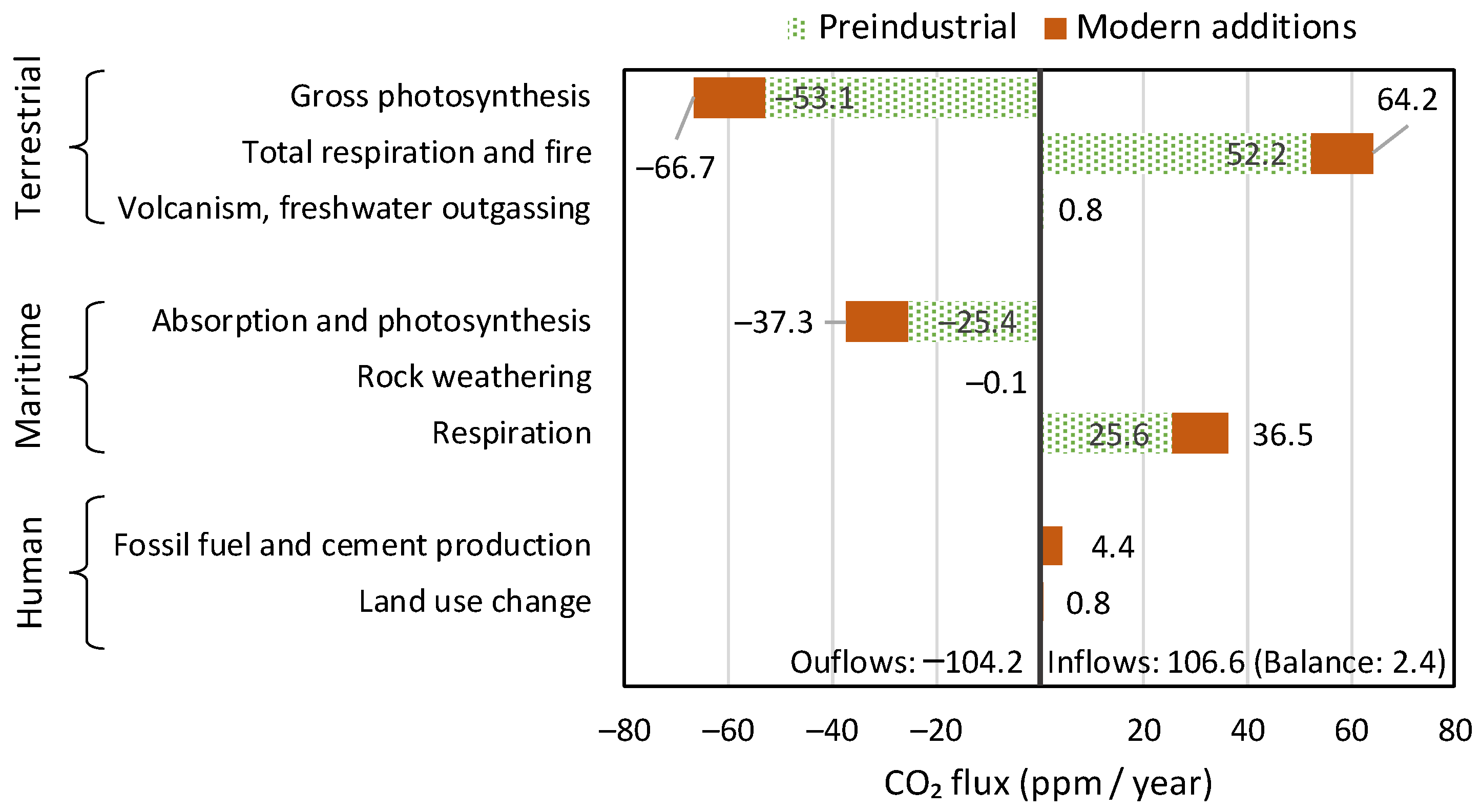
- Human activities are responsible for only 4% of carbon emissions.
- The vast majority of changes in the atmosphere since 1750 (red bars in the graph) are due to natural processes, respiration and photosynthesis.
- The increases in both CO2 emissions and sinks are due to the temperature increase, which expands the biosphere and makes it more productive.
- The terrestrial biosphere processes are much stronger than the maritime ones in terms of both production and absorption of CO2.
- The CO2 emissions by merely the ocean biosphere are much larger than human emissions.
- The modern (post 1750) CO2 additions to pre-industrial quantities (red bars in the right half of the graph, corresponding to positive values) exceed the human emissions by a factor of ~4.5. In the most recent 65 years, covered by measurements, the rate of natural emissions is ~3.5 times greater than the CO2 emissions from fossil fuels.
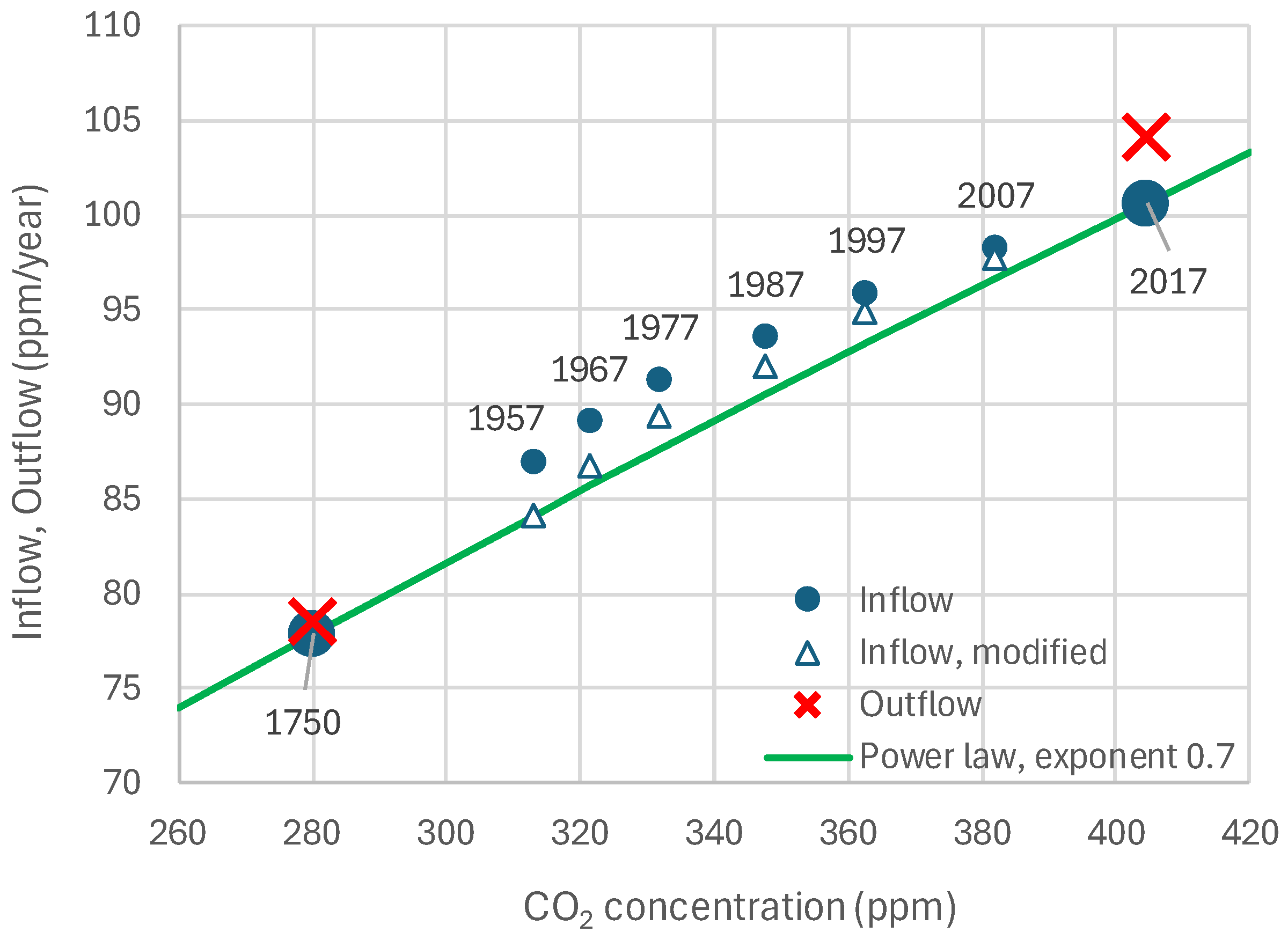
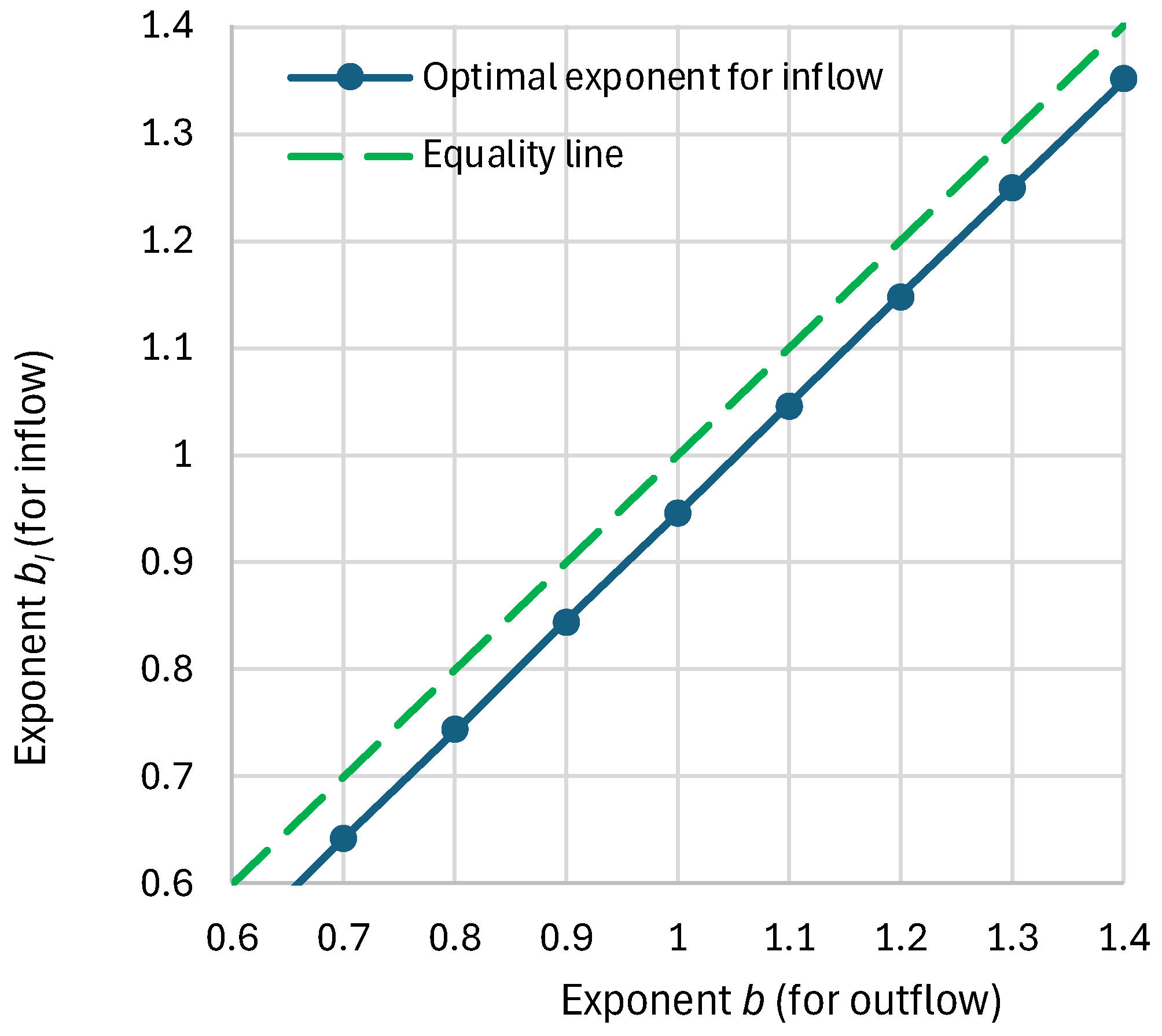
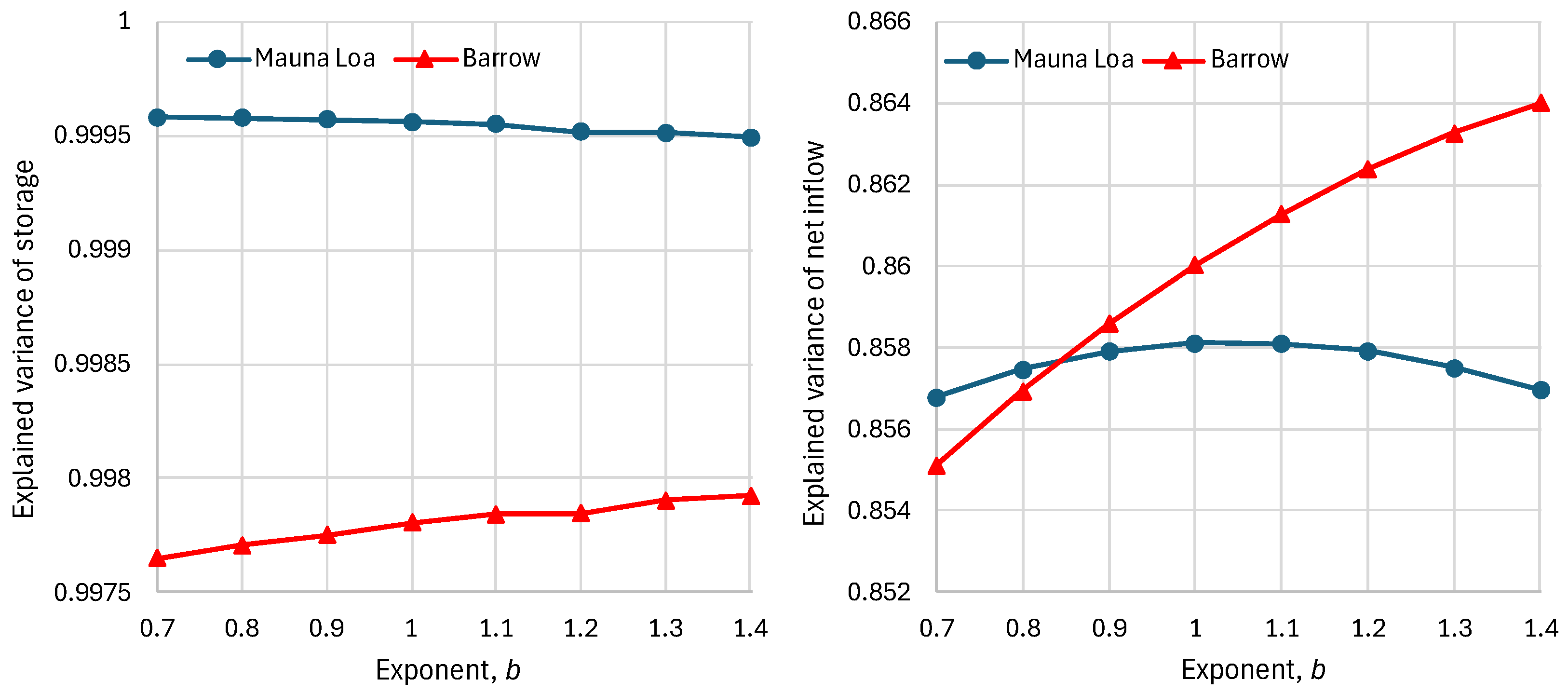
4.3. Model and Its Fitting Methodology
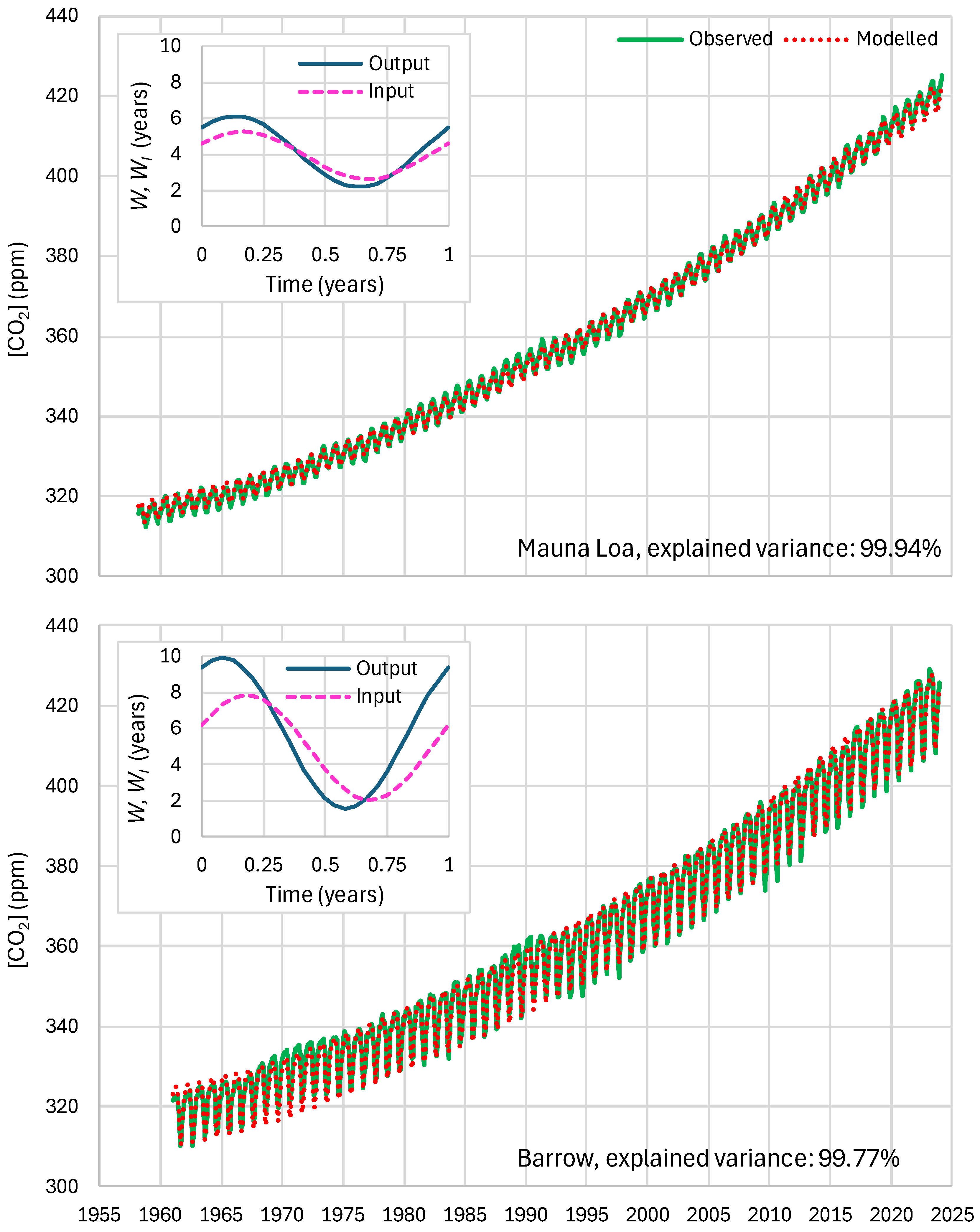
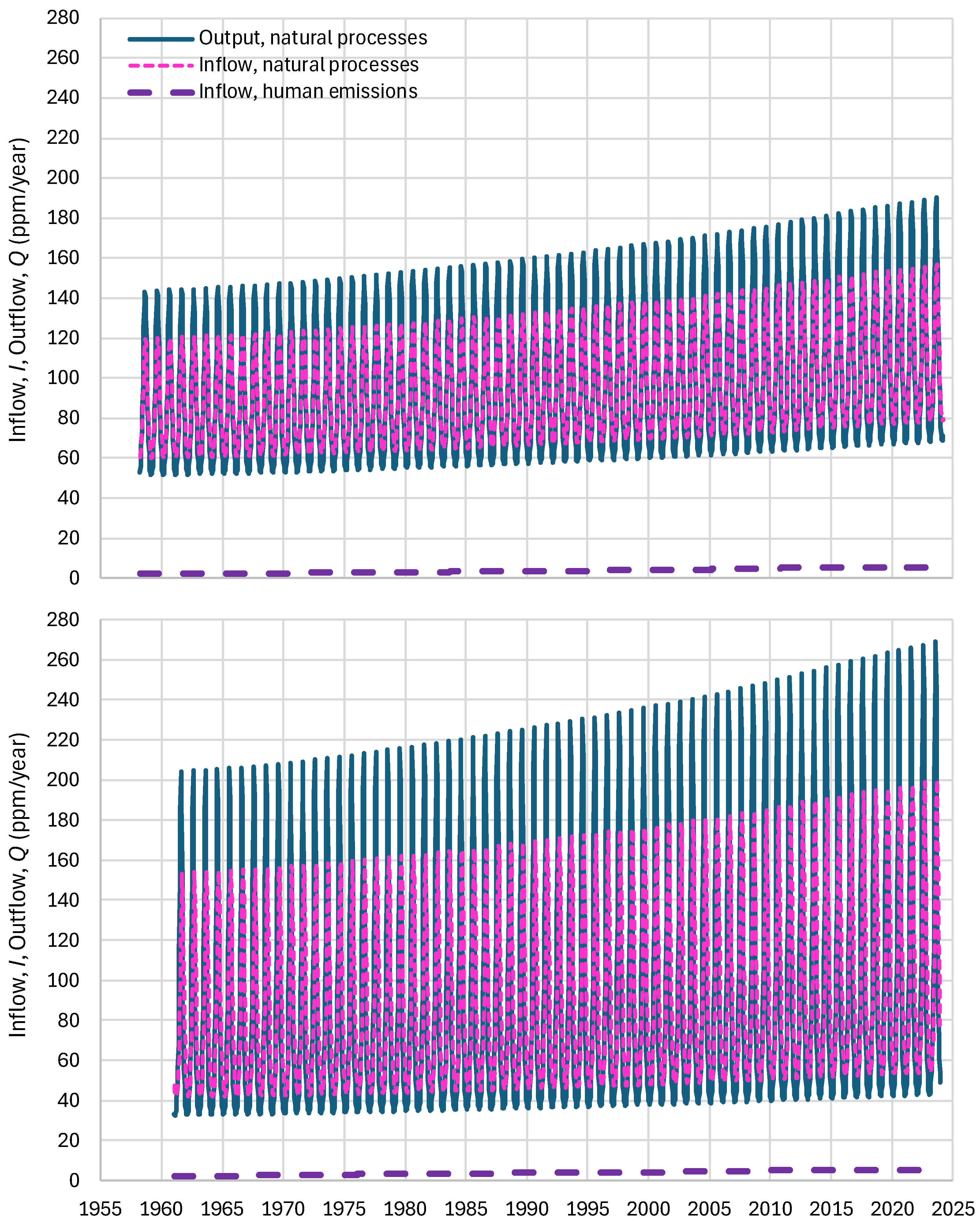
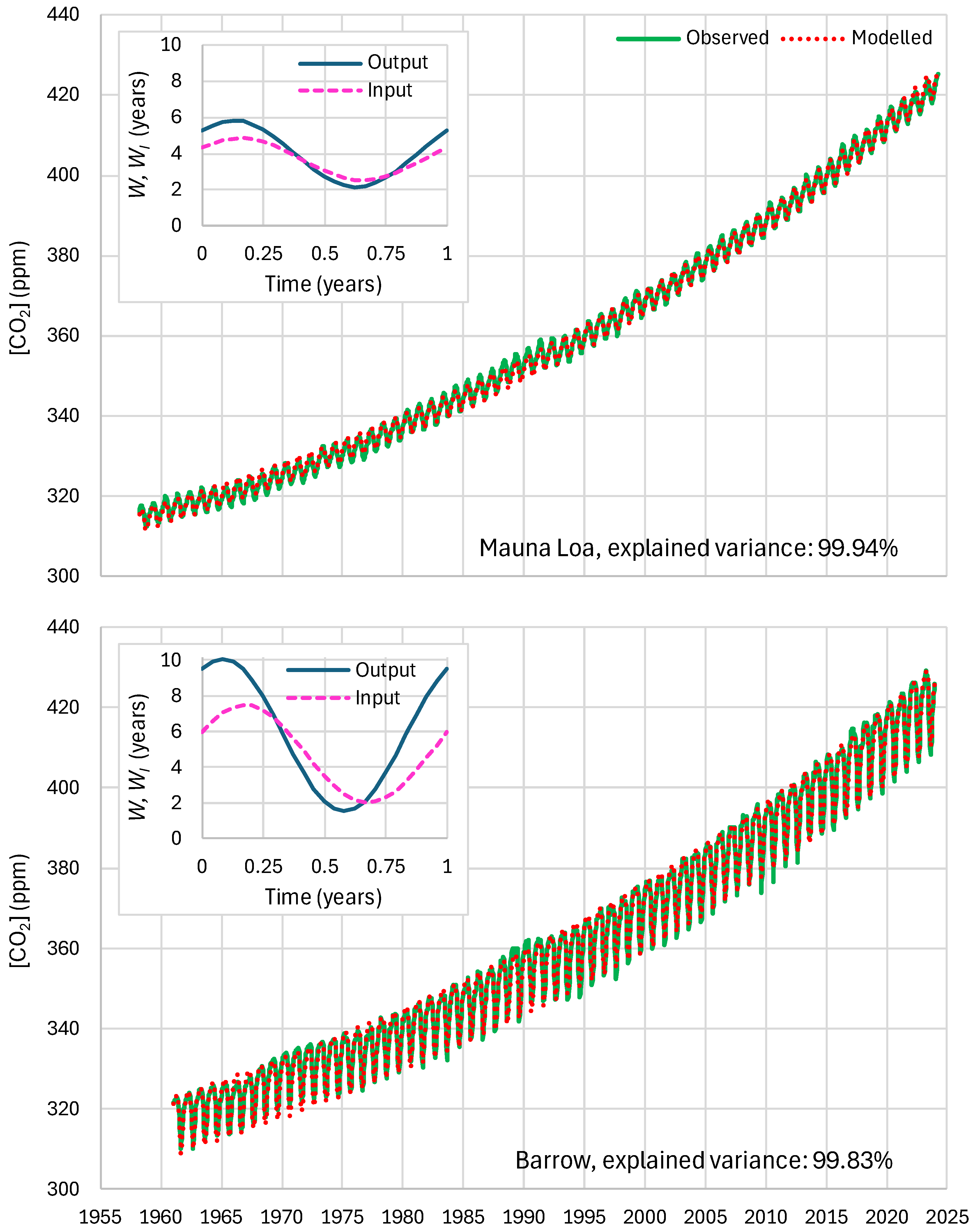
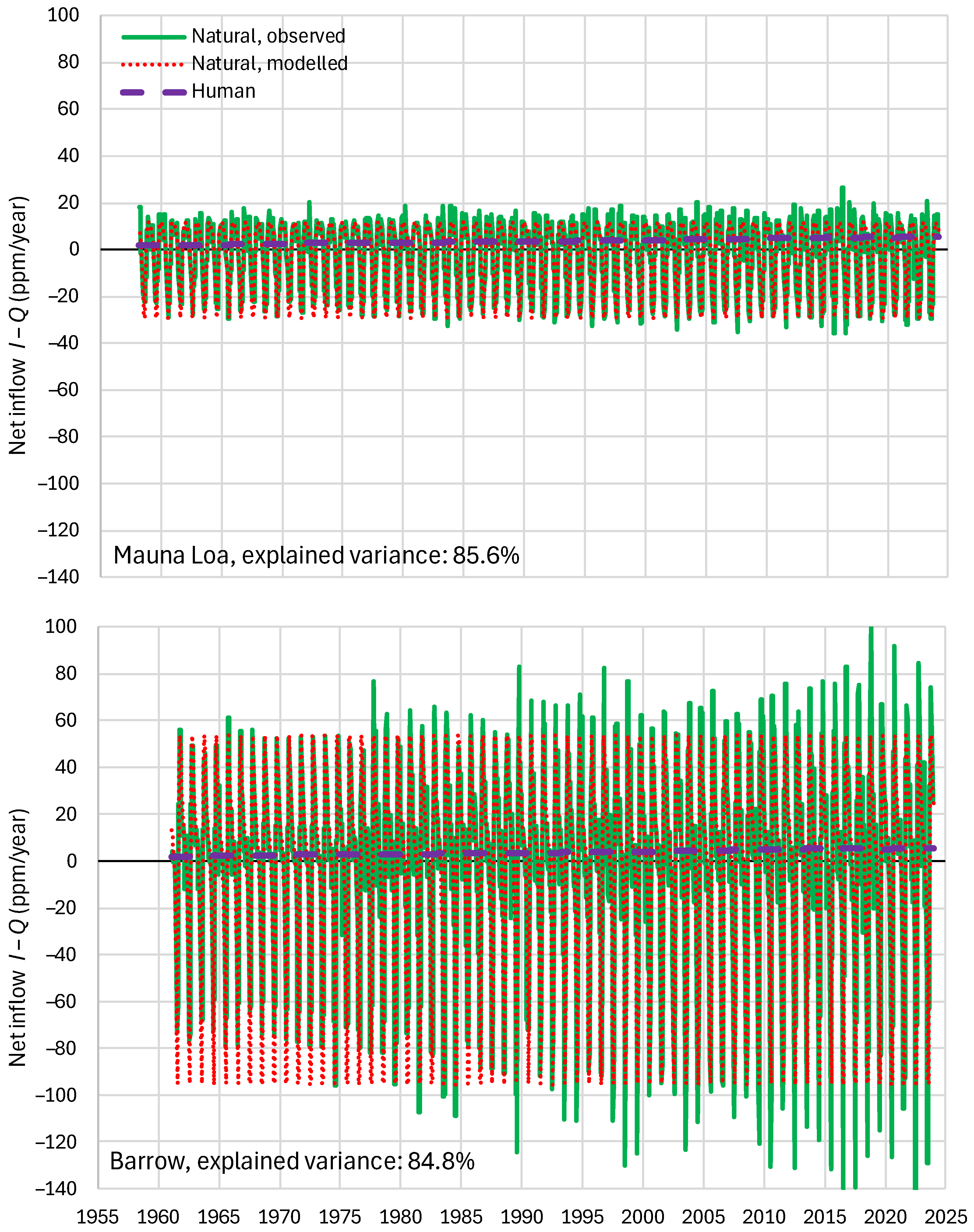
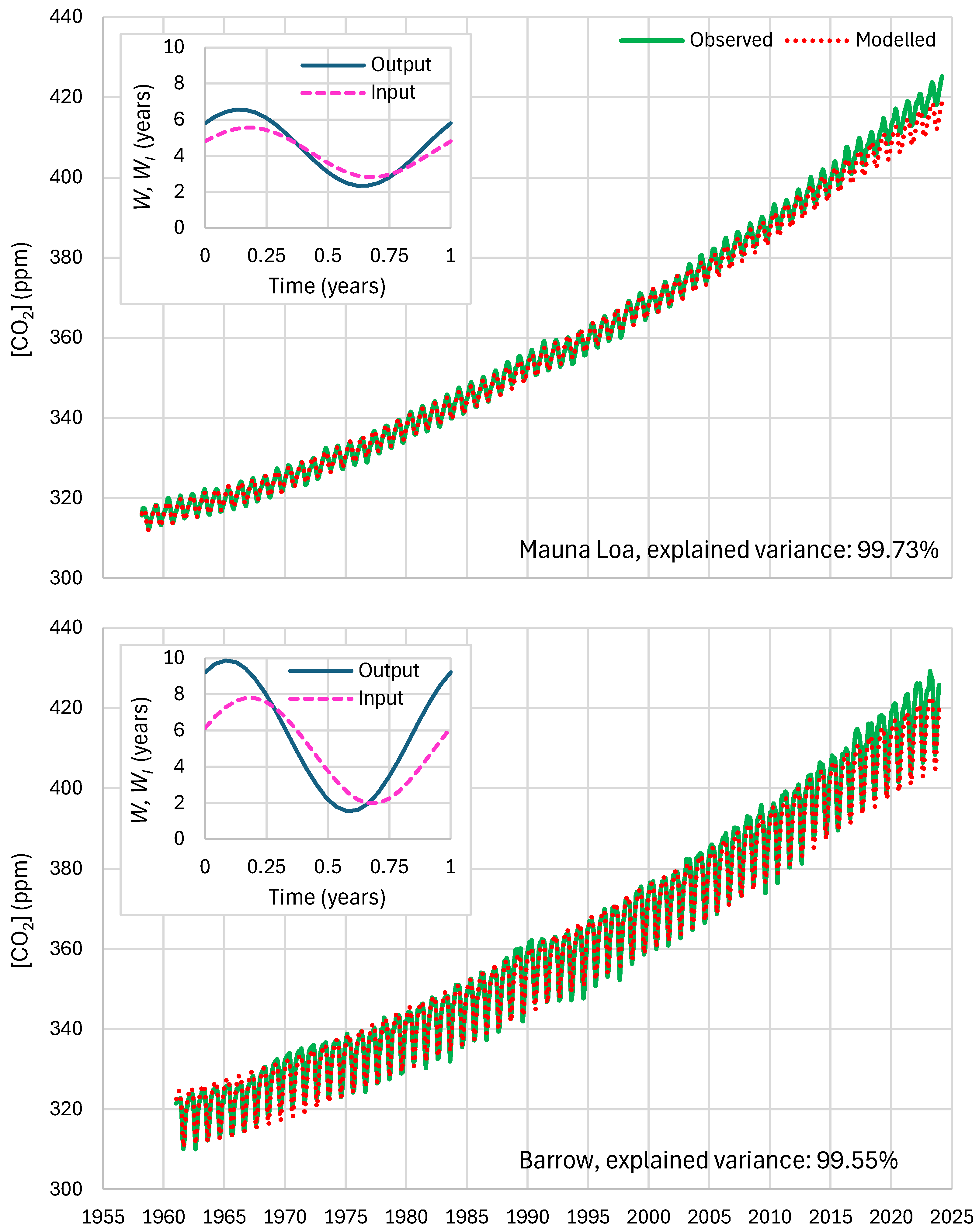
4.4. Results of Final Modeling
4.5. Results for Imaginary Cases
- Human emissions are disregarded, and only natural processes are considered.
- The natural processes are neglected, and only the anthropogenic emissions are considered.
- In addition to anthropogenic emissions, natural outputs (but no inputs) are also considered.
- All processes are considered, but the biosphere expansion is neglected.
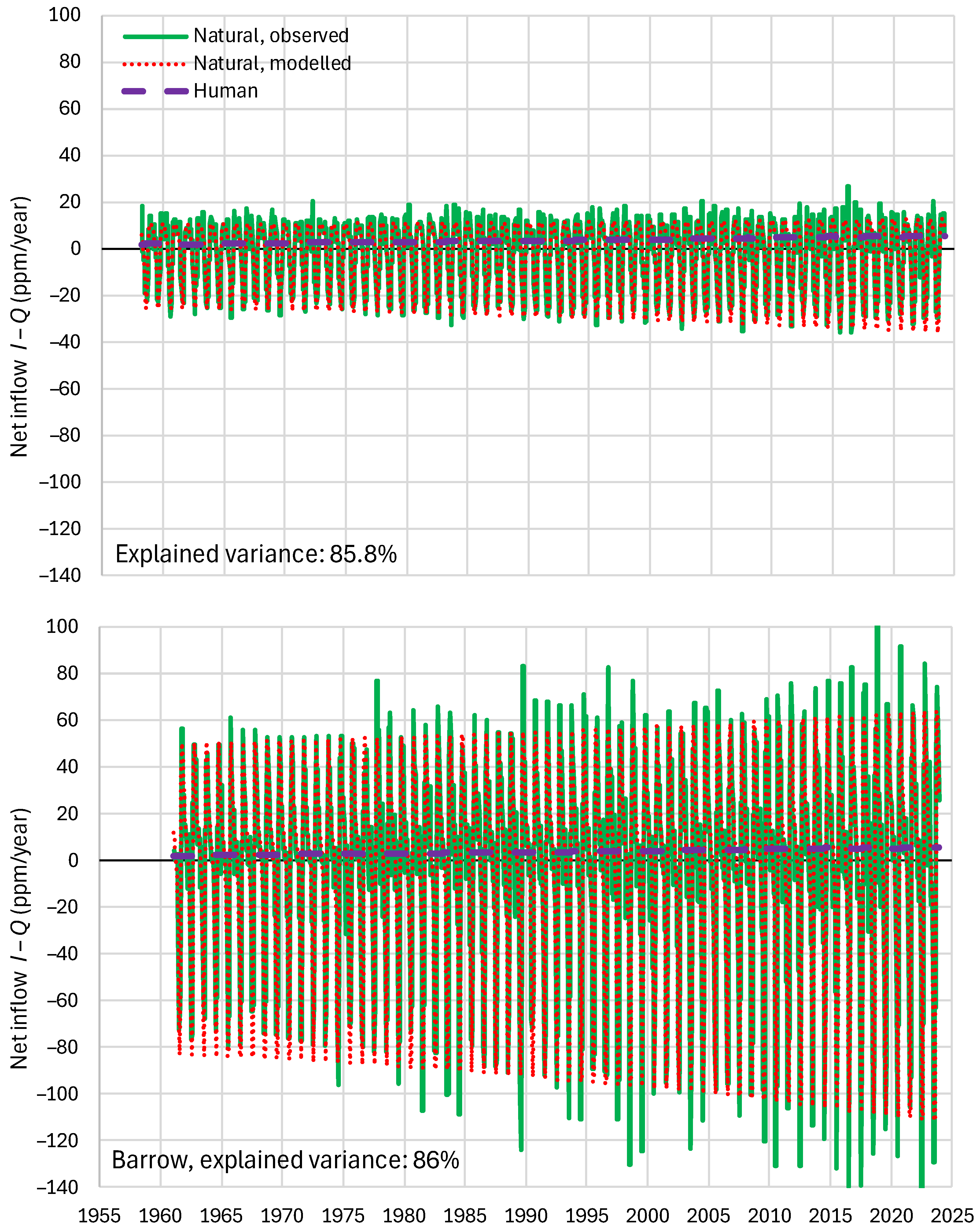
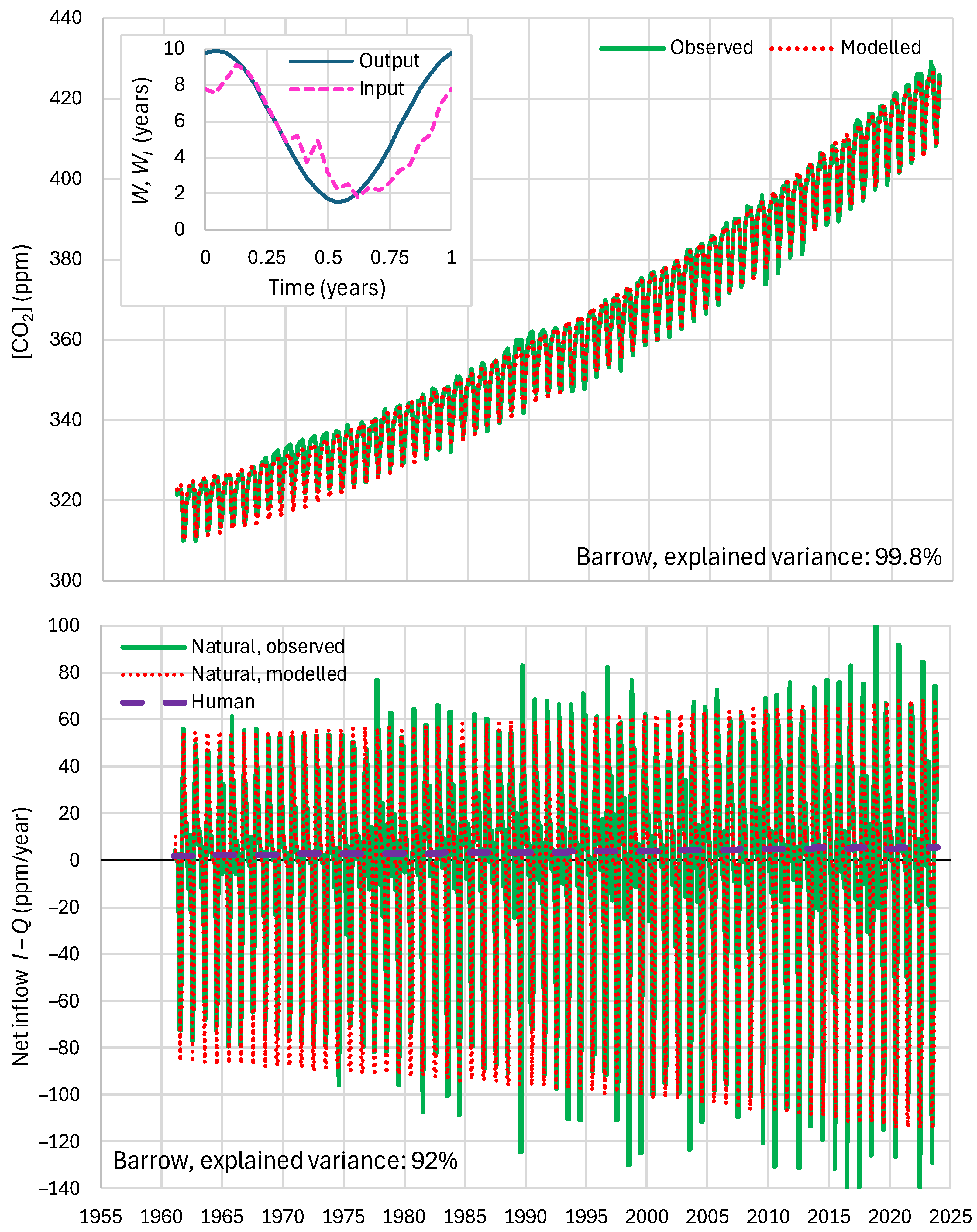
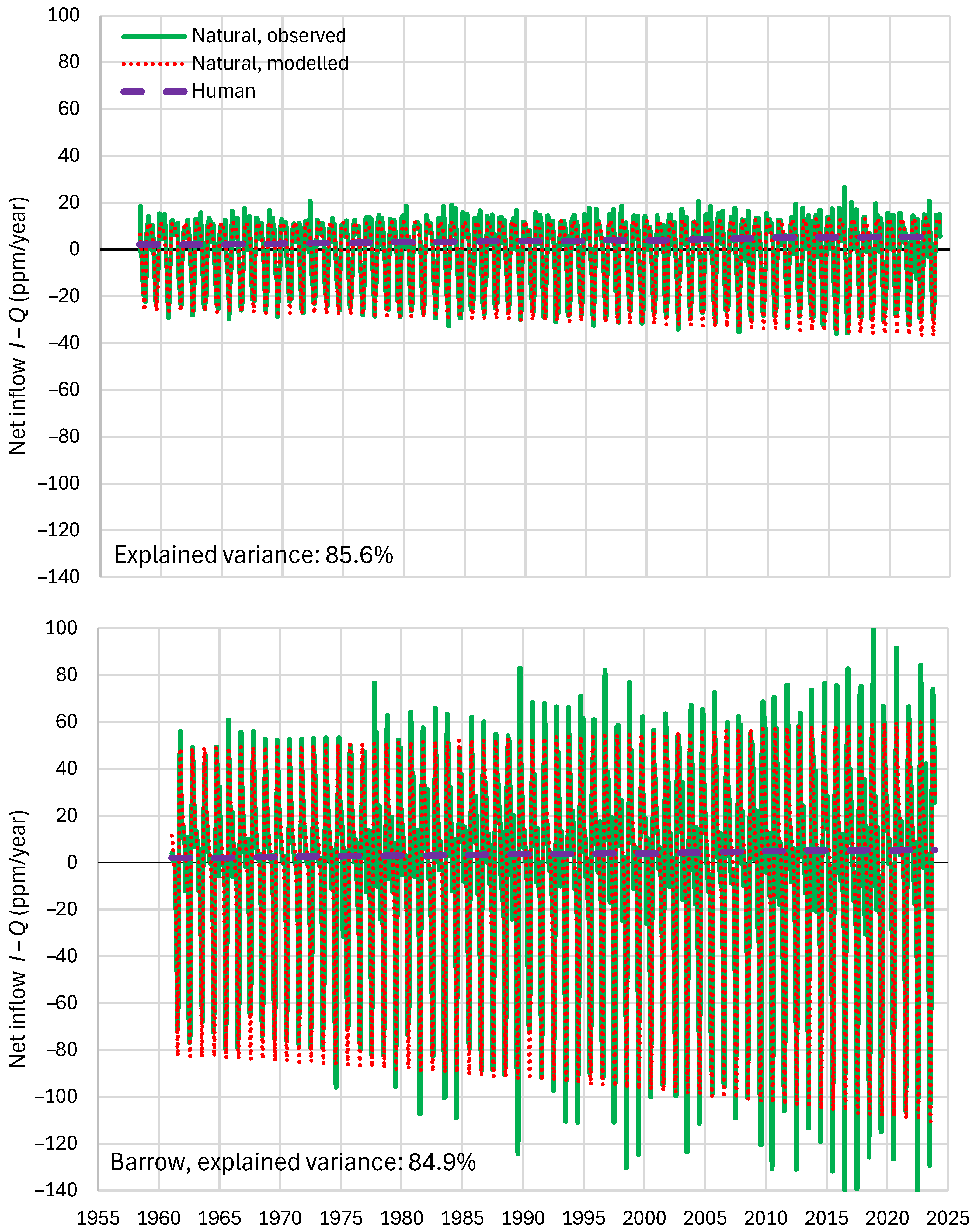
4.6. RRR Validation
5. Discussion and Further Results
5.1. Residence Times
5.2. Anthropogenic Emissions Remaining in the Atmosphere: Total Mass
Over the past six decades, the average fraction of anthropogenic CO2 emissions that has accumulated in the atmosphere (referred to as the airborne fraction) has remained nearly constant at approximately 44%.
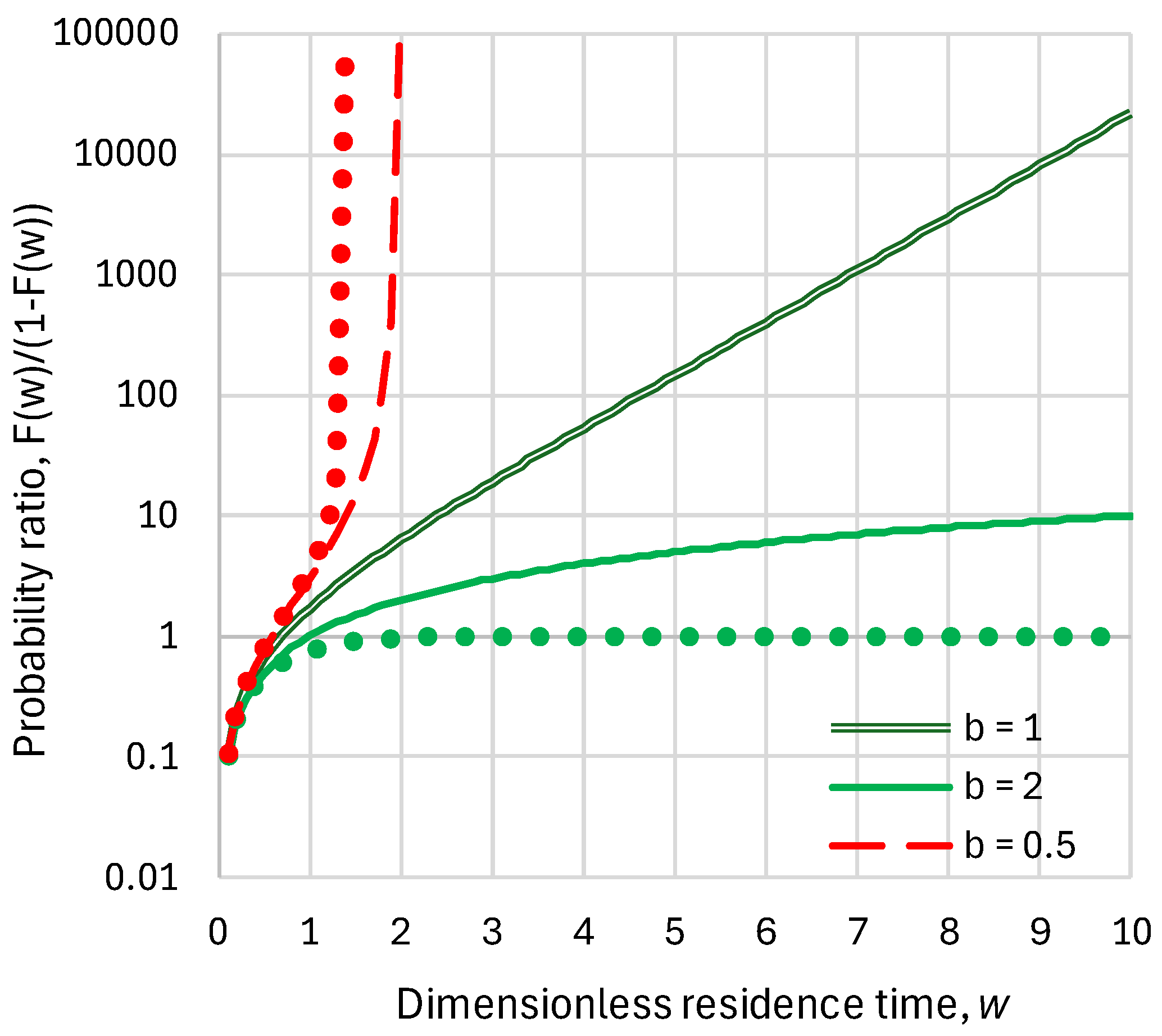
5.3. Anthropogenic Emissions Remaining in the Atmosphere: Probabilistic Assessment of Characteristic Times
- The probability that a molecule remains after 1000 years is , where we have used Equation (29) to evaluate the .
- The probability that out of molecules none remain after 1000 years is , and the probability that at least one molecule remains is . Given that as , , for small (as in our case), we have .
- According to IPCC [32] (Figure 5.12), the atmospheric CO2 amounts to 870 Pg C = g C. Thus, the mass of CO2 is g (where 44 and 12 are the molecular masses of CO2 and C, respectively). The number of moles is .
- The Avogadro constant is , and thus the number of CO2 molecules in the atmosphere is .
- Hence, the probability that after 1000 years, at least one out of the molecules remains in the atmosphere is .
- A probability is virtually no different from an impossibility. Hence, we can be certain that none of the molecules existing in the atmosphere now, whether due to an “emitted CO2 pulse” or existing before it, will remain after 1000 years—let alone after “ten thousand years” or after “several hundred thousand years”.
- To make this probability a reasonable rarity of 1% () that a single molecule out of the remains in the atmosphere, we need to make . This would occur at time such that , which yields years.
6. Conclusions
- It defines and clarifies the relevant quantities, including the characteristic time lags, such as residence and response times, which are often confused in the literature. (The Glossary presented below summarizes the related concepts and their definitions.)
- It refines the case of a reservoir with linear dynamics, which admits analytical solutions for all related variables, and rederives and streamlines these analytical solutions.
- It classifies the cases of a reservoir with nonlinear dynamics, studies some special cases that admit analytical solutions, and provides working approximations of the outflow and the residence time, including its probability distribution and statistical characteristics.
- It provides an exact solution for the instantaneous response function and the response time, whether for the linear or nonlinear case.
- It proposes a framework for model fitting, based on observed data, for several cases, whether with linear or nonlinear dynamics.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Glossary
Appendix A. Alternative Approximations of a Sublinear or Superlinear Reservoir
Appendix B. Notes on the Sum of Exponential Functions as a Response Function
| Term | ||||
|---|---|---|---|---|
| 0.2173 | 0.224 | 0.2824 | 0.2763 | |
| (years) | ∞ | 394.4 | 36.54 | 4.304 |
Appendix C. Indirect Validation of the RRR Results Using 14C Isotopic Data
This study explores the plausibility of this concept, which results in much shorter atmospheric residence times, 4-5 years, than the magnitude larger outcomes of the usual global carbon cycle models which are adjusted to fit the assumption that anthropogenic emissions are primarily the cause of the observed rise in atmospheric CO2. The continuum concept is consistent with the record of the seasonal photosynthesis swing of atmospheric CO2 which supports a residence time of about 5 years, as also does the bomb C14 decay history. The short residence time suggests that anthropogenic emissions contribute only a fraction of the observed atmospheric rise, and that other sources need be sought.
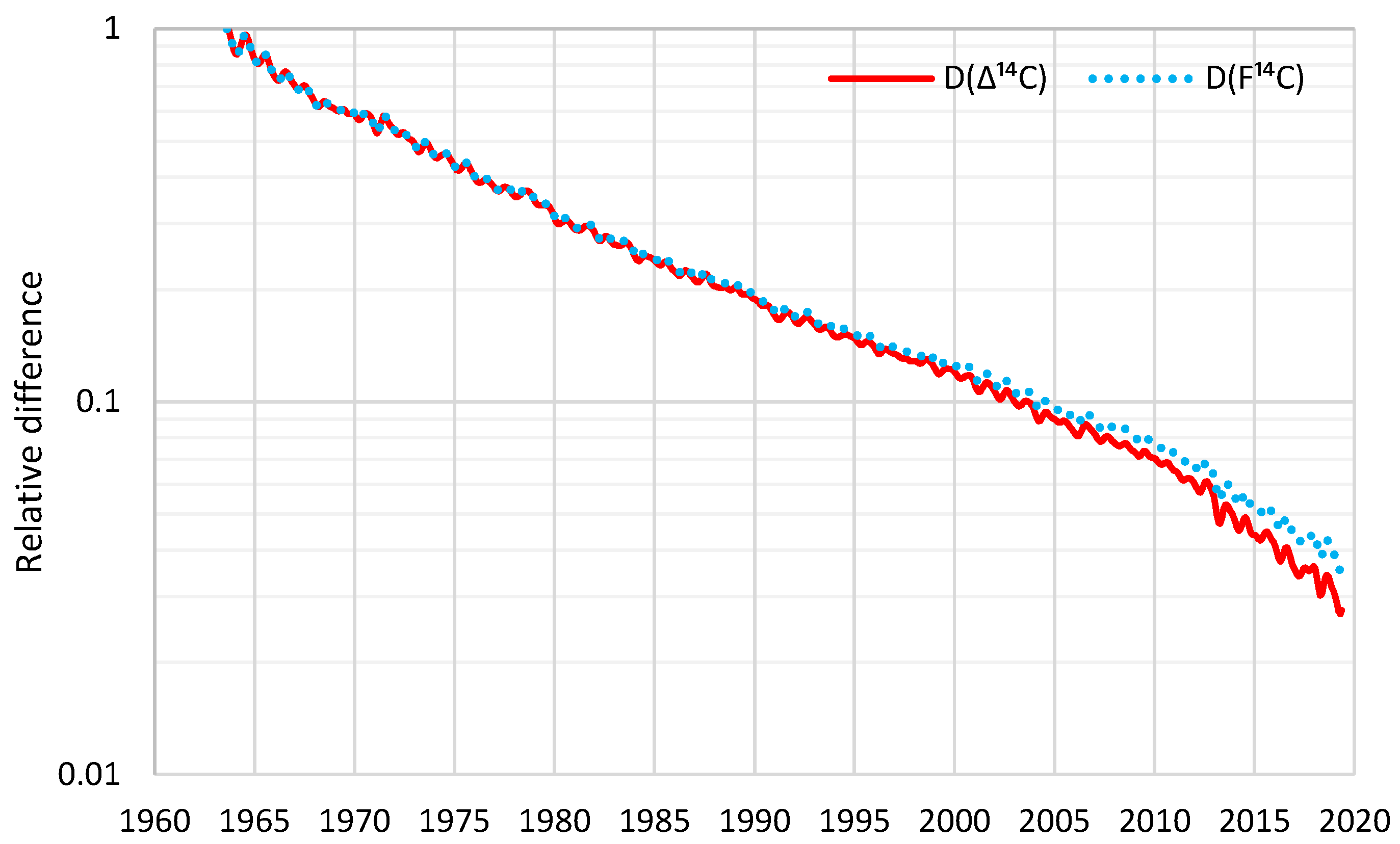
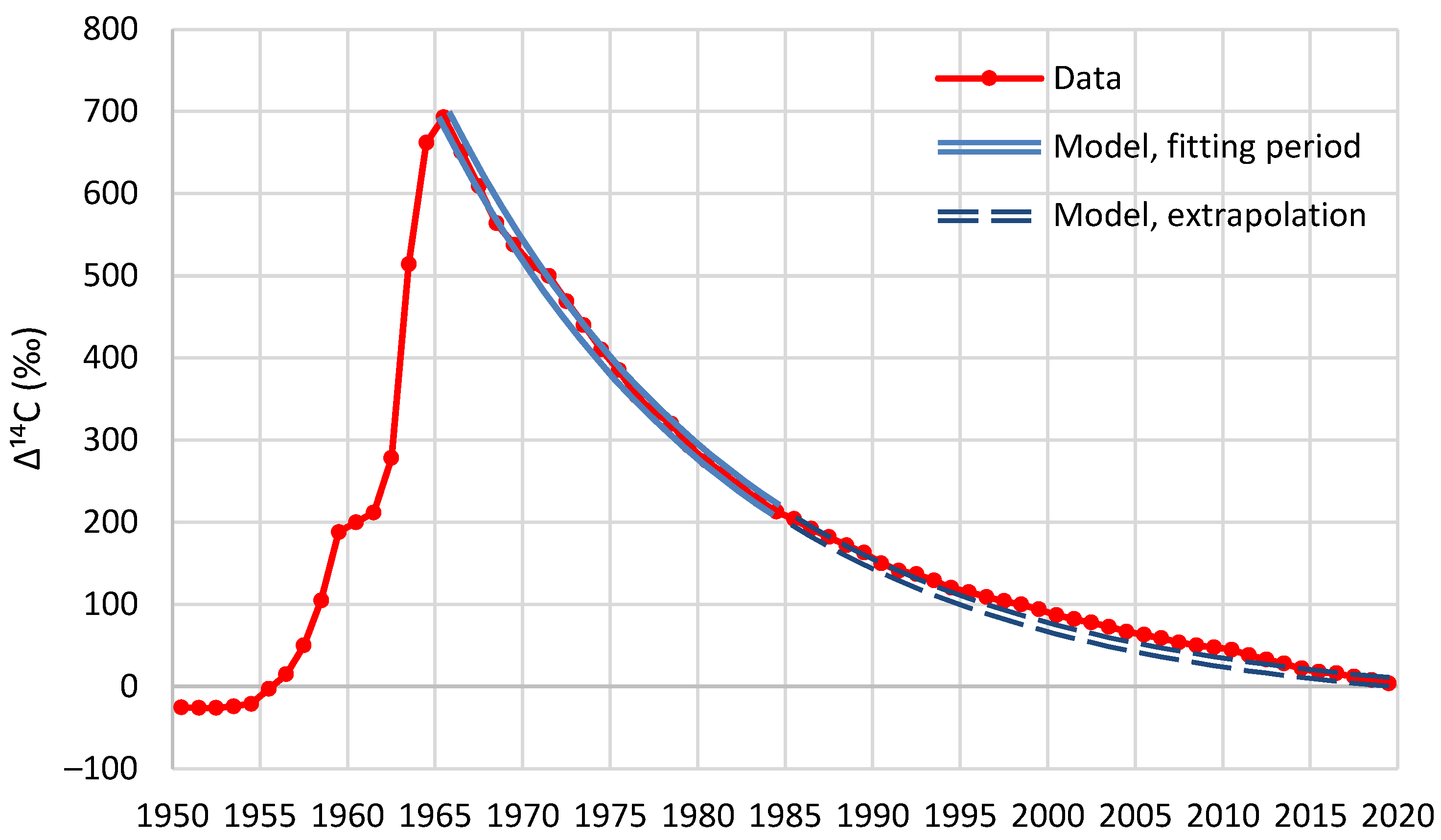
Decreases in atmospheric Δ14C from the mid-1960s to mid-1980s are mainly due to rapid exchange between the atmosphere and the biosphere and oceans […], while combustion of fossil fuels free of 14C is the main causal factor for the Δ14C decline since the late 1980s and early 1990s […]. Since the early and late 2000s, the atmospheric Δ14C values have been lower than those of the surface waters in the North and South Pacific Gyres, respectively, indicating the oceans might become a net 14C source (instead of a net 14C sink) of the atmosphere […]The last data points in our compiled monthly data at 2019.375 have respective F14C values of 1.0084 and 1.0195 for the NH and SH (see Supplementary Tables 2a–e), which are very close to the pre-bomb F14C value of slightly lower than 1. This indicates that clean-air F14C is likely to reach the pre-bomb value in the early 2020s […].
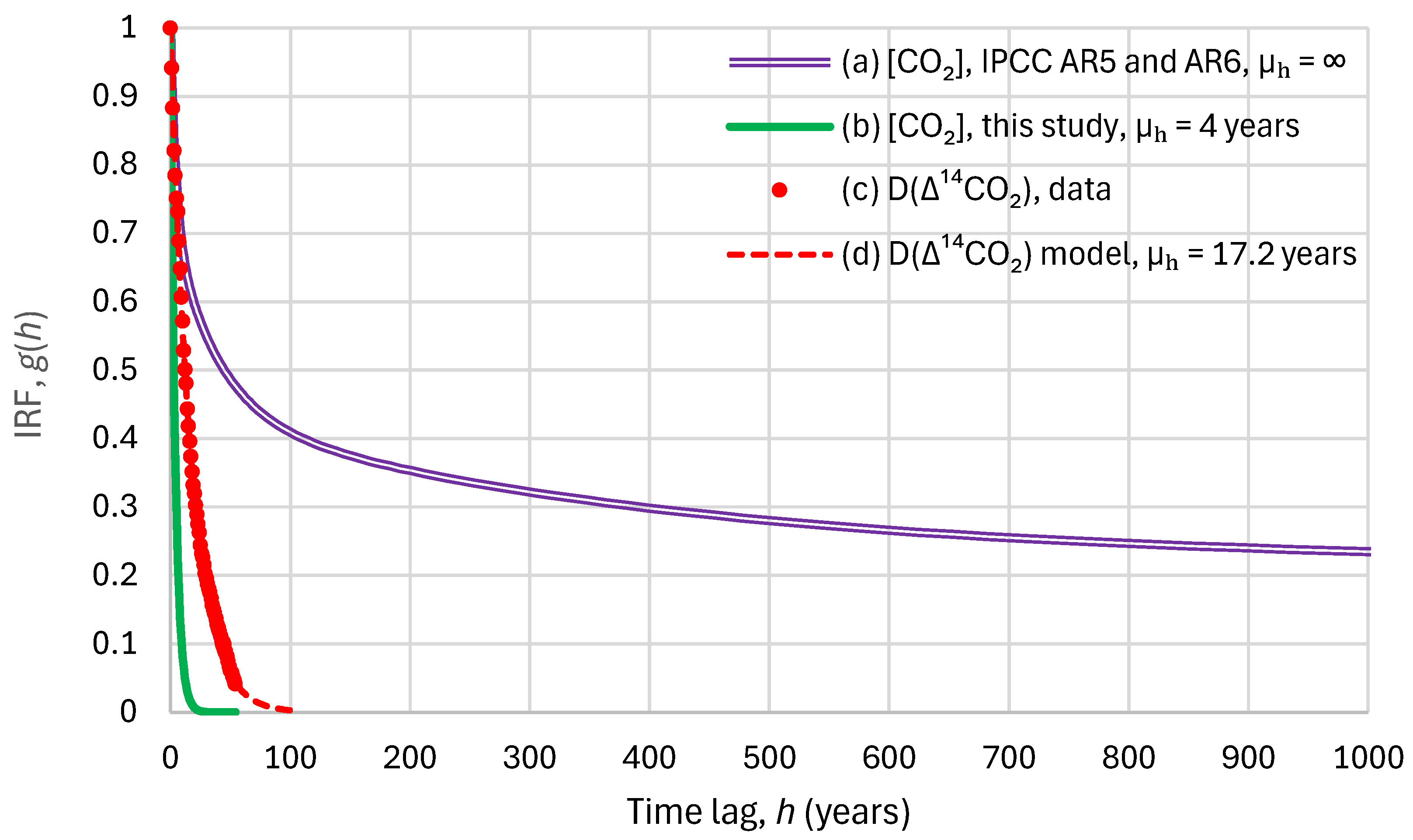
- The absorption of the heavier isotope 14C is subject to a function known as fractionation, that is, isotope discrimination. In particular, photosynthesis, during the exchange of O2 and CO2, discriminates against the heavier isotopes, and, as a result, 14C remains in the atmosphere for longer periods.
- As already noted above, most of the 14C produced by nuclear weapons testing was injected into the stratosphere, and the transport from the stratosphere to the troposphere is a slow process, substantially increasing the time lags.
- While, by its definition, the IRF presupposes zero inflows after the impulse, in reality, there were additional 14C inflows due to anomalous neutron flux (corresponding to a systematic increase of 5–10% over the last 30 years, according to Harde and Salby [74]). The fact that these 14C inflows were not considered in the model led to an artificial increase in the actual response time.
References
- Stendhal. The Life of Henry Brulard [Vie de Henry Brulard]; Sturrock, J., Translator; The New York Review of Books: New York, NY, USA, 1995; ISBN 978-1-681371-22-1. Available online: https://archive.org/details/stendhal-life-of-henry-brulard/ (accessed on 30 April 2024).
- Müller-Neuhof, B.; Betts, A.V.G.; Wilcox, G. Jawa, Northeastern Jordan: The first 14C dates for the early occupation phase. Z. Für Orient-Archäologie 2015, 8, 124–131. [Google Scholar]
- Fahlbusch, H. Early dams. Proc. ICE—Eng. Hist. Herit. 2009, 162, 13–18. [Google Scholar] [CrossRef]
- Makarewicz, C.A.; Finlayson, B. Constructing community in the Neolithic of southern Jordan: Quotidian practice in communal architecture. PLoS ONE 2018, 13, e0193712. [Google Scholar] [CrossRef]
- Bible, Genesis, 41. Available online: https://www.bible.com/el/bible/2503/GEN.41.GRCBRENT?parallel=392 (accessed on 30 April 2024).
- Bell, B. Climate and the History of Egypt: The Middle Kingdom. Am. J. Archaeol. 1975, 79, 223–269. [Google Scholar] [CrossRef]
- Said, R. The River Nile: Geology, Hydrology and Utilization; Pergamon Press: Oxford, UK, 1993. [Google Scholar]
- Hurst, H.E. Long term storage capacities of reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 776–808. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Wallis, J.R. Noah, Joseph, and operational hydrology. Water Resour. Res. 1968, 4, 909–918. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Stochastics of Hydroclimatic Extremes—A Cool Look at Risk, 3rd ed.; Kallipos Open Academic Editions: Athens, Greece, 2023; p. 391. ISBN 978-618-85370-0-2. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Onof, C.; Kundzewicz, Z.W.; Christofides, A. On Hens, Eggs, Temperatures and CO2: Causal Links in Earth’s Atmosphere. Sci 2023, 5, 35. [Google Scholar] [CrossRef]
- Peachey, B. Mitigating human enhanced water emission impacts on climate change. In Proceedings of the 2006 IEEE EIC Climate Change Conference, Ottawa, ON, Canada, 9–12 May 2006. [Google Scholar] [CrossRef]
- Sherwood, S.C.; Dixit, V.; Salomez, C. The global warming potential of near-surface emitted water vapor. Environ. Res. Lett. 2018, 13, 104006. [Google Scholar] [CrossRef]
- Li, X.; Peachey, B.; Maeda, N. Global warming and anthropogenic emissions of water vapor. Langmuir 2024, 40, 7701–7709. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Relative importance of carbon dioxide and water in the greenhouse effect: Does the tail wag the dog? Preprints 2024, 2024040309. [Google Scholar] [CrossRef]
- Klemeš, V. Watershed as semiinfinite storage reservoir. J. Irrig. Drain. Div. 1973, 99, 477–491. [Google Scholar] [CrossRef]
- Liu, Z.; Todini, E. Assessing the TOPKAPI non-linear reservoir cascade approximation by means of a characteristic lines solu-tion. Hydrol. Process. 2005, 19, 1983–2006. [Google Scholar] [CrossRef]
- Fenicia, F.; Savenije, H.H.G.; Matgen, P.; Pfister, L. Is the groundwater reservoir linear? Learning from data in hydrological modelling. Hydrol. Earth Syst. Sci. 2006, 10, 139–150. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Revisiting the global hydrological cycle: Is it intensifying? Hydrol. Earth Syst. Sci. 2020, 24, 3899–3932. [Google Scholar] [CrossRef]
- Nash, J.E.; Farrel, J.P. A graphical solution of the flood-routing equation for linear storage-discharge relation. Eos Trans. Am. Geophys. Union 1955, 36, 319–320. [Google Scholar]
- Langbein, W.B. Queuing theory and water storage. J. Hydraul. Div. 1958, 84, 1–24. [Google Scholar] [CrossRef]
- Nash, J.E. Systematic determination of unit hydrograph parameters. J. Geophys. Res. 1959, 64, 111–115. [Google Scholar] [CrossRef]
- Dooge, J. Linear Theory of Hydrologic Systems; No. 1468; Agricultural Research Service, US Department of Agriculture: Washington, DC, USA, 1973. Available online: https://books.google.com/books?id=iVgTfUhBi2gC (accessed on 20 April 2024).
- Klemeš, V. Probability distribution of outflow from a linear reservoir. J. Hydrol. 1974, 21, 305–314. [Google Scholar] [CrossRef]
- Klemeš, V.; Borůvka, L. Output from a cascade of discrete linear reservoirs with stochastic input. J. Hydrol. 1975, 27, 1–13. [Google Scholar] [CrossRef]
- Basha, H.A. Nonlinear reservoir routing: Particular analytical solution. J. Hydraul. Eng. 1994, 120, 624–632. [Google Scholar]
- Paik, K. Analytical derivation of reservoir routing and hydrological risk evaluation of detention basins. J. Hydrol. 2008, 352, 191–201. [Google Scholar] [CrossRef]
- Nematollahi, B.; Niazkar, M.; Talebbeydokhti, N. Analytical and numerical solutions to level pool routing equations for sim-plified shapes of inflow hydrographs. Iran. J. Sci. Technol. Trans. Civ. Eng. 2022, 46, 1–15. [Google Scholar] [CrossRef]
- Basha, H.A. Routing equations for detention reservoirs. J. Hydraul. Eng. 1995, 121, 885–888. [Google Scholar] [CrossRef]
- Berry, E.X. Human CO2 emissions have little effect on atmospheric CO2. Int. J. Atmos. Ocean. Sci. 2019, 3, 13–26. [Google Scholar]
- IPCC. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- IPCC. Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021; p. 2391. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Onof, C.; Christofides, A.; Kundzewicz, Z.W. Revisiting causality using stochastics: 1. Theory. Proc. R. Soc. A 2022, 478, 20210835. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Onof, C.; Christofides, A.; Kundzewicz, Z.W. Revisiting causality using stochastics: 2. Applications. Proc. R. Soc. A 2022, 478, 20210836. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Stochastic assessment of temperature—CO2 causal relationship in climate from the Phanerozoic through modern times. Math. Biosci. Eng. 2024, 21, 6560–6602. [Google Scholar] [CrossRef]
- Salby, M.L. Physics of the Atmosphere and Climate; Cambridge University Press: New York, NY, USA, 2012. [Google Scholar]
- Humlum, O.; Stordahl, K.; Solheim, J.E. The phase relation between atmospheric carbon dioxide and global temperature. Glob. Planet. Chang. 2013, 100, 51–69. [Google Scholar] [CrossRef]
- Harde, H. Scrutinizing the carbon cycle and CO2 residence time in the atmosphere. Glob. Planet. Chang. 2017, 152, 19–26. [Google Scholar] [CrossRef]
- Harde, H. What humans contribute to atmospheric CO2: Comparison of carbon cycle models with observations. Earth Sci. 2019, 8, 139–159. [Google Scholar]
- Poyet, P. The Rational Climate e-Book, 2nd ed.; ResearchGate; ISBN 978-99957-1-929-62022. Available online: https://www.researchgate.net/publication/347150306 (accessed on 30 April 2024).
- Stallinga, P. Residence time vs. adjustment time of carbon dioxide in the atmosphere. Entropy 2023, 25, 384. [Google Scholar] [CrossRef] [PubMed]
- Joos, F.; Roth, R.; Fuglestvedt, J.S.; Peters, G.P.; Enting, I.G.; von Bloh, W.; Brovkin, V.; Burke, E.J.; Eby, M.; Edwards, N.R.; et al. Carbon dioxide and climate impulse response functions for the computation of greenhouse gas metrics: A multi-model analysis. Atmos. Chem. Phys. 2013, 13, 2793–2825. [Google Scholar] [CrossRef]
- Joos, F.; Bruno, M.; Fink, R.; Siegenthaler, U.; Stocker, T.F.; Le Quere, C.; Sarmiento, J.L. An efficient and accurate representation of complex oceanic and biospheric models of anthropogenic carbon uptake. Tellus B 1996, 48, 397–417. [Google Scholar] [CrossRef]
- Archer, D.; Brovkin, V. The millennial atmospheric lifetime of anthropogenic CO2. Clim. Chang. 2008, 90, 283–297. [Google Scholar] [CrossRef]
- Archer, D.; Eby, M.; Brovkin, V.; Ridgwell, A.; Cao, L.; Mikolajewicz, U.; Caldeira, K.; Matsumoto, K.; Munhoven, G.; Mon-tenegro, A.; et al. Atmospheric lifetime of fossil fuel carbon dioxide. Annu. Rev. Earth Planet. Sci. 2009, 37, 117–134. [Google Scholar] [CrossRef]
- MIT Climate Portal Writing Team Featuring Guest Expert Ed Boyle, How Do We Know How Long Carbon Dioxide Remains in the Atmosphere? MIT Climate Portal. 2023. Available online: https://climate.mit.edu/ask-mit/how-do-we-know-how-long-carbon-dioxide-remains-atmosphere (accessed on 30 April 2024).
- Buis, A. The Atmosphere: Getting a Handle on Carbon Dioxide, NASA’s Jet Propulsion Laboratory. 2019. Available online: https://science.nasa.gov/earth/climate-change/greenhouse-gases/the-atmosphere-getting-a-handle-on-carbon-dioxide/ (accessed on 30 April 2024).
- Berry, E. Why Climate Change Is a Fraud. Available online: https://edberry.com/why-climate-change-is-a-fraud/ (accessed on 30 April 2024).
- Myhre, G.; Shindell, D.; Bréon, F.-M.; Collins, W.; Fuglestvedt, J.; Huang, J.; Koch, D.; Lamarque, J.-F.; Lee, D.; Mendoza, B.; et al. Anthropogenic and natural radiative forcing supplementary material. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; p. 1535. Available online: https://www.ipcc.ch/report/ar5/wg1/chapter-8sm-anthropogenic-and-natural-radiative-forcing-supplementary-material/ (accessed on 30 April 2024).
- Strassmann, K.M.; Joos, F. The Bern Simple Climate Model (BernSCM) v1.0: An extensible and fully documented open-source re-implementation of the Bern reduced-form model for global carbon cycle–climate simulations. Geosci. Model Dev. 2018, 11, 1887–1908. [Google Scholar] [CrossRef]
- Luo, X.; Xia, T.; Huang, J.; Xiong, D.; Ridoutt, B. Radiative forcing climate footprints in the agricultural sector: Comparison of models from the IPCC 5th and 6th Assessment Reports. Farming Syst. 2023, 1, 100057. [Google Scholar] [CrossRef]
- Keeling, C.D.; Piper, S.C.; Whorf, T.P.; Keeling, R.F. Evolution of natural and anthropogenic fluxes of atmospheric CO2 from 1957 to 2003. Tellus B Chem. Phys. Meteorol. 2011, 63, 1–22. [Google Scholar] [CrossRef]
- Scripps CO2 Program, Sampling Station Records. Available online: https://scrippsco2.ucsd.edu/data/atmospheric_co2/sampling_stations.html (accessed on 30 April 2024).
- Keeling, C.D.; Piper, S.C.; Bacastow, R.B.; Wahlen, M.; Whorf, T.P.; Heimann, M.; Meijer, H.A. Exchanges of Atmospheric CO2 and 13CO2 with the Terrestrial Biosphere and Oceans from 1978 to 2000. I. Global Aspects; SIO Reference Series, No. 01-06; Scripps Institution of Oceanography: San Diego, CA, USA, 2001; p. 88. [Google Scholar]
- Keeling, C.D.; Piper, S.C.; Bacastow, R.B.; Wahlen, M.; Whorf, T.P.; Heimann, M.; Meijer, H.A. Atmospheric CO2 and 13CO2 exchange with the terrestrial biosphere and oceans from 1978 to 2000: Observations and carbon cycle implications. In A History of Atmospheric CO2 and Its Effects on Plants; Ehleringer, J.R., Cerling, T.E., Dearing, M.D., Eds.; Springer: New York, NY, USA, 2005; pp. 83–113. [Google Scholar]
- Ritchie, H.; Roser, M. CO2 Emissions. OurWorldInData.org. 2020. Available online: https://ourworldindata.org/co2-emissions (accessed on 30 April 2024).
- Global Carbon Budget (2023)—With Major Processing by Our World in Data. “Annual CO2 Emissions—GCB” [Dataset]. Global Carbon Project, “Global Carbon Budget” [Original Data]. Available online: https://ourworldindata.org/co2-and-greenhouse-gas-emissions (accessed on 30 April 2024).
- International Energy Agency. CO2 Emissions in 2023. 2024. Available online: https://iea.blob.core.windows.net/assets/33e2badc-b839-4c18-84ce-f6387b3c008f/CO2Emissionsin2023.pdf (accessed on 30 April 2024).
- Koutsoyiannis, D.; Kundzewicz, Z.W. Atmospheric temperature and CO2: Hen-or-egg causality? Sci 2020, 2, 83. [Google Scholar] [CrossRef]
- Patel, K.F.; Bond-Lamberty, B.; Jian, J.L.; Morris, K.A.; McKever, S.A.; Norris, C.G.; Zheng, J.; Bailey, V.L. Carbon flux estimates are sensitive to data source: A comparison of field and lab temperature sensitivity data. Environ. Res. Lett. 2022, 17, 113003. [Google Scholar] [CrossRef]
- Robinson, C. Microbial respiration, the engine of ocean deoxygenation. Front. Mar. Sci. 2019, 5, 533. [Google Scholar] [CrossRef]
- Klemeš, V. Operational testing of hydrological simulation models. Hydrol. Sci. J. 1986, 31, 13–24. [Google Scholar] [CrossRef]
- Granger, C.W. Investigating causal relations by econometric models and cross-spectral methods. Econometrica 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Vournas, C. Revisiting the greenhouse effect—A hydrological perspective. Hydrol. Sci. J. 2024, 69, 151–164. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Net isotopic signature of atmospheric CO2 sources and sinks: No change since the Little Ice Age. Sci 2024, 6, 17. [Google Scholar] [CrossRef]
- Graven, H.; Keeling, R.F.; Rogelj, J. Changes to carbon isotopes in atmospheric CO2 over the industrial era and into the future. Glob. Biogeochem. Cycles 2020, 34, e2019GB006170. [Google Scholar] [CrossRef] [PubMed]
- Hua, Q.; Turnbull, J.C.; Santos, G.M.; Rakowski, A.Z.; Ancapichún, S.; De Pol-Holz, R.; Hammer, S.; Lehman, S.J.; Levin, I.; Miller, J.B.; et al. Atmospheric radiocarbon for the period 1950–2019. Radiocarbon 2022, 64, 723–745. [Google Scholar] [CrossRef]
- Kondev, F.G.; Wang, M.; Huang, W.J.; Naimi, S.; Audi, G. The NUBASE2020 evaluation of nuclear physics properties. Chin. Phys. C 2021, 45, 030001. [Google Scholar] [CrossRef]
- Starr, C. Atmospheric CO2 residence time and the carbon cycle. Energy 1993, 18, 1297–1310. [Google Scholar] [CrossRef]
- Berry, E.X. The impact of human CO2 on atmospheric CO2. Sci. Clim. Chang. 2021, 1, 1–46. [Google Scholar]
- Berry, E.X. Nature Controls the CO2 Increase. Sci. Clim. Chang. 2023, 3, 68–91. [Google Scholar]
- Salby, M.; Harde, H. Control of atmospheric CO2-Part I: Relation of carbon 14 to the removal of CO2. Sci. Clim. Chang. 2021, 1, 177–195. [Google Scholar]
- Salby, M.; Harde, H. Control of atmospheric CO2- Part II: Influence of Tropical Warming. Sci. Clim. Chang. 2021, 1, 197–213. [Google Scholar]
- Harde, H.; Salby, M. What controls the atmospheric CO2 level. Sci. Clim. Chang. 2021, 1, 54–69. [Google Scholar]
- Andrews, D.E. Correcting an error in some interpretations of atmospheric 14C data. Earth Sci. 2020, 9, 126–129. [Google Scholar]
- Reimer, P.J.; Brown, T.A.; Reimer, R.W. Discussion: Reporting and calibration of postbomb 14C data. Radiocarbon 2004, 46, 1299–1304. [Google Scholar]
- Currie, L.A.; Stafford, T.W.; Sheffield, A.E.; Klouda, G.A.; Wise, S.A.; Fletcher, R.A.; Donahue, D.J.; Jull, A.T.; Linick, T.W. Microchemical and molecular dating. Radiocarbon 1989, 31, 448–463. [Google Scholar]
- Stenström, K.; Skog, G.; Georgiadou, E.; Genberg, J.; Mellström, A. A Guide to Radiocarbon Units and Calculations. Lund University, Department of Physics, Internal Report LUNFD6(NFFR-3111)/1-17/(2011). 2011. Available online: https://portal.research.lu.se/files/5555659/2173661.pdf (accessed on 30 July 2024).

| Site | (Years) | (Years) | ||||||
|---|---|---|---|---|---|---|---|---|
| Mauna Loa | 1 | 5.445 | 1.973 | 2.115 | 0.953 | 5.247 | 1.462 | 2.855 |
| Barrow | 1 | 5.757 | 4.181 | 1.370 | 0.953 | 5.149 | 3.104 | 1.633 |
| Site | (Years) | (Years) | ||||||
|---|---|---|---|---|---|---|---|---|
| Mauna Loa | 1 | 5.399 (5.445) | 2.126 (1.973) | 2.092 (2.115) | 0.935 (0.953) | 5.164 (5.247) | 1.578 (1.462) | 2.858 (2.855) |
| Barrow | 1 | 5.710 (5.757) | 4.174 (4.181) | 1.368 (1.370) | 0.935 (0.953) | 5.134 (5.149) | 2.207 (3.104) | 1.594 (1.633) |
| ↓Site | (ppm) | (ppm/year) | ||||
|---|---|---|---|---|---|---|
| Period→ | All | 1958–2002 | 2003–2023 | All | 1958–2002 | 2003–2023 |
| Calibration over the entire period | ||||||
| Mauna Loa | 99.94 | 99.82 | 99.64 | 85.81 | 87.25 | 83.30 |
| Barrow | 99.77 | 99.25 | 99.16 | 85.30 | 85.82 | 84.64 |
| Calibration over the period 1958–2002 | ||||||
| Mauna Loa | 99.73 | 99.90 | 96.24 | 85.57 | 87.46 | 82.25 |
| Barrow | 99.55 | 99.44 | 95.88 | 84.85 | 86.18 | 83.13 |
| Site | , Beginning Year | , Ending Year | ||||
|---|---|---|---|---|---|---|
| Calibration over the entire period | ||||||
| Mauna Loa | 2.20 | 6.15 | 4.17 | 3.68 | 3.68 | 3.70 |
| Barrow | 1.55 | 9.91 | 5.73 | 3.91 | 3.94 | 3.95 |
| Calibration over period 1958–2002 | ||||||
| Mauna Loa | 2.32 | 6.57 | 4.45 | 3.91 | 3.93 | 3.98 |
| Barrow | 1.53 | 9.88 | 5.70 | 3.89 | 3.92 | 3.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koutsoyiannis, D. Refined Reservoir Routing (RRR) and Its Application to Atmospheric Carbon Dioxide Balance. Water 2024, 16, 2402. https://doi.org/10.3390/w16172402
Koutsoyiannis D. Refined Reservoir Routing (RRR) and Its Application to Atmospheric Carbon Dioxide Balance. Water. 2024; 16(17):2402. https://doi.org/10.3390/w16172402
Chicago/Turabian StyleKoutsoyiannis, Demetris. 2024. "Refined Reservoir Routing (RRR) and Its Application to Atmospheric Carbon Dioxide Balance" Water 16, no. 17: 2402. https://doi.org/10.3390/w16172402
APA StyleKoutsoyiannis, D. (2024). Refined Reservoir Routing (RRR) and Its Application to Atmospheric Carbon Dioxide Balance. Water, 16(17), 2402. https://doi.org/10.3390/w16172402







