Investigation of Improved Energy Dissipation in Stepped Spillways Applying Bubble Image Velocimetry
Abstract
:1. Introduction
2. Materials and Methods
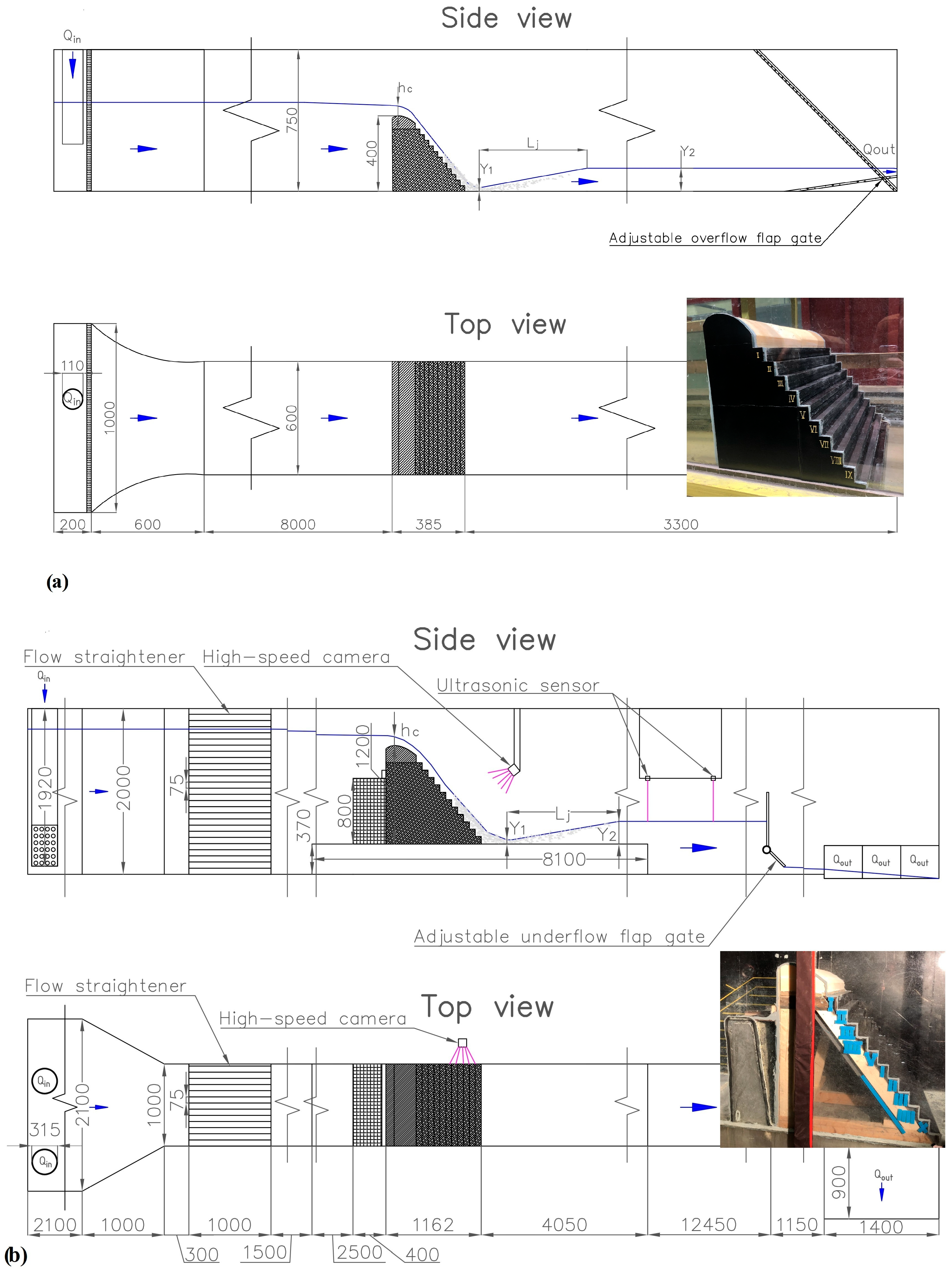
2.1. Experimental Set-Up and Procedure
2.2. Crest Splitters
2.3. Procedure for BIV
2.4. Experiment Parameters
3. Experimental Results
3.1. Post-Processing of the Flow Characteristics
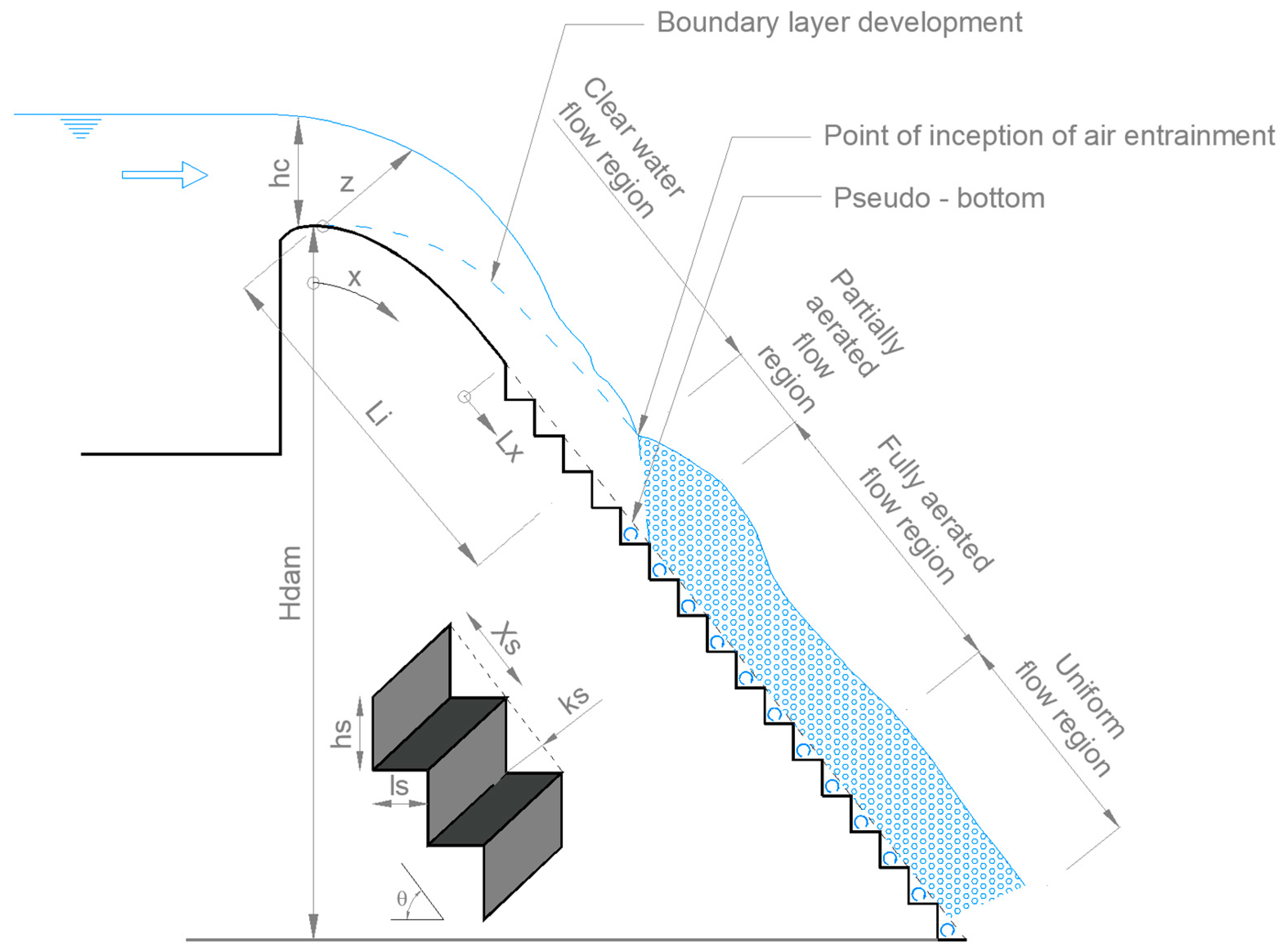
3.2. Inception of Free-Surface Aeration
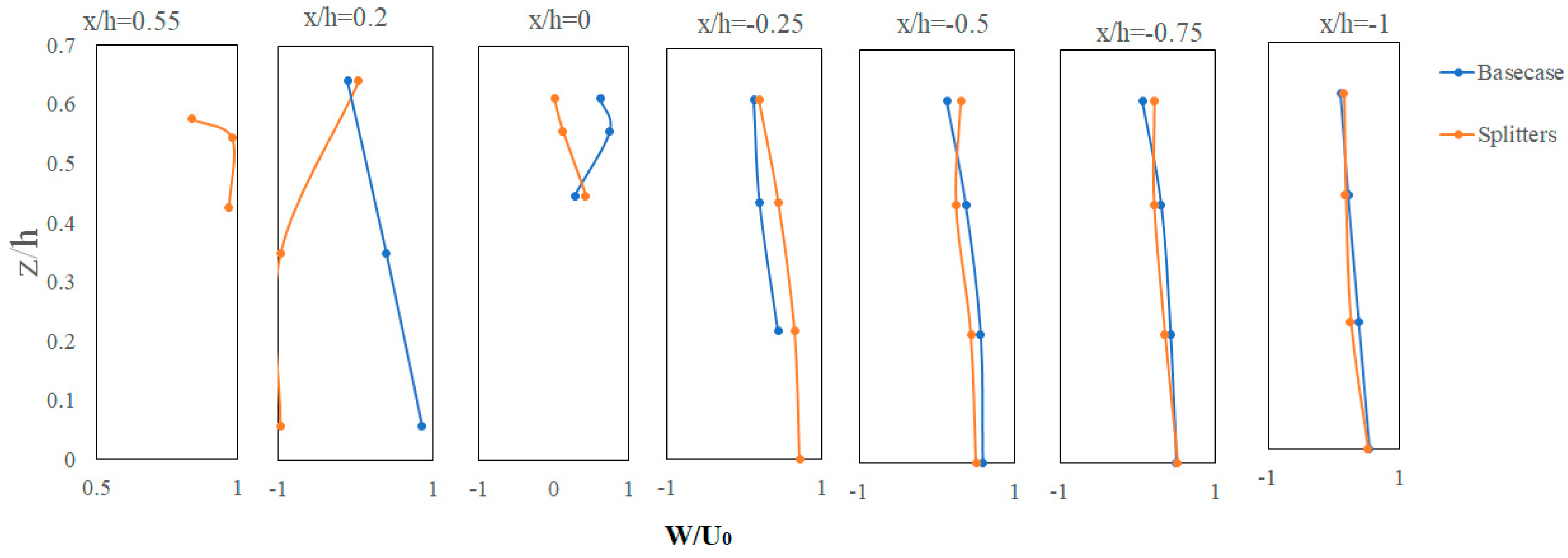
3.3. Velocity Profiles over Step Edges
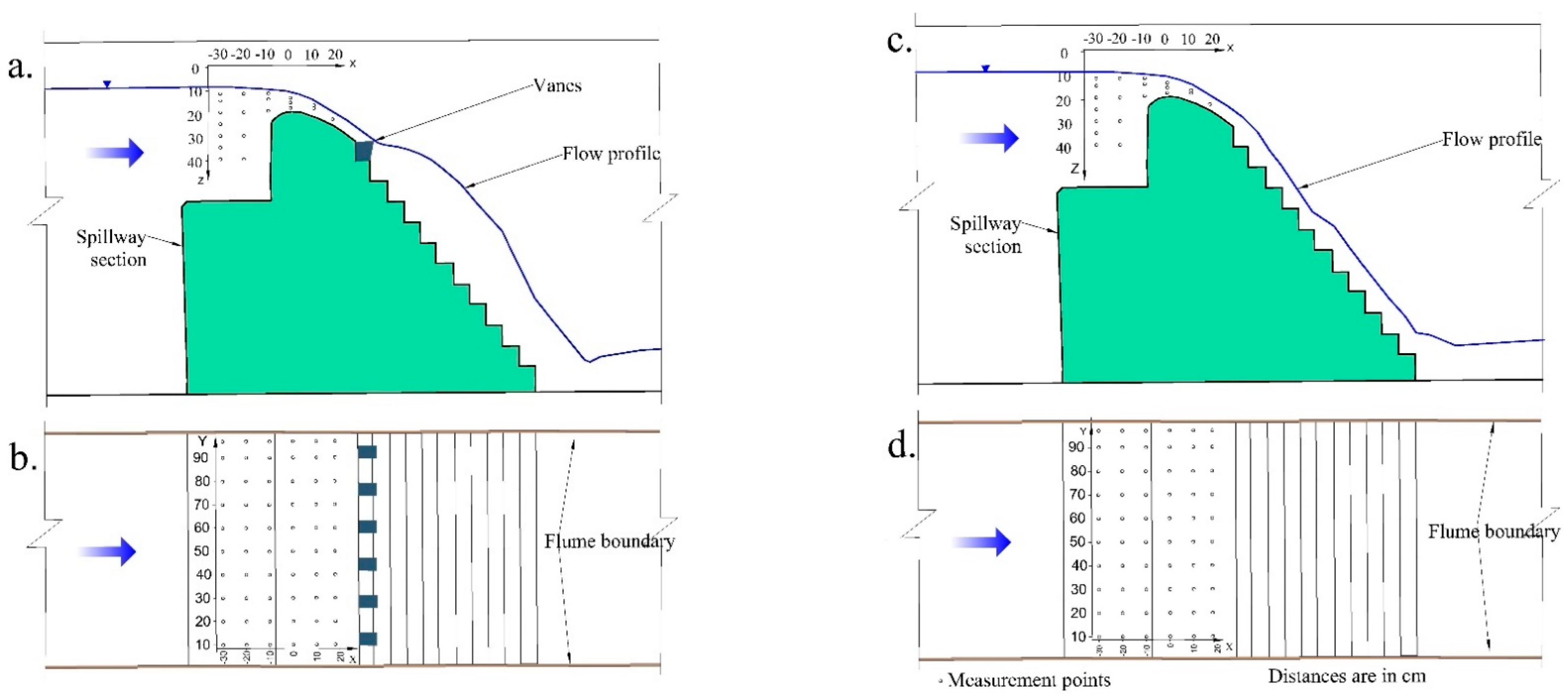
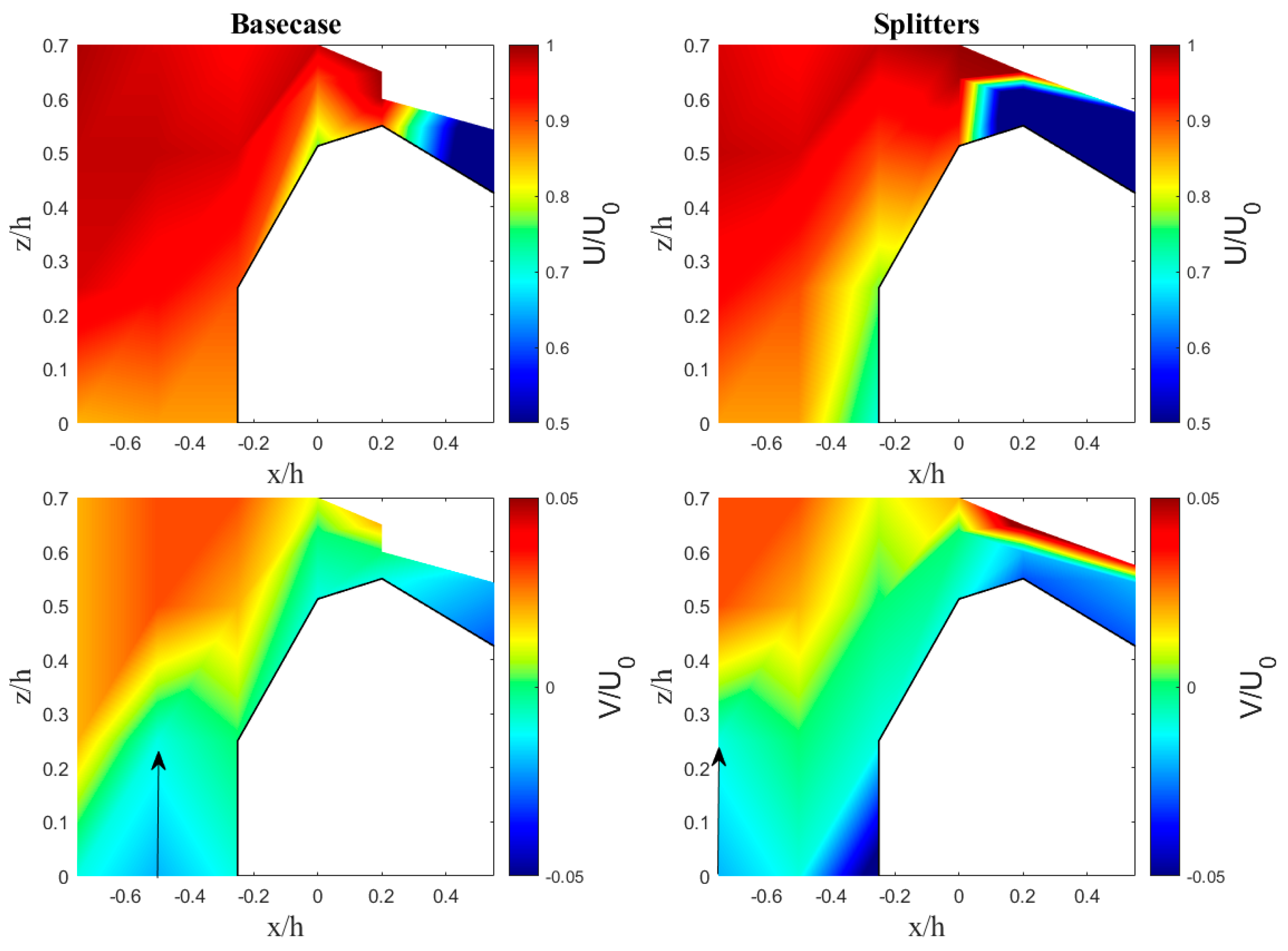
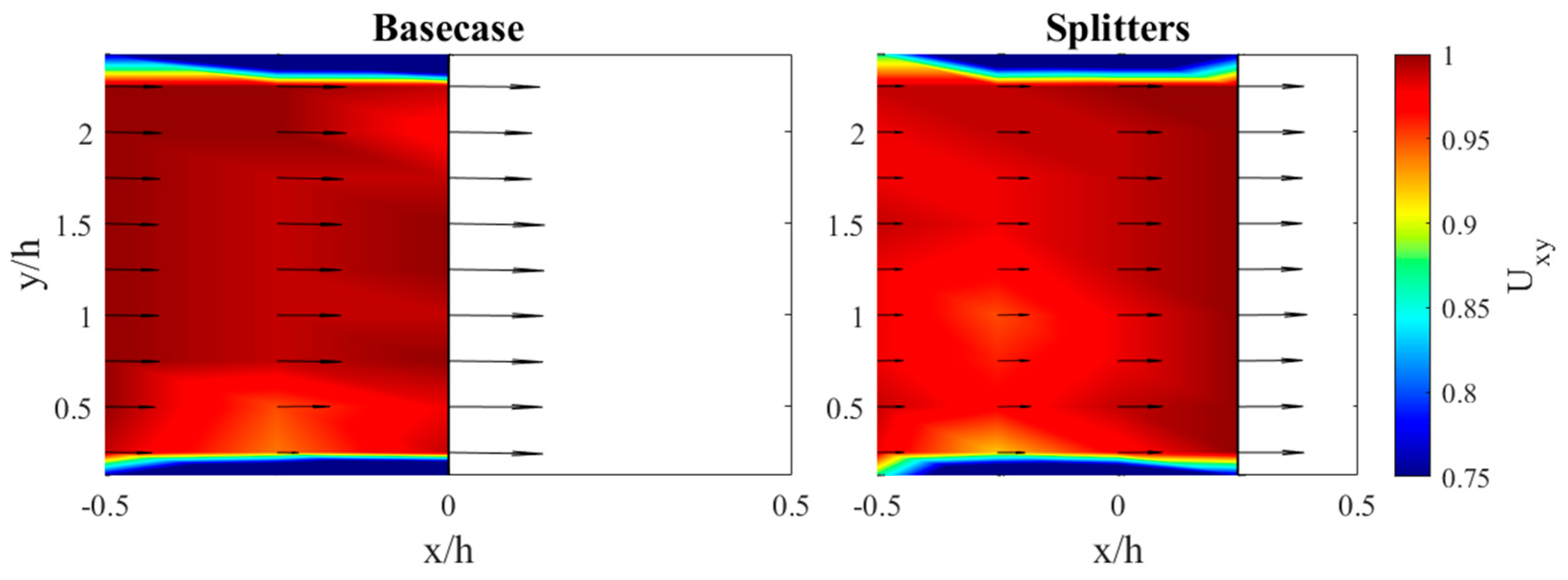
3.4. Flow Patterns on Ogee Crest
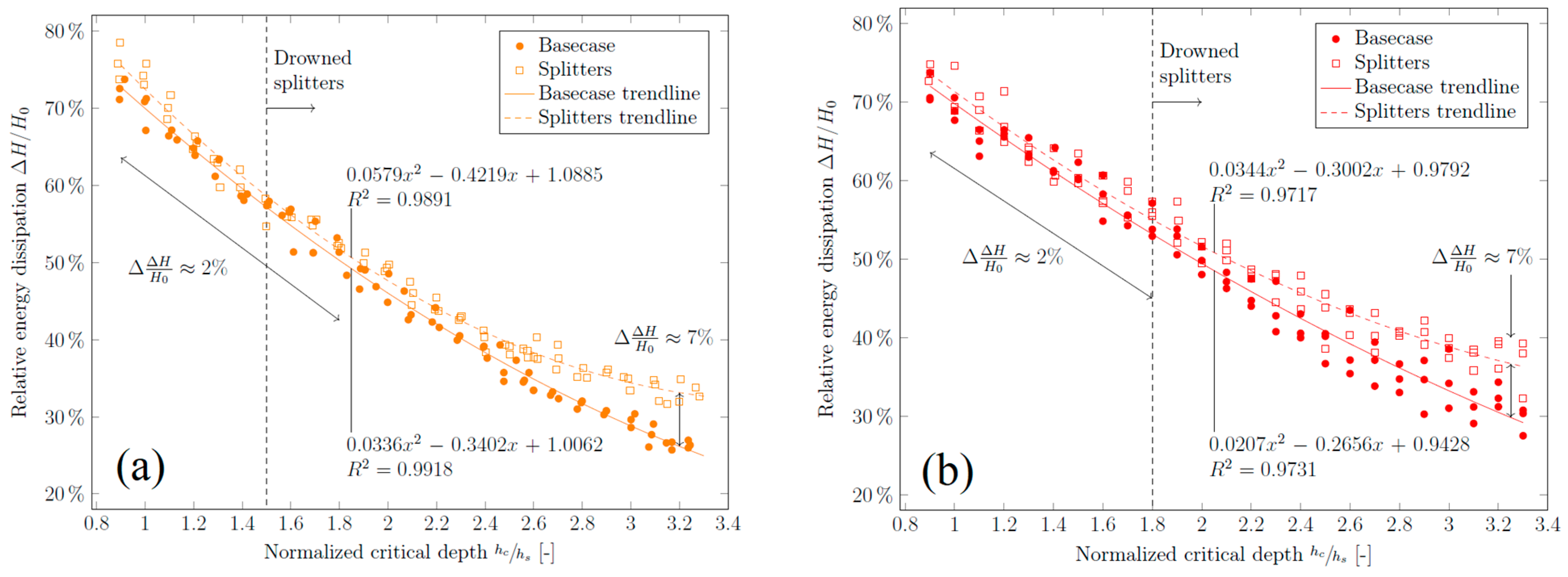
3.5. Energy Dissipation
4. Discussion
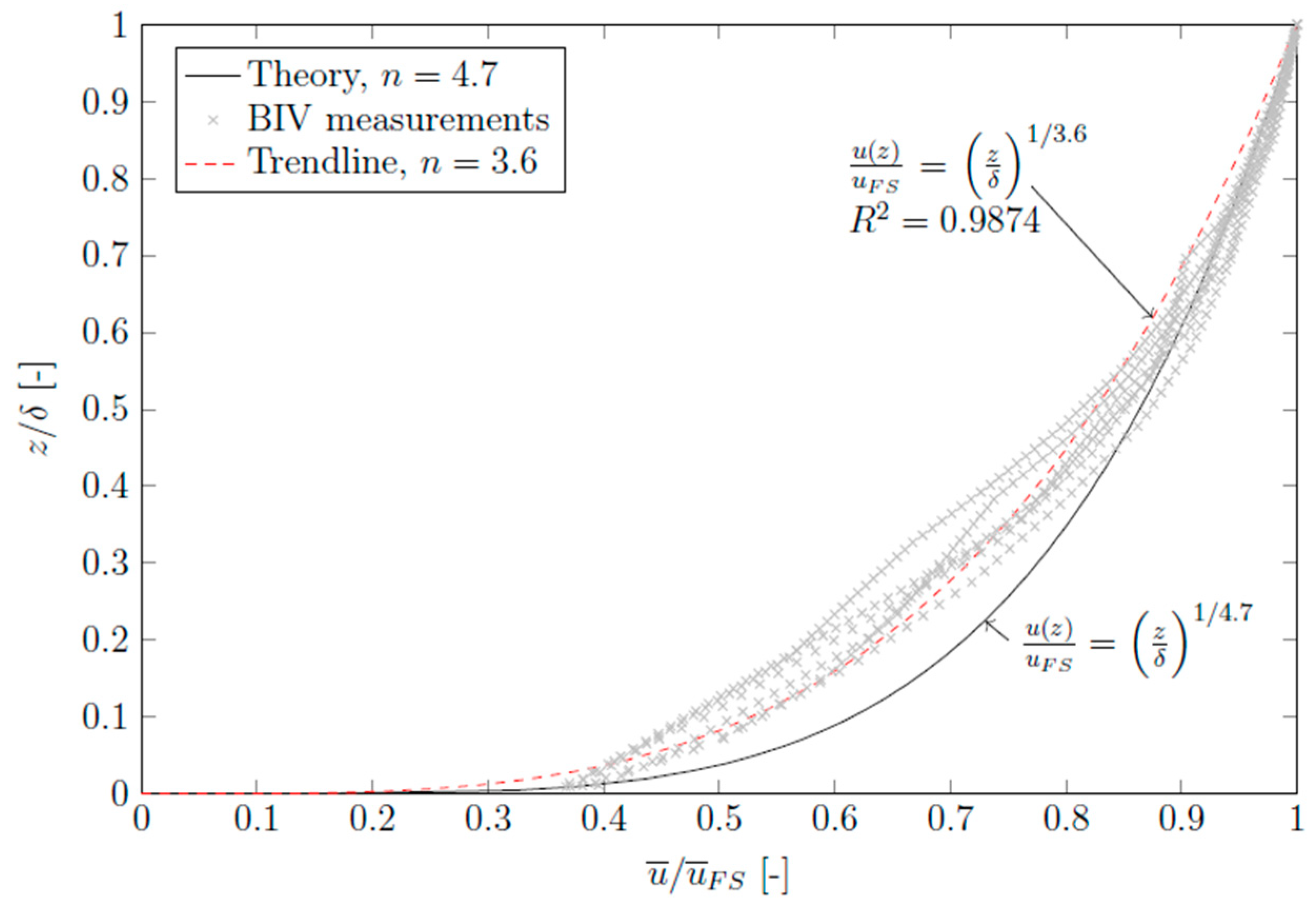
4.1. Flow Regimes and Velocity Distribution in the Step Edges
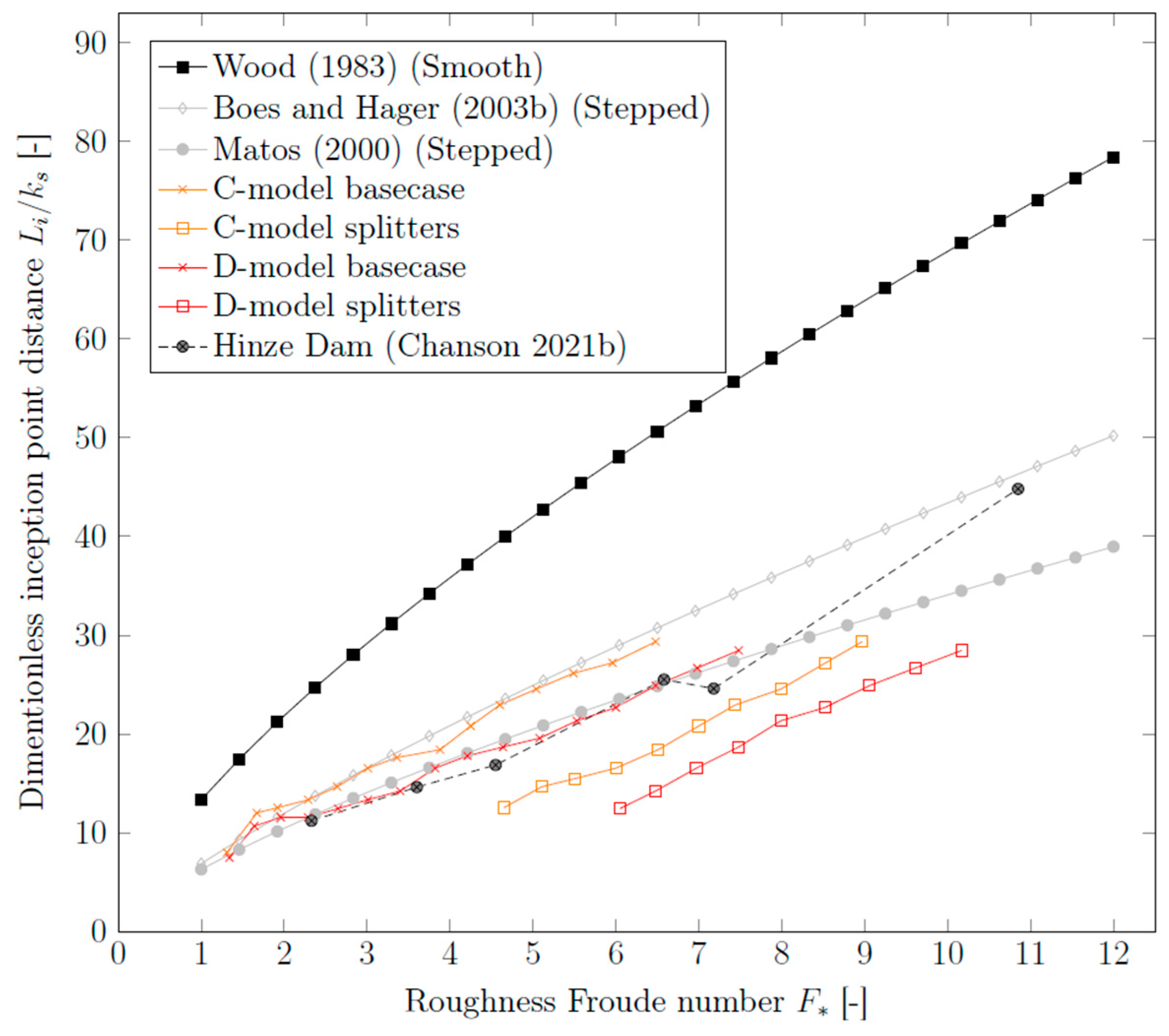
4.2. Length of Inception and Cavitation Potential
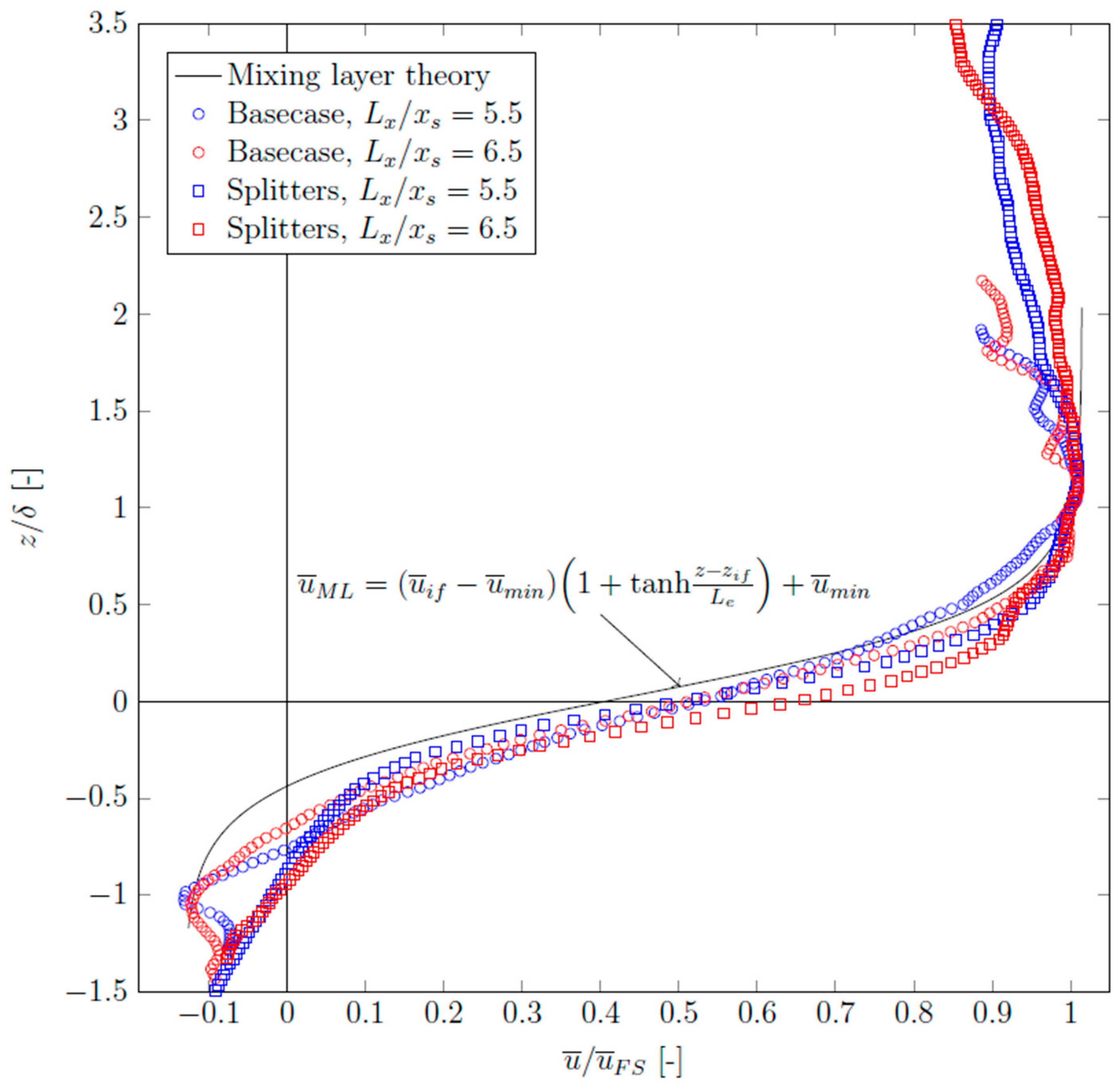
4.3. Effect of Crest Splitters on Velocity Patterns above the Ogee Crest and Energy Dissipation
4.4. Scale Effects and Uncertainty
5. Conclusions
- −
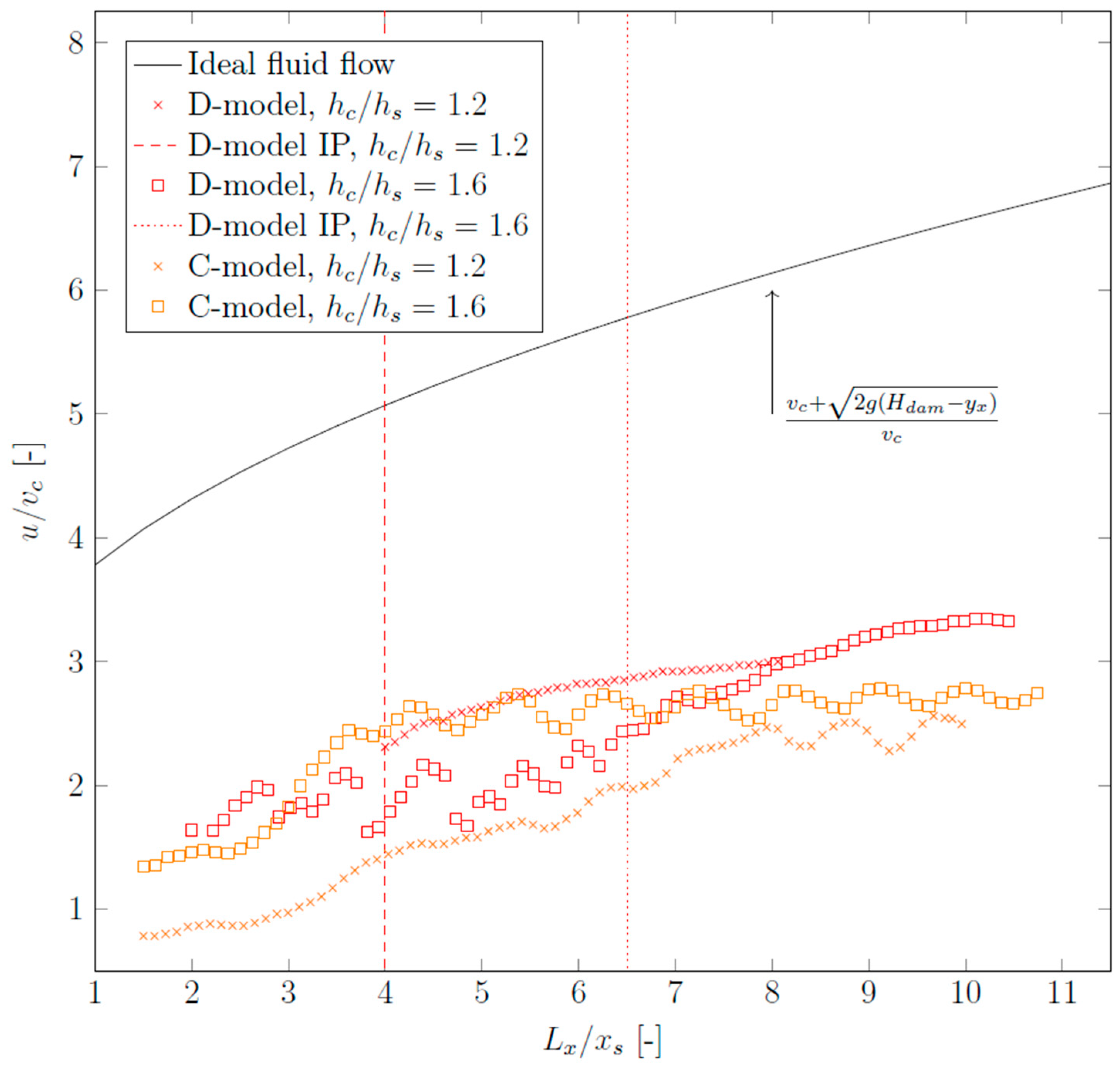
- In the experiments, it was observed that the flow region developed in shear flow consists of a turbulent boundary layer, with ideal fluid flow above it. A rapidly changing flow movement was observed along the steps. Bernoulli’s principle was used to calculate the energy distribution, assuming that the flow moved in the downward direction.
- −
- The splitters were found to increase relative energy dissipation by 7%. In addition to enhancing energy dissipation, the splitters reduced the length of inception to = 10, thereby lowering the potential for subsequent cavitation. This resulted in an increase in the maximum allowable unit discharge. Consequently, crest splitters can be considered a practical, viable, and cost-effective measure to improve energy dissipation in stepped spillways, applicable to both existing dams and new projects.
- −
- In the experiment with the splitter, the horizontal velocity vector u around the ogee crest showed a significant decrease. Additionally, the vertical velocity vector v contributed to turbulence by changing direction, resulting in decreased average velocities in front of and behind the ogee crest, thereby reducing energy on the downstream side of the spillway.
- −
- BIV was found to be a straightforward and highly effective technique for accurately measuring and determining flow characteristics in aerated flow conditions, likely the best practice for such applications. BIV enables the collection of large quantities of high-quality data with standard camera equipment, allowing for the extraction of detailed information and the production of dense plots without the need for commercial software or extensive processing capabilities.
- −
- The scale effects observed in this study align well with established theory. Severe scale effects were noted in the air–water flow in the smaller-scaled model, underscoring the importance of using a larger scale to accurately study highly turbulent two-phase flow conditions. The findings closely correspond to established theory regarding the valid length scales for studying highly turbulent two-phase flow under Froude similitude.
- −
- While the smaller C-Model appears unfit for the study of two-phase flow, the change in relative energy dissipation from the base case to the splitter configuration is nearly identical for the two different scale models, supporting the findings in the primary D-Model.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Notations
| Flume width [L] | |
| Air concentration at the pseudo-bottom [-] | |
| Air concentration at the pseudo-bottom at the point of inception [-] | |
| Mean air concentration at point of inception [-] | |
| D | Flow depth [-] |
| Equivalent clear water hydraulic diameter in the quasi-uniform zone [-] | |
| Darcy–Weisbach friction factor [-] | |
| Froude number, [-] | |
| Roughness Froude number [-] | |
| Gravitational acceleration [L/T2] | |
| H | Ogee height [L] |
| Local energy head [L] | |
| Vertical distance from the starting point of the inception [L] | |
| Height of flume [L] | |
| Total head [L] | |
| Critical depth, [L] | |
| Height of the step [L] | |
| Normal height of the step [L] | |
| Characteristic mixing layer length scale [L] | |
| Longitudinal distance from the top of the crest to the inception point [L] | |
| Length of the step [L] | |
| Longitudinal distance from the top of the first step [L] | |
| Power-law exponent [-] | |
| Number of steps along the chute [-] | |
| Pressure at flow surface [N/m2] | |
| Vapor pressure [M/LT2] | |
| Water discharge [L3/T] | |
| Maximum water discharge [L3/T] | |
| Unit water discharge [L2/T] | |
| Upstream radius 1 for ogee weir [L] | |
| Upstream radius 2 for ogee weir [L] | |
| Reynolds number [-] | |
| Hydraulic radius [L] | |
| Streamwise water velocity [L/T] | |
| Time-averaged streamwise velocity [L/T] | |
| Incoming velocity to the hydraulic jump [L/T] | |
| Air–water mixture velocity at the flow depth [L/T] | |
| Free-stream velocity [L/T] | |
| Velocity at the infection point [L/T] | |
| Air–water mixture velocity [L/T] | |
| Time-averaged mixture velocity [L/T] | |
| Minimum velocity in the mixing layer [L/T] | |
| Mixing layer velocity [L/T] | |
| Weber number [-] | |
| X, Y, Z | Distances in x, y, z directions, respectively [L] |
| Dimensionless distance from the inception point [-] | |
| Longitudinal distance between two step edges [L] | |
| Step edge elevation above the datum [L] | |
| Flow depth with 90% air concentration [L] | |
| Inflection point elevation above pseudo-bottom [L] | |
| Mixture depth at point of inception [L] | |
| u, v, w | Instantaneous velocity components [L/T] |
| Mean velocity components [L/T] | |
| Average approach flow velocity [L/T] | |
| Non-dimensional mean resultant velocity [-] | |
| ΔH | Energy dissipation rate [-] |
| Boundary layer thickness [L] | |
| Correction factor for the singular loss when the flow changes direction from the stepped spillway to the horizontal bed [-] | |
| Angle of the slope of the chute [] | |
| Length scale factor in Froude similitude [-] | |
| Density of water [M/L3] | |
| Cavitation index [-] | |
| Critical cavitation index [-] |
References
- Chanson, H. Hydraulics of Stepped Chutes and Spillways; Balkema Publ: Lisse, The Netherlands, 2001; ISBN 9058093522. [Google Scholar]
- Kokpinar, M.A. Flow over a stepped chute with and without macro-roughness elements. Can. J. Civ. Eng. 2004, 31, 880–891. [Google Scholar] [CrossRef]
- Zhang, G.; Chanson, H. Application of local optical flow methods to high-velocity free-surface flows: Validation and application to stepped chutes. Exp. Therm. Fluid Sci. 2018, 90, 186–199, ISSN 0894-1777. [Google Scholar] [CrossRef]
- Sánchez-Juny, M.; Estrella, S.; Matos, J.; Bladé, E.; Martínez-Gomariz, E.; Bonet Gil, E. Velocity Measurements in Highly Aerated Flow on a Stepped. Water 2022, 14, 2587. [Google Scholar] [CrossRef]
- Kramer, M. Velocities and Turbulent Stresses of Free-Surface Skimming Flows over Triangular Cavities. J. Hydraul. Eng. 2023, 149, 04023012. [Google Scholar] [CrossRef]
- Rajaratnam, N. An experimental study of air entrainment characteristics of the hydraulic jump. J. Inst. Eng. 1962, 42, 247–273. [Google Scholar]
- Murillo, R.E. Experimental Study of the Development Flow Region On Stepped Chutes. Ph.D. Thesis, University of Manitoba, Winnipeg, MB, Canada, 2006. [Google Scholar]
- Ohtsu, I.; Yasuda, Y. Characteristics of flow conditions on stepped channels. In Proceedings of the 27th IAHR Congress, San Francisco, VA, USA, 10–15 August 1997; pp. 583–588. [Google Scholar]
- Amador, A.; Sánchez-Juny, M.; Dolz, J. Characterization of the Nonaerated Flow Region in a Stepped Spillway by PIV. ASME J. Fluids Eng. 2006, 128, 1266–1273. [Google Scholar] [CrossRef]
- Bung, D.; Valero, D. Optical flow estimation in aerated flows. J. Hydraul. Res. 2016, 54, 575–580. [Google Scholar] [CrossRef]
- Kramer, M.; Chanson, H. Optical flow estimations in aerated spillway flows: Filtering and discussion on sampling parameters. Exp. Therm. Fluid Sci. 2019, 103, 318–328. [Google Scholar] [CrossRef]
- Lopes, P.; Leandro, J.; Carvalho, R.; Daniel, D. Alternating skimming flow over a stepped spillway. Environ. Fluid Mech. 2017, 17, 303–322. [Google Scholar] [CrossRef]
- Leandro, J.; Bung, D.; Carvalho, R. Measuring void fraction and velocity fields of a stepped spillway for skimming flow using non-intrusive methods. Exp. Fluids 2014, 55, 1732. [Google Scholar] [CrossRef]
- Wright, H.C.; Cameron-Ellis, D.G. Energy dissipation provisions for stepped spillways: Are additional measures necessary? A southern african perspective. In Proceedings of the SANCOLD Annual Conference 2018, Pretoria, South Africa, 3–7 November 2018. [Google Scholar]
- Chanson, H. Energy dissipation on stepped spillways and hydraulic challenges—Prototype and laboratory experiences. J. Hydrodyn. 2022, 34, 52–62. [Google Scholar] [CrossRef]
- Boes, R.M.; Hager, W.H. Two-Phase Flow Characteristics of Stepped Spillways. J. Hydraul. Eng. 2003, 129, 661–670. [Google Scholar] [CrossRef]
- USBR Design of Small Dams. Water Resources Technical Publication, third edition. 1987. Available online: https://www.osti.gov/biblio/29108 (accessed on 19 August 2024).
- Mikalsen, L.; Thorsen, K. Improved Energy Dissipation in Stepped Spillways—Hydraulic Model Study Applying Bubble Image Velocimetry. Master’s Thesis, NTNU, Trondheim, Norway, 2023. [Google Scholar]
- Robert, D. The dissipating of the energy of a flood passing over a high dam. Civ. Eng. = Siviele Ingenieurswese 1943, 1943, 48–92. [Google Scholar]
- William, T.; Stamhuis, E. PIVlab—Towards User-friendly. Affordable and Accurate Digital Particle Image Velocimetry in MATLAB. J. Open Res. Softw. 2014, 2, 30. [Google Scholar] [CrossRef]
- Bor, A. Experimental investigation of 90° intake flow patterns with and without submerged vanes under sediment feeding conditions. Can. J. Civ. Eng. 2022, 49, 452–463. [Google Scholar] [CrossRef]
- Goring, D.G.; Nikora, V.I. Despiking acoustic doppler velocimeter data. J. Hydraul. Eng. 2002, 128, 117–126. [Google Scholar] [CrossRef]
- Hunt, S.; Kadavy, K. Inception Point for Embankment Dam Stepped Spillways. J. Hydraul. Eng. 2012, 139, 60–64. [Google Scholar] [CrossRef]
- Hunt, S.L.; Kadavy, K.C.; Hanson, G.J. Simplistic Design Methods for Moderate-Sloped Stepped Chutes. J. Hydraul. Eng. 2014, 140, 04014062. [Google Scholar] [CrossRef]
- Wood, I. Uniform Region of Self—Aerated Flow. J. Hydraul. Eng. 1983, 109, 447–461. [Google Scholar] [CrossRef]
- Matos, J. Hydraulic design of stepped spillways over RCC dams. In Hydraulics of Stepped Spillways; Minor, E.H., Hager, W., Eds.; CRC Press: London, UK, 2000; ISBN 9781003078609. [Google Scholar]
- Amador, A.; Sánchez-Juny, M.; Dolz, J. Developing Flow Region and Pressure Fluctuations on Steeply Sloping Stepped Spillways. J. Hydraul. Eng. 2009, 135, 1092–1100. [Google Scholar] [CrossRef]
- Meireles, I.; Renna, F.; Matos, J.; Bombardelli, F. Skimming, Nonaerated Flow on Stepped Spillways over Roller Compacted Concrete Dams. J. Hydraul. Eng. 2012, 138, 10. [Google Scholar] [CrossRef]
- Takahashi, M.; Ohtsu, I. Aerated flow characteristics of skimming flow over stepped chutes. J. Hydraul. Res. 2012, 50, 427–434. [Google Scholar] [CrossRef]
- Frizell, K.; Renna, F.; Matos, J. Cavitation Potential of Flow on Stepped Spillways. J. Hydraul. Eng. 2015, 141, 630–636. [Google Scholar] [CrossRef]
- André, S. High Velocity Aerated Flow on Stepped Chutes with Macro-Roughness Elements. Ph.D. Thesis, EPFL, Lausanne, Switzerland, 2004. [Google Scholar] [CrossRef]
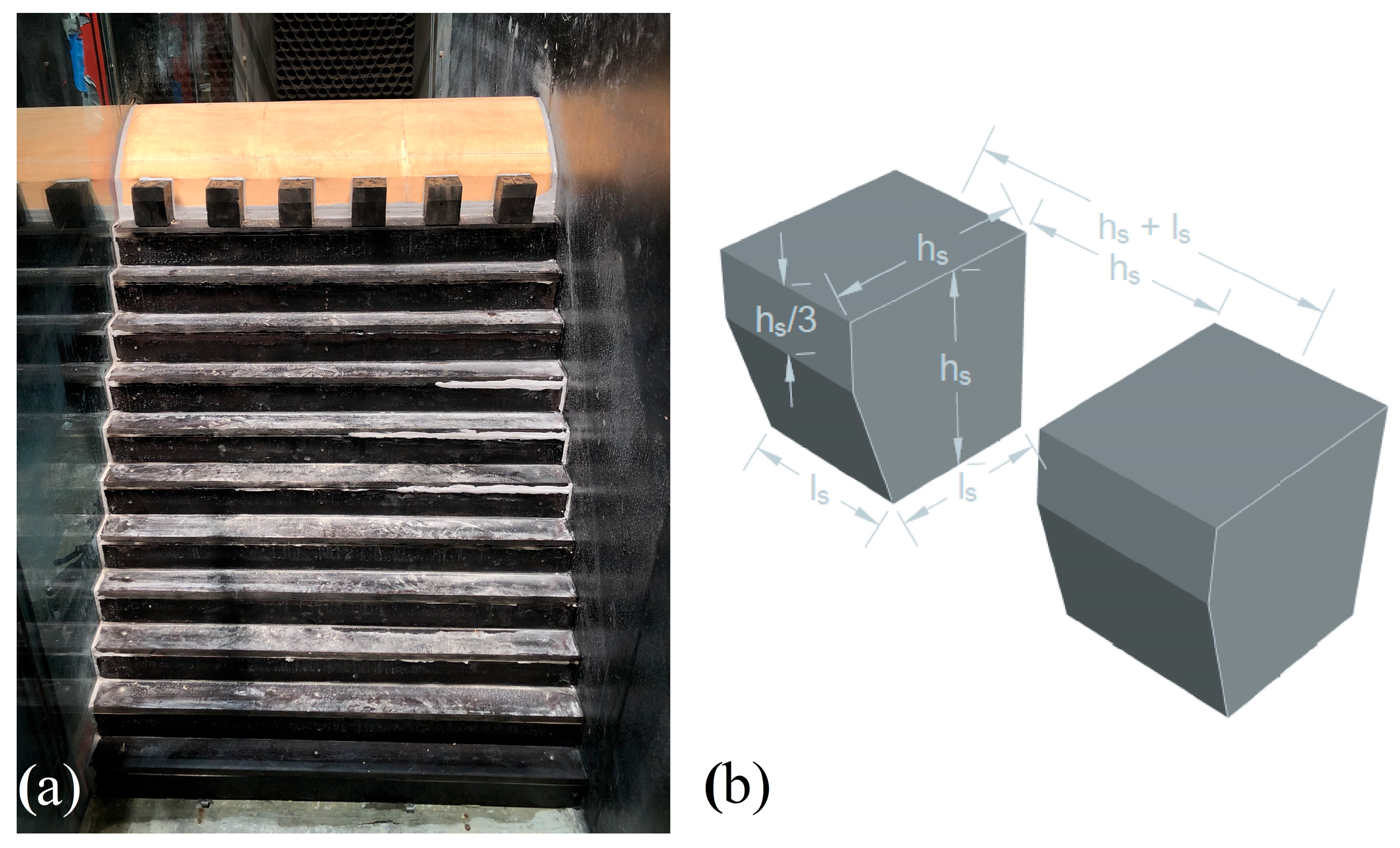






| Name | Scale | H (m) | hs (m) | Hf (m) | Bf (m) | Qmax (m3/s) |
|---|---|---|---|---|---|---|
| Prototype | 01:01 | 20 | 1.5 | - | - | - |
| C-Model | 01:50 | 0.4 | 0.03 | 0.75 | 0.6 | 0.058 |
| D-Model | 01:17 | 1.2 | 0.09 | 2 | 1 | 0.51 |
| Dimension | Length (m) | Relative Size |
|---|---|---|
| Height | 1.5 | hs |
| Top length | 1.5 | hs |
| Bottom length | 1.2 | ls |
| Width | 1.2 | ls |
| Gap | 1.5 | hs |
| Vertical face | 0.5 | hs/ 3 |
| Model | λf (-) | Q (L/s) | hc/hs (-) | Re (-) | W (-) |
|---|---|---|---|---|---|
| C-Model | 50 | 7.2–58 | 0.6–3.2 | 1.2 × 104–9.5 × 104 | 32–62 |
| D-Model | 17 | 61–510 | 0.6–3.3 | 6.1 × 104–5.1 × 105 | 106–179 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mikalsen, L.M.; Thorsen, K.H.; Bor, A.; Lia, L. Investigation of Improved Energy Dissipation in Stepped Spillways Applying Bubble Image Velocimetry. Water 2024, 16, 2432. https://doi.org/10.3390/w16172432
Mikalsen LM, Thorsen KH, Bor A, Lia L. Investigation of Improved Energy Dissipation in Stepped Spillways Applying Bubble Image Velocimetry. Water. 2024; 16(17):2432. https://doi.org/10.3390/w16172432
Chicago/Turabian StyleMikalsen, Lars Marius, Kasper Haugaard Thorsen, Aslı Bor, and Leif Lia. 2024. "Investigation of Improved Energy Dissipation in Stepped Spillways Applying Bubble Image Velocimetry" Water 16, no. 17: 2432. https://doi.org/10.3390/w16172432
APA StyleMikalsen, L. M., Thorsen, K. H., Bor, A., & Lia, L. (2024). Investigation of Improved Energy Dissipation in Stepped Spillways Applying Bubble Image Velocimetry. Water, 16(17), 2432. https://doi.org/10.3390/w16172432






