Hydrodynamic Modelling in a Mediterranean Coastal Lagoon—The Case of the Stagnone Lagoon, Marsala
Abstract
:1. Introduction
2. Materials and Methods
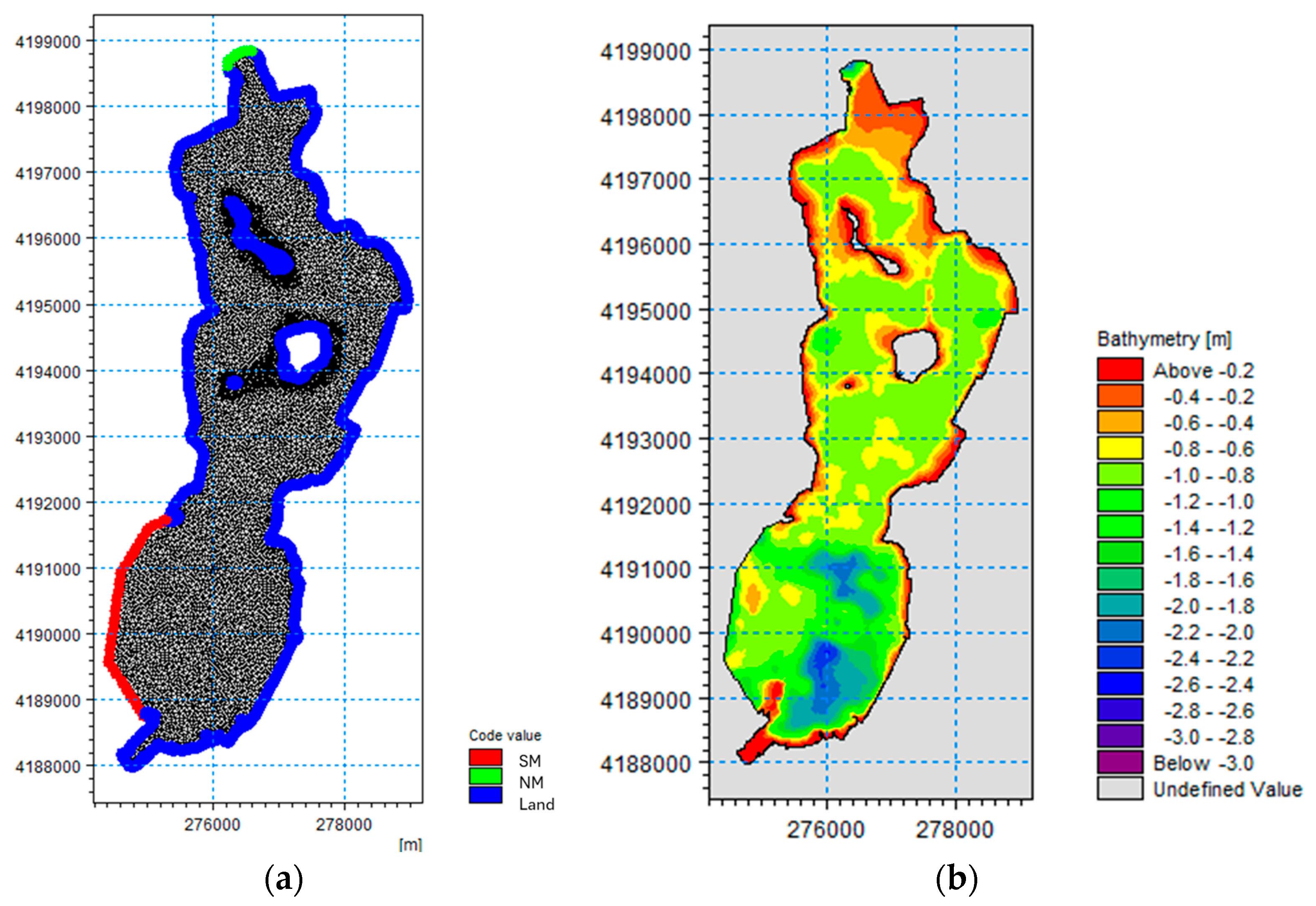
2.1. Study Area
2.2. Numerical Model
- = atmospheric pressure [kg/m/s2];
- = flux density in the x and y direction, respectively [m3/s/m];
- = gravity acceleration [m/s2];
- = water depth [m];
- = surface elevation [m];
- C = Chezy resistance [m1/2/s];
- = water density [kg/m3];
- = components of effective shear stress;
- = Coriolis parameter [s−1];
- = wind friction factor;
- = wind speed and x component [m/s].
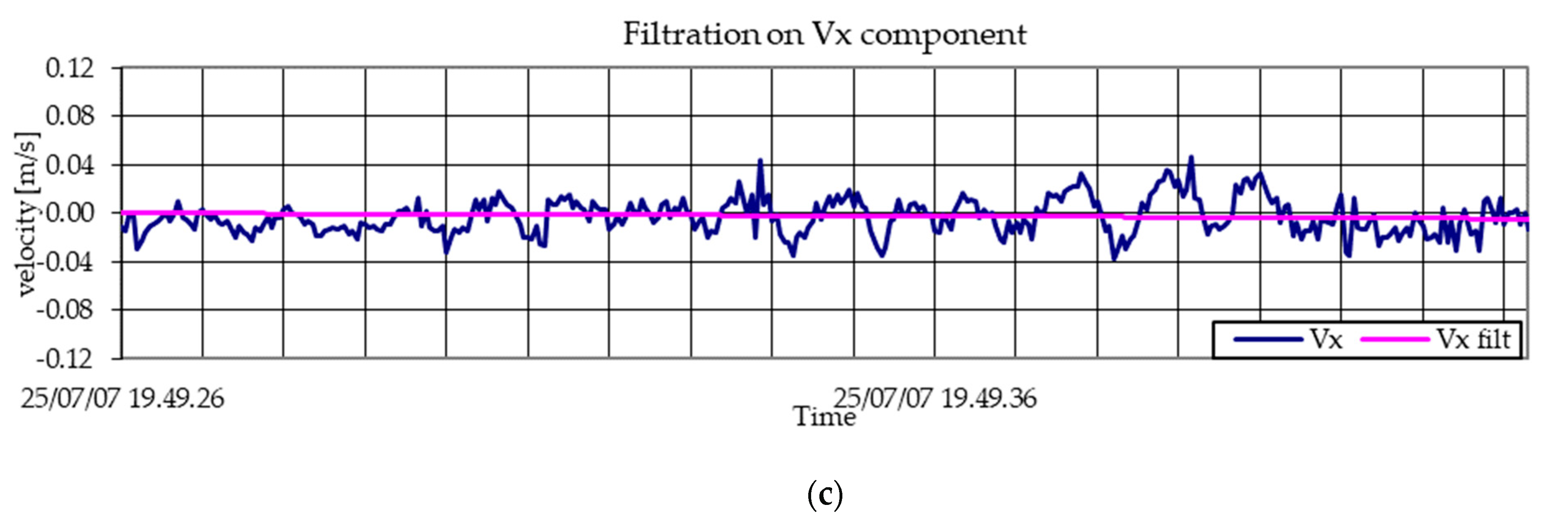
2.3. Field Data
3. Results and Discussion
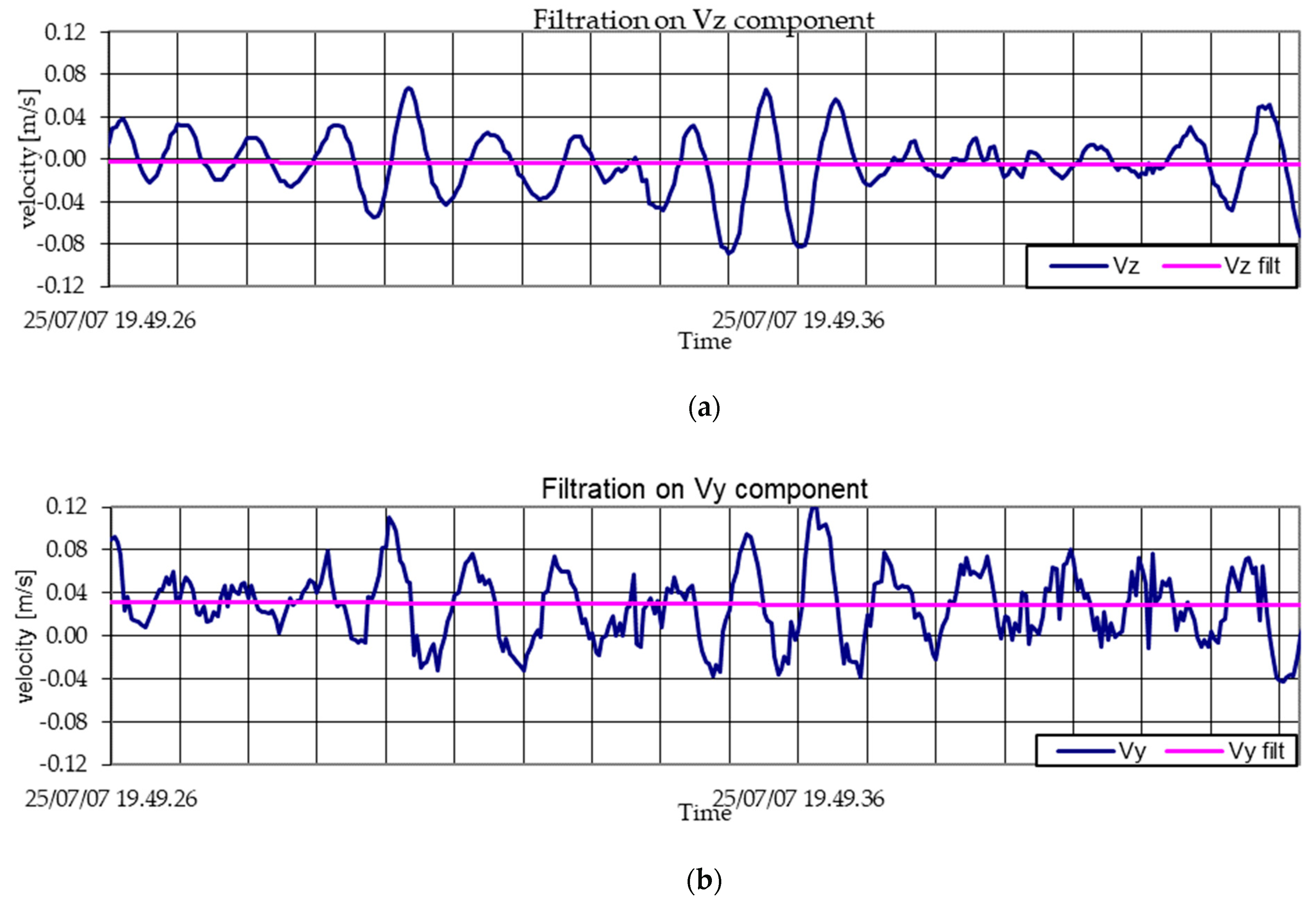
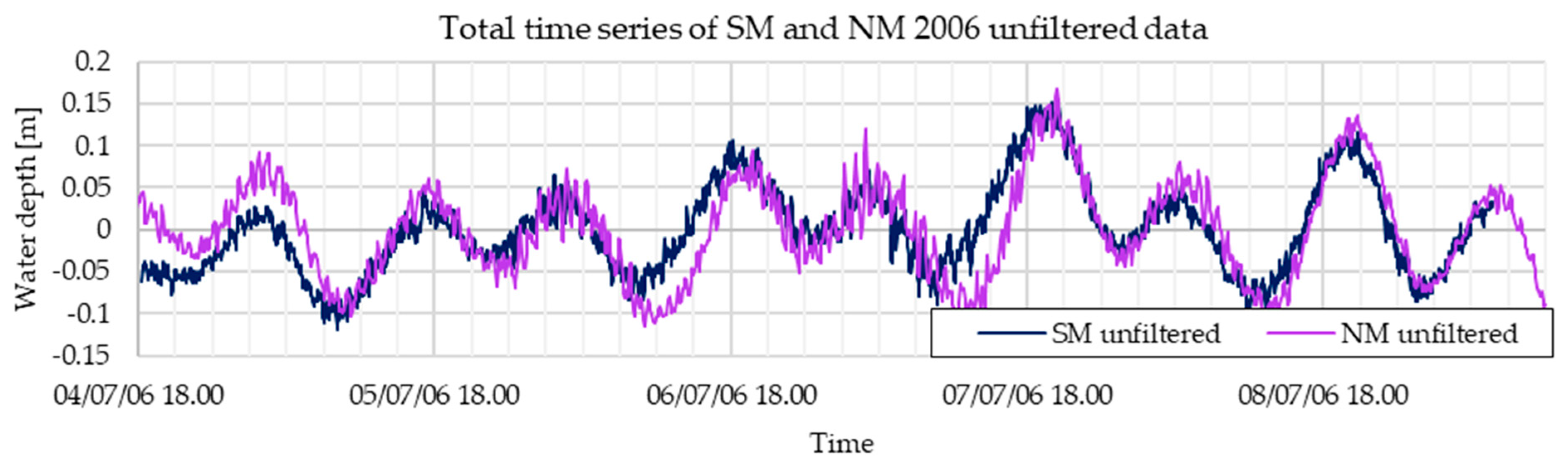
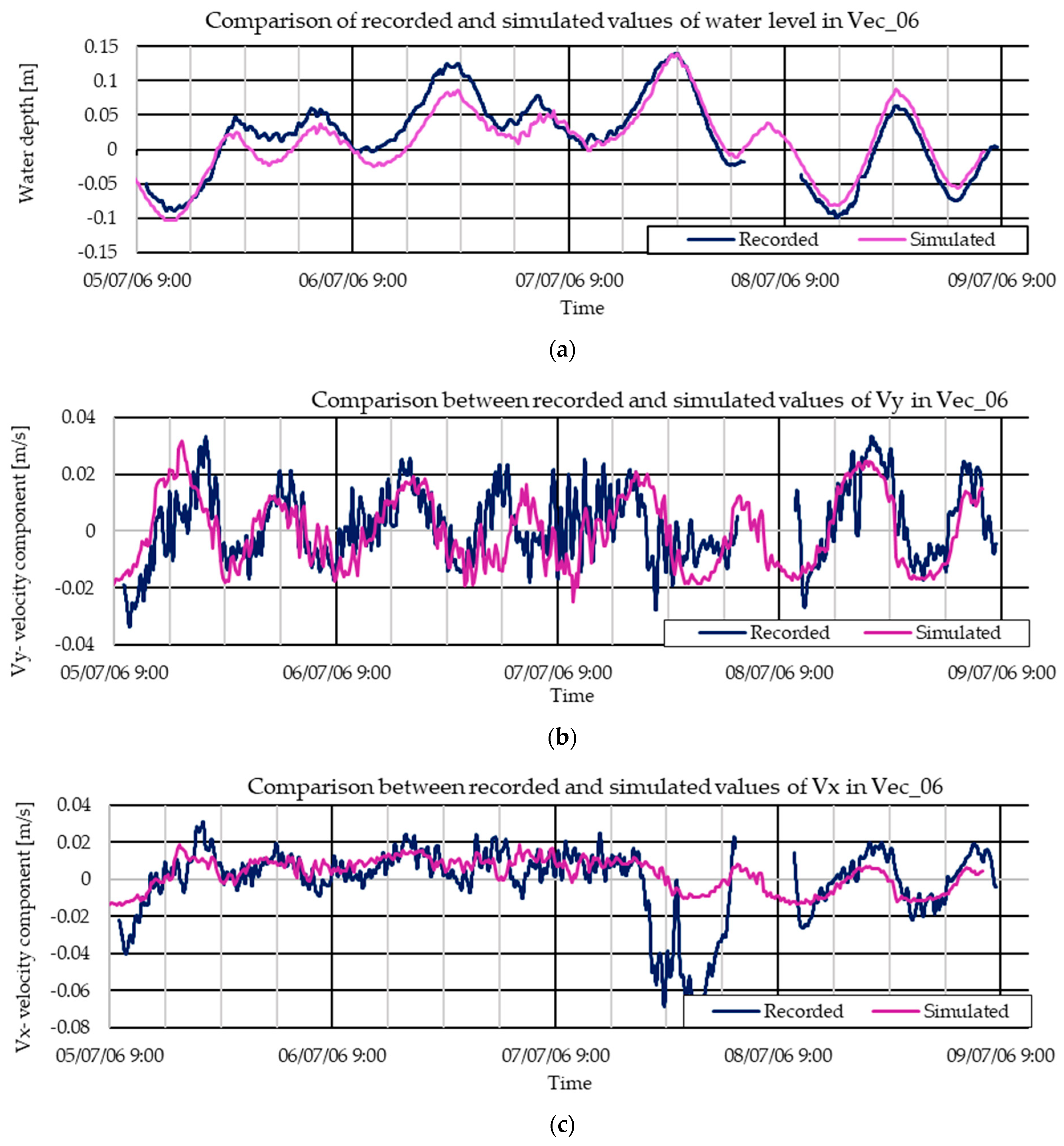
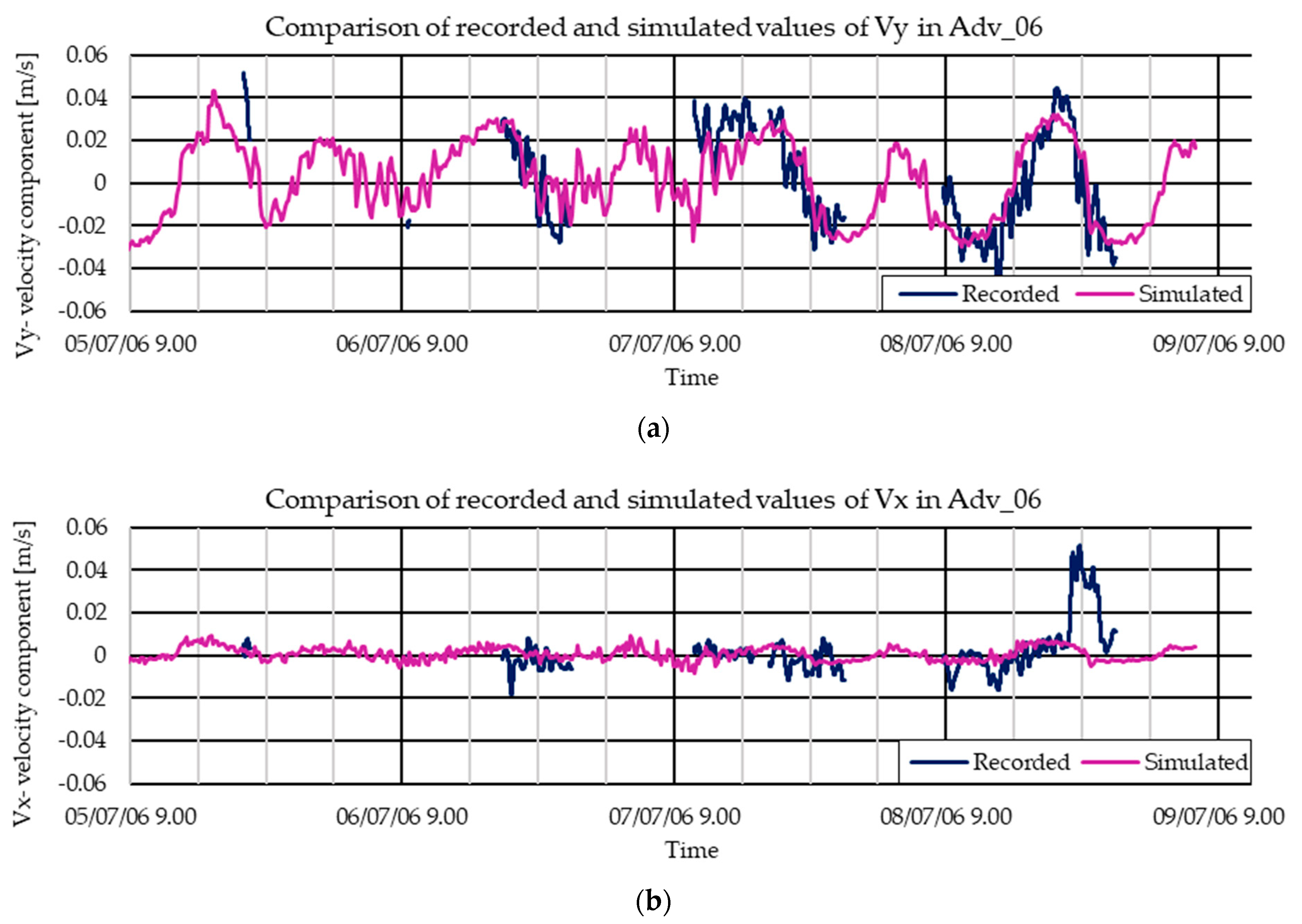
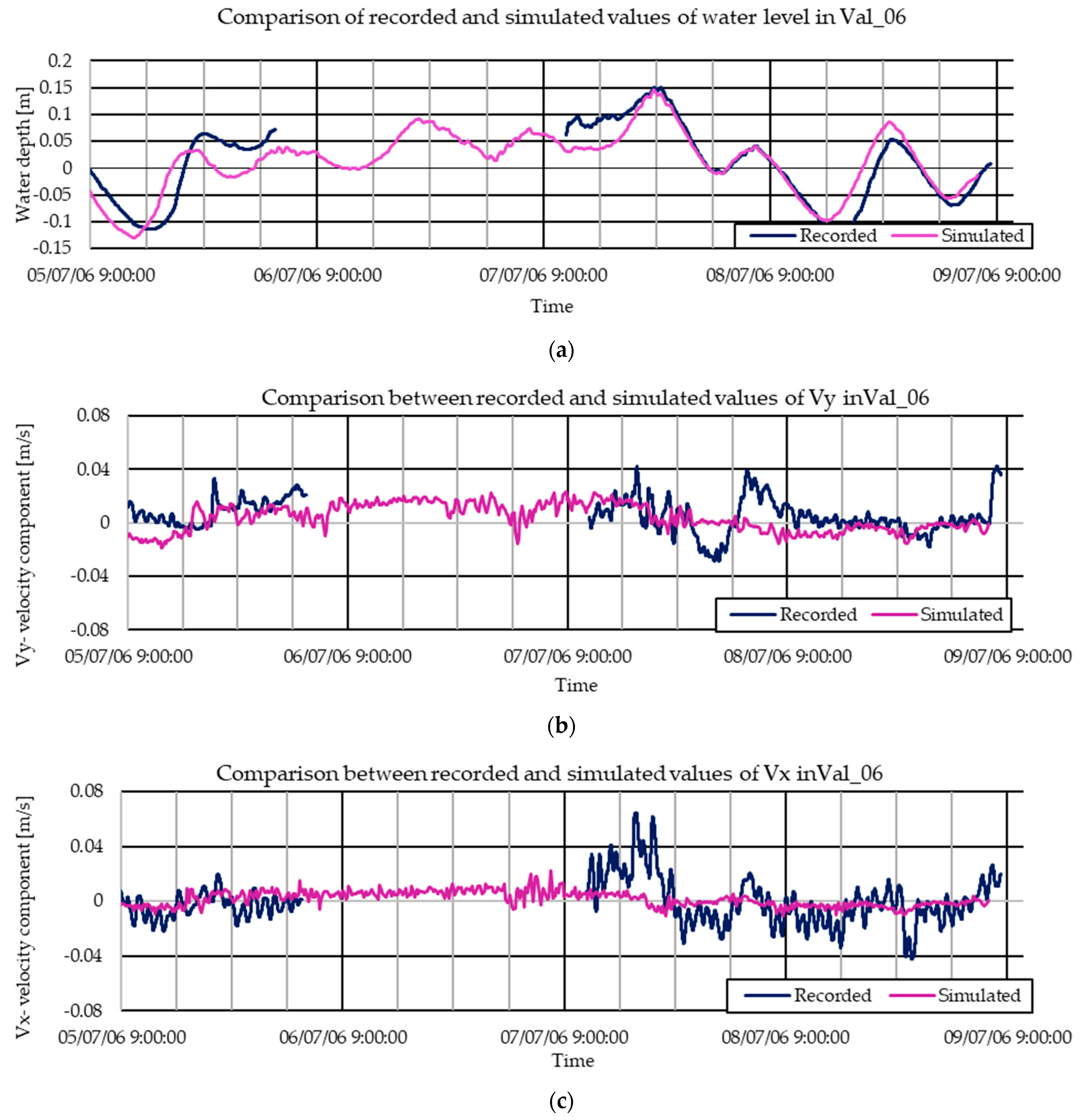
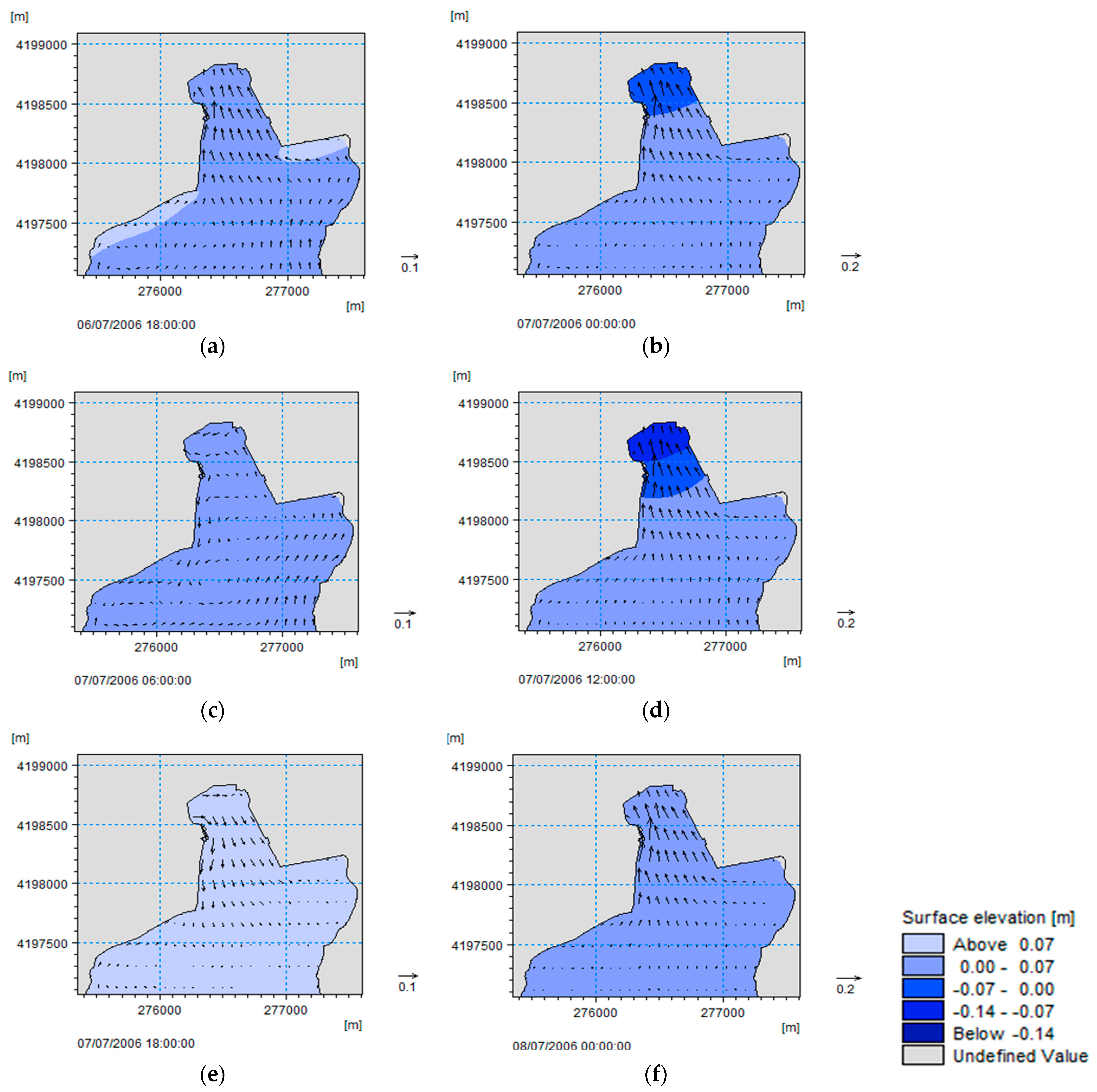
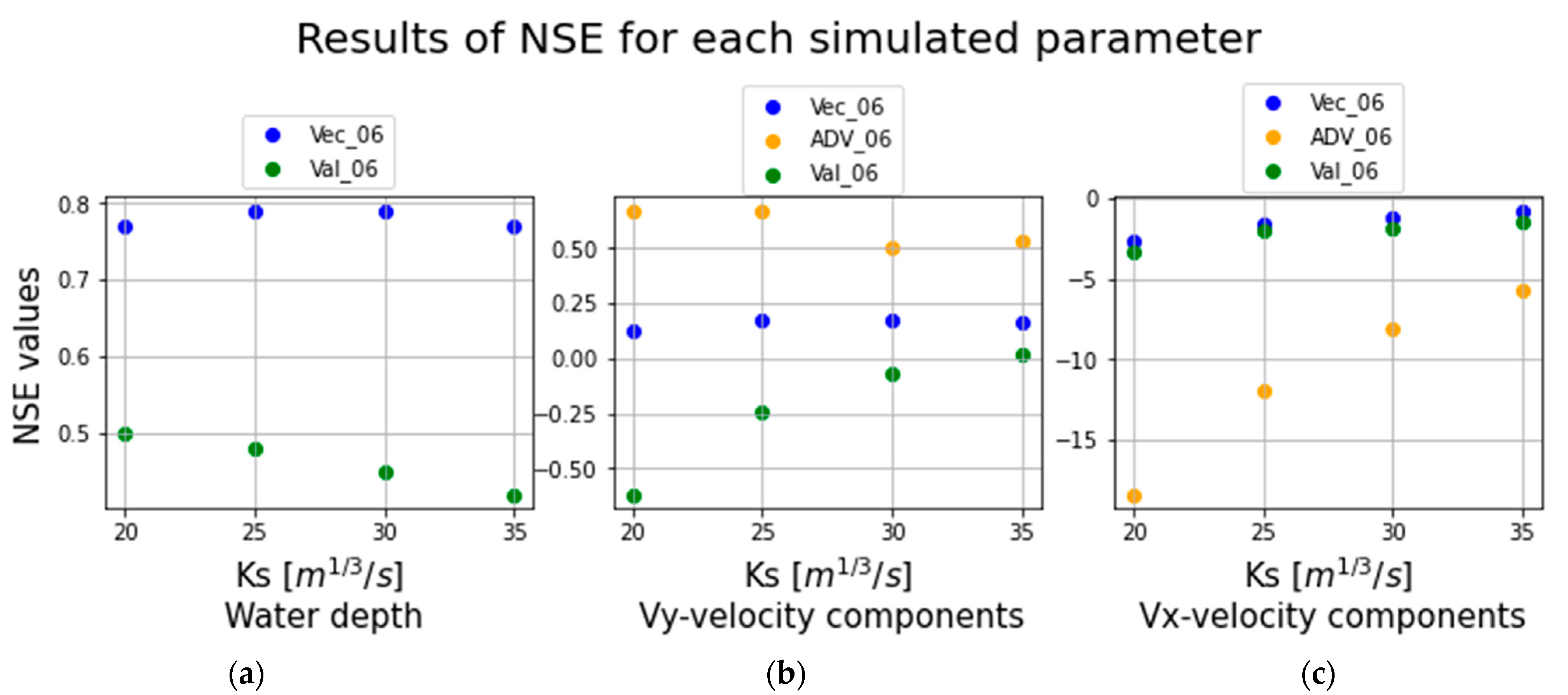
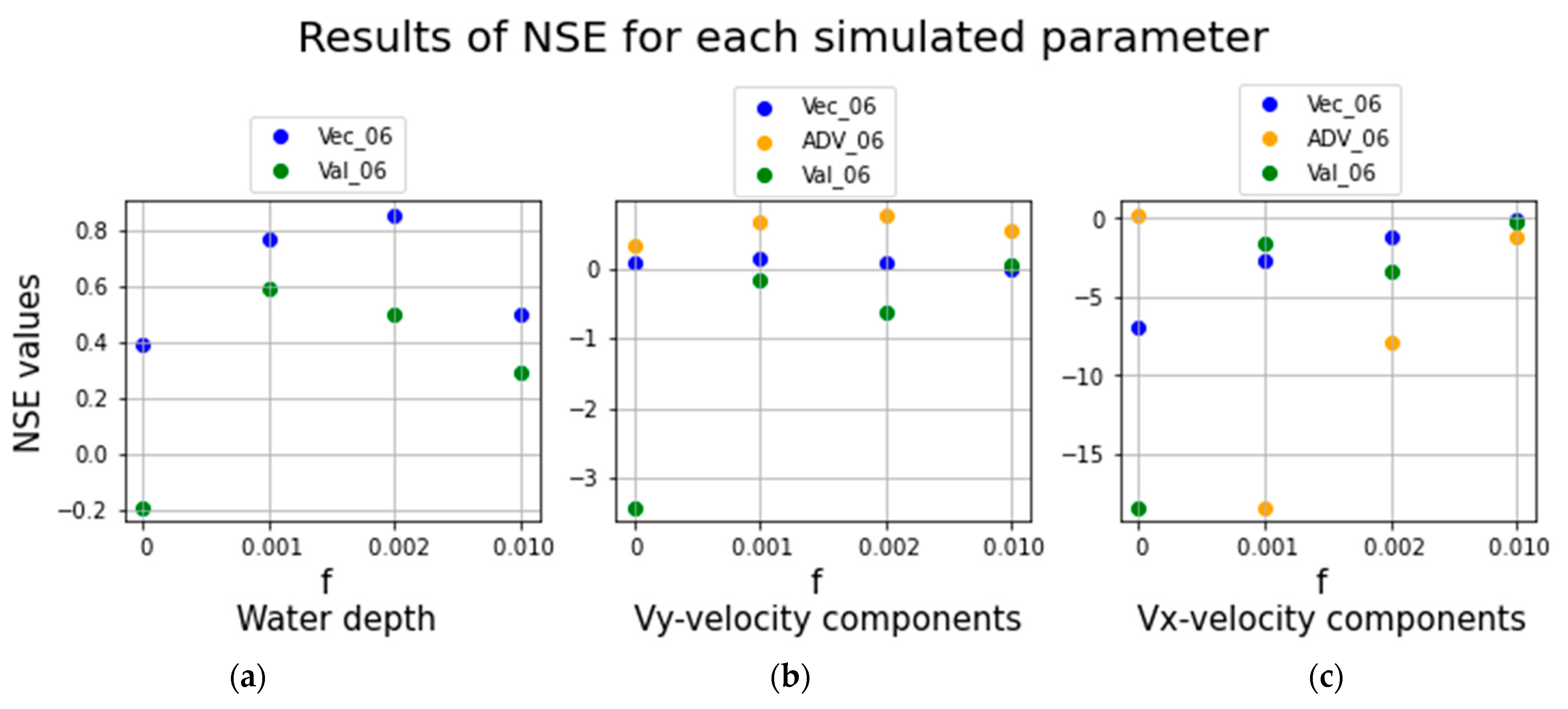
3.1. Calibration with 2006 Data
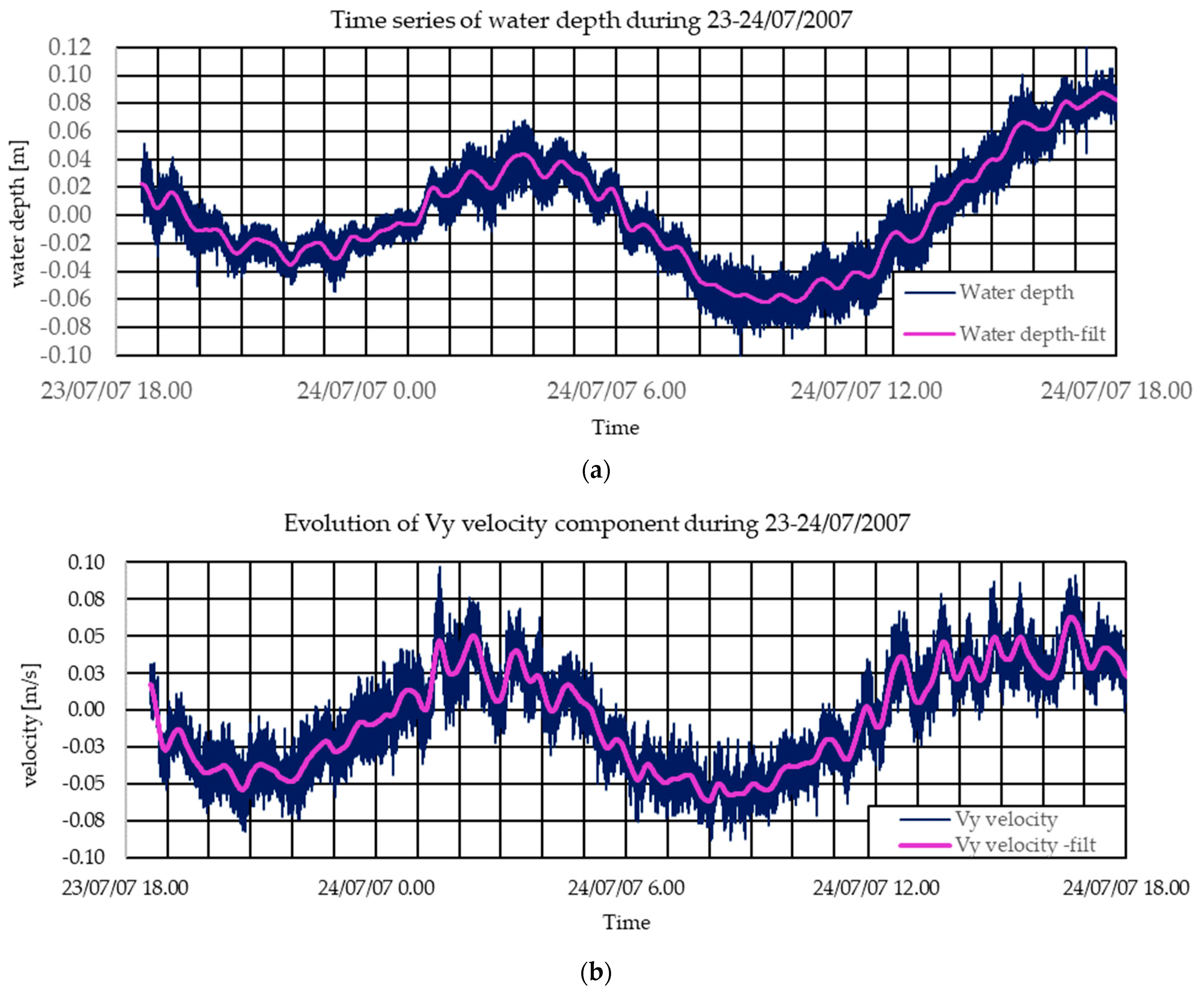
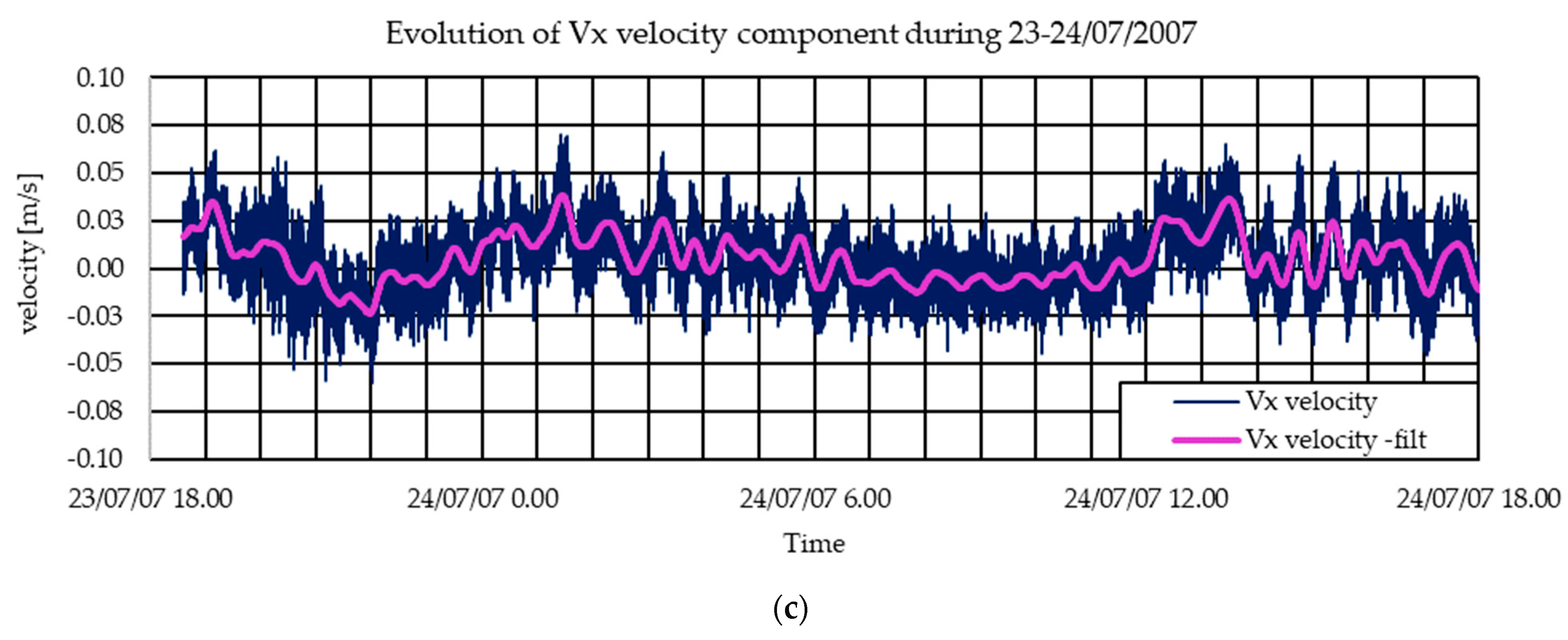
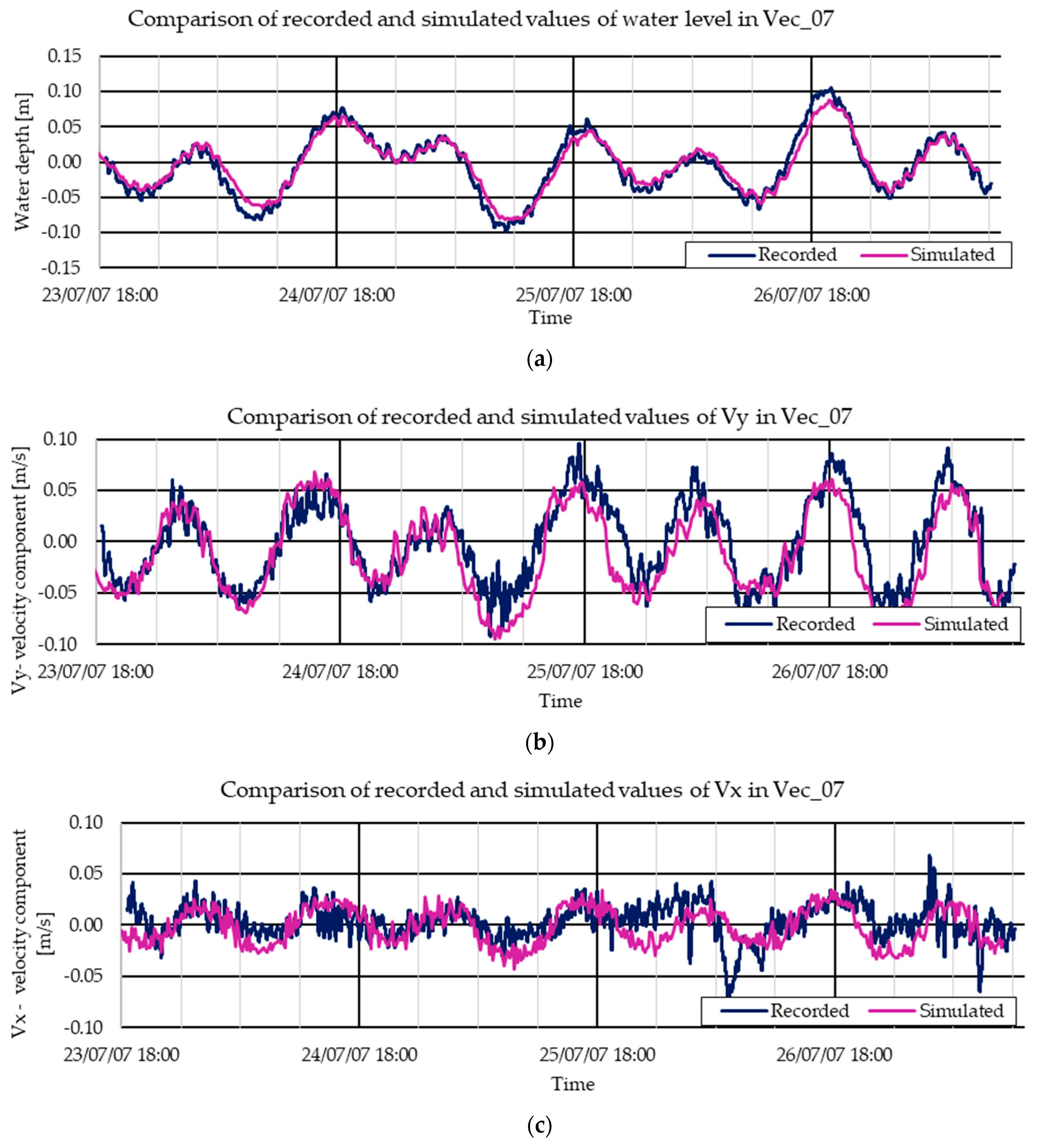
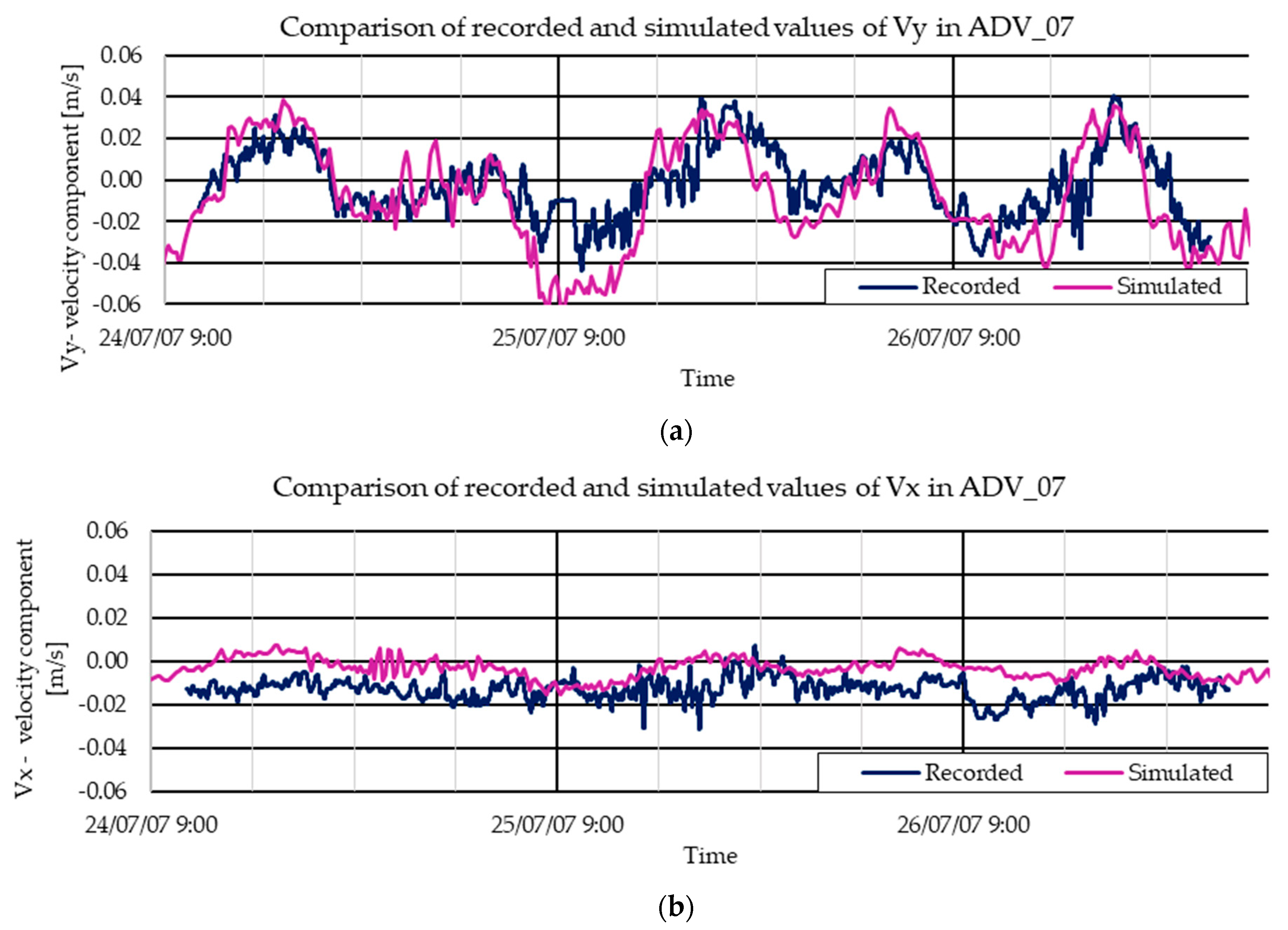
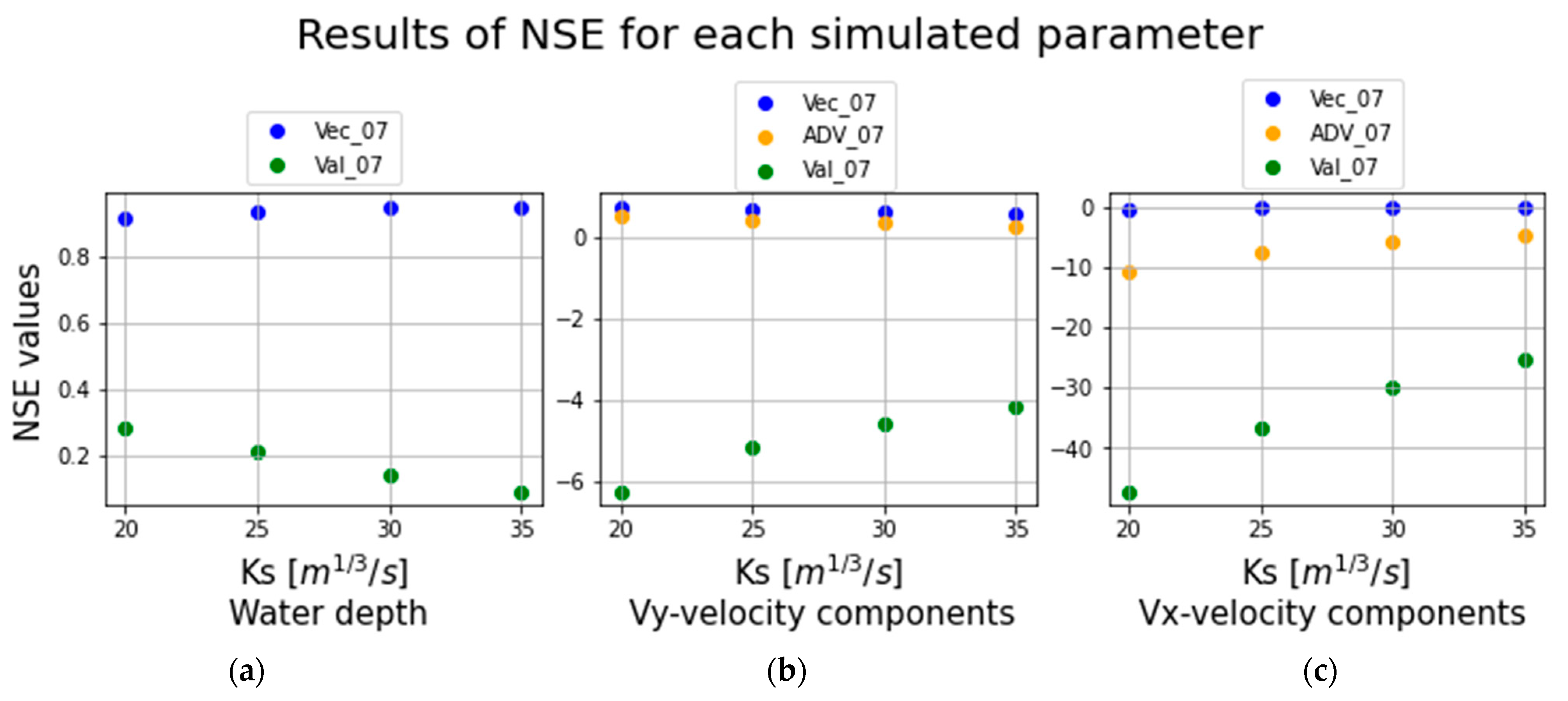
3.2. Validation with 2007 Data
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Statistics of 2006 and 2007 Simulation Efficiency
| Water Level | Vx Velocity Component | Vy Velocity Component | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Station | RMSE | R2 | SI | RMSE | R2 | SI | RMSE | R2 | SI |
| Vec_06 | 0.02 | 0.88 | 1.01 | 0.01 | 0.39 | −6.26 | 0.01 | 0.35 | 5.07 |
| Val_06 | 0.03 | 0.74 | −3048.96 | 0.00 | 0.09 | −2.22 | 0.01 | 0.07 | 1.77 |
| Adv_06 | - | - | - | 0.00 | 0.10 | 0.63 | 0.02 | 0.00 | −1.78 |
| Adv_07 | - | - | - | 0.00 | 0.02 | −0.35 | 0.02 | 0.59 | −7.69 |
| Val_07 | 0.03 | 0.57 | −129.00 | 0.00 | 0.04 | −0.34 | 0.02 | 0.00 | 1.25 |
| Vec_07 | 0.01 | 0.96 | −1.64 | 0.02 | 0.21 | 4.9 | 0.02 | 0.77 | −10.64 |


References
- Inácio, M.; Barboza, F.R.; Villoslada, M. The Protection of Coastal Lagoons as a Nature-Based Solution to Mitigate Coastal Floods. Curr. Opin. Environ. Sci. Health 2023, 34, 100491. [Google Scholar] [CrossRef]
- La Loggia, G.; Calvo, S.; Ciraolo, G.; Mazzola, A.; Pirrotta, M.; Sarà, G.; Tomasello, A.; Vizzini, S. Influence of Hydrodynamic Conditions on the Production and Fate of Posidonia oceanica in a Semi-Enclosed Shallow Basin (Stagnone Di Marsala, Western Sicily). Chem. Ecol. 2004, 20, 183–201. [Google Scholar] [CrossRef]
- Paugam, C.; Sous, D.; Rey, V.; Meulé, S.; Faure, V.; Boutron, O.; Luna-Laurent, E.; Migne, E. Wind Tides and Surface Friction Coefficient in Semi-Enclosed Shallow Lagoons. Estuar. Coast. Shelf Sci. 2021, 257, 107406. [Google Scholar] [CrossRef]
- Mancuso, F.P.; Bernardeau-Esteller, J.; Spinelli, M.; Sarà, G.; Ruiz, J.M.; Calvo, S.; Tomasello, A. Life on the Edge: Adaptations of Posidonia oceanica to Hypersaline Conditions in a Mediterranean Lagoon System. Environ. Exp. Bot. 2023, 210, 105320. [Google Scholar] [CrossRef]
- Pascolo, S.; Petti, M.; Bosa, S. On the Wave Bottom Shear Stress in Shallow Depths: The Role of Wave Period and Bed Roughness. Water 2018, 10, 1348. [Google Scholar] [CrossRef]
- Petti, M.; Bosa, S.; Pascolo, S.; Uliana, E. An Integrated Approach to Study the Morphodynamics of the Lignano Tidal Inlet. J. Mar. Sci. Eng. 2020, 8, 77. [Google Scholar] [CrossRef]
- Pavlova, A.; Myslenkov, S.; Arkhipkin, V.; Surkova, G. Storm Surges and Extreme Wind Waves in the Caspian Sea in the Present and Future Climate. Civ. Eng. J. 2022, 8, 2353–2377. [Google Scholar] [CrossRef]
- Simantiris, N.; Avlonitis, M. Effects of Future Climate Conditions on the Zooplankton of a Mediterranean Coastal Lagoon. Estuar. Coast. Shelf Sci. 2023, 282, 108231. [Google Scholar] [CrossRef]
- Larroudé, P.; Doua, M. Comparison of Sediment Transport Formulae with Monthly 2DH Simulation on a Sandy Beach and on a Beach with Noneroded Sea Bed Zone. In Proceedings of the Littoral 2010—Adapting to Global Change at the Coast: Leadership, Innovation, and Investment, London, UK, 21–23 September 2010; EDP Sciences: London, UK, 2011; p. 12006. [Google Scholar]
- Ondiviela, B.; Losada, I.J.; Lara, J.L.; Maza, M.; Galván, C.; Bouma, T.J.; Van Belzen, J. The Role of Seagrasses in Coastal Protection in a Changing Climate. Coast. Eng. 2014, 87, 158–168. [Google Scholar] [CrossRef]
- Cavallaro, L.; Lo Re, C.; Paratore, G.; Viviano, A.; Foti, E. Response of Posidonia oceanica to Wave Motion in Shallow-Waters-Preliminary Experimental Results. Coast. Eng. Proc. 2011, 32, 49. [Google Scholar] [CrossRef]
- Leonardi, N.; Carnacina, I.; Donatelli, C.; Ganju, N.K.; Plater, A.J.; Schuerch, M.; Temmerman, S. Dynamic Interactions between Coastal Storms and Salt Marshes: A Review. Geomorphology 2018, 301, 92–107. [Google Scholar] [CrossRef]
- Mahapatro, D.; Panigrahy, R.C.; Panda, S. Coastal Lagoon: Present Status and Future Challenges. Int. J. Mar. Sci. 2013, 3, 178–186. [Google Scholar] [CrossRef]
- Mulhern, J.S.; Johnson, C.L.; Martin, J.M. Is Barrier Island Morphology a Function of Tidal and Wave Regime? Mar. Geol. 2017, 387, 74–84. [Google Scholar] [CrossRef]
- Li, X.; Huang, M.; Wang, R. Numerical Simulation of Donghu Lake Hydrodynamics and Water Quality Based on Remote Sensing and MIKE 21. ISPRS Int. J. Geo-Inf. 2020, 9, 94. [Google Scholar] [CrossRef]
- Pillai, U.P.A.; Pinardi, N.; Alessandri, J.; Federico, I.; Causio, S.; Unguendoli, S.; Valentini, A.; Staneva, J. A Digital Twin Modelling Framework for the Assessment of Seagrass Nature Based Solutions against Storm Surges. Sci. Total Environ. 2022, 847, 157603. [Google Scholar] [CrossRef]
- Jacob, B.; Dolch, T.; Wurpts, A.; Staneva, J. Evaluation of Seagrass as a Nature-Based Solution for Coastal Protection in the German Wadden Sea. Ocean Dyn. 2023, 73, 699–727. [Google Scholar] [CrossRef]
- Simonetti, I.; Cappietti, L. Influence of Inlets Morphology and Forcing Mechanisms on Water Exchange between Coastal Basins and the Sea: A Hindcast Study for a Mediterranean Lagoon. J. Mar. Sci. Eng. 2022, 10, 1929. [Google Scholar] [CrossRef]
- Schoen, J.H.; Stretch, D.D.; Tirok, K. Wind-Driven Circulation Patterns in a Shallow Estuarine Lake: St Lucia, South Africa. Estuar. Coast. Shelf Sci. 2014, 146, 49–59. [Google Scholar] [CrossRef]
- Fourniotis, N.T.; Leftheriotis, G.A.; Horsch, G.M. Towards Enhancing Tidally-Induced Water Renewal in Coastal Lagoons. Environ. Fluid Mech. 2021, 21, 343–360. [Google Scholar] [CrossRef]
- Smagorinsky, J. General Circulation Experiments with the Primitive Equations: I. The Basic Experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Ciraolo, G.; Ferreri, G.B.; Loggia, G.L. Flow Resistance of Posidonia oceanica in Shallow Water. J. Hydraul. Res. 2006, 44, 189–202. [Google Scholar] [CrossRef]
- Nepf, H.M. Hydrodynamics of Vegetated Channels. J. Hydraul. Res. 2012, 50, 262–279. [Google Scholar] [CrossRef]
- Kundu, P.K.; Cohen, I.M. Fluid Mechanics, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2008; ISBN 978-0-12-381399-2. [Google Scholar]
- Niedda, M.; Greppi, M. Tidal, Seiche and Wind Dynamics in a Small Lagoon in the Mediterranean Sea. Estuar. Coast. Shelf Sci. 2007, 74, 21–30. [Google Scholar] [CrossRef]
- Kobayashi, N.; Raichle, A.W.; Asano, T. Wave Attenuation by Vegetation. J. Waterw. Port Coast. Ocean Eng. 1993, 119, 30–48. [Google Scholar] [CrossRef]
- Etminan, V.; Ghisalberti, M.; Lowe, R.J. Predicting Bed Shear Stresses in Vegetated Channels. Water Resour. Res. 2018, 54, 9187–9206. [Google Scholar] [CrossRef]
- Neumeier, U.; Ciavola, P. Flow Resistance and Associated Sedimentary Processes in a Spartina Maritima Salt-Marsh. J. Coast. Res. 2004, 202, 435–447. [Google Scholar] [CrossRef]
- Sambe, A.N.; Sous, D.; Golay, F.; Fraunié, P.; Marcer, R. Numerical Wave Breaking with Macro-Roughness. Eur. J. Mech.-BFluids 2011, 30, 577–588. [Google Scholar] [CrossRef]

| Instruments Characteristics and Acquiring Period | ||||||
|---|---|---|---|---|---|---|
| Station | Instrument | Measure | Period (s) | Mean Water Depth (m) | Starting Time | Ending Time |
| South Mouth (SM) | Valeport 808 EM | Pressure | 120 | 0.60 | 04/07/2006 4:17 23/07/2007 17:54 | 09/07/2006 7:45 27/07/2007 12:12 |
| Vec 06 | Vector Aanderaa | Pressure Velocity Wind | 60 60 60 | 1.30 | 05/07/2006 10:05 | 09/07/2006 7:00 |
| Adv 06 | Nortek ADV | Velocity | 5 | 1.25 | 08/07/2006 8:43 | 09/07/2006 00:00 |
| Val 06 | Valeport 808 EM | Pressure Velocity | 20 20 | 1.25 | 04/07/2006 14:45 | 09/07/2006 8:22 |
| North Mouth (NM) | Ott Thalimedes | Level | 300 | 0.60 | Always recording | |
| Vec 07 | Vector | Pressure Velocity | 10 10 | 1.50 | 23/07/2007 18:35 | 27/07/2007 11:00 |
| Adv 07 | Nortek ADV LSI Lastem | Velocity Wind | 10 5 | 1.30 | 24/07/2007 11:04 | 27/07/2007 00:41 |
| Val 07 | Valeport 808 EM | Pressure Velocity | 20 20 | 1.00 | 24/07/2007 08:16 | 27/07/2007 10:19 |
| NSE | h—Depth | Vy Velocity | Vx Velocity |
|---|---|---|---|
| Vec_06 | 0.77 | 0.13 | −2.63 |
| Adv_06 | 0.67 | −18.37 | |
| Val_06 | 0.50 | −0.62 | −3.37 |
| NSE | h—Depth | Vy Velocity | Vx Velocity |
|---|---|---|---|
| Vec_07 | 0.92 | 0.72 | −0.32 |
| Adv_07 | 0.50 | −10.57 | |
| Val_07 | 0.28 | −6.27 | −47.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ingrassia, E.; Nasello, C.; Ciraolo, G. Hydrodynamic Modelling in a Mediterranean Coastal Lagoon—The Case of the Stagnone Lagoon, Marsala. Water 2024, 16, 2602. https://doi.org/10.3390/w16182602
Ingrassia E, Nasello C, Ciraolo G. Hydrodynamic Modelling in a Mediterranean Coastal Lagoon—The Case of the Stagnone Lagoon, Marsala. Water. 2024; 16(18):2602. https://doi.org/10.3390/w16182602
Chicago/Turabian StyleIngrassia, Emanuele, Carmelo Nasello, and Giuseppe Ciraolo. 2024. "Hydrodynamic Modelling in a Mediterranean Coastal Lagoon—The Case of the Stagnone Lagoon, Marsala" Water 16, no. 18: 2602. https://doi.org/10.3390/w16182602
APA StyleIngrassia, E., Nasello, C., & Ciraolo, G. (2024). Hydrodynamic Modelling in a Mediterranean Coastal Lagoon—The Case of the Stagnone Lagoon, Marsala. Water, 16(18), 2602. https://doi.org/10.3390/w16182602









