Parameters Variation of Natural Gas Hydrate with Thermal Fluid Dissociation Based on Multi-Field Coupling under Pore-Scale Modeling
Abstract
:1. Introduction
2. Materials and Methods
2.1. Lattice Boltzmann Method for Convection Simulation
2.2. Lattice Boltzmann Method for Phase Change
2.3. Lattice Boltzmann Method for Hydrate Reaction
2.4. Lattice Boltzmann Method for an Unstable Simulation
3. Results and Discussions
3.1. Simulation Verifying by Reaction Rate
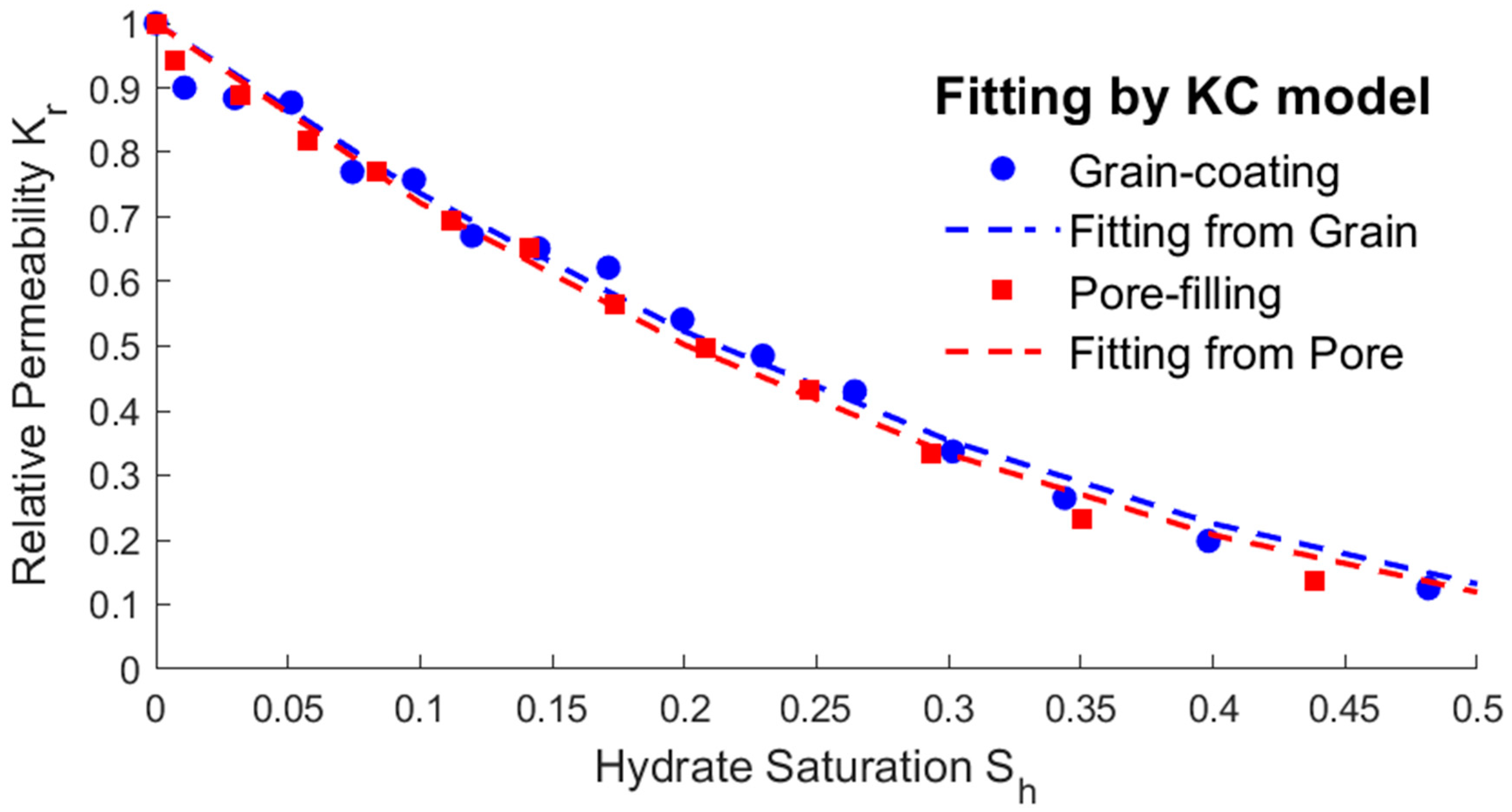
3.2. Relationship between Saturation and Permeability
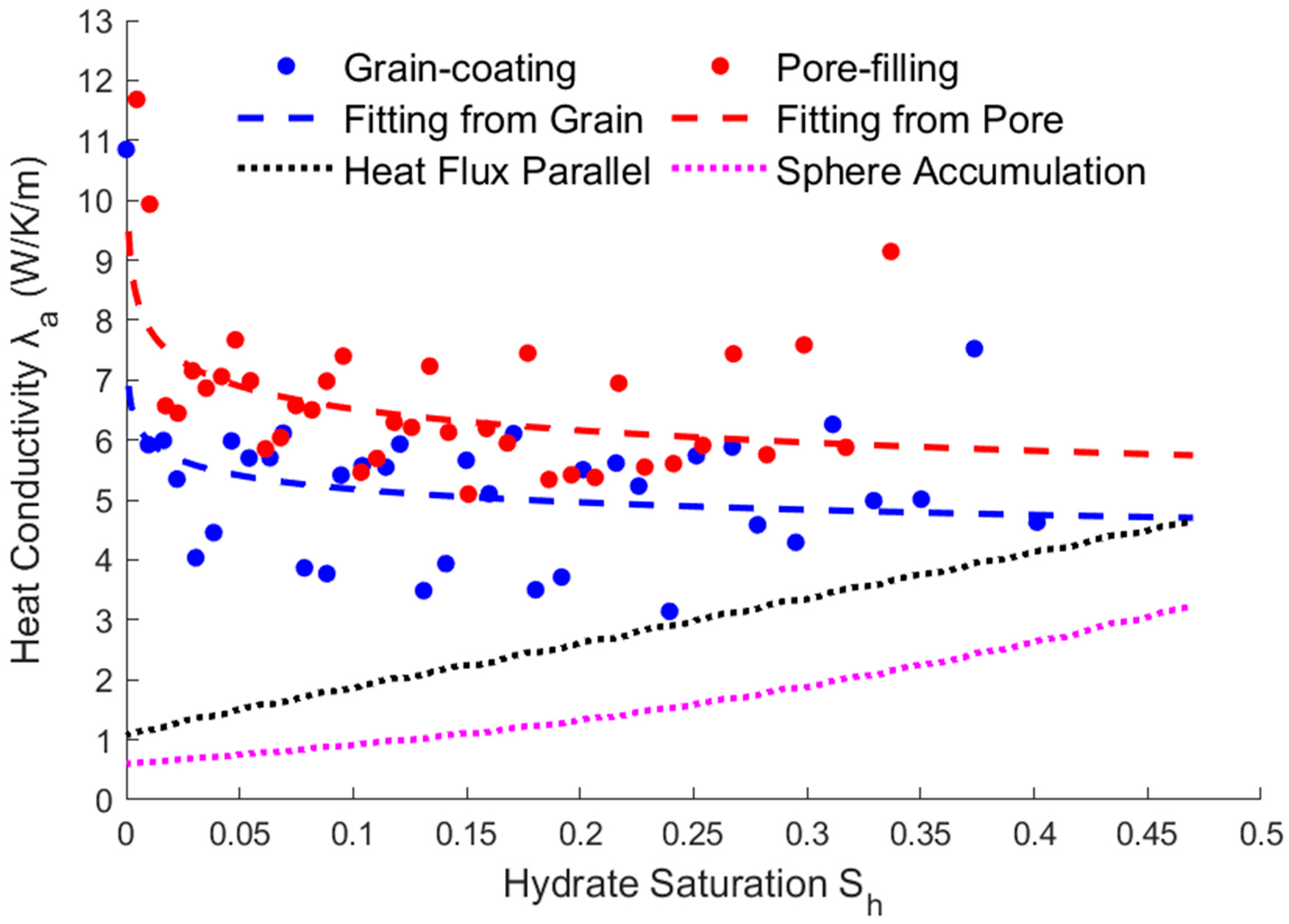
3.3. Relationship between Saturation and Heat Conductivity
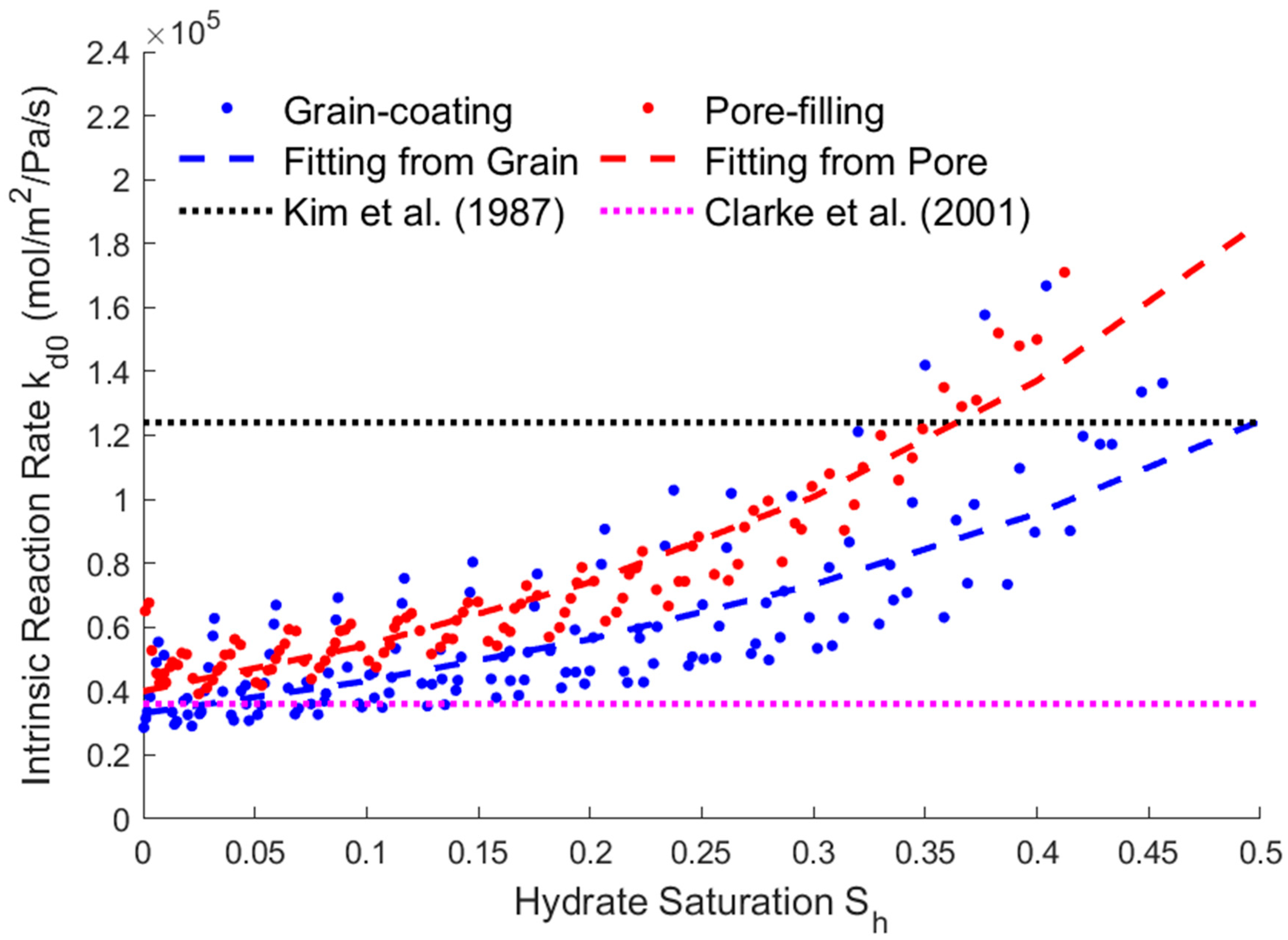
3.4. Relationship between Saturation and Reaction Rate
4. Conclusions
- (1)
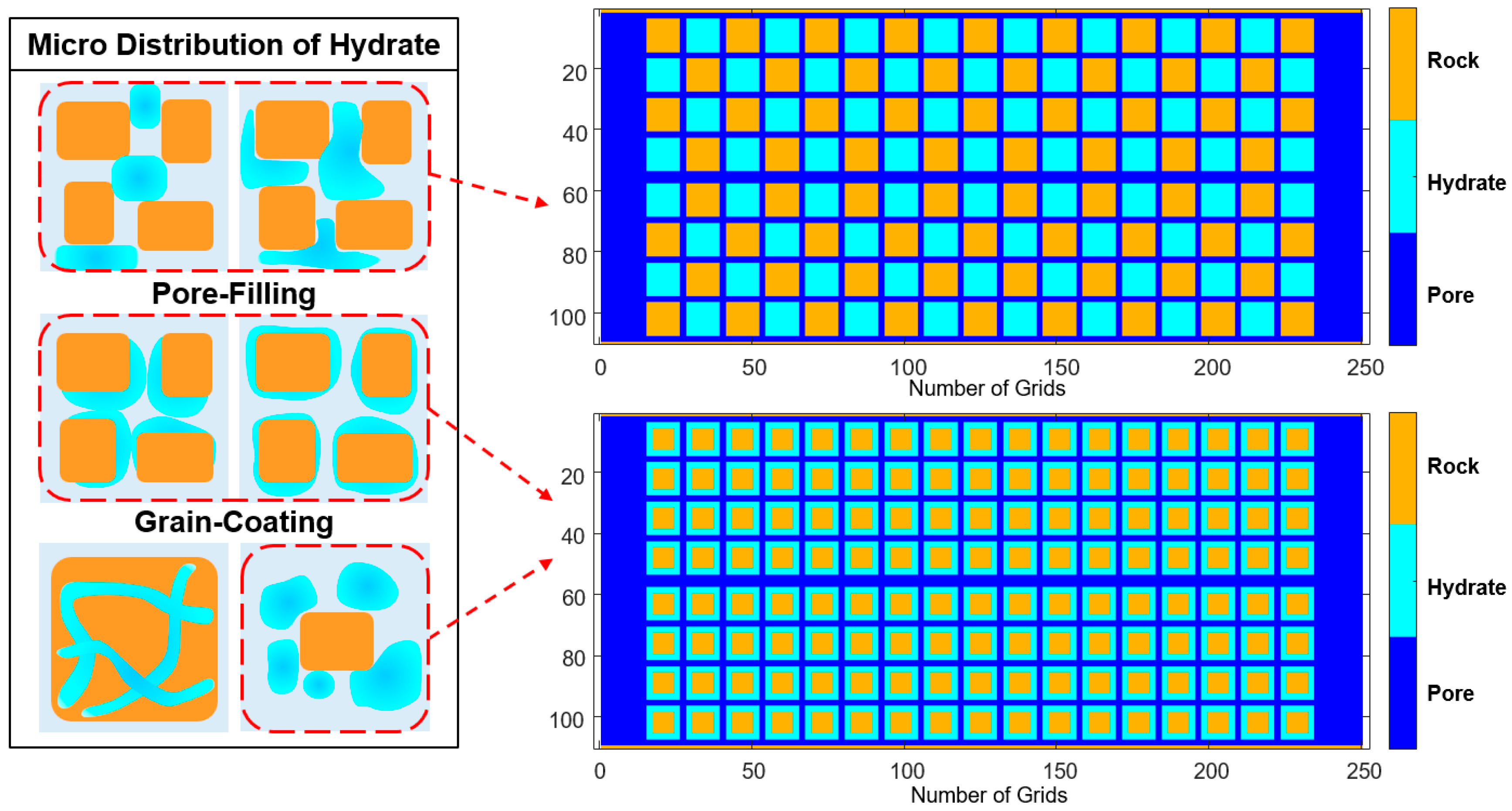
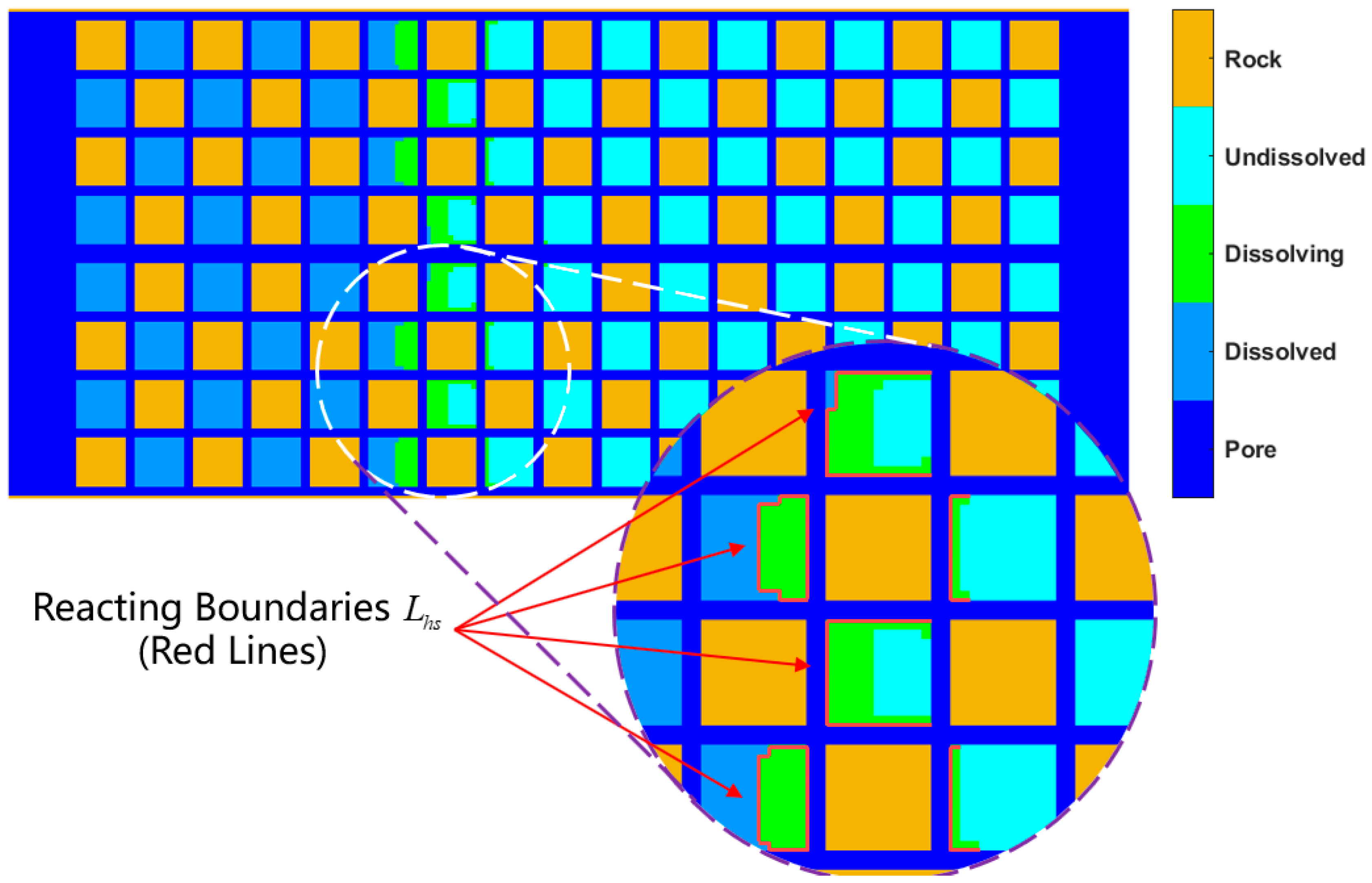
- When DDF-LBM simulates conjugate convection, the relaxation frequency of the thermal lattice in the pores needs to be modified to consider the simultaneous existence of thermal diffusion and thermal convection. The modification is necessary when simulating forced convection heat transfer; otherwise, the calculated results will be much smaller. When describing the changes in fluid–solid boundaries, we must first determine whether the current solid hydrate lattices have reached the P-T phase equilibrium condition and then determine whether the cumulative internal energy absorbed by the current lattice exceeds the heat required for its reaction. The lattices that have reached phase equilibrium conditions but do not satisfy the cumulative endothermic conditions are dissolving solid hydrate lattices, and their contact boundaries with the flowing lattices are the reacting contact areas in the K-B model. The reaction contact area can be directly obtained from the structural field simulation results, so that the effect of dissociation endothermicity on internal energy transfer in the convective heat transfer process can be described at the microscale.
- (2)
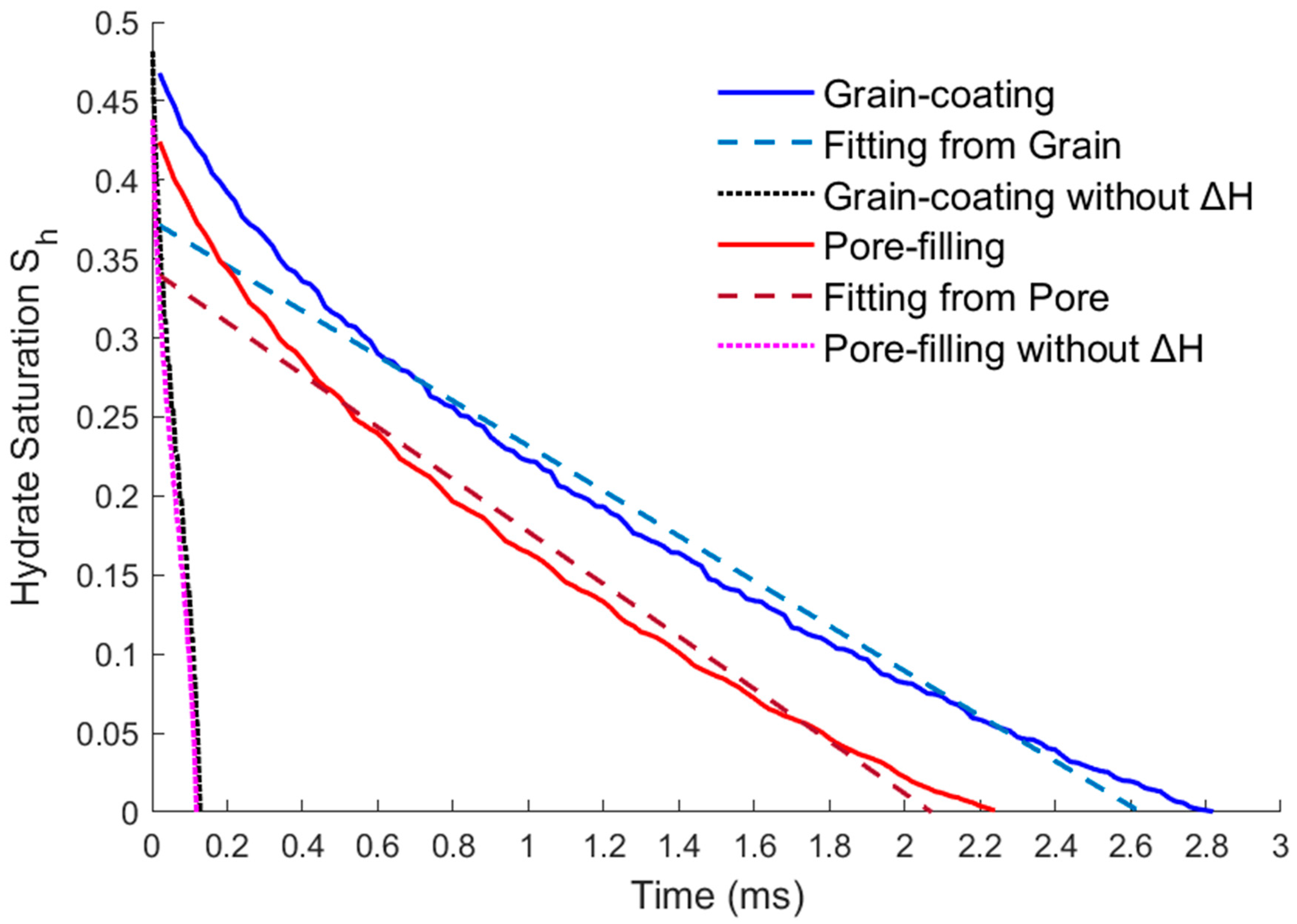
- By comparing the results of heating dissociation experiments in closed containers in other literature, the hydrate dissociation rate under the thermal fluid injection conditions simulated in this paper is higher than the result of only heat absorption on the surface. This is because the dissociation rate obtained from the experiments in the literature was based on surface heat diffusion only and did not take into account the actual situation of thermal fluid flowing under the porous structure of the reservoir. Therefore, the activation reaction rate calculated by DDF-LBM is more consistent with the real reservoir situation. Comparing the dissociation rates of the grain-coating type and the pore-filling type, although the hydrate structures and initial saturations of the two models are different, their dissociation rates are basically the same due to the same boundary conditions of the injection flow velocity and temperature. It is shown that the DDF-LBM simulation with THMC multi-field coupling in this paper can approximately and accurately describe the hydrate dissociation process when thermal fluid injected into porous media.
- (3)
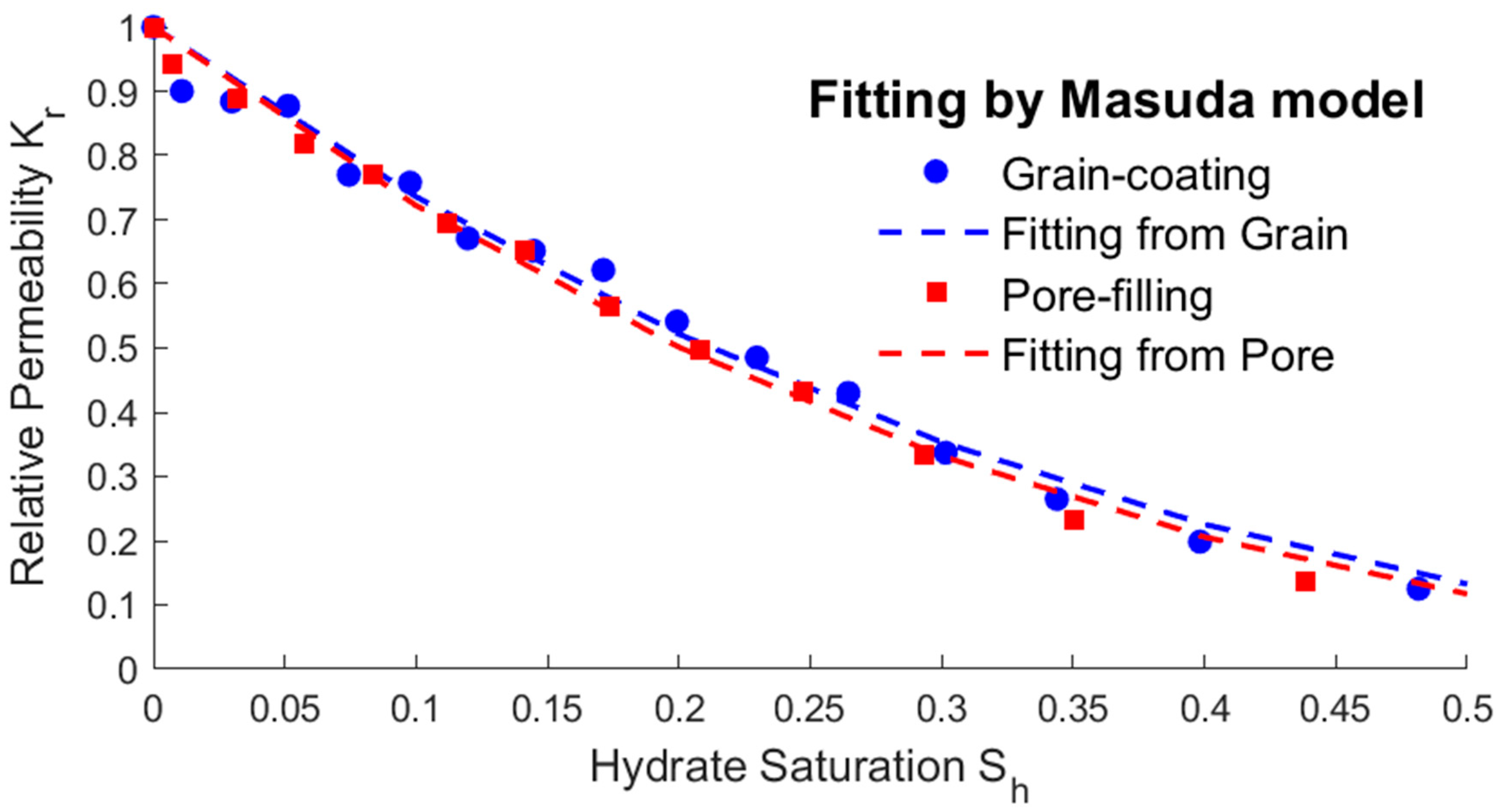
- The modified expressions of the key physical parameters of THMC multi-field coupling can be obtained by fitting the hydrate saturation with the average permeability, effective thermal conductivity, and intrinsic reaction rate. The fitting results show that the parameters’ trending of two different storage structures are the same. The average permeability increases as the saturation decreases, and the relative permeability has an exponential relationship with the saturation. The effective thermal conductivity increases slightly with the decreasing saturation and increases substantially when most of the hydrates are dissolved. Therefore, there is an approximate linear or exponential relationship between the effective thermal conductivity and the saturation, and a power exponential equation was used for fitting in this paper. The intrinsic reaction rate decreases with the decreasing saturation, which is different from the fixed value given by the K-B model in the literature. This is because the model does not fully consider the impact of the temperature gradient and reaction contact area on the results at the microscale, so the K-B model can be further modified. The above modified expressions of the key parameters can provide necessary references for simulating the real-time full coupling of thermal fluid injection into hydrates under macros-scale conditions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Z.; Zhang, Y.; Peng, Z.; Shan, Z.; Sun, B.; Sun, J. Recent advances in methods of gas recovery from hydrate-bearing sediments: A Review. Energy Fuels 2022, 36, 5550–5593. [Google Scholar] [CrossRef]
- Wang, X.; Sun, B.; Wang, Z.; Gao, Y.; Li, H. Coupled heat and mass transfer model of gas migration during well cementing through a hydrate layer in deep-water regions. Appl. Therm. Eng. 2019, 163, 114383. [Google Scholar] [CrossRef]
- Wang, Z.; Liao, Y.; Zhang, W.; Sun, B.; Sun, X.; Deng, X. Coupled temperature field model of gas-hydrate formation for thermal fluid fracturing. Appl. Therm. Eng. 2018, 133, 160–169. [Google Scholar] [CrossRef]
- Rathnaweera, T.D.; Wu, W.; Ji, Y.; Gamage, R.P. Understanding injection-induced seismicity in enhanced geothermal systems: From the coupled thermo-hydro-mechanical-chemical process to anthropogenic earthquake prediction. Earth-Sci. Rev. 2020, 205, 103182. [Google Scholar] [CrossRef]
- Li, Q.; Liu, J.; Wang, S.; Guo, Y.; Han, X.; Li, Q.; Chen, Y.; Dong, Z.; Li, X.; Zhang, X. Numerical insights into factors affecting collapse behavior of horizontal wellbore in clayey silt hydrate-bearing sediments and the accompanying control strategy. Ocean Eng. 2024, 297, 117029. [Google Scholar] [CrossRef]
- Li, Q.; Cheng, Y.; Li, Q.; Ansari, U.; Liu, Y.; Yan, C.; Lei, C. Development and verification of the comprehensive model for physical properties of hydrate sediment. Arab. J. Geosci. 2018, 11, 325. [Google Scholar] [CrossRef]
- Huang, J.; Yin, X.; Barrufet, M.; Killough, J. Lattice Boltzmann simulation of phase equilibrium of methane in nanopores under effects of adsorption. Chem. Eng. J. 2021, 419, 129625. [Google Scholar] [CrossRef]
- Liu, Y.; Hou, J.; Zhao, H.; Liu, X.; Xia, Z. A method to recover natural gas hydrates with geothermal energy conveyed by CO2. Energy 2018, 144, 265–278. [Google Scholar] [CrossRef]
- Kim, H.C.; Bishnoi, P.R.; Heidemann, R.A.; Rizvi, S.S. Kinetics of methane hydrate decomposition. Chem. Eng. Sci. 1987, 42, 1645–1653. [Google Scholar] [CrossRef]
- Sun, X.; Luo, T.; Wang, L.; Wang, H.; Song, Y.; Li, Y. Numerical simulation of gas recovery from a low-permeability hydrate reservoir by depressurization. Appl. Energy 2019, 250, 7–18. [Google Scholar] [CrossRef]
- Moridis, G.J. User’s Manual for the Hydrate v1.5 Option of TOUGH+ v1.5: A Code for the Simulation of System Behavior in Hydrate-Bearing Geologic Media; Lawrence Berkeley National Laboratory: California, CA, USA, 2014. [Google Scholar]
- Karani, H.; Huber, C. Lattice Boltzmann formulation for conjugate heat transfer in heterogeneous media. Phys. Rev. E 2015, 91, 023304. [Google Scholar] [CrossRef] [PubMed]
- Huo, Y.; Rao, Z. Lattice Boltzmann simulation for solid–liquid phase change phenomenon of phase change material under constant heat flux. Int. J. Heat Mass Transf. 2015, 86, 197–206. [Google Scholar] [CrossRef]
- He, Y.L.; Liu, Q.; Li, Q.; Tao, W.Q. Lattice Boltzmann methods for single-phase and solid-liquid phase-change heat transfer in porous media: A review. Int. J. Heat Mass Transf. 2019, 129, 160–197. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, C.; Zhang, K.; Zhang, L.; Yao, J.; Sun, H.; Yang, Y. Pore-scale investigation of methane hydrate dissociation using the lattice Boltzmann method. Water Resour. Res. 2019, 55, 8422–8444. [Google Scholar] [CrossRef]
- Ji, Y.; Kneafsey, T.J.; Hou, J.; Zhao, J.; Liu, C.; Guo, T.; Wei, B.; Zhao, E.; Bai, Y. Relative permeability of gas and water flow in hydrate-bearing porous media: A micro-scale study by lattice Boltzmann simulation. Fuel 2022, 321, 124013. [Google Scholar] [CrossRef]
- Ross-Jones, J.; Gaedtke, M.; Sonnick, S.; Meier, M.; Rädle, M.; Nirschl, H.; Krause, M.J. Pore-scale conjugate heat transfer simulations using lattice Boltzmann methods for industrial applications. Appl. Therm. Eng. 2021, 182, 116073. [Google Scholar] [CrossRef]
- Zhang, J.; Yin, Z.; Khan, S.A.; Li, S.; Li, Q.; Liu, X.; Linga, P. Path-dependent morphology of CH 4 hydrates and their dissociation studied with high-pressure microfluidics. Lab A Chip 2024, 24, 1602–1615. [Google Scholar] [CrossRef]
- Yang, J.; Xu, Q.; Liu, Z.; Shi, L. Pore-scale study of the multiphase methane hydrate dissociation dynamics and mechanisms in the sediment. Chem. Eng. J. 2022, 430, 132786. [Google Scholar] [CrossRef]
- Woods, L.C. An Introduction to the Kinetic Theory of Gases and Magnetoplasmas; Oxford University Press: London, UK, 1993. [Google Scholar]
- Li, J.; Liang, Z.; Wang, Z.; Bao, W. Molecular dynamics simulation of decomposition of methane hydrate and interfacial characteristics in nanostructure region. Int. J. Thermophys. 2020, 41, 13. [Google Scholar] [CrossRef]
- Guo, B.; Zhang, P.; Zhang, H. Mathematical modeling of heat transfer from geothermal reservoirs to gas hydrate reservoirs. In Proceedings of the Applied Energy Symposium: MIT A+ B, Cambridge, MA, USA, 5–8 July 2022. [Google Scholar]
- Mohamad, A.A. Lattice Boltzmann Method: Fundamentals and Engineering Applications with Computer Codes, 2nd ed.; Springer: London, UK, 2019. [Google Scholar]
- Gaedtke, M.; Abishek, S.; Mead-Hunter, R.; King, A.J.; Mullins, B.J.; Nirschl, H.; Krause, M.J. Total enthalpy-based lattice Boltzmann simulations of melting in paraffin/metal foam composite phase change materials. Int. J. Heat Mass Transf. 2020, 155, 119870. [Google Scholar] [CrossRef]
- Kamath, V.A.; Holder, G.D. Dissociation heat transfer characteristics of methane hydrates. AIChE J. 1987, 33, 347–350. [Google Scholar] [CrossRef]
- Masuda, Y. Numerical calculation of gas-production performance from reservoirs containing natural gas hydrates. In Proceedings of the SPE Asia Pacific Oil & Gas Conference & Exhibition, Kuala Lumpur, Malaysia, 14–16 April 1997. [Google Scholar]
- Dai, S.; Seol, Y. Water permeability in hydrate-bearing sediments: A pore-scale study. Geophys. Res. Lett. 2014, 41, 4176–4184. [Google Scholar] [CrossRef]
- Zhu, W.; Kan, A.; Chen, Z.; Zhang, Q.; Zhang, J. A modified Lattice Boltzmann method for predicting the effective thermal conductivity of open-cell foam materials. Int. Commun. Heat Mass Transf. 2022, 133, 105957. [Google Scholar] [CrossRef]
- Qin, X.; Cai, J.; Zhou, Y.; Kang, Z. Lattice Boltzmann simulation and fractal analysis of effective thermal conductivity in porous media. Appl. Therm. Eng. 2020, 180, 115562. [Google Scholar] [CrossRef]
- Clarke, M.; Bishnoi, P.R. Determination of the activation energy and intrinsic rate constant of methane gas hydrate decomposition. Can. J. Chem. Eng. 2001, 79, 143–147. [Google Scholar] [CrossRef]

| Parameters | Symbols | Value with Units |
|---|---|---|
| Kinetic viscosity | 1 × 10−6 m2/s | |
| Heat diffusivity of liquid | 1.31 × 10−7 m2/s | |
| Thermal conductivity of rock | 2.0 W/m/K | |
| Thermal conductivity of hydrate | 9.0 W/m/K | |
| Thermal conductivity of liquid | 0.55 W/m/K | |
| Density of hydrate | 920 kg/m3 | |
| Density of rock | 2650 kg/m3 | |
| Specific heat of rock | 1.0 kJ/kg/K | |
| Specific heat of hydrate | 2.08 kJ/kg/K | |
| Inlet temperature | 293 K | |
| Phase change temperature | 274 K | |
| Original temperature | 271 K | |
| Inlet velocity | 0.1 m/s | |
| Original pressure | 2.3 MPa | |
| Length scale | 2 × 10−7 m | |
| Time scale | 2 × 10−8 s | |
| Height | 10 × 10−7 m | |
| Activation energy | 81 kJ/mol | |
| Reaction heat absorption | 52 kJ/mol | |
| Phase equilibrium curve |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Wang, Z.; Ji, H. Parameters Variation of Natural Gas Hydrate with Thermal Fluid Dissociation Based on Multi-Field Coupling under Pore-Scale Modeling. Water 2024, 16, 2734. https://doi.org/10.3390/w16192734
Li Z, Wang Z, Ji H. Parameters Variation of Natural Gas Hydrate with Thermal Fluid Dissociation Based on Multi-Field Coupling under Pore-Scale Modeling. Water. 2024; 16(19):2734. https://doi.org/10.3390/w16192734
Chicago/Turabian StyleLi, Zhengyi, Zhiyuan Wang, and Hongfei Ji. 2024. "Parameters Variation of Natural Gas Hydrate with Thermal Fluid Dissociation Based on Multi-Field Coupling under Pore-Scale Modeling" Water 16, no. 19: 2734. https://doi.org/10.3390/w16192734
APA StyleLi, Z., Wang, Z., & Ji, H. (2024). Parameters Variation of Natural Gas Hydrate with Thermal Fluid Dissociation Based on Multi-Field Coupling under Pore-Scale Modeling. Water, 16(19), 2734. https://doi.org/10.3390/w16192734






