Water and the Origin of Life

Abstract

This article reviews all the major stages in the origins of life, from the emergence of matter in the initial Big Bang to the modern, civilized human being. On an immaterial level, it is proposed and explained how consciousness necessarily takes precedence over matter. Next, we explain how consciousness, with its ability to process information, selected the water molecule to breathe life into the periodic table of elements. We also explain why the notion of entropy allows us to evolve, “Die Entropie der Welt strebt einem Maximum zu” (second principle), and, therefore, takes precedence over the notion of energy, which, on the contrary, encourages us to preserve what we have, “Die Energie der Welt bleibt konstant” (first principle). This is followed by a discussion of the importance of quantum coherence and the need to rely on a second quantization formalism for a proper understanding of the physical–biochemical properties of water. Moreover, throughout the argument developed on the best and most fundamental things science has to offer, care is taken to link this knowledge to the great philosophies of the West (Greece), the East (China and India), and even to practices of a shamanic nature (Africa and America). Hence, finally, we propose reconsidering all musical practice within the framework of the diapason of water at a frequency of 429.62 Hz, as well as all therapeutic practice on the basis of seven clearly identified and established frameworks of thought.

1. Introduction

This paper suggests that life is an inevitable phenomenon from the moment the three following ingredients mix: water, mineral ions derived from the elements (Na, K, Mg, Ca, B, V, Cr, Mn, Fe, Co, Ni, Cu, Zn, Mo, Si, P, S, Se, F, Cl, and I), and organic matter based on the quadrette (C, H, O, and N). As it is stars that synthesize atomic nuclei and electrons that neutralize the positive electric charges of these nuclei, life can only be a phenomenon of a profoundly quantum nature. Furthermore, as the water molecule is by far the largest constituent of a cell, the theory of relativity also comes into play. To understand this substance with the formula H₂O, we need to call on the quantum physics of second quantization fields, and not on the quantum physics of first quantization. Finally, one last science is absolutely necessary to explain the complexity of the living world, as follows: the thermodynamics of irreversible processes [1,2]. These different ingredients are, more often than not, largely ignored by conventional biologists, who see the living cell as an object obeying the following laws of classical physics: Newton’s equations for the mechanical aspect and Maxwell’s equations for the electromagnetic aspect. As for the reactivity aspect, it draws heavily on the thermodynamics of chemical equilibria, focusing on the notion of energy. The entropy aspect is only taken into account to model chemical potential via the notions of enthalpy H(P,V) and “free” energies known as Gibbs G(T,P) or Helmholtz F(T,V). Because of these theoretical limitations, one phenomenon closely linked to life remains a profound mystery—consciousness. While consciousness is clearly manifest in human beings, there is growing evidence to suggest that it also exists in animals, plants, and even in the single-celled world of bacteria.

Here, we propose to place biology in a quantum, relativistic, and entropic framework, while including the phenomenon of consciousness from the outset. This has, of course, already been conducted and published in previous scientific articles, where all the technical and scientific details can be found. Our aim, therefore, is not to repeat what has already been said, but rather to glue the pieces together to provide a coherent overview of the inexorability of the vital phenomenon, both in its purely material (mechanical or chemical) and immaterial aspects (electromagnetism or psyche via the notion of consciousness). Let it be clear that we have no pretension of asserting that this is a theoretically demonstrated and experimentally validated vision. Rather, it is a synthetic proposal designed to orient future biological research on a clear physicochemical basis, in line with the laws of modern physics. In other words, it is a paradigm shift that places the quantum vacuum and its interfacial material agent, the water molecule, at the center of the game, rather than on its periphery as a mere filler for the holes created by organic and/or inorganic matter, so do not be overly surprised if we start with some basic physics notions. For, like a painter faced with a blank canvas or a musician faced with an empty score, a framework must be put in place so as not to spill over into purely philosophical or religious considerations. Because, as soon as we talk about consciousness, religion is not far away… Thus, it is imperative to put in place solid safeguards rooted in science and not in dogmatism of any kind. Once the framework is in place, it will be time to fill it with a palette that draws on tangible, weighable matter, of course, but also on non-matter (imponderable waves and fields) and the mixed concept of information, which is equally weighable (entropy) and imponderable (memory and consciousness).

We are well aware that the origin of life is an intensely debated subject, both in science and in religion. Indeed, for some, life may well be the result of extraterrestrial intervention. If this were the case, everything we say here would obviously be wrong and biased by our anthropocentric nature. Our first working hypothesis will, therefore, be to assume that, since the appearance of planet Earth in the solar system, no extraterrestrial life form has come to interfere with the basic physicochemical processes as we are about to describe them as simply and succinctly as possible. In this review, we will also attempt to blend the scientific and philosophical approaches. After all, there is no guarantee that science is the best route to knowledge. It is up to each and every one of us to decide and choose what suits us best, in the light of what we are about to present.

2. Water and Life in Greek Philosophy

2.1. Empirical Approach: The Six Elements

The city of Miletus Ionia (Asia Minor) was the cradle of a monistic philosophy which explained, in a language accessible to all, that there was a single primordial substance or element. This primordial substance contained within itself a principle that created the visible world, as follows: movement. As everything was matter for the Milesians, including the soul or thought (ψυχὴ, psychê), the question of emptiness did not even arise. For Thales of Miletus, the founder of this way of thinking, the primary, animate element is the water of the River Oceanos (Ωκεανος), hence, the idea of an Earth floating on an ocean. Thales sees water as the permanent basic element that ensures the constitution and transformation of all things. His apothegm is that “All is water, all is one”. According to Diogenes Laërtius (c.300 C.E.), it was Thales who first enunciated the precept “Gnothi Seauton” (Γνῶθι σεαυτόν) meaning “know thyself”, which is engraved at the entrance to the temple of Delphi at the foot of Mount Parnassus. We see here, then, the close link that exists, from the outset, between life in the form of pure consciousness or cells and liquid water.

Anaximander of Miletus, a disciple of Thales, prefers to place the origin of all things in perpetual circular motion, which cannot be preceded by anything else. Thus, in the beginning, matter appears in the form of a neutral element more subtle than water but denser than air, which Anaximander calls Apeiron (Aπειρον). This Apeiron is imperceptible to the senses and unbounded. It can be resolved into the following pair of states: hot/cold on the one hand and dry/wet on the other. Each world, thus, adopts a spherical shape with a cold central core (Earth) surrounded by wet (Water), then dry (Air), and finally hot (Fire). Like Anaximander, Anaximenes of Miletus wanted to place movement at the origin of things, but he was looking for something that could be perceived by the physical senses, and which was unbounded and in perpetual agitation. Since the element Air possesses all these qualities, he posited that “everything comes from air, and everything returns to it”. This view that, without air, there would be no life, resonates today in the fundamental division between living beings that breathe air and those that can live in anaerobic conditions.

In 494 B.C.E., the city of Milet was taken and ravaged by the Persians, putting an end to the development of the empiricist and monistic Milesian philosophy. However, this philosophy was to be found again, still in Ionia, but further north in the city of Clazomenae, in a dualistic form from which Socrates, Plato, and Aristotle drew, and, by the same token, all our contemporary thought. Anaxagoras of Clazomenae posited that “nothing is born and nothing perishes, but things that already exist combine and then separate again”. The novelty introduced by Anaxagoras is Intelligence or Spirit (Νοῦς, Nous), an infinite non-material thing quite distinct from the Milesian material psyche, which is the initial driving force, the very principle of movement. This spirit is non-limited and allied to nothing, but it exists on its own, possessing the capacity to discriminate, not to generate. It has the ability to rotate material principles (Υλη, Hylê) called homeomeres, which are infinite in number and infinitely small at the same time. It follows from this that the void cannot exist for Anaxagoras. Thus, the Spirit (Νοῦς) separating itself from the Whole (Παν, Pan) at one point triggers a whirling movement (Περιχωρησις, perichoresis) that gradually spreads throughout the Universe and continues to do so to this day. Under the effect of Νοῦς, heavier bodies, like Earth, are carried downwards. The lighter ones, like fire or ether (αἰθειν, aithein), move upwards. Air and water are in the middle.

Between the cities of Milet and Clazomenae lies the town of Colophon, where the bard Xenophanes of Colophon sang the praises of a single God. One great whole, present in all things, being both ψυχη and νοῦς. For Xenophanes, mud, a mixture of earth and water, is the origin of the universe, which has no beginning and no end. Man, like the universe, is a mixture of earth and water. South of Colophon and north of Miletus, we find another poet, Heraclitus of Ephesus, known as “the obscure” because he was particularly difficult to understand. Indeed, Heraclitus was one of the first philosophers to use symbolic language, where logos (Λογος, logos) implies an underlying harmony of opposites. This implies, metaphorically speaking, the laws of eternal (αἰωνα, aiona) change. From all things the one and from the one all things. For Heraclitus, all matter comes from fire and will return to fire, the archetype of the eternally changing substratum. Fire is eternally alive, because it has always existed and always will. All becoming is the fruit of discord (ἐριν, érin) and necessity (χρεων, khreon). Heraclitus was the first to give a creative image of time. His favorite image is that of the river seen as a dynamic system in perpetual change, but one that nevertheless possesses its own law of organization and existence. Since nothing is permanent and everything is movement, Heraclitus’ apophthegm would be “Πάντα ῥεῖ, Penta rhei”.

Empedocles of Akragas was the last “empiricist” philosopher, heir to the Ionian tradition. For his part, he sought an adequacy between sensory perception and the intrinsic reality of Nature (Φυσεως, Phuseôs). For Empedocles, it is the senses that teach the true nature of things. Like many of his colleagues, he took the view that nothing can absolutely come into existence from nothingness, and that what is cannot perish. The Whole (το Παν, to Pan) is seen as an absolute continuum that leaves no room for the void, and is expressed in a fourfold reality (fire, air, water, and earth), which are the “roots of all things”. Each root (στοιχεια, stoikheia) displays the property of quantitative invariance. In order to provide the necessary impetus for the movement without which all creation would be impossible, Empedocles also considers two complementary “producing causes” to explain the transformation of roots. On the one hand, attraction (φιλια, philia) unites the multiple into one. On the other, repulsion (νεικος, neikos) divides the one into the many. Attraction reigns over Sphairos, that is, the sphere of the intelligible, whereas repulsion reigns over the Cosmos. In other words, the sensible world. As with Anaxagoras, roots assemble and dissociate according to a law of conservation of content, generating variable forms. All creation is the fruit of chance encounters and the necessity of symmetries imposed by repulsion, but with a memory (ἀναμνησις, anamnêsis) that leads roots to seek each other out in order to find each other again thanks to attraction.

2.2. Dogmatic Approach: Matter, Emptiness, and Movement

Figure 1, on the left, summarizes these different empiricist philosophies, in which emptiness (Apeiron), consciousness (Nous), matter (Water, Air, Earth), energy (Fire), and force (Attraction/Repulsion) play, in turn, the roles of creative principles. In 540 B.C.E., the Persian conquest forced the Ionians to flee to the far west and found the city of Elea. It was here that Parmenides posited that there are two paths to knowledge. The first is the path of Truth (ἀληθειης, aleitheiês) based on reason. It corresponds to the intrinsic state of nature, a state totally independent (objective) of its observer. Thus, it is with Parmenides that a driving principle (ψυχη, psykhê) appears, capable of giving life (ζωη, Zoê), spirit (νους, nous), and thought (φρονησις, phronêsis) to any material structure. The consequence is that there is a single, eternal (ἀτελεστον, ateleston), and immobile (ἀτρεμες, atremes) Being (το ἐον, to eon). In short, something that is uncreated (ἀγενητον, agenêton) and also imperishable (ἀνωλεθρον, anôlethon), which preserves itself no matter what, allowing us, by reference, to reason about the world. Moreover, Being is non-divisible (οὐλομελε, oulomele, global, without separate members) and homogeneous (ὁμοιον, omoion). Consequently, Being is continuous and One, and, therefore, emptiness does not exist. Since Being possesses all attributes, it possesses, in particular, the attribute of being the limit, and, as such, it cannot be infinite. Thus, this completed Being that fixes eternal permanence is clearly opposed to Anaximander’s infinite Apeiron, a generator of intrinsic change.

The second path to truth is the path of opinion (δοξῶν, doxôn) based on the senses. This path, which we must be wary of, is opposed to the path of truth, which is sure. So, while Being is, opinion teaches Non-Being. To the eternity of Being and its permanence, it opposes birth, death, and change. Similarly, instead of the immobility and globality of Being, opinion makes us believe in the locality of movement. To the present, it opposes the past and the future, and to unity, variety. Finally, to the homogeneity and continuity of Being, opinion shows us the heterogeneity and discontinuity of the world. For his part, Zeno of Elea was a fervent disciple of Parmenides. It was he who invented dialectics with his reasoning by the absurd, reductio ad absurdum, to counter the attacks of his master Parmenides’ opponents. Zeno thus posed four paradoxes (dichotomy, Achilles and the tortoise, arrow, and stadium) in relation to the infinite divisibility of space and time. The conclusion of Zeno’s four paradoxes is clear—whatever hypotheses imply the continuity or discontinuity of time and space, it is impossible to account for motion. Therefore, motion is an illusion. Parmenides’ arguments on the rational necessity of believing that Being exists and conserves itself were also taken up by Melissus of Samos. But Melissus questions the spatial finiteness of this Being, concluding that the spherical, perfect, homogeneous, and immobile nature of Being is non-limited.

In opposition to Parmenides’ realism, there was also the esoteric school of Pythagoras of Samos, a mystico-religious philosopher and contemporary of Zarathustra (628–551 B.C.E.), Buddha (563–483 B.C.E.), and Confucius (551–479 B.C.E.). Around 530 B.C.E., he founded a politico-religious school in Crotone (southern Italy), teaching musical harmony, metallurgy, the rule of proportion in painting, sculpture and architecture, and the existence of biological, meteorological, and astronomical cycles. Nothing Pythagoras taught was to be written down or divulged to the uninitiated. There were two classes of initiates, the mathematicians (μαθηματικοι, mathêmatikoi), privileged students in the knowledge of the Master’s thoughts, and acousmaticians (ἀκουσματικο, acousmatiko), listeners capable of knowing a little of this teaching. The Τετρακτυς, a triangle formed from the first four integers, the sum of which is the Decade, the sacred number, was the sign of belonging to the Pythagorean group, for whom “All is number”. Unlike Parmenides, the interval filled by the void played just as important a role as the One. The role of the void was to distinguish numbers, their nature, their elements, their parts, and their individuality. As the void fills everything, penetrates everything, and embraces everything, it could very well be a reality, a primordial principle on a par with the One. The existence of even (2n = n + 0 + n) and odd (2n + 1 = n + 1 + n) numbers led to a logical grouping of concepts, as follows: One (εν, en), Odd (περιττον, peritton), Male (αρρεν, arren), Rectilinear (ευθη, euthê), Square (τετραγωνον, tetragônon), Limited (περας, peras), Good (αγαθον, agathon), Luminous (φως, phos), Straight (δεξιον, dexion), or Motionless (ηρεμουν, êremoun). In contrast, there were Many (και πληθον, kai plêthon), Even (και αρτιον, kai artion), Female (και θυλη, kai thulê), Curved (και καμπυλον, kai kampulon), Rectangular (και ετερομηκες, kai eteromêkes), Unlimited (και απειρον, kai apeiron), Evil (και κακον, kai kakon), Dark (και σκοτον, kai skotos), Left (και αριστερον, kai aristeron), or Mobile (και κινουμενουν, kai kinoumenoun). For the Pythagoreans, there was also an immaterial soul (ψυχη, psychê) with the memory of past lives (ἀναμνησις anamnesis) quite distinct from the physical body.

Philolaus was a pupil of Pythagoras, the only survivor of the fire at the Crotone School around 450 B.C.E. It was he who first associated the tetrahedron with fire, the octahedron with air, the icosahedron with water, the cube with earth, and the dodecahedron with a fifth element, ether. Archytas, a pupil of Philolaus, defined arithmetic, geometric, and harmonic progressions as the foundations of musical rules. He also placed himself at the end of the sky delimited by the fixed stars, and asked himself whether it was possible to extend his hand or a stick. Since nothing seemed to stand in the way of this gesture, he deduced that, despite its apparent perfection, the Universe could only be infinite.

For Parmenides, emptiness and motion do not exist, whereas for Heraclitus, emptiness and motion are real things. Atomism arose from the desire of the philosopher Leucippus to reconcile the views of Parmenides and Heraclitus. He described the Universe in terms of a vacuum and microscopic, inseparable, unalterable Parmenidean worlds—atoms. Thus, concerned with symmetry, Leucippus gave Being, seen as an atom, the attribute of Fullness, and Non-Being that of the Void (κενον, kenon) existing between atoms. The One, thus, remains unique, but due to the existence of the Void, it can divide into a multitude of fragments of infinitely varied forms. These “atoms”, inseparable and invisible because of their smallness, are in perpetual motion. This brilliant idea was taken up by Democritus of Abdera, whose philosophy is known to us thanks to Epicurus, the last representative of Greek philosophy, and Lucretius, a great admirer of Epicurus. For Democritus, “Nothing comes from nothing; nothing that exists can be annihilated. All change is the aggregation or disintegration of parts. Nothing happens by chance, but everything has its reason and its necessity”. Atoms are infinite in number and infinitely diverse in form. Falling eternally through immense space, the largest and fastest collide with the smallest. The resulting lateral movements and whirlpools (δινήν, dinên) are the beginning of the world’s formation. It follows that the World had no beginning and will have no end. Nor is there any indication that there is only one world. The soul, on the other hand, is made up of subtle, smooth, round atoms, similar to those of fire. These atoms are the most mobile of all, and from their movement, which penetrates the whole body, come the phenomena of life. No cause or force was required to impose their initial movement on the atoms, for their movement is eternal, both in the past and in the future.

While Democritus takes matter and emptiness as his starting point, the first sophist, Protagoras (c.490–c.420 B.C.E.), no longer takes the object, external nature, as his starting point, but rather sensation. For a sophist, for a given event, there are as many protagonists as there are opinions, each constituted by what they have experienced. Thus, “man is the measure of all things, of those that are, of their existence, of those that are not, of their non-existence”. No single opinion can bring together all lived experiences. So, there is no truth in itself. There are only truths particular to each individual. The sophist Gorgias (483–375 B.C.E.) goes beyond Protagoras’ pessimism, moving towards nihilism. He does this via the three following principles: first, that there is nothing. The second, that even if there is something, that something is unknowable to man. Thirdly, that even if this something is knowable, it cannot be divulged or communicated to others.

By shifting the debate from the object to the subject, the sophists’ way of thinking would, of course, send shockwaves through all Greek thought. This would prompt Socrates to assert, ironically, that “all I know is that I know nothing” (Ἓν οἶδα ὅτι οὐδὲν οἶδα, En oida oti ouden oida). It is also an ethical injunction to look inward, “Know thyself”. Becoming aware of one’s ignorance is the indispensable first step on the path to knowledge. Just as the emptiness of matter enables us to distinguish between all things, the emptiness of ideas enables us to distinguish between science (επιστήμη, epistêmê) and opinion or belief (doxa). Socrates claims to know nothing and have nothing to teach. For him, only dialogue (διάλογος, dialogos) between two consciences, two reasons, or two logos can bring forth novelty and enable mutual enrichment. So, we can no longer content ourselves with poetic fragments in the style of Heraclitus or Parmenides. Since Socrates, thinkers’ assertions have had to be justified by rigorous arguments. This is because they have to be put through the Socratic maieutic sieve. Hence, the birth of the scientific way of thinking, a formidable tool at the service of certainty, establishing that there is an order of reality that transcends both the senses and the opinions of reason that interpret them. This dogmatism underpins virtually all philosophies, whether pre-Socratic, as in Thales, Parmenides, or Pythagoras, or post-Socratic, as in Plato and Aristotle. Dogmatism reached its most perfect and well-defined form in the Middle Ages with Saint Thomas of Aquinas (1227 C.E.–1274 C.E.).

2.3. Skeptical and Causal Approaches

To oppose all dogmatic positions, Pyrrho of Elea, whose philosophy was handed down to us by Sextus Empiricus (160–210 C.E.), claimed that nothing is certain, and that every proposition can be opposed by an equally probable contrary proposition. Therefore, the wise man must stick to examination and abstain from judgment (ἐποχή, epoché) (σκέψεις, skepsis). Hence, the name skeptics, followers of the no–yes, no–no philosophy. Skeptics distinguish between good things, bad things, and indifferent things, based on what appears to them. The skeptic denounces the vanity of any dogmatic search for causes. He is, thus, a precursor of the positivist, who holds to scientific knowledge alone, without any value judgments. In the end, it was the Socratic maieutic that enabled us to move beyond the nihilistic discourse of the sophists and the abstention from judgment of the skeptics. But above all, it crystallized the debate between the supporters of emptiness (Pythagoras and the atomists) and the opponents of emptiness (Empedocles and Anaxagoras) in favor of the latter.

Plato, born Aristocles, who met Socrates at the age of 20, was shocked by the latter’s death. In fact, Socrates calmly drank a lethal decoction of hemlock after being sentenced to death by the People’s Court of Athens for impiety and corruption of youth. Plato wondered how false speeches could be more persuasive than true ones. He used the Allegory of the Cave to explain his tripartite vision of nature. There are the intelligible forms, the ideas (εἶδος, eidos), which are the immutable models of sensible things. These ideas are merely the images of intelligible forms projected onto a spatial medium. In other words, a material upon which the action of the demiurge is exerted, enabling sensible things to appear. Plato believes in the existence of Non-Being, like Leucippus and Democritus, but he never quotes Democritus, for whom Non-Being is identified with emptiness (κενόν, kenon). Plato rejects this concept. He speaks of something that is both a receptacle and a material, a thing capable of mediating between the sensible and the intelligible, which he calls extent (la chora, χώρα). Extent, then, is not empty space, but the permanent matter of the universe. Thus, Plato agreed with Socrates that the general, as one and stable, can alone be the object of science. He also agreed with Heraclitus that the sensible world was in a state of perpetual change. His world of ideas corresponded to the Eleatian definition of Being, as follows: One, unchanging, free from multiplicity and change. But, at the same time, he agreed with Democritus (without ever naming him) on the multiplicity of things.

Plato’s pupil, Aristotle, recognized that the goal of science is to know the principles and causes of being. But Aristotle rejected the idea of a universal separate from individuals. For, as the idea is outside things, to know the idea is not to know the thing. Here, there is no question of substituting another intelligible world for the sensible one. Rather, we simply need to determine the point of view from which we must consider the sensible world in order to find it intelligible. Aristotle, thus, sees philosophy as the science of Being in general. Physics, on the other hand, is the science of material beings in motion or capable of receiving motion. Thus, Aristotle contrasts form, which particularizes, with ideas, which generalize. He posits that Being is composed of an indeterminate material cause (cf. Pythagorean even numbers) that exists in potential, and this material cause is associated with an essential or formal cause that exists in act (cf. Pythagorean odd numbers). Matter (ὕλη, hylê) and form (μορφή, morphê) are, therefore, along with privation, the principles that coexist in substance (ουσία, ousia), but which can only be isolated by abstraction. So, unlike Plato, who identifies matter and extent in a theory of the appearance of sensible forms from pre-existing intelligible forms, Aristotle develops a theory of matter as the substratum of change. For Aristotle, the act is the realization of the possible, which requires a driving cause that generates movement and a final cause that stops it in its tracks. This movement is considered as continuous and infinitely divisible. It can occur in the three following ways: spatial displacement (A → A), displacement in quantity A by evolution (∆A), and displacement in quality by alteration (A → B). Hence, the Aristotelian apothegm, “Everything moved is necessarily moved by something”. But there cannot be an infinite series of principles. We must, therefore, necessarily stop at a first cause, God, who communicates motion without having received it. From this first principle, there is an infinite chain of causes and effects in time (displacement), in magnitude (evolution), and in the succession of beings (alteration). Like his master Plato, Aristotle fought against the idea that the void could exist. The basic idea stemmed from the fact that “the quantity that surpasses another quantity is composed, first of the quantity by which it surpasses the other, and then of the very quantity it surpasses”. Thus, 5 = 3 + 2, where 3 is the quantity separating 5 from 2, which is the quantity surpassed. But if I write that 5 = 5 + 0, the latter appears to be composed of itself and nothing, which is rather awkward. The void can have no proportion to the full, so it does not exist. This leads us to regard the void as a Non-Being, suggesting that it is a privation rather than something in itself.

3. Life Versus Inert Matter

It was important to review the philosophies behind the development of our “modern” science. It is no exaggeration to say that, before Aristotle, there was a veritable ferment of ideas. Then, from Aristotle onwards, this ferment came to an abrupt halt. The reason for this abrupt halt is the idea that, if the void exists, it can only be a deprivation of matter, and not a thing in itself existing independently of matter. Worse still, the very idea that the vacuum could create matter was simply inconceivable. The basic question was, “Why is there something rather than nothing?” This totally echoes the question that interests us here, “How could life have arisen from non-living things?” As these are very difficult questions, the temptation to invoke the existence of an immaterial divinity that substitutes for the void or is the only one capable of procuring life is great.

3.1. There Are No Supernatural Beings

Let us now take a look at modern science. According to Figure 1, there are the five following main currents of thought:

• The pre-Socratic Empiricist movement, based on the theory of the four elements (Earth/Water/Air/Fire) and beginning with Thales and Xenophanes. This trend was taken up, in part, by post-Socratic Aristotelian realism.
• Pre-Socratic esotericism (Tetrahedron, Octahedron, Cube, Icosahedron, and Dodecahedron). This trend begins with Pythagoras and continues with Socrates towards Platonic idealism (ideas) or towards Aristotelian realism (duality of matter and form), where emptiness is deprivation.
• The pre-Socratic Rationalist movement, which denies movement and, therefore, emptiness, since, without emptiness, there can be no movement. This trend derives from the ideas of Parmenides. It culminates in the idea that Being can only be limitless and, therefore, infinite.
• The pre-Socratic constructivist trend, which puts the human being at the center of the game. This trend asserts that there can be no absolute truth, since the human being is the measure of all things. This gave rise to post-Socratic skepticism, in which observation is all that counts. Since the void cannot be observed, it does not exist.
• The post-Socratic Atomist movement, which takes up the starting point of rationalism. But here, instead of denying the existence of motion, since it is clearly observable, we deduce that the void must also exist. Hence, atoms of matter move in a non-material vacuum.

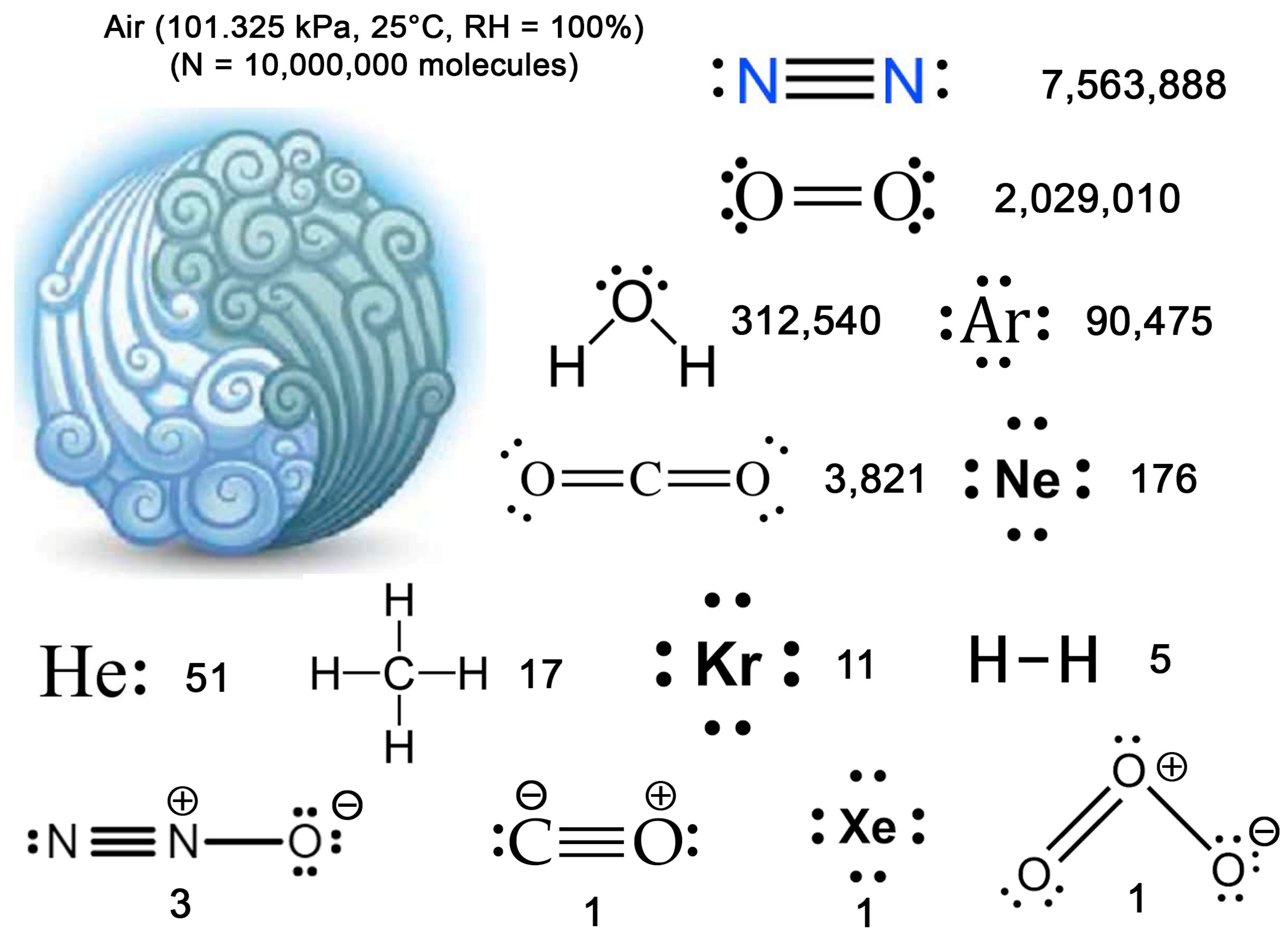
3.2. Air Always Contains Water

First of all, it is clear that the empiricist trend is problematic. We know today that, under ambient conditions of temperature (T = 20 °C) and pressure (P = 101.325 kPa), air always contains water. Figure 2 summarizes what we know today about this element called “air”. For simplicity’s sake, we chose to use only whole numbers. To achieve this, we took the composition of a dry atmosphere [3] and calculated the quantity of water vapor present in the air at a temperature of 25 °C, a pressure of 101,325 Pa, and a relative humidity of 100%. That is, P(air) = 98,158 Pa and P(H₂O) = 3167 Pa [4]. We then calculated the number of each of the fourteen molecules present in the atmosphere, for a total of 100,000 air molecules. This showed that the water molecule came in third place, just after the oxygen molecule. Of course, we assumed a relative humidity of 100%. So here, we determined the maximum number of water molecules that can be present at 25 °C at sea level. But even in a hot desert, there will always be some humidity, up to 2%. With such a relative humidity, we calculated P(air) = 101,324 Pa and P(H₂O) = 0.634 Pa [4], which still corresponded to 63 water molecules compared with one Xenon molecule and 182 Neon molecules. Water is, thus, becoming very rare, but is still very much present. In other words, it is completely unrealistic to consider air without a single molecule of water in it. Of course, this fundamental fact disqualifies air as an elementary constituent of all matter. After all, there will always be a non-zero quantity of water in air.

3.3. Earth Is Always Hydrated

The same applies to the “element” earth. Figure 3 shows the total amount of water present on planet Earth. Here too, imagining a totally anhydrous earth is totally unrealistic. There will always be moisture in the Earth’s soil. For comparison with Figure 2, we considered an average soil composition. Once again, we calculated the molar fractions of the main elements and the proportion of water molecules. For the calculation, a typical soil was assumed to be 50% void and 50% dry matter. The 50% void contains either air (25%) or water (25%). For the inorganic solid part based on the elements (Si, Al, O, H + Fe, Mn, Ca, Mg, Na, and Cl), we took a mixture of sand (40%), silt (40%), and clays (20%). The sand and silt were essentially composed of quartz with the formula SiO₂ and a molar mass of 60.08 Da. For the clay, we instead considered a kaolinite Al₂Si₂O₅(OH)₄ with a molar mass of 258 Da. Hence, there was an average molar mass of 60.08 × 0.8 + 258 × 0.2 = 99.7 Da for the dry soil. A typical value for organic matter is 14 mg per gram of dry soil [5]. If we assume that this organic fraction is essentially a mixture of an equal mass of amino acids belonging to proteins (average molar mass of 110 Da per amino acid) and glucose (molar mass of 180.156 Da), we calculate an average molar mass of 137 Da. Consequently, for a soil with a density of 2.66 g·cm⁻³ and 50% porosity, we would expect to find 1.33 g of dry mineral matter with an average molar mass of 99.7 Da in a volume of 1 cm³ when saturated with water. Then, 0.25 cm³ = 0.25 g of water with a molar mass of 18.01 Da, and again, 0.25 cm³ = 0.27925 mg of air with an average molar mass of 28.97 Da. Finally, we would expect 18.62 mg of organic matter with an average molar mass of 137 Da. Hence, the figures are shown in Figure 3.

3.4. Morphogenic Water

We can see that, when we hold a handful of earth in our hand, we are essentially holding an equimolar mixture of water and matter, with very little air. Let us suppose that this air is flushed away by substituting water during a heavy rainfall, for example. We would then obtain, still for 10,000 molecules of “Earth”, 6732 molecules of water, 3235 molecules of mineral rock, and 55 molecules of organic matter. The conclusion is that what we call “earth” is more water than rock. This is why plants can grow even when no liquid water is visible. Hence, the term “morphogenic” water [6]. This is a reminder of the fundamental fact that water can be found in vast quantities in a wide variety of forms, but without revealing that they are, molecularly speaking, essentially just water. Indeed, the term “morphogenic” was coined from two Greek roots. On the one hand, the root “morphos”, meaning “form”. On the other, the root “genos”, meaning “creator”. So, morphogenic water is the water that gives rise to all the forms we can observe in the natural world around us. To convince yourself of this, all you have to do is thoroughly dehydrate any material form. It will then be reduced to powder. The only exceptions are materials formed from mineral particles such as quartz or clay, where water is not found inside their crystalline structures, but rather on the outside. In this case, it is possible to retain the original shape throughout the dehydration process, in order to obtain totally anhydrous glasses or ceramics.

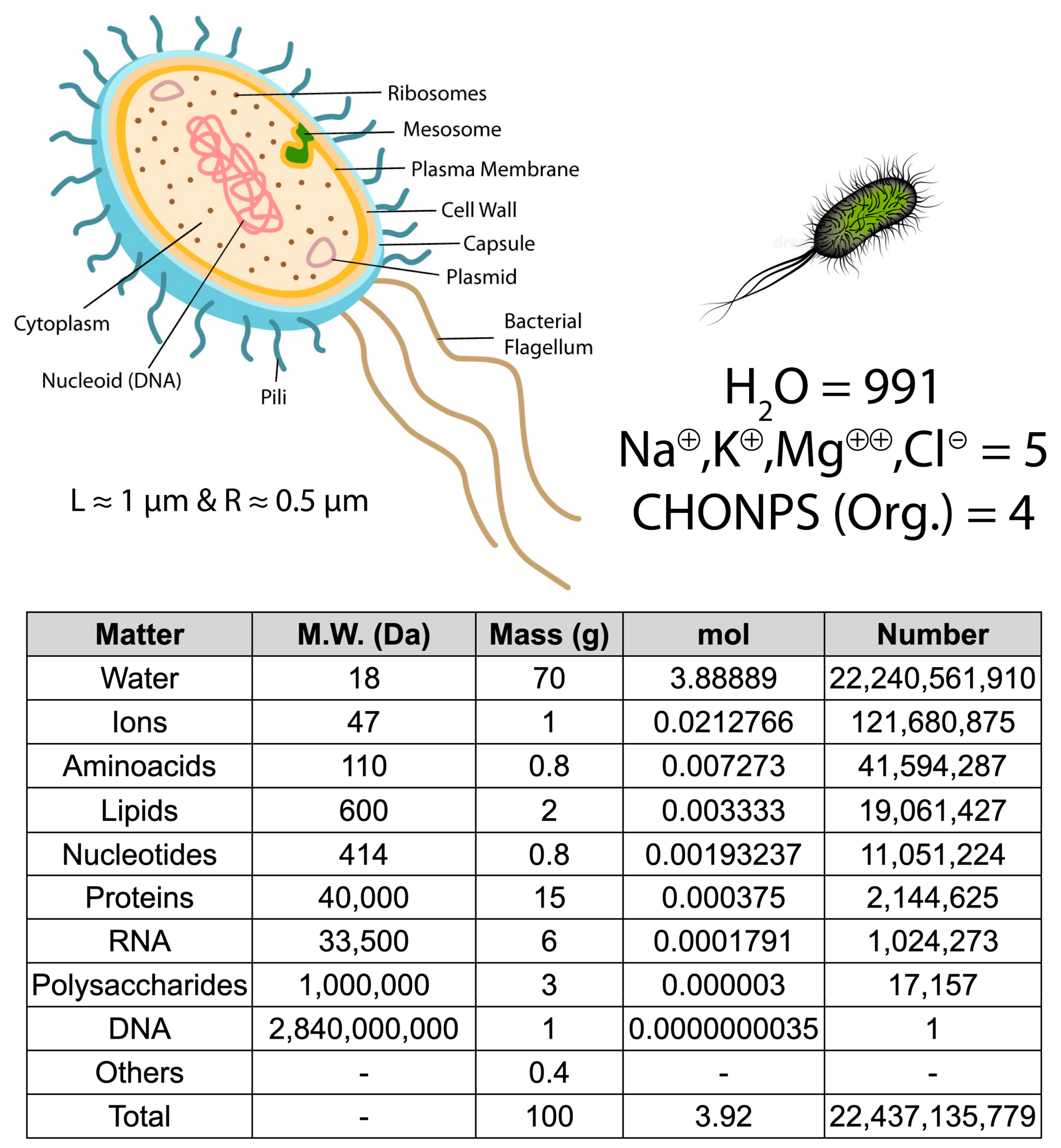
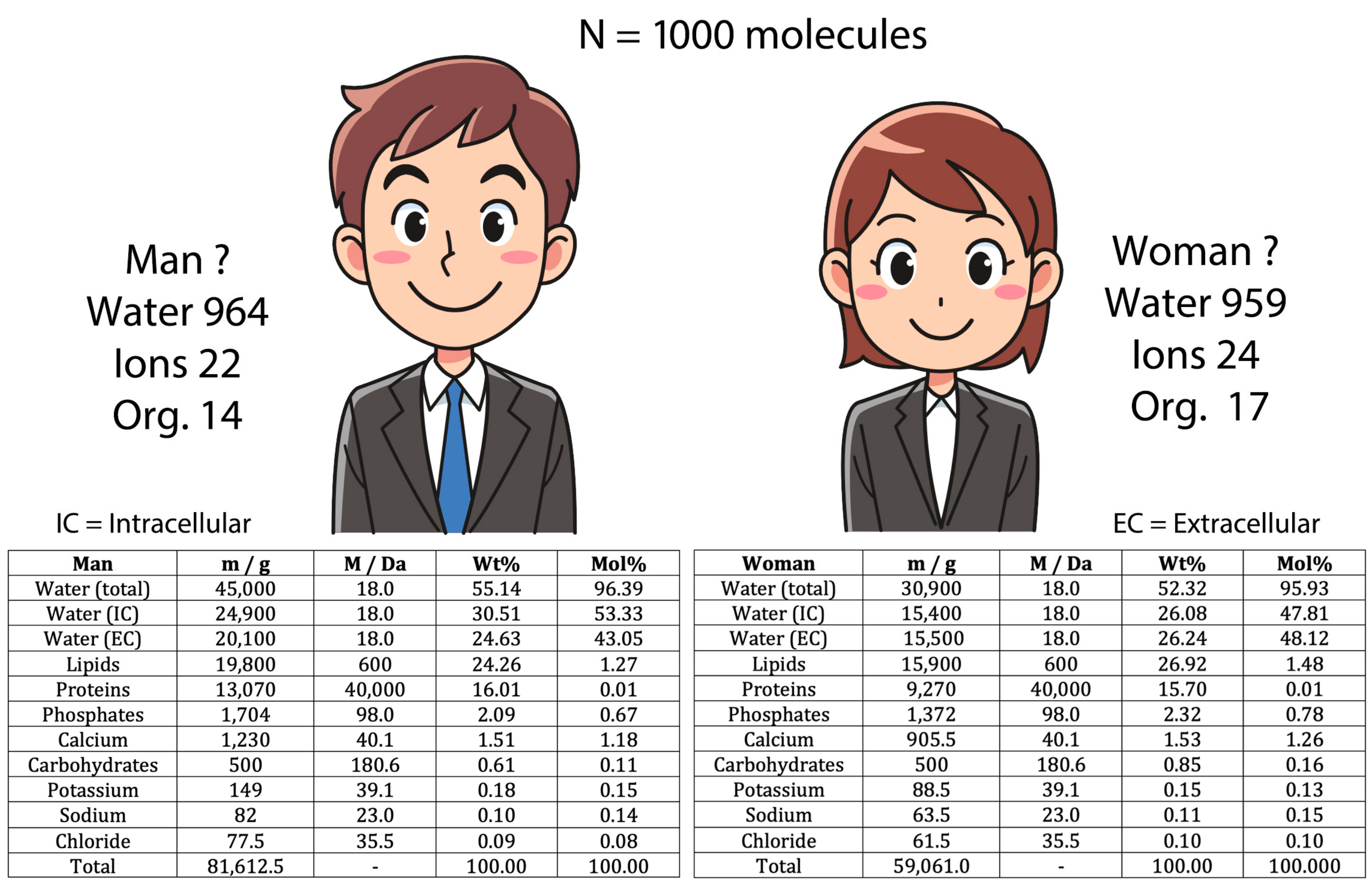
3.5. Molar Composition of a Living Being

Let us take a look at an extreme case of an object that, from the outside, does not look like water. Yet, it is essentially water. We are talking here about a living cell of the prokaryotic type (see Figure 4). Taking a bacterium like Escherichia coli, what we see is a cylindrical body covered with very fine hairs. Several flagella emerge from the cylinder, enabling the bacterium to move around independently. In short, we are dealing with a living being, not inert matter subject to external disturbances. Now, let us take a look at what we find inside this bacterium (see the table accompanying Figure 4). This table lists the main constituents and their relative proportions [7]. As we have become accustomed to doing, let us transform all the measured masses into moles. The result is indisputable. This living thing is 99.1 mol% water. In other words, if we count to 1000, we will find 991 water molecules, 5 mineral ions, and 4 molecules based on highly varied combinations of carbon, hydrogen, oxygen, nitrogen, phosphorus, or sulfur (CHONPS). In other words, E. coli bacteria can be summed up as a drop of slightly salty water “polluted” by a few rare organic molecules. Or, if you prefer, that all biology books, no matter how thick, speak, in brief, of only 4‰ of the matter present. All the rest, or 994‰ of this matter, is a matter of water containing minerals.

This applies to all living beings. Take a human being, for example. If we look inside and out, we see skin, organs, and bones. But if we take into account that all these objects are made up of cells, we would expect water to be the predominant molecule. Figure 5 lists the molecules present in a human body [8]. The relative molar proportions totally confirm this point of view. Thus, a man, boils down to 964 mol‰ of water molecules, containing 22 mol‰ of dissolved minerals and 14 mol‰ of molecules based on the CHONPS elements. For women, it is slightly different. There is a little less water (959 mol‰) and more minerals (24 mol‰) or organic molecules (17 mol‰). So, there is an awful lot of water in a male or female human being. In fact, the novelty for bodies made of eukaryotic cells, compared to a simple prokaryotic bacterium, is that there are the two following types of water: immobile intracellular water and extracellular water that moves. It is in this respect that men differ from women. In a man, there is slightly more intracellular water (533 mol‰) than in a woman (478 mol‰). Which means, of course, that we have the opposite situation for extracellular water, as follows: 430 mol‰ in men versus 481 mol‰ in women. In other words, the sexualization of human beings is primarily linked to water, more than to the shape of organs or the XX or XY nature of chromosomes. Even with surgery to change sex (organs) or the genetic manipulation of chromosomes, male bodies will always have more extracellular water than female ones.

4. Chinese Philosophy and the Tao

4.1. Chinese Culture Versus Western Culture

Returning now to Figure 1, we can greatly simplify the Western materialistic vision of nature. Indeed, we now know that there are only the two following fundamental “elements” to consider: Water and Fire. It is at this precise point that we should forget Western science for a moment. In the East, other, perhaps more relevant, philosophies have emerged. We are referring here to the Chinese civilization summarized in Figure 6. But first, a few dates must be specified. Figure 1 shows that in Greece, everything began in the first millennium B.C.E.

Chinese culture began as early as the third millennium B.C.E., with the Longshan culture (3000–1900 B.C.E.) in the lower basin of the Yellow River (Huang He). During the same period, in Europe, the Bronze Age began in Greece and the Aegean Sea (3500–2000 B.C.E.). In the Near East, the Jiroft civilization flourished in Iran (3200–2100 B.C.E.), followed by the Archaic dynasties of Mesopotamia (2900–2340 B.C.E.). The Indian subcontinent saw the blossoming of the Indus Valley civilization in India and Pakistan (2600–1900 B.C.E.). In America, vast cultural and religious complexes were built on the central coast of Peru (2600–1800 B.C.E.). Lastly, Africa saw the construction of the great pyramids in Egypt (2700–2000 B.C.E.).

4.2. Tao (1), Dynamic Yin/Yang Duality (2), and He Harmony (3)

All this is to highlight that Chinese culture far precedes Western culture, where the notion of elements refers to concepts of form, substance, and quality. In China, on the other hand, we tend to speak of agents of transformation, and, therefore, of processes or changes. These changes refer to the cosmos, the terrestrial world, and human nature. To sum up, in China, we assume the existence of a fundamental principle forming and animating the universe, breathing life into it, the one, called Tao. Tao then creates the yin–yang pair associated with the number two. Yang is a masculine, sonorous principle (music) symbolized by the Sun, associated with all that is bright, luminous, and hot (gas) and is always in motion. In contrast, Yin is feminine and silent (rite), symbolized by the Moon, associated with all that is dark, obscure, and cold (solid) and is at rest. But because of the Tao in the background, Yang and Yin are by no means static principles. On the contrary, they are dynamic entities that allow for Ch’i or Q’ì to circulate. When Ch’i circulates, what is light and clear tends to rise towards the sky. What is dark and heavy, on the other hand, tends to fall to the ground. A well-known symbol of this dynamic Yin/Yang duality is the “Tàji Tú”, which features two spirals of opposite chirality. One is white, the other black. But both are interlocked, with black and white dots superimposed. Hence, the dynamic, since at any moment, the white spiral can become black and vice versa.

Of course, such a constantly shifting Yin/Yang dynamic calls for a state of balance and harmony, “He”, associated with the number three and the geometric figure of the triangle. Hence, the saying, “Never two without three”. There are two ways of representing this ternary principle. The first is in the form of the “Tai Chi” symbol, represented by a white center around which two spirals wind, one yellow, turning to the left, the other black, turning to the right. Here, the dynamic has been stabilized by the presence of the Tai Chi center. The second representation is an equilateral triangle. Here, the base symbolizes the Yin/Yang duality and the third vertex of the “He”, achieving a perfectly balanced synthesis between the two opposing vertices. Of course, the perfect ternary symmetry evokes the idea that the “He”, “Yin”, and “Yang” aspects are totally indistinguishable, forming a unity that recalls the existence of the “Tao”. If the Yin/Yang pair refers to the Earth/Sky pair, the Yin/He/Yang triplet indicates that, between Heaven and Earth, there is a middle ground. This middle ground, symbolizing the harmony of the Earth/Sky pair, could very well be the human being. Hence, the existence of three types of “energy”. The first, Yang (Ch’i), is of a respiratory nature, breathing life into us. The second, Yin (Jing), is of a sexual nature, authorizing reproduction. The third, He (Chen), is spiritual in nature, animating the immortal soul of every human being.

4.3. Invisibility (n ≤ 3) and Visibility (n ≥ 4)

In Taoist philosophy, everything that is one, two, or three is invisible and inaccessible to the human senses. This is why the summits of Chinese pyramids are always truncated to symbolize such inaccessibility. For, as explained in the Tao Te Ching, the number three is capable of producing all things, “The Tao produced One; One produced Two; Two produced Three; Three produced All things. All things leave behind them the Obscurity (out of which they have come), and go forward to embrace the Brightness (into which they have emerged), while they are harmonized by the Breath of Vacancy.” [9].

Among them, the very first, the number four, restores the dynamic introduced by the number two. But this new dynamic is an accessible movement of an earthly nature represented by the four cardinal points (South, West, North, and East). Each of these four cardinal points is associated with a legendary animal associated with the four seasons, with one pair (South/North) represented by the Red Phoenix (Summer)/Black Turtle (Winter) pair, which is associated with the duality of Heaven (Yang) and Earth (Yin). A second pair (West/East), represented by the White Tiger (Autumn)/Green Dragon (Spring) pair, is associated with the duality of Water (Yin) and Fire (Yang). It is at this precise point, the Water/Fire duality, that Chinese and Greek philosophers find themselves on the same wavelength. This also applies to the other pair, which is formulated as Heaven/Earth in China and Air/Earth in Greece. Is Air not in Heaven, the opposite of Earth?

The difference between the two philosophies is that the four Greek elements emerge from virtually nowhere. The four cardinal directions, on the other hand, have the Yin/Yang duality and the unity of the Tao as their backdrop. From this point of view, Chinese philosophy appears far more rational and convincing than Greek philosophy. But it is also the way that it follows the numerical progression that makes it even more convincing. For example, for the number five, we tend to think of the five “elements” of Wu-Xing (five-pointed star), but this would be a serious mistake. The temptation is great, since three of these agents (Fire, Water, and Earth) coincide with three of the Greek elements. Only Air is eliminated from the Chinese pentacle. The reason is simple, since Air actually appears in the form of Heaven in the number four, which precedes the number five. It would, therefore, be totally illogical to include it again at this higher level. So, how do we understand these five agents?

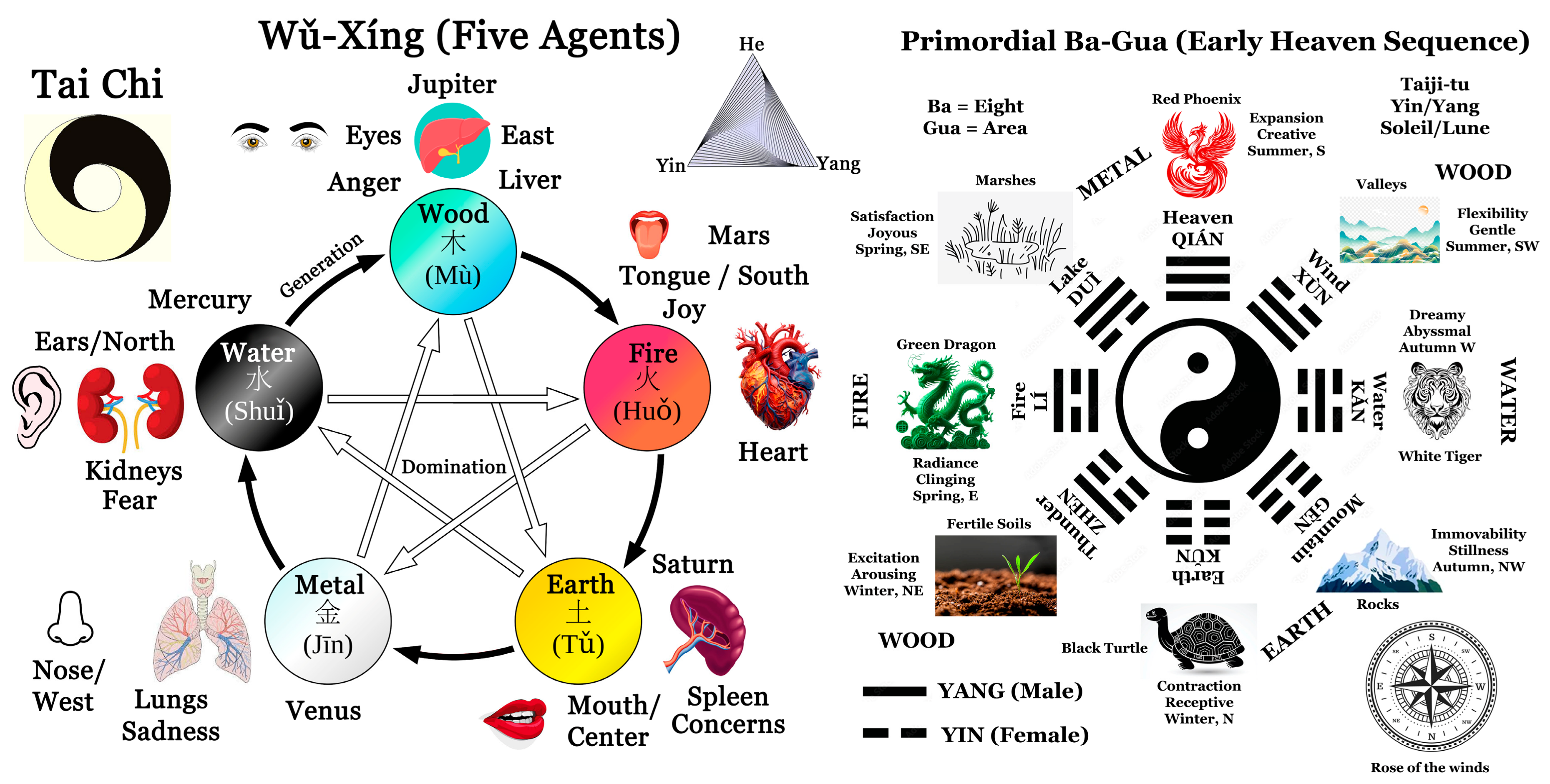
4.4. The Five Chinese Elements (Wu-Xing)

The idea is to understand that the number four is intimately associated with life on Earth. The Earth is dark, while the Sky is clear and luminous when the Sun shines. As chapter 42 of the Tao Te Ching makes clear, all things tend to move from darkness to light. As the number four is associated with the Earth, it is only logical that it should tend towards the next level up, the number five, which must, therefore, be associated with Heaven. What do we see moving in the sky apart from the Sun (Yang) and Moon (Yin)? The answer, of course, is the stars. But a careful observer of the heavens will note that these “stars”, observable as points of light, are of two types. The vast majority of these points of light form unchanging patterns in time, called “constellations”, which move as a whole through rotation. On Earth, however, everything is in constant motion, thanks to the harmony brought about by the breathing of the void. So, all we have to do is search the sky to see if there are any luminous points animated by the breathing of the void, never occupying the same place from night to night. If so, this could hold the key to the successor of the number four.

Indeed, all is well, for there are exactly five points of light moving against a fixed, unchanging background of stellar constellations. These are, of course, the five planets of the solar system visible to the naked eye. Starting with the Sun, these are as follows: Mercury, Venus, Mars, Jupiter, and Saturn. Symbolically, the number five refers to the letter X, formed by two inclined branches meeting at a point. This letter also appears if we project a square-based pyramid from its apex, where the four triangular faces meet. The number five, thus, reveals a center, whereas the number three reveals a median. It is, therefore, a higher degree of harmony that brings stability. Such a center, organizing two pairs of opposing Yin/Yang polarity, is obviously reminiscent of the undifferentiated Tao. Here we find the attributes of the planet Mercury, whose sex is both male (Yang) and female (Yin). Mercury, i.e., intelligence, is, therefore, an organizing center between the pair of Mars (Yang) and Venus (Yin) on the one hand, and the pair of Jupiter (Yang) and Saturn (Yin) on the other. But we can also refer to the organizing center of the human heart. Here, the pair of opposites becomes the pair of Kidneys (Yin) and Spleen (Yang) on the one hand, and the second pair of Lungs (Yin) and Liver (Yang) on the other.

4.5. Higher Levels (n > 5)

As you may have gathered, in Chinese philosophy, even numbers are dynamic in nature. Therefore, they belong to the earthly realm. In contrast, odd numbers are static in nature, belonging to the celestial realm with its unchanging stellar constellations. So, the successor to the number five must refer to a higher level of terrestrial organization, a level where we expect to find the dynamic impetus of the number two. On the other hand, the harmony brought about by the number five, symbolized by the letter X, must not be broken. There is only one solution—the octahedron, a geometric figure with six vertices and eight triangular faces, which, like the square-based pyramid, is again represented in projection by the letter X. This new figure, or geometry, allows us to achieve a perfect balance between the three following directions of the Earth: Right/Left, Front/Back, and Top/Bottom. Thus, the six figure organizes the dynamic exchanges between Heaven and Earth, shaping the world in which life expresses itself.

With the number seven, we find celestial stability in the form of a new organizing center. Geometrically speaking, we add a center to the octahedron, where the three directions defined by the number six intersect (7 = 1 + 6). This organizing center is the spark of life that can either start or stop. Here, we find the Yin/Yang fusion expressed through the pairing of Life (Yang) and Death (Yin). To be alive is to accept that we must die one day. But, at the same time, it means admitting that it is always possible to be reborn if you have died. The number seven represents the attainment of a perfection that can be seen in the celestial image of the Sun, Moon, Mercury, Venus, Mars, Jupiter, and Saturn, i.e., 7 = 2 + 5, but also in the earthly image of Heaven, Middle, Earth, Spring, Summer, Autumn, and Winter, i.e., 7 = 3 + 4.

The number eight represents the distribution and terrestrial organization of the formidable vital energy underpinned by the number seven (8 = 7 + 1). But it is also the number of double differentiation (8 = 4 + 4), symbolized by the eight-pointed compass rose. The four intermediate directions (SE, NE, NW, and SW) here refer to the fact that, when the Earth accumulates, mountains are created by the accumulation of rocks. Between two mountains, there is usually a valley in which the air is set in motion, generating wind. Mutually reinforcing winds can lead to thunderstorms, with thunder and lightning shattering rocks and transforming them into fertile soil. Last but not least, mountains facilitate the condensation of water in the form of snow on high ground, which then melts and gathers in the deepest valleys to form lakes or marshes. The result is a new, clearly terrestrial quaternity (Mountain/Vent/Thunder/Lake) rotated by 45° in relation to the quaternity (South/East/North/West) expressed in the Sky. This is where we find the primordial Ba Gua or Pa Kua of Taoism or Feng Shui. This geometric figure of octagonal symmetry can also be deduced from the eight trigrams of the Yi Jing, as shown in Figure 6 on the right. This figure geometrically expresses the numerical identity 2³ = 2 × 2 × 2 = 8. Another geometric figure, the cube, with its eight vertices, expresses a double quaternity (8 = 4 + 4) indistinguishable from the square when projected onto a plane along one of its six square faces.

Ba Gua is a tool for checking whether qi (or chi) is flowing properly through the body. As the number eight is associated with healing, this is another tool for rebalancing the energies circulating in the house where you live. In Taoism, we find here all eight immortals. These embody the dynamism associated with victory over earthly death (number four), through perfect union with the essence of life (another extra- or intra-terrestrial number four). All this is through the following eight figures representative of Chinese society:

• The military man, Zhon LiQuin, leader of the group, who uses his fan to resurrect dead people.
• The woman, He XiangGu, holding in her hand a lotus that represents spiritual fulfillment and watches over the family’s health.
• The vigilante, Lü DongBing, an alchemist who, with his sword, symbolizes moral rectitude combined with knowledge and wisdom. He is the patron saint of poets.
• The beggar, Lan CaiHe, holding a basket of flowers, symbolizing happiness and longevity. He is the patron saint of gardeners.
• The scholar, Han XiangZi, writer and civil servant, always carries a flute. He is, therefore, the patron saint of musicians.
• The ugly, shaggy, bedraggled cripple, Tie GuaiLi. He holds a gourd, symbol of immortality, filled with the elixir of long life. He is the patron saint of the sick.
• The old man, Zhang GuoLao, who wards off evil spirits with his “YuGu” cylindrical drum. He is the patron saint of painters.
• The great nobleman, Cao GuoJiu, who purifies the world with his two jade plates. He is the patron saint of actors.

After the earthly number eight, symbolizing the possibility of rebirth after death, we move on to the number nine, which brings us back to celestial stability. Geometrically, we again consider the cube, but, as before, we include the center (9 = 8 + 1). The immaterial celestial aspect of the number nine is symbolized by the nine following orifices of the human body: two eye cavities, two ear cavities, two nasal cavities, one mouth, one vagina in women or one urethra in men, and, finally, one anus (9 = 2 × 3 + 3 = 6 + 3). The number nine thus asserts itself as a complete completion, a finishing touch, in the completion of the One. Nine, thus, represents the exhaustion of numbers. It symbolizes the achievement of completeness. For everything has been deployed, organized, and completed. Hence, in humans, the nine months of pregnancy, or, in cats, the nine weeks before giving birth.

4.6. Cycles of Creation and Domination

Nine, therefore, symbolizes the greatest expression of Yang. But, at the same time, its exhaustion. Hence, the need to return to unity, symbolized by the number 10 (10 = 1 + 0 = 1), a number that can be associated with Wu-Xing and its five agents, as follows: Wood, Fire, Earth, Metal, and Water. Note that three of the five agents (Earth, Water, and Fire) are also present in the octagonal Ba Gua. So, for the latter, we can also consider that the wood element splits into a pair (Wind and Thunder) and the metal element into a pair (Lake and Sky). This leaves two opposing pairs (fire and water) and (earth and mountain), i.e., 8 = 4 × 2 instead of 4 + 4.

But in Wu-Xing, the five agents are involved in five cycles of creation and five cycles of domination (Figure 6 left), i.e., 10 = 5 × 2 = 5 + 5. On a strictly numerical level, we can appreciate the elegant solution to the crisis generated by the number five and the basic instability linked to the number two, i.e., 10 = 5 × 2 or 7 = 5 + 2. It is well known, but it is worth remembering. So, to create fire, you need wood, and once burnt, the wood will have generated ashes, i.e., earth. These ashes are made up of metal cations, which, when buried in the ground, can be reduced to metal. When the metal comes to the surface, drops of water appear. This water is necessary for the wood to grow again. It is all perfectly logical, and there is no divinity involved in the process of creating one element from another. The result is a five-stage generation cycle in the shape of a regular pentagon.

But alongside this Yin cycle of generation, there is also a Yang cycle of domination, which takes the dual form of the star pentagon. Thus, fire dominates metal, since it melts it. Metal, in turn, dominates wood, as it enables it to be cut into pieces. Wood dominates earth, as it lifts and pierces it as it grows. Earth dominates water, as it channels it and prevents it from flowing away. Finally, water dominates fire, since it can extinguish it.

All this is, of course, applicable to the human body. Figure 6 shows the analogy between the five agents, i.e., the five main organs (Heart, Spleen, Lungs, Kidneys, and Liver) of a Yin nature. Here, the Liver communicates its energy to the Heart, which, in turn, communicates it to the Spleen, which passes it on to the Lung, which sends it to the Kidney, before returning to the Liver. Alternatively, this is the Yang cycle of the five emotions. Thus, joy dominates sadness, since it makes it disappear. Furthermore, when you are angry, becoming sad makes the anger disappear. Anger, on the other hand, is a reaction to the presence of worries. These are eliminated as soon as we become afraid. Finally, as soon as you are afraid, you cannot be happy, which brings us back to where we started. Through this type of correspondence and the two movements of generation and domination, it is possible to cure a large number of illnesses, both physical and psychological. For this, natural derivatives of minerals, plants, or animals are used.

5. The Atomic Vacuum

The main advantage of Chinese philosophy over Greek philosophy is that the two antagonistic pairs of Water/Fire and Heaven (Air)/Earth do not emerge from nothing. They originate in an undifferentiated unity, the Tao, which is simultaneously feminine and masculine in nature. On the other hand, the notion of emptiness escapes Taoism altogether. The term “undifferentiated” refers to something that exists and is not empty. In other words, Chinese arithmetic starts with the number one and forgets the number zero. Yet, as we saw above, to explain the movement of atoms, Greek philosophy needs the void. If you prefer, the notion of negative quantity has no place in Chinese philosophy. It is all about the positive, the tangible, and the manifest, concepts born of three things imperceptible to our five senses, but also “full”. The unity of the Tao, the duality of Yin/Yang, and the median term, He harmony, which leads to the possibility of creating everything via a trinity.

As already mentioned, modern science validates the atomic theory of matter, and, therefore, the underlying notion of emptiness, which is absent from Taoism. Hence, the rejection of this elegant vision of the structure of the visible universe, where there is no place for the void. This is particularly striking in medicine, where, in the West, all illness is treated with chemical molecules made up of atoms, and not according to Taoist philosophy based on an intangible Yin/Yang duality. In this section, I propose to show that, via the science known as quantum field physics, or second quantization physics, we can forget the notion of the atom, and that, fundamentally, everything is a matter of a vacuum capable of vibrating.

5.1. Instability of the Atom

The best way to introduce this subject is to return to the atom, the elementary constituent of all matter. In chemistry, these ideas are finalized in the periodic table of elements drawn up by the chemist Dmitri Mendeleev (Figure 7). But let us forget this table for a moment, and focus on the first box bearing the symbol “H” for the hydrogen atom. At the beginning of the twentieth century, just when we thought we had completely elucidated the nature of matter, a terrible crisis arose. This crisis was linked to the discovery of a tiny particle of matter that explained the existence of electrical and magnetic phenomena, the electron. This particle of matter in fact carries a negative elementary electric charge -e = −1.602176634 × 10⁻¹⁹ C. These “electrons” were discovered in 1899 by British physicist Sir Joseph John Thomson (1856–1940). His discovery was rewarded with the Nobel Prize in Physics in 1906.

Then, in 1911, New Zealand physicist and chemist Ernest Rutherford (1871–1937), the father of nuclear physics, discovered the atomic nucleus, which carries an electric charge of the opposite sign to that of the electron, and is, therefore, positive. In 1914, he hypothesized that the nucleus of hydrogen, the lightest known atom, was made up of a single, positively charged particle, which he named the proton. In 1914, we learned that the most abundant atom in the universe, the source of all other elements synthesized in the heart of stars, is composed of a single proton with a positive charge +e. Around this proton “orbits” a single electron of an opposite electric charge -e. All is well, except, of course, for Coulomb’s law, the validity of which cannot be called into question. This law stipulates that two electric charges of opposite signs must attract each other with a force proportional to the inverse of the square of the distance separating the two charges. Because of this law, the hydrogen atom simply cannot exist! If, by any chance, a proton with a positive electric charge sees an electron with a negative electric charge in its vicinity, it will inevitably attract it to itself (see Figure 8, top left). In the end, the only stable configuration will be a proton that has swallowed an electron, i.e., a neutron n°. This second particle does exist, but was not discovered until 1932 by British physicist James Chadwick (1891–1974).

In 1914, such instability came as a great surprise. Above all, we were totally unable to explain the electron cloud’s size of around 0.1 nm = 10⁻¹⁰ m. This is a huge value compared to the size of the nucleus, which is around 1 fm = 10⁻¹⁵ m. A very mysterious force seemed to hold the electron in an orbit far away from the nucleus, preventing it from crashing into it. To understand the scale of the problem, the nucleus, which concentrates all the atom’s mass, has a volume of 10⁻⁴⁵ m³. This compares with a volume of 10⁻³⁰ m³ for the electron cloud. In short, 99.9999999999999% of an atom is empty space! So, why so much vacuum? The atom would appear stable instead of imploding on itself, without a lifetime of the order of 0.1 ns = 10⁻¹⁰ seconds and releasing an enormous amount of light.

However, there was a hint that the situation was not quite so catastrophic. In fact, according to Maxwell’s theory, the “vacuum” did not seem quite empty, since, to allow the propagation of light, it had to possess an electrical impedance Z₀ = µ₀·c ≈ 377 Ω, with µ₀ = 4π·10⁻⁷ kg·m·A⁻²·s⁻² (magnetic permeability of the vacuum) and c = 299,792,458 m·s⁻¹ (propagation speed of light in vacuum). A new science was, indeed, about to be born. It is best to quote the revealing words of French mathematician Henri Poincaré (1854–1912), “One of the most astonishing discoveries that physicists have announced in recent years is that matter does not exist…”. [10].

5.2. The Février-Destouches Theorem

The solution to the mystery arrived in 1924 with the advent of quantum mechanics. But rather than rehash the well-known history, let us jump straight to the founding principle of this science, known as “contextuality”. This was stated in 1946, “There is no such thing as a state variable” [11]. Remember that every value of a state variable, such as the internal energy U in thermodynamics or the Hamilton function H in mechanics, corresponds to an exactly defined value for every other variable. The Février-Destouches theorem [11], therefore, dictates that, if an observable system possesses a state variable, then statements of measurement results on this system must follow classical Aristotelian Boolean logic. Namely, identity, contradiction, and excluded third. In such a case, determinism is said to exist, since all quantities are simultaneously measurable. Hence, the use of so-called “real” numbers, which open up the possibility of differential and integral calculus, unlike “integer” numbers, where this kind of calculation is impossible. This is the situation encountered in classical Newtonian or relativistic physics, thermodynamics, or electromagnetism (Maxwell’s equations).

It is precisely at this level that something very remarkable happens. For, many natural things are measured with integers, not real numbers. So, when a cell divides, you obtain two cells, then four, then eight, and so on. You will never obtain 3.1416 cells. Similarly, an apple tree will always yield an integer number of apples, and a family will always be made up of an integer number of individuals. Above all, when a hydrogen atom is excited, it emits only certain frequencies that can be indexed by integers. Between two emission lines, there is only darkness, no light. In the same way, between the number one and the number two, there is nothing at all, just emptiness. As we saw above, an atom is, in fact, essentially empty, containing a whole number of protons, neutrons, and electrons.

The triumphant physics of the entire nineteenth century was based on the use of infinitely divisible real numbers. It is perfectly incapable of explaining the integers used by spectroscopists to index the absorption or emission lines of atoms. It was this same physics which, in 1914, forbade these very atoms to exist. There was only one way out—give up on real numbers and develop a new physics in which integers would play a leading role. Integers have been used since the dawn of time to count and answer the following question: “How many…”? The Latin word for “how many” is “quantum”. Hence, the name “quantum mechanics” was given to this new physics that was to restore stability to the atom and explain why it responds with discontinuous integers. The father of this quantum theory was the German physicist Max Planck (1858–1947).

5.3. Ultraviolet Catastrophe

The latter was obsessed with the problem of the ultraviolet catastrophe in the radiation spectrum of the “black body”. In fact, we knew that, at low temperatures, a black body could emit in the infrared. At very high temperatures (T > 10,000 K), its color ranged from red to blue. The problem was that it never emitted in the ultraviolet at room temperature (T ≈ 300 K), as predicted by Maxwell’s theory. Something forced the radiation density to decrease exponentially with temperature. There was nothing in Maxwell’s equations to identify that something. All that was known was that, at low temperatures, experiments showed that radiation density increased with the square of the frequency. This experimental fact was well and truly predicted by Maxwell’s theory.

We were, therefore, faced with a theory that was both true and false. Planck, in a flash of genius, wondered whether it was the calculation procedure, involving the calculation of an integral, that needed to be called into question. Integral calculation presupposes the use of real numbers. What would happen if we used integers instead of real numbers to index light emission frequencies? So, Planck replaced the integration procedure with the calculation of an infinite but convergent series. This time, the solution obtained was perfectly in line with the experimental curves. Furthermore, at low frequencies, we find the radiation density predicted by Maxwell’s theory. At high frequencies, we find an exponential decay that avoids the ultraviolet catastrophe.

In doing so, a new universal constant, Planck’s constant (symbol h ≈ 663 zJ·fs = 6.63 × 10⁻³⁴ J·s), made a sensational appearance in physics. Now, it turns out that this constant has the dimension of an action, M·L²·T⁻¹, a well-known quantity in Lagrangian mechanics. Here, to predict the trajectory of a moving object, we seek to minimize its action integral. From a practical point of view, action is defined as energy E multiplied by time ∆t. But since the inverse of a duration measured in seconds is a frequency f measured in hertz (Hz), it follows that we can write the following: E = h·f. Here, energy is no longer seen as something dependent on mass and velocity, but rather as something associated with vibration. In the case of light, what vibrates are immaterial entities, the electric field E or the magnetic induction B. The conceptual leap, then, is to think that, as an atom is essentially made up of a vacuum, the latter would be more a vibration of the vacuum than a material thing. In short, everything in nature would be vibration rather than matter… Then, the integer n would express the idea that, in nature, any change implies the involvement of, at the very least, a quantum of action h, perhaps more (n × h), but never less (n ≥ 1).

5.4. Complex Numbers

This is where we need to return to the Février-Destouches theorem, since, in order to have the right to manipulate real numbers, there must be a state variable. On the other hand, as soon as there are quantities that are not simultaneously measurable in law, there can be no state variable. Essential indeterminism then arises, as certain pairs of propositions cannot be joined by the conjunction and (∧), according to the rules of classical propositional calculus. In this case, it is necessary to use complementarity logic rather than Boolean logic. The practical consequence is that we must then abandon the use of real numbers and instead use an algebra based on complex numbers.

Now, a complex number is actually a pair of real numbers, the first called the “real part” and the second the “imaginary part”. In other words, while the real number is represented by a straight line, the complex number is represented by a plane. What can you do in a plane that you cannot do on a straight line? The answer is that you can rotate. Basically, real numbers allow you to make translations, while complex numbers allow you to make rotations. Of all the possible rotations, there is one in particular that takes the real number line in a perpendicular direction. This rotation, represented by the symbol “i”, has the following property: i² = i × i = −1. The fact that we obtain the number −1 after squaring is due to the fact that, if we turn twice by an angle of 90° in the same direction, we end up on the starting straight line. But if this straight line is oriented to the right, it ends up oriented to the left after the double 90° rotation. Hence, the −1 sign. To shift the axis back to its original orientation, therefore, we need to perform operation i four times, as follows: i⁴ = i² × i² = (−1) × (−1) = 1. There is nothing mysterious about this once it is understood that a complex number, z = a + i × b, is a two-dimensional number, and not a one-dimensional number like a real number. The operation known as “conjugation”, which consists of changing the sign in front of the symbol “i”, means that the rotation must be in the opposite direction, i.e., from right to left.

But complex numbers z = a + i × b also have another, non-Cartesian representation, known as “polar”. Here, the same number z can also be seen as an arrow with a certain length r and a certain angle φ, with the axis measuring the real part. Furthermore, when the arrow rotates with a constant angular velocity, the movement of its tip projected along two perpendicular directions generates two vibrations 90° out of phase with each other. In other words, the real part x corresponds to a cosine function, while the imaginary part y corresponds to a sine function, i.e., z = a + i × b = r × exp(iφ) = r × cos φ + i × sin φ. Consequently, to assert that “everything is vibration” is to admit that physical reality must be described with complex numbers rather than real numbers. It then follows, according to the Février-Destouches theorem, that there is no such thing as a state variable. In other words, this means that, in law, there are two quantities that cannot be measured simultaneously. This gives rise to an essential indeterminacy, which implies that certain forecasts are subject to error, and must, therefore, be expressed in terms of probabilities rather than certainties.

5.5. Entropy, Position, and Momentum

All that remains is to find this pair of non-simultaneously measurable quantities. To do this, we simply need to forget the notion of energy for a moment and focus on the concept of entropy S, a physical quantity introduced in 1854 by Prussian physicist Rudolf Clausius (1822–1888). For, thanks to Clausius, we have the second principle of thermodynamics, which states that, during any material transformation, the entropy of a system can only increases, as follows: ∆S = ∆Q/T ≥ 0. Here, ∆Q is the amount of heat exchanged during the transformation and T is the absolute temperature measured in Kelvin (K). Behind this inequality lies the fundamental principle that heat always flows from the hot body to the cold body. The opposite process, in which the cold body spontaneously gives up heat to the hot body, can never be observed.

But, thanks to the kinetic theory of gases, we know that all matter is made up of atoms in motion for a certain temperature T ≥ 0. Now, according to the laws of mechanics, every atom is defined by its position q and by its momentum p = m × v, where m is a mass moving at velocity v. This is called a “microstate”. For a macrostate characterized by a given volume V and temperature T, there exists a set of microstates W, all compatible with the macrostate in question. Thus, in 1875, Austrian physicist Ludwig Boltzmann (1844–1906) established a link between the entropy S of a system and its number of accessible microstates, as follows: S = k_B × Ln W, where k_B = 1.380649 × 10⁻²³ J·K⁻¹ is a universal constant which Max Planck called Boltzmann’s constant in 1900.

Now, due to Brownian motion, any atom is equiprobably located at any point of a certain volume V = L³. Hence, a positional indeterminacy ∆q = L along the x, y, or z directions. This corresponds to a number of positional states W_q ∝ V^N = (∆q)^3N. On the other hand, the kinetic theory of gases gives us the probability density of observing a certain velocity v at a temperature T. This, with a width at half-height, which is, therefore, a good measure of the indeterminacy on velocities ∆v. Hence, an indeterminacy on the momentum ∆p = m × ∆v, corresponding to a number of dynamic states W_p ∝ (∆p)^3N. Total indeterminacy in terms of the positions and quantities of motion will, therefore, be given by the product W_q × W_p = (∆q × ∆p)^3N. Note that the product of a position L and a momentum M·L·T⁻¹ is homogeneous with an action M·L²·T⁻¹. We see that there is a minimal action, h, for a change to be observed. So, by dividing the product W_q × W_p by this quantum of action, we obtain the total number of microstates W = (∆q × ∆p/h)^3N compatible with the macrostate under consideration. It follows logically from this that:

S = k_B × Ln(∆q × ∆p/h)^3N ≥ 0 ⇒ 3N × k_B × Ln(∆q × ∆p/h) ≥ 0 ⇒ ∆q × ∆p/h ≥ 1 ⇔ ∆q × ∆p ≥ h

A fundamental “indeterminacy” relationship between position and impulse is, thus, obtained. It is then easy to derive another one, linking time t and energy U (Figure 8, right). We can clearly see how the existence of the action quantum h alone ensures the existence of pairs of non-simultaneously measurable quantities. Although h is very small, its value is not zero. It is, therefore, impossible to simultaneously have the following: ∆q = ∆p = ∆U = ∆t = 0. Since the pairs (p, q) and (U, t) are not simultaneously measurable with infinite precision, there can be no state variable associated with the quantities p, q, U, and t. According to the Février-Destouches theorem, this absence of a state variable means that the Boolean logic associated with real numbers must be abandoned. Instead, we adopt the wave logic associated with complex numbers. Hence, the need for “wave” mechanics based on the algebra of complex numbers rather than the algebra of real numbers.

5.6. Wave/Corpuscle Duality

Figure 8 shows another way of understanding this famous wave–corpuscle duality. Consider a perfectly monochromatic wave with wavelength λ = h/p = h/m × v, i.e., (∆p = 0). The immediate consequence is that it is, then, impossible to locate it precisely, since it repeats identical to itself to infinity. Now, let us consider the addition of a number of vibrations that do not have quite the same wavelengths. We see that, at the origin (x = 0), all waves are in phase. The more waves of different frequencies added together, the greater the amplitude. Elsewhere, due to phase shifts, amplitudes only decrease. In the end, after adding an infinite number of vibrations, all the amplitude is now concentrated at the origin, with no spread to the right or left (∆x = 0). The constituent waves are, thus, transformed into a perfectly localizable corpuscle.

In short, the introduction of the action quantum h solves not only the problem of the ultraviolet catastrophe, but also the problem of the atom’s instability. Indeed, we know that the nucleus has a size of 1 fm. So, let us suppose that an electron with a negative electrical charge happens to wander onto the positively charged nucleus. The indeterminacy about its position then becomes very small ∆q ≈ 10⁻¹⁵ m. But then, the minimum indeterminacy on its momentum is the following: ∆p ≈ h/∆q. Now, we know that the energy of attraction between a proton and electron at a distance d is worth E = e²/4πε₀d ≈ −231(zJ)/d(nm). So, with d = 10⁻⁶ nm, it follows that E = −231 fJ. Now, an electron with a mass m_e ≈ 10⁻³⁰ kg and able to possess a momentum ∆p = h/∆q has the following minimum kinetic energy: K_min = h²/2m_e × ∆q² ≈ 33 × 10⁶ fJ. In other words, the kinetic energy of repulsion here is a hundred thousand times greater than the energy of attraction! Under such conditions, the electron has absolutely no chance of staying on the nucleus. But can it go very far? No, of course not, because, as it moves further away, the indeterminacy of its position increases, which mechanically diminishes the indeterminacy of its momentum. For example, if the electron finds itself at a distance of 1 nm = 10⁻⁹ m, its minimum kinetic energy becomes the following: K_min = h²/2m_e×∆q² ≈ 2.2 zJ compared to an attraction energy of −231 zJ. Here, attraction clearly wins out…

This shows that, for the electron of the hydrogen atom, the equilibrium distance where attraction and repulsion compensate each other must be close to 10 pm = 10⁻¹¹ m. For, at this distance, we find K_min ≈ 22 aJ against E ≈ −23 aJ. In fact, a more rigorous quantum calculation gives a₀ ≈ 53 pm for the size of a hydrogen atom. Thanks to quantum action, furnaces no longer emit gamma rays and atoms regain the right to exist. In short, the world, as we observe it, finds its meaning and familiarity. However, the price of a stable atomic world is high. We have to give up using real numbers, however attractive they may be. Everything has to be thought of in terms of complex numbers with a real part and an imaginary part. But, as the term implies, this means that part of reality becomes unobservable in principle. To recover observable real numbers, we need to eliminate this imaginary part. In concrete terms, this means that, once you have rotated to the left and left observable reality, you need to rotate to the right to return to observable reality. Mathematically speaking, this means evaluating the product z × z*, so that all that remains is the square of the modulus of the number z, which is obviously a real number. As a complex number can also be seen as a probability wave, we find a wave-like unreality (complex number) coexisting with a corpuscular reality (real number).

In other words, when no attempt is made to observe the system, it evolves with a complex probability amplitude generally denoted as ψ(x,y,z,t). However, as soon as a measurement is made on this system (observation), this wave function collapses to give an observable probability density of ψ(x,y,z,t) × ψ*(x,y,z,t). Consequently, although the object is, first and foremost, a wave, we can only observe a world made up of particles whose motion obeys the rules of probability calculus. In mathematical terms, this means that each physical quantity must be associated not with a real number, but with a quantum operator denoted as Ô, for example. This operator can act on any function ψ(x,y,z,t), giving a new function of ψ’(x,y,z,t) = Ôψ(x,y,z,t) = λ × ψ(x,y,z,t), where λ is a real number, called the “eigenvalue” of the Ô operator. It is this real eigenvalue λ that can be measured experimentally, which can be indexed by an integer n. Suppose there exists another operator  such that [Ô,Â] = Ô·Â − Â·Ô = i·Û. Here, Û is the “commutator” operator. Then, the product of the quantum indeterminacy on the quantity Ô (∆O) by that on the quantity  (∆A) will be such that ∆O·∆A ≥ ½|U| (Heisenberg’s uncertainty principle). Applied to the two quantities position and momentum, this gives ∆p·∆x ≥ ℏ/2, with ℏ = h/2π.

5.7. Quantum Phase

There is another, more imaginative way of understanding the appearance of integers in a world of continuity. In fact, we have known since antiquity, and since the work of Pythagoras, that, behind every vibrating string, there are whole numbers. These are called harmonics. They are what make music so original. In music, this integer n indicates the number of times the string’s amplitude of vibration cancels out between its left and right ends. Note that an electron confined in a potential well of width a (Figure 8) behaves, in fact, rather like a vibrating string of fixed length. However, in three dimensions, as in the case of the hydrogen atom, triplets of integers are needed to characterize all the vibrational states allowed (see the interference diagrams in Figure 8, left). So, rather than seeing a corpuscle endowed with a mass m, velocity v, momentum p = m × v, and energy E, we will speak instead of its wavelength λ = h/p, frequency f = v/λ, pulsation ω = 2π × f, or phase φ. Note, moreover, that this phase has no corpuscular equivalence, since it exists only when complex numbers are considered. Physically speaking, it is an angle that lies between zero and 2π and allows us to account for the interference properties that exist only with waves. As the phase is linked to a complex number, it is impossible to measure it, unlike frequency, which is linked to a real number called “energy”, and wavelength, which is linked to a real number called “momentum”.

A first crucial consequence of the finitude of the quantum of action is that an observer never sees the world as it is. They always see a world modified by their presence. An example of this is the image of an artist rhinoceros who wants to paint the landscape they observe (Figure 8, bottom). Of course, they will never be able to paint the landscape as it is. After all, there is always a rhinoceros horn stuck in the background. If the horn is not there, we can legitimately deduce that it was not a rhinoceros that painted the landscape. Whenever we observe, there will always be a clue somewhere in the measurements to show that an observer was, indeed, there, and that their presence modified the landscape.

A second consequence is that, above a certain size scale, there will always be a quantum blur. In other words, if we try to observe too much detail, we will not see anything. This is, of course, linked to the wave–corpuscle duality, but applied to light and not to matter. Indeed, Maxwell’s deterministic equations validate, without any possible discussion, the idea that light is a wave of an electromagnetic nature. But, in fact, light is only a wave when it propagates without interacting with matter. On the other hand, as soon as it interacts, it can only do so as a corpuscule (“photoelectric” effect). Hence, the existence of zero-mass “corpuscles” of light called “photons”, invented by German physicist Albert Einstein (1879–1955).

So, suppose we are looking to see the trajectory of an electron of mass m_e gravitating around a proton, as in the hydrogen atom. In quantum mechanics, the mean electron orbital size depends on the square of an integer n and the Sommerfeld constant α ≈ 1/137, i.e., <r> = ℏ × n²/(α × m_e × c), with ℏ = h/2π. Moreover, the average binding energy <E> at this distance <r>, on the other hand, varies as <E> = ½(α/n)²·m × c². Now, to make the observation, I need a light source, because if I do not illuminate my system, I will not see anything. To “see” the electron, the light must interact with it. Obviously, this presupposes a shock between the photon sent and the electron. So, there is a transfer of some momentum ∆p = h/λ, where λ = c/f is the wavelength associated with the photon of energy E = h × f. This transfer of momentum between photon and electron corresponds to an increase in the electron’s kinetic energy ∆K ≈ (∆p)/2m²_e ≈ h²/(2m_e × λ²). On the other hand, if I do not want my photon to be diffracted, the photon’s wavelength must be much smaller than the mean radius <r> of the electron orbit, a condition for having a sharp image. I can, therefore, hope, at best, that λ ≈ <r>, which will lead to a kinetic energy transfer ∆K ≈ 4π²<E>/n². So, for n = 1, I am, therefore, imparting to the electron a kinetic energy some 36 times greater than its binding energy, removing any hope of observing its supposed trajectory. As a result, the atomic world will remain veiled from us forever.

5.8. Being Empty and Impenetrable

How can something full of “emptiness” be perceived as a hard, impenetrable object? To understand this, we turn to an object called Roue de bicyclette, made in 1913 by French artist Marcel Duchamp (1887–1968). It is a bicycle wheel mounted on a stool. Here, if the wheel is stationary, it is easy to pass your hand through its spokes without injury, and, therefore, apprehend the vacuum that constitutes it. But in quantum physics, the state of rest does not exist, because of the finiteness of the quantum of action. So, the wheel is constantly turning “in a vacuum”. But once the wheel is spinning at a sufficiently high frequency, it is impossible to pass your hand between the spokes without hurting yourself. Thus, an object full of “emptiness” has become, through the magic of movement, a hard, impenetrable thing. This analogy explains how an atom can be “empty” and behave like a hard, impenetrable thing in measurements, if its vibratory frequency is high enough. It is also worth noting that this same emptiness is found in the spectrum of light frequencies emitted by an atom when excited by electromagnetic radiation. Hence, the famous “quantum leaps”, in flagrant opposition to the Aristotelian credo, “Natura non facit saltus”.

It is worth noting that there is nothing in quantum mechanics to specify at what size scale we should switch from quantum probabilism to strict classical determinism. All we know is that even molecules with a molar mass as high as 7000 daltons (Da) still behave like probability waves, and not as objects with deterministic behavior [12]. Consider that the molar mass of a water molecule is barely 18 Da. The average molar mass of an amino acid, the basic building block of every protein, is 110 Da. The average molar mass of a nucleotide, the building block of DNA, is 300 Da. Even the molar mass of a phospholipid, the main constituent of cell membranes, is just 775 Da. In short, every molecule in a living cell must be seen as a probability wave. But, strangely enough, biologists are still not trained in this quantum physics, even though it has been fully formalized since 1926.

The essential reason is that the quantum phase φ cannot be measured. Only a phase difference ∆φ can give rise to observable effects. In fact, this is in no way specific to quantum mechanics. For, when we send out an electromagnetic wave, the latter brings energy via the square of the electric field E or the square of the magnetic flux density B. But the fields E and B are also associated with a scalar potential V and a vector potential A, which are only defined to within one integration constant. Only potential differences can, therefore, be measured, just as only phase differences can be observed, in the form of interference patterns. In the Aharonov–Bohm effect, for example, an interference pattern is obtained when an electron beam split into two secondary beams passes through a region where the magnetic flux density B is zero, but the associated vector potential A is non-zero [13].

In conclusion, there is an important difference between a deterministic point of view using only real numbers and a quantum point of view requiring the use of complex numbers. So, if a deterministic physicist wants to know the position of a particle, he will say, “It is here at position x and time t”. In contrast, a quantum physicist would say, “It is necessarily somewhere, and let x be the result of measuring its most probable position at time t”. The quantum physicist is, therefore, careful to distinguish between the three following concepts: the state, noted |a>, characterized by a label, the operator Â, associated with the measurement process, and the result, a, of the following measurement: Â|a> = a|a>. Note that complex numbers are used here in the definition of the  operator, but that the so-called “eigenvalue”, a, is a real number. On a practical level, the  operator is either a square matrix (Heisenberg representation) or a differential operator (Schrödinger representation). In the Heisenberg representation, the state |a> is identified with a vector evolving in a discrete, infinite-dimensional space. In Schrödinger’s representation, on the other hand, it is a wave function ψ(x, y, z, t). In fact, it does not matter—both representations lead to the same end result.

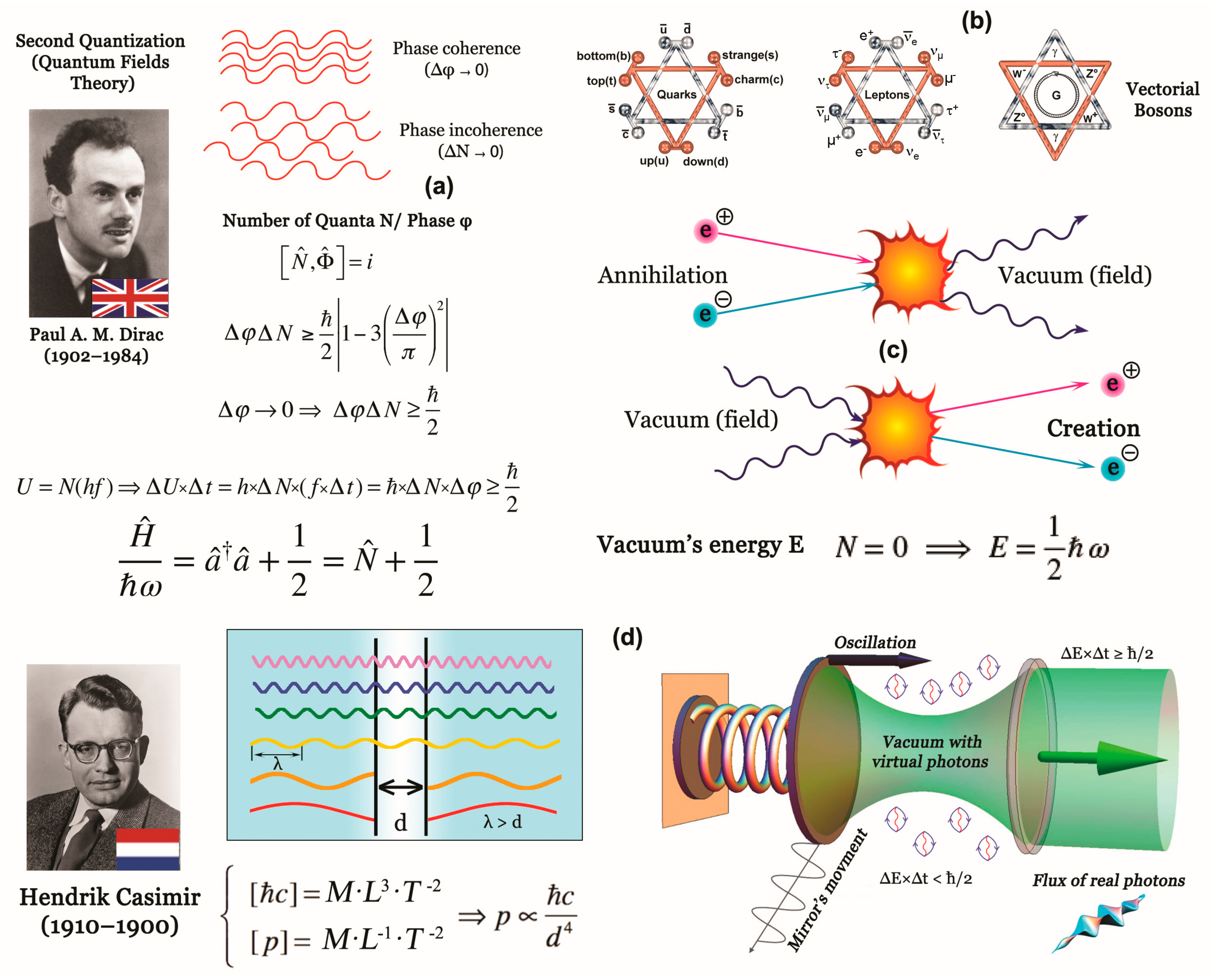
6. Second Quantification

The first quantification explains the stability of the atom, and, therefore, the stability of the observable world. You might think that we have reached the end of the road. In fact, this is not true, because the first quantification does not explain why ice H₂O floats on liquid water, also being H₂O. Without this essential property of water, there could be no life on Earth. So, to justify this crucial property of water, it is imperative to resort to a second quantification. Moreover, there remains the thorny problem of the size scale at which we leave the probabilistic framework of the atomic and molecular world to return to the deterministic framework of macroscopic objects familiar to our five physical senses. As we have already said, there is nothing in the formalism that allows us to set such a limit. Worse still, there are phenomena (superfluidity or superconductivity) where matter behaves quantum-like, even on a macroscopic scale. Here, we usually get away with saying that this only concerns very low temperatures. However, superconductors also seem to exist at high critical temperatures… In short, some physicists would like quantum physics to remain confined to very small scales.

6.1. Ether, the Fifth Greek Element

But, as we shall see, this is impossible. The starting point was mentioned earlier, when we saw that a vacuum vibrating at very high frequencies could be perceived as something hard and impenetrable. In fact, rather than talking about a vacuum, it would be better to talk about “ether”. Greek philosophy already spoke of it. The existence of the ether is, therefore, nothing new in itself. In fact, the notion was taken up by German philosopher Immanuel Kant (1724–1804) in 1755. He assumed the existence of an elementary substance filling space, within which all bodies could be resolved. Following the general development of physics from Descartes to Euler, Kant assumed that this substance is closer to force or energy than to matter. Except that, being more subtle, it is more difficult to detect with instruments. Then, from 1788/9, he had the audacity to dematerialize his ether and make it a fundamental transcendental material. Ether was, therefore, not a body, as it could change neither place nor form.

In the nineteenth century, ether came back into play following the establishment of Maxwell’s equations. For light to be an electromagnetic transverse wave, it had to be able to vibrate a physical ether that was supposed to fill the vacuum, but this ether had to be both extremely tenuous and stiffer than steel to justify light’s extremely high propagation speed (c = 298,792,458 m·s⁻¹). To verify the existence of this ether, American physicists Albert Michelson (1852–1931) and Edward Morley (1838–1923) studied, between 1881 and 1889, if variations in the speed of light could be detected using a device based on light interference. But the final result was that no variations could be observed, i.e., the speed of light always remained constant. Albert Einstein used this crucial result as a basis for deducing, in 1905, that ether did not exist. Only the vacuum existed.

Unfortunately for Einstein, this conclusion was far too hasty, as his analysis had ignored the phenomenon of gravitation. So, ten years later, in 1915, as part of his theory of general relativity, he realized that masses could bend this supposedly empty space–time. The following is what he wrote in a speech delivered on 5 May 1920 at the Reich University in Leiden [14]:

“In summary, we can say: According to the general theory of relativity, space is endowed with physical qualities; so, in this sense an ether exists. According to the general theory of relativity, space without ether is unthinkable; Because in such a system there would not only be no propagation of light, but also no possibility of the existence of scales and clocks, and therefore no spatial-temporal distances in the sense of physics. However, this ether must not be thought of as having the characteristic property of ponderable media of consisting of parts that can be traced through time; the concept of movement may not be applied to him”.

6.2. Uncertainty Relations between Time/Energy and Phase/Number of Quanta

So, after all, Kant was right, and the ether does exist. In this new way of thinking, matter does not exist in its own right. On the other hand, it can always be created or annihilated from this relativistic ether. In quantum physics, any state of energy E can be associated with a frequency f = E/h. Each state also has a quantum phase φ = ω × t = 2πf × t = 2πE × t/h. Consider, then, the total energy E associated with a total number of quanta N, as follows: E = N × h × f. It follows that any fluctuation in energy ∆E lasts for a period of time ∆t = ∆φ/2πf. Therefore, this corresponds to a fluctuation in the number of quanta ∆N = ∆E/h × f. Now, we see (Figure 8) that ∆E × ∆t ≥ ℏ/2. Therefore, it follows that ∆N × hf × ∆φ/2πf ≥ ℏ/2, or after simplification, the following: ∆N × ∆φ ≥ ½. We have, thus, achieved our goal. For, let us remember, the quantum phase is an unobservable entity and, therefore, immaterial in nature. Similarly, the number N can designate both a number of particles, which are, after all, immaterial probability waves when unobserved, and a number of photons, equally immaterial. As for the factor ½, this is a pure number with no physical content that will take the same value in an atom as in a galaxy.

Consequently, we have just found a new pair of variables (N, φ), where precise knowledge of one leads to complete indeterminacy of the other. Once again, according to the Février-Destouches theorem, if there is a pair of non-simultaneously measurable quantities, we must, once again, renounce determinism and adopt the probabilistic point of view. Except, this time, the indeterminacy relation no longer involves a ridiculously small quantum of action. In short, there are no size or temperature limits. In this new way of thinking, quantum physics must be applied to all scales, from the smallest particle to the entire universe.

6.3. Matter Does Not Exist

Let us take a closer look at how this new way of thinking works. As indicated, we have abandoned the principle of conservation of mass so dear to Lavoisier. In fact, this is permissible insofar as we place ourselves in a relativistic framework, for mass m is an independent attribute of energy E only within the framework of the Galilean mechanics group Gal(3,1). As soon as we work with the relativistic Poincaré group ISO(3,1), we are dealing with an overgroup of Gal(3,1). In ISO(3,1), mass and energy are two equivalent ways of describing the same property of inertia with respect to motion, since E = m·c². In practical terms, this means that, on the scale of an elementary particle, it is possible to make it appear from the quantum ether. For, as Figure 9 shows, this ether must be seen, on a scale of 10⁻³⁵ m, as a medium filled with energy fluctuations, of an average amplitude ∆E.

Hence, the possibility of creating any mass ∆m = ∆E/c², as soon as the ether fluctuation is large enough. Such a particle that magically emerges from the ether is called a “virtual” particle. Now, for such a fluctuation to remain unobservable, i.e., virtual, it suffices that ∆N × ∆φ ≤ ½. Either ∆E × ∆t < ℏ/2 or ∆m ≤ ℏ/2c² × ∆t. This shows us that a virtual particle of mass ∆m can be created from the ether, provided that its lifetime is ∆t ≤ ℏ/2∆m × c². Furthermore, since ∆x = c × ∆t, the size scale ∆x at which a virtual particle can be created is such that ∆x ≤ ℏ/2∆m×c. Let us translate this using complex numbers, the only ones allowed in quantum physics. So, let us consider a quantum state, denoted |n>, which contains a number n of quanta. Let â be the so-called “creation” operator, capable of creating a new state of the ether, denoted as |n + 1>, now containing (n + 1) quanta.

6.4. Creation and Annihilation

Now let us take a look at complex numbers rather than real numbers. For, as Figure 8 shows, creating a virtual particle from the ether with a complex probability amplitude z means that there necessarily exists a conjugate amplitude z*, where the rotation is reversed. There is, therefore, a so-called “adjoint” annihilation operator, ↠(read “a-dagger”), which returns to the starting state by annihilating the quanta that was just created. This operator can, thus, bring the ether back to its fundamental state, denoted as |0>. At this point, it is impossible to go any further and destroy the ether, i.e., â†|0> = 0. This means that a vacuum can never be annihilated, since it is impossible to be less than nothing. Consequently, the ether is the only tangible, indestructible reality that fills the entire universe and is the source of everything.

Now, by combining these two creation â and annihilation ↠operators, we can create a third, ↷â that leaves the ether in its |n> state. Very simply, this new operator allows us to count quanta, one by one. As these notions may seem very abstract, let us return to the problem of atomic stability. In the context of the first quantization, matter is indestructible. As we have already seen, the indeterminacy relation ∆p × ∆x ≥ ℏ/2 prevents the electron from merging with the nucleus. To be more precise, it is the same electron that spirals towards the nucleus or flees it as a result of the impossibility of being confined to a very small volume. In the second quantization, things are very different. In this relativistic world, there are two types of particles. The first type is called matter, and the second type is called antimatter. This stems from the fact that, for a particle at rest (p = 0), there are two states, one with positive energy, E = +m₀ × c², and the other with negative energy, E = −m₀ × c². So, if there is an electron with an electric charge −e, there must also exist a positron of the same mass, but with a positive electric charge +e. When an electron meets a positron, they can annihilate each other to give back vacuum and release an energy equal to the sum of the disintegrated masses, i.e., 2m₀.

Let us now investigate at what size scale ∆x it is possible to create such an electron/positron pair via a fluctuation in the ether. Here, we have ∆m = 2m₀ ≈ 2 × 10⁻³⁰ kg, and so it will suffice that ∆x ≤ ℏ/4m₀ × c ≈ 8.33 × 10⁻¹⁴ m. Consequently, an electron spiraling towards a nucleus with a maximum size of 10⁻¹⁴ m will not have time to reach it, because, before it does, there is a good chance that it will encounter an electron/positron pair from the fluctuations of the quantum ether. The falling electron can then be annihilated by the positron emerging from the ether. The electron leaving the ether, which was virtual, now becomes real. It can then use the kinetic energy of confinement to escape the attraction of the nucleus. In short, this creates the illusion that it is the same electron that falls and leaves again.

Indistinguishability is one of the other charms of quantum physics. If you are faced with two electrons that are identical in every way, it is impossible to know which one is on the left and which one is on the right. To find out, you have to observe them. If, by any chance, you do not observe them, they may very well exchange positions! Basically, this means that an atom is a dynamic structure that constantly disintegrates and reintegrates at a very high frequency. The characteristic time of this process is given by ∆t = ∆x/c ≈ 3 × 10⁻²² s. So, Marcel Duchamp’s bicycle wheel spins so fast that, on our scale of seconds, we have the impression of stable, hard, and impenetrable atoms. In fact, this is an illusion, since all we have is ether vibrating at a very high frequency.

6.5. The Atomic Nucleus and the Casimir Effect

In fact, this process of permanent creation/annihilation also applies to the atomic nucleus. To say that it is made up of protons and neutrons is a misnomer. For it, too, is an even higher-frequency vibration of the ether. In fact, there are particles called “pions” that exist in three “flavors”. There is the negative pion, denoted as π-, with a mass of ∆m = 2.51 × 10⁻²⁸ kg, which is capable when it encounters a proton of transforming it into a neutron. Knowing that ℏ/2c ≈ 1.7 × 10⁻⁴³ m·kg⁻¹, this can occur spontaneously via an ether fluctuation as soon as ∆x ≈ 6.8 × 10⁻¹⁵ meters for a duration ∆t = ∆x/c ≈ 2.3 × 10⁻²³ s. Since the positive pion, denoted as π+, is the antiparticle of the negative pion, any neutron can, after encountering a positive pion, become a proton on the same size and time scales. Finally, there is also a neutral pion, denoted as π° with mass ∆m = 2.43 × 10⁻²⁸ kg, which is capable, when it encounters a neutron, of transforming it into another neutron, or transmuting a proton into another proton, again on the same size and time scales.

The atomic nucleus is, therefore, no more material than its direct descendant, the atom. It simply vibrates on a smaller scale and at a higher frequency than the atom. Of course, since every molecule is made up of atoms, it too is a vibratory structure of the ether. We can, thus, move up the scale to arrive at the entire universe, which, observed at a size scale of 10⁻¹⁵ meters and a time scale of 10⁻²³ s, does not stop, at the level of its elementary components, disintegrating and rebuilding itself. What is remarkable is that, in spite of this, we observe large-scale structures that can exist over very long durations. Figure 9 shows that, while these energetic fluctuations in the ether are not directly observable, they do have tangible, observable effects (Lamb effect and static or dynamic Casimir effects).

The static Casimir effect can be understood by looking at two boats placed side by side in a harbor. As the water in the harbor is constantly agitated, long-wave ripples are excluded from the space between two hulls. This is not the case for short-wave ripples. As a result, the two boats move closer together, requiring tires to prevent them from colliding. The same effect occurs in the quantum vacuum, where two mirrors highlight the spontaneous approach. In the dynamic Casimir effect, on the other hand, light can be made to emerge from this vacuum. All it takes is for one of the two mirrors to oscillate at a certain frequency relative to the second, immobile mirror. All this shows that this quantum world, unobservable in principle, is, nonetheless, capable of having very tangible and real effects.

6.6. Quantum Coherence on a Macroscopic Scale

This brings us directly to the notion of coherence, which is the other facet of these relativistic vibrations of an ether, as, so far, we have essentially been talking about the indeterminacy aspect of the number of particles, ∆N, involved in the condition of visibility, ∆N × ∆φ ≥ ½, or invisibility (ether), ∆N × ∆φ < ½. We must, therefore, now turn to the coherence aspect via indeterminacy on the quantum phase, ∆φ. This is, of course, much more difficult, since the quantum phase, φ, is, in itself, fundamentally unobservable. Indeed, only phase differences (interference) can be observed.

This brings us directly to the notion of the quantum field. To help visualize the concept, we can take, as an example, a wheat field made up of a large number N of wheat ears. Each ear has an amplitude (its height) and a phase φ (with its orientation relative to the ground). Energy is also required, in this case, the wind, which can blow over the wheat field with varying degrees of force. This situation already makes it clear that there are two states for the field, a state in which there is no wind, and a state in which the wind blows with a certain force. When the wind is zero, it is easy to count the ears (∆N = 0). The consequence is that the orientation of the ears of corn can be arbitrary (∆φ → ∞). But, if now the wind blows, some ears all take the same direction (∆φ → 0), and it becomes impossible to count them (∆N → ∞). In fact, the field as a whole is traversed by these magnificent coherence waves, which make it undulate in a quite striking way.

This shows us that phase coherence is a phenomenon that can be demonstrated on our macroscopic scale. In any case, there are always two states. The first state is the one in which things can be counted, because there is no coherent collective motion. The second is where coherent collective movements appear, making it very difficult, if not impossible, to count things. In this case, well-defined spatial or temporal structures appear, which merely reflect the underlying phase coherence. This coherence can occur at any size scale. For example, at the scale of the infinitely large, a galaxy is simply a coherent field of stars, while the night sky is an incoherent field of the same stars. Now, on the scale of the infinitely small, the atomic nucleus is a coherent field of protons and neutrons, while the nuclear explosion is an incoherent field of these same nucleons.

Similarly, a molecule can be seen as a coherent field of atoms, whereas a mixture of dioxygen and dihydrogen is an incoherent field of the same atoms. In fact, as soon as the size scale becomes atomic or molecular, we speak of a quantum field. It is, then, imperative to use complex numbers to describe the behavior of atoms or molecules (wave/corpuscle duality). For macroscopic examples, we can use real numbers and simply speak of “fields”, as soon as we consider a large number of objects as a whole.

7. Ether in Greek and Hindu Philosophy

We have just seen that modern Western science validates the idea that the only real component of the universe is the relativistic ether. Furthermore, the physics of second quantification introduces a mathematical formalism based on three operators, capable of creating, conserving, and destroying all matter. This brings us to an ancient civilization which, almost word for word, embodies everything that modern physics has patiently developed since 1927, when physicist Paul Adrien Maurice Dirac perfected the formalism of quantum electrodynamics (see Figure 9).

7.1. Hindu Civilization

Hindu civilization began in the Neolithic period as early as 7000 B.C.E. The archaeological site of Mehrgarh in Pakistani Baluchistan, west of the Indus Valley, already bears witness to agricultural practices. Between 5500 B.C.E. and 4800 B.C.E., pottery appeared, along with a ceramic and metallurgical industry. The site was deserted around 2600 B.C.E.–2000 B.C.E., after the appearance of the Indus Valley civilization. This civilization concentrated around the city of Harappa between 3000 B.C.E. and 1600 B.C.E. (Bronze Age), in what is today the Punjab in Pakistan. Then, during the period from 1500 B.C.E. to 600 B.C.E., Vedism appeared, and the Shruti literature of “revealed knowledge” flourished. This literature was initially oral, and took shape with the writing of the four Vedas. The first was the Rigveda or Veda of stanzas. This was followed by the Yajurveda, or Veda of formulas, and the Samaveda, or Veda of melodies. Finally, came the Atharvaveda, specifically dedicated to the knowledge and use of the mineral, plant, and animal worlds for healing. It was this fourth Veda that gave birth to Ayurveda. Around 500 B.C.E., the Buddhist period gave a strong impetus to the exploration of Ayurveda. Then, between 600 B.C.E. and 500 C.E., the Brahminic religion, also known as ancient Hinduism, developed. During this period, society was divided into the four following castes (varna): priests (Brahmins), priests, teachers, and lawyers. Even later, around 100–300 C.E., the “Sanatana dharma”, meaning “eternal law”, developed, laying the foundations of modern Hinduism. Then, around the year 1000 C.E., the “Yoga” school of Hinduism appeared.

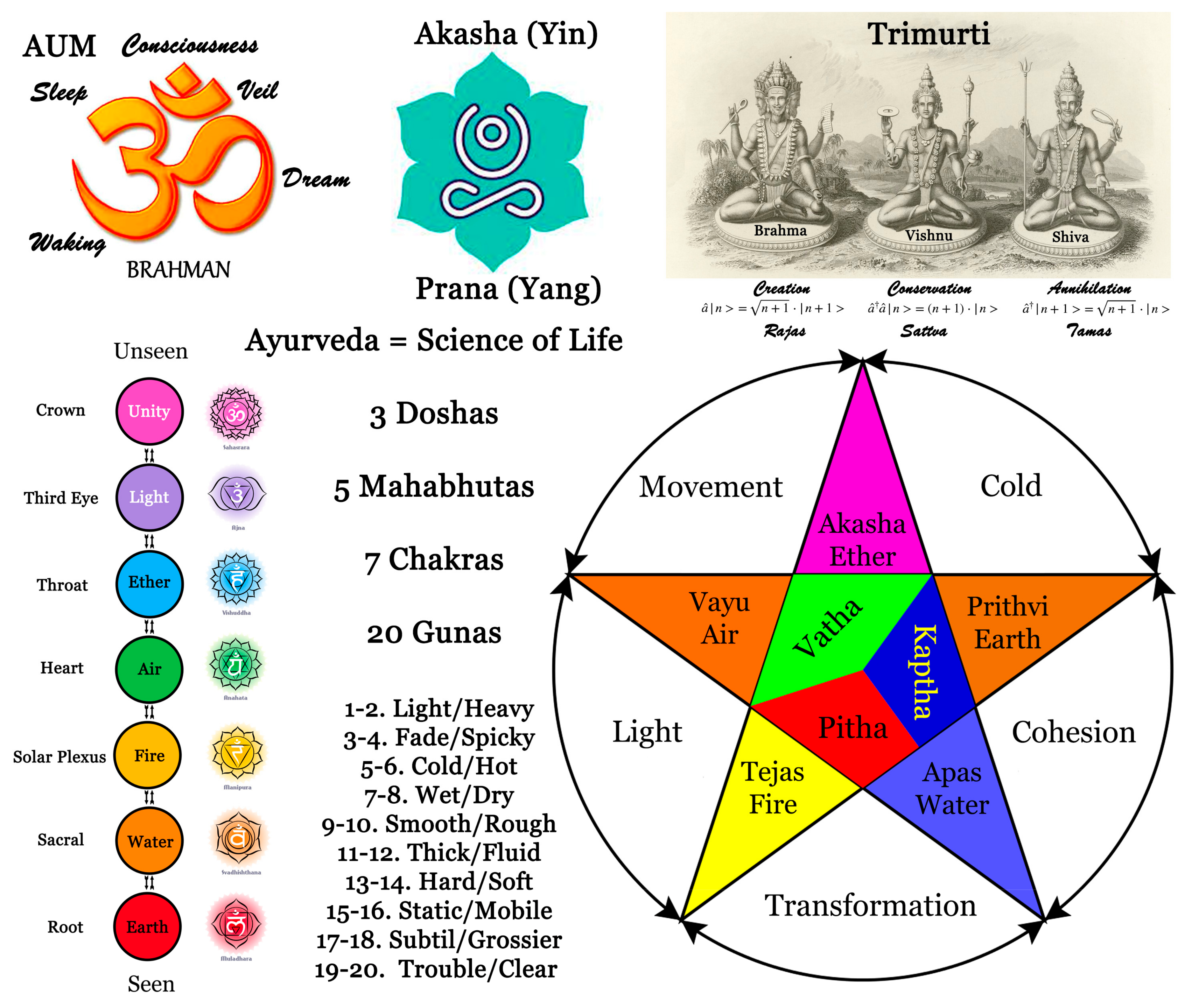
7.2. The Primordial Sound AUM

Early Hindu cosmology bears a strong resemblance to Chinese cosmology. At the very beginning, there is only Brahman or Prajapati, the Absolute, the undifferentiated One, without beginning or end, the Hindu equivalent of the Chinese Tao. It is impossible, then, to represent him, for he is not a divinity. The best way to think of Brahman is as a vibration, a primordial sound, the creator of all things. This sound is pronounced AUM or Ôm (Figure 10). Then, if we take the pronunciation Ôm, Brahman splits in two, giving rise to Prâna on the one hand, the energy equivalent to Chinese “Yang”, and Akasha on the other, the substance equivalent to Chinese “Yin”. Then, comes the Trimurti, which corresponds to the ternary AUM structure of the fundamental vibration. Here, we find the three following deities: Brahma the creator (initial letter ‘A’), Shiva the destroyer (final letter ‘M’), and Vishnu the preserver (middle letter ‘U’). It is at this level that there is a strong resonance with quantum field physics (Figure 10), since quantum field physics has three basic operators. There is the one that creates a new |n + 1> state from the |n> state, the one that annihilates this state to return to the starting state, and finally, the one that maintains the initial state |n>.

Just as in China, where anything can be created from the number three, this divine ternary structure AUM has many variations in India. For example, one of them corresponds to the three “Gunas” of yoga, as follows: Rajas (activity, desire), Sattva (purity, knowledge), and Tamas (darkness, destruction). Here, the sound “AUM” is supposed to maintain the balance between these three Gunas. As in China, odd numbers are associated with stable things. Of these, the following 3, 5 and 7 play a prominent role.

For example, the primordial sound AUM (Figure 10) can be analyzed according to five states. Three earthly states, waking, sleeping, and dreaming, beneath a fourth state (veil symbolizing spirit), and masking a fifth ultimate reality, consciousness. According to Ayurveda, there is a “Pancha Maha Bhutas”, with the word “Pancha” meaning the number “five”, the word Maha meaning “great”, and the word Bhutas meaning “Substances”. This expression can, therefore, be translated as the five fundamental categories of substances or five primordial states of matter. Consequently, the universe, like man, is made up of five fundamental elements, “mahabutas” (Figure 10). The three following of these are shared with the Chinese: fire, water, and earth. But here, air replaces wood and ether replaces metal. It would seem, then, that the Hindus understood that wood was, in fact, nothing more than solidified air (CO₂). Similarly, they would have understood that metal could come from the earth, but also fall from the sky, in the form of meteorites. So, as in China, there are five elements, at the cost of a few changes in order to involve extraterrestrial matter, absent from purely terrestrial Chinese philosophy.

7.3. The Three Doshas of Ayurveda

Ayurveda’s great originality lies in its introduction of a principle of stability via a trinity of three “doshas”. Ether, acting on air, generates the wind “Vâta”, authorizing the movement of matter. Fire, acting in concert with water, generates steam, “Pitta”, capable of digesting or transforming all forms of matter. Finally, earth, acting in concert with water, generates the mud “Kâpha”, which enables things to link together to achieve a state of equilibrium. The result is the number eight (5 + 3 = 8), which is even and, therefore, unstable. Hence, the need for reincarnation (death followed by rebirth), which provides the opportunity to heal the karma accumulated in a previous life.

On the other hand, to divide a pentagon into three pieces, quadrilaterals must be used. So, each dosha is quaternary in nature, meaning that something is in progress via their action on the five elements. This gives rise to the 5 × 4 = 20 “adi gunas”, pairs of opposites attributed to substances or even circumstances. This describes our apprehension of the world and helps us to restore our balance and health when it is disturbed. As in Chinese medicine, natural derivatives of minerals, plants, or animals are used to restore the disturbed balance.

On the other hand, unlike Chinese philosophy, Hindu philosophy is also obsessed with the number seven, associated with the idea of perfection. Thus, the universe is likened to a cosmic egg floating on a primeval ocean, stratified into seven domains. In the upper zone, we find three regions, forming the Bhumi, where matter reigns (Earth, Atmosphere, and Sky). Above this, we find four celestial regions (Svarga) where there is only light. A total of 4 + 3 = 7 domains. In its lower zone (Patala), the egg contains seven regions filled with jewels and lakes, but the last and seventh region is populated by demons and snakes (Nagas). The Earth itself is made up of seven continents surrounded by seven seas.

The number seven is also found in yoga, in the form of the seven chakras. Logically, yoga associates the five Ayurvedic elements with the first five chakras. Just as logically, to achieve a certain kind of beauty, the sixth chakra is associated with light. To achieve perfection, a seventh chakra is evoked. This allows us to see the world as a unity in which the elements and light have no existence of their own. Rather, they exist only because they are in a constant relationship with one another via an underlying unity. For Buddhists, this unity is called “emptiness”, but the basic idea remains the same. Thus, the union of beauty (6) and unity (1) naturally leads to a form of perfection (7 = 6 + 1).

7.4. The Number Zero and Emptiness

Where Hindus differ from the Chinese is in mathematics, for it was they who invented the number zero to represent the absence of quantity, i.e., emptiness (shunya). More precisely, the Chinese, but also the Babylonians, were aware of zero as a position. Around 400 B.C.E., the Babylonians used two small square brackets to indicate that a place in a number was vacant. This made it possible to distinguish the number 27 from the number 207. However, it was impossible to distinguish between 27 and 270, and it is in this ability to distinguish between these two numbers that the Hindu originality lies. In 628 C.E., the mathematician Brahmagupta defined zero (shunya, meaning “void” or “nothingness” in Sanskrit) as the subtraction of a number by itself, i.e., a − a = 0. Hence, a + 0 = a, a − 0 = a, and a × 0 = 0. He even understands that division by zero leads to infinity. Indeed, in Buddhist philosophy, the concept of “shunya” is central to achieving nirvana, hence, the great innovation of seeing zero as a number in its own right and not as an empty position in a non-zero number. Until 2018, the oldest representation of the number zero was an inscription on a temple wall in Gwalior, India. Since then, the carbon-14 dating of an ancient text known as the “Bakhshali manuscript” has pushed back the date of the explicitly symbolized zero by 500 years. In this text, hundreds of zeros are indicated by a dot, a symbol that later evolved into the current representation of a circle with nothing in the middle.

It is amusing to note that zero, as a number, did not exist in Europe until the X^e century C.E. So, when the Gregorian calendar was developed in the VI^e century C.E., we went directly from year −1 to year +1. Hence, the historians’ calendar, in which the year 0 does not exist, which differs from the astronomers’ calendar, which has a year zero. In ephemeris calculations, the year zero is the one immediately preceding the first year of the Christian era, i.e., year −1. The presence of zero means that a period extending from a date in year m to the same date in year n has a duration of n-m years. Thus, the time interval separating 1 March of year −1 from 1 March of year +1 in the astronomical calendar lasts two years. In contrast, the interval between these same dates in a calendar without a zero year (such as the Revolutionary, Gregorian, or Julian calendars) lasts just one year. This is why we entered the third millennium on 1 January 2001, rather than 1 January 2000, when we were still in the second millennium, which ended at midnight on 31 December 2000.

Unlike the Greeks, who hardly ever went beyond 10,000, the Hindus had names for numbers that could be gigantic, such as 10¹⁷ or 10⁵³. This was because, mathematically speaking, the inverse of the number zero corresponds to infinity, as follows: 1/0 = ∞. As a result, irrational numbers like √2 did not scare them in the least. Thus, in 800 B.C.E., the Indian mathematician Baudhayana enumerated the theorem unjustly attributed to Pythagoras as follows: “The area produced by the diagonal of a rectangle is equal to the sum of the area produced by it on two sides”. He even gave an approximate value for the length of this diagonal, “The measure must be increased by a third and decreased by a quarter. This is its diagonal approximately”. Or, in modern notation, √2 ≈ 1 + 1/3 + 1/3 × 4 − 1/3 × 4 × 34 = 577/408 ≈ 1.414216, to be compared with the exact value rounded to six decimal places, 1.414214. Finally, he also gave a way for finding a circle whose area is the same as that of a square, “Draw half its diagonal about the center towards the East–West line; then describe a circle together with a third part of that which lies outside the square”.

7.5. The Five Platonic Solids

Today, we know that the peoples of western India are all descended from “Indo-European” ancestors. So, it is perfectly logical that the five following elements of Greek philosophy are absolutely identical to those of Ayurveda: ether, fire, air, water, and earth. However, with the Greeks, one of these five elements, ether, was given a special status. At this point, it is worth returning to Plato’s philosophy (Figure 11). For this philosopher, each element could be associated with a regular polyhedron, and everything had to be made up of triangles to ensure stability. The simplest solid was the four-vertex tetrahedron, formed by assembling four equilateral triangles. Now, four is the number of action, of unstoppable progress. Plato, therefore, logically associated this solid with the element of fire, which always tends to spread. The second solid with the fewest triangles was the octahedron, with eight equilateral triangular faces. Here, we find the number four of action in the fact that 8 = 4 × 2, and that each vertex is formed by the meeting of four triangles. The notion of beauty was also present in the fact that an octahedron has six vertices. What element could be more stable than fire, yet always in motion—air, of course.

Still in terms of triangles, the next solid was the cube, with six square faces and eight vertices, with each vertex being common to three faces. To form the square, two isosceles triangles had to be associated by their hypotenuse. A cube is, therefore, made up of 6 × 2 = 12 isosceles triangles. As 1 + 2 = 3, the cube was clearly associated with something very stable and a source of beauty, the element earth (crystals). The fourth solid was the icosahedron, formed of 20 equilateral triangles, with 5 triangles at each of the 12 vertices. Here, we find the numbers two (2 + 0 = 2), five, and three (1 + 2 = 3), i.e., something both stable (3) and unstable (2), a source of permanent crisis (5). Water, with its irresistible tendency to flow while remaining at rest in a watertight container, fits the bill perfectly.

Plato could, therefore, be very pleased with such a correspondence. But his mathematical science told him that there was a fifth solid made up of 12 regular pentagons with three faces meeting at each of the 20 vertices. As with the squares of the cube, he had to cut a pentagon into triangles. This was made possible by two identical isosceles triangles and a third one different from the first two (see Figure 11). Thus, a pentagonal dodecahedron had 12 × 3 = 36 triangles, a number reducible to the number 9 (3 + 6 = 9). This last solid had to evoke something new, something different from the other four. The decision was, therefore, taken to conceal the existence of this fifth element, which corresponded to what Plato called “quintessence” and what Aristotle called “ether”. Only the initiated knew about this fifth element, while the uninitiated were content with the other four material elements.

Indeed, for Plato, the number of action is four, while five is the number of crisis. So, as we have seen, the Chinese identify four elements (wood, fire, metal, and water) with four seasons (spring, summer, autumn, and winter) and four cardinal points (east, south, west, and north). But they do not stop there, invoking the center of the cardinal cross for their fifth element, earth. This, of course, obliges them to introduce the following fifth season: the end of summer, known in the West as “Indian summer”. For his part, Plato found it more logical to reject the center outside the Earth, thus retaining only four cardinal points for orientation on the Earth’s surface and four seasons. From then on, the crisis linked to the number five becomes external and spiritual for Plato and the Hindus, with a race to the spiritual directed towards a quintessence outside ourselves. For the Chinese, on the other hand, this crisis is more earthly, and is oriented towards the material.

The problem with this view is that, apparently, there is nothing beyond quintessence. For Pythagoras, it was quite clear that the crisis of five meant moving towards beauty (6) and perfection (7). This philosophy of quintessence (5 = 4 + 1) lacked a principle for achieving perfect earthly stability (3) (7 = 4 + 3). This is obviously in stark contrast to the Eastern solution (7 = 5 + 2), where perfection is sought within us (via the notion of center), and not outside us in an inaccessible quintessence. This was also different from the Hindu solution, which united beauty and unity (7 = 6 + 1). In fact, on a purely religious level, the solution (5 = 4 + 1) went very well with the existence of an inaccessible “God” (1) sending his “Son” to earth to be crucified (4). Then, there was a whole concept of medicine, humourism, also based on the number four (Figure 11).

7.6. The “Tria Prima”

How do you introduce the number three under these conditions? Paracelsus provided the solution, introducing a “tria prima” (sulfur, mercury, and salt). These three principles are obviously reminiscent of the three Ayurvedic doshas, reintroduced here in a Westernized version. Within this ternary, the mercurial principle acts as a compressive force from the outside (soul). To balance this external pressure, the sulfuric principle acts, in contrast, as an expanding force from within (spirit). The result is a state of equilibrium in the personality that can be modulated by salt (body). This union of the material (four elements) and the spiritual (three principles) enables a certain form of perfection to be achieved once again (7 = 4 + 3).

But this totally idealistic vision of nature was opposed by the materialistic vision of Democritus. Plato hated Democritus so much that, after his death, he planned to burn all his books. For Democritus, there are only the two following primary elements: atoms and the void. Atoms, which form matter, are indivisible and invariable, eternal, and perpetually in motion. They differ only in shape, size, position, and order. All bodies are combinations of atoms, and their separation leads to their destruction. It could be said that atoms are avatars of the Chinese Yang, with the void playing the role of Yin, and bodies formed of atoms demonstrating the existence of a He, a harmony, via the bond that unites two atoms with each other (chemical bond). For Democritus, the soul is made up of fiery, light, spherical atoms and disappears after death. There is, therefore, no life in the afterlife, and no organizing God. There are only countless atoms eternally moving in the infinite void. Without too much exaggeration, Plato can be said to have been the precursor of fascism, which requires the presence of leaders with all the power to direct a people of slaves. Democritus, on the other hand, was a representative of ancient democracy and a fierce opponent of slave aristocracy. Hence, Plato’s hatred of Democritus. Epicurus and later Lucretius tried to propagate Democritus’ materialism. But it was Plato’s idealism, taken up by Aristotle, that triumphed until the advent of quantum physics, which rehabilitated atoms and their intrinsic emptiness.

8. Ether and Consciousness

To talk about the origin of life, it is imperative to understand that, just like our universe, life has non-material, even spiritual aspects, as well as purely material ones. While this is particularly obvious in humans, it is much less so in bacteria. For simplicity’s sake, these two inseparable aspects of the vital phenomenon will be labelled as follows: “matter” for everything visible and tangible, and “consciousness” for everything invisible and immaterial.

It would be a serious methodological error not to take into account this fundamental duality between matter and consciousness. In fact, we are naive enough to believe that the difficulties we encounter when we try to talk about the origin of life are intimately linked to our failure to take this fundamental duality into account. But that is far from enough, for it is also imperative to understand that consciousness is not an emergent property of matter. This follows from the observation of the logical postulate that any phenomenon pre-existing another can participate in the creation of the latter, whereas the opposite is impossible. Indeed, if we accept this basic postulation, then we can only arrive at the logical conclusion that the space–time–matter framework used by conventional science is capable of emerging from a non-local consciousness according to a precise hierarchical cascade [15]. If we wish to transcend this fundamental duality, there is only one concept that can do so without any contradictions—the concept of the void, or rather the ether. Hence, the need, before speaking of consciousness or matter, to have a precise idea of the nature of this ether at the origin of all things and all thought, and to make a clear distinction between the three concepts of nothingness, emptiness/ether, and vacuity.

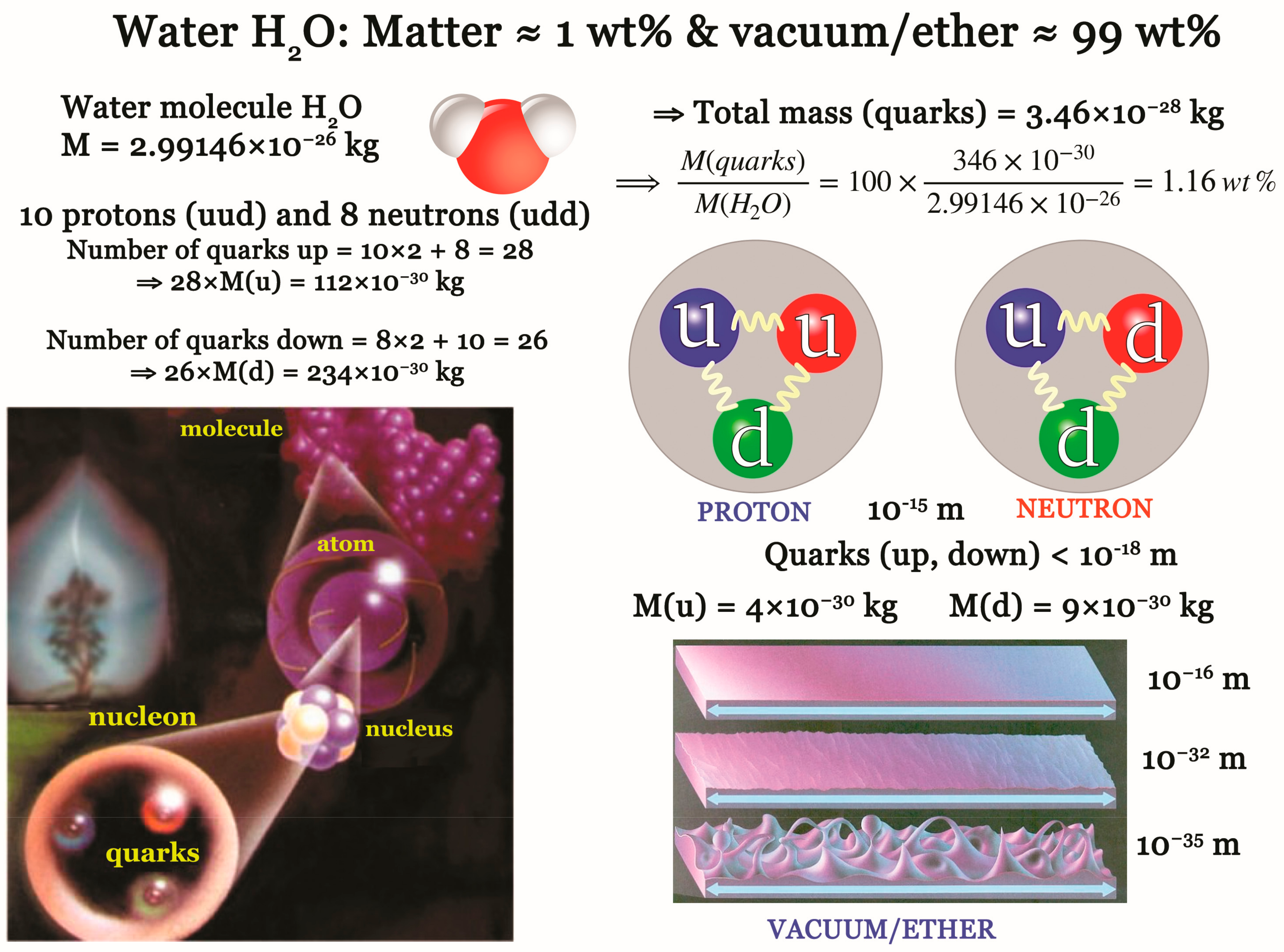
8.1. Nothingness, Emptiness/Ether, and Vacuity

In fact, nothingness is easily identified with “nothing”, i.e., with the set of things that are impossible. An example of nothingness is the statement that 1 + 1 = 3. If such a thing were true, then the world as we know it simply could not exist. For our living world to exist, it is imperative that 1 + 1 = 2, and nothing else. This may seem obvious, but it is precisely because it is obvious that this basic fact is so often overlooked. As soon as something is concealed, there is the danger of “talking about nothing”. In fact, we can recognize in the identity 1 + 1 = 2 the notion of identical reproduction leading to growth, a notion that applies just as much to an idea as to a living cell.

Let us move on to the notion of emptiness/ether, which is very clearly distinguished from the notion of nothingness. To be empty is not to be “nothing”, but rather to be “primitive”, i.e., to be “at the origin” of something quite concrete. To take the previous example, I can easily create emptiness by assuming that 1 − 1 = 0. Here we find the notion of sexual reproduction by birth. Two very concrete and differentiated things (1 and −1) decide to unite intimately to create an entirely new thing (0) that cannot be identified with the two “parents”.

Finally, there is the notion of vacuity. To grasp this new notion, which is neither “nothing” nor “emptiness”, I will refer to set theory and the so-called “Peano–Cantor” construction (Figure 12). This construction assumes that the empty set, denoted as Ø, exists, and, as it contains no elements, its number of elements, or cardinal, is zero. If you prefer, I am dealing with the previous “new” thing, but one that has not yet materialized. Aristotle would say that it exists “in potential”. Nowadays, we would say that it exists “in consciousness”. Let us now consider the set A, which contains the empty set as its only element, and is, therefore, of cardinal 1. The two sets Ø and A are clearly different in nature, since A contains one element Ø, while Ø contains nothing at all. Aristotle would say that the “new” thing now exists “in act”, whereas a contemporary scientist would speak of existence in the form of a cell. In concrete terms, set A can be seen as a drawer containing an empty bag, and so cannot itself be empty, since it contains a bag… So, we do indeed have two things, an empty bag and a drawer containing this empty bag, which makes it possible to define a new set B of cardinal 2 formed by the union of these two different elements. True, but this new set B, added to the first two, Ø and A, in turn, defines a new set of cardinal 3 and so on, ad nauseam (see Figure 12).

This ingenious construction shows that emptiness, by virtue of its very existence, is capable of generating an infinite number of things, all of which are hollow shells fitted together like a set of Russian dolls. It is this interlocking of empty things that we refer to as “vacuity”. It does not matter whether you use the column on the left, which, with its succession of different letters, masks the nesting and emptiness of things, or the column on the right, which shows that all you need is one powerfully creative thing, the empty whole Ø. In fact, it does not really matter which labels we choose to place at each stage of the interlocking process, because all this applies to everything, material or spiritual. The construction of Peano–Cantor is, in fact, summed up very well by the Zen koan, “Mu Soku Wu, Wu Soku Mu”, which could be translated as “From the void everything can spring, and this everything can always return to the creative void”.

The Peano–Cantor construction teaches us that we can very well be both empty (Ø) and non-empty, i.e., an arbitrary nesting of equally empty things. In this way, we experience the non-duality that is the very essence of vacuity, which corresponds to the Western ouroboros, the ensô of Zen Buddhism, or the ying/yang symbol of Taoist philosophy (see Figure 12). There are also ribbons that have only one side, such as the Moebius ribbon, or the Klein bottle, which has neither an inside nor an outside. Vacuity can be reduced neither to a self nor to a lack of self. As a middle way, vacuity is a way of not being trapped either in the idea that things exist or in the idea that things do not exist. Existence and non-existence are a dualism that is imbued in our concepts and our ways of thinking and speaking. To be empty, then, is not to be non-existent. It is to be devoid of permanent identity.

So, to speak of a thing, you need at least three words, two words to describe the thing and the non-thing, and a third word to unite the thing and the non-thing into a meta-thing, a substance that lies behind the thing, but is neither the thing nor the non-thing. Chinese philosopher Lao Tzu’s Tao-te-king XLII-1 is very clear on this point, as follows:

“The Tao produced One, One produced Two, Two produced Three, Three produced ten thousand beings…”. If you are unfamiliar with Eastern philosophies, you may also refer Plato’s Timaeus. In this work, Plato speaks of expanse (la chôra, χώρα), the permanent matter of the universe, which participates simultaneously in the sensible and the intelligible. Thus, we find the principle of identity (A: the Model, which is always identical to itself), the principle of contradiction (non-A: the copy, different from the Model), and the chôra, which is neither the Model nor its copy, but is of a “third kind”, neither A nor non-A, which ultimately remains unintelligible, by reason of the excluded third. It is for this reason that the notion of the included third symbolized by the chôra is rejected, forcing us to make do with the Aristotelian place (τόπος, topos) that suits the disjunctive logic of the excluded third perfectly. The chôra can, thus, be seen as the milieu in which the becoming occurs [16]. It should also be remembered that, as early as the III^e century C.E., Indian logicians developed tetralemmes, which, on the contrary, allow for the inclusion of the third party according to the four following lemmas: 1. A (affirmation); 2. non-A (negation); 3. neither A nor non-A (neither affirmation nor negation); and 4. both A and non-A (both affirmation and negation). In a more scientific sense, the problem of vacuity or chôra reappears fully in quantum physics in the form of the wave–corpuscle duality, which must be understood as non-duality, in the sense discussed above.

8.2. The Water Molecule and the Void

In fact, it took a long time to accept the existence of the vacuum and, above all, the fact that the vacuum and matter are two facets of the same reality. Indeed, it is matter which, by its presence, defines where there is a void and where there is not. It is the void which, in turn, by its presence or absence, gives meaning and form to matter. Remove the void, and all becomes shapeless chaos, for behind the existence of the void lies the notion of movement. How do we recognize that something is alive? By the fact that it has an autonomous movement with no apparent motor. Another crucial point is that all living matter is essentially made up of a single substance, water. Behind this substance lies the vacuum. Indeed, according to the Standard Model, which counts the material and non-material particles that populate the universe, there are, on the one hand, quarks, the constituents of atomic nuclei. On the other hand, electrons neutralize the positive electric charge brought by the protons formed by the “uud” combination (Figure 13). There is another “udd” combination, with zero electric charge, which defines the neutron. However, when we calculate the mass balance between the quarks and electrons making up the water molecule and the molecule itself, it is clear that these “observable” particles make up only 1.2% of the total mass. In other words, 98.8% of the mass of a water molecule comes from the vacuum or ether that constitutes it.

Such a fact is obviously shocking to a mind firmly anchored in matter. For an Indian mind, however, it is a no-brainer. In fact, it is self-evident. As soon as one wishes to associate the ether with a tangible reality, it becomes impossible to evacuate consciousness from the problem of the origin of life. Since the ether is empty of matter, while being something in itself, capable of creating all matter, the only thing it is capable of containing is information. What does consciousness do? It manipulates information. Let us take a closer look.

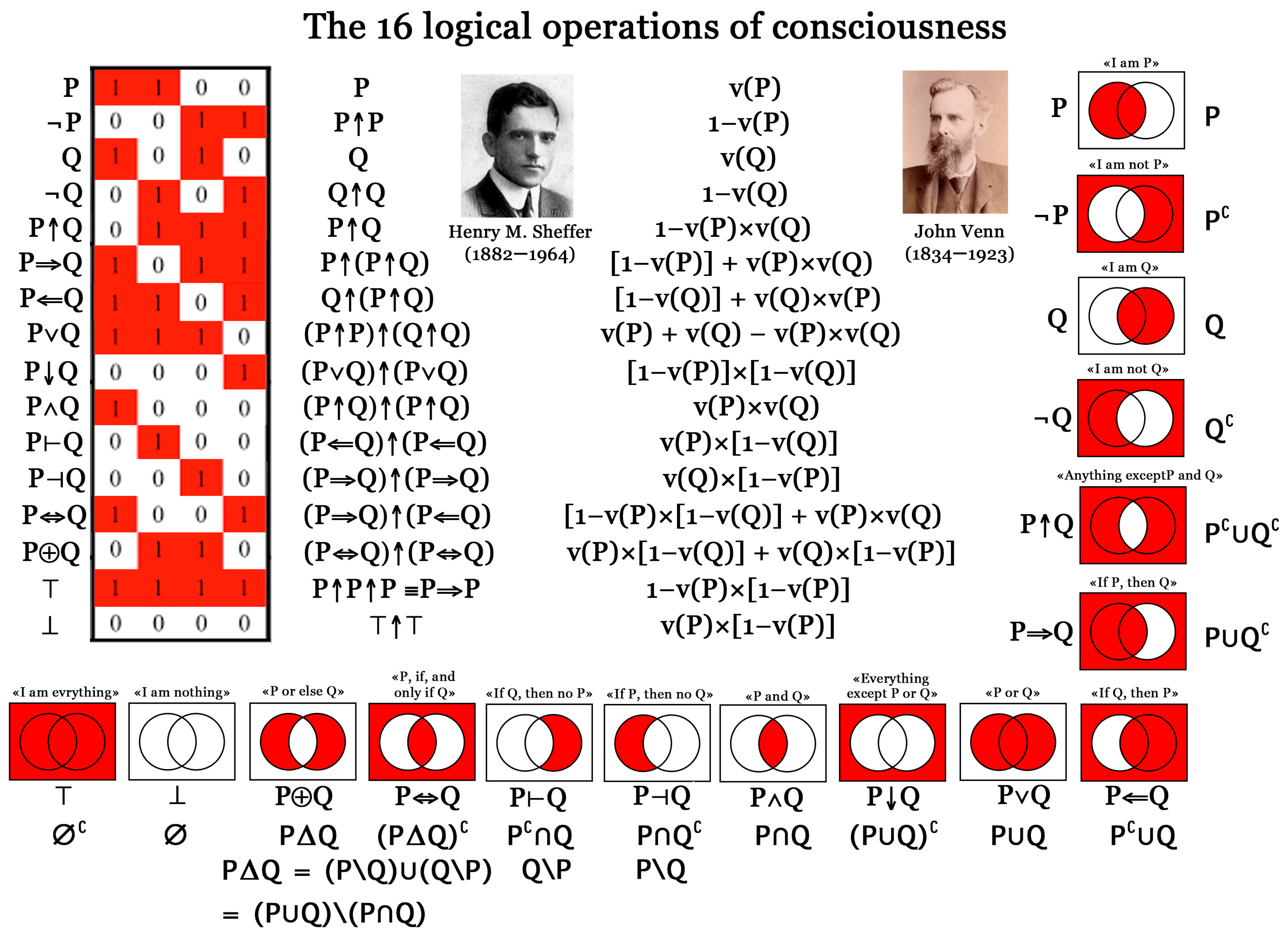
8.3. The Sheffer Bar

It was proven in 1913 by the American mathematician Henry Maurice Sheffer (1882–1964) that Boolean algebra could be defined using a single binary operator called NAND (non-conjunction). Such an operator can be represented by an ascending bar (↑) or “Sheffer bar”. Figure 14 summarizes what is said here. This rather remarkable property has made NAND gates crucial to modern digital electronics, enabling the manufacturing of flash memory and the design of high-performance computing processors, since all binary logic operations can be encoded with this single logic connector. Recall that, if P and Q are two true or false propositions (binary logic), then v(P↑Q) = 1 in all cases unless v(P) = v(Q) = 1, in which, case v(P↑Q) = 0. In this framework, if P represents any statement such as “I am”, the three following primitive concepts immediately emerge:

• Negation: ¬P = P↑P or “I am not”.
• The tautology: ⊤ = (¬P↑P) = P↑P↑P or “I am what I am”.
• The contradiction: ⊥ = ¬⊤ = (⊤↑⊤) = P↑P↑P↑P↑P or “I am what I am not”.

Our starting point, then, is that these three concepts form the basis of all identification principles, i.e., of all consciousness. Negation allows us to define our exterior, and tautology our interior. Contradiction, on the other hand, posits the existence of incompleteness. In other words, there are, as a matter of principle, propositions that are undecidable on the sole level of logic, in accordance with Gödel’s theorem of 1931. The other attributes of consciousness then follow logically as soon as we apply the operation of non-conjunction to two different statements, P and Q. First and foremost, we can, for example, give a precise meaning to the notion of causality in the form of a principle of implication, as follows:

• Implication: (P ⇒ Q) = P↑(P↑Q)

If we pose Q = P, we find the tautology in a new form (P ⇒ P), which can be translated as “If I, then I”. Above all, causality allows us to posit the existence of time as an endless chain of causes (P) and effects (Q). Irreversibility is naturally introduced here by the fact that the truth table of (P ⇒ Q) is different from that of (Q ⇒ P). Implication also uncovers another crucial attribute of consciousness, inhibition, in the following form:

• Inhibition: (P⊣Q) = (P ⇒ Q) ↑ (P ⇒ Q) = [P↑(P↑Q)]↑[P↑(P↑Q)]

Note that Implication and Inhibition are dual notions, since we can write the following: (P⇒Q) = (P⊣Q) ↑ (P⊣Q)

Thus, causality posits the existence, in principle, of an active, expansive “Yang” mode operating by implication. This mode complements a passive, contractive “Yin” mode operating by inhibition. From a neuronal point of view, this means the existence of the two following modes of autonomy: sympathetic or active, and parasympathetic or inhibitory, as well as alternation between a waking state (active consciousness) and a sleeping state (passive consciousness).

Another attribute of consciousness is its ability to distinguish between what is similar (equivalence) and what is different (incompatibility), as follows:

• Equivalence: (P ⇔ Q) = [(P↑P)↑(Q↑Q)↑(P↑Q)]
• Incompatibility: (P ⊕ Q) = (P↑P)↑(Q↑Q)↑(P↑Q)↑(P↑P)↑(Q↑Q)↑(P↑Q)

For completeness, consciousness also possesses the ability to bring things together (synthesis) according to an operation of conjunction (P∧Q) = (P↑Q)↑(P↑Q). Or, on the contrary, to separate them (analysis) according to a disjunction operation (Q∨P) = (P↑P)↑(Q↑Q). It is obviously quite remarkable that all these attributes of consciousness derive from the givenness of a single logical operation, non-conjunction. From a symbolic point of view, this non-conjunction, a fundamental attribute of consciousness, has been repeatedly represented in the form of the Ouroboros, the snake that bites its own tail. Its circular shape clearly defines an exterior (negation), an interior (tautology), and a fundamental incompleteness. The beginning coincides with the end (contradiction). The tautological aspect of consciousness can be summed up by the following statement: “Only consciousness can be conscious”.

8.4. Three Logics of Consciousness

In this respect, it should be noted that consciousness is capable of proceeding according to three different types of logic, depending on the meaning given to contradiction. There is the classical mode of thought, which allows for reasoning by the absurd and deduces from a contraction (¬P⇒⊥) that P or ¬¬P are valid (elimination of double negation) [17]. This is the rational and coherent way of thinking of active consciousness, based on Boolean algebra.

The second way of thinking is intuitionistic logic [18]. This conforms to a quantum way of thinking that posits that contradictions exist (such as wave–corpuscle duality, for example), but that from a contradiction that is false by nature, we can deduce any proposition (⊥⇒P). This principle of explosion, characteristic of Heyting algebras, is at the root of notions such as the Big Bang for inert matter or biodiversity for living matter. In the intuitionist mode, double negation has an autonomous status different from that of the assertion (on the other hand, it is always true that ¬¬¬P = ¬P). This is the unconscious way of thinking that makes the decoding of dreams so difficult for active consciousness.

The third way of thinking is that of minimal logic, which provides no special treatment for contradiction [19]. As a result, minimal logic makes no distinction between the formula ⊥ and any other formula F. In fact, if we assign no special role to contradiction, we can make any formula F play the role of this contradiction, by defining negation as P ⇒ F. Here, we recognize a highly original mode of thinking for consciousness, where everything is affirmed and nothing is denied, which we could, therefore, call “full consciousness”.

8.5. Information and Meaning

As the Palo Alto school of psychology, funded by Gregory Bateson, has shown, it is absolutely impossible not to communicate [20]. In fact, any silence or omission can have far-reaching consequences. To raise our level of consciousness, we need to be able to communicate, i.e., exchange information, using a language that can be either digital or analog. Information is, therefore, not a primary trait of consciousness, but always a secondary effect of conscious (digital) and reflective (analog) sensitivity. Hence, the conclusion that consciousness precedes the notion of information, and is, therefore, hierarchically superior to it.

This leads us to consider the two following levels of language: “object language”, which speaks of concrete objects, and “metalanguage”, which takes language itself as its object. While object language is particularly well-suited to digital communication in terms of content, it is, in fact, totally devoid of meaning. Hence, the role of metalanguage, which is a language designed to give meaning to object language. This is in the context of analog, not just digital, communication. This is also in line with Gödel’s incompleteness theorem, which states that there is no such thing as a self-contained language. So, to define the truth of an object language L, we need to go up to the ML level (metalanguage), which alone has the resources to refer to all the expressions of L. The truth for L is, therefore, to be found in ML, and not in L. Similarly, the truth for ML will be found in MML up to a regression to infinity.

In other words, a language cannot contain an adequate predicate of truth for itself, and the definition of truth cannot be defined within it. Truth must be defined in a higher language. All communication has two aspects, content (or passive information) and relation (or active information). As the relation orders the content, the relation can only be a meta-communication. It is also important to understand that, in any communication, one of the subjects may have more information at his disposal than the other, even if the latter thinks it has just as much. So, it is dangerous to believe that the other has the same amount of information as yourself. However, they will also draw the same conclusions. The problem with analog messages is that they lack many of the elements that make up the morphology and syntax of digital language. It is up to the translator to insert the missing elements. When translating analog material into digital, we need to introduce the logical truth functions that are absent from communication in the analog mode. This is particularly true of negation, which, as we have seen, does not exist in minimal logic and underpins communication in the active analog mode. All communication exchanges are, therefore, symmetrical or complementary, depending on whether they are based on equality or difference.

Moreover, in any cognitive act, we need to distinguish between the fact of perceiving (passive information or digital object language) and the fact of understanding what we have perceived (active information or analogical metalanguage). Active information brings us back to the notion of meaning, which can be defined as information in a context. It is also possible to assert that “A bit of information is definable as a difference which makes a difference” [21]. Although so similar in nature that they are often confused in common parlance, passive and active information do not act at the same level. From a thermodynamic point of view, we find this duality of information in entropy, which measures the quantity of information available at a digital level [22]. The other partner is complexity or thermodynamic depth, which corresponds to the quantity of information rejected at an analog level during the process leading to the physical materialization of an object [23].

Here, we find the notion of exformation processed by consciousness but not transmitted, which defines context [24]. Since it is meaning that gives information its value, active information (meaning, exformation) is chronologically prior to passive information (content) and, therefore, hierarchically superior to it. By recognizing this fundamental duality in the notion of information, we reconcile the two following interpretations of entropy: thermodynamic according to Shannon–Von Neumann, defined at the digital level of object language, and cybernetic according to Wiener–Schrödinger, defined at the analog level of metalanguage [25]. The mistake not to be made here is to believe that we can obtain meaning (cybernetic entropy) simply by changing the sign of nonsense (thermodynamic entropy). We must also reject the equation of entropy with disorder and negentropy with order, because disorder is not in matter, but in the consciousness of the observer of matter. Entropy and information cannot be defined without context. Information measures our degree of surprise, and there are more surprises in disorder than in order. Something that does not surprise us is necessarily orderly. So, information is only clearly defined when we explain what we mean by order. One of the consequences of Gödel’s incompleteness theorem is that it is impossible to know whether there is order in disorder. The notions of order and disorder are, therefore, subjective, since they are situated at the level of metalanguage and not object language.

8.6. Energy or Entropy?

In thermodynamics, entropy is identified with the energy available per degree of freedom (position or motion) via Boltzmann’s constant, while, according to the first principle, the energy of the universe is constant, and its entropy can only increase during the spontaneous transformations of closed physical systems. This is achieved through the production of heat, so that energy can be distributed over the greatest possible number of degrees of freedom available in the system under consideration. However, it is information that is responsible for this process [26]. Any flow of entropy (or information) allows structures to emerge through self-organization [27]. It follows logically, then, that it is information/entropy that channels energy towards ever more harmonious complexity (meaning) and, ultimately, towards life. We can, thus, affirm that the role of information is chronologically prior and, therefore, hierarchically superior to that of energy.

Physicist John Archibald Wheeler’s position that everything in the universe is made of information, “It from bit”, therefore, seems perfectly legitimate [28]. It should also be noted that the duality observed at the level of language and information is also found at the level of energy. In relativistic theory, mass m and energy E are equivalent according to the famous Poincaré–Einstein equation, E = m·c², where c is the speed of light in a vacuum. On the other hand, quantum theory teaches us that this same energy can also be seen as a frequency according to the Planck–Einstein relation, E = h·f, where h is the quantum of action. It follows that any mass can be interpreted as a vibration, and vice versa. Since time, seen as a succession of causes and effects, is prior to information, itself prior to energy, we can deduce the following: matter, which is characterized by a non-zero mass at rest seen as energy, has a hierarchical status inferior to energy seen as the inverse of time (frequency).

Material bodies are, therefore, logically at the bottom of our hierarchy. This means that the neuron, which is the material structure processing information by the means of energy in every living being, is also at the bottom of the hierarchy. It cannot, therefore, generate the consciousness that lies at the top of the hierarchy. We have, thus, demonstrated that consciousness predates meaning, which predates information, which predates energy, which predates the material neuron. Moreover, consciousness operates according to three logics (classical, intuitionistic, and minimal). The neuron, on the other hand, is found in the brain, intestines, and heart, and operates at the level of digital object language, obeying classical logic. It follows, therefore, that the neuron is not the only channel for the expression of consciousness. Intuitionist logic, which posits that any proposition can be deduced from a contradiction, accounts for the creativity of consciousness when it expresses itself through the energy/matter channel. Similarly, the body, which is incapable of lying, necessarily uses the third analogical channel of expression, which operates according to a minimal logic, since, here, the concept of negation simply does not exist. To localize consciousness at the level of a single organ, the brain, is, therefore, a perfectly illogical attitude, given the proposed hierarchy based on the existence of a single logical connector, the non-conjunction, authorizing three modes of handling contradiction.

9. Water and Information

Upstream, we have the consciousness capable of processing information, and downstream, we have the living cell, made up essentially of water at over 99 mol%. This naturally raises the question of whether water might act as an interface between vacuum/ether information and biological information. As this point has already been dealt with in another paper [29], we will restate only the essentials here. Establishing conceptual and logical links between consciousness and information also has the advantage of providing an obvious and simple explanation for the appearance of quantum physics in the visible universe. Furthermore, the three notions of particles, fields, and information fit perfectly with the three types of consciousness (digital, analog, and non-dual). Now, a question that has a crucial bearing on our understanding of consciousness is the following: what happens after death? The father of electromagnetism, James Clerk Maxwell, made it clear on his deathbed that he felt that what he had achieved had been achieved by something greater than himself.

9.1. Electromagnetism and Group Theory

At this stage, the idea is to propose that this thing inside us that goes far beyond us is the information available in the void/ether, information accessible through our three forms of consciousness (digital, analog, and non-dual). To demonstrate this, we need only refer to group theory. In modern physics, every law can be seen as a consequence of the existence of an underlying symmetry group, and, when we look for the symmetry group that leaves Maxwell’s famous equations invariant, we come across the ISO(4,2)⊗U(2)⊗U(2) group characterized by 6 × 5/2 + 2² + 2² = 23 generators. What interests us here are the 15 infinitesimal generators of the ISO(4,2) subgroup, where the acronym ISO stands for “Inhomogeneous Special Orthogonal” group. Among them are the following seven generators of the Gal(3,1) subgroup underlying Galilean physics: three spatial translations, three spatial rotations, and one translation in time. Thus, the (3,1) doublet refers to the fact that we live in a three-dimensional space (3) to which a temporal dimension (1) has been added. In short, to describe any purely mechanical phenomenon, it is imperative to consider a triplet of real numbers (x, y, and z). This allows us to distinguish, in space, between right and left (x-axis), front and back (y-axis), and up and down (z-axis). But this is not enough. We also need to add another real number to distinguish between the past, present, and future (time t). The fact that this fourth coordinate is not integrated with the other three is linked to the fact that time always flows from the past to the future, and never in the opposite direction.

The French mathematician Henri Poincaré then added three other generators leading to the ISO(3,1) Lorentz subgroup. This, in the form of three Lorentz generators, the boosts mixing each of the three spatial coordinates (x, y, and z) with the temporal coordinate (t). The consequence is that space and time can now mix. Hence, the relativistic notion of space–time. But, to preserve the impossibility of going back in time, the time coordinate becomes the imaginary part of a complex number describing this mixture of space and time. In practical terms, this means that we have now unified mechanical and electromagnetic phenomena. It also means that we have gone from three Casimir invariants for Gal(3,1), mass (spatial translations), energy (temporal translation). and spin (spatial rotations), to just two, mass/energy with E = m·c² and spin, for ISO(3,1). But the fact is that there is an ISO(4,2) supergroup including ISO(3,1) as a subgroup. As its symbol indicates, this supergroup adds a fourth space coordinate s and a second time coordinate ψ, associated with five new infinitesimal generators. The first generator corresponds to dilation in space or time, and the other four to conformal symmetries that preserve angles between two arbitrary directions.

The new spatial coordinate s is used to specify the size scale (small/large) at which the system under study is considered. For space, this corresponds to the number of particles in an inert system or the number of cells in a living system. So, for a crystal, you only need to define the crystal lattice to know everything, whereas, for a living being, it is the cell that suffices. For time, this scale coordinate means that it is enough to limit ourselves to a frequency range covering an octave (factor 2). Hence, transposing from octave to octave does not change the musical rendering. Now, we also need to know what the second time coordinate ψ represents. It is here that I propose to bring consciousness into play. So, in addition to time t, measured by a clock, there would be time ψ measured by consciousness. Roughly speaking, ψ would indicate at what level of reincarnation and, therefore, at which information level we are located in the void/ether. Unlike the other five coordinates, this is a matter of proposition and speculation, not certainty, but it is precisely the purpose of this paper to see how far we can go with such a hypothesis.

9.2. The Universe Is a 6D Continuum

Therefore, we consider our universe to form a 6D continuum (6 = 4 + 2) with four spatial coordinates (abscissa, ordinate, coordinate, and scale) and two temporal coordinates (time and level of information/consciousness). What motivates us here is that the characteristic of time is that it cannot be reversed, and, by the same token, the level of information cannot be reversed, for, according to Shannon’s theory, this level is defined by I = Σ_i p_i·ln p_i, where p_i represents the probability of having a certain piece of information i among a whole set of information. Similarly, we know that, in statistical thermodynamics, the entropy of a system is defined as S = k_B × Σ_i p_i·ln p_i, where p_i now represents the probability of observing a certain microstate (x, y, z, and t) in space and time. Just as it is impossible to go back in time, it is, in fact, impossible to decrease the entropy of the universe, which can only increase. The k_B constant (Boltzmann’s constant) is, here, simply a scaling constant, allowing us to determine whether we are working with matter or with pure information via consciousness. There are, thus, two dimensions for time, one, t, associated with energy E, and the other, ψ, associated with entropy/information S.

In summary, we propose the existence of three types of continuums, denoted as M⁴, C⁵, and V⁶ hereafter. The M⁴ continuum corresponds to Minkowski’s spacetime limited to the quadruplet (x, y, z, and i·c·t). The C⁵ continuum is a conformally symmetrical space characterized by five coordinates (x, y, z, i·c·t, and s), with the last coordinate (s) referring to a position in the size scale (small/large). From a mathematical point of view, by combining the dilation symmetry operation with the translation and rotation symmetries, it is possible to construct a mass-conjugate quantum eigentime operator. This coordinate then makes it possible to speak of birth and death in an absolute sense. It is, thus, meaningful to assert that a given mass appeared here (place of birth) at a precise moment (date of birth) and disappeared there (place of death) at a later moment (date of death), and all this can be repeated ad nauseam.

Whether we are in M⁴ or C⁵, we are still describing the observable universe at an object-oriented level. The existence of a larger embedding space, V⁶, would allow for a supra-consciousness to operate on a virtual information field. Another crucial point is that the use of dilation symmetry operators may also be linked to the fact that a conscious being is free to operate changes in measurement units without altering the observed system. In short, all units are equal… The fact that the information field V⁶ is fundamentally scale-invariant is just another way of saying that space, time, and matter do not exist by themselves. Hence, the not-so-surprising assertion that matter is a mere illusion and does not exist in its own right. There is, therefore, a fundamental equation W = k_B·T = h·f = m·c² = e·U = (2h·α/e)·I = G·m²/D, indicating that matter can always be associated with the same energy W via interactions of a thermal, vibratory, mechanical, electrical (voltage U), magnetic (electric current I), and gravitational (mass m and distance D) nature. This, with a set of universal constants k_B = 0.0138 zJ·K⁻¹, h = 663 zJ·fs, c = 299,792,458 m·s⁻¹, e = 0.16 aC, α = 1/137, and G = 66.7384 pJ·kg⁻²·m, which are valid whatever the scale of observation.

9.3. Life and the Fifth Dimension of Scale

For quantum physics, this suggests introducing a new scale wave function ψ(x,y,z,t,s), taking its values not only in space (x,y,z) and time (t), but also in scale (s). Now, by squaring the amplitude of such a scale wave ψ(x,y,z,t,s)·ψ*(x,y,z,t,s), we should obtain the probability of observing the mass of a system at any scale of observation. Using quantum scale operators, it is then possible to write a generalized Schrödinger equation whose solutions are waves propagating with time in scale, as well as in space. We then find that the square of the ratio of the amplitudes of the fastest pair of these scale waves (the first two harmonics) is related by a universal constant N = ¼exp(4π²/ln2) ≈ 10²⁴. This justifies the order of magnitude of Avogadro’s constant, N_A = 6.022 × 10²³ mol⁻¹, which sets the size of atoms in relation to that of macroscopic bodies. The inclusion of other harmonics in the description slightly modifies the value, but not the exponent.

In other words, V⁶ must be seen as an entity that exists beyond space, time, and matter and is the ultimate source of all types of reality. It would contain, in the form of bit strings, all past, present, and future events in our universe. The ether of general relativity is, therefore, the physical substate of V⁶, upon which it is physically possible to write or read bits of information as on any type of memory. In other words, everything is possible in V⁶, even the non-physical things that are commonly visualized during dreams as chimeras, monsters, or other nonsense for the conscious “self” evolving in a C⁵ subspace. The ether V⁶ is also the repository of all mathematical ideas, all scientific theories, all works of art, all pieces of music, and all deities—in other words, the common source of inspiration for everyone involved in art, science, or spirituality.

With regard to the mechanism for reading from or writing to such an ether, we can refer to quantum-loop gravity by stating that the ether can exist in the two following distinct states: looped (bit 1) or unlooped (bit 0). It is also possible to define a quantum of spatial area A_P = ħ·G/c³ (where ħ = h/2π is Dirac’s constant) and, therefore, also a quantum of length L_P = A_P^½ = (ħ·G/c³)^½, as well as a quantum of temporal area t_P² = A_P/c². Knowing the age of the universe t_U = 4.3 × 10¹⁷ s, it follows that the memory capacity of our universe C⁵ embedded in the ether V⁶ is currently about M = (c·t_U/L_P)⁴ = c¹⁰·t_U⁴/(ħ·G)² ≈ 10²⁴⁴ bits. Alternatively, the ether of general relativity can be replaced by the vacuum of quantum theory. At the level of the information stored in V⁶, this does not matter. However, after projection into a subspace C⁵, where energy matters, the two points of view do not agree. This stems from the fact that mass M scales with length L in general relativity (M = G·L/c²), while it scales with the inverse of a length (M = h·c/L) in quantum physics. Hence, the difficulty of marrying these two theories together.

That said, we can now turn to the crucial role played by the water molecule in this picture. First of all, the distinction between inert and living things lies in the ability of a given material system to explore the fifth dimension. This is by allowing changes in size through a metabolism that enables duplication, and to memorize what has been acquired by being able to process information (consciousness) in a sixth dimension. In contrast, an inert thing is limited in its evolution by the M⁴ subspace. It follows that neurons, being made of matter, surely hold in M⁴ a form of local consciousness, the conscious “self”, embedded in a supra-consciousness that extends in V⁶ far beyond the brain, heart, or gut. Furthermore, neurons acting at the level of object-oriented language obey Boolean binary logic. Consequently, there should be at least one other channel of expression involving the whole body obeying intuitionistic logic (meta-consciousness). Finally, a third channel could also be identified, involving the mind/body combination in the V⁶ field and obeying minimal logic, where negation simply does not exist.

On the other hand, there is experimental evidence that water is capable of storing, in the form of an electromagnetic signal, the information needed to produce, from separate nucleotides, a molecule as complex as DNA [30,31,32,33]. For some ten years, this claim always came from the same research group, until an independent group confirmed such a possibility [34]. Obviously, in an M⁴ continuum, such a claim appears, on a theoretical level, totally unfounded. But, in a V⁶ continuum, nothing is very surprising. The mechanism authorizing such a phenomenon was put forward as early as 1988 [35] and refined in 1995 [36], then in 2012 [37], and finally amended definitively in 2018 [38]. We briefly recall it here.

9.4. Coherence Domains (CDs)

The starting point is the possibility of generating an attractive force between two mirrors proportional to the inverse of the power of four of their distance d (static Casimir effect) [39]. Such a force (Figure 9d) arises from the exclusion of all wavelengths greater than d. In another experiment, unobservable virtual photons filling the quantum ether can be transformed into real photons (dynamic Casimir effect) [40]. All that is needed is to set one of the two mirrors in relativistic motion (Figure 9d). The existence of such virtual photons within the quantum ether is ensured via the existence of an operator N, an operator whose eigenvalues correspond to the number of quanta with pulsation ω = ∆φ/∆t, where φ is the unobservable quantum phase angle related to the internal state of each quantum.

Under these conditions, the reduced Hamiltonian can be written as follows: H/ħω = N + ½. Hence, when the quantum field is in its ground state (empty), there is the existence of a so-called “zero-point” energy ZPE = ½ħω, with ω = ∆φ/∆t and corresponding to N = 0 [41]. Moreover, there is non-commutation between the quantum number operator N and the phase angle operator Θ, [N,Θ] = −i. There is, therefore, an indeterminacy relation ∆N × ∆φ ≥ ½, responsible for quantum coherence at all scales, including a macroscopic one [42,43]. With W = N × ħω or ∆W = ħω × ∆N, any uncertainty ∆N, such that ∆N × ∆φ ≥ ½, leads to an energy uncertainty such that ∆W × ∆t ≥ ½ ħ. It is, therefore, possible, in quantum field theory, to temporarily violate the sacrosanct principle of energy conservation, but only for a short time ∆t < ħ/∆W.

These considerations apply, of course, to all types of matter. Matter seen not by a chemical formula, but rather, equivalently, by its frequency spectrum. Such a spectrum is easy to obtain thanks to a whole range of different spectroscopic techniques. The question that now arises is to, once again, consider the water molecule, the most abundant molecule in the universe, but no longer with its formula H₂O, rather via the frequency spectrum associated with such a stoichiometric formula [42] (Figure 15a). The interest here is that the water molecule is a very small entity, with a diameter close to 0.3 nanometers. Consequently, the energy levels of the first excited states do not form a continuum, but rather a ladder with widely spaced rungs. Thus, there is a first excited level at an energy ∆W = 1120 zJ for an ionization energy of 2022 zJ. This level, however, cannot be used, as it corresponds to anti-bonding states of the O-H bond. If it were used, there would be a non-negligible risk of OH• hydroxyl radicals appearing.

The idea is, therefore, in order to achieve virtual excitations using vacuum energy, to use non-bonding Rydberg levels located on the oxygen atom, of the 5d orbital type. This is because, such a level, located at an energy ∆W = 1934 zJ above the ground state of the water molecule, is capable of giving a coherence gap of the same order of magnitude as the energy of the hydrogen bond [29]. Hence, a self-excitation wavelength λ(μm) = 198.645/∆W(zJ), i.e., λ ≈ 0.1 μm = 100 nm and a lifetime ∆t < ħ/∆W = 106/1937 fs ≈ 10⁻¹⁶ s, since ħ ≈ 106 zJ.fs. Now, the power P radiated by an electron of mass m_e ≈ 10⁻³⁰ kg, subjected to acceleration a and velocity v = a×τ_e, is written as P = (m_e ×·a)·v = ⅔·ħ × (a/c)², with α ≈ 1/137, Sommerfeld’s fine structure constant. Hence, there is a characteristic relaxation time τ_e = ⅔α·ħ/(m_e × c²) ≈ 10⁻²³ s, since m_e×c² ≈ 82 fJ. The number of water molecules affected by such virtual excitation extracted from the vacuum during a time lapse ∆t ≈ 10⁻¹⁶ s, is, therefore, ∆N ≈ 10⁻¹⁶/10⁻²³ = 10⁷. This also means that the maximum uncertainty on the phase angle φ common to these N_CD ≈ 10 million water molecules forming a “coherence domain” (CD) of size λ is such that ∆φ ≈ ½∆N, i.e., ∆φ < 5 × 10⁻⁸ rad. On the other hand, in order to minimize the increased electron repulsions via these excited states, this cannot occur in volume, but rather in the vicinity of any 2D interface [43].

More precisely, Figure 15b shows that, when a water molecule in its gaseous state interacts with the quantum vacuum via one of its excited states, the diameter of its electron cloud increases. Here, the only possibility is to wait long enough for relaxation back to the ground state. The energy required for excitation is then returned to the vacuum. In the liquid state, however, the scenario is different. Here, van der Waals forces mean that molecules are relatively close together. As a result, if a water molecule becomes excited, it expands as expected, but its electron cloud then overlaps that of a neighboring molecule. As a result of this partial overlap, quantum entanglement can occur, leading to the possibility of cross-relaxation. In other words, instead of returning the borrowed photon to the vacuum, it is transferred to the water molecule entangled near the van der Waals. Thus, the first molecule relaxes, while the second, in turn, becomes excited (Figure 15c). Of course, this mechanism does not stop there, which means that the initial photon borrowed from the vacuum passes from molecule to molecule, without returning there. However, after around 10 million transfers, the process reaches its limits, and the vacuum ultimately reclaims the photon that it was kind enough to supply to the first water molecule. In short, some 10 million molecules, for a brief moment, share the same photon extracted from the vacuum. As a result of this sharing, the quantum vacuum is able to act as a “glue” between around 10 million water molecules (coherence domain). Figure 15d shows how this glue can be represented within the framework of a second quantization formalism, via so-called “virtual” photons circulating ceaselessly between water molecules, thereby rendering them totally indistinguishable and united by the same quantum phase.

As this is very technical, we could also say that there is a perpetual game of soccer between the vacuum, which plays the role of playing field and referee, the water molecules, which are the players, and the photons, which play the role of balloons. In classical physics, there is obviously nothing equivalent, hence, the invention of an ad hoc term, where this “glue” is called the “hydrogen bond”. In short, this is a simple word to translate this subtle, perpetual interplay involving vacuum, light, and matter. This is why this glue is found not only in liquid water, but also in a large number of biological molecules (DNA, RNA, proteins, and sugars) fundamental to life. As water and biopolymers use exactly the same glue, it is no exaggeration to say that “water is life”.

9.5. Water Is Life

Therefore, if scientists were serious and consistent, they would integrate all the available data acquired during years of theoretical and experimental work on liquid water, the water that wets, quenches, and gives life (Figure 15e). We are a long way from the formula H₂O. Let us recap—H for hydrogen, D for deuterium, T for tritium, and O for oxygen, with three digits, 16, 17, or 18, indicating which isotopologue we are dealing with. Next, the arrows indicate the spin state of the H, D, or T atoms (ortho or para water). The dots ‘.’ stand for the aqueous physical vacuum, something different from nothingness. The Greek letter γ stands for the coherent glue or “hydrogen bond” between water molecules, whereas the letter γ’ stands for the coherent glue of a covalent nature between different types of atoms. Finally, the positive charge (hydronium ion H₃O^⊕) appears as soon as an oxygen atom is surrounded by three γ’ glues and a single γ glue, while the negative charge appears if that same oxygen atom is surrounded by three γ glues and a single γ’ glue (hydroxide ion OH^⊖). In pure, neutral water, these two ions are always in equal amounts, hence, pH = 7. If there is an imbalance, we speak of an “acidic” (excess of H₃O^⊕ ions) or “basic” (excess of OH^⊖ ions) medium. It is important to realize, however, that as soon as these species are no longer in exactly equal concentration, the thing we are manipulating is no longer water, but something else we call an “acid” or “base”. Scientifically speaking, the drawing represents what is known as a “coherence domain”, which may contain several million water molecules, although there are barely 17 represented.

For those who still have trouble visualizing what a coherence domain is, this is represented in Figure 15f. Here, the same phenomenon is reproduced on a macroscopic scale, with grains of sand playing the role of water molecules and a vibrating plate playing the role of the quantum vacuum. But this is also true of starlings in the sky or schools of fish. In the case of starlings (water molecules), air plays the role of the quantum vacuum, the vibratory support. For schools of fish (water molecules), it is seawater itself that, once again, plays the role of the quantum vacuum, a vibratory support. Let us now look at the practical consequences of this new way of thinking about hydrogen bonding.

Thus, a mammalian cell has a mass m ≈ 1 ng [44], for a volume of 10⁻⁹ cm³, a diameter D ≈ 12 μm, and a surface area A ≈ πD² ≈ 500 μm². As already mentioned, such a cell is made up of more than 99 mol% morphogenic water of density d ≈ 1 g·cm⁻³. Furthermore, such a cell is covered by a hydration shell strongly associated with its lipid bilayer. If these water molecules are excited by vacuum/ether at λ ≈ 0.1 μm, the number of coherence domains amounts to N_DC = 2·A/λ² ≈ 2 × 500/0.01 = 100,000. The factor two takes into account both extracellular and intracellular water shells. Depending on what is embedded in such a lipid bilayer, there may be regions where coherence is activated (bit 1), and other regions where coherence is absent (bit 0). Hence the possibility of encoding information. Furthermore, a coherence gap δW ≈ 42 zJ [37] corresponds to an associated wavelength λ(μm) = 198.645/42 ≈ 4.7 μm, falling into the infrared region of the electromagnetic spectrum. The energy required to modify the coherence state in these aqueous domains could, therefore, very well be supplied by the Sun/Earth couple. For, the Sun illuminates the Earth at 0.5 μm, with re-emission by the latter at around 10 μm.

This is also in line with the observation that any hydrophilic surface has an exclusion zone (EZ-water) that converts IR radiation into an electrical potential [45]. In other words, the water layers surrounding a cell can store information that can be written, erased, or read using infrared radiation. Knowing that 1 byte = 8 bits, the total memory capacity of these water layers is estimated at N_DC/8 ≈ 10 ko. With 3.72 × 10¹³ cells in a human body [44], the memory capacity of membranes would, therefore, be close to 3.72 × 10¹⁷ bytes = 372 Po. We can also consider the reference value of 36 L of water, average between men and women from the adult white American population (20–79 years) [46]. However, the hydration shell of intracellular biopolymers consists of a maximum of four water monolayers [41], i.e., a thickness of around 1 nm, since a water molecule has a diameter of around 0.3 nm. Hence, there is a volume of V_DC ≈ 1 × 100 × 100 = 10⁴ nm³ per coherence domain and, therefore, 8 × 10⁴ nm³ per byte of information. Since 1 L = 10²⁴ nm³, we find for 36 L of intracellular and extracellular water or interstitium [47] a total of 36 × 10²⁴/8 × 10⁴ bytes = 450 Eo.

In addition to cell membranes and the interstitium, consider the human intestine, known to contain around 3.8 × 10¹³ prokaryotes [48]. A prokaryotic cell has a diameter ten times smaller than that of a eukaryotic cell, i.e., a surface area 100 times smaller (A’ = A/100 = 5 µm²). Hence, it has a storage capacity at λ = 0.1 µm, estimated at 2A’/8λ² ≈ 10/(8 × 0.01) = 125 bytes. Therefore, for the human intestine, we find a total of 3.8 × 125 × 10¹³ = 4.75 × 10¹⁵ bytes = 4.75 Po. With around 5 × 10³⁰ prokaryotes on earth [49], we find a total of 6.25 × 10³² bytes. By comparison, for a total of 8.1 × 10⁹ human beings in 2024 [50], each carrying 4.5 × 10²⁰ bytes in their bodies, we only obtain a total of M(t) = 4.5 × 8.1 × 10²⁹ bytes = 3.645 × 10³⁰ bytes.

9.6. Consciousness and Bandwidth

For consciousness, memory capacity is not enough. For, one must also take into account the bandwidth BW(t) = dM(t)/dt [51]. For a human being, we find BW(t) ≈ 1 Mo·s⁻¹, coming mainly from the sense of vision [24], or for about 100 years of existence, about 3156 × 10⁹ s, and, therefore, a total of 3156 × 10⁹ × 10⁶ = 3156 × 10¹⁵ bytes ≈ 3.2 Po. This corresponds to just 1% of the memory capacity of the body’s membranes. Even assuming a bandwidth of external stimuli of 100 Go·s⁻¹, corresponding to all that is possible to record during an entire human lifetime [29], we find 32 × 10¹⁸ bytes = 32 Eo, or just 10% of the body’s 450 Eo. Hence, this is the consciousness that is required to make sense of this raw data stored in every human body and define what is usually referred to as “context” [52]. The role of the conscious “I” is to discard a large part of this context that is not transmitted (exformation) [24]. We know that the average water turnover of a sedentary adult is 3256 mL per day, or 37 μL·s⁻¹ [53]. So, if water is, indeed, the information carrier in the human body, we calculate a bandwidth of BW(t) = 37 × 10¹⁸/8 × 10⁴ = 462.5 To·s⁻¹, since V_CD = 10⁴ nm³ and 1 μL = 10¹⁸ nm³. This value is 12 times lower than the global Internet traffic estimated for the year 2025 at 181 Zo [54], i.e., 181 × 10²¹/3.156 × 10⁷ ≈ 5.735 Po·s⁻¹. However, we can also consider the movement of water inside the body, independent of external losses. Now, in Homo Sapiens, blood is distributed to cells by around 10⁹ capillaries of an internal diameter of D_C = 3.5 μm for a total cross-sectional area of A_C = 6 m² [55]. On the other hand, the largest artery of the heart is the aorta, with a mean diameter of D_A = 30 mm [56], associated with a mean blood flow velocity of v_A = 76 cm·s⁻¹ [57]. Knowing that ¼π·D_A²·v_A = A_C·v_C = 537 cm³·s⁻¹ = 537 × 10²¹ nm³·s⁻¹, i.e., v_C = 89.5 cm·s⁻¹, it follows that BW(t) = 537 × 10²¹/8 × 10⁴ = 6.7 Eo·s⁻¹, a throughput 1000 times greater than the entire global internet forecast for the year 2025.

Clearly, the most likely place where such information flows exist is in cell membranes. This means that any cell membrane could be the host of a local consciousness, and intelligence is expected in amoebae, for example, as has been observed experimentally with the plasmodium mold Physarum polycephalum [58]. This mold has also been shown to be able to anticipate periodic events [59]. Since the osmotic coefficient of the permeability of a lipid bilayer for water is around 100 μm·s⁻¹ [60], it comes for a surface area A (prokaryote) = 5 μm² a bandwidth BW(t) = 5 × 100 × 10⁹/8 × 10⁴ = 6.25 Mo·s⁻¹. So, for all terrestrial prokaryotes, we expect that BW_pro (t) = 5 × 6.25 × 10³⁶ ≈ 3.1 × 10³⁷ bytes·s⁻¹. By comparison, humanity, as a whole, is characterized by BW_hum (t) = 6.7 × 10¹⁸ × 7.7 × 10⁹ ≈ 5.2 × 10²⁸ bytes·s⁻¹. In other words, the human contribution to the Earth’s global consciousness is just one part per billion (ppb). In fact, in view of these enormous bandwidths, it should be obvious that we are talking here about consciousness at an object-oriented, i.e., largely unconscious, level. Consequently, for the blood circulating in our capillaries, we can speak of a personal unconscious, or even Freud’s “id” [61], whereas for the water that circulates on the membranes of prokaryotes, we are probably confronted with Jung’s collective unconscious [62].

When it comes to consciousness at a meta-level, we leave the object-oriented digital mode and land in an analog mode associated with muscular movements or the electromagnetic signals emitted by the brain, gut, and heart. However, we know from the invariance of Maxwell’s equations under the symmetry operations of the ISO(4,2)⊗U(2)⊗U(2) mathematical group that all electromagnetic reality should be embedded in an ether V⁶. Fitting consciousness into the restrictive framework of a Minkowski M⁴ space is generally perceived as a “difficult problem” [63]. There is also the free will of living beings, which can be described as a “difficult issue” [64].

9.7. Minerals, Plants, Animals, and Humans

In the ether V⁶, on the other hand, there should be no problems or difficult issues related to consciousness. Here, each conscious being occupies a certain volume, with highly significant bits that never change and other bits that can be reconfigured according to experiences on a C⁵ hyper-surface at a given location (coordinates x-, y-, and z-), at a given moment (coordinate t-), and at a given scale in space and time (coordinate s-). Using the language of group theory, reducing reality to a space C⁵ means separating the group ISO(4,2) with infinitesimal generators describing an external world from the group U(2)⊗U(2) with finite generators and describing the internal world of elementary particles (strong and weak interaction). Consequently, our approach is consistent with physicalism, as well as dualism.

As explained above, the s-coordinate of C⁵ is crucial in differentiating between living things and inert things. Thus, a rock has an existence in space and time at a given scale, but lacks the software in V⁶ enabling it to develop on its own. In other words, for inert matter, space V⁶ and its subspace M⁴ seem to be completely disconnected due to a too low a water content. A seed, on the other hand, also has an existence in M⁴. But, more importantly, it possesses in V⁶ a small ROM containing downloadable instructions on how to grow over time. Such a ROM enables it to change size, optimally managing matter and energy via metabolism. At birth, the necessary information stored in V⁶’s ethereal substance is transferred as ROM to the DNA and as RAM to the hydration shells of membranes and biopolymers. Upon death, this information is transferred to the hydration shells of the terrestrial microbiota or animals that have devoured the living being. The same applies to animals, but here, the ROM in V⁶ can be updated via their metabolism in C⁵. This is precisely why animals, unlike plants, have the ability to move in C⁵ in search of food. As animals, humans are also able to reconfigure their software in V⁶ thanks to their metabolism in C⁵. However, they have the additional ability to do so after mentally focusing their attention (through meditation, for example) on a particular set of bits in V⁶, in a state generally referred to as “mindfulness”.

9.8. Relations with Eastern Philosophies

This would mean that humans have the ability to mentally access the internal world of matter covered by U(2)⊗U(2) symmetry, whereas animals are condemned to use only the ISO(4,2) part of reality. As the generators of the U(2)⊗U(2) group are integrative and differential in nature, they couple the macrocosm with the microcosm at all scales. Further work is, therefore, needed to fully understand their role in nature. During the exchange of information between space V⁶ and hyper-surface C⁵, the conscious being has the feeling of being traversed by a pure energy that could be identified with the “Prana” or “Qi” of Eastern civilizations. Such an information-driven flow would be perceived as entropy by a Western mind. Consequently, the shift in scale can only be experienced as energy, as the presence of matter locally breaks the ISO(4,2) symmetry, reducing it to ISO(3,1) with the appearance of a force called gravitation, necessary to restore full symmetry on a global scale.

This modeling of the phenomenon of consciousness appears, therefore, intimately linked to gravitation, as proposed by the Orch-R model of consciousness [65]. Such a reduction from ISO(4,2) symmetry in C⁵ to ISO(3,1) symmetry in M⁴ can be identified with the collapse of the wave function in quantum physics. As cognitive neuroscientist Marcel Kinsbourne quotes, “What makes any problem difficult is that something false but attractive stands in its way” [64]. Here, the thing that is false but attractive is obviously the fact that matter exists by itself. As explained earlier, the fact that matter does not exist and is an illusion has been lucidly perceived by great scientists such as Henri Poincaré, Max Planck, Werner Heisenberg, Erwin Schrödinger, and John Wheeler. In our approach, Einstein’s call to think at a higher level [66] means replacing the ISO(3,1) group with its ISO(4,2) supergroup.

Of course, Eastern philosophies did not wait for the discovery of group theory or quantum physics to reach the conclusion that matter was an illusion and that ultimate reality was to be found in consciousness. Fortunately, Western science, based on powerful mathematical models, comes to exactly the same conclusion. These considerations are also fully in line with Hinduism’s concept of multiple lives. For, here, karma corresponds to the traces left in V⁶ by conscious beings experiencing multiple life forms in C⁵. This is also consistent with shamanism, with V⁶ becoming the spirit world. More generally, this is consistent with all altered states of consciousness where one has direct access to the invisible reality of V⁶ without having to experience death, the “normal” gateway to it automatically. Another consequence is that near-death experiences (NDEs) or out-of-body experiences (OBEs) should be seen as actual journeys into V⁶ with the help of consciousness, and not as unreal mental images generated by an oxygen-starved brain. Finally, all this points to at least three different ways of healing when you are ill. Healing can happen in M⁴ through the use of material drugs or stimuli of an electromagnetic nature (for example). Healing can also occur in C⁵ due to water’s ability to store or transmit various and sundry information. Finally, healing can also occur in V⁶ via purely informational means involving consciousness (placebo effect, among others).

10. Water, Consciousness, and Life

Now, we come to the crux of this paper. How can we understand the phenomenon of life in 2024? Figure 16 summarizes the main point. The central idea defended here is that consciousness gave birth to life, and not the other way round. However, a certain number of stages is necessary to go from the very beginning—consciousness—to the final end—life on earth. Among the five intermediate stages, the immaterial concept of information and that material thing called “water” appear to be closely linked. To imagine life without consciousness is simply impossible. Whatever the context—bacterium, plant, animal, or human being—each entity participates in its own way and with its own skills in raising the overall level of consciousness of this planet called “Earth”.

10.1. The Five Metric Dimensions

In the foregoing, we have already shown that each entity on Earth can be assigned a bandwidth expressed in bytes per second, and this information is never lost. Rather, it is stored in the ether, also known as the “quantum vacuum”, according to the state of coherence (bit 1) or incoherence (bit 0) of a Planck cell. The existence of such cells is assured by the two following theories central to contemporary physics: quantum physics and general relativity.

Within this framework, it is possible to identify the five following “fundamental dimensions”: mass M, length L, time T, temperature Θ, and electric charge Q. Opposite these five fundamental dimensions, we can contrast the five following universal constants:

• The universal gravitational constant: [G] ≡ M⁻¹·L³·T⁻²
• The quantum of action, also known as Planck’s constant: [h] ≡ M·L²·T⁻¹
• The speed of light in the vacuum/ether: [c] = L·T⁻¹
• The entropy quantum, also known as Boltzmann’s constant: [k_B] = M·L²·T⁻²·Θ⁻¹
• Coulomb’s constant: [k_C] = M·L³·T⁻²·Q⁻²

The constant [G] is used to describe the interaction between immobile masses. The action quantum [h] describes the interaction between moving masses with a certain velocity v. The constant [c] tells us that there are light “particles” (photons) with no mass, but with a very characteristic speed limit. The entropy quantum [k_B] guarantees the existence of something called “heat”, capable of setting masses in motion spontaneously and not initiated by shocks between masses. Finally, Coulomb’s constant [k_C] guarantees the existence of charges responsible for non-mechanical, non-luminous, or non-calorific phenomena such as electricity (immobile charges) or magnetism (moving charges). The latter constant is linked to the existence of a quantum of charge e, such that e² = αℏc/k_C, where ℏ = h/2π and α is a dimensionless pure number such that 1/α = 137.03599911…, called the “Sommerfeld constant”. This constant [k_C ], in turn, is intimately related to the so-called “ether permittivity”, denoted as ε₀, with 1/k_C = 4πε₀. Note that we prefer the term “ether” here to its equivalent the word “vacuum”, which can give the unfortunate impression that there is nothing there. For, in fact, in this void/ether, there is, indeed, something that is, information, but this is neither visible nor tangible to the physical senses. Consciousness is the only way to access this information, provided that we have a communication interface—which, in the material world, is provided by water.

Everything is, therefore, in place to divide the vacuum/ether into elementary cells called “Planck cells” with an “elementary” area A_P = ℏG/c³ or an elementary volume V_P = [(ℏG/c)^½]³, depending on whether we are at a matter/ether interface (A_P) or in pure ether (V_P). For, as explained above, in modern physics, matter has no existence of its own, being merely a more or less intense excitation of the underlying ether that permeates everything material or non-material. As Figure 16 reveals, a chain of seven key concepts underpins everything that can happen in our universe, from immaterial consciousness to material life. First, there is the basic substrate—the ether or quantum vacuum, whichever you prefer to call it. Then, this ether is merely a substrate for this thing we call “information”, which can exist in the two following states: “true = 1” or “false = 0”. The size scale here is L_P = (ℏG/c)^½ = 1.616 × 10⁻³⁵ m. Even if this size scale seems extraordinarily small, thought allows us to imagine the existence of an arbitrary number of perfectly unobservable quantum blocks of even smaller size. However, even at this size, we can assume that the laws of quantum physics remain valid. So, as soon as a Planck cell encodes the bit “1”, then all the constituent sub-blocks all share the same quantum phase (coherence). On the other hand, if bit “0” is encoded, there is no phase correlation between the various sub-blocks (incoherence). Note that, at this stage, this information is in its raw state, totally devoid of meaning. But if, at this level, the true or false states of Planck cells cannot be measured individually, it is still possible to associate a global total information quantity I = Σ_i (p_i × Ln p_i) by assigning each cell a probability p_i of being, for example, in a “true” state. Then, by multiplying this sum I by the entropy quantum k_B, we recover an entropy of a more thermodynamic nature. This assumes that there is matter in motion somewhere, so that we can define a temperature T, via the average kinetic energy of the particles making up this decorative matter.

10.2. Life and Water

To move towards life, we must now, via consciousness, give meaning to this raw information, i.e., define a context. A context is also information, but it is information that is not intended to be transmitted. Hence, it has another name, exformation, which is information that remains in the ether with the cloud of the entity who will play the role of transmitter. This is where it all happens. The basic tool for sorting out what is to be transmitted and what is not is the Sheffer bar, a binary logical operation that can be considered the primary source of all other logical operations. This is where the notion of energy comes in, because this sorting does not happen by itself. It requires work and a certain level of activity, not only in the mathematical sense, but also in the thermodynamic sense (concentration gradients). Hence, this is another piece of information, carefully processed and purified, worthy of being transmitted to a receiver that can only be water. This substance is material in nature, making up 99.1 mol% of all living cells.

For, if an information receiver is to be present, the best thing is for it to envelop, like its ancestor, the ether, anything that is not water. This automatically solves the problem of which direction to send the information calculated by the consciousness. In fact, whatever the direction, there will always be water to receive and store this information. Here, again, this is a great economy of means. It is the same phase coherence mechanism as for the mother ether. We have just changed scale. Instead of manipulating the immaterial sub-domains of a Planck cell, we manipulate coherence domains made of water molecules, as seen previously. Anyway, in both cases (ether and water), we can memorize a sequence of numbers, 0 and/or 1. The only difference is that this can be conducted in 3D for ether, but only in 2D for water. So, what we are referring to here is “morphogenic” water, and not water with the formula H₂O. This is why this H₂O formula is drawn with thick letters in non-uniform colors, to clearly suggest that this is not ultrapure liquid water. Ideally, of course, the water should be attached to lipid membranes, which can form by self-assembly as soon as a material of an oily nature is dispersed in liquid water, but this is not mandatory, for it can also be any gas/water interface involving one or more gaseous substances (air) mixed with water. The only difference is that the information stored in lipid bilayers is far more stable than that stored in gas/water interfaces, which disappear rapidly as soon as the temperature rises too high.

Ultimately, it is this informed morphogenic water that gives rise to all the extremely sophisticated nanostructures found in a living cell, all wrapped up in a membrane bilayer that clearly differentiates between intracellular and extracellular media. After all, it is all water, 964 mol‰ for a man and 975 mol‰ for a woman. The rest of the story involves concentration gradients involving one or more of the 19 ions encountered in a cell. More particularly, the pair Na^⨁ in the extracellular medium and K^⨁ in the intracellular medium is used to generate a membrane electrical potential. It is worth noting that organic matter only appears in the very last place, and that, among all possible and imaginable molecules, two appear absolutely vital and inescapable. These two kinds of molecules correspond to proteins embedded in the lipid bilayer. The role the first one is to form a tunnel able to transfer water from the intracellular to the extracellular environment and vice versa. These tunnels are called “aquaporins”. The other kind will also act as a tunnel, but here, to allow inorganic ions to pass through the lipidic barrier. This is in order to modulate membrane electrical potentials as effectively as possible. This second kind of tunnel is called an “ion pump”. So, with just a few proteins, the basic blueprint of life is in place. The rest is simple decoration, which will evolve over time to become ever more efficient and effective.

10.3. Entropy in Thermodynamics

With such a background in mind, it appears that biology is currently plagued by several fossil concepts that may be responsible for this difficulty in elucidating the basic mechanisms of life. A careful examination of the origins of thermodynamics has identified these following fossil concepts [2]:

• The assumption that heat is a form of energy.
• Equating entropy with disorder.
• Equating death with states of maximum entropy.
• The assimilation of Adenosine Tri-Phosphate (ATP) into the energy currency of living cells.
• The non-recognition of entropy as a state function of the entire universe.
• Belief that so-called “free” energies are a form of energy.
• Ignorance of the basic principles of quantum physics and, in particular, of the importance of intrinsic spin.
• Confusion between three different forms of reversibility.
• Failure to recognize that irreversibility lies at the heart of living systems.

Basically, these fossil concepts have been safely tucked away in a cupboard. Then, the fact remains that life is deeply rooted, through the concept of entropy, in quantum physics on the one hand and cosmology on the other. This is in perfect accord with everything we have just said. Namely, that life is not an emergent property of matter. Rather, it has always been a fundamental property of a universe filled with particles and fields subject to consciousness. It was, therefore, proposed to retain only Ludwig Boltzmann’s clear definition of entropy. The latter is expressed only in terms of the multiplicity of microstates Ω, S = k_B × Ln Ω, with a second principle expressed in its most general possible form. This form is applicable to any type of macro-state, i.e., ∆S(universe) ≥ 0.

Concerning entropy, we recall that this concept was coined in the mid-nineteenth century to predict how a chemical system comes to undergo spontaneous evolution over time. The problem is that the so-called “second principle” (∆S ≥ 0) designates the gaseous state as the final product of all evolution in a closed system. This is perfectly at odds with the direct observation of biological systems, for the latter undergo spontaneous evolution from a gaseous state characterized by maximum entropy towards highly complex structures, displaying considerably lower entropies. Hence, this is an apparent violation of the sacrosanct second principle of thermodynamics. However, it is also perfectly permissible to consider the Earth as an open system rather than a closed one. If this were the case, it would be capable of undergoing a spontaneous (local) decrease in entropy, but only if the excess entropy could be effectively exported to the entire universe via infrared photons imperceptible to the human senses [2]. If the entropy exported in the form of invisible infrared radiation is much higher than the entropy decrease observed on Earth, then the appearance of life on this planet becomes fully compliant with the second law.

The consequences of such a broader viewpoint, taking into account all types of process (reversible and irreversible), have been studied in depth [1], and will not be repeated here. The central idea is that the first condition for the spontaneous appearance of life on Earth is the existence of a metabolism, taking the form of thermodynamic cycles capable of generating large amounts of entropy by degrading low-entropy molecular systems (food) into high-entropy molecular compounds (waste). Two possible cycles have been identified, based on the very low entropy of the Earth’s metallic core. This is in order to generate reducing gases (such as H₂, CO, NH₃, or H₂S) thanks to the low entropy of solar radiation (food) and for the simultaneous production, as waste products, of solid minerals (serpentine, metal sulfides, magnetite, or even goethite) or gases such as water vapor or carbon dioxide. The large entropy flux generated by these processes can, then, be used to build low-entropy molecular systems based on reduced carbon species and soluble phosphates, which are observed in all living cells [2]. Another consequence of this approach is the recognition of the ubiquitous role played by water in all aspects of life, through the concept of “water activity”.

10.4. Membranes, Genes, and Metabolism

Three major events have marked the evolution of the Universe. The first is the Big Bang, which saw the appearance of matter and light in the form of stars. A star is basically something that burns hydrogen to form the atoms that make up all matter. However, hydrogen is not really an atom, since it has no nucleus. Let us recall here that a nucleus is defined as an assembly of protons and neutrons, and while deuterium D is indeed an atom with a nucleus, its lighter isotope H is not, since it has no neutrons. In fact, the hydrogen atom is an assembly of two elementary particles. One is made up of quarks (the proton p^⨁) and the other is the electron (e^⊖), which is a lepton. Quarks and leptons are themselves creatures of the ether (or, if you prefer, of the quantum vacuum), created by a fluctuation which, for want of a better term, will be assumed to be random. This is fundamental, because this simple fact will confer on chemical combinations of the H₂ or indeed H₂O type, quite original properties. This can be compared to other molecules with only two or three constituent atoms, because, as we saw above, beyond three, we leave the sphere of “elementary” processes generating “motion” to enter that of processes generating very diverse and varied “structures”.

At the very beginning of this article, we saw that to ensure stability, it is imperative to obey a ternary logic of the thesis–antithesis–synthesis type. For example, we know (Figure 7) that hydrogen and oxygen are the two most abundant elements (green boxes) in the universe and, thus, on Earth. What happens when a dihydrogen molecule H₂ (thesis) meets a dioxygen molecule O₂ (antithesis)? You obtain a triatomic synthesis, in the form of two H₂O water molecules. Hence, it is not possible to have life without this really extraordinary substance that is water. But this is not enough. To store information, water has to be morphogenic. So, it must also contain, at the very least, air bubbles, if consciousness is to unfold in all three spatial dimensions. The price to pay, however, is low stability in relation to outside temperature. If, on the other hand, we move into two dimensions, by attaching the water to a non-gaseous lipidic surface, then we can develop hardware systems capable of storing information permanently, but only if the temperature is neither too high nor too low. Hence, the second event, the formation of the solar system following an accident 4.5 billion years ago, but also the choice of planet Earth, both close enough (thesis) and far enough (antithesis) from a star (Earth–Sun system), and, of course, the choice of water as the ultra-majority constituent of all life forms (at least 96 mol% in humans).

• If we accept that life does not escape the constraints imposed by physics, we would expect any form of life to express itself within a framework that allows for the following:
• Control of space (meter), which requires the use of membranes.
• Control of time (seconds), which requires genes.
• Control of mass kilogram), which implies the existence of a metabolism.
• Control of electrical charge (amperes) via membranes allowing concentration gradients for ionic species.
• Control of temperature (kelvin) to initiate polymerization reactions.
• Control of the number of molecules (mole) via membranes, genes, and metabolism.
• Control of light flux (candela) via chromophores (photosynthesis).

Hence the close symbiosis between the three following prerequisites:

• Membranes that provide the awareness of existence in relation to an external environment. Hence, the need to know how to manage lipids.
• Genes that enable experience to be passed on to new generations upon physical death. Here, it is the management of nucleic acids capable of supporting a genetic code that comes into play.
• A metabolism that allows us to build ourselves from the information contained in our genes, from birth to death. As we shall see, this requires mastery of phosphorylation.

10.5. Elements Essential to Life

Now, let us suppose that these three prerequisites have been fulfilled. How do we develop, now, non-gaseous interfaces that can immobilize these water molecules, which are just waiting to move? The answer lies in creating nanostructures via covalent interactions based on other sufficiently abundant elements such as carbon, nitrogen, or sulfur (Figure 7). About 3900 Myr ago, the relentless bombardment of the Earth by meteorites finally came to an end. At this time, carbon is found in the air in the form of methane CH₄, carbon monoxide CO, and carbon dioxide CO₂. For nitrogen, again in the air, we have dinitrogen N₂ and ammonia NH₃ giving rise to the ammonium cation NH₄^⊕ in water or hydrogen cyanide HCN, which, in water, gives rise to the cyanide anion CN^⊝. Finally, there is sulfur, found in air either as hydrogen sulfide H₂S or as the hydrogen sulfide anion or bisulfide HS^⊝ in water (sea ≈ 10⁻² M).

Five other highly abundant elements with a strong affinity for water complete the picture, as follows: sodium (Na), potassium (K), magnesium (Mg), calcium (Ca), and chlorine (Cl). Unsurprisingly, elements with a metallic character will end up as cations (thesis), as follows: sodium Na^⊕ (>10⁻¹ M), potassium K^⊕ (≈10⁻² M), calcium Ca^2⊕ (≈ 10⁻³ M), and magnesium Mg^2⊕ (≈10⁻² M), while chlorine, a non-metal, would form the chloride anion Cl^⊝ (>10⁻¹ M). With these four metallic species (Na, K, Mg, and Ca) and the six non-metallic elements (C, H, O, N, S, and Cl), we have ten of the eleven elements absolutely essential to life (red circles in Figure 7). The eleventh element, phosphorus, which is also absolutely essential, is less abundant than the other ten (yellow). Above all, it is rarely found in the air, even though it is also a non-metal. Its preferred place is, therefore, water in the form of HPO₄^2⊝ phosphate anions (<10⁻⁵ M).

Then, there are also the 14 elements that are essential to life, but only in trace amounts. They are marked with a blue square in Figure 7. Finally, the seven elements marked with a white triangle are only essential for certain species [67]. Here, with regard to the origin of life, within a reducing atmosphere, we would highlight the following in particular:

• Iron, in the form of ferrous Fe^2⊕ ions (≈ 10⁻⁷ M)
• The divalent cations Mn^2⊕ (≈10⁻⁷ M) and Zn^2⊕ (≈10⁻¹² M)
• The monovalent cations Cu^⊕ (≈10⁻²⁰ M), Co^⊕ (≈10⁻¹³ M), and Ni^⊕ (≈10⁻¹² M)
• Thiolates anions such as MoS₄^2⊝ (≈10⁻¹⁰ M) and WS₄^2⊝ (≈10⁻⁹ M)
• Vanadates VO^2⊕ (≈0.3 × 10⁻⁷ M)

These elements, along with perhaps one or two others, are the only ones of interest in possible initial organic systems, with sulfide-rich anoxygenic seawater.

Now, there must necessarily have been a primitive organization of all this prebiotic chemistry before reproductive life, because reproductive life requires a code that can only “code” a pre-existing system. On the one hand, we have lipids and proteins (metabolism), which clearly act as “material”. On the other, we have nucleic acids (replication), which can act as “software”. Then, to play the role of electricity circulating between the components, we have everything we need in the way of water holding dissolved inorganic ions. Hence, the third event is the appearance of life on Earth 3.9 to 3.5 Gyr ago.

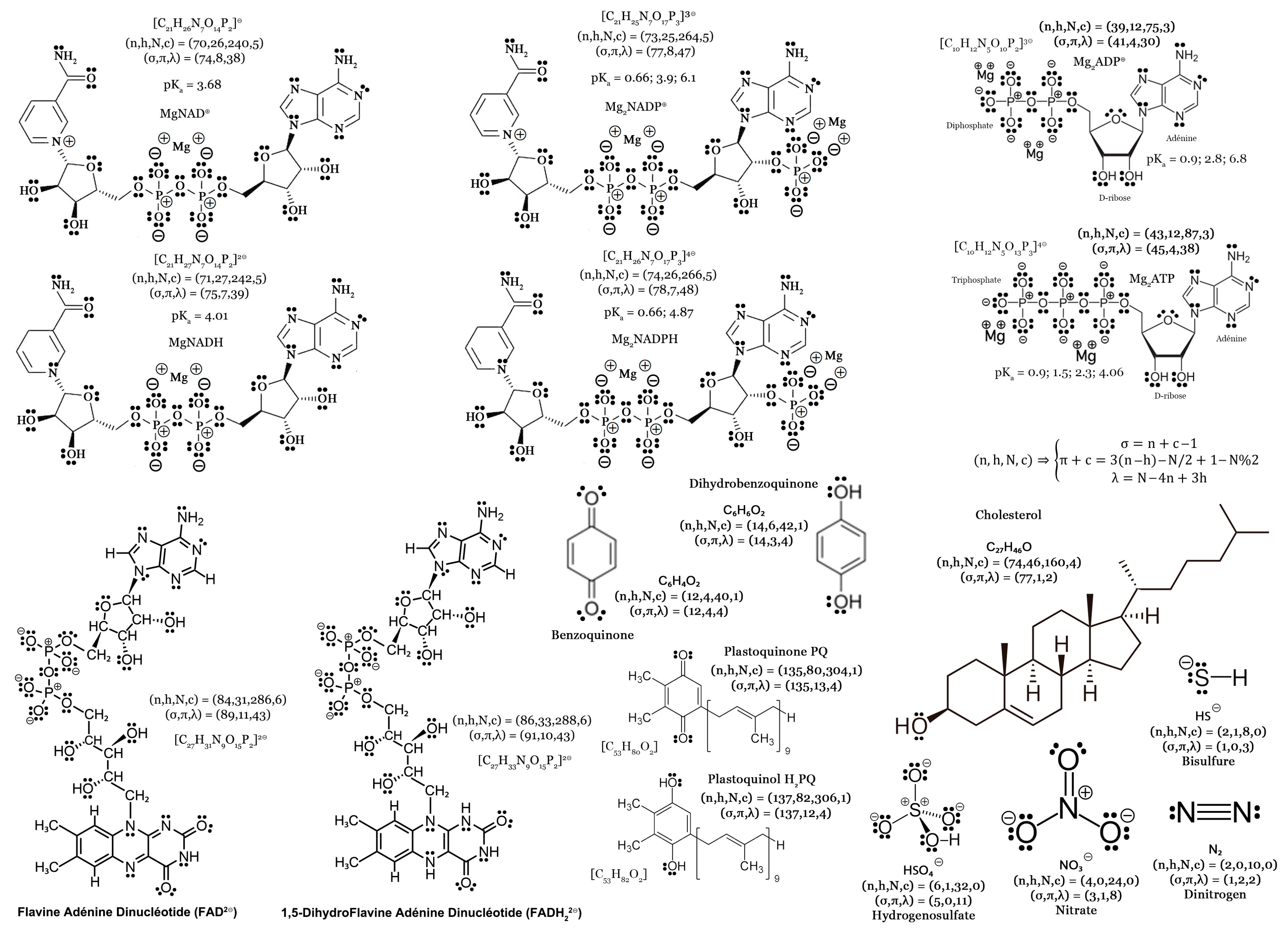
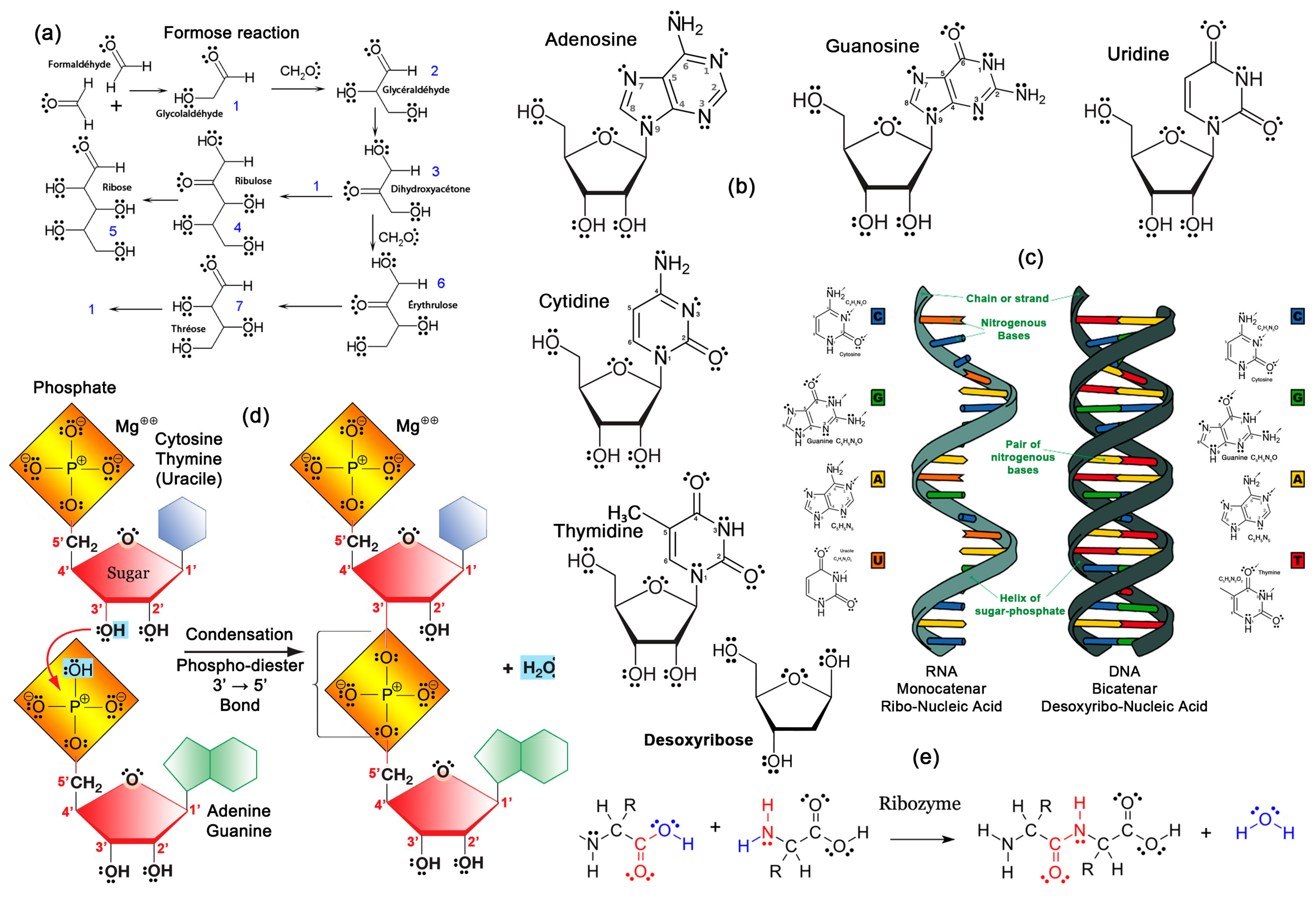
10.6. Three Fundamental Condensation Reactions

If we think of the ternary relationship between proteins (thesis), nucleic acids (antithesis), and metabolism (synthesis), the same problem immediately arises. Protein synthesis cannot have taken place in solution, because, in order to condense two amino acids, a water molecule must be eliminated as follows:

R-NH₂ + HO-CO-R’ = R-NH-OC-R’ + H₂O

The simple law of mass action, therefore, prohibits the formation of any chemical bond of a peptide nature in water. The same constraint also applies to the phosphodiester bond that produces polynucleotides as follows:

MgO₃P-O-Cb-OH + (HO)-Cb-O-PO₂K = MgO₃P-O-Cb-O-KPO₂-O-Cb + H₂O

Here, the symbol Cb represents a carbohydrate (sugar) such as ribose (RNA) or deoxyribose (DNA). RNA and DNA are also molecules capable of replication (replicators), and can code for proteins via a genetic code. Finally, no metabolism would be possible without the phosphorylation reaction, which also eliminates a molecule of water, as follows:

MgO₃P-OH + HO-X = MgO₃P-O-X + H₂O

Here, X can be an amino acid, any small molecule bearing a hydroxyl function, or even another phosphorus derivative to obtain a polyphosphate. Fortunately, nature has found a universal solution to enable all these reactions, crucial for any living being, to take place. The idea is actually quite simple—all that is needed is to create compartments isolated from the surrounding aqueous environment. This need must have arisen even before the need to refer to codes. A code will only become essential when it comes to reproduction, whereas to live, the code is useless. Consequently, the appearance of a code that guarantees continuity requires that the system already has sufficient persistence to give it time to evolve.

To make these compartments, nature has fallen back on the eternal recipe of the ternary, but here, it is applied to very special molecules, fatty acids. It is a fact that any covalent association between a hydrophilic molecule (polar head, thesis) and another hydrophobic one (tail, antithesis) can give rise, via self-assembly reactions, to extremely sophisticated nanostructures (synthesis) (Figure 17) [68]. Of course, these systems become self-assembled thanks to non-covalent forces (van der Waals forces and hydrogen bonds) that are intrinsically weak compared with chemical bonds of a covalent nature, but they have the great advantage of being cooperative. In other words, as the number of self-assembled objects in a nanostructure increases, so does the probability of adding a new object of the same kind.

10.7. The Serpentinization Reaction

Now, how can we make fatty acids under prebiotic conditions? This is where we need to talk a little bit about serpentinites, which are water-rich rocks composed mainly of minerals from the serpentine group (chrysotile, lizardite, and antigorite). They are found on almost every continent. Such a rock with the formula Mg₃Si₂O₅(OH)₄ is obtained as a result of the relatively low-temperature hydration of peridotite, the main rock of the upper mantle, composed of magnesium-rich olivine and orthopyroxene (Figure 18). Ultramafic rocks and serpentinites are abundant in the oldest Archean greenstone belts (3.81–3.70 Ga) on Earth. Serpentinization is a natural process that releases hydrogen and other reduced gases, creating a unique deep-sea ecosystem [69]. It is, thus, assumed that this serpentinization reaction would have provided favorable environments for the abiotic production of lipid chains or amino acids, all that is needed is for seawater to come into contact with the oceanic crust at hydrothermal vents with temperatures ranging from 100 °C to 400 °C via fissures and crevasses. The chemical constituents of the seawater involved in this serpentinization are water and carbon dioxide dissolved as bicarbonate ions, while the constituents of the Earth’s crust are ferrous ions contained in olivines. Accordingly, seismic data indicate that fluids can percolate to depths of 500 m below the seafloor, reaching temperatures of between 150 °C and 200 °C.

Under these conditions, the ferrous Fe^2⊕ ion in rocks is capable of reducing water to produce ferric ions in the form of magnetite Fe₃O₄ or goethite (FeOOH), with wastes as brucite Mg(OH)₂ and “serpentine”. It was, thus, estimated that one cubic meter of olivine could deliver around 500 moles of dihydrogen during serpentinization. Moreover, the vast majority of rocks making up the Earth’s oceanic crust consist of olivine or pyroxene, minerals which can also take part in the serpentinization reaction. This serpentinization reaction, therefore, most likely occurred as soon as there were oceans on Earth. Furthermore, it has been estimated that the total volume of the Earth’s oceans passes through its hydrothermal vents approximately every 100,000 years. So, the vast number of ferrous ions that make up the Earth’s electron reservoir for producing dihydrogen via serpentinization is in no danger of being depleted. Serpentinization delivers, and has always delivered, a non-negligible quantity of dihydrogen that can be used as a source of electrons for the primary production of organic matter in undersea ecosystems. With hydrothermal vents, we also know that serpentinization can geochemically reduce carbon dioxide into methane CH₄. This same geochemical process could, therefore, have perfectly fostered an energy metabolism based on chemical reactions involving carbon compounds and releasing large amounts of entropy as found in methanogenic or acetogenic bacteria. These reactions could also have been accelerated by cofactors and enzymes. Serpentinization can occur in both hot, acidic black smokers and colder, alkaline vents. These two types of hydrothermal vents could, therefore, have offered pH gradients that were quite similar to those present in Hadean oceans. The lower temperature in the vicinity of the vents could provide favorable conditions to support abiotic synthesis and the accumulation of reduced carbon compounds.

10.8. Basic Organic Chemistry

Hence, there is a possibility that the following molecules, crucial for all metabolism, appeared around 4 billion years ago (Figure 18): methane (CH₄), formaldehyde H₂CO (H₂C=:O:), hydrocyanic acid HCN (H-C≡N:), iso-cyanic acid HNCO (H-N:=C=:O:), acetylene C₂H₂ (H-C≡C-H), and hydroxy-cyanamide CH₂N₂O (H-:O:-:NH-C≡N:) from dihydrogen H₂, bicarbonate ions HCO₃^⊝, and dinitrogen N₂ (:N≡N:). Note that most of these reactions require the removal of one or more water molecules. For the same reasons as above, therefore, they cannot occur in water. But there is no problem here, as serpentine is a lamellar structure that can intercalate the hydrophilic chemical species between two sheets, thus isolating them from the surrounding aqueous medium. Of course, it is also possible to manufacture fatty acids according to the following balance sheet:

HCO₃^⊝ + n CO + (2n + 1) H₂ = C_nH_2n+1 CO₂^⊝ + (n + 1) H₂O

So, let us start with the possibility of making membranes from fatty acids. Such molecules are, in fact, ideal for forming an enormous variety of nanostructures via self-assembly reactions (Figure 18). Here, the fatty acid is characterized by its volume V, the area A swept by its carboxylate polar head, and the maximum length L of the fully stretched hydrocarbon chain [68]. Now, let R be the radius of the cavity in which the fatty acid will be solubilized in water. For a spherical cavity, we have a topological condition R = 3V/A ≤ L. It follows, then, that a criterion for having a spherical micelle is that the stacking parameter PP = V/(L·A) is such that PP ≤ ⅓. If PP > ⅓, the system will seek to reduce its curvature. So, for a cylinder, we will have a new criterion R = 2V/A ≤ L, i.e., PP ≤ ½. If PP > ½, the idea is to make closed spherical bilayers with a radius equal to twice the hydrocarbon chain length L, R = 3V/2A ≤ L, i.e., PP ≤ ⅔. If PP > ⅔, a new topology can, then, be a planar bilayer, such that R = V/A ≤ L i.e., PP ≤ 1. Finally, if PP > 1, the surface area of the polar head is too small to form bilayers, and inverted micellar structures are then obtained. Among all these topologies, evolution has retained spherical vesicle- or liposome-type bilayers, which partition water into compartments. On the one hand, there is the water inside the compartment, which will later become intracellular water. This first type of water is capable of rejecting the sodium ions Na^⊕ or calcium Ca^⊕⊕, as well as the chloride ion Cl^⊝ and the oxygen molecule O₂ outside it [70]. On the other hand, all living organisms persist in accumulating certain elements, essentially C, N, H, P, S, K, Mg, and Fe. The second type of water is water outside the compartment, which will later become extracellular water. The problem of the emergence of life, then, boils down to how metabolism, replicators, and enzymatic systems could develop, all attached to the same membrane system. In other words, without membranes and water, no life is possible…

11. The Prebiotic Soup

The complexity of the problem of the origin of life stems from the fact that the useful markers of biological evolution cannot be the traditional organic chemicals, such as DNA, RNA, proteins, or even complex metabolites. In fact, it is only the very small carbon molecules, CO₂ and CH₄, that can be called environmental markers. Alas, these molecules are not directly controllable by cells. Hence it is impossible to track their changes over the period of time stretching from 4.0 Gyr to the present day. One peculiarity is that CH₄, formed as a result of the reductive degradation of organic molecules, reacts very slowly with oxygen.

This leaves only molecules such as N₂, NH₃, O₂, and the soluble ions SO₄^2⊝ and H₂PO₄^⊝ as long-term markers, via the modification of their isotopic composition linked to any cellular evolution. As far as metal cations are concerned, we can particularly track changes in environmental availability and use of the ions Mg^2⊕, Ca^2⊕, Zn^2⊕, Mn^2⊕, Fe^2⊕, Co^⊕, Ni^⊕, and Cu^⊕ (Cu^2⊕) which are incorporated, mainly, into proteins.

11.1. Importance of Inorganic Ions

It is, therefore, time to recall the role of these species in a cell [67]. Figure 19 shows the structures of the main metalloproteins. First and foremost are the Na^⊕ and K^⊕ ions, which are systematically involved in the regulation of osmotic equilibrium. Indeed, all cells reject Na^⊕ (10⁻³ M), Cl^⊝ (10⁻³ M), and Ca^2⊕ (10⁻⁶ M) compared to seawater concentrations. Then comes magnesium Mg^2⊕, which is involved in the glycolytic pathway (enolase), in all kinases, in most syntheses, in all signaling (transcription factors), in DNA/RNA structures, and in light capture (chlorophylls). In fact, it appears that adenosine triphosphate (ATP) is always close to 10⁻³ M, very close to the concentration of free Mg^2⊕. It follows that MgATP should be the active agent in most reactions. This homeostasis also applies to mobile coenzymes such as NADH, and certainly to the cytoplasmic pH of cells. The concentration of free cytoplasmic Ca^2⊕ ions is always below 10⁻⁶ M, and there are no intracellular Ca^2⊕-binding proteins in early cells. Certain cellular gradients were, therefore, established early in life and included the use of proton gradients to drive many non-spontaneous activities. On the other hand, the Ca^2⊕ ion stabilizes the membrane and wall, and may be involved in certain signaling activities.

The ferrous ion Fe^2⊕, for its part, is involved in the reverse citric acid cycle, CO₂ incorporation, signaling transcription factors, the control of protein synthesis (deformylation), and light capture (hemes and ferredoxins). Manganese Mn^2⊕ is involved in the photolysis of water to release dioxygen O₂. The Ni^⊕ ion is found in the cofactor F430 of the enzyme methyl coenzyme M reductase (MCR), which is involved in the final stage of methanogenesis by archaea, as follows: CH₃-S-CoM + HS-CoB = CH₄ + CoM-S-S-CoB. The Co^⊕ ion, meanwhile, is found in cobalamin, an enzyme involved in the methyl radical metabolism -CH₃. Finally, the elements molybdenum (Mo) and tungsten (W) enable oxygen atom transfer at a low oxidation/reduction potential. Hence, there is a possibility of incorporating oxygen to obtain carboxylates from aldehydes, without using oxygen itself. Two ions, Zn^2⊕ and Cu^2⊕, have virtually no internal role. However, they are both excellent evolutionary markers, for, in the most primitive single-cell anaerobes, the unavailable oxygen and copper cannot be used. Hence, the absence of their protein partners. On the other hand, in unicellular aerobic prokaryotes, calcium and the proteins with which it associates are little or not at all utilized. However, calcium signaling is becoming increasingly important in unicellular eukaryotes, where new calcium-binding proteins are emerging. Finally, multicellular organisms use more Ca-, Zn-, Cu-, and Fe-based proteins and many elements outside the cell in controlled fluids, where new regulated proteins are emerging.

Anaerobic organism types are generally considered to be the most primitive organisms. As for the “material” side, all these cells, they have free concentrations of K^⊕ (10⁻¹ M), Mg^2⊕ (10⁻³ M), and Fe^2⊕ (10⁻⁷ M), and mainly use the ferrous ion Fe^2⊕ with some cobalt and nickel, but very little manganese and zinc, and, most probably, never any copper- or calcium-based ions in the intracellular environment.

11.2. Self-Replicating Molecules

On the “software” side, there is a possibility of obtaining purine and pyrimidine bases. For example, we know that hydrocyanic acid polymerization can lead to adenine (A): 5 HCN = C₅H₅N₅. If one molecule of HCN is replaced by one molecule of isocyanic acid HNCO, guanine (G) can be made as follows: 4 HCN + HNCO = C₅H₅N₅O. If acetylene is used in combination with isocyanic acid HNCO, uracyl (U) can be obtained as follows: C₂H₂ + 2 HNCO = C₄H₄N₂O₂. With hydroxy-cyanamide CH₂N₂O or formaldehyde H₂CO, the following molecules can be obtained:

• Cytosine C (DNA): C₂H₂ + CH₂N₂O + HCN = C₄H₅N₃O
• Thymine T (DNA): C₂H₂ + HNCO + HCN + H₂CO = C₅H₆N₂O₂
• Nicotinamide (NAD): 2 C₂H₂ + 2 HNCO + H₂ = C₆H₆N₂O + H₂O
• Isoalloxazine (FAD, FMN): 3 C₂H₂ + 4 HNCO = C₁₀H₆N₄O₂ + 2 H₂O

On a practical level, adenine and guanine, the two nitrogenous bases involved in RNA formation, can also be easily produced using an ice/hydrogen cyanide eutectic (H₂O/HCN) and sunlight. The ice/urea eutectic (H₂O/NH₂CONH₂), for its part, could produce pyrimidine, cytosine, and uracil, other key constituents of the RNA molecule. Via the bases (U, A, G, C, and T), it became possible to have the “software” function ensuring the replication of information, in addition to the “hardware” function of the metabolic type (NAD, FAD, and FMN). All this, of course, is in the morphogenic water that orchestrates all this ionic, molecular, and self-assembly chemistry in the background. All these more or less reduced molecules must be available in the vicinity of “hydrothermal” vents, due to the serpentinization reaction.

Thanks to serpentinization, planet Earth had an almost inexhaustible source of reduced hydrocarbon matter, unaffected by random lightning strikes or equally random meteorite bombardments. In order to develop, life was, thus, able to address the far more delicate issue of molecular replication. One of life’s obsessions will, of course, be to develop its capacity to store information and, above all, to stabilize it. Evolution will require us not to rely on water/gas or water/oil interfaces, which are far too labile. Indeed, while these interfaces are ideal for emerging from molecular chaos and managing the movement necessary for life, they do not ensure stability over four eons. As species evolve, we need to recognize the different entities we are dealing with. Hence, there is an imperative need to reproduce identically so that the information patiently acquired is not lost. With modern biology, we know that the final solution consists of a DNA/(RNA)/protein triplet, using nucleic acids of the RNA (ribonucleic acid) or DNA (deoxyribonucleic acid) type for genetic information on the one hand, and proteins for regulation and structural function on the other. This is where we come up against the chicken-and-egg problem. Since nucleic acid replication is dependent on protein enzymes, these same enzymes depend on the existence of nucleic acids in order to exist. This clearly means that, at the origin of life, another system predominated. But which of the following is capable of self-replication: nucleic acids or proteins? The answer here is quite clear—nucleic acids.

This leaves the problem of non-enzymatic nucleotide synthesis and non-enzymatic polymerization to form RNAs with random sequences. Another problem is the non-enzymatic copying and/or replication of RNA. Finally, there is the problem of the emergence, via natural selection, of a set of functional catalysts made of RNA. This is a set that is able to maintain exponential growth in a prebiotic environment. This hypothesis of an “RNA world” is, therefore, very promising, even if all the details are still a long way from being elucidated [71,72,73]. What seems certain, however, is that life could not have arisen within oceanic water masses. For, here, the level of dilution is such that it is highly unlikely that long polymeric chains of RNA or proteins could have formed. A more serious hypothesis, therefore, seems to be a combination of clay and water or the formation of a eutectic with ice so that the organic matter had a chance of polymerizing [74].

Indeed, the evaporation of acidic nucleotide solutions leads to complex mixtures containing very short oligonucleotides in which the 2′-5′ and 3′-5′ phosphodiester bonds are random. The presence of external activating agents such as montmorillonite, therefore, seems indispensable. Montmorillonite is a mineral composed of hydrated aluminum-magnesium silicate, with the formula (Na,Ca)_0.3(Al,Mg)₂Si₄O₁₀(OH)₂·nH₂O, belonging to the smectite group of the phyllosilicate family. It is also known as terre de Sommières. This aluminosilicate lamellar clay swells easily, enabling it to accommodate large molecules between its sheets so that it can catalyze the formation of phosphodiester bonds from previously activated ribonucleotides in this way. Montmorillonite is also capable of accelerating the conversion of fatty acid micelles into vesicles, and RNA adsorbed on this clay can be encapsulated in these vesicles.

The other hypothesis is the development of life in the vicinity of oceanic hydrothermal vents that could provide favorable conditions to support abiotic synthesis and the accumulation of reduced carbon compounds [75]. With regard to the prebiotic manufacturing of RNA, one problem has long been that the condensation of sugar (ribose) and nucleobase (purines and pyrimidines) does not work [72]. However, a recent paper was able to show how to avoid this sugar and base condensation step [76]. Therefore, it was possible to spontaneously assemble pyrimidine ribonucleotide monomers from molecules that are plausible on a purely prebiotic level. On the other hand, as there is still no credible prebiotic synthesis pathway for purine ribonucleotides, there is currently no convincing evidence for total prebiotic RNA synthesis on primitive Earth. On the one hand, yields are still far too low and, on the other, we always obtain racemic mixtures and not the biologically dominant D-nucleotide. Nevertheless, research continues apace, and, no doubt, a solution will eventually be found and published.

11.3. The RNA World

It is, therefore, clear that nucleic acid synthesis, duplication, and mutation are the driving forces of evolution. This is because, according to Watson and Crick [77], nucleic bases may be paired with the following schemes: A…T, A…U, and C…G. Hence, there is a property that a polynucleotide is capable of directing the synthesis of a complementary strand starting from mononucleotides or small oligonucleotides. Hence, it is hypothesized that RNA acted as a precursor to proteins and DNA, in the sense that it can act both as a catalyst (like protein enzymes) and as a vector for genetic information. In 1986, the idea was born of an autonomous organism made entirely of RNA and capable of carrying out all vital functions, such as catalysis, heredity, recombination, and evolution, thanks to this single molecule. This followed the discovery of catalytic RNA molecules, ribozymes, capable of carrying out enzymatic reactions [78,79].

The ribozymes found in living organisms today play a vital role, even if they are rather limited in the range of reactions they can catalyze. The best-known ribozyme is the ribosome [80], and it has now been demonstrated that peptide bond formation during protein synthesis is catalyzed by the RNA of the ribosome, without the direct intervention of the protein itself [81]. These same ribozymes also catalyze RNA splicing. RNA is, therefore, both a transporter of genetic information and an enzyme. The existence of ribozymes consisting of RNA has, thus, made plausible the existence of a primitive RNA world in which all enzymes were RNAs with no proteins [82]. Because the catalytic site that synthesizes proteins must have preceded the proteins themselves, ribosomes and, consequently, ribozymes must predate protein enzymes.

The existence of an RNA world greatly simplifies the problem of the origin of life on Earth, for it avoids asking questions about the origins of all the other molecular components found in a cell, because DNA and proteins are only consequences of processes of natural selection in a prebiotic soup full of ribozymes. However, this hypothesis casts an opaque veil between current biochemistry and prebiotic chemistry. In the context of the RNA world hypothesis, the problem of the origin of life on Earth begins with the question of non-enzymatic nucleotide synthesis. As far as sugars are concerned, we have the “Formose reaction”, in which formaldehyde is polymerized [83]. This is probably in the presence of inorganic catalysts based on lamellar magnesium and aluminum hydroxides according to the following balance: n H₂CO = HOCH₂-[CH(OH)]_n−2-CHO. Hence, this results in sugars (Figure 20) such as ribose (n = 5) or glucose (n = 6). This Formose reaction is of great interest, for it is the only example of a cyclic autocatalytic process taking place in an aqueous medium capable of converting a very simple substance, formaldehyde, into a mixture of complex molecules, most of which are important biochemical molecules.

11.4. The Fundamental Role of Phosphorylation

Another major concern for the emergence of life is that the phosphate ion is incorporated into all nucleotides and many lipids, as well as being a component of many metabolites. We are talking here about phosphorylation, a process that activates molecules and causes them to react with each other, something they would be reluctant to do were it not for the following crucial reaction:

∆ + R-OH + HO-P(O)X₂ ⇄ R-O-P(O)X₂ + H₂O

The interesting thing is that this type of reaction can occur in both directions, as indicated by the double arrow. However, esterification with water elimination is an endothermic process that absorbs heat (symbol ∆). Furthermore, such esterification generates one molecule of water, which requires an anhydrous medium for the reaction to take place, as it just impossible to eliminate water if you are already in water. On the other hand, the opposite reaction, hydrolysis, consumes water and spontaneously releases heat. As always, we find the water without which life would be impossible. Of course, it is impossible to carry out these reactions, which, nowadays, require proteins that did not exist on primitive Earth. Hence the phosphorylating bottleneck, as phosphorylation is absolutely essential to the formation of any complex biomolecule, and, at present, there is no known alternative. Moreover, in the sea, the phosphate ion cannot exceed around 10⁻⁶ M due to the presence of calcium ions. Cellular phosphate requirements can, therefore, only be met by excluding calcium from the intracellular medium and pumping phosphate into the cells, where the concentration of free calcium is greatly reduced.

One trick is, therefore, to use the hydrolysis of the pyrophosphate ion [P₂O₇]^4⊝, which is a spontaneous process. For, as we know, the Earth’s crust contains around 5 × 10¹³ kg of phosphate minerals [84], most of which are in the form of apatite Ca₅(PO₄)₃(X)₂, where X is a hydroxide ion OH^⊝ or a fluoride ion F^⊝. Upon heating, apatite generates pyrophosphate ions [P₂O₇]^4⊝ (PP) or more condensed polyphosphates (Poly-P). Hence, the name litho-phosphorylation is used to describe this inorganic phosphorylation, as opposed to catalytic phosphorylation, which requires enzymes and cells. It is, therefore, almost certain that the world of nucleic acids could not have existed in the primitive ocean, as, here, the enormous amount of water would lead to strong dilution and inhibit any esterification reaction. Instead, it could very well have developed in terrestrial saline polar pools subject to hydrothermal activity. This is because, on Earth, periodic freezing can form eutectics capable of significantly concentrating any prebiotic soup. Furthermore, a relatively cold frozen environment is more favorable for the stability of condensed nucleic acids and self-assembling membranes than a warm one. It follows that the first proto-cellular vesicles (hereinafter referred to as PCVs) were more likely to be psychrophilic (cold-loving) or mesophilic (lukewarm-loving) than thermophilic (warm-loving). So, at the end of this prebiotic soup phase, we expect to find in these pools two types of molecules destined for a great future. On the one hand, replicases, which are nucleotidyl-transferases catalyzing the following reaction: nucleoside triphosphate + RNA_n ⇌ PPi + RNA_n+1, where PPi designates one of the acid–base forms of the pyrophosphate ion. The other molecule was a non-specific kinase capable of transferring a phosphate ion from a polyP or PyroP to activate nucleotides or other molecules such as amino acids.

11.5. Biology Versus Artificial Intelligence (AI)

As we said earlier, before matter-based life, there was immaterial consciousness (information). Nowadays, artificial intelligence (AI) has infiltrated all areas of our daily lives. Here too, there is a clear distinction between hardware and software. Let us remember that hardware includes all the parts made of matter, whereas software refers to the components that enable us to process that intangible thing we call “information”. Figure 7 shows the main elements necessary for life, but also, thanks to the little icon of a cell phone, the elements that are mandatory for AI. The idea here is that, if such a dichotomy exists today with AI, it must also have been present at the very beginning with the first forms of life. Hence, there is a certain correspondence between computer science on the one hand and biology on the other. Of course, if you have the hardware but not the software, there is no life. All we have are physicochemical transformations subject to the laws of thermodynamics (abiotic metabolism). Conversely, if you have the software without the hardware, there is no life either. We just have “viruses” waiting for the hardware to arrive so they can replicate. This inability of viruses to be autonomous means that their metabolic function is more primitive than their replicative function.

RNA replication without the aid of an enzymatic protein is a major feature of the RNA world hypothesis. It seems likely, but not necessarily certain, that the synthesis of a complementary RNA from a preformed RNA template, without the intervention of an informational catalyst, played a role in bringing about an RNA world. Thus, if a polynucleotide is incubated at a sufficiently low temperature with an appropriate mixture of complementary mononucleotides or small oligonucleotides, double- or triple-helix complexes are obtained in most cases. The complexes are structurally similar to double- or triple-stranded nucleic acids, but with an interrupted chain. The problem is that both 3′-5′ and 2′-5′ linkages are usually obtained. Here too, sugar phosphorylation seems to favor the formation of 3′-5′ links to the detriment of 2′-5′ links. On the other hand, all prebiotic synthesis leads to ribonucleotides in the form of racemates. However, the L-enantiomers of activated nucleotides are highly effective inhibitors of any matrix synthesis involving D-enantiomers. Unfortunately, this is a major obstacle to any self-replication of polynucleotides using plausible prebiotic monomeric substrates.

For life to start, there must, therefore, have been a natural selection of a set of functional catalysts made of RNA that, taken together, were able to maintain exponential growth in a prebiotic environment. In evolutionary terms, we know that the large ribosomal subunit had only 20 proteins instead of 31 at the time when the bacterial kingdom began to diverge from the archaeal and eukaryotic kingdoms. The first ribosome was, therefore, very probably made entirely of RNA. On the other hand, eubacteria share only 20 proteins of the large ribosomal subunit with eukaryotes and archaea. This suggests that ribosomal proteins were late evolutionary additions. The peptidyl transferase center, 3–4 nm in size, is conserved in all three kingdoms of the tree of life, and contains no globular proteins, but only a large number of linear protein chains. This is very convincing evidence for the existence of a primitive RNA world.

Unfortunately, the invention of protein synthesis was the beginning of the decline of the RNA world. We now know that RNA is capable of catalyzing many reactions. We have even been able to develop a catalytic RNA which has most of the essential properties of RNA polymerase. When presented with a single-stranded RNA template as an RNA primer in a mixture of the four nucleotide triphosphates, the complementary strand of the template is obtained. At present, it is impossible to copy templates with more than 14 residues, although the in vitro copying of much longer RNAs is conceivable. However, the intractable problem of separating the double-stranded product of the copying reaction remains to be resolved before a second round of copying can be initiated.

We saw earlier that life as we know it today required the three following prerequisites: membranes to differentiate between inside and outside, genes to transmit any information acquired through natural selection, and a metabolism based on catalysts for non-spontaneous reactions such as phosphorylation. On a strictly molecular level, ribonucleic acids (RNAs) have the particularity of being able to combine two of the three prerequisites. By joining together in a double helix, they can perform the genetic function of replication. By remaining single-stranded and folding on themselves, they become catalysts at the origin of metabolism (Figure 20). On the other hand, these RNAs cannot play the role of membranes, the preserve of lipids alone. Hence, there is the idea that nucleic acids “invented” proteins by drawing on the intelligence and consciousness associated with lipid membranes. Consequently, some 3.9 billion years ago, a self-replicating RNA world may have emerged from a mixture of mud, ice, and various organic molecules.

11.6. Selfish Viruses and Kinases

However, this RNA-based world soon came up against the problem of the proliferation of selfish, self-replicating entities—viruses. Indeed, many viruses can reproduce without the intervention of lipids, whereas without lipids, a cell cannot reproduce. What enabled the emergence of cellular life from a viral world was, therefore, a symbiosis between nucleic acids, lipids and proteins. Of course, once lipids had invented proteins, viruses were able to use them to their advantage to build capsids to protect their RNA or DNA genetic material, thus becoming virions. Later, when cell membranes were well developed, some virions also found it useful to surround themselves with a lipid membrane, borrowed from cells, in order to better infect their target host cells. Thus, cells capable of autonomous reproduction and self-replicating viruses, the genetic parasites of cells, live side by side, for better or for worse. The best comes from horizontal gene transfer, ensuring a good genetic diversity. The worst is cell death through the hijacking and plundering of reproductive capacities.

If we liken the genetic reproduction system of a cell to a computer system, this is perfectly consistent with Gödel’s theorem, “No program that does not alter the operating system of a computer can detect all the programs that are capable of doing so”. In other words, viruses are inevitable, no matter what protection systems we devise against them. So, there is no point in fighting viruses, and we will just have to content ourselves with containing them to their role as genetic mixers.

As we know, it is the association of a long lipophilic tail covalently linked to a hydrophilic head that enables lipid membranes to form spontaneously by self-assembly, provided that they are in water. Two particularly interesting topologies are planar bilayers (membranes) and bilayer or multilayer vesicles (liposomes). Depending on the conditions of temperature, pressure, pH, and electrolyte concentration, these two topologies can interconvert into one another. As far as the RNA/membrane association is concerned, it is imperative that the RNAs are placed on the outside of the vesicles and not on the inside. This is to ensure competition for the external nutrient medium with other non-encapsulated RNAs. The first step towards the formation of a proto-organism is, therefore, to be able to attach RNAs to the outside of a membrane. The next step is to encapsulate this primitive vesicle, decorated on its outer surface, in another vesicle to ensure its protection. As evolution has taken place in the meantime, we will be thinking of equipping this outer envelope with pores to ensure and control the passage of food. At the same time, viral nucleic acids from the external environment will be prevented from using the patiently elaborated internal machinery for their own replication.

In those remote times, each sub-glacial saltwater pond could be the site of enormous genetic variability, which varied greatly from pond to pond. This biodiversity within sheets of clay was well protected from frost and, above all, from the intense ultraviolet radiation emitted by the sun, for there was no ozone layer to absorb this radiation, which could pass unhindered through the Earth’s atmosphere. Furthermore, thermally generated polyphosphates, tri-metaphosphates, and pyrophosphates could be periodically leached to colder areas, much to the delight of PCVs competing greedily for such a source of phosphorus.

In fact, we know that RNAs of at least 50 nucleotides can form spontaneously upon contact with clay or phosphate mineral surfaces. In particular, phosphate minerals can activate monomers, while clay, such as montmorillonite, catalyzes their condensation. A genetic code is, therefore, not yet required. All that is required is for the first enzyme to be a non-specific phosphotransferase capable of activating amino acids (proto-amino-acyl-tRNA synthetase) and indifferently adding nucleotides (replicase) or amino acids in the 3′ position. Under these conditions, a single, relatively short self-replicating polymer would suffice for life to begin. Indeed, in its double-stranded form, the self-replicating polymer can perform the function of a gene. In its single-stranded form, however, it or its complement become a “nucleozyme”, i.e., an accumulator providing the functions of replicase, proto-peptidyl transferase, proto-amino-acyl-tRNA synthetase, and also proto-tRNA due to self-complementarity. The replicase function, i.e., the addition of a nucleotide at the 3′ position, would be a process requiring the presence of a template or boss, whereas the addition of an amino acid at this same 3′ position would be totally free, requiring no template. The addition of the amino acid in the 3′ position would, thus, enable the nucleozymes to cling to the negatively charged clay and phosphate mineral surfaces via the positively charged amine function below pH9, instead subjecting them to the chaotic Brownian motion prevailing in the aqueous solution. This greatly favors the replicase function, considerably increasing the probability of encounters. Finally, given the non-specificity of the putative phosphotransferase function, these nucleozymes can also transfer phosphate ions directly from mineral polyphosphates to amino acids, nucleosides, or nucleotides in order to activate them, thus becoming polyphosphate kinases.

11.7. Birth of Proto-Amino-acyl-Transferases

On a molecular level, it turns out that the central part of a ribonucleotide is formed by a D-aldopentose. In other words, a sugar containing five carbon atoms, one aldehyde function -CHO, and four -OH groups. Hence the presence of three centers of chirality leading to the four following pairs of enantiomers: (D,L)-ribose, (D,L)-arabinose, (D,L)-xylose, and (D,L)-lyxose (Figure 21). For each of the four diastereoisomers, the carbon atom bearing the aldehyde function is numbered 1′, while the last carbon atom bearing the primary alcohol function is numbered 5′. During the cyclization of the sugar to form a pyranose ring, the alcohol function on carbon 4′ reacts with the aldehyde function on carbon 1′ to form the following hemiacetal function: RO-CH(OH)-R’, leading to an α-isomer if the OH function of the hemiacetal group is on the opposite side of the pyranose ring to the alcohol function 5′, or to a β-isomer if these two functions are on the same side of the pyranose ring. In the case of ribonucleotides, we have the D-β-ribopyranose isomer. The hemiacetal carbon atom 1′ is used to attach a purine base (adenine or guanine with nine carbon atoms, denoted 1–9) or a pyrimidine base (cytosine, thymine, or uracil with six carbon atoms, denoted 1–6), while the alcohol functions 5′ and 3′ are used to attach phosphate groups. The OH function on carbon 2′ remains unused in the ribonucleotides that form RNA, and is even replaced by a single hydrogen atom in the deoxyribonucleotides that form DNA. However, because their phosphate groups are attached to carbohydrates, nucleozymes are naturally excluded from the interior of lipid bilayers. This condemns them to eternal wandering on their polar surfaces, with no hope of binding.

It is precisely at this point that a decisive invention will take place, tipping the balance definitively in favor of protocells to the detriment of viruses. When a strand of DNA or RNA is synthesized, nucleotides are always condensed in the 5′ → 3′ direction for reading in the opposite 3′ → 5′ direction, because the template strand and the synthesized strand are always complementary and antiparallel. The great innovation of around 3.9 billion years ago was, therefore, to condense the 3′ alcohol function of the sugar with a polyphosphate-activated amino acid. This transformed the nucleozyme into a proto-amino-acyl-transferase, putting a stop to its growth. This birth of “runt” nucleozymes did not initially upset the ruthless world of nucleic acids, until one day, when one of these runts learned to condense its terminal amine function with the acid function of another amino acid. In doing so, it became a proto-peptidyl transferase. In short, this new catalyst was capable of creating a peptide bond between two amino acids. Of course, this was a real revolution compared with the transfer of a single amino acid to an RNA in the 3′ position via a proto-amino-acyl-transferase. Indeed, the cooperation between these two brothers, with the elder activating an amino acid and the younger welding it to a terminal amine position, will give this new type of nucleozyme a new capacity for growth. But this time, instead of making an RNA, we will have a hybrid molecule, with an RNA chain on one side (thesis) and a peptide chain on the other (antithesis) that can be lengthened at will (synthesis).

11.8. Birth of a Lipophilic Genetic Code

The nucleozymes concerned by this revolution are those with an amino acid in the 3′ terminal position authorizing the growth of a protein chain. They are, therefore, the direct ancestors of the large ribosomal subunits that possess the catalytic peptidyl transferase function. The basic idea is, once again, very simple. It has to do with the lipophilic nature of the interior of lipid bilayers, which spontaneously attract any sufficiently long hydrocarbon chain. Among the amino acids used by today’s cells, five appear to have a very marked lipophilic character, as follows: alanine (Ala), valine (Val), proline (Pro), leucine (Leu), and isoleucine (Ile). This is because their saturated side chains lack hydrophilic functions. Logically, these are also the amino acids each encoded by at least four different codons (N = G, A, C, or U) for alanine (GCN), valine (GUN), and proline (CCN), three codons AUPy/A for isoleucine (Py = pyrimidine base C or U), and no less than six codons for the highly lipophilic amino acid leucine (CUN and UUPu, Pu = purine base G or A). We can, therefore, assume that the original function of the large ribosomal subunit was not to make proteins. Rather, it was to add as many lipophilic residues as possible to the 3′ end of nucleozymes. This was to enable them to anchor themselves via this lipophilic tail in the lipid bilayers of abiotically synthesized vesicles. Such anchoring would enable these nucleozymes to still be itinerant, while, at the same time, providing them with a surface upon which to continue increasing their genetic diversity in two-dimensional encounters, rather than the three-dimensional encounters seen in solution.

Anchoring on the same membrane surface will also make it possible to move from a single ancestor with all functions to an entity made up of four specialized nucleozymes. Nucleozymes are encoded by four separate genes, paving the way for the independent optimization of each of the four following basic phosphotransferase activities: replicase, proto-amino-acyl-tRNA synthetase, proto-peptidyl transferase, and proto-tRNA. The first proto-tRNAs were probably helical hairpins with a three- or four-nucleotide terminal unmatched loop. This loop would later become the anticodon loop, with a marked preference for G and C bases over A and U bases. This applies to the first two codon positions. The third position is generally considered, on a purely semantic level, to be redundant. The coding itself probably started after the association of a new RNA acting as proto-mRNA to hold the proto-tRNA to the nucleozyme acting as peptidyl transferase. The specificity of the code could be minimal, simply selecting the most lipophilic amino acid possible from the pre-biotic soup. A precursor of the small ribosomal subunit rRNA was probably also selected at this time to stabilize the mRNA/tRNA assembly. The pairing between mRNA and small rRNA was most likely a very rudimentary initiation mechanism. It is likely that the first two amino acids to be encoded were valine and alanine, given their abundance in meteorites [72]. The strong conservation of the tRNA structure implies that, before becoming a true rRNA, the proto-tRNA already possessed 75 nucleotides folded into a cloverleaf shape, and that genes of a similar length could have encoded signal peptides with up to 25 amino acids. The emergence of the mixed nucleic acid-protein world can, therefore, be summarized in the following five stages:

• The appearance of a nucleozyme with a replicase function (R)
• The appearance of a nucleozyme with a polyphosphate kinase function (K)
• The appearance of a nucleozyme with a peptidyl-transferase (P) function, acting as a proto-grand-RNA capable of adding amino acids to the 3′ ends of R, K, and itself.
• The appearance of GC pair-rich duplicators acting as proto-tRNAs and preferentially binding to hydrophobic amino acids.
• The appearance of proto-mRNAs and proto-small rRNAs to help proto-tRNAs bind to proto-peptidyl transferase.

It follows that a rudimentary peptide synthesis directly capable of evolving into the current coding system could start with just four different genes, two encoding proto-rRNA, one proto-tRNA, and one proto-mRNA. If we add a gene encoding the replicase function and one the kinase function, we obtain a minimal PCV with six genes capable of evolving into a real cell later on.

At this stage of evolution, only the five most lipophilic amino acids were selected to form a hydrophobic tail capable of anchoring genes or nucleozymes to the outer surface of a lipid bilayer vesicle. This PCV would have used 11 of the 64 possible NYN codons to select these five lipophilic amino acids, using Y = U as the code for the most lipophilic amino acids (isoleucine, leucine, and valine) and Y = C for the less lipophilic amino acids (alanine and proline). So, let us see how to obtain such amino acids under prebiotic conditions. Let us start with the ten simplest amino acids requiring just one molecule of carbon dioxide and having no sulfur atoms, as follows:

n CO + CO₂ + q HCN + m H₂ + γ = C_n+q+1H_2(m−n)+qN_qO₂ + n H₂O

The only amino acid requiring no carbon monoxide (n = 0) is glycine (Gly) with q = 1 and m = 2. The six following amino acids require a single molecule of HCN (q = 1): alanine (Ala, n = 1, m = 4), proline (Pro, n = 3, m = 7), valine (Val, n = 3, m = 8), leucine and isoleucine (Leu, Ile, n = 4, m = 10), and phenylalanine (Phe, n = 7, m = 12). The two following amino acids require two molecules of HCN (q = 2): lysine (Lys, n = 3, m = 9) and tryptophan (Trp, n = 8, m = 13). Finally, a single amino acid requires three molecules of HCN (q = 3), as follows: histidine (His, n = 2, m = 5). We see that our five highly lipophilic amino acids are indeed there.

11.9. Mixed Lipophilic/Hydrophilic Genetic Code

The advantage of a code based solely on highly lipophilic amino acids is that it can tolerate many translation errors. This is without altering the main aim, which was to have a chain long enough to anchor itself in the lipid bilayer of any vesicle. Once the genetic code for the lipophilic residues had been fine-tuned, hydrophilic domains had to be added to the membrane surface very quickly. This was to enable the attachment of critical hydrophilic molecules such as polyphosphates. This led to the development of five new proto-tRNAs to select hydrophilic amino acids such as serine (UCN/AGPy), threonine (ACN), glycine (GGN), aspartic acid (GAPy), and glutamic acid (GAPu). We have already seen how to obtain glycine. For the other four amino acids, an additional molecule of carbon dioxide is logically required to obtain a second group of eight “oxidized” amino acids, as follows:

n CO + 2 CO₂ + q HCN + m H₂ + γ = C_n+q+2H_{2(m−n−k)+q}N_qO_4-k + (n + k) H₂O

The two amino acids that do not require carbon monoxide (n = 0, m = 4 and k = 1) are serine (Ser) with q = 1 and asparagine (Asn) with q = 2. We can also add arginine with n = 0, m = 7, k = 2, and q = 4. Then come the following three amino acids that require only a single molecule of CO (n = 1): aspartate (Asp with q = 1, m = 4, k = 0), threonine (Thr, q = 1, m = 6, k = 1), and glutamine (Gln, q = 2, m = 6, k = 1). Finally, the last two amino acids, as follows: glutamate (Glu, n = 2, q = 1, m = 6, k = 0) and tyrosine (Tyr, n = 6, q = 1, m = 12, k = 1). This leaves the two sulfur-containing amino acids, where their synthesis involves carbon oxysulfide COS (:O:=C=:S:) formed by reacting carbon dioxide with hydrogen sulfide H₂S, as follows: CO₂ + H₂S = COS + H₂O. Hence, the following balance, where COS replaces one molecule of CO:

(n−1) CO + CO₂ + COS + q HCN + m H₂ + γ = C _n+q+1H_2(m−n)+qN_qO₂S + n H₂O

So, with one molecule of HCN (q = 1), we obtain cysteine (Cys, n = 1, m = 4) and methionine (Met, n = 3, m = 8).

Thus, a proto-mRNA rich in CG codes on the 5′ side and rich in AU codes on the 3′ side could have encoded the synthesis of a lipophilic signal peptide possessing a hydrophilic tRNA-supporting surface domain. The fact that many glucokinases and several families of ATP-binding proteins have aspartic acid, glycine, and threonine as key amino acids supports this scenario. It was at this stage that the first proto-amino-acyl-tRNA synthetases appeared, capable of binding a specific amino acid to a tRNA with the appropriate anticodon, whereas, until now, it was the tRNA itself that took on this task (self-loading). By the means of a set of 10 proto-amino-acyl-tRNA synthetases using between 22 and 27 of the 64 codons available, a PCV would already be capable of encoding a wide variety of large enzymes or structural proteins capable of complex folding.

11.10. Ligase, Endonuclease, and Exonuclease

A PCV can, therefore, begin protein synthesis as soon as it has six replicative nucleic acids on the outer surface of its membrane. It is highly probable, however, that two additional genes encoding a ligase and an endonuclease had to be added relatively early in order to be able to manipulate the genes. The ligase enables a bond to be formed between the 5′-phosphate group of a nucleic acid segment and the 3′-OH group of the preceding segment on the same strand. Ligases are essential for linking the various replicating entities into a continuous chromosome, ensuring their unity in the event of any fragmentation of the lipid membrane. Ligases are also used to combat viruses attempting to parasitize the PCV.

Endonucleases, on the other hand, are indispensable for cutting nucleic acid into shorter fragments. Ribonuclease P (RNase P), for example, is an endonuclease present in all living cells, whose function is the maturation of transfer RNAs. Like the ribosome, it acts as a ribozyme capable of cleaving an RNA sequence on the 5′ side of tRNA precursors, releasing the 5′ extension and the monophosphate-matured 5′ tRNA. RNase P plus a second nucleozyme cleaving its tRNA adjacent to the 3′ end is, indeed, indispensable for cutting into functional genes a chromosome made up of mRNAs, rRNAs punctuated by tRNAs. However, the replication of a relatively long chromosome would pose problems for a nucleozyme. As a result, multigenic chromosomes could not evolve without the appearance of an RNA- or DNA-polymerase-type protein. Since primases perform little differentiation between ribo- and deoxy-ribonucleotides and require no complex machinery for initiation, there is a good chance that a primase was the first RNA- or DNA-polymerase protein. In fact, primase is capable of synthesizing an RNA primer de novo from a double strand of nucleic acids, unlike DNA polymerases, which are only capable of elongating an already partially double-stranded region by adding a nucleotide to an already present 3′ hydroxyl end. Thus, the primase enables the synthesis of short RNA segments, which are then used as primers by the replicative DNA polymerase. We can, therefore, remember that a chromosome can only evolve if a ligase, an RNase P, a second endonuclease, and a protein polymerase are available. It was at this stage that a clear distinction was made between replication and transcription. The invention of polymerases, peptidyl transferases, and amino-acyl-tRNA synthetases marked the end of the RNA world, which, in the end, was very brief [84].

It is worth noting that an exonuclease must also have been invented at this stage of evolution. This is an enzyme capable of cutting nucleic acids (DNA or RNA). The prefix “exo” specifies that this cut is made from one end, one nucleotide at a time, and in a 5′ to 3′ direction. This makes it possible to digest other replicators in an extremely dynamic and unforgiving world. Thanks to this dozen or so amino acids, the first enzymes were able to appear. Hence, this was a very primary metabolism, but sufficient to ensure the “material” part, not forgetting that there is also a purely “inorganic” part to this same metabolism. This includes sodium (Na), potassium (K), calcium (Ca), magnesium (Mg), iron (Fe), manganese (Mn), chlorine (Cl), and phosphorus (P). There are, of course, others, but as we are interested in origins, it is clear for these that their concentrations in intracellular water must have been closely maintained and regulated throughout evolution [85]. Here, it is rocks eroded by the water cycle that can provide these elements. Examples include dolomite (Ca_1−xMg_x)CO₃, hydroxyapatite Ca₅(PO₄)₃(OH), rhodochrosite (MnCO₃), pyrite (FeS₂), and rock salt (Na,K)Cl. Once dissolved in water, all these ions end up stored in the oceans.

11.11. Chirality and Solubility

Moreover, let us also recall the unique chirality of amino acids (all L-) and sugars (all D-) as a signature of life. This empirical fact has fascinated scientists and laymen alike since Pasteur’s first careful separation of enantiomorphs crystals of a tartrate salt in 1848 [86,87]. Recent studies investigating a plausible new prebiotic pathway to proteinogenic peptides have shown that the creation of a peptide bond favors the ligation of L-monomers with D-monomers. This finding seems problematic for the prebiotic emergence of homochiral L-peptides. However, it has, nevertheless, been shown that this heterochiral preference provides a mechanism for enantiomeric enrichment in homochiral chains [88,89]. Symmetry breaking, chiral amplification, and chirality transfer occur for all reactants and products in competitive multi-component reactions. Indeed, solubility considerations justify further chemical purification and increased chiral amplification. Experimental data and kinetic modeling support this plausible biotic mechanism for the emergence of homochiral biological polymers. The dipeptide- and pyridoxal-mediated kinetic resolution of racemic amino acids provides a plausible prebiotic route to proteinogenic amino acids enriched in L-type enantiomers. The kinetic resolution of racemic precursors, therefore, appears to be a general route to enantiomeric enrichment under prebiotic conditions. If, in the near future, this explanation of kinetic resolution proves to be wrong, there would still remain the explanation based on the influence of a powerful supernova explosion [90,91].

Finally, there is also the problem of the aggregation of organic polymers in water above a certain critical concentration. Fortunately, adenosine triphosphate (ATP) has been shown to possess the properties of a biological hydrotrope [92]. In other words, this molecule can both prevent the formation of protein aggregates and dissolve aggregates already formed. This chemical property manifests itself at physiological concentrations of between 5 and 10 mM. So, as well as being a source of phosphate for biological reactions at micro-molar concentrations, ATP at milli-molar concentrations could help to keep proteins in solution. This could explain, in part, why the ATP molecule is present at very high concentrations in living cells.

12. Photosynthesis and Expansion of the Genetic Code

We also know that there was originally no oxygen in the Earth’s primitive atmosphere. There was, however, a lot of hydrogen sulfide H₂S, as a result of numerous volcanic eruptions. Hence, the precipitation of certain metal cations with a strong affinity for sulfur, leading to the formation of highly water-insoluble sulfides. Therefore, there were very low concentrations of the following elements, in the following order [84]:

Cu < Zn < Ni < Co < Fe < Mn and Mo < W

This is why strict anaerobes today are still very low in Cu, Zn, and Mo compared to the elements Fe, Mn, and Mg, which were available at 10⁻⁶ M or thereabouts and were abundant in primitive cells.

12.1. Photosystem-II, Chlorophylls, and Carotenoids

Three billion years ago, life on Earth depended on organic molecules produced by lightning or geothermal sources, with the risk of rapid depletion. Once photosynthesis was discovered, life on Earth really took off. The idea was to combine carbon dioxide in the air with water to create carbohydrates. Today, photosynthesis is the foundation of life on Earth. Every living organism on Earth, with a few exotic exceptions, depends on this reaction.

Thanks to the combination of hardware metabolism and software replication, it has become possible to produce an enzyme called “photosystem-II” [93]. This enzyme is the first link in the photosynthesis chain. It is made up of a set of proteins (25–30 subunits) which absorb light energy via a set of membranes called the “thylakoid”, from the Greek thylakos, meaning “sack”. In the chloroplasts of green plants, this membrane network is organized into grana (granum in the singular). Light-absorbing proteins are located on the inner surface of the grana’s thylakoid membrane. To achieve their function, they use different molecules called “chlorophylls”, from the Greek khlôrós (“green”) and phúllon (“leaf”). The most common chromophore is chlorophyll-a, formed from a porphine molecule surrounding a magnesium ion, attached to a C₂₀ terpenoid alcohol, phytol (see Figure 22).

Porphine: 8 C₂H₂ + 3 HNCO + HCN = C₂₀H₁₄N₄ + 3 H₂O

Chlorophyll is a hydrophobic molecule that can be anchored to a lipid membrane. The five following reactions are required to produce chlorophyll-a:

• Proto-porphyrin-IX: 15 C₂H₂ + 4 HNCO = C₃₄H₃₄N₄O₄
• Mg-Proto-porphyrin-IX: C₃₄H₃₄N₄O₄ + Mg^⊕⊕ = C₃₄H₃₂MgN₄O₄ + 2 H^⊕
• Divinyl proto-chlorophillide “a”: C₃₄H₃₂MgN₄O₄ + CH₃OH = C₃₅H₃₄MgN₄O₄ + H₂O
• Monovinyl chlorophillide “a”: C₃₅H₃₄MgN₄O₄ + H₂O₂ = C₃₅H₃₄MgN₄O₅ + H₂O
• Phytol: 13 CH₄ + 7 CO = C₂₀H₄₀O + 6 H₂O
• Chlorophyll-a: C₃₅H₃₄MgN₄O₅ + C₂₀H₄₀O = C₅₅H₇₂MgN₄O₅ + H₂O

I have used chlorophyll-a as an example, because it is a universal molecule found in all species capable of photolysis of water (plants, algae, and cyanobacteria). This chlorophyll-a has the characteristic of strongly absorbing wavelengths of 460 nm and 664 nm. The advantage of decorating porphin with methyl groups -CH₃ (4 for chlorophyll-a) is that one can be oxidized to an aldehyde function (-CHO), as follows:

• Chlorophyllide-b or -f: C₃₅H₃₄N₄O₅ + O₂ = C₃₅H₃₂N₄O₆ + H₂O
• Chlorophyll-b or -f: C₃₅H₃₂N₄O₆ + C₂₀H₄₀O = C₅₅H₇₀MgN₄O₆ + H₂O
• Chlorophyllide-d: C₃₅H₃₄MgN₄O₅ + O₂ = C₃₄H₃₂MgN₄O₆ + H₂CO
• Chlorophyll-d: C₃₄H₃₂MgN₄O₆ + C₂₀H₄₀O = C₅₄H₇₀MgN₄O₆ + H₂O

As a result, for chlorophyll-b (plants and green algae), the molecule still absorbs at 460 nm, but the second absorption shifts from 664 nm to 647 nm. This gives it an olive-green color. It is also more soluble in aqueous media than chlorophyll-a, due to the presence of the carbonyl group. In terrestrial plants, chlorophyll-b is mainly found around photosystem II. In the case of chlorophyll-f, found in cyanobacteria, absorption at 460 nm disappears, while absorption at 664 nm doubles to 727 and 745 nm. For chlorophyll-d, also found in cyanobacteria, absorption at 460 nm splits at 401 and 405 nm, while absorption at 664 nm rises to 696 nm.

In addition to chlorophyll molecules, there are also carotenoids, which have a long chain of carbon–carbon double bonds, forming a set of highly colored molecules that also capture light, as follows:

• Lycopene (red): 16 C₂H₂ + 2 C₂H₄ + 4 CH₄ = C₄₀H₅₆
• Astaxanthin (pink): 14 C₂H₂ + 2 C₂H₄ + 4 CH₄ + 4 CO = C₄₀H₅₂O₄
• Lutein, canthaxanthin, zeaxanthin (yellow): 16 C₂H₂ + 6 CH₄ + 2 CO = C₄₀H₅₆O₂

After capturing light photons, chlorophylls or carotenoids transmit their energy to an active center, called the OEC, to split the water molecule into hydrogen ions, electrons, and oxygen as follows:

2 H₂O + γ = 4 H^⊕ + 4 e^⊖ + O₂↑

This gas then forms bubbles which, when they burst, release oxygen into the atmosphere. This reaction is the source of all the oxygen we breathe today. Hydrogen ions, meanwhile, are used to fuel the synthesis of a molecule of adenosine triphosphate or ATP (Mg₂P₃O₉) via the enzyme ATP-synthase, as follows:

MgHP₂O₆ (ADP) + MgHPO₄ (P_i) + 2 H^⊕(out) = Mg₂P₃O₉ (ATP) + H₂O + 2 H^⊕(in)

Electrons, in turn, are transmitted along a chain of electron-carrying proteins to reduce two molecules of plastoquinone (PQ) to plastoquinol (H₂PQ), as follows:

4 H^⊕ + 4 e^⊖ + 2 PQ = 2 H₂PQ

The core of photosystem-II, known as the OEC, is a cluster of four manganese ions Mn^2⊕ and one calcium ion Ca^2⊕ linked by a µ₂-oxo bridge, three µ₃-oxo bridges, and a µ₄-oxo bridge [94]. This is a cluster that seizes the two water molecules and removes four electrons from them. The binding site of the two water molecules is not known with certainty, but it is highly likely that the gateway is at the level of the calcium ion. This OEC is surrounded by histidines, aspartates, and glutamates, which hold it in place. Right next to the cluster is a key chlorophyll molecule that establishes a tyrosine bridge with the water-binding site. When it absorbs light, one of the electrons in this chlorophyll is excited to a higher energy. This excited electron then jumps down, through several other pigmented molecules, to a first plastoquinone A and finally to plastoquinone B. When it obtains enough electrons, this small quinone is released from the photosystem and delivers its electrons to the next link in the electron transfer chain. Following this electron loss, the upper half of the OEC is tasked with replacing it with a lower-energy electron from water. Therefore, it extracts an electron from the water and passes it on to the amino acid tyrosine, which then sends it to the chlorophyll, making it ready to absorb another photon.

Of course, the whole process would not be very efficient if plants had to wait for photons to reach that special chlorophyll in the reaction center. Fortunately, the energy of an electron excited by light is easily transferred thanks to the phenomenon of resonance between two molecules close enough together. This is why photosystems feature large antennae filled with light-absorbing molecules. This enables them to capture light and transfer the light energy captured to the interior of the OEC.

12.2. Photosystem-I, ATP, and NADPH

Let us now consider photosystem-I, the second reaction center used by cyanobacteria, algae, and plants [95]. It is located on the outer surface of the thylakoid membrane of the grana. It is a trimeric complex which forms a large disc embedded in the membrane, with large flat faces exposed above and below the membrane. Each of the three subunits of photosystem-I is a complex of a dozen proteins, which, together, support and position over a hundred cofactors. Some of these cofactors are shown in green (chlorophylls) and orange (carotenoids). They are exposed around the perimeter of the complex, while many others are buried within it. In contrast to photosystem-II, here, there is a higher concentration of chlorophyll-a than chlorophyll-b. In cyclic photophosphorylation, photosystem-I synthesizes ATP, and in non-cyclic photophosphorylation, it synthesizes NADPH. The heart of photosystem-I is an electron transfer chain (ETC), composed of chlorophyll (green), phylloquinone (orange), and three iron–sulfur clusters (yellow and red at the top) called “ferredoxins” [96]. Ferredoxins are electron transfer proteins containing one or more active sites consisting of two or four iron atoms linked together by sulfide bridges and bound to organic matter by four cysteine sulfhydryl groups. There is, therefore, no photolysis of water here.

The two chlorophyll molecules at the bottom catch the light first. In doing so, an electron is excited into a higher-energy state. Normally, this electron would quickly de-excite, giving off heat or releasing a new photon of a slightly lower energy. But before this can happen, the electron is transferred to the cofactor chain. At the top, the electron is transferred to a small ferredoxin protein, which then forwards it to the other stages of photosynthesis. At the bottom, the hole left by this stray electron is filled by an electron from another protein, plastocyanin. This plastocyanin is found in the cytochrome-b6f complex (Cyt-b6f), whose function is to accumulate protons in the thylakoid lumen during the transfer of high-potential electrons from photosystem-II to photosystem-I. The Cyt-b6f complex receives the plastoquinone produced by photosystem-II and sends it to copper-based plastocyanin (CuPC), which ensures electron transfer and proton accumulation as follows:

H₂PQ + 2 CuPC^2⊕ + 2 H^⊕ = PQ + 2 CuPC^⊕ + 4 H^⊕

Photosystem-I receives electrons from plastocyanin or cytochrome-b6f on the lumenal side of the thylakoid membrane and uses light energy to transfer them across the membrane to a ferredoxin on the stromal side. Note that it is normally more difficult to add an electron to ferredoxin than to plastocyanin. This is where photosystem-I uses the energy of light to force the electron from plastocyanin to ferredoxin. Figure 22 shows the photosystem-I cofactor chain when the protein is made transparent. These “antenna” molecules each absorb light and transfer the energy to their neighbors. Before long, all the energy is routed to the three reaction centers, where it is captured to create activated electrons. The central electron transfer pathway features chlorophyll, colored from green to yellow, associated with orange phylloquinone (vitamin K) molecules, and iron–sulfur clusters colored red and yellow. In the surrounding antenna, chlorophyll is colored in green, magnesium in turquoise, and beta-carotene in pink.

Thanks to these two major inventions, photosynthetic cells have unlimited access to two key metabolism molecules, ATP and NADPH. Indeed, if we forget the details, the following is the balance of the Calvin cycle represented in Figure 22:

3 Mg₂[C₅H₈O₁₁P₂] + 3 H₂O + 3 CO₂ = 6 Mg[C₃H₄O₇P]^⊖ + 6 H^⊕

6 Mg[C₃H₄O₇P]^⊖ + 6 Mg₂P₃O₉ + 6 H^⊕ = 6 Mg₂[C₃H₄O₁₀P₂] + 6 MgHP₂O₆

6 Mg₂[C₃H₄O₁₀P₂] + 6 Mg₂NADPH = 5 Mg[C₃H₅O₆P] + Mg[C₃H₅O₆P] + 6 Mg₂NADP^⊕ + 6 MgPO₄^⊖₂

5 Mg[C₃H₅O₆P] + 2 H₂O = 3 Mg[C₅H₉O₈P] + 2 MgHPO₄^⊖

3 Mg[C₅H₉O₈P] + 3 Mg₂P₃O₉ = 3 Mg₂[C₅H₈O₁₁P₂] + 3 MgHP₂O₆

Sum of the 5 above equations:

5 H₂O + 3 CO₂ + 9 Mg₂P₃O₉ + 6 Mg₂NADPH =

Mg[C₃H₅O₆P] + 9 MgHP₂O₆ + 6 Mg₂NADP^⊕ + 2 MgHPO₄ + 6 MgPO₄^⊖

Or: 5 H₂O + 3 CO₂ + 9 ATP + 6 NADPH = GAP + 9 ADP + 6 NADP^⊕ + 8 P_i

It is easy to see how ATP and NADPH molecules can be used to produce a molecule of glyceraldehyde-3-phosphate (GAP or G3P). GAP is an aldo-triose, an important metabolic intermediate in glycolysis and gluconeogenesis, as well as in tryptophan biosynthesis. For example, it enables the production of fructose diphosphate, which can then be used to manufacture glucose, sucrose, starch, and other carbohydrates (anabolism). Remember that anabolism is the set of non-spontaneous chemical reactions involving reduction (supply of electrons), leading to the formation of the body’s constituents from the simple elements of digestion. Catabolism, on the other hand, is the phase of metabolism during which relatively large, complex molecules are broken down, by oxidation, into smaller, simpler ones. On the catabolic side, GAP is also involved in a step of glycolysis to produce pyruvate.

The invention of photosynthesis explains the development of copper-hungry aerobic bacteria, which prefer molybdenum to tungsten. Indeed, the key enzymes that use copper as a cofactor in functional catalytic reactions are the following: cytochrome-c oxidase (mitochondrial respiratory chain); superoxide dismutase-1 (free radical eradication); lysyl oxidase (speed-limiting steps in the collagen and elastin cross-linking reaction); and tyrosinase (melanin formation). It took around 2 Gyr for the concentration of free oxygen in the atmosphere to increase significantly, let us say, up to 1% of current levels 500 million years ago [97]. The main species involved in this oxidation were, on the non-metal side, a powerfully reducing molecule such as H₂S and its derivative ion HS^⊝, which found themselves reduced to sulfate ions SO₄^2⊝. In the case of metallic species, it is the free Fe^2⊕ ferrous ions that will be oxidized to ferric Fe^3⊕ ions with a very low solubility (≈10⁻¹⁷ M). Hence, the precipitation of banded iron formations (BIF) in surface geological minerals, or of baryte BaSO₄.

Other chemical species that will disappear include the very low-solubility cuprous ion Cu^⊕, which will be replaced by the much better-solubility cupric ion Cu^2⊕ (≈10⁻¹⁰ M). The last two species are thiomolybdate and thiotungstate, which will be replaced by the oxo-anions MoO₄^2⊝ (≈10⁻⁷ M) and WO₄^2⊝ (≈10⁻⁹ M). Thus, the sea became very rich in molybdenum and vanadium at the start of ocean oxygenation, since, in the order of sulfide oxidation, vanadium comes before molybdenum. The other divalent species do not change in nature, but see their solubility increase, as follows: Zn^2⊕ (<10⁻⁸ M); Ni^2⊕ (<10⁻⁹ M); and Co^2⊕ (≈10⁻¹¹ M), except for manganese, Mn^2⊕ (≈10⁻⁹ M). The result of this oxidation is that seawater gained one pH unit from pH ≈ 7 ([H^⊕ ] ≈ 10⁻⁷ M) about 4 Gyr ago to pH ≈ 8 ([H^⊕ ] ≈ 10⁻⁸ M) 2 Gyr later.

12.3. Genotype and Chemotype Changes

Another problem was that life always needed hydrogen, which became very scarce in an oxidizing environment. Hence, the discovery that water could be a source of hydrogen, producing oxygen as a waste product. It was this rejection of oxygen, along with that of Na^⊕, Ca^2⊕, Cl^⊝ (and perhaps Mn^2⊕) ions, that created a very strong environmental pressure pushing in, chemically speaking, an ever-more oxidized direction. But for nascent life, oxygen’s first effect is that of a poison, through its partially reduced products such as superoxide O₂^•⊝ and peroxide in the form of hydrogen peroxide H₂O₂. Consequently, even before oxygen or these derivatives were used, a mechanism had to be developed to protect against these “reactive oxygen species” (ROS). Hence, the very early appearance, in anaerobes, of enzymes eliminating not only dioxygen O₂ via reduction by NADH, but also the superoxide ion or via iron- and manganese-based superoxide dismutases. Later in evolution, these three products will find a use thanks to the following universal ternary progression: Poison/Protective device/Use of the “poison”. Some prokaryotes even developed new metabolic pathways to utilize poisons derived from the “poison” oxygen. Hence, the exploitation of new non-metal states, such as SO₄^2⊝ or even NO₃^⊝, and the systematic use of newly available metals such as zinc and copper. New sub-classes of aerobic chemotypes have, thus, emerged, including sulfate-, nitrogen-, and nitrate-dependent bacteria. But there are also “siderophores” (from the Greek pherein and sideros meaning “to transport iron”). These are powerful Fe^3⊕-chelating agents, synthesized and secreted by micro-organisms in particular, to enable them to draw on the iron essential for their development. The result is increasingly complex organisms.

As a result, the first organisms were gradually confronted with an increasingly hostile environment. The Na^⊕, Cl^⊝, and Ca^2⊕ ions were still present in the sea, but became increasingly active as they lost access to C, N, S, Se, and Fe^2⊕. There was also a growing presence of oxygen and its non-metallic products, as well as a number of increasingly available transition metal ions. In chemical terms, we would say that the chemotype was changing, by analogy with genotype, which refers to individual species and the specific genes that define them. Animals with nerves found a whole new use for the Na^⊕ and Cl^⊝ in these fluids, requiring new proteins to pump these ions. All these characteristics could, of course, be attributed to new DNA sequences.

Nonmetals other than sulfur were also oxidized, in particular the original carbon monoxide CO, as well as nitric oxide NO or ammonia NH₃, which were replaced by carbon dioxide CO₂ and nitrate ions NO₃^⊝. From a genetic point of view, this phototrophic proto-cellular world that evolved between 3850 and 3500 Myr was based on a set of 20–30 genes [84]. It was during this phase that the genetic code was extended and completed, with the coding firstly of tyrosine (Tyr,) phenylalanine (Phe), cysteine (Cys), histidine (His), and aspargine (Asn). This was followed by glutamine (Gln), lysine (Lys), tryptophan (Trp), arginine (Arg), methionine (Met), and selenocysteine (Sec).

12.4. Prokaryotes and Eukaryotes

All in all, it took around 400 Myr to go from an inanimate prebiotic soup to a replicative PCV based on lipid membranes that was capable of internal metabolism. The next step was the appearance of the first cell, equipped with a double membrane and capable of autonomous movement. Three major inventions were responsible for this PCV → bacterial transition, which took place 3500 Myr ago. These were the invention of peptidoglycan, the synthesis of lipopolysaccharides or endotoxins, and the development of flagella. It would seem that a total of 2000 genes would be sufficient to encode such a bacterium [98]. For the sake of brevity, Figure 23 shows the chronology of the diversification of this extraordinarily varied bacterial world.

A major innovation in the evolution of the bacterial world was the replacement, some two billion years ago, of peptidoglycan by glycerol. This gave rise to a new class of cells known as “eukaryotes”. The increased flexibility of their outer membrane, due to the inclusion of cholesterol, enabled them to digest prokaryotes, obviating the need to synthesize the chemicals essential to both groups. This increasingly led to symbioses, in which the higher organism was a source of certain basic foods needed by the lower organism. The latter very often supplied the higher organism with more complex molecules, coenzymes, for example flavin, or molecules such as ammonia, which were difficult to produce from dinitrogen N₂.

As seen previously, prokaryotes were forced to create an abrupt Ca^2⊕ ion gradient ranging from around 10⁻³ M on the outside to less than 10⁻⁶ M on the inside. In eukaryotes, the Ca^2⊕ ion was allowed to reach 10⁻³ M in endoplasmic reticulum vesicles, but the same cytoplasm/environment gradient had to be maintained. These huge gradients are ideal for conversion and use in new signaling devices, particularly when coupled to internal cytoplasmic signaling, for example, by phosphates. This is how eukaryotic cells gain knowledge of changes in their external environment, advantageous or disadvantageous, through the opening of calcium entry channels in the cytoplasm.

Thus, a fascinating new chemical feature emerged with the eukaryotic revolution. Because of the rigidity of their cell wall, prokaryotes had a certain awareness of changes in their external environment, but this was very slow. Hence, their main response, also very slow, which was the mutation and development of their genes. In contrast, with their highly flexible cell membrane, eukaryotes could react very quickly to external events. The result was more or less reversible changes in form and metabolism, and very few changes in genes. This is representative of the eternal duality between hardware (metabolism) and software (genes). When hardware evolves very quickly, software changes very little. But as soon as the hardware stagnates, it is the software that becomes more refined.

At the enzymatic level, the eukaryotic revolution saw the development of Zn^2⊕-dependent transcription factors (zinc fingers), while, in order to combat the highly toxic reactive oxygen species, a new protective enzyme, superoxide dismutase based on copper and zinc appeared. The free zinc in cells is still slightly below 10⁻¹⁰ M, and free copper, meanwhile, has remained at around 10⁻¹⁵ M by necessity. This is in sharp contrast to the superoxide dismutases of prokaryotes, which are still largely based on iron or manganese. Eukaryotes have also come to depend on bacteria for the other elements as essential to life as carbon, namely nitrogen. Eukaryotes cannot obtain nitrogen from dinitrogen, and many are unable to denitrify nitrates. A large part of the new communication system for organic molecules is, therefore, linked to the increasing availability of two metal ions, zinc and copper. The lives of higher animals are totally dependent on plants for food and bacteria for digestion and coenzymes (vitamins), which means that animals lose several metabolic pathways.

At the same time, bacteria develop extra-vesicular compartments such as the thylakoid, which allows for the localized production of protons and, thus, a highly acidic environment with an internal pH locally below 5.0. This occurs while maintaining the pH of the cytoplasm slightly above 7.0. Similarly, the subsequent device for oxidative phosphorylation will replace the pH gradient with an external membrane potential. Another example of evolutionary adaptation is provided by the anammox bacterium, which oxidizes toxic ammonia with nitric oxide inside a separate vesicle. Then, another remarkable switch in the tree occurred 850 Ma ago.

12.5. Apparition of Archaea

Back in the 1970s, Carl Woese was working on a seemingly innocuous subject—finding a way to classify this richly diverse bacterial world. But, while this seemed an obvious task, it turned out that bacteria had, so far, resisted all attempts at classification. The traditional method of looking for differences in appearance, structure, or metabolism had failed miserably. All bacteria look and act very much alike, and this makes it very difficult to establish a chronology for their appearance. Big names in microbiology have thrown in the towel on this problem, but Woese had the following idea: to use the RNA of their ribosomes, because he knew that most ribosomal RNA mutations had catastrophic consequences for the offspring, who, therefore, sought to avoid these mutations at all costs. As a result, changes in ribosomal RNA occur very rarely. However, after several billion years of microbial life on Earth, such mutations do eventually occur, making this a molecule of great interest for understanding relationships that extend far back in time. Hence, a decade of painstaking work to sequence ribosomal RNA into small pieces and identify them. Then, something unexpected happened. A colleague named Ralph Wolf suggested that Woese use his method to study an unusual group of methane-producing bacteria. Although these bacteria form pasty clumps with a wide variety of shapes, their biochemistry and metabolism seemed very similar. However, when Woese studied the RNA sequences of these “methanogens”, they turned out not to be bacteria at all. In fact, they lacked the complete oligonucleotide sequences normally found in bacteria. Thinking that the samples had been contaminated, he studied new ones. But the result was confirmed, and Woese found that the methanogens were not bacteria, although morphologically speaking, they resembled bacteria. However, Woese was well aware that morphology meant nothing for bacteria, and that only their molecules could tell them apart. The molecules showed that methanogens resembled no other prokaryote or eukaryote. In short, they were a new kingdom, the “archaea”, forming a third branch of life [99].

After all this hard work, Woese had just discovered a new world of microbes, which, to our eyes, looked like bacteria. But, in fact, they were so unique, biochemically speaking, that they turned out to be closer to eukaryotes than to bacteria. Woese’s observations were, of course, greeted with great skepticism. In fact, archaea are ubiquitous in hydrothermal vents, salt lakes, ice, seawater, soil, and, of course, the human body. In many ways, archaea are more like eukaryotes than bacteria. In fact, eukaryotes are life forms that house their DNA packaged in nuclei. The eukaryote group includes just about every living thing except archaea and bacteria. Archaea possess RNA- and DNA-polymerases, enzymes that replicate DNA and RNA, but in a simpler version than that found in eukaryotes. Their single circular chromosome can have more than one origin for replication, like eukaryotes, in marked contrast to bacteria.

In fact, bacteria condense their DNA inside the cell to protect it, thanks to a protein called “Gyrase”, which winds up their DNA like a coil. Archaea do the same, but wind their DNA around proteins called histones. Again, these appear to be simplified versions of the histones employed by eukaryotes to perform this crucial task. Bacteria, on the other hand, do not possess histones. This obvious similarity between archaea and eukaryotes has led some to suggest the existence of a symbiosis between mitochondria and chloroplasts. But, in addition, other symbioses or an even more mysterious chimerism seems to have taken place between archaea and bacteria. This gave rise to the first proto-eukaryotic cell. This may, thus, mean that eukaryotes actually evolved from archaea, an idea that was to be hotly debated.

The outer membranes of archaea, on the other hand, are very different from anything else on Earth. Indeed, the membrane lipids of bacteria and eukaryotes have the same general structure. A phosphate group attached to a glycerol molecule forms the head of the lipid, while fatty chains form the tail. As in bacteria, the glycerol hydroxyl heads are linked to the fatty acid chains by ester bonds. Archaeal membrane lipids are very different from those of bacteria and eukaryotes (Figure 24). Archaea have tails made of branched isoprene-based units instead of fatty acids, and are 20-carbon phytanyl-type. These lipid tails can be branched in extremely complex ways or even incorporate cycles leading to very strange shapes that bacterial or eukaryotic membrane lipids can never adopt. Moreover, phytanyl tails are attached to glycerol using ether bonds, which are much more heat-resistant than ester bonds. Finally, their glycerol is of an opposite chirality to the glycerol of bacterial or eukaryotic lipid membranes.

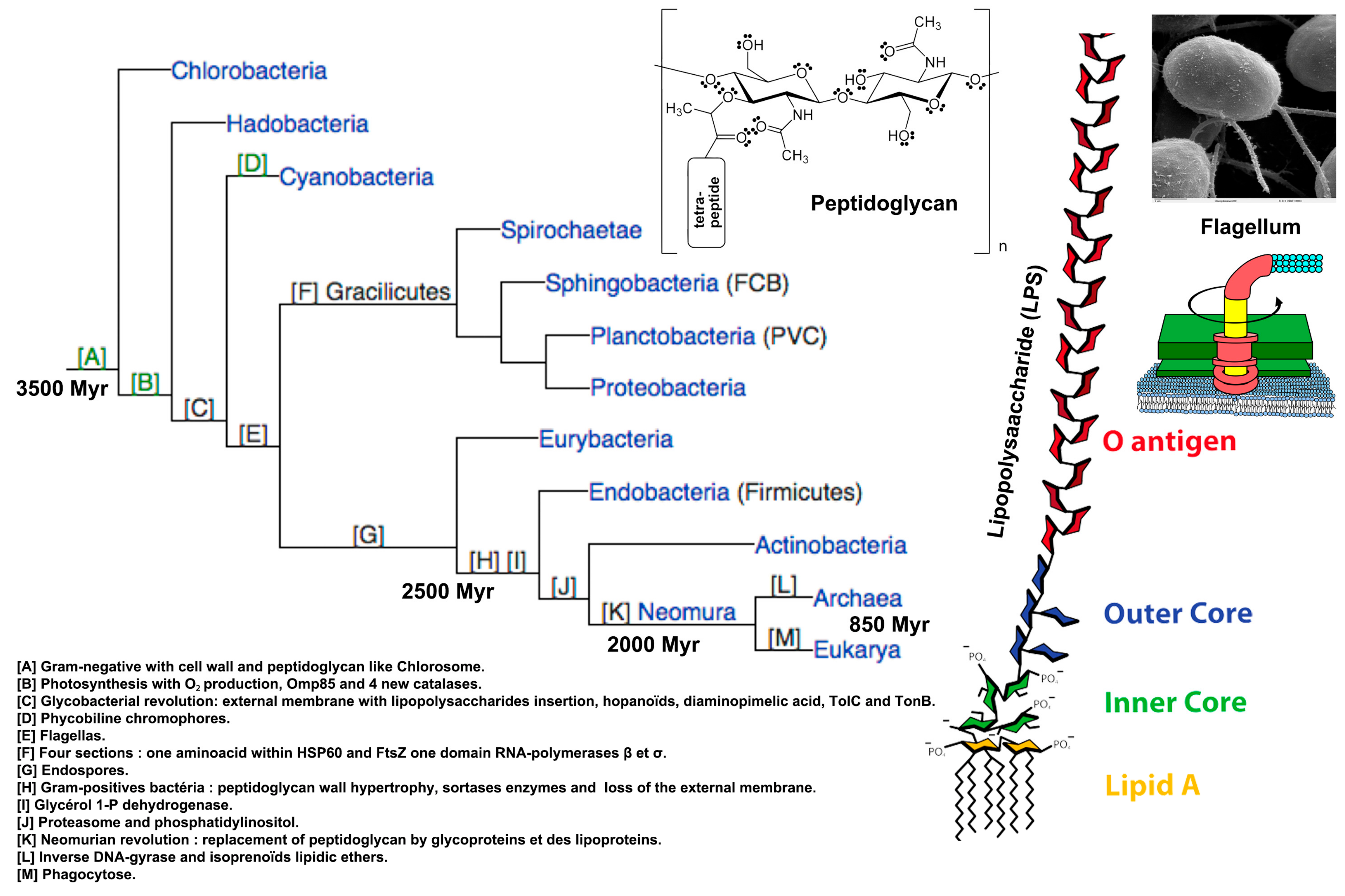
12.6. Bacteria, Eukaryotes, and Archaea

So, the fact that archaeal and bacterial enzymes use glycerol molecules with an opposite chirality implies that bacteria and archaea split up a very long time ago indeed. Some archaeal lipids also have a property that is rarely, if ever, encountered in eukaryotes or bacteria. Bacteria and eukaryotes have membranes made of lipid bilayers, where the upper lipids are independent of the lower ones. In contrast, archaeal phytanyl tails can be covalently linked to each other to form a lipid monolayer with two heads and a single body—a veritable membrane hydra. It is probably this feature that enables Archean lipid monolayers to withstand the scorching acidic infernos in which hyperthermophilic archaea manage to survive. Such is the case of Pyrolobus fumarii, the only known representative of the Pyrolobus genus belonging to the Crenarchaeota phylum, which can live and multiply at temperatures of up to 113 °C. Growth is impossible at temperatures below 90 °C. This facultative aerobic, chemolithoautotrophic species was first discovered in 1997 in the vicinity of a submarine hydrothermal vent on the Atlantic Ridge [100]. A microbe of the same family, Geogemma barosii, managed to survive and reproduce in an autoclave at 121 °C for 10 h, dying only when the temperature reached 130 °C [101,102]. Between 121 °C and 130 °C, it could not reproduce, but remained alive and resumed growth as soon as the temperature dropped. Before its discovery, no cell could survive 15 min at such temperatures. Experiments suggest that there may be archaea species that can tolerate temperatures of 140–150 °C. The ability to survive at 121 °C is crucial for medicine, as this is the temperature chosen to sterilize medical equipment. Fortunately, Geogemma barosii cannot survive at 37 °C, making it non-infectious. It uses dihydrogen H₂ as an electron donor and Fe(III) as an electron acceptor, reducing it to Fe(II) in the form of magnetite.

Contrary to our own genetic and protein machinery, our lipids resemble those of bacteria and not those of archaea, which could be an indication of very ancient chimerism. No archaea are known to be parasitic or pathogenic, but this is not to say that they do not exist. Archaea existed long before we discovered them, and today, we find that they really are everywhere. Bacteria and eukaryotes have developed myriads of pernicious parasites, and it seems very strange that an entire field of life should be devoid of them. Could the chemistry of archaea be so unique that they are ill-equipped to survive inside advanced organisms? This does not seem to be the case. So why is this the case? Is there something fundamental about their metabolism or chemistry? The Archean species most likely to act pathogenically as a parasite is Nanoarcheum equitans, the world’s second-smallest unicellular being (400 nm in diameter for a genome of 490,885 nucleotides) after Mycoplasma genitalium (200–300 nm in diameter). It was discovered in 2002 in a hydrothermal vent and grows at a temperature of 80 °C with a saline concentration of 2% [103]. It is found all over the world, in hydrothermal vents, in Yellowstone’s colored lake, in Iceland, and under the Arctic Ocean. Wherever it is found, it seems to live exclusively on the surface of larger archeans such as Ignicoccus, which can house up to ten N. equitans individuals on its lipid mantle. In fact, Nanoarcheum does not seem to be able to manufacture its own lipids, nucleotides, or amino acids—everything seems to come from Ignicoccus. On the other hand, N. equitans can repair its own DNA and manufacture its own DNA, RNA, and proteins.

This is not to say that archaea are free of parasites and pathogens. On the contrary, many archaea find themselves on the menu of other micro-organisms, or can be infested by a very broad spectrum of DNA viruses. When archaea were first discovered, they were considered to be strange and bizarre. They live in salt ponds, hydrothermal vents, burning acid lakes, and methane-infested swamps. So, they are not normal microbes. Square, flat archaea have been discovered that divide into sheets like postage stamps and live in real brines. They use proteins called bacterio-rhodopsin, which are structurally and functionally similar to the rhodopsin protein of the vertebrate eye, the one that enables energy to be generated from light. Other species of salt-loving archaea have a variety of polyhedral shapes that can even change shape between generations. But like most microbes, archaea are difficult to cultivate in the laboratory. When the search for archaeal DNA began, these microbes were found just about everywhere. This includes normal places like seawater and the ocean, ocean sediments, and soil, as well as the intestines or vaginas of mammals. Archaea can constitute up to 40% of the microbial biomass in the oceans, although bacteria are around three times more numerous and can constitute up to 20% of the total mass of terrestrial biomass. Despite their heat-loving reputation, archaea are also found in all the coldest spots on the planet, including Arctic seawater and ice. Much to our surprise, we found giant filamentous archaea so large they could be seen with the naked eye living on mangrove roots. We found methanogenic archaea that interact with protozoa in the intestines of cows and termites to help these organisms break down cellulose to recover energy. We have even found an archaeon living in symbiosis with a sponge.

At the molecular level, archaea differ quite markedly in their use of nickel, particularly at the level of the cofactor F430. Of particular interest are the four coenzymes linked to the porphyrin skeleton and to metal ions, as follows: heme (Fe), coenzyme B12 (Co), chlorophyll (Mg), and factor F430 (Ni). Indeed, these four components involving invariable metal ions act as if they were four new elements. Porphyrin may well have appeared before cells even existed. Note that the F430 (Ni) factor only appears in archaea that do not produce chlorophyll (Mg), which makes it possible to distinguish between sub-chemotypes. Another example of coenzyme development is that of the tungsten (W) and molybdenum (Mo) dithiolate complexes, where the (W) complex is present in archaea. Early on, molybdenum was precipitated in the form of its sulfide MoS₂. Similarly, the chemistry of nickel, cobalt, and tungsten hardly developed over the course of evolution, to such an extent that these elements disappeared from many higher organisms. Around 2 Gyr ago, the first truly complex single cells with multiple compartments appeared simultaneously in all lineages, from the first aerobic bacteria and archaea to plants (using light), fungi, and animals [98].

13. Frames of Consciousness

In this section, before concluding, we will take a step back, for our main proposition here is that we must not decorrelate the phenomenon of consciousness, which is essentially spiritual in nature, from that of biological evolution, which is materialistic in essence. This is particularly important, given that we have very recently been confronted with a major crisis in materialistic scientific medicine with the so-called COVID-19 crisis. This is not the place to discuss the sociological issues that led to such a crisis. What is clear, however, is that, during this crisis, the immaterial side of our ideas, rooted in quantum field physics (also known as the second quantization), and the spiritual side, linked to the notion of consciousness, were totally sidelined or even ignored. It is our conviction that this must not happen again. If we truly wish to evolve towards a more harmonious society that respects nature, whether this nature is expressed in bacterial, plant, animal, or human form, it becomes crucial to constantly refer to the triptych of consciousness, information, and water. Consequently, in parallel with this proposed overhaul of the origin of life, we might also consider the parallel evolution of human societies, and, by the same token, the evolution of so-called artistic practices. Among these artistic practices, there is one that deserves a closer look—medicine, or rather, the art of curing living beings from the moment they are declared “sick”.

13.1. Is Medicine a Science?

Here, too, we need to be realistic, and not blind ourselves to the facts. If medicine were truly scientific in nature, disease would not exist. Or, at least, it would be cured with a 100% success rate. In particular, we would not have all these medical studies demanding complete anonymity and double- or triple-blind procedures. If such precautions are necessary, it is because medicine does not hold all the cards. In addition, there is always the unanimously recognized phenomenon called the “placebo effect”. We are talking here, of course, about the therapeutic effect obtained through the administration of various substances and procedures that have no specific effect on the disease being treated [104,105,106]. If the placebo effect does exist, then medicine can only be an art, the art of healing, and not a science. The relevance of our formulation of the origin of life then becomes clear. If life is, indeed, produced by consciousness, then spontaneous healing becomes possible thanks to this universal consciousness, whether we call it “Tao” or “Ether”. Chinese medicine, Ayurveda, and other so-called “energetic” medicines can no longer be dismissed with a simple shrug of the shoulders.

13.2. Relationship between the Two Numbers Three and Seven

If we look at the problem of life from this angle, we can identify seven modes of thought [107], giving rise to seven major types of medicine. The first question that arises is why exactly seven, and not ten or fourteen? One reason is that the number seven appears in many remarkable natural phenomena. For example, during or after rain, a rainbow can appear, which is a breakdown of sunlight into the seven main following colors: red, orange, yellow, green, blue, indigo, and violet. At first glance, such a division may seem rather arbitrary, except that we owe it to the great British physicist Sir Isaac Newton (1643–1727 E.C.). Indeed, in his second major book on the physical sciences, Newton deals with optics and the refraction of light. In this work, Newton analyzes the fundamental nature of light, its diffraction, and the behavior of color mixtures. To clarify the subject, he proposes linking the fundamental rules of light to those of the musical scale, composed of seven notes [108]. For the color spectrum is, then, considered to be made up of just five colors, as follows: red, yellow, green, blue, and violet. In an attempt to reconcile music and science, he decided to add orange between red and yellow, and to separate violet into two colors, indigo and mauve. Hence, the seven colors of the rainbow, which are in perfect harmony with the seven notes of earthly music or the seven wandering stars in the sky, Sun, Moon, Mercury, Venus, Mars, Jupiter, and Saturn, noted since ancient times. It also resonates with the seven alchemical metals, gold, silver, quicksilver, copper, iron, tin, and lead, or the seven alchemical operations, Calcinatio, Solutio, Coagulatio, Sublimatio, Circulacio, Mortificatio, and Putrefactio. Moreover, if we refer to the Bible, Elohim creates the heavens and the Earth in six days, then rests and sanctifies on the seventh (Genesis 1–2:4). There is also the New Testament and its apocalypse. Here, the seventh trumpet announces the resurrection of the dead and the Last Judgment. Then, come the seven plagues, which correspond to the seven vials of divine wrath poured out by the seven angels into the world. In the ancestral traditions of India, as we saw above, the Vedic scriptures and yogic practices have, for millennia, described seven chakras or seven wheels of life influencing our physical and spiritual existence. Finally, in Chinese culture, the number seven is synonymous with neutrality, with both positive and negative aspects. Thus, seven is written as (七—qī) and pronounced similarly to the words 起 (qǐ—to rise, to begin) and 气 (qì—vital energy). It is, therefore, considered to be a lucky number for relationships. But it is also sometimes seen as an ominous sign, because the seventh month is “the month of ghosts”. During this period, tradition dictates that the spirits held in the underworld are released… Hence, ultimately, a neutral thing.

All this means that the number seven seems to be the link between the subtle spiritual world and the physical, material world. This is why, in 2020, I proposed to distinguish seven frames of thought [6,107]. The starting point is that what matter and spirit have in common is the use of whole numbers to express themselves. Matter, quantitatively, as a sum of units via quantum physics, and mind, more qualitatively, as a division of a single unit (philosophy). On the philosophical side, we have the number zero, which, for our Ancients, symbolized the entire universe in its unmanifested, latent, potential, and invisible state. The symbol of the ouroboros, the snake biting its own tail, is a perfect illustration of this. However, another number, one, could also play this role. However, it described a manifest, real, and visible state of this same universe. Here, the snake has stopped biting its own tail, and can unfold as a ripple that has no beginning and no end. In short, we have a unit, the one, and thus, an essence for everything that follows. The number two, on the other hand, was the number of discriminations. In other words, a manifestation of polarity, allowing us to differentiate between the head and tail of the cosmic serpent. This polarity is, of course, a source of instability, of perpetual oscillation between right and left. In short, as soon as two appears, nothing can ever be the same again. The virtual (0) and the real (1) interpenetrate deeply.

Hence, the need to seek a compromise expressed by the number three, which is the production number of all tangible and stable things. The Egyptians engraved it in stone in the form of a triangle (pyramids), while the Greeks founded philosophy on the notions of thesis, antithesis, and synthesis. It is said, “Never 2 without 3”? The triangle is, in fact, the first creator of regular three-dimensional solid shapes such as the tetrahedron, octahedron, and icosahedron. It is at this level that an eminently remarkable geometric construction based precisely on the number three comes into play. The idea is to consider its first three powers, as follows: 3⁰ = 1, 3¹ = 3, and 3² = 9, and to draw three concentric circles (A, B, and C). Here, the second (B) should have a diameter three times that of the first (A). As for the third (C), its diameter will, again, be triple that of the second (B). Then, starting at any point on circle C, a tangent can be traced to the small inner circle A, extending it until reaching the middle circle B (Figure 25). At this point, a new tangent can be traced to circle A, which takes us back to another point on circle C. We then repeat the same operation from this new point, seven times. Remarkably, by the seventh time, we are right back where we started.

13.3. The First Five Frames of Thought

The result is a double seven-pointed star (Figure 25). All we need to do now is associate each outer branch of this star with a specific way of thinking, and a medical technique associated with it. For example, the most primitive way of thinking is shamanism, which can be summed up by the phrase “All is Spirit”. Within this framework, the treatment method is similar to the various shamanic trance techniques.

The second frame of thought appeals to materialism, with its apothegm “All is Matter”. The emphasis here is on everything that is concrete and visible. In other words, everything that can be seen, heard, touched, smelled, or tasted. Herbal medicine (phytotherapy) fits in perfectly with this way of thinking about the world. The various pharmacopoeias of China, Ayurveda, Africa, Europe, the Caribbean, and Polynesia validate this way of healing.

The third frame of thought is determinism. This framework is linked to the idea that nothing happens by chance and can always be understood through logical, coherent reasoning. Here, natural events are subject to a set of mathematical equations that allow us to predict, with certainty, what will happen given a given set of initial conditions. We recognize here the framework of scientific thought developed from the 17th^e century onwards, mainly in Europe, with its apothegm, “Everything is equation”. This is a framework that presupposes that, alongside matter, there can also be light. This is the framework of modern science, and its so-called “allopathic” medicine, in which disease is fought using drugs that have an effect opposite to the pathological phenomena. Here, the remedy can be natural or synthetic, i.e., manufactured through the ingenuity of the human mind, whatever the case may be. The only problem was that, at the beginning of the twentieth century, this deterministic framework of thought proved totally inadequate to describe phenomena on the scale of a billionth of a meter (nanometer).

Hence, the birth of the fourth frame of thinking, probabilism, in which the deterministic equations of the macroscopic world are replaced by probabilistic equations of the microscopic world derived from quantum physics. Here, the apothegm “Everything is vibration” reigns, meaning that reality is described either in terms of “corpuscles” or “wave functions”. In other words, there is a wave–corpuscle duality, and because of such duality, it is impossible to predict everything with certainty, as in frame #3. Hence, of course, new treatment techniques that take this wave aspect into account, and the name “quantum therapies”. It is, at this point, that the scientific community splits into two distinct groups. The first group validates the idea that the quantum revolution of the 1930s should be taken into account in medicine. However, this should only apply to medical techniques for diagnosing disease, such as X-rays, positron emission tomography (PET-Scan), or magnetic resonance imaging (MRI). In surgery, this includes the use of coherent light lasers to cut tissue, vaporize thrombi in arteries, or detect cancerous tumors, etc. On the other hand, this first group categorically refuses to admit that probability waves can be used for treatment [109]. A second group, on the other hand, admits this possibility and relies on machines that aim to harmonize or balance the energy flow of body and mind. Here, the line is relatively blurred between devices using waves of an electromagnetic nature and devices with no active electronic components. Hence, the skepticism of the first group, who prefer to stick to the fact that quantum laws only apply to atoms and molecules, and certainly not to other bodies operating on a macroscopic scale.

But before we say anything more about this heated debate between conventional and quantum medicine, let us note that this fourth probabilistic framework is based entirely on a physics of first quantization, illustrated by the concept of wave–corpuscle duality. From the foregoing, we know that there is a fifth frame of thought in which matter is considered not to exist in its own right, being merely a very-high-frequency vibration of a relativistic ether. Hence, the name immaterialism, which is based on quantum field theory and the maxim “all is coherence”. Here, there are no more waves or corpuscles, only “quantum fields”, which, depending on experimental conditions, can create particles or waves at will in a four-dimensional space–time, from a quantum vacuum that is the ultimate source of all reality. In this paper, we propose to link homeopathic medicine, which uses more or less diluted aqueous solutions, to this fifth frame of thought, but also all the so-called “energetic” medicines where the physical body is subjected to energetic exercises, such as Yoga or Qi Gong, Tui Na massage, or acupuncture. It would be madness to deny that these often ancient “holistic” techniques are ineffective. On the other hand, allowing them to have their own framework of thought, with its clear apothegm rooted in modern physics, can only be beneficial to all.

13.4. Music and the Sixth Frame of Thought

It should be noted that a very large majority of physicists believe that this fifth framework is sufficient to describe all physical reality. However, a small minority, including myself, believe that this framework also has its limitations, as it does not take into account symmetry operations of the “dilation” type, which imply that the object under study remains invariant through a change of scale (vide supra). It is at this sixth level that new so-called “scaling waves” come into play, enabling the same physical system to recognize itself at different scales of size and duration [110]. For this sixth frame of thought, we would have a new apothegm, “All is harmony”. The associated treatment method would be the use of music (music therapy), hence, the name “musicalism”, for, here too, it is imperative to find a place for all agricultural techniques using music to minimize viral or bacterial attacks on plants. If these musical techniques do indeed work for plants [111,112], there is no reason why they should not also apply to animals and human beings.

It is in this sixth frame of thought that we can consider water as being capable of providing a sound reference or tuning fork. Indeed, in the fifth dimension of the universe, masses must synchronize on a musical scale, as energy can be expressed in two different and intrinsically equivalent ways. On the one hand, any mass m can be considered as energy according to the relation E = m·c², where c = 299,792,458 m·s⁻¹ is the propagation speed of light in a vacuum. On the other hand, according to quantum physics, any energy can be considered as a frequency f, according to the relation E = h × f, where h = 6.62607015 × 10⁻³⁴ J-s represents Planck’s quantum of action. Assuming that the same energy E is involved in both cases, it follows that m × c² = h × f. This means that any mass m can be associated with a characteristic frequency f, and vice versa. However, for molecules, mass is usually expressed in Daltons (Da = g-mol⁻¹), which means we need to go through Avogadro’s constant, N_A = 6.02214076 × 10²³ mol⁻¹, to obtain a mass m expressed in kilograms (kg). Hence, the following fundamental relationship:

f/Hz = k_MF × M(/Da), with k_MF = c²/(1000 × N_A × h) = 2.25234272 × 10²⁴ (Hz·Da⁻¹).

So, for a water molecule of mass m = 18.01528 Da, we rigorously calculate a quantum frequency f = 4.0577 × 10²⁵ Hz. This is where the notion of scale invariance comes into play, coupling the world of the infinitely small to our macroscopic scale. In music, this invariance of scale is expressed by the principle of octave identity, recognized since Antiquity. At the frequency level, this principle corresponds to division or multiplication by a factor of two. As the quantum frequencies of molecules are really very high, the most convenient way is to use the base-2 logarithm function, noted log₂, which allows us to write the following: f₀/2⁷⁶ (Hz) = 2.980951 × (m/Da). Then, as m[H₂O] = 18.01528 Da, there comes f₀(H₂O) = 53.70267 Hz. Since this frequency is too low to correspond to an A4 tuning fork, we simply raise it by three octaves to obtain a value of 429.62 Hz known as the “water tuning fork”. This gives a value close to the average, 430.5 Hz, between the lowest (404 Hz) and highest (457 Hz) pitches used in Western music [113]. Of course, this kind of calculation can be performed for any chemical molecule. Hence, the possibility of transforming any substance whose chemical composition is known into a sequence of musical notes. Then, from these notes, it is possible to derive a mode to create a totally harmonized accompaniment according to musical laws. A collection of musical pieces, all tuned to the tuning fork of water, is now available for free download from the Internet [114].

13.5. Information and the Seventh Frame of Thought

Finally, the seventh and last framework of thought will be symbolism, in order to account for the capacity of consciousness to manipulate information and give it meaning [29]. This framework is, of course, the most general, since its apothegm is “Everything is information”. As we have seen, this information can be stored both in the ether and in the coherence domains that can appear when water undergoes virtual excitations from this same ether. This framework has everything it takes to support a final form of healing, which consists, when faced with an illness, in persuading oneself that it is possible to cure via any substance or technique, or even by the sheer force of thought. This is the placebo effect, which obliges adherents to the third frame of thought to carry out randomized, double-blind studies to validate the therapeutic effect of a medicinal substance. Thus, the placebo effect completes the panoply of medical techniques that can be used to overcome all kinds of illnesses.

The point of Figure 25 is to provide a sound, practical basis for any kind of medical practice. This is crucial, insofar as, in the field of medicine, it is often difficult to distinguish between a genuine desire to heal and a desire to make substantial profits. After all, a person in poor health will have an innate and spontaneous tendency to undergo whatever it takes to get better. Hence, the possible abuse of therapists in providing expensive treatments of a dubious efficacy. In fact, this rather perverse aspect of medicine and pharmacy was long thought to be non-existent, or merely the ravings of publicity-hungry minds. However, since the COVID-19 crisis, it has become clear that science and medical research are not always beyond reproach, as demonstrated by the “Lancetgate” affair [115].

Prior to this major crisis in medicine, it was, of course, the questioning of the efficacy of homeopathy, a medicine proposed by Samuel Hahnemann as early as 1796, that attracted all the attention. Yet, prestigious researchers such as Jacques Benvéniste and the 2008 Nobel Prize winner for Medicine, Luc Montagnier, have carried out highly advanced and sophisticated fundamental scientific research. On the basis of their duly published findings, homeopathic treatment consists of using only the information contained in any remedy, instead of the material itself. Of course, if such therapeutic information is stripped of its natural support, the molecule, it must be transferred to another medium, and that other medium is water or sugar. Provided that we place ourselves within the framework of so-called second quantization quantum field physics, where matter is perceived as a vibration of the ether, there is nothing extraordinary about this transfer between a dissolved molecule and the solvent that takes it in. The physics of coherence domains [37,38] provides a solid and indisputable scientific basis for this phenomenon. Paradoxically, equally “immaterial” practices such as acupuncture, Qi Gong, and yoga have not come under the same attack as homeopathy. So, it is time to make medical debates less dogmatic and more dispassionate.

14. Conclusions

We have come to the end of this little journey from the Big Bang to the advent of the Internet, with the following order:

Big Bang → Light → Hydrogen → Stars → Atoms → Water → Planets → Metabolism → Lipids → RNA → Viruses → Ribozyme → Proteins → Bacteria, Archaea → Eukaryotes → Sex → Plants → Animals → Humans → Computers → Internet.

What sets this paper apart from others on the same subject is that it gives pride of place to the notion of consciousness. This immaterial consciousness pre-exists matter and drives it via a substance with extraordinary properties—water. In this process, we encountered and discussed the philosophical foundations of all the great human civilizations. From this, we have drawn the following universal ternary recipe: thesis–antithesis–synthesis, for evolving while maintaining efficiency and stability. Water, with its formula H₂O, is an excellent illustration of this highly creative trinity. For example, seeing O as the basic antithesis of the acidity provided by H, or seeing O as the oxidizing antithesis of the reduction provided by H, not to mention the electronegativity associated with O, the antithesis of the electropositivity associated with H. Hence, the ability to solvate both anionic and cationic species and to form micelles with non-polar solutes. The water molecule is, thus, a synthesis of the greatest likelihood of bringing about that priceless thing we call life.

However, there is more to water, the substance that makes up the vast majority of living cells, for it is also an association between an oxygen atom and two non-atoms of hydrogen. The fact that hydrogen is not an atom, but an association between three quarks (proton) and a lepton (electron), means that, to understand water, we have to deal with the physics of second quantization, a physics where the wave or the corpuscle have no tangible reality, since here, only the quantum vacuum or ether exists, the generator or annihilator of all things. In short, throughout this article, I have tried to reframe biology in its most fundamental terms—consciousness and water. Hence, the possible unification of age-old medical practices that have largely proved their worth, such as shamanic trance, phytotherapy, allopathy, classical or quantum electro-magnetotherapy, homeopathy, music therapy, and even placebo therapy. In other words, no single medicine can claim to hold the secret to good health and longevity. This article calls for a reconciliation between all therapists, whatever their country of origin or philosophical convictions.

Another original feature of this paper is the care taken to ensure that not only are the “bonding” electrons (chemical bonds) always shown alongside the atoms, but so are the “non-bonding” doublets generally overlooked in most biology treatises. Similarly, for formulas involving phosphorus, the crucial element without which there can be no life, we have systematically used the strict octet rule with its formal charges. This is because quantum chemical methods have confirmed that the single bonds between elements in the first row are weak, while multiple bonds are strong [116]. For elements in the second or higher row, however, the opposite is true. Here, single bonds are strong, while multiple bonds are weak. The “extended valence” (violation of the octet rule) observed in the compounds of the elements of the top main group has little to do with the availability of d-orbitals, but is rather due to the size of these atoms and, thus, to the reduced steric hindrance between ligands and, to a lesser extent, to the lower electronegativity of heavy atoms. Here, a model based on the concept of electron-rich multicentric bonds is certainly closer to reality than one involving hybrid orbitals with the participation of d-orbitals. XO bonds in phosphane oxides, sulfoxides, and related compounds are best formulated as semi-polar bonds rather than true double bonds. Hence, the absence of any P=O double bonds in this article, and, by implication, the clear highlighting of the electron richness of the P-O bond, which implies the possibility of a strong multicentric resonance on the tetrahedral PO₄ entity. After all, reasoning with false schemes that are unrepresentative of chemical reality is unhealthy, and can only lead to errors in subsequent analysis. See Appendix A for further details and examples.

This article also opens up the possibility of seeing the water molecule not only as an essential biological reference, but also as a fascinating musical one. Indeed, any conversion of musical notes into sound frequencies calls for a universal tuning fork of 440 Hz. However, there is nothing in physics to justify such a value. On the other hand, it is relatively easy to transform the average isotopic mass of a water molecule into a sound frequency of 429.62 Hz, according to the laws of physics. This article, therefore, strongly urges all composers and musicians to adopt this new musical reference value in place of the purely commercial 440 Hz. Those who have already conducted this have confirmed that this water pitch provides a much deeper musical experience than the standard 440 Hz pitch. Of course, this is only a suggestion, and is unlikely to be proven. For that, we would need to have enough statistical data to see exactly what is going on. So, it is still too early to draw any definitive conclusions, but in the meantime, there is nothing to stop you trying.