Simulation and Evaluation of Runoff in Tributary of Weihe River Basin in Western China
Abstract
:1. Introduction
2. Regional Overview and Model Establishment
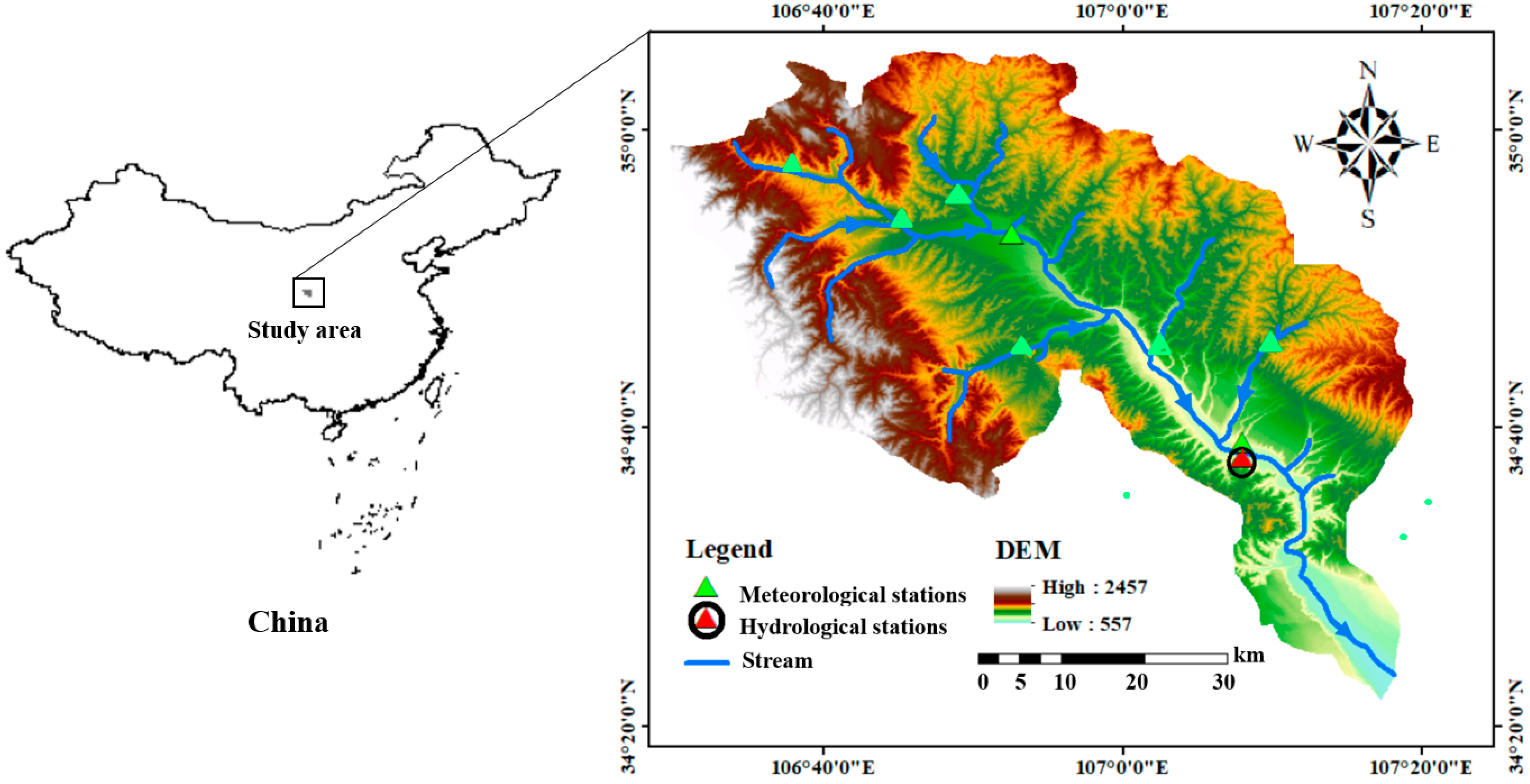
2.1. Regional Overview
2.2. SWAT Model Construction
2.3. Database and Hydrological Response Unit
2.4. Parameter Sensitivity Evaluation
3. Results and Discussion
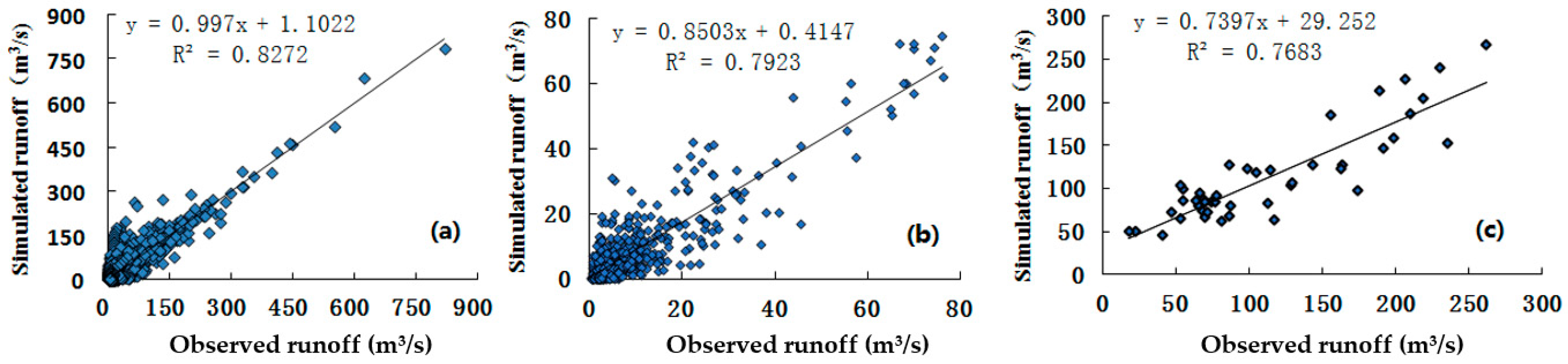
3.1. Runoff Simulation Evaluation
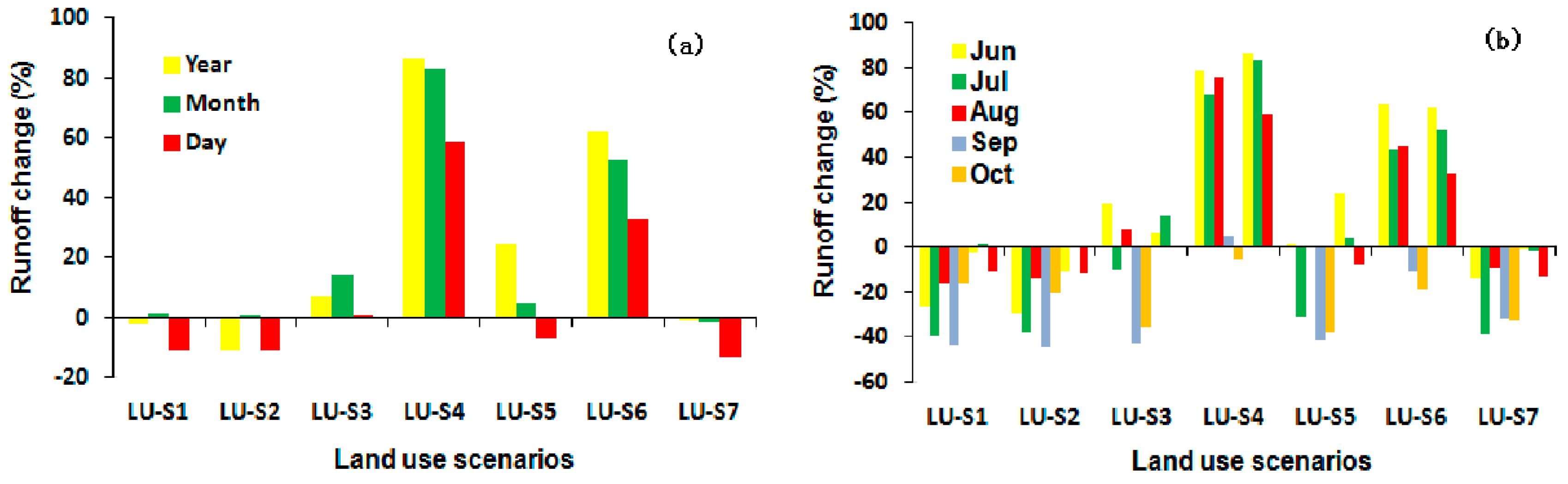
3.2. Runoff Simulation under Land Use Changes
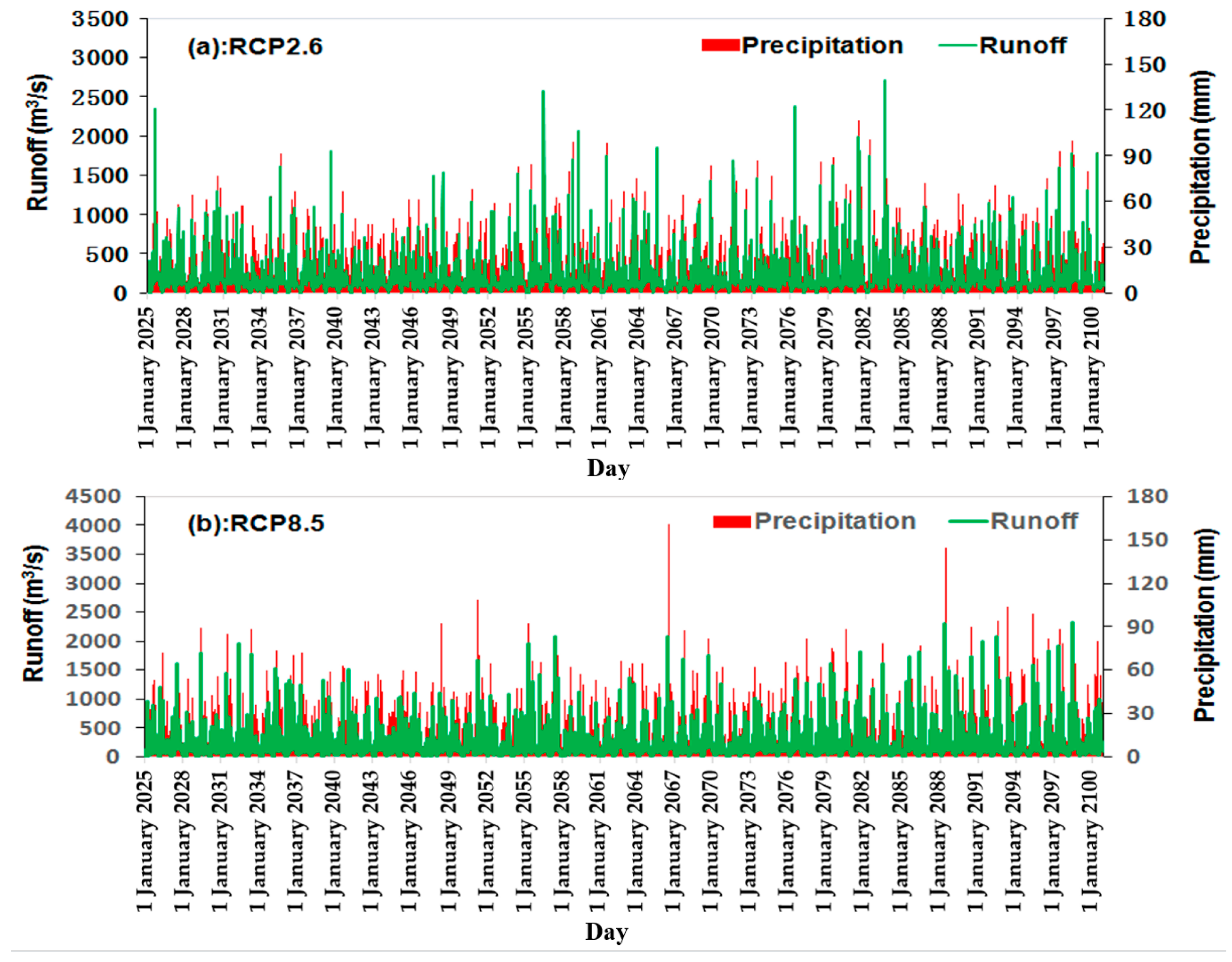
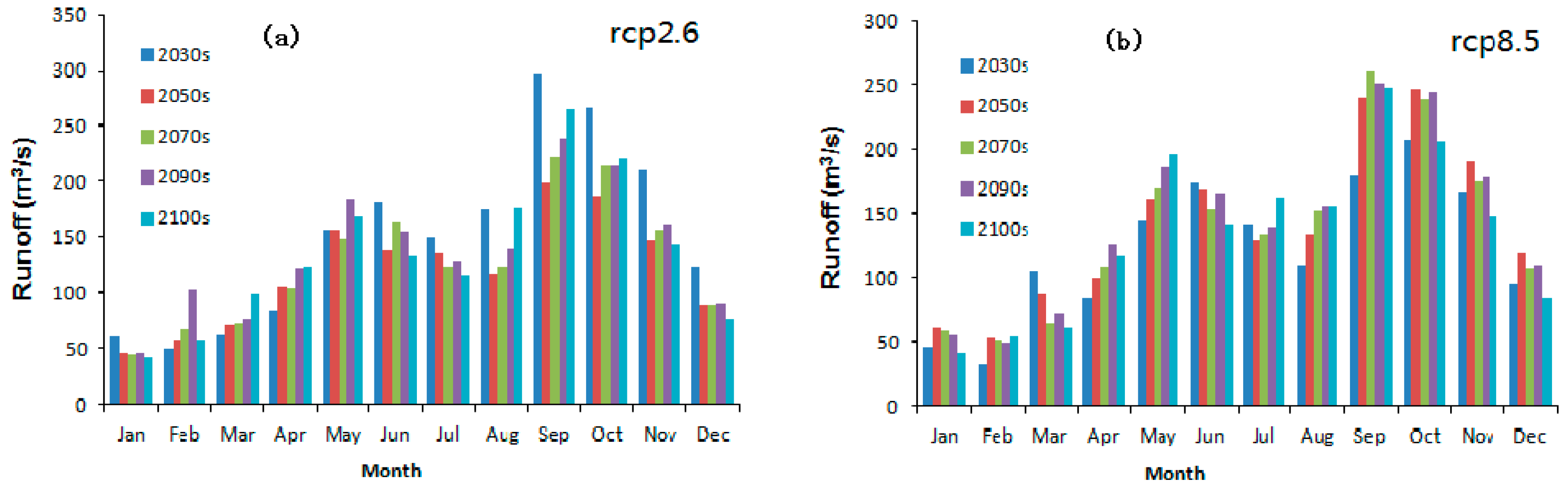
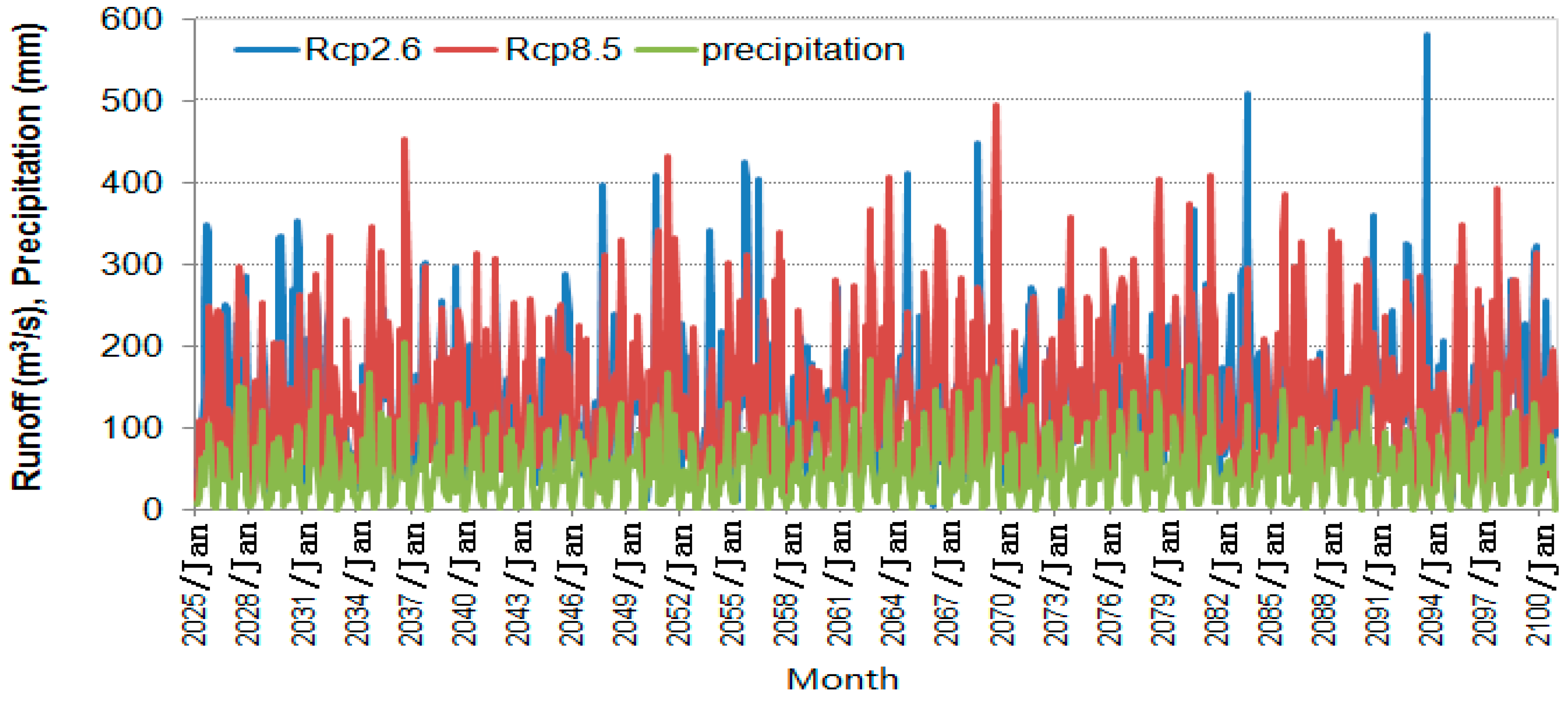
3.3. Runoff Response to Climate
3.4. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Danneberg, J. Changes in runoff time series in Thuringia, Germany–Mann-Kendalltrend test and extreme value analysis. Adv. Geosci. 2012, 31, 49–56. [Google Scholar] [CrossRef]
- Liu, Y.G.; Yu, K.K.; Zhao, Y.Q.; Bao, J.C. Impacts of Climatic Variation and Human Activity on Runoff in Western China. Sustainability 2022, 14, 942. [Google Scholar] [CrossRef]
- Liu, Y.; Wen, Y.; Zhao, Y.; Hu, H. Analysis of Drought and Flood Variations on a 200-Year Scale Based on Historical Environmental Information in Western China. Int. J. Environ. Res. Public Health 2022, 19, 2771. [Google Scholar] [CrossRef]
- Sun, T.; Yang, Y.-M.; Wang, Z.-G.; Yong, Z.-W.; Xiong, J.-N.; Ma, G.-L.; Li, J.; Liu, A. Spatiotemporal variation of ecological environment quality and extreme climate drivers on the Qinghai-Tibetan Plateau. J. Mt. Sci. 2023, 20, 2282–2297. [Google Scholar] [CrossRef]
- Cinto Mejía, E.; Wetzel, W.C. The ecological consequences of the timing of extreme climate events. J. Ecol. Evol. 2023, 13, e9661. [Google Scholar] [CrossRef]
- Liu, Y.G.; Wang, N.L.; Wang, L.G.; Zhao, Y.Q.; BoWu, X. Application of GIS in regional ecological risk assessment of water resources. Environ. Eng. Manag. J. 2013, 12, 1465–1474. [Google Scholar] [CrossRef]
- Liu, Y.G.; Zhang, J.H.; Zhao, Y.Q. The Risk Assessment of River Water Pollution Based on a Modified Non-Linear Model. Water 2018, 10, 362. [Google Scholar] [CrossRef]
- Li, Z.; Shao, Q.; Xu, Z.; Xu, C. Uncertainty issues of a conceptual water balance model for a semi-arid watershed in northwest China. Hydrol. Process. 2013, 27, 304–312. [Google Scholar] [CrossRef]
- Huang, S.; Huang, Q.; Chen, Y. Quantitative estimation on contributions of climate changes and human activities to decreasing runoff in Weihe River Basin, China. Chin. Geogr. Sci. 2015, 25, 569–581. [Google Scholar] [CrossRef]
- Zhang, P.; Liu, R.; Bao, Y.; Wang, J.; Yu, W.; Shen, Z. Uncertainty of SWAT model atdifferent DEM resolutions in a large mountainous watershed. Water Res. 2014, 53, 132–144. [Google Scholar] [CrossRef]
- Forsythe, N.; Fowler, H.; Blenkinsop, S.; Burton, A.; Kilsby, C.; Archer, D.; Harpham, C.; Hashmi, M. Application of a stochastic weather generator to assess climate change impacts in a semi-arid climate: The Upper Indus basin. J. Hydrol. 2014, 517, 1019–1034. [Google Scholar] [CrossRef]
- Hao, Z.C.; Xie, H.H.; Huang, G.R.; Qin, J.; Jie, H. Spatial Scale Analysis of the TOPMODEL Model. J. Glaciol. Geocryol. 2010, 32, 587–592. [Google Scholar]
- Xin, X.; Tian, Q.A.; Xiao, D.L. Application of a Fractional Instantaneous Unit Hydrograph in the TOPMODEL: A Case Study in Chengcun Basin, China. Appl. Sci. 2023, 13, 2245. [Google Scholar]
- Ni, A.Q.; Jun, Y.Z.; Xu, G.W.; Cui, J.; Song, Y.-X.; Sun, X.-Y. A modified TOPMODEL introducing the bedrock surface topographic index in Huangbengliu watershed, China. J. Mt. Sci. 2022, 19, 3517–3532. [Google Scholar]
- Yi, X.; Shu, S.P.; Agnès, D.; Ciais, P.; Gumbricht, T.; Jimenez, C.; Poulter, B.; Prigent, C.; Qiu, C.; Saunois, M. Author Correction: Gridded maps of wetlands dynamics over mid-low latitudes for 1980–2020 based on TOPMODEL. Sci. Data 2022, 9, 3517–3532. [Google Scholar]
- Farid, B.; Hadi, M.F.; Touraj, S.; Haghighi, A.T.; Talebi, A. Spatial–temporal analysis of landslides in complex hillslopes of catchments using Dynamic Topmodel. Acta Geophys. 2022, 70, 1417–1432. [Google Scholar]
- Kazmi, D.H.; Li, J.; Rasul, G.; Tong, J. Statistical downscaling and future scenario generation of temperatures for Pakistan region. J. Theor. Appl. Climatol. 2015, 120, 341–350. [Google Scholar] [CrossRef]
- Liu, Z.; Martina, M.L.V.; Todini, E. Flood forecasting using a fully distributed model: Application of the TOPKAPI model to the Upper Xixian Catchment. Hydrol. Earth Syst. Sci. 2005, 9, 347–364. [Google Scholar] [CrossRef]
- Deng, P.; Li, Z.J.; Liu, Z.Y. Numerical algorithm of distributed TOPKAPI model and its application. Water Sci. Eng. 2008, 1, 14–21. [Google Scholar] [CrossRef]
- Iqra, A.; Javed, I.; Li, J.S. Modeling Hydrological Response to Climate Change in a Data-Scarce Glacierized High Mountain Astore Basin Using a Fully Distributed TOPKAPI Model. Climate 2019, 7, 127. [Google Scholar]
- Ragettli, S.; Pellicciotti, F. Calibration of a physically based, spatially distributed hydrological model in a glacierized basin: On the use of knowledge from glaciometeorological processes to constrain model parameters. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Hengade, N.; Eldho, T. Assessment of LULC and climate change on the hydrology of Ashti Catchment, India using VIC model. J. Earth Syst. Sci. 2016, 125, 1623–1634. [Google Scholar] [CrossRef]
- Diwan Mohaideen, M.M.; Varija, K. Improved vegetation parameterization for hydrological model and assessment of land cover change impacts on flow regime of the Upper Bhima basin, India. J. Acta Geophys. 2018, 66, 697–715. [Google Scholar] [CrossRef]
- Hengade, N.; Eldho, T.I.; Ghosh, S. Climate change impact assessment of a river basin using CMIP5 climate models and the VIC hydrological model. J. Hydrol. Sci. J. 2018, 89, 596–614. [Google Scholar] [CrossRef]
- Lilhare, R.; Déry, S.J.; Stadnyk, T.A.; Pokorny, S.; Koenig, K.A. Warming soil temperature and increasing baseflow in response to recent and potential future climate change across northern Manitoba, Canada. Hydrol. Process. 2022, 36, e14748. [Google Scholar] [CrossRef]
- Carvalho, V.S.O.; da Cunha, Z.A.; Alvarenga, L.A.; Beskow, S.; de Mello, C.R.; Martins, M.A.; de Oliveira, C.d.M.M. Assessment of land use changes in the Verde River basin using two hydrological models. J. S. Am. Earth Sci. 2022, 118, 103954. [Google Scholar] [CrossRef]
- Zhou, Q.; Chen, L.; Singh, V.P.; Zhou, J.; Chen, X.; Xiong, L. Rainfall-runoff simulation in karst dominated areas based on a coupled conceptual hydrological model. J. Hydrol. 2019, 471, 524–533. [Google Scholar] [CrossRef]
- Hiep, N.H.; Luong, N.D.; Nga, T.T.V.; Hieu, B.T.; Ha, U.T.T.; Du Duong, B.; Long, V.D.; Hossain, F.; Lee, H. Hydrological model using ground- and satellite-based data for river flow simulation towards supporting water resource management in the Red River Basin, Vietnam. J. Environ. Manag. 2018, 80, 346–355. [Google Scholar] [CrossRef]
- Lee, H.E.; Shim, S.; Choi, Y.; Bae, Y.S. NADPH oxidase inhibitor development for diabetic nephropathy through water tank model. Kidney Res. Clin. Pract. 2022, 41, S89–S98. [Google Scholar] [CrossRef]
- Guang, S.L.; Toraharu, W.; Takeshi, S. Two-phase Flow Analysis for Small-scale Ballast Water Tank Model by Hydraulics Experiment and Simulations. IOP Conf. Ser. Earth Environ. Sci. 2022, 972, 012048. [Google Scholar]
- Shi, X.L.; Li, Y.; Yang, Z.Y. Response of runoff on land use/cover change in Nuomin river basin based on SWAT model. J. Water Resour. Water Eng. 2016, 27, 65–69. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, N.; Zhang, J.; Wang, L. Climate change and its impacts on mountain glaciers during 1960–2017 in western China. J. Arid. Land 2019, 11, 537–550. [Google Scholar] [CrossRef]
- Chen, X.L.; Huang, G.R. Runoff simulation of Feilaixia watershed of Beijiang River based on SWAT Mod. J. Water Resour. Water Eng. 2017, 28, 1–7. [Google Scholar]
- Rahman, K.; Maringant, C.; Beniston, M.; Widmer, F.; Abbaspour, K.; Lehmann, A. Streamflow Modeling in a Highly Managed Mountainous Glacier Watershed Using SWAT: The Upper Rhone River Watershed Case in Switzerland. Water Resour. Manag. 2013, 27, 323–339. [Google Scholar] [CrossRef]
- Akansha, K.; Manoj, K.J. Hydrological Simulation in a Forest Dominated Watershed in Himalayan Region Using SWAT Model. Water Resour. Manag. 2013, 27, 3005–3023. [Google Scholar]
- Anaba, L.A.; Banadda, N.; Kiggundu, N.; Wanyama, J.; Engel, B.; Moriasi, D. Application of SWAT to assess the effects of land use change in the Murchison Bay Catchment in Uganda. Comput. J. Water Energy Environ. Eng. 2017, 6, 24–40. [Google Scholar]
- Ze, P.Z.; Qing, Z.W.; Qing, Y.G.; Xiao, X.; Mi, J.; Lv, S. Research on the optimal allocation of agricultural water and soil resources in the Heihe River Basin based on SWAT and intelligent optimization. Agric. Water Manag. 2023, 279, 108177. [Google Scholar]
- Mendonça, F.S.D.; Natália, P.S.D.; Proença, R.O.D.; Di Lollo, J.A. Using the SWAT model to identify erosion prone areas and to estimate soil loss and sediment transport in Mogi Guaçu River basin in Sao Paulo State, Brazil. Catena 2023, 222, 106872. [Google Scholar]
- Verma, K.S.; Prasad, D.A.; Verma, K.M. An Assessment of Ongoing Developments in Water Resources Management Incorporating SWAT Model: Overview and Perspectives. Nat. Environ. Pollut. Technol. 2022, 21, 1963–1970. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, Y.; Zhao, Y.; Long, Y. Using SWAT Model to Assess the Impacts of Land Use and Climate Changes on Flood in the Upper Weihe River, China. Water 2022, 14, 2098. [Google Scholar] [CrossRef]
- Manoj, J. SWAT: Model use, calibration, and validation. Environ. Sci. Geosci. 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Wu, H.J.; Chen, B. Evaluating uncertainty estimates in distributed hydrological modeling for the Wenjing River watershed in China by GLUE, SUFI-2, and ParaSolmethods. Ecol. Eng. 2015, 76, 110–121. [Google Scholar] [CrossRef]
- Lu, Z.; Zou, S.; Xiao, H.; Zheng, C.; Yin, Z.; Wang, W. Comprehensive hydrologic calibration of SWAT and water balance analysis in mountainous watersheds in northwest China. J. Phys. Chem. Earth A/B/C 2015, 56, 79–82. [Google Scholar] [CrossRef]
- Yesuf, H.M.; Melesse, A.M.; Zeleke, G.; Alamirew, T. Streamflow prediction uncertainty analysis and verification of SWAT model in a tropical watershed. Environ. Earth Sci. 2016, 75, 806. [Google Scholar] [CrossRef]
- Zuo, D.P.; Xu, Z.X. Distributed hydrological simulation using SWAT and SUFI-2 in the Wei river basin. J. Beijing Norm. Univ. (Nat. Sci.) 2012, 48, 490–496. [Google Scholar]
- Guo, Y.; Amo, L.i.Z.; Boateng, M.; Deng, P.; Huang, P. Quantitative assessment of the impact of climate variability and human activities on runoff changes for the upper reaches of Weihe River Stochastic. Environ. Res. Risk Assess. 2014, 8, 333–346. [Google Scholar] [CrossRef]
- Zhang, L.; Karthikeyan, R.; Bai, Z.; Srinivasan, R. Analysis of streamflow responses to climate variability and land use change in the Loess Plateau region of China. Catena 2017, 154, 1–11. [Google Scholar] [CrossRef]








| Parameter | Definition | S | p | Order |
|---|---|---|---|---|
| BF-C | Base flow coefficient | 7.4890 | 0.0035 | 1 |
| SOL-AW | Soil available water capacity | 6.1902 | 0.0735 | 2 |
| CN2 | Runoff curve coefficient | 9.3272 | 0.0002 | 3 |
| SOL-ECC | Soil evaporation compensation coefficient | 5.1393 | 0.1377 | 4 |
| BAN-BRC | Base flow coefficient of bank regulated storage | 0.6197 | 0.5349 | 5 |
| MSF-RC | Manning slope flow coefficient | 4.3573 | 0.1952 | 6 |
| GRO-RC | Shallow groundwater runoff coefficient | 0.6973 | 0.5931 | 7 |
| SOL-AHC | Soil conductivity of saturated water | 5.7720 | 0.0739 | 8 |
| V-ECC | Vegetation evapotranspiration compensation coefficient | 2.9348 | 0.3571 | 9 |
| REVAPMN-C | Re-evaporation coefficient of shallow aquifer | 0.5438 | 0.6393 | 10 |
| SUR-RC | Surface runoff lag coefficient | 0.4981 | 0.7126 | 11 |
| SM-C | Maximum snowmelt coefficient | 0.3362 | 0.7593 | 12 |
| STMI-C | Minimum temperature for snowmelt | 0.2461 | 0.8913 | 13 |
| BOI-MEF | Biological mixing efficiency factor | 0.0737 | 0.9251 | 14 |
| T-DR | Temperature drop rate | 0.0259 | 0.9481 | 15 |
| Parameter | Ranges | Optimal Value | Sensitivity Order |
|---|---|---|---|
| BF-C | 0–1 | 0.4733 | 1 |
| SOL-AW | 0–1 | 0.6495 | 2 |
| CN2 | 20–50 | 39.3275 | 3 |
| SOL-ECC | 0–1 | 0.5543 | 4 |
| BAN-BRC | 0–1 | 0.36487 | 5 |
| MSF-RC | 0–0.5 | 0.039 | 6 |
| GRO-RC | 100–1000 | 649.402 | 7 |
| SOL-AHC | 10–500 | 41.43783 | 8 |
| V-ECC | 0–1 | 0.27392 | 9 |
| Land Use Type | Land Use Change Scenario | ||||||
|---|---|---|---|---|---|---|---|
| LU-T1 | LU-T2 | LU-T3 | LU-T4 | LU-T5 | LU-T6 | LU-T7 | |
| Cultivated land | 0 | 0 | 3086 | 0 | 0 | 0 | 1216 |
| Woodland | 1956 | 743 | 0 | 0 | 743 | 743 | 743 |
| Grassland | 1130 | 2343 | 0 | 0 | 1130 | 1130 | 1130 |
| Waters | 62 | 62 | 62 | 62 | 62 | 62 | 62 |
| Residential area | 4 | 4 | 4 | 4 | 1217 | 4 | 4 |
| Low-density residential area | 45 | 45 | 45 | 45 | 45 | 45 | 45 |
| Transport land | 17 | 17 | 17 | 17 | 17 | 1230 | 17 |
| Wasteland, bare land | 3 | 3 | 3 | 3089 | 3 | 3 | 0 |
| Temperature Change | Precipitation Change | ||||
|---|---|---|---|---|---|
| −25% | −10% | 0 | +10% | +25% | |
| −2 °C | C-S1 | C-S2 | C-S3 | C-S4 | C-S5 |
| −1 °C | C-S6 | C-S7 | C-S8 | C-S9 | C-S10 |
| 0 | C-S11 | C-S12 | C-S0 | C-S13 | C-S14 |
| +1 °C | C-S15 | C-S16 | C-S17 | C-S18 | C-S19 |
| +2 °C | C-S20 | C-S21 | C-S22 | C-S23 | C-S24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Su, Y.; Wang, L.; Zhao, Y. Simulation and Evaluation of Runoff in Tributary of Weihe River Basin in Western China. Water 2024, 16, 221. https://doi.org/10.3390/w16020221
Liu Y, Su Y, Wang L, Zhao Y. Simulation and Evaluation of Runoff in Tributary of Weihe River Basin in Western China. Water. 2024; 16(2):221. https://doi.org/10.3390/w16020221
Chicago/Turabian StyleLiu, Yinge, Yang Su, Lingang Wang, and Yaqian Zhao. 2024. "Simulation and Evaluation of Runoff in Tributary of Weihe River Basin in Western China" Water 16, no. 2: 221. https://doi.org/10.3390/w16020221






