Integrated Subsurface Hydrologic Modeling for Agricultural Management Using HYDRUS and UZF Package Coupled with MODFLOW
Abstract
1. Introduction
2. Materials and Methods
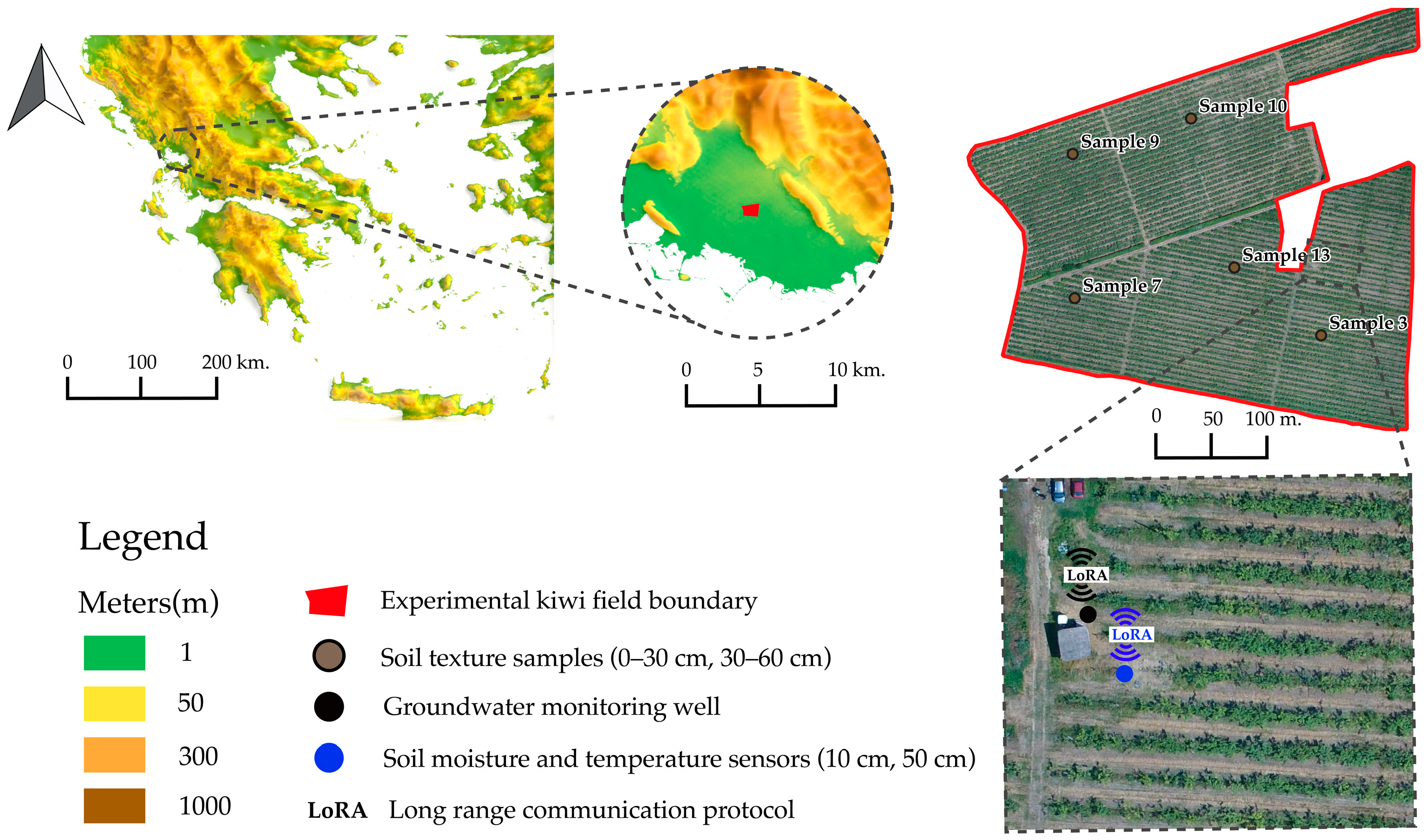
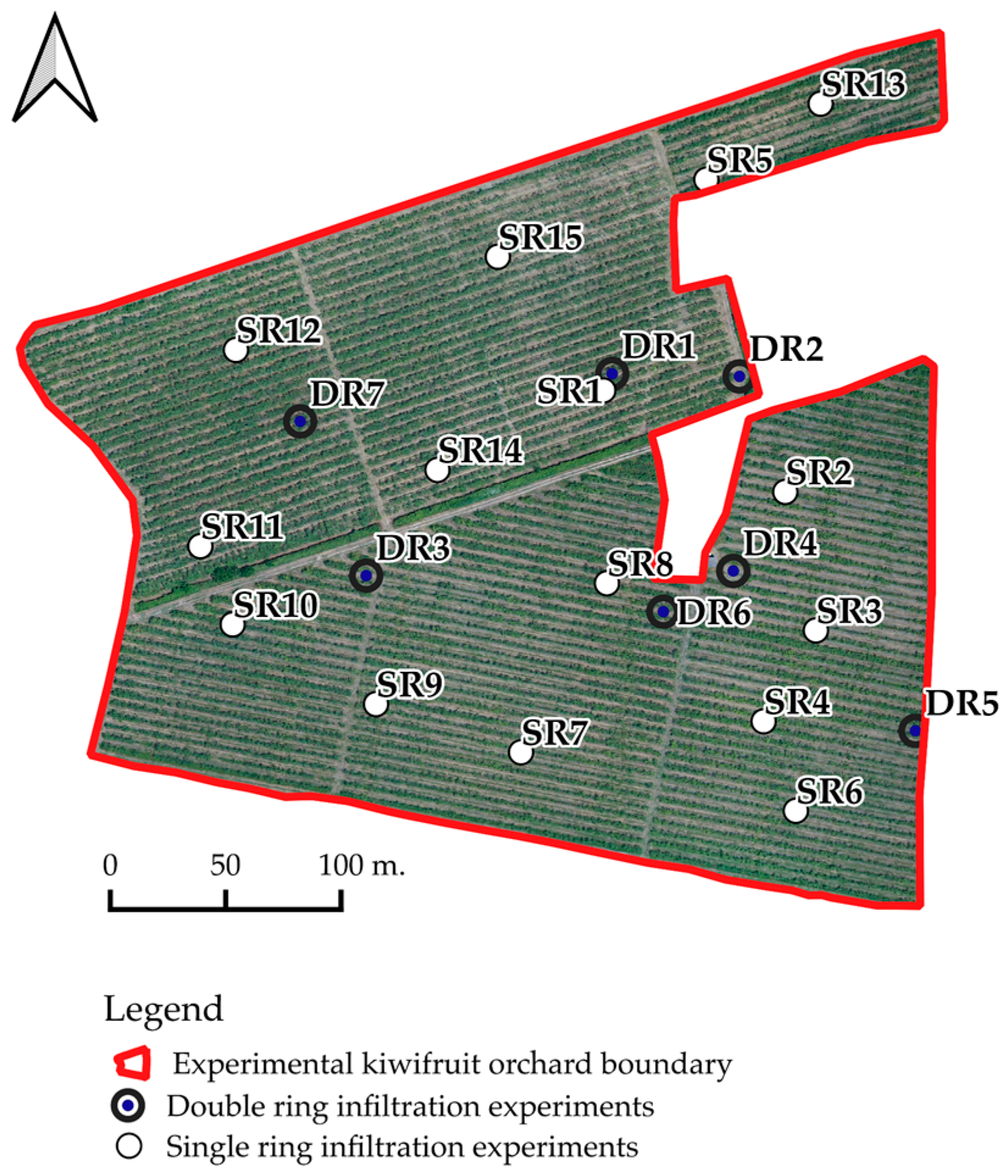
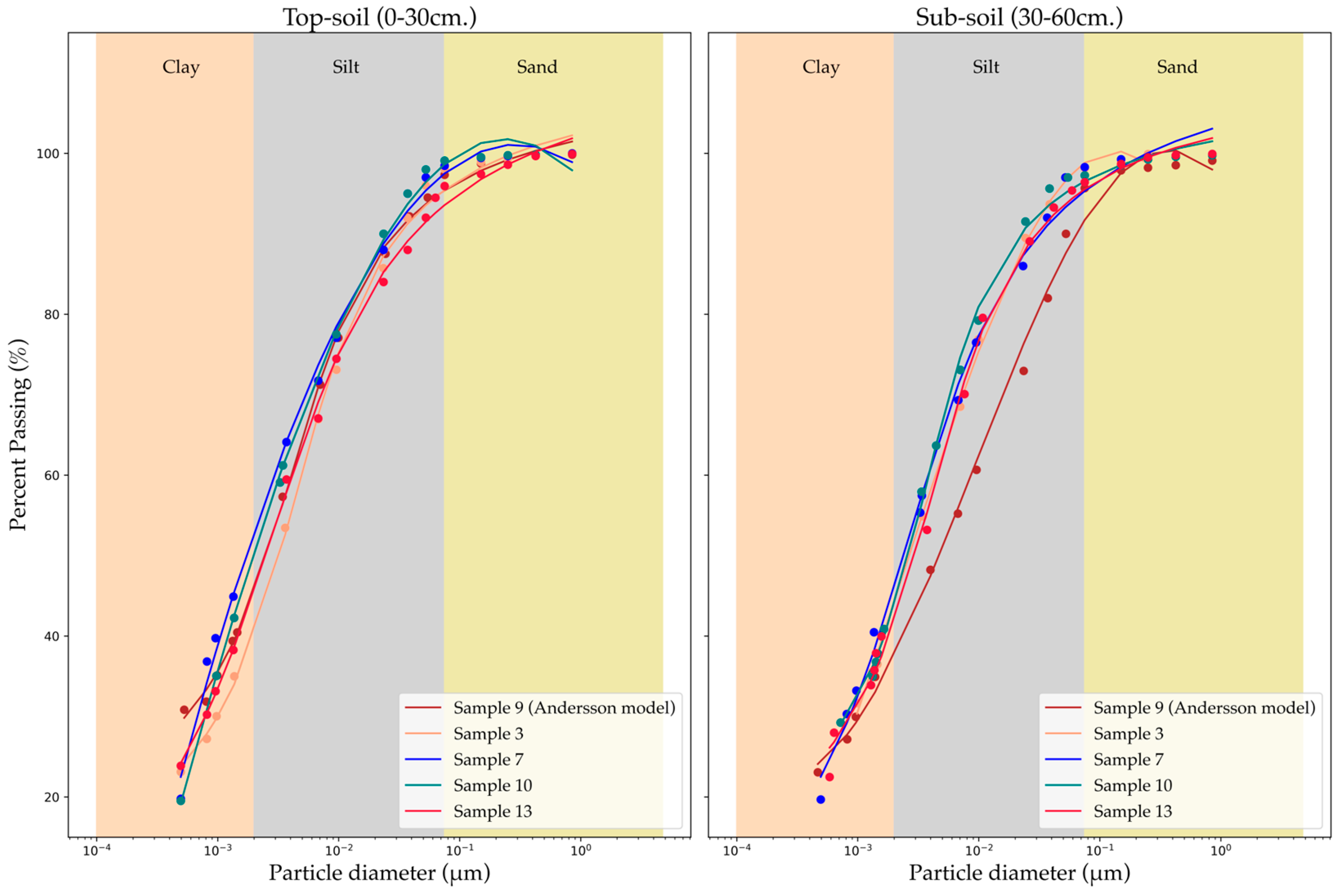
2.1. Particle Soil Distribution Analysis and Infiltration Experiments in the Field
2.2. Groundwater and Soil Moisture Monitoring in the Field
2.3. Unsaturated Zone Flow Modeling
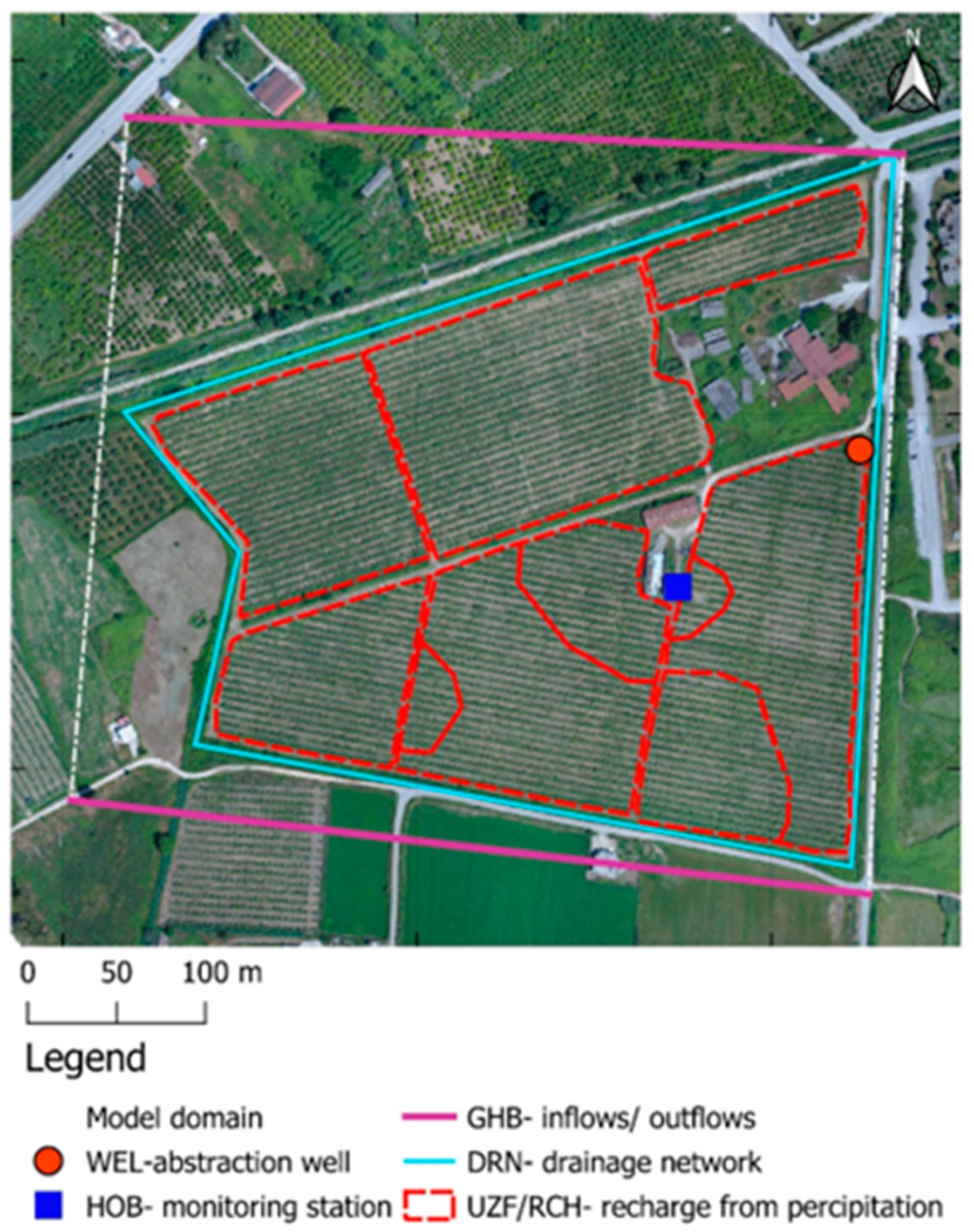
2.4. Groundwater Flow Modeling
- Newman boundary conditions.
- Abstraction well (WEL: Well package): a mean pumping rate of 520 m3/day (every three days) was selected during the irrigation period, according to the irrigation practice that is followed for the specific kiwi field.
- Percolation of precipitation (RCH: Recharge package): the specific package was utilized for groundwater recharge from precipitation and irrigation fluxes that was calculated as an output of the HYDRUS model. For the case where the Unsaturated Zone Flow (UZF) package was utilized, the RCH package remained inactive.
- Cauchy boundary conditions.
- Lateral inflows/outflows from/to the aquifer (GHB: General Head Boundary): GHB was used to interpret the inflows and outflows from and to the surrounding aquifer of the study area. GHB was placed at the northern and southern part of the study field, following the groundwater flow pattern.
- Drainage network (DRN: Drain package): the elevation of the drainage network was defined through measurements during field research.
3. Results–Discussion
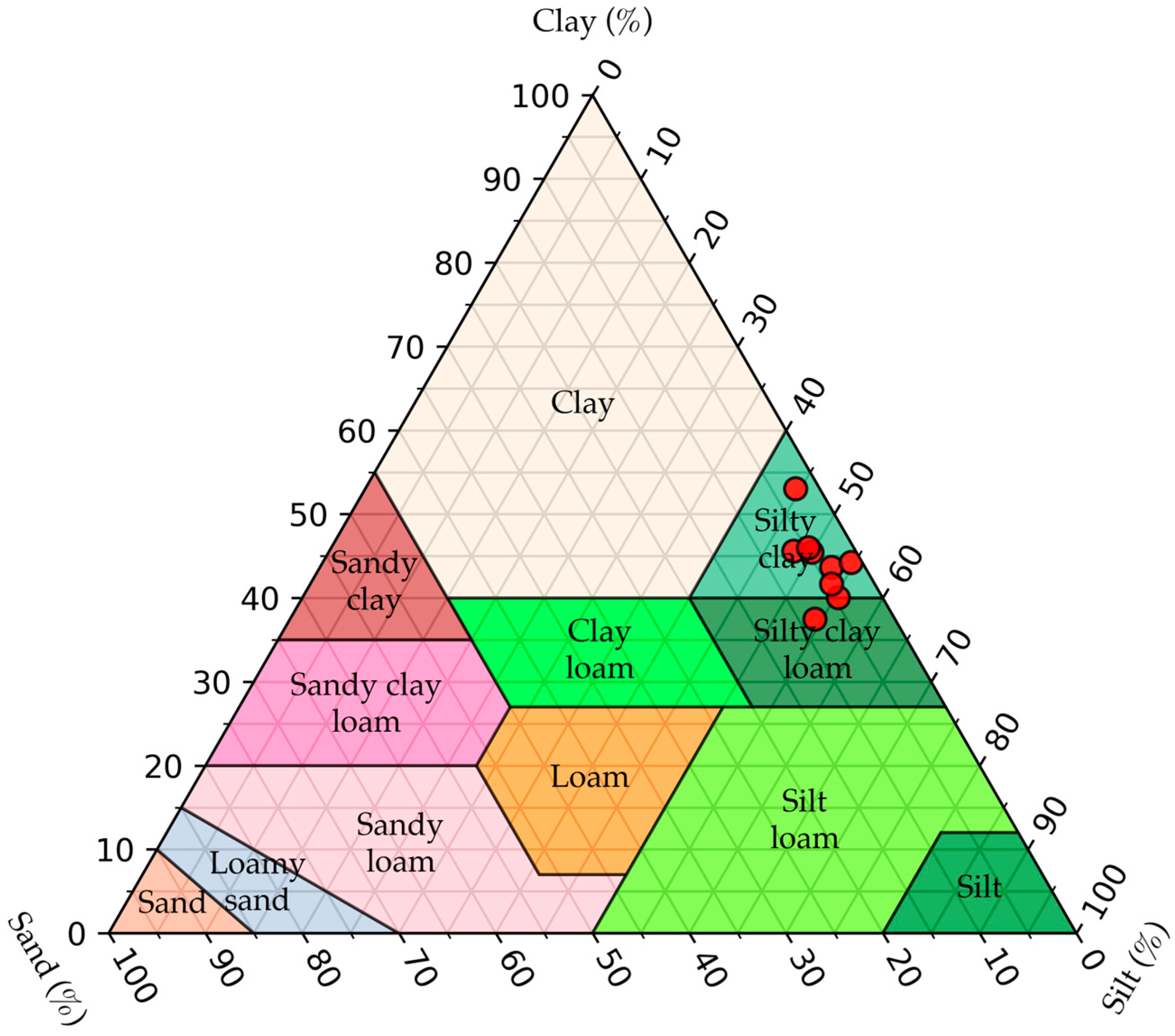
3.1. Particle Soil Distribution Analysis
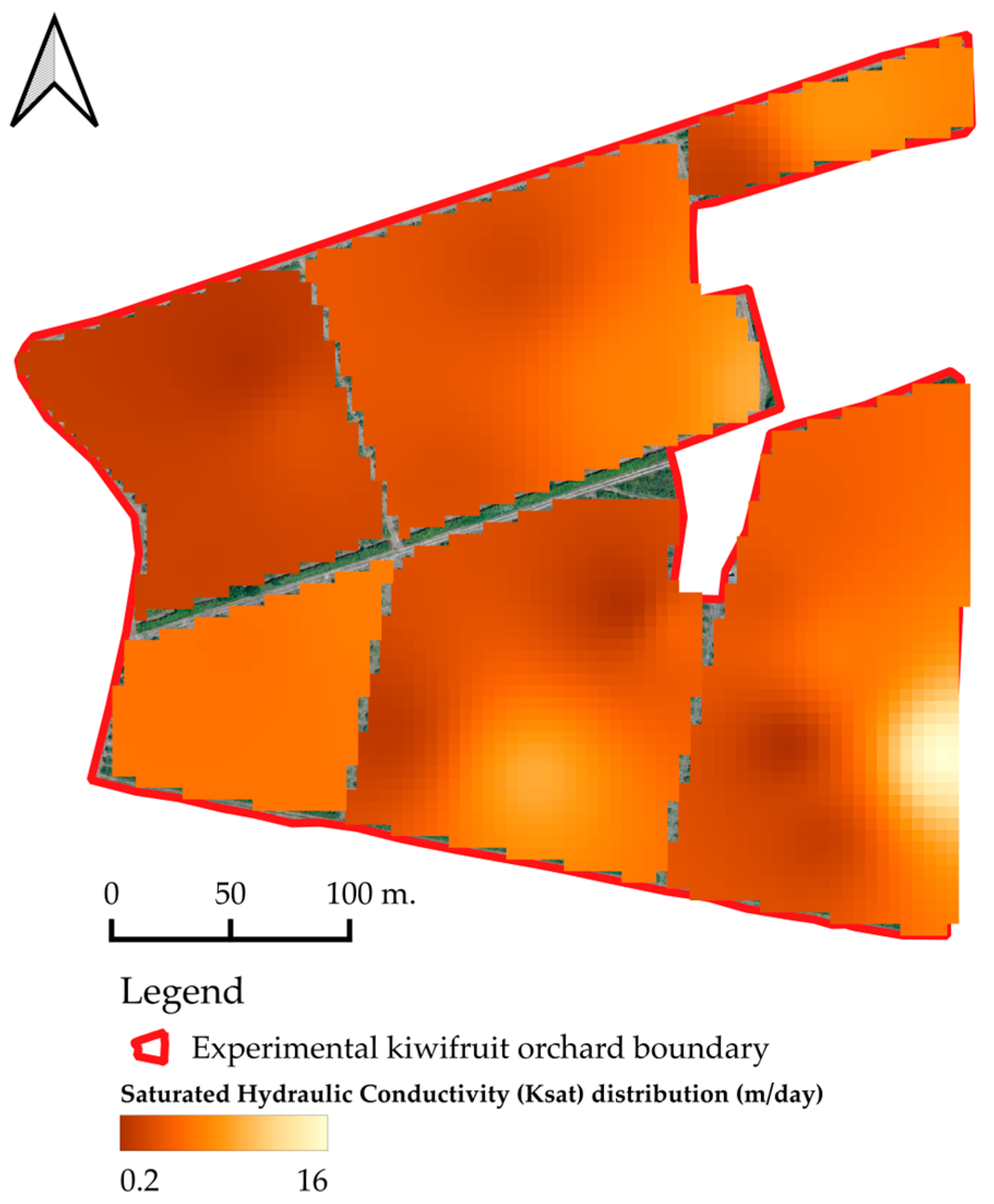
3.2. Field Infiltration Rates Modeling—Ksat Estimation
3.3. Coupled Unsaturated Zone Flow and Groundwater Flow Modeling
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wada, Y.; van Beek, L.P.H.; Bierkens, M.F.P. Nonsustainable Groundwater Sustaining Irrigation: A Global Assessment. Water Resour. Res. 2012, 48, W00L06. [Google Scholar] [CrossRef]
- Vörösmarty, C.J.; Douglas, E.M.; Green, P.A.; Revenga, C. Geospatial Indicators of Emerging Water Stress: An Application to Africa. AMBIO 2005, 34, 230–236. [Google Scholar] [CrossRef] [PubMed]
- Wang-Erlandsson, L.; Tobian, A.; van der Ent, R.J.; Fetzer, I.; te Wierik, S.; Porkka, M.; Staal, A.; Jaramillo, F.; Dahlmann, H.; Singh, C.; et al. A Planetary Boundary for Green Water. Nat. Rev. Earth Environ. 2022, 3, 380–392. [Google Scholar] [CrossRef]
- Vereecken, H.; Amelung, W.; Bauke, S.L.; Bogena, H.; Brüggemann, N.; Montzka, C.; Vanderborght, J.; Bechtold, M.; Blöschl, G.; Carminati, A.; et al. Soil Hydrology in the Earth System. Nat. Rev. Earth Environ. 2022, 3, 573–587. [Google Scholar] [CrossRef]
- Maréchal, J.C.; Dewandel, B.; Ahmed, S.; Galeazzi, L.; Zaidi, F.K. Combined Estimation of Specific Yield and Natural Recharge in a Semi-Arid Groundwater Basin with Irrigated Agriculture. J. Hydrol. 2006, 329, 281–293. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Reedy, R.C.; Stonestrom, D.A.; Prudic, D.E.; Dennehy, K.F. Impact of Land Use and Land Cover Change on Groundwater Recharge and Quality in the Southwestern US. Glob. Chang. Biol. 2005, 11, 1577–1593. [Google Scholar] [CrossRef]
- Kendy, E.; Zhang, Y.; Liu, C.; Wang, J.; Steenhuis, T. Groundwater Recharge from Irrigated Cropland in the North China Plain: Case Study of Luancheng County, Hebei Province, 1949–2000. Hydrol. Process. 2004, 18, 2289–2302. [Google Scholar] [CrossRef]
- Meredith, E.; Blais, N. Quantifying Irrigation Recharge Sources Using Groundwater Modeling. Agric. Water Manag. 2019, 214, 9–16. [Google Scholar] [CrossRef]
- Nastev, M.; Rivera, A.; Lefebvre, R.; Martel, R.; Savard, M. Numerical Simulation of Groundwater Flow in Regional Rock Aquifers, Southwestern Quebec, Canada. Hydrogeol. J. 2005, 13, 835–848. [Google Scholar] [CrossRef]
- Krogulec, E. Evaluation of Infiltration Rates within the Vistula River Valley, Central Poland. Acta Geol. Pol. 2010, 60, 617–628. [Google Scholar]
- Gumuła-Kawęcka, A.; Jaworska-Szulc, B.; Szymkiewicz, A.; Gorczewska-Langner, W.; Pruszkowska-Caceres, M.; Angulo-Jaramillo, R.; Šimůnek, J. Estimation of Groundwater Recharge in a Shallow Sandy Aquifer Using Unsaturated Zone Modeling and Water Table Fluctuation Method. J. Hydrol. 2022, 605, 127283. [Google Scholar] [CrossRef]
- Pawlowicz, M.; Balis, B.; Szymkiewicz, A.; Šimůnek, J.; Gumuła-Kawęcka, A.; Jaworska-Szulc, B. HMSE: A Tool for Coupling MODFLOW and HYDRUS-1D Computer Programs. SoftwareX 2024, 26, 101680. [Google Scholar] [CrossRef]
- Mirlas, V.; Kulagin, V.; Ismagulova, A.; Anker, Y. MODFLOW and HYDRUS Modeling of Groundwater Supply Prospect Assessment for Distant Pastures in the Aksu River Middle Reaches. Sustainability 2022, 14, 16783. [Google Scholar] [CrossRef]
- Xiao, X.; Xu, X.; Ren, D.; Huang, Q.; Huang, G. Modeling the Behavior of Shallow Groundwater System in Sustaining Arid Agroecosystems with Fragmented Land Use. Agric. Water Manag. 2021, 249, 106811. [Google Scholar] [CrossRef]
- Carranza, C.; Nolet, C.; Pezij, M.; van der Ploeg, M. Root Zone Soil Moisture Estimation with Random Forest. J. Hydrol. 2021, 593, 125840. [Google Scholar] [CrossRef]
- Feddes, R.A.; Kabat, P.; Van Bakel, P.J.T.; Bronswijk, J.J.B.; Halbertsma, J. Modelling Soil Water Dynamics in the Unsaturated Zone—State of the Art. J. Hydrol. 1988, 100, 69–111. [Google Scholar] [CrossRef]
- Schaap, M.G.; Leij, F.J.; van Genuchten, M.T. Rosetta: A Computer Program for Estimating Soil Hydraulic Parameters with Hierarchical Pedotransfer Functions. J. Hydrol. 2001, 251, 163–176. [Google Scholar] [CrossRef]
- Tóth, B.; Weynants, M.; Nemes, A.; Makó, A.; Bilas, G.; Tóth, G. New Generation of Hydraulic Pedotransfer Functions for Europe. Eur. J. Soil Sci. 2015, 66, 226–238. [Google Scholar] [CrossRef]
- Van Looy, K.; Bouma, J.; Herbst, M.; Koestel, J.; Minasny, B.; Mishra, U.; Montzka, C.; Nemes, A.; Pachepsky, Y.A.; Padarian, J.; et al. Pedotransfer Functions in Earth System Science: Challenges and Perspectives. Rev. Geophys. 2017, 55, 1199–1256. [Google Scholar] [CrossRef]
- Zhang, Y.; Schaap, M.G. Weighted Recalibration of the Rosetta Pedotransfer Model with Improved Estimates of Hydraulic Parameter Distributions and Summary Statistics (Rosetta3). J. Hydrol. 2017, 547, 39–53. [Google Scholar] [CrossRef]
- Ritter, A.; Hupet, F.; Muñoz-Carpena, R.; Lambot, S.; Vanclooster, M. Using Inverse Methods for Estimating Soil Hydraulic Properties from Field Data as an Alternative to Direct Methods. Agric. Water Manag. 2003, 59, 77–96. [Google Scholar] [CrossRef]
- Farthing, M.W.; Ogden, F.L. Numerical Solution of Richards’ Equation: A Review of Advances and Challenges. Soil Sci. Soc. Am. J. 2017, 81, 1257–1269. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary Conduction of Liquids through Porous Mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Or, D.; Lehmann, P.; Assouline, S. Natural Length Scales Define the Range of Applicability of the Richards Equation for Capillary Flows. Water Resour. Res. 2015, 51, 7130–7144. [Google Scholar] [CrossRef]
- Camporese, M.; Paniconi, C.; Putti, M.; Orlandini, S. Surface-Subsurface Flow Modeling with Path-Based Runoff Routing, Boundary Condition-Based Coupling, and Assimilation of Multisource Observation Data. Water Resour. Res. 2010, 46, W02512. [Google Scholar] [CrossRef]
- Kollet, S.J.; Maxwell, R.M. Integrated Surface–Groundwater Flow Modeling: A Free-Surface Overland Flow Boundary Condition in a Parallel Groundwater Flow Model. Adv. Water Resour. 2006, 29, 945–958. [Google Scholar] [CrossRef]
- Yeh, G.-T.; Shih, D.-S.; Cheng, J.-R.C. An Integrated Media, Integrated Processes Watershed Model. Comput. Fluids 2011, 45, 2–13. [Google Scholar] [CrossRef]
- Niswonger, R.G.; Prudic, D.E.; Regan, R.S. Documentation of the Unsaturated-Zone Flow (UZF1) Package for Modeling Unsaturated Flow Between the Land Surface and the Water Table with MODFLOW-2005; U.S. Geological Survey: Reston, VA, USA, 2006. [Google Scholar]
- Twarakavi, N.K.C.; Šimůnek, J.; Seo, S. Evaluating Interactions between Groundwater and Vadose Zone Using the HYDRUS-Based Flow Package for MODFLOW. Vadose Zone J. 2008, 7, 757–768. [Google Scholar] [CrossRef]
- Beegum, S.; Šimůnek, J.; Szymkiewicz, A.; Sudheer, K.P.; Nambi, I.M. Updating the Coupling Algorithm between HYDRUS and MODFLOW in the HYDRUS Package for MODFLOW. Vadose Zone J. 2018, 17, 180034. [Google Scholar] [CrossRef]
- Szymkiewicz, A.; Gumuła-Kawęcka, A.; Šimůnek, J.; Leterme, B.; Beegum, S.; Jaworska-Szulc, B.; Pruszkowska-Caceres, M.; Gorczewska-Langner, W.; Angulo-Jaramillo, R.; Jacques, D. Simulations of Freshwater Lens Recharge and Salt/Freshwater Interfaces Using the HYDRUS and SWI2 Packages for MODFLOW. J. Hydrol. Hydromech. 2018, 66, 246–256. [Google Scholar] [CrossRef]
- Xu, X.; Huang, G.; Zhan, H.; Qu, Z.; Huang, Q. Integration of SWAP and MODFLOW-2000 for Modeling Groundwater Dynamics in Shallow Water Table Areas. J. Hydrol. 2012, 412–413, 170–181. [Google Scholar] [CrossRef]
- Šimůnek, J.; Brunetti, G.; Jacques, D.; van Genuchten, M.T.; Šejna, M. Developments and Applications of the HYDRUS Computer Software Packages since 2016. Vadose Zone J. 2024, 23, e20310. [Google Scholar] [CrossRef]
- Celia, M.A.; Bouloutas, E.T.; Zarba, R.L. A General Mass-Conservative Numerical Solution for the Unsaturated Flow Equation. Water Resour. Res. 1990, 26, 1483–1496. [Google Scholar] [CrossRef]
- Collenteur, R.; Vremec, M.; Brunetti, G. Interfacing FORTAN Code with Python: An Example for the Hydrus-1D Model. In Proceedings of the EGU General Assembly 2020, Online, 4–8 May 2020. [Google Scholar]
- Zhang, X.; Wendroth, O.; Matocha, C.; Zhu, J.; Reyes, J. Assessing Field-Scale Variability of Soil Hydraulic Conductivity at and near Saturation. CATENA 2020, 187, 104335. [Google Scholar] [CrossRef]
- Mason, D.D.; Lutz, J.F.; Petersen, R.G. Hydraulic Conductivity as Related to Certain Soil Properties in a Number of Great Soil Groups—Sampling Errors Involved. Soil Sci. Soc. Am. J. 1957, 21, 554–560. [Google Scholar] [CrossRef]
- Öztekin, T.; Erşahin, S. Saturated Hydraulic Conductivity Variation in Cultivated and Virgin Soils. Turk. J. Agric. For. 2006, 30, 1–10. [Google Scholar]
- Nimmo, J.R.; Schmidt, K.M.; Perkins, K.S.; Stock, J.D. Rapid Measurement of Field-Saturated Hydraulic Conductivity for Areal Characterization. Vadose Zone J. 2009, 8, 142–149. [Google Scholar] [CrossRef]
- Gupta, S.; Hengl, T.; Lehmann, P.; Bonetti, S.; Or, D. SoilKsatDB: Global Database of Soil Saturated Hydraulic Conductivity Measurements for Geoscience Applications. Earth Syst. Sci. Data 2021, 13, 1593–1612. [Google Scholar] [CrossRef]
- Rice, R.; Milczarek, M.; Keller, J. A Critical Review of Single Ring Cylinder Infiltrometers with Lateral Flow Compensation. In Proceedings of the 14th Biennial Symposium on Managed Aquifer Recharge, Orange, CA, USA, 31 July–1 August 2014. [Google Scholar]
- Bouwer, H.; Back, J.T.; Oliver, J.M. Predicting Infiltration and Ground-Water Mounds for Artificial Recharge. J. Hydrol. Eng. 1999, 4, 350–357. [Google Scholar] [CrossRef]
- Su, L.; Wang, Q.; Shan, Y.; Zhou, B. Estimating Soil Saturated Hydraulic Conductivity Using the Kostiakov and Philip Infiltration Equations. Soil Sci. Soc. Am. J. 2016, 80, 1463–1475. [Google Scholar] [CrossRef]
- Bilas, G.; Dionysiou, N.; Karapetsas, N.; Silleos, N.; Kosmas, K.; Misopollinos, N. Development of a National Geodatabase (Greece) for Soil Surveys and Land Evaluation Using Space Technology and GIS. In Proceedings of the EGU General Assembly 2016, Vienna Austria, 17–22 April 2016; p. EPSC2016-12889. [Google Scholar]
- European Soil Data Centre (ESDAC) Soil Map of Greece—ESDAC—European Commission. Available online: https://esdac.jrc.ec.europa.eu/content/soil-map-greece-0 (accessed on 6 September 2024).
- Misopolinos, N.; Syllaios, N.; Zalidis, G.; Matsi, T.; Bilas, G.; Karapetsas, N.; Giannousios, A.; Tavakoglou, V.; Stratakis, G.; Dionusiou, O.; et al. Collection and Registration of Added Value Information; Final Report; Epirus region, Technological Institute 630 of Arta, Faculty of Agriculture, Forestry and Natural Environment Aristotele University of Thessaloniki: Thessaloniki, Greece, 2008. [Google Scholar]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World Map of the Köppen-Geiger Climate Classification Updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef] [PubMed]
- Mamassis, N.; Mazi, K.; Dimitriou, E.; Kalogeras, D.; Malamos, N.; Lykoudis, S.; Koukouvinos, A.; Tsirogiannis, I.; Papageorgaki, I.; Papadopoulos, A.; et al. OpenHi.Net: A Synergistically Built, National-Scale Infrastructure for Monitoring the Surface Waters of Greece. Water 2021, 13, 2779. [Google Scholar] [CrossRef]
- Cipriani, G.; Messina, R.; Vizzotto, G.; Testolin, R. Harvest Time and Storage of ‘Soreli’ Kiwifruit (Actinidia chinensis Planch.). Acta Hortic. 2018, 1218, 459–464. [Google Scholar] [CrossRef]
- Dichio, B.; Tuzio, A.C.; Xiloyannis, C.; Rigo, G.; Lovato, R.; Comuzzo, G.; Frezza, R.; Macor, D.; Cipriani, G.; Testolin, R.; et al. The New Yellow-Fleshed Kiwifruit (Actinidia chinensis pl.) “Soreli”: Conclusions from Six Years of Cultivation in Different Climatic Areas. Acta Hortic. 2015, 1096, 149–154. [Google Scholar] [CrossRef]
- McAneney, K.J.; Judd, M.J. Observations on Kiwifruit (Actinidia chinensis Planch.) Root Exploration, Root Pressure, Hydraulic Conductivity, and Water Uptake. N. Z. J. Agric. Res. 1983, 26, 507–510. [Google Scholar] [CrossRef]
- Gandar, P.W.; Hughes, K.A. Kiwifruit Root Systems 1. Root-Length Densities. N. Z. J. Exp. Agric. 1988, 16, 35–46. [Google Scholar] [CrossRef]
- Hughes, K.A.; Wilde, R.H. The Effect of Poor Drainage on the Root Distribution of Kiwifruit Vines. N. Z. J. Crop Hortic. Sci. 1989, 17, 239–244. [Google Scholar] [CrossRef]
- Hughes, K.A.; De Willigen, P.; Gandar, P.W.; Clothier, B.E. Kiwifruit Root Systems: Structure & Function. Acta Hortic. 1992, 297, 383–390. [Google Scholar] [CrossRef]
- Bardet, J.-P. Experimental Soil Mechanics; Prentice Hall: Upper Saddle River, NJ, USA, 1997; ISBN 978-0-13-374935-9. [Google Scholar]
- Cisty, M.; Celar, L.; Minaric, P. Conversion Between Soil Texture Classification Systems Using the Random Forest Algorithm. Air Soil Water Res. 2020, 8, 67–75. [Google Scholar] [CrossRef]
- Shangguan, W.; Dai, Y.; García-Gutiérrez, C.; Yuan, H. Particle-Size Distribution Models for the Conversion of Chinese Data to FAO/USDA System. Sci. World J. 2014, 2014, 109310. [Google Scholar] [CrossRef]
- Esmaeelnejad, L.; Siavashi, F.; Seyedmohammadi, J.; Shabanpour, M. The Best Mathematical Models Describing Particle Size Distribution of Soils. Model. Earth Syst. Environ. 2016, 2, 1–11. [Google Scholar] [CrossRef]
- Burt, R.; Soil Survey Staff. Soil Survey Field and Laboratory Methods Manual; Soil Survey Investigations; U.S. Department of Agriculture, Natural Resources Conservation Service: Washington, DC, USA, 2014. [Google Scholar]
- Kostiakov, A.Ν. The Dynamics of the Coefficient of Water Percolation in Soils and the Necessity for Studying It from a Dynamic Point of View for Purpose of Amelioration. Soc. Soil Sci. 1932, 14, 17–21. [Google Scholar]
- Philip, J.R. The Theory of Infiltration: 1. The Infiltration Equation and Its Solution. Soil Sci. 1957, 83, 345. [Google Scholar] [CrossRef]
- Kahlon, M.S.; Lal, R.; Ann-Varughese, M. Twenty Two Years of Tillage and Mulching Impacts on Soil Physical Characteristics and Carbon Sequestration in Central Ohio. Soil Tillage Res. 2013, 126, 151–158. [Google Scholar] [CrossRef]
- Ma, D.; Wang, Q.; Shao, M. Analytical Method for Estimating Soil Hydraulic Parameters from Horizontal Absorption. Soil Sci. Soc. Am. J. 2009, 73, 727–736. [Google Scholar] [CrossRef]
- Ghosh, R.K. A Note on Lewis-Kostiakov’s Infiltration Equation. Soil Sci. 1985, 139, 193. [Google Scholar] [CrossRef]
- WIKA. Submersible Pressure Sensor High-Performance Model LH-20; WIKA: București, Romania, 2024. [Google Scholar]
- Pagano, A.; Croce, D.; Tinnirello, I.; Vitale, G. A Survey on LoRa for Smart Agriculture: Current Trends and Future Perspectives. IEEE Internet Things J. 2023, 10, 3664–3679. [Google Scholar] [CrossRef]
- Brooks, R.H.; Corey, A.T. Hydraulic Properties of Porous Media; Colorado State University: Fort Collins, CO, USA, 1964; Volume 3. [Google Scholar]
- Pan, T.; Hou, S.; Liu, Y.; Tan, Q. Comparison of Three Models Fitting the Soil Water Retention Curves in a Degraded Alpine Meadow Region. Sci. Rep. 2019, 9, 18407. [Google Scholar] [CrossRef]
- Memari, S.S.; Clement, T.P. PySWR—A Python Code for Fitting Soil Water Retention Functions. Comput. Geosci. 2021, 156, 104897. [Google Scholar] [CrossRef]
- Durner, W.; Priesack, E.; Vogel, H.-J.; Zurmühl, T. Determination of Parameters for Flexible Hydraulic Functions by Inverse Modeling. In Proceedings of the International Workshop on Characterization and Measurement of the Hydraulic Properties of Unsaturated Porous Media; University of California: Berkeley, CA, USA, 1999. [Google Scholar]
- Stankovich, J.M.; Lockington, D.A. Brooks-Corey and van Genuchten Soil-Water-Retention Models. J. Irrig. Drain. Eng. 1995, 121, 1–7. [Google Scholar] [CrossRef]
- Lenhard, R.J.; Parker, J.C.; Mishra, S. On the Correspondence between Brooks-Corey and van Genuchten Models. J. Irrig. Drain. Eng. 1989, 115, 744–751. [Google Scholar] [CrossRef]
- Fuentes, C.; Haverkamp, R.; Parlange, J.-Y. Parameter Constraints on Closed-Form Soilwater Relationships. J. Hydrol. 1992, 134, 117–142. [Google Scholar] [CrossRef]
- Rawls, W.J.; Brakensiek, D.L.; Saxtonn, K.E. Estimation of Soil Water Properties. Trans.-Am. Soc. Agric. Eng. 1982, 25, 1316–1320. [Google Scholar] [CrossRef]
- Vereecken, H.; Kamai, T.; Harter, T.; Kasteel, R.; Hopmans, J.; Vanderborght, J. Explaining Soil Moisture Variability as a Function of Mean Soil Moisture: A Stochastic Unsaturated Flow Perspective. Geophys. Res. Lett. 2007, 34, L22402. [Google Scholar] [CrossRef]
- Harbaugh, A.W. MODFLOW-2005: The U.S. Geological Survey Modular Ground-Water Model—The Ground-Water Flow Process. In Techniques and Methods; US Geological Survey: Reston, VI, USA, 2005. [Google Scholar] [CrossRef]
- Winston, R.B. ModelMuse Version 4: A Graphical User Interface for MODFLOW 6; U.S. Geological Survey: Reston, VI, USA, 2019. [Google Scholar]
- Pouliaris, C.; Kofakis, P.; Chrysanthopoulos, E.; Myriounis, C.; Markantonis, K.; Koltsida, E.; Pappa, D.; Kaliampakos, D.; Perdikaki, M.; Kallioras, A. Conflicting Ecosystem Services within Coastal Na.tural Hydrosystems. The Case of Louros-Arachthos-Amvrakikos, W. Greece. In Proceedings of the EGU22, the 24th EGU General Assembly, Vienna, Austria, 23–27 May 2022; p. EGU22-12011. [Google Scholar]
- Chrysanthopoulos, E.; Pouliaris, C.; Tsirogiannis, I.; Kofakis, P.; Kallioras, A. Development of Soil Moisture Model Based on Deep Learning. In Proceedings of the Recent Advances in Environmental Science from the Euro-Mediterranean and Surrounding Regions, 4th ed.; Ksibi, M., Sousa, A., Hentati, O., Chenchouni, H., Lopes Velho, J., Negm, A., Rodrigo-Comino, J., Hadji, R., Chakraborty, S., Ghorbal, A., Eds.; Springer Nature Switzerland: Cham, Switzerland, 2024; pp. 477–479. [Google Scholar]
- Koltsida, E.; Panagiotaropoulos, K.; Perdikaki, M.; Pouliaris, C.; Kallioras, A. Development of an Integrated Simulation Platform of the Agricultural Ecosystems and Hydrological Processes; Final Report. “e-Pyrros: Development of an Integrated Monitoring Network for Hydro-Environmental Parameters within the Hydro-Systems of Louros-Arachthos-Amvrakikos for the Optimal Management and Improvement of Agricultural Production.”; N.T.U.A. Research Committee: Athens, Greece, 2022. [Google Scholar]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Lehmann, P.; Leshchinsky, B.; Gupta, S.; Mirus, B.B.; Bickel, S.; Lu, N.; Or, D. Clays Are Not Created Equal: How Clay Mineral Type Affects Soil Parameterization. Geophys. Res. Lett. 2021, 48, e2021GL095311. [Google Scholar] [CrossRef]
- Gerke, H.H.; van Genuchten, M.T. A Dual-Porosity Model for Simulating the Preferential Movement of Water and Solutes in Structured Porous Media. Water Resour. Res. 1993, 29, 305–319. [Google Scholar] [CrossRef]
- Van Liew, M.W.; Arnold, J.G.; Garbrecht, J.D. Hydrologic Simulation on Agricultural Watersheds: Choosing Between Two Models. Trans. ASABE 2003, 46, 1539–1551. [Google Scholar] [CrossRef]
- Leterme, B.; Gedeon, M.; Laloy, E.; Rogiers, B. Unsaturated Flow Modeling with HYDRUS and UZF: Calibration and Intercomparison. In Proceedings of the MODFLOW and More 2015: Modeling a Complex World, Golden, CO, USA, 31 May–3 June 2015. [Google Scholar]





| Parameter | Parameter Name | Parameter Value |
|---|---|---|
| Horizontal Hydraulic Conductivity (Top Layer) | HK_Lay1 | 5.2 m/day |
| Horizontal Hydraulic Conductivity (Bottom Layer) | HK_Lay2 | 10.43 m/day |
| Specific Storage (Top Layer) | SS_Lay1 | 0.00023 m−1 |
| Specific Storage (Bottom Layer) | SS_Lay2 | 2.1 × 10−5 m−1 |
| Specific Yield (Top Layer) | SY_Lay1 | 0.3 |
| Specific Yield (Bottom Layer) | SY_Lay2 | 0.2 |
| Hydraulic Conductance (General Head Boundary) | GHB_cond | 8.64 m/day |
| Infiltration Points | m (Kostiakov) | n (Kostiakov) | m * | n * | Ksat * (m/day) | Ksat * (Kostiakov Parameters) (m/day) |
|---|---|---|---|---|---|---|
| DR1 | 14.040 | 0.728 | 14.004 | 0.576 | 6.374 | 21.035 |
| DR2 | 12.415 | 0.827 | 12.205 | 0.625 | 9.417 | 17.489 |
| DR3 | 14.284 | 0.573 | 17.087 | 0.495 | 6.236 | 15.632 |
| DR4 | 28.032 | 0.585 | 29.470 | 0.517 | 3.021 | 14.437 |
| DR5 | 26.960 | 0.752 | 24.224 | 0.610 | 16.237 | 44.61 |
| DR6 | 34.861 | 0.599 | 37.235 | 0.520 | 4.369 | 21.064 |
| DR7 | 1.784 | 0.980 | 1.01 | 0.906 | 2.937 | 6.4156 |
| Infiltration Points | m (Kostiakov) | n (Kostiakov) | m * | n * | Ksat * (m/day) | Ksat (Kostiakov) (m/day) |
|---|---|---|---|---|---|---|
| SR1 | 11.163 | 0.699 | 10.198 | 0.584 | 5.144 | 14.180 |
| SR2 | 16.295 | 0.630 | 16.107 | 0.541 | 3.896 | 13.025 |
| SR3 | 10.264 | 0.739 | 9.256 | 0.604 | 5.854 | 16.003 |
| SR4 | 4.177 | 0.753 | 4.214 | 0.584 | 2.146 | 6.940 |
| SR5 | 11.160 | 0.580 | 11.454 | 0.518 | 1.255 | 5.388 |
| SR6 | 2.153 | 0.791 | 2.138 | 0.605 | 1.374 | 4.2065 |
| SR7 | 15.013 | 0.728 | 12.615 | 0.620 | 9.295 | 22.201 |
| SR8 | 17.291 | 0.510 | 18.225 | 0.497 | 0.258 | 1.001 |
| SR9 | 0.585 | 0.972 | 0.305 | 0.929 | 0.951 | 2.056 |
| SR10 | 5.297 | 0.858 | 4.105 | 0.705 | 5.394 | 13.205 |
| SR11 | 2.027 | 0.828 | 1.803 | 0.648 | 1.661 | 4.553 |
| SR12 | 0.377 | 0.819 | 0.316 | 0.659 | 0.314 | 8.189 |
| SR13 | 17.795 | 0.689 | 16.307 | 0.580 | 7.897 | 21.415 |
| SR14 | 2.086 | 0.912 | 1.398 | 0.786 | 2.67 | 6.171 |
| SR15 | 4.17 | 0.753 | 4.21 | 0.584 | 2.146 | 6.94 |
| HYDRUS | UZF [18] | UZF [74] | |
|---|---|---|---|
| r | 0.8 | 0.803 | 0.803 |
| R2 | 0.64 | 0.644 | 0.645 |
| RMSE (m) | 0.186 | 0.187 | 0.187 |
| MODFLOW-HYDRUS | MODFLOW-UZF [74] | MODFLOW-Toth [18] | |
|---|---|---|---|
| Storage | 52,347.12 | 59,834.629 | 59,806.2 |
| Head-Dependent Boundaries | 187,056.5 | 242,706.64 | 243,091 |
| Recharge | 93,745.68 | 55,290.02 | 55,653.539 |
| Storage | −70,883.4 | −81,906.875 | −82,208.6 |
| Pumping wells | −98,831.2 | −98,831.156 | −98,831.156 |
| Drains | −8793.86 | −6427.26 | −6442.2241 |
| Head-Dependent Boundaries | −154,587 | −123,056.6 | −122,715 |
| Evapotranspiration | - | −48,068.3 | −48,020.484 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chrysanthopoulos, E.; Perdikaki, M.; Markantonis, K.; Kallioras, A. Integrated Subsurface Hydrologic Modeling for Agricultural Management Using HYDRUS and UZF Package Coupled with MODFLOW. Water 2024, 16, 3297. https://doi.org/10.3390/w16223297
Chrysanthopoulos E, Perdikaki M, Markantonis K, Kallioras A. Integrated Subsurface Hydrologic Modeling for Agricultural Management Using HYDRUS and UZF Package Coupled with MODFLOW. Water. 2024; 16(22):3297. https://doi.org/10.3390/w16223297
Chicago/Turabian StyleChrysanthopoulos, Efthymios, Martha Perdikaki, Konstantinos Markantonis, and Andreas Kallioras. 2024. "Integrated Subsurface Hydrologic Modeling for Agricultural Management Using HYDRUS and UZF Package Coupled with MODFLOW" Water 16, no. 22: 3297. https://doi.org/10.3390/w16223297
APA StyleChrysanthopoulos, E., Perdikaki, M., Markantonis, K., & Kallioras, A. (2024). Integrated Subsurface Hydrologic Modeling for Agricultural Management Using HYDRUS and UZF Package Coupled with MODFLOW. Water, 16(22), 3297. https://doi.org/10.3390/w16223297






